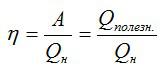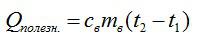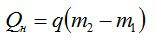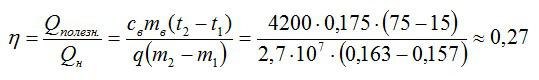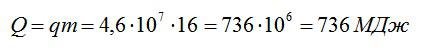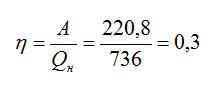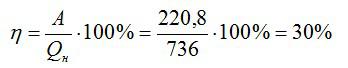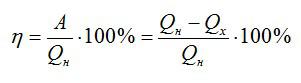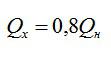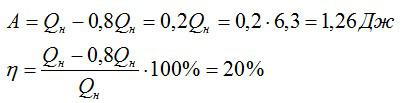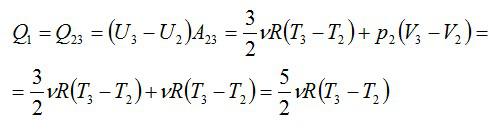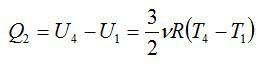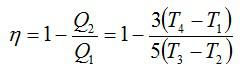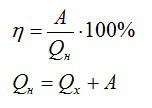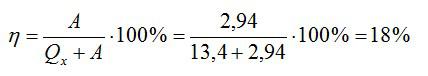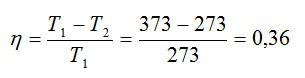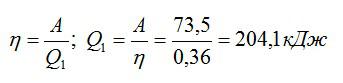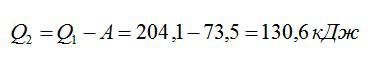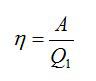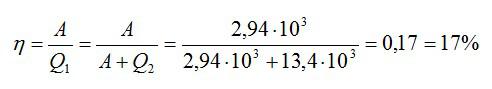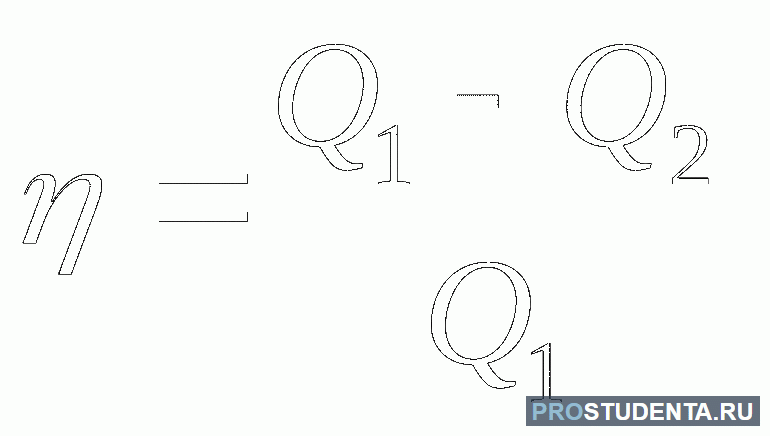Как найти время по формуле кпд

У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.

Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.

Задачи по физике на КПД теплового двигателя

Задача на вычисление КПД теплового двигателя №1

Условие 

Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.

Решение

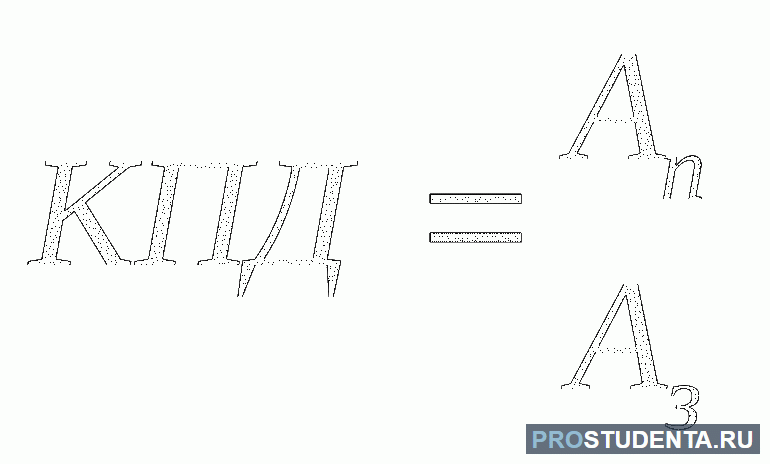
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:

Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:

Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.

Подставляем значения и вычисляем:

Ответ: 27%

Задача на вычисление КПД теплового двигателя №2

Условие

Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.

Решение

Найдем общее количество теплоты, которое произвел двигатель:

Теперь можно рассчитать КПД:

Или, умножая на 100, получаем значение КПД в процентах:

Ответ: 30%.

Задача на вычисление КПД теплового двигателя №3

Условие

Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.

Решение

КПД идеальной тепловой машины:

По условию:

Вычислим сначала работу, а затем КПД:

Ответ: 20%; 1,26 Дж.

Задача на вычисление КПД теплового двигателя №4

Условие

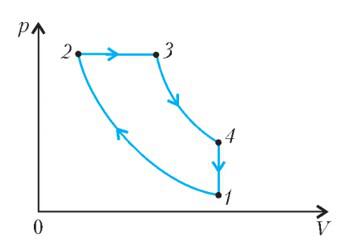
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.

Решение

Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.

Аналогично:

Получим результат:

Ответ: См. выше.

Задача на вычисление КПД теплового двигателя №5

Условие

Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.

Решение

Запишем формулу для КПД:

Отсюда:

Ответ: 18%

Вопросы на тему тепловые двигатели

Вопрос 1. Что такое тепловой двигатель?

Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.

Вопрос 2. Приведите примеры тепловых двигателей.

Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:

• ракетный двигатель;
• авиационный двигатель;
• газовая турбина.

Вопрос 3. Может ли КПД двигателя быть равен единице?

Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.

КПД реальных двигателей редко превышает 30%.

Вопрос 4. Что такое КПД?

Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.

Вопрос 5. Что такое удельная теплота сгорания топлива?

Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.

Задачи и вопросы на цикл Карно

Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.

Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).

Задача на цикл Карно №1

Условие

Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.

Решение

Рассчитаем КПД цикла: 

С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:

Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:

Ответ: 0,36; 204,1 кДж; 130,6 кДж.

Задача на цикл Карно №2

Условие

Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.

Решение

Формула для КПД цикла Карно:

Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:

Ответ: 17%.

Задача на цикл Карно №3

Условие

Изобразите цикл Карно на диаграмме и опишите его

Решение

Цикл Карно на диаграмме PV выглядит следующим образом:

• 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
• 2-3. Адиабатическое расширение, тепло не подводится;
• 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
• 4-1. Адиабатическое сжатие.

Ответ: см. выше.

Вопрос на цикл Карно №1

Сформулируйте первую теорему Карно

Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.

Вопрос на цикл Карно №2

Может ли коэффициент полезного действия в цикле Карно быть равным 100%?

Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.

Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.

Каждый механизм, совершающий работу, затрачивает на её выполнение определённую энергию. Её разница с потребляемой для этого мощностью называется коэффициентом полезного действия. Для физики формула, определяющая это значение, является фундаментальной. С её помощью рассчитывают эффективность энергетических процессов. Можно утверждать, что этот параметр занимает важное место в характеристиках любого технического устройства.

Оглавление:

• Общие сведения и определения
• Нахождение полезного действия
• Тепловые и электродвигатели
• Решение задач

Общие сведения и определения

Энергия — это характеристика, являющаяся скалярной величиной и служащая мерой различного перемещения и взаимодействия материи при переходе в ту или иную форму. С фундаментальной точки зрения, она состоит из импульса и его момента, связанных с неоднородностью времени. В физике понятие «энергия» применяется для замкнутых систем.

Как было установлено опытным путём из-за независимости физических законов от момента времени, энергия не исчезает и не появляется из ничего, она просто есть и переходит из одного состояния в другое. Это утверждение называется Законом сохранения. В математике это правило эквивалентно системе дифференциальных уравнений, описывающих их динамику и обладающих первым интегралом движения, симметричного относительно сдвига во времени.

Чтобы система совершила работу, она должна получить энергию снаружи. То есть на неё должен воздействовать импульс. Но не вся получаемая энергия идёт на достижение нужной цели. По факту она разделяется на два вида:

• затрачиваемая — полная величина, которая была взята извне;
• полезная — та, что не затрачивается на преодоление различных сил.

Например, пусть необходимо поднять груз. Другими словами, совершить работу. Для того чтобы достичь заданной цели, нужно преодолеть ряд сил: тяжести, трения. Эти затраты и считаются неполезными. Так, для механических устройств энергия затрачивается на преодоление сил, возникающих при контакте поверхностей, в электричестве — на сопротивление проводников. Вот такого типа потери и называют затратными.

В соответствии с Законом сохранения, взятая системой энергия не может просто исчезнуть. Поэтому и рассчитывают, какое количество её было трансформировано в другую «побочную» форму. Если общую работу обозначить за A, то можно записать равенство: A = Aп + Aз, где Aз — работа затраченная, а Aп — полезная. Так как идеальных систем не существует, то всегда Aз > Aп.

Научное общество с давних времён занимается проблемой уравнивания этих величин. Периодически появляются сведения об изобретении «вечного двигателя». Это устройство, у которого вся потребляемая энергия идёт на выполнение полезного действия. К сожалению, сегодняшние возможности и знания не позволяют полностью исключить затраты. Поэтому все такие изобретения являются ложными, а перед учёными стоит задача свести потери к минимуму.

Нахождение полезного действия

Если затраченную работу увеличить в несколько раз, то на это же число возрастёт и взятая полезная энергия. Если бы механизм был идеальный, то их отношение равнялось единице. Но так как в реальности оно всегда меньше, то соотношение Ап к Аз используется для описания качества. Этому параметру и присвоили название КПД. Расшифровка этой аббревиатуры звучит как «коэффициент полезного действия».

Другими словами, если нужно найти КПД по формуле, то следует просто вычислить отношение: η = Ап / Аз. Для обозначения характеристики применяют букву греческого алфавита η (эта). Таким образом, полезным действием называют физическую величину, равную отношению работы, выполненной самим механизмом, к затраченной энергии по приведению его в действие. Измерять КПД принято в процентах.

Если система тел способна совершить работу, то говорят, что она обладает энергией. Измеряется она в джоулях. Существует несколько видов энергии, с помощью которых можно определять работу, а значит, и вычислять КПД. Наиболее часто приходится исследовать две энергии:

1. Потенциальную — ею называется энергия взаимодействия тел или частей одной физической частицы. Её вычисление зависит от принятой системы. Для тела, поднятого над землёй, она будет равна: Eп = mgh. То есть приобретённая потенциальная энергия — это полезная работа. Например, её сообщают телу при поднятии его по наклонной плоскости.
2. Кинетическую — это та энергия, которой обладает движущееся тело. Она пропорциональна массе тела и квадрату его скорости: Ек = mv² / 2.

Следует отметить, что при расчёте работы, связанной с потенциальной энергией, имеет значение уровень, от которого она отсчитывается.

На первый взгляд кажется, что эта ситуация приводит к неоднозначностям. Но это не так, потому что работа равняется не самой энергии, а её изменению. При этом существует закономерность, что уменьшение потенциальной энергии приводит к увеличению кинетической. Это правило действует и в обратную сторону.

Тепловые и электродвигатели

Тепловыми машинами называют механизмы, которые преобразовывают внутреннюю энергию в механическую работу. Это ветряные и водяные мельницы, устройства, работающие от всевозможного топлива. К основным частям любого теплового двигателя относят:

• нагреватель — приспособление с высокой температурой по отношению к окружающей среде;
• рабочее тело — часть, непосредственно выполняющая поставленную задачу, например, газ или пар;
• охладитель.

Количество теплоты, полученной от нагревателя телом, будет равно совершённой работе плюс изменение внутренней энергии: Q = A + Δ U. Максимальное КПД такого устройства будет, когда ΔU = 0. Внутренняя энергия газов зависит от температуры. Значит, при совершении работы она не должна изменяться. Другими словами, происходящий процесс должен быть изотермическим.

Становится понятным, что для повышения КПД нужно, чтобы работа по сжатию была меньше той, которую совершает тело при расширении. Достичь это можно охлаждением: A = Q1 — Q2. В это время часть энергии будет возвращаться в систему. Значит, КПД равно: η = (Q1 — Q2) / Q1. При этом наибольший коэффициент находится по формуле: η = (T1 — T2) / T2, где T1 и T2 — температуры нагревателя и охладителя соответственно.

У электродвигателей потери энергии обусловлены нагреванием проводников при прохождении по ним электрического тока, а также воздействием паразитных магнитных потоков. Кроме этого, дополнительный расход энергии может затрачиваться на механические потери, вызванные элементами двигателя.

У электромашины КПД может изменяться от 10% до 99%. Находят его через следующее отношение: η = P2 / P1, где P2 — механическая мощность, а P — подводимая к двигателю. Нужно отметить, что эффективность эксплуатации двигателя сильно упадёт, если его применять для обеспечения движения механизма, обладающего более низким коэффициентом полезной энергии.

Повышение КПД электрической машины возможно путём использования качественных деталей, например, подшипников качения, крыльчаток с уменьшенным сопротивлением воздуху. Для снижения нагрева применяют сверхпроводники, обладающие малым сопротивлением. Магнитные потери уменьшают применением электромагнитной стали с высокой степенью изоляции.

Решение задач

Любое вычисление коэффициента полезного действия сводится к нахождению отношений работы. Так как это безразмерная величина, ответ записывают в процентах. Существует ряд типовых задач, позволяющих лучше разобраться в теории и понять, для чего можно использовать знания на практике. Вот некоторые из них:

1. На стройке с помощью рычажного механизма паллету массой 190 кг подняли на один метр. При этом длинное плечо опустилось на два метра. Найти КПД, учитывая, что приложенная сила к рычагу составила 1000 ньютон. Для решения этого задания нужно рассчитать полную и полезную работу. Так как общая энергия характеризуется силой, которая была приложена к плечу рычага, то найти её можно из выражения: Аз = F * S = 1000 Н/кг * 2 м = 2000 Дж. В то же время полезная работа — это та, что позволила поднять груз. Находится она следующим образом: Ап = mgh = 190 кг * 1 м * 10 Н/кг = 1900 Дж. Отсюда искомая сила равна: n = 1900 Дж / 2000 Дж = 0,95 * 100 = 95%.
2. Производительность насоса составляет 300 литров в минуту при подаче воды на 20 метров. Найти, какая мощность мотора, если КПД устройства составляет 80%. Для того чтобы выполнить расчёт, понадобится знать плотность воды. Она составляет 1000 кг / м³. Решать эту задачу нужно следующим образом. Полезная работа при поднятии воды насосом равняется: Aп = P * s1 = mgh, где m — масса воды, которую можно найти, зная плотность и объём. Тогда Ап = p * V * h = 1000 кг / м³ * 0,3 м³ * 20 м = 60 000 Дж. Полную же затраченную энергию можно найти по формуле: Аз = n * t. Отсюда: n = Ап / Аз = Ап / n * t = 60 000 Дж / 0,8 * 60с = 1250 Вт.
3. Куб массой 200 кг поднимают по наклонной доске. Высота отклонения от горизонтальной линии составляет полтора метра, а длина пути — десять метров. Определить необходимую силу, если КПД составляет 60%. Полезная работа в этом случае находится из произведения веса куба и высоты: Aп = mgh. Полная же энергия рассчитывается так: Аз = F * l. Эти выражения можно подставить в формулу нахождения КПД и из неё уже выразить искомую силу: F = mgh / n = (200 кг * 10 Н/кг * 1,5 м) / (0,6 * 10 м) = 3000 / 6 = 500 Н.

Таким образом, при решении задач необходимо сначала правильно определить полезную и полную работу. Для этого нужно разобраться, с какой целью используется тот или иной механизм. Ведь за всю энергию принимается та, которая совершается самим устройством.

Вычисление полезной работы через КПД

Измерять КПД принято в процентах. Например, КПД 35%, означает, что почти две трети энергии пошли на ненужные траты, стали рассеянным в пустую теплом, были потрачены на истирание деталей машины, образование искр и т. п.

Важно. 35% совсем не плохой КПД. У паровозов первой половины 20 века он составлял всего 10%. Лишь одна десятая образующегося при сгорании топлива тепла шла на перемещение состава, остальное рассеивалось в атмосфере. Среднеэксплуатационный КПД у современных тепловозов 20-22%. КПД машин на бензиновом ДВС равен 25%. КПД дизеля – 33%. Хорошо на этом фоне выглядит КПД электромобилей. Он у них около 90%.

В формуле нахождения полезной работы да в физике в основном КПД обозначают буквой из греческого алфавита η (эта).

Полезная работа в физике и ненужные траты энергии

Прежде чем говорить о том, как найти полезную работу в физике, следует сказать о ней самой. Дело в том что полезная работа в физике – величина очень даже субъективная. Она напрямую связана с человеческим восприятием, с тем, чего нам нужно получить от системы. Поэтому часто, когда говорят о КПД, имеют в виду различные технические устройства, а не природные объекты.

Хотя технологии постоянно развиваются избежать значительных потерь энергии всё же не удаётся. Получается, что:

Aзатр > Aполез

Aзатр – затраченная работа, Aполез – полезная работа, та что идёт на осуществление нужного нам процесса.

Как бы мы ни пытались уменьшить ненужные потери энергии, полностью от них избавиться не получиться. Непреодолимой преградой для этого является первый закон термодинамики. Из него явственно следует, что КПД любого устройства и механизма ни при каких обстоятельствах не может быть больше единицы и даже стать равным ей.

Мощность представляет собой работу, совершённую за единицу времени. В связи с этим КПД можно посчитать как отношение входной мощности системы к выходной. Т. е.

η = Pвх/Pвых.

Как найти полезную работу в физике используя формулы для разных физических процессов

Вид формул, как найти полезную работу в физике, зависит от природы физических явлений, использующихся для преобразования затраченной энергии в нужную.

Как найти полезную работу в физике механической системы

Лучше всего это показать на конкретном примере. Допустим, нам требуется найти КПД процесса, при котором мальчик вкатывает санки весом 4 кг на горку длиной 12, высотой 2 м. Он прикладывает для этого силу, равную 15 Н.

Решение:

Напомним, что общая формула для КПД

η = (Aполез/Aзатр) * 100%

Aполез в нашем случае равна потенциальной энергии (Eп), которую нужно потратить на то, чтобы поднять санки на высоту, т. е.  Aполез = m*g*h.

Затраченная мальчиком работа равна произведению силы на перемещение, т. е. Aзатр = F*S.

Подставляем в общую формулу для КПД

η = (m*g*h*100)/(F*S)

При подстановке численных значений получаем

η = 4*9,8*2/15*12 * 100% = 78,4/180 * 100% ≃ 43,6 %

Из этого примера ясно, чему равна полезная работа в физике механической системы, выраженная через КПД.

Формула полезной работы в физике термодинамической системы

Именно по ней судят об эффективности тепловых машин. Допустим, нам нужно отыскать КПД тепловой машины, рабочее тело которой берёт от нагревателя 20кДж, а холодильнику отдаёт 10кДж.

Решение:

Тепловая машина работает следующим образом: нагреватель передаёт определённое количество теплоты рабочему телу, оно из-за этого расширяется, совершая тем самым механическую работу. Однако в последнюю переходит далеко не вся часть переданной тепловой энергии. Чтобы вернуть систему в исходное состояние и начать новый цикл приходится использовать холодильник.

Из выше сказанного можно сделать вывод, что Aполез равна разности энергии взятой от нагревателя и энергии, забранной холодильником, т. е.

Aполез = Qнагревателя – Qхолодильника

Затраченная работа равняется количеству той теплоты, которая была сообщена нагревателю.

Если всё это подставим в формулу для КПД, то получим

[eta=(text { Qнагревателя }-text { Qхолодильника })^{*} 100 / text { Qнагревателя }]

После подстановки численных значений будем иметь

η = (20 – 10)/20*100% = 50%

Теперь ясно, как определить полезную работу в физике термодинамической системы.

Формула полезной работы в физике электродинамической системы

Очень важный класс явлений. Каждый день все пользуются самыми разными электрическими устройствами: телевизором, компьютером, телефоном и т. д. Но мы рассмотрим случай попроще. Вычислим КПД электрического чайника. Допустим воде было передано 22176 Дж тепла за 2 мин. Напряжение в электросети стандартное 220 В. Сила тока равняется 1,4 А.

Решение:

Aполез будем считать работу, которая пошла на нагрев воды. Хотя она нам и дана из условия, формулу вспомнить всё равно не будет лишним.

• Q = cm(tконечная-tначальная)
• Q — количество теплоты [Дж]
• c — удельная теплоёмкость вещества [Дж/кг*˚C]
• m — масса [кг]
• tконечная — конечная температура [˚C]
• tначальная — начальная температура [˚C]
• Работа тока вычисляется по формуле
• A = (I^2)*Rt = (U^2)/R *t = UIt
• A — работа электрического тока [Дж]
• I — сила тока [А]
• U — напряжение [В]
• R — сопротивление [Ом]
• t — время [c]

В нашем примере она примет вид

η = Q/A *100% = Q/UIt *100%

Переводим минуты в секунды и, подставляя численные значения, получаем

η = 22176/220*1,4*120 *100% = 60%

Формула полезной работы электродинамической системы будет:

Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную или затраченную работу A_з и полезную работу A_п. Если, например, наша цель — поднять груз массой m на высоту h, то полезная работа — это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:

    A_п = F_тh = mgh.      (24.1)

Если же мы применяем для подъема груза блок или какой-либо другой механизм, то, кроме силы тяжести груза, нам приходится преодолевать еще и силу тяжести частей механизма, а также действующую в механизме силу трения. Например, используя подвижный блок, мы вынуждены будем совершать дополнительную работу по подъему самого блока с тросом и по преодолению силы трения в оси блока. Кроме того, выигрывая в силе, мы всегда проигрываем в пути (об этом подробнее будет рассказано ниже), что также влияет на работу. Все это приводит к тому, что затраченная нами работа оказывается больше полезной:

A_з > A_п

Полезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм.

Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется коэффициентом полезного действия механизма.

Сокращенное обозначение коэффициента полезного действия — КПД.

Чтобы найти КПД механизма, надо полезную работу разделить на ту, которая была затрачена при использовании данного механизма.

Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой η (читается «эта»):

    η =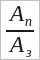* 100%    (24.2)

Поскольку числитель A_п в этой формуле всегда меньше знаменателя A_з, то КПД всегда оказывается меньше 1 (или 100%).

Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их массу. В тех случаях, когда трение ничтожно мало и используемые механизмы имеют массу, пренебрежимо малую по сравнению с массой поднимаемого груза, коэффициент полезного действия оказывается лишь немного меньше 1. В этом случае затраченную работу можно считать примерно равной полезной работе:

    A_з ≈ A_п     (24.3)

Следует помнить, что выигрыша в работе с помощью простого механизма получить нельзя.

Поскольку каждую из работ в равенстве (24.3) можно выразить в виде произведения соответствующей силы на пройденный путь, то это равенство можно переписать так:

    F₁s₁ ≈ F₂s₂     (24.4)

Отсюда следует, что,

выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот.

Этот закон называют «золотым правилом» механики. Его автором является древнегреческий ученый Герон Александрийский, живший в I в. н. э.

«Золотое правило» механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.

Так, например, благодаря этому правилу мы сразу можем сказать, что рабочему, изображенному на рисунке 47, при двукратном выигрыше в силе для подъема груза на 10 см придется опустить противоположный конец рычага на 20 см. То же самое будет и в случае, изображенном на рисунке 58. Когда рука человека, держащего веревку, опустится на 20 см, груз, прикрепленный к подвижному блоку, поднимется лишь на 10 см.

1. Почему затраченная при использовании механизмов работа оказывается все время больше полезной работы? 2. Что называют коэффициентом полезного действия механизма? 3. Может ли КПД механизма быть равным 1 (или 100%)? Почему? 4. Каким образом увеличивают КПД? 5. В чем заключается «золотое правило» механики? Кто его автор? 6. Приведите примеры проявления «золотого правила» механики при использовании различных простых механизмов.

КПД теплового двигателя рассчитывается по формуле $eta = frac{A_п}{Q_1}$ или $eta = frac{Q_1 — Q_2}{Q_1} cdot 100 %$, где
$A_п$ — полезная работа,
$Q_1$ — количество теплоты, полученное от нагревателя,
$Q_2$ — количество теплоты, отданное холодильнику.

Когда говорят о коэффициенте полезного действия теплового двигателя, часто используют понятие мощности или полезной мощности: $N = frac{A_п}{t}$. Эту величину в жизни использовать удобнее, чем говорить о полезной работе. 

На данном уроке мы разберем решение задач, используя формулы, приведенные выше.

Для решения задач, в условиях которых, говорится о сжигании топлива ($Q = qm$), вам понадобятся табличные значения удельной теплоты сгорания топлива.

Задача №1

Какая работа совершена внешними силами при обработке железной заготовки массой $300 space г$, если она нагрелась на $200 degree C$?

$A — ?$

Показать решение и ответ

Скрыть

Задача №2

Приняв, что вся тепловая энергия угля обращается в полезную работу, рассчитайте какого количества каменного угля в час достаточно для машины мощностью $733 space Вт$?

$m — ?$

Показать решение и ответ

Скрыть

Задача №3

Нагреватель за некоторое время отдает тепловому двигателю количество теплоты, равное $120 space кДж$. Тепловой двигатель совершает при этом полезную работу $30 space кДж$. Определите КПД теплового двигателя.

$eta — ?$

Показать решение и ответ

Скрыть

Задача №4

Нагреватель  отдает тепловому двигателю за $30 space мин$ количество теплоты, равное $460 space МДж$, а тепловой двигатель отдает количество теплоты, равное $280 space МДж$. Определите полезную мощность двигателя.

Показать решение и ответ

Скрыть

Задача №5

Паровой молот мощностью $367 space кВт$ получает от нагревателя в час количество теплоты, равное $6720 space МДж$. Какое количество теплоты в час получает холодильник?

$Q_2 — ?$

Показать решение и ответ

Скрыть

Задача №6

Мопед, едущий со скоростью $20 frac{км}{ч}$, за $100 space км$ пути расходует $1 space кг$ бензина. КПД его двигателя равен $22 %$. Какова полезная мощность двигателя?

$N — ?$

Показать решение и ответ

Скрыть

Задача №7

Определите КПД двигателя внутреннего сгорания мощностью $36.6 space кВт$, который сжигает в течение одного часа $10 space кг$ нефти.

Показать решение и ответ

Скрыть

Паровая машина мощностью $220 space кВт$ имеет КПД $15 %$. Сколько каменного угля сгорает в ее топке за $8 space ч$?

Показать решение и ответ

Скрыть

Задача №9

Современные паровые механизмы расходуют $12.57 space МДж$ в час на $735 space Вт$. Вычислите КПД таких механизмов.

$eta- ?$

Показать решение и ответ

Скрыть

Задача №10

Мощность дизельного двигателя $367 space кВт$, КПД $30 %$. На сколько суток непрерывной работы хватит запаса нефти $60 space т$ такому двигателю?

$t — ?$

Показать решение и ответ

Скрыть