4 февраля 2014
Итак, сегодня мы продолжаем изучать задачи на движение. Перед нами — сложная (для многих учеников она реально сложная) задача B14 на движение по эскалатору. Из урока вы узнаете, как не «подвисать» при решении подобных задач, а также не выполнять лишних действий. Все-таки текст задачи сводится к системе уравнений, да и ответ тоже находится не сразу. В общем, смотрите видео — и берите на вооружение!
Задача B14. Маша спустилась по движущемуся вниз эскалатору за 36 секунд. По неподвижному эскалатору с той же скоростью относительного него она спустится за 1 минуту 3 секунды. За сколько секунд она спустится, стоя на ступеньках движущегося эскалатора?
Как видите, основная проблема данной задачи — неизвестно общее расстояние, т.е. длина эскалатора. В некотором смысле эта задача очень похожа на движение по воде: при спуске скорости эскалатора и человека складываются. Однако, в отличие от задач на движение, здесь недостаточно просто решить систему — требуется еще и понять, какую именно величину записывать в ответ.
Смотрите также:
- Задача B14 про эскалаторы: считаем ступеньки
- Тест по задачам B14: легкий уровень, 2 вариант
- Тест к уроку «Сложение и вычитание дробей» (средний)
- Периодические десятичные дроби
- Изюм и виноград (смеси и сплавы)
- ЕГЭ 2022, задание 6. Касательная к графику функции
Условие
B12. Эскалатор метро движется со скоростью 0,75 м/с. Найдите время, за которое пассажир переместится на 20 м относительно земли, если он сам идет в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета, связанной с эскалатором.
Решение
1 способ. По условию дано перемещение пассажира относительно земли, т.е. Δrton = 20 м. Так как задана скорость пассажира в СО, связанной с эскалатором, то υc = υesk = 0,75 м/с; υtop = υpass = 0,25 м/с. Время найдем по формуле (~t = frac{Delta r_{tonx}}{upsilon_{tonx}}) (т.к. дано перемещение Δrton и НЕ ЗАБЫВАЙТЕ принцип соответствия).
Найдем υton. Запишем закон сложения скоростей в векторном виде (~vec upsilon_{ton} = vec upsilon_c + vec upsilon_{top} = vec upsilon_{esk} + vec upsilon_{pass}) и в проекции на ось 0X: υtonx = υesk + υpass (рис. 1). Так как υton x > 0, то Δrton x > 0. Тогда (~t = frac{Delta r_{ton}}{upsilon_{esk} + upsilon_{pass}}) ; t = 20 с.
2 способ. Время найдем по формуле (~t = frac{Delta r}{upsilon_{pass}}) , где Δr = 20 м – перемещение пассажира относительно земли. Найдем скорость υpass.
Так как задана скорость пассажира в СО, связанной с эскалатором, то воспользуемся законом сложения скоростей в следующем виде[~vec upsilon_{pass} = vec upsilon_{esk} + vec upsilon_{pass/esk}] , где υesk = 0,75 м/с – скорость эскалатора; υpass/esk = 0,25 м/с – скорость пассажира в СО, связанной с эскалатором. Тогда в проекции на ось 0Х: υpass x = υesk + υpass/esk > 0 (рис. 1). После подстановки получим (~t = frac{Delta r}{upsilon_{esk} + upsilon_{pass/esk}}) ; t = 20 с.
Рис. 1
Эскалатор метро движется со скоростью 0,75 м/с. Найти время, за которое пассажир переместится на 20 м относительно земли, если он сам идет в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета, связанной с эскалатором
Задача из пособия: Рымкевич А.П. 10-11 класс
Механика
Решение
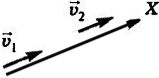
Скорости направлены вдоль прямой в одну сторону. Проекция скорости пассажира на направление движения эскалатора в системе отсчета, связанной с землей, равна сумме проекций скоростей эскалатора и пассажира относительно эскалатора на то же направление:
0,75 м/с + 0,25 м/с = 1 м/с.
Воспользуемся формулой
То есть время перемещения пассажира на 20 м относительно земли — это частное от деления этого пути на его скорость относительно земли:
Первое
Второе
В этой статье собраны задачи про эскалаторы. Пассажиры метро чего только на них не выделывают, и каких только способов подняться и спуститься не придумали! Встретятся и задачи на постоянную скорость, и задачи на относительность движения.
Задача 1.
Пассажир поднимается по неподвижному эскалатору метрополитена за время мин, а по движущемуся вверх – за
минуты. Сможет ли он подняться по эскалатору, движущемуся с той же скоростью вниз? Если да, то за какое время?
Итак, дана, по сути, собственная скорость пассажира. Ее можно найти, зная время его подъема и обозначив длину расстояния от нижней точки до верхней за :
Когда эскалатор движется вверх, то скорости пассажира и эскалатора сложатся, и относительно земли пассажир будет двигаться со скоростью , где
— скорость движения эскалатора. Тогда время подъема станет равным
:
Отсюда можно определить скорость эскалатора:
Если пассажиру вздумается идти вверх по эскалатору, то скорость эскалатора вычтется из его собственной скорости, и общая скорость подъема станет равной , тогда время подъема:
Ответ: 6 минут.
Задача 2.
Человек спускается по движущемуся вниз эскалатору. В первый раз он насчитал ступенек, второй раз, двигаясь в ту же сторону со скоростью относительно эскалатора втрое большей, он насчитал
ступенек. Сколько ступенек он насчитал бы на неподвижном эскалаторе?
Так как в первом случае и во втором случае человек бежал с разной скоростью, то и время он затрачивал разное. Кроме того, он пробегает в каждом случае и разный путь, поскольку эскалатор тоже движется, и с каждой секундой расстояние, которое отделяет человека от конца эскалатора, все время сокращается. Поэтому пусть в первом случае наш пассажир двигался со скоростью и прошел путь
за время
, а во втором случае скорость движения
, время движения
и
— пройденное расстояние. Тогда:
Пути, пройденные в первом и втором случае, разные, но перемещение-то одно и то же! Человек достиг цели: спустился сверху вниз. Обозначим перемещение . Тогда относительно земли человек в первом случае движется со скоростью
, где
— скорость эскалатора, а во втором случае
:
Подставим найденное время:
Разделим на
:
Найдем отношение скорости человека к скорости эскалатора, разделив на :
Тогда можно подставить:
Откуда расстояние , выраженное в числе ступенек,
.
Ответ: 100.
Задача 3.
Эскалатор метро спускает идущего по нему человека за время мин. Если человек будет двигаться относительно эскалатора вдвое быстрее, то он спустится за
с. Сколько времени будет спускаться человек, стоящий на эскалаторе?
Пусть сначала скорость спуска человека относительно эскалатора равна , тогда во второй раз она будет
. Скорость эскалатора обозначим за
. Поскольку в обоих случаях и человек, и эскалатор движутся в одну сторону, то скорости будут складываться. Поэтому время первого спуска равно:
А время второго спуска будет
Если человек на эскалаторе просто стоит, то он и движется со скоростью эскалатора, ее нам и надо найти. Составим из этих двух уравнений систему и решим ее.
Уравняем коэффициенты:
Вычтем из первого второе уравнение:
Теперь можно определить и время спуска, если человек стоит на эскалаторе. Оно будет равно
Ответ: 90 с.
Задача 4.
Два человека одновременно вступают на эскалатор с противоположных сторон и движутся навстречу друг другу с одинаковыми скоростями относительно эскалатора м/с. На каком расстоянии от входа на эскалатор они встретятся? Длина эскалатора 100 м, его скорость
м/с.
Если наши пассажиры встретились, то, следовательно, прошли весь эскалатор: часть – один, а часть – второй. Тот, что двигался в ту же сторону, что и эскалатор, относительно земли перемещался со скоростью , а тот, что шел навстречу движению – со скоростью
. Таким образом, скорость сближения двух людей равна
. Таким образом, время их движения равно:
За это время тот, что шел в одну сторону с эскалатором, прошел
А тот, что шел навстречу движению эскалатора, прошел
Таким образом, если вход на эскалатор там, где ступил на него первый пассажир (что логично), то встретятся они в 87,5 м от этого места.
Ответ: 87,5 м.
Задача 5.
Эскалатор метро движется со скоростью м/с. Пассажир заходит на эскалатор и начинает идти по его ступеням следующим образом: делает шаг на ступеньку вперед и два шага по ступенькам назад. При этом он добирается до другого конца эскалатора за время
с. Через какое время пассажир добрался бы до конца эскалатора, если бы шел другим способом: делал два шага вперед и один шаг назад? Скорость пассажира относительно эскалатора при движении вперед и назад одинакова и равна
м/с. Считать размеры ступеней много меньше длины эскалатора.
Итак, пусть человек затрачивает время для того, чтобы шагнуть на одну ступеньку. Тогда сначала он будет двигаться со скоростью
, поскольку в итоге шагает назад на одну ступеньку, и делает это за тройное время. Иначе говоря, скорость человека в первом случае равна
. Движется он в сторону, противоположную движению эскалатора, поэтому его скорость относительно земли равна
. В конце концов он добирается до нижней точки, то есть совершает перемещение
:
Если бы он шел вторым способом, то скорость относительно эскалатора была бы , а относительно земли
. Время перемещения тогда составило бы:
Ответ: 50 с.
4 комментария
Илья
✉️
25.04.2017 09:54:15
В задаче н2 в разделе эскалаторы непонятно из условия, ни в каком направлении двигается пассажир, ни по направлению движения эскалатора, ни против.
Анна Валерьевна
✨
25.04.2017 11:51:55
Поправила. Спасибо!
Наталья
✉️
06.10.2018 11:48:22
задачу 2 можно сделать проще. )
В первом случае на каждую пройденную человеком ступень уезжает хорошо ступеней эскалатора. И так 50 раз:
50 (1+х)
во втором случае — на каждую пройденную ступень уедет в три раза меньше:
75 (1+х/3)
Приравняем, решим, получим х=1 и
50 (1+х)= 100
Все!
Анна Валерьевна
✨
06.10.2018 12:46:52
Спасибо большое! Красиво.
Эскалатор метро движется со скоростью 0,75 м/с. Найти время, за которое пассажир переместится на 20 м относительно земли, если он сам идет в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета, связанной с эскалатором
Данная задача находится в разделе
Решебник Рымкевич на странице № 3
<<< Предыдущая задача из Рымкевич
Гусеничный трактор Т-150 движется с максимальной скоростью 18 км/ч. Найти проекции векторов скоростей верхней и нижней части гусеницы на оси X и X1. Ось X связана с землей, ось X1 — с трактором. Обе оси направлены по ходу движения трактора
Следующая задача из Рымкевич >>>
Два поезда движутся навстречу друг другу со скоростями 72 и 54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда




