Связь между скоростью и фактором Лоренца γ (и, следовательно, замедлением времени движущихся часов).
Замедление времени, предсказываемое специальной теорией относительности , часто подтверждается экспериментами по времени жизни частиц. Согласно специальной теории относительности, скорость часов C, перемещающихся между двумя синхронизированными лабораторными часами A и B, как видит лабораторный наблюдатель, замедлена по сравнению с тактовой частотой лабораторных часов. Поскольку любой периодический процесс можно рассматривать как часы, время жизни нестабильных частиц, таких как мюоны, также должно быть затронуто, так что движущиеся мюоны должны иметь большее время жизни, чем покоящиеся. Разнообразные эксперименты, подтверждающие этот эффект, были выполнены как в атмосфере, так и в ускорителях частиц . Другой тип экспериментов по замедлению времени — это группа экспериментов Айвса – Стилвелла по измерению релятивистского эффекта Доплера .
Атмосферные испытания
а) Просмотр в S
б) Вид в S ′
c) Диаграмма Лёделя (чтобы уменьшить различия, использовалось 0,7c вместо 0,995c)
Теория
Возникновение мюонов вызвано столкновением космических лучей с верхними слоями атмосферы, после чего мюоны достигают Земли. Вероятность того, что мюоны могут достичь Земли, зависит от их периода полураспада , который, в свою очередь, модифицирован релятивистскими поправками на две величины: а) среднее время жизни мюонов и б) расстояние между верхней и нижней атмосферой (на поверхности Земли). . Это позволяет напрямую применить сокращение длины к покоящейся атмосфере в инерциальной системе отсчета S и замедление времени к покоящимся мюонам в S ′.
- Замедление времени и сокращение длины
Длина атмосферы : Формула сжатия определяется выражением , где L 0 — собственная длина атмосферы, а L — ее сокращенная длина. Поскольку атмосфера в S находится в состоянии покоя, мы имеем γ = 1 и измеряется ее собственная длина L 0 . Поскольку он движется в S ′, мы имеем γ> 1 и измеряем его сжатую длину L ′ .
Время распада мюонов : Формула замедления времени такова , где T 0 — собственное время часов, движущихся с мюоном, соответствующее среднему времени распада мюона в его собственной системе отсчета . Поскольку мюон покоится в S ′, мы имеем γ = 1, и его собственное время T ′ 0 измеряется. Как движется в S, то есть у> 1, поэтому его надлежащее время короче по времени T . (Для сравнения можно рассмотреть другой мюон, покоящийся на Земле, называемый мюоном-S. Следовательно, его время распада в S короче, чем у мюона-S ‘, в то время как оно больше в S’.)
- В S мюон-S ‘имеет большее время распада, чем мюон-S. Следовательно, мюон-S ‘имеет достаточно времени, чтобы пройти надлежащую длину атмосферы, чтобы достичь Земли.
- В S ‘мюон-S имеет большее время распада, чем мюон-S’. Но это не проблема, так как атмосфера сжата относительно ее надлежащей длины. Следовательно, даже более быстрое время распада мюона-S ′ достаточно для того, чтобы его преодолела движущаяся атмосфера и достигла Земля.
- Диаграмма Минковского
Мюон возникает в начале координат (A) в результате столкновения излучения с верхними слоями атмосферы. Мюон покоится в S ′, поэтому его мировая линия — это ось ct′. Верхние слои атмосферы покоятся на S, поэтому его мировая линия является осью ct. На осях x и x ′ присутствуют все события, одновременные с A в S и S ′ соответственно. Мюон и Земля встречаются в D. Поскольку Земля находится в состоянии покоя в S, ее мировая линия (идентичная нижней атмосфере) проводится параллельно оси ct, пока она не пересечет оси x ‘и x.
Время: интервал между двумя событиями, присутствующими на мировой линии одних часов, называется собственным временем , важным инвариантом специальной теории относительности. Поскольку происхождение мюона в точке A и встреча с Землей в точке D происходит на мировой линии мюона, только часы, движущиеся вместе с мюоном и, таким образом, покоящиеся в S ‘, могут указывать собственное время T’ 0 = AD . Из-за своей инвариантности также в S согласовано, что эти часы показывают именно то время между событиями, и поскольку они здесь находятся в движении, T ‘ 0 = AD короче, чем время T, указанное часами, находящимися в S. Это может можно увидеть на более длинных интервалах T = BD = AE, параллельных оси ct.
Длина: Событие B, где мировая линия Земли пересекает ось x, соответствует в S положению Земли одновременно с появлением мюона. C, где мировая линия Земли пересекает ось x′, соответствует в S ′ положению Земли одновременно с появлением мюона. Длина L 0 = AB в S больше, чем длина L ‘= AC в S’.
Эксперименты
Результаты эксперимента Фриша – Смита . Кривые, рассчитанные для и .
Если замедления времени не существует, то эти мюоны должны распадаться в верхних областях атмосферы, однако из-за замедления времени они присутствуют в значительном количестве и на гораздо более низких высотах. Сравнение этих количеств позволяет определить среднее время жизни, а также период полураспада мюонов. — количество мюонов, измеренное в верхних слоях атмосферы на уровне моря, — это время пробега в системе координат покоя Земли, за которое мюоны пересекают расстояние между этими областями, и — это среднее собственное время жизни мюонов:
Росси – Холл эксперимент
В 1940 году на озере Эхо (3240 м) и Денвере в Колорадо (1616 м) Бруно Росси и Д. Б. Холл измерили релятивистский распад мюонов (которые они считали мезонами ). Они измерили мюоны в атмосфере, движущиеся выше 0,99 c ( c — скорость света). Росси и Холл качественно подтвердили формулы для релятивистского импульса и замедления времени. Знание импульса и времени жизни движущихся мюонов позволило им вычислить и их среднее собственное время жизни — они получили ≈ 2,4 мкс (современные эксперименты улучшили этот результат до ≈ 2,2 мкс).
Эксперимент Фриша – Смита
Гораздо более точный эксперимент такого рода был проведен Дэвидом Х. Фришем и Смитом (1963), которые измерили приблизительно 563 мюона в час за шесть запусков на горе Вашингтон . Измеряя их кинетическую энергию, были определены средние скорости мюонов от 0,995 до 0,9954 с. Мишень находилась в Кембридже, штат Массачусетс, с разницей в высоте 1907 м, которую должны пройти мюоны примерно за6,4 мкс . Предполагая, что среднее время жизни составляет 2,2 мкс, только 27 мюонов достигли бы этого места, если бы не было замедления времени. Однако в Кембридж приходило примерно 412 мюонов в час, в результате чего коэффициент замедления времени составлял8,8 ± 0,8 .
Фриш и Смит показали, что это согласуется с предсказаниями специальной теории относительности: фактор замедления времени для мюонов на горе Вашингтон, движущихся от 0,995 c до 0,9954 c, составляет приблизительно 10,2. Их кинетическая энергия и, следовательно, их скорость уменьшались, пока они не достигли Кембриджа, до 0,9881 c и 0,9897 c из-за взаимодействия с атмосферой, уменьшая фактор расширения до 6,8. Таким образом, между началом (≈ 10,2) и целью (≈ 6,8) средний коэффициент замедления времени составляет8.4 ± 2 было определено ими, что согласуется с измеренным результатом в пределах погрешности (см. Приведенные выше формулы и изображение для расчета кривых затухания).
- Прочие эксперименты
С тех пор в студенческих экспериментах было проведено множество измерений среднего времени жизни мюонов в атмосфере и замедления времени .
Испытания ускорителей и атомных часов
Замедление времени и симметрия CPT
Гораздо более точные измерения распада частиц были выполнены в ускорителях частиц с использованием мюонов и различных типов частиц. Помимо подтверждения замедления времени, симметрия КПН была подтверждена путем сравнения времен жизни положительных и отрицательных частиц. Эта симметрия требует, чтобы скорости распада частиц и их античастиц были одинаковыми. Нарушение CPT-инвариантности также приведет к нарушению лоренц-инвариантности и, следовательно, специальной теории относительности.
| Пион | Каон | Мюон |
|---|---|---|
| Дурбин и др. (1952)
Eckhause et al. (1965) Nordberg et al. (1967) Гринбург и др. (1969) Ayres et al. (1971) |
Burrowes et al. (1959)
Нордин (1961) Боярский и др. (1962) Lobkowicz et al. (1969) Отт и др. (1971) Skjeggestad et al. (1971) Geweniger et al. (1974) Carithers et al. (1975) |
Ланди (1962)
Meyer et al. (1963) Eckhause et al. (1963) Баландин и др. (1974) |
Сегодня замедление времени частиц обычно подтверждается в ускорителях частиц наряду с тестами релятивистской энергии и импульса , и его учет является обязательным при анализе экспериментов с частицами при релятивистских скоростях.
Парадокс близнецов и движущиеся часы
Bailey et al. (1977) измерили время жизни положительных и отрицательных мюонов, проходящих по петле в мюонном накопителе ЦЕРНа . Этот эксперимент подтвердил как замедление времени, так и парадокс близнецов , то есть гипотезу о том, что часы, отправляемые и возвращающиеся в исходное положение, замедляются по сравнению с часами в состоянии покоя. Другие измерения парадокса близнецов также связаны с гравитационным замедлением времени.
В эксперименте Хафеле-Китинга настоящие атомные часы с цезиевым пучком облетели весь мир, и были обнаружены ожидаемые различия по сравнению со стационарными часами.
Гипотеза часов — отсутствие эффекта ускорения
Гипотеза часов утверждает, что степень ускорения не влияет на величину замедления времени. В большинстве упомянутых выше экспериментов распадающиеся частицы находились в инерциальной системе отсчета, т.е. без ускорения. Однако в Bailey et al. (1977) частицы испытывали поперечное ускорение до ~ 10 18 g . Поскольку результат был таким же, было показано, что ускорение не влияет на замедление времени. Кроме того, Roos et al. (1980) измерили распад барионов сигма , которые подвергались продольному ускорению от 0,5 до 5,0 · 10 15 g . И снова не было измерено никаких отклонений от обычного замедления времени.
Смотрите также
- Тесты специальной теории относительности
Рекомендации
Внешние ссылки
- Робертс, Т; Schleif, S; Длугош, JM (редактор) (2007). «Что является экспериментальной основой специальной теории относительности?» . Часто задаваемые вопросы по Usenet Physics . Калифорнийский университет, Риверсайд .CS1 maint: дополнительный текст: список авторов ( ссылка )
- Замедление времени — эксперимент с мю-мезонами
- Бониццони, Илария; Джулиани, Джузеппе, Интерпретации экспериментаторами экспериментов по «замедлению времени»: 1940-1970 около, arXiv : Physics / 0008012
Лабораторная работа № 6
Цель
работы: изучение
процессов при замыкании и размыкании
электрической цепи, имеющей индуктивность
и сопротивление; определение постоянной
времени
-цепи.
Приборы
и материалы:
лабораторный стенд, имеющий набор
объектов на плате, генератор сигналов,
осциллограф, набор соединительных
проводов.
1. Краткая теория
Электрический ток, текущий в любом
контуре, создает пронизывающий этот
контур магнитный поток. При изменениях
силы тока изменяется также и магнитный
поток, вследствие чего в контуре возникает
ЭДС самоиндукции
.
Это приводит к тому, что установление
тока при замыкании цепи и убывание тока
при размыкании цепи происходит не
мгновенно, а постепенно.
Рассмотрим
цепь с не зависящей от силы тока
индуктивностью
,
сопротивлением
и источником тока
(рис. 6.1). Такая цепь называется
-цепью.
В литературе [1]
показано, что при подключении к цепи
источника тока функция, описывающая
нарастание тока, имеет вид:
. (6.1)
А
функция, описывающая убывание тока
после отключения источника тока:
.
(6.2)
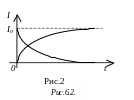
Графики возрастания и убывания тока
при замыкании и размыкании цепи приведены
на рис. 6.2. Скорость возрастания или
убывания тока характеризуется величиной,
имеющей размерность времени:
,
(6.3)
которую называют постоянной времени
—цепи.
Заменив в (6.1) и в (6.2)
через
,
получим:
, (6.4)
. (6.5)
В соответствии с формулой (6.5)
есть время, в течение которого сила тока
уменьшается в
раз. Из (6.3) и (6.5) видно, что чем больше
индуктивность цепи
и меньше ее сопротивление
,
тем больше постоянная времени
и тем медленнее спадает ток в цепи.
2. Методика выполнения работы
В данной работе к
-цепи
в качестве источника тока подключается
генератор прямоугольных импульсов. В
результате этого, действие переднего
фронта прямоугольного импульса аналогично
подключению к цепи источника
,
а действие заднего фронта – отключению
от цепи источника
.
В соответствии с выше сказанным, сигнал
будет иметь не строго прямоугольную
форму. Его передний фронт будет описываться
выражением (6.4), а задний фронт – выражением
(6.5).
В работе, используя изображения импульса
на экране осциллографа, измеряется
напряжение на сопротивлении
как функция времени
:
для переднего и заднего фронтов импульса.
Используя (6.4), (6.5) и закон Ома, можно
получить следующие выражения:
, (6.6)
. (6.7)
Построив графики функции
и
от времени
,
находят тангенс угла наклона каждого
из графиков
и в обоих случаях определяют постоянную
времени
.
Сравнивают полученные результаты.
3. Выполнение упражнений и обработка результатов измерений Задание. Определить постоянную времени -цепи.
1. Подготовка экспериментальной
установки к работе
Перед началом измерений следует
ознакомиться с работой генератора
сигналов и электронного осциллографа.
1
.1.
Соберите электрическую схему (рис.6.3),
состоящую из генератора сигналов
,
катушки индуктивности
,
резистора
и осциллографа. Резистор и катушка
индуктивности входят в состав
соответственно магазина сопротивлений
и магазина индуктивностей, находящихся
на плате лабораторного стенда. Используя
ручки регулировки генератора сигналов,
подготовьте его к работе в качестве
источника прямоугольных импульсов.
Значения сопротивления
,
индуктивности
и частоты сигналов генератора указываются
преподавателем.
1.2. После проверки электрической схемы
преподавателем или инженером приступите
к выполнению задания.
2. Определение постоянной времени
-цепи
2.1. Включите осциллограф и генератор
сигналов. Дайте приборам прогреться
около 5 минут.
2.2. Используя ручки регулировки генератора
сигналов и органов управления
осциллографом, добейтесь устойчивого
изображения сигнала на экране осциллографа.
2.3. Зарисуйте осциллограмму.
2.4. По экрану осциллографа произведите
измерения напряжения
в различные моменты времени для переднего
и заднего фронта импульса (по 10 точек
для каждого фронта импульса). Точки
следует брать в наиболее искривленных
участках осциллограммы. Результаты
измерений занести в таблицу 6.1. Следует
отметить, что для начального момента
времени
=0
имеем: в случае переднего фронта импульса
=0
и
=0;
в случае заднего фронта импульса
=
и
=0.
Таблица
6.1
|
№ п/п |
Для переднего |
Для заднего фронта |
||||||
|
, |
, мс |
, |
, |
, мс |
, |
|||
2.4. Постройте графики зависимостей
для переднего фронта и
для заднего фронта импульса.
2.5. По построенным графикам определите
постоянные времени
для переднего фронта и для заднего
фронта импульса, как величины обратные
тангенсам углов наклона полученных
прямых. Сравните полученные значения
между собой и со значением, рассчитанным
по формуле:
.
2.6. Оставив неизменным значение
индуктивности, повторить измерения еще
для трех сопротивлений отличных от
первоначального значения.
2.7. Оставив неизменным первоначальное
значение сопротивления, повторить
измерения еще для трех катушек, значения
индуктивностей которых отличны от
первоначального.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Электрическая цепь RC
Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе,
согласно закону Ома, составит U/R, где U — напряжение заряда конденсатора.
Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и
противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:
Решаем дифференциальное уравнение C(dU/dt)= -U/R

Из таблицы интегралов здесь используем преобразование
Получаем общий интеграл уравнения: ln|U| = — t/RC + Const.
Выразим из него напряжение U потенцированием: U = e-t/RC * eConst.
Решение примет вид:
U = e-t/RC * Const.
Здесь Const — константа, величина, определяемая начальными условиями.
Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону
e-t/RC.
Экспонента — функция exp(x) = ex
e – Математическая константа, приблизительно равная 2.718281828…
Постоянная времени τ
Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U,
в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения UC и определится выражением:

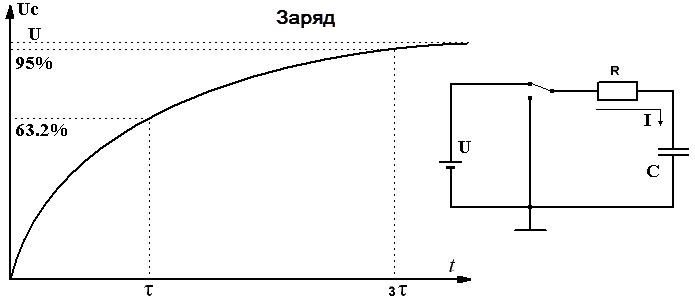
Тогда напряжение UC на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:
UC = U(1 — e-t/RC)
При t = RC, напряжение на конденсаторе составит UC = U(1 — e-1) = U(1 — 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.
Постоянная времени τ = RC
За время τ конденсатор зарядится до (1 — 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 — 1/e3)*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 — 1/e5)*100% ≈ 99% значения U.
Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R,
тогда в цепи пойдёт ток разряда конденсатора.
Напряжение на конденсаторе при разряде будет составлять UC = Ue-t/τ = U/et/τ.
За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.
За время 3τ конденсатор разрядится до (1/e3)*100% ≈ 5% от значения U.
За время 5τ до (1/e5)*100% ≈ 1% значения U.
Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.
Замечания и предложения принимаются и приветствуются!
Содержание:
- Определение и формула времени
- Особенности времени как физической величины
- Особенности времени как физической величины
- Единицы измерения времени
- Примеры решения задач
Определение и формула времени
В понятие времени отражаются такие свойства мира как постоянное развитие, изменение его в сознании человека. Процессы идут в определенной последовательности, при этом имеют определённую продолжительность.
Определение
Время – физическая величина, отражающая свойство материальных процессов иметь определенную продолжительность,
следовать друг за другом в установленной последовательности и развиваться этапно. Обозначают время буквой t.
Особенности времени как физической величины
Время неотделимо от материи и ее движения, так как является ее формой существования. Нет смысла говорить о времени самом по себе, так как в отрыве от материальных процессов течение времени становится бессодержательным. Только исследование процессов, происходящих в материальном мире и их взаимосвязей, делает понятие времени физически содержательным.
В череде процессов, происходящих в природе, особенное место занимают повторяющиеся процессы (повторение дней и ночей, дыхание, перемещение звезд по небосводу и т. д). Исследование и сравнение подобных процессов между собой ведет к идее о длительности материальных процессов, сравнение их длительности приводит к идее об их измерении.
Эталоном измерения является периодический процесс, который называют часами. Существуют системы отсчета, в которых возможно введение единого времени с достаточной для практики точностью. Введение единого времени хорошо подтверждается экспериментом. Теория дает возможность предсказать отклонения единого времени, что можно проверить эмпирически.
Длительность физического процесса, который происходит в некоторой точке, определяют при помощи часов, которые располагают в той же точке. При этом применяется прямое сравнение, сравниваются длительности процессов, которые текут в одной точке. Измерение длительности сводят к фиксации начала и окончания рассматриваемого процесса на шкале процесса, который принимают за эталонный. При этом говорят как о фиксации показаний часов в момент начала и окончания процесса, и это не имеет отношения к фактическому месту нахождения часов (процесса) в точке рассмотрения.
Синхронизация часов и изучения законов распространения физических сигналов развивались параллельно, при этом происходили взаимные уточнения и дополнения. Синхронизацию проводят при помощи сигналов, которые распространяются с конечной скоростью. Этот метод использует определение постоянной скорости: если из точки, в которой часы показывают t0, исходит сигнал, перемещающийся со скоростью v=const, то тогда, когда сигнал придет в точку на расстоянии s, часы в этой точке должны показать время:
$$t=t_{0}+frac{s}{v}(1)$$
Такая синхронизация согласуется с синхронизацией с использованием световых сигналов. Тогда часы синхронизируются по формуле:
$$t=t_{0}+frac{s}{c}(2)$$
где c=299792,4562 км/с – скорость света, которая не зависит от скорости источника и приемника по всем направлениям пространства одинакова.
Особенности времени как физической величины
Перемещение ($bar{s}$), равно:
$$bar{s}left(t_{2}, t_{1}right)=bar{s}left(t_{2}right)-bar{s}left(t_{1}right)(3)$$
где $bar{s}(t_2)$ – радиус-вектор в момент времени
$t_2, bar{s}(t_1)$ – радиус-вектор в момент времени
$t_1$ .
Мгновенная скорость ($bar{v}$):
$$bar{v}=frac{d bar{s}}{d t}(4)$$
Мгновенное ускорение ($bar{a}$):
$$bar{a}=frac{d bar{v}}{d t}(5)$$
Единицы измерения времени
Основной единицей измерения момента силы в системах СИ и СГС является: [t]=c
Единицы измерения времени основываются на периоде вращения Земли около своей
оси и вокруг Солнца, Луни вокруг Земли. Внесистемные единицы измерения времени: час, минута, сутки и т.д.
Примеры решения задач
Пример
Задание. Движения двух тел заданы уравнениями: и s1(t)=5t и s2(t)=150-10t. Найдите время встречи.
Решение. В точке встречи s1(t)=s2(t). Приравняем правые части функцийx(t), имеем:
$$5 t=150-10 t rightarrow 15 t=150 rightarrow t=10$$
Ответ. t=10 c

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
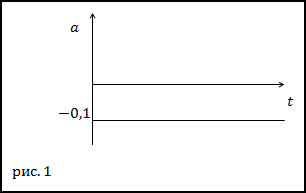
Задание. Движение материальной точки, задано уравнением: x=4t-0,05t2 .
В какой момент времени, скорость точки равна нулю? Коэффициенты имеют размерности: 4 м/с, 0,05м/с2 .
Изобразите графики зависимости модуля ускорения от времени.
Решение. В условиях задачи задана функция x(t), скорость можно найти как:
$$v=frac{d x}{d t}=4-0,1 t(2.1)$$
Приравняем скорость к нулю, найдем время:
$$4-0,1 t=0 rightarrow t=frac{4}{0,1}=40(c)$$
Определим, какова зависимость модуля ускорения от времени, для этого возьмем производную по времени от функции v(t) (2.1):
$$a(t)=frac{d v}{d t}=-0,1(2.2)$$
Тогда график зависимости a(t) имеет вид:
Ответ. t=40 c
Читать дальше: Формула длины волны.
«Формула времени. Решение задач»
Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.
Время обозначается как t. Единица измерения времени – с (секунды).
Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.
При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v0) / a или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v0).
Решение задач через формулу времени
Задача № 1.
Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

Задача № 2.
Двигаясь с ускорением 5 м/с2 скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?
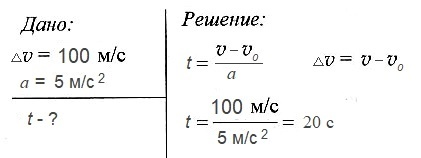
Задача № 3.
Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t1 = 3 ч, а плот то же расстояние – за время t0 =12 ч. Какое время t2 затратит моторная лодка на обратный путь?
Решение. Обозначим расстояние между пунктами А и В через L, скорость моторной лодки относительно воды через vл , а скорость течения через vт. Тогда t0 = L / vт , t1 = L / (vл + vт) , t2 = L / (vл — vт) . Исключая из записанной системы уравнений L, vл и vт
находим
Ответ: 6 ч.
Конспект урока «Формула времени. Решение задач».
Следующая тема: «».














![begin {align} M _ { mathrm {Newton}} & = N exp left [-Z / T_ {0} right] \ M _ { mathrm {SR}} & = N exp left [- Z / left ( gamma T_ {0} right) right] end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/523baef4ab77b16caaa4f3dadbfa1b448132a3ff)