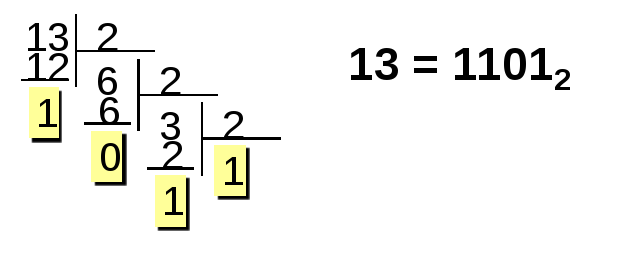Тема 3: Представление
целых чисел в компьютере.
Представление числовой информации в
компьютере
Любая информация (числа,
текстовая, графическая и т. д.) представляется
в ЭВМ в виде двоичных кодов фиксированной
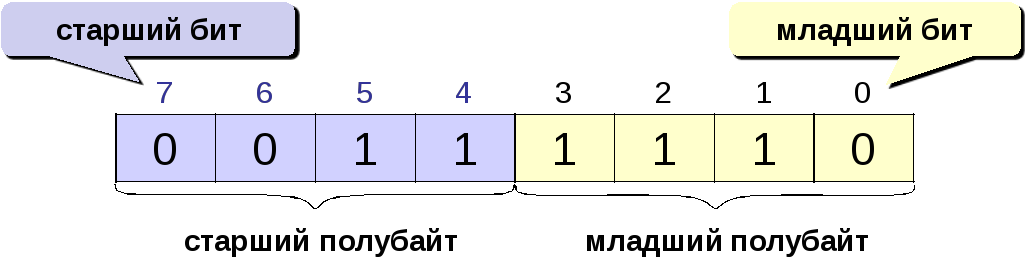
или переменной длины. Отдельные элементы
двоичного кода, имеющие значение 0 или
1, называют битами.
Двоичный код состоящий из 8 разрядов
носит название байта.
Целые числа могут
представляться в компьютере со знаком
или без знака.
Представление целых чисел без знака
в компьютере
Целые числа без знака обычно занимают
в памяти компьютера один,
два или 4 байта.
В однобайтовом формате
числа принимают значения от
000000002
до 111111112.
В двубайтовом формате —
от 00000000 000000002
до 11111111 111111112.
В четырехбайтовом — от
00000000 00000000 00000000 000000002
до 11111111 1111111 11111111 111111112
Диапазоны значений целых чисел без
знака
|
Формат |
Диапазон |
|
|
Запись с |
Обычная |
|
|
1 |
0 … 28–1 |
0 … 255 |
|
2 |
0 … 216–1 |
0 … 65535 |
|
4 |
0 … 232–1 |
0…429967295 |
Например,
в однобайтовом формате число 62=1111102
имеет вид:
В двубайтовом формате число 1402=101011110102
имеет вид:
Пример 1. Для хранения целого числа
без знака используется один
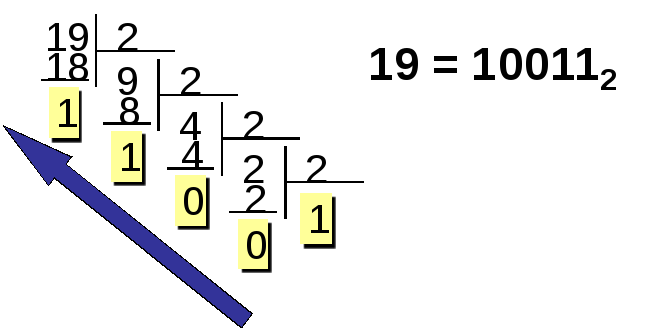
байт. Записать представление числа 19 в
компьютере.
1 шаг: Переведем число 19 из десятичной
системы счисления в двоичную.
2 шаг:
Так как для представления числа в
компьютере выделен 1 байт, то код числа
должен содержать 8 знаков (8 бит). Поэтому
впереди числа дописываем 3 незначащих
нуля.
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
Задания.
1. Запишите числа в беззнаковом коде
(формат 1 байт):
а) 31; б)
163; в) 65; г) 128.
2. Найдите десятичные
представления чисел, записанных в
беззнаковом коде:
а) 0 1011000;
б) 1 0011011; в) 0 1101001;
г) 1 1000000.
Представление целых чисел со знаком
Так же как беззнаковые целые числа целые
со знаком обычно занимают в
памяти компьютера один, два
или 4 байта.
Диапазоны значений целых чисел со
знаком
|
Формат |
Диапазон |
|
|
Запись с |
Обычная |
|
|
1 |
–27 … |
–128 … 127 |
|
2 |
–215 … |
–32768 … |
|
4 |
–231 … |
–2147483648 … |
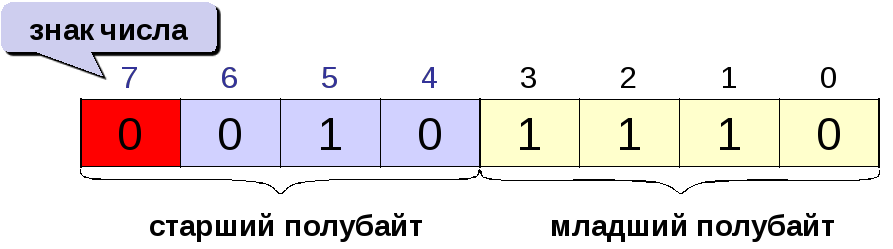
Самый левый (старший бит)
разряд определяет знак числа.
Если
он равен 0, число положительное, если 1,
то отрицательное.
Например,
в однобайтовом формате число 46=1011102
имеет вид:
В ЭВМ в целях упрощения
выполнения арифметических операций
применяют специальные коды для
представления чисел. Использование
кодов позволяет свести операцию вычитания
чисел к арифметическому сложению кодов
этих чисел. Применяются прямой,
обратный
и дополнительный
коды чисел. Дополнительный код используется
для хранения чисел в запоминающем
устройстве ЭВМ. Обратный и дополнительный
коды используются для замены операции
вычитания операцией сложения, что
упрощает устройство арифметического
блока ЭВМ.
Прямой код.
Прямой код двоичного числа совпадает
по изображению с записью самого числа.
Значение знакового разряда для
положительных чисел равно 0, а для
отрицательных чисел 1.
Обратный код.
Обратный код для
положительного числа совпадает с прямым
кодом. Для отрицательного числа все
цифры числа заменяются на противоположные
(1 на 0, 0 на 1), а в знаковый разряд заносится
единица.
Дополнительный код.
Дополнительный код
положительного числа совпадает с прямым
кодом. Для отрицательного числа
дополнительный код образуется путем
получения обратного кода и добавлением
к младшему разряду единицы.
Например, в однобайтовом формате числа
27 и -27 имеют вид:
|
Число |
Прямой |
Обратный |
Дополнительный |
|
27 |
00011011 |
00011011 |
00011011 |
|
-27 |
10011011 |
11100100 |
11100101 |
Пример 1. Найти прямой, обратный и
дополнительный код представления числа
13 в однобайтном формате.
1 шаг: Переведем число 13 из десятичной
системы счисления в двоичную.
2 шаг: Для представления
числа в компьютере выделен 1 байт. Старший
бит занимает знак числа – 0. Сам код
числа должен занимать 7 бит. Таким образом
прямой код числа 13
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
Так как для положительных чисел прямой,
обратный и дополнительный код совпадает,
то ответ 00001101.
Пример 2. Найти прямой, обратный и
дополнительный код представления числа
-23 в однобайтовом формате.
1 шаг: Переведем число -23 из десятичной
системы счисления в двоичную. Получим
-2310=-101112
2 шаг: Прямой код числа в однобайтовом
формате, учитывая, что старший бит
занимает знак числа -1, имеет вид
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
3 шаг: Найдем обратный код числа -23,
заменив все цифры числа на
противоположные (1 на 0, 0 на 1), а в знаковый
разряд заносится единица. Имеем,
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
4 шаг: Найдем дополнительный код
числа -23, добавив 1 к младшему
разряду обратного кода.
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
Ответ:
прямой код – 10010111; обратный – 11101000;
дополнительный – 11101001.
Так
вот, прямой
обратный и дополнительный код — это
модели представления целых чисел,
как положительных, так и отрицательных.
Примеры записи некоторых чисел во всех
трех восьмиразрядных кодах показаны в
таблице ниже.
|
Число |
Прямой |
Обратный |
Дополнительный |
|
0 |
00000000 |
00000000 |
00000000 |
|
1 |
00000001 |
00000001 |
00000001 |
|
-1 |
10000001 |
11111110 |
11111111 |
|
5 |
00000101 |
00000101 |
00000101 |
|
-5 |
10000101 |
11111010 |
11111011 |
|
8 |
00001000 |
00001000 |
00001000 |
|
-8 |
10001000 |
11110111 |
11111000 |
|
120 |
01111000 |
01111000 |
01111000 |
|
-120 |
11111000 |
10000111 |
10001000 |
|
127 |
01111111 |
01111111 |
01111111 |
|
-127 |
11111111 |
10000000 |
10000001 |
Во
всех трех кодах старший разряд указывает
на знак числа и он равен единице, если
число отрицательное и нулю в противном
случае. Остальные разряды содержат
представление модуля числа. Различие
между кодами наблюдается именно в
способах представления модуля. Для
положительного числа модуль во всех
трех кодах представляется одинаково —
это просто естественная запись двоичного
числа.
Для отрицательных чисел, в обратном
коде это просто поразрядная инверсия
прямого кода, а в дополнительном — к
обратному коду, как к числу, просто
прибавляется единица.
Распространёнными
формами представления чисел со знаками
является их представление в прямом,
обратном и дополнительном коде.
Прямой
код числа образуется кодированием знака
числа нулём, если число положительно и
единицей, если число отрицательно (для
двоичной системы)
Для общего случая
(q — 1) — если число отрицательно, и 0 — если
число положительно. q — основание системы
счисления.
Код знака записывается
перед старшей цифрой числа и отделяется
от неё точкой:
-1.01 = 1.101
Прямой, обратный
и дополнительный коды положительных
чисел совпадают между собой.
Обратный
код отрицательного числа образуется
из прямого кода, заменой его цифр на их
дополнения до величины q-1. Код знака
сохраняется без изменения.
Пример
:
+12310 =
0.123пр =
0.123об.
-12310 =
9.123пр =
9.876об
+3А7С0016 =
0.3А7С00пр =
0.3А7С00об.
-3А7С0016 =
F.3А7С00пр=
F.C583FFоб.
-1012 =
1.101пр =
1.010об.
Замена
цифр их дополнениями для двоичной
системы совпадает с операцией инверсии,
то есть нули заменяются единицами,
единицы — нулями. Знак принимает значение,
равное единице.
Дополнительный код
отрицательного числа образуется из
обратного увеличением на 1 его младшего
разряда. При этом перенос из знакового
разряда игнорируется.
Пример:
+23610 =
0.236пр.=
0.236об.=
0.236доп.
-23610 =
9.236пр.=
9.763об.=
9.764доп.
-1012=
1.101пр.=
1.010об=
1.011доп.
-3А7С16=
F.3А7Спр=
F.C583об.=
F.C584доп.
Правила
перевода из прямого кода в обратный и
из обратного в прямой, а также из прямого
в дополнительный и из дополнительного
в прямой совпадают между собой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Видеоурок:
Представление чисел в компьютере.
Представление целых чисел
Число в математике: 101111111010
— количество цифр в записи числа может быть сколь угодно большим;
— у любого целого числа есть следующее и предыдущее число.
Число в компьютере: 00110001
Количество цифр (разрядов) ограничено памятью, выделенной для его хранения.
Размер памяти определяет величину самого большого числа.

Беззнаковое представление можно использовать только для неотрицательных целых чисел.

Способ представления целых чисел обеспечивает:
— эффективное расходование памяти;
— повышение быстродействия;
— повышение точности вычислений за счёт введения операции деления нацело с остатком.
Представление числа в привычной для человека форме «знак – величина», при которой старший
разряд ячейки отводится под знак, а остальные разряды — под цифры числа, называется прямым кодом.

Работа с числами в прямом коде требует особых алгоритмов:
• для действия «вычитание»;
• для особой обработки знакового разряда.
В прямом коде можно хранить числа, но работа с ними требует более сложной архитектуры
центрального процессора.
Дополнительный код числа
Сумма отрицательного числа и его модуля равна 0.

Выделим под значение | x | один байт памяти компьютера.

Сколько надо прибавить, чтобы получить 0?
Произведем вычисления: 100000000 – 10011000.

Дополнительный n-разрядный код отрицательного числа равен 2n — | x |

Обратите внимание, что цифры в числах | x | и 2n — | x | инверсивны. Прибавим единицу.

Запишем алгоритм определения дополнительного n-разрядного кода отрицательного числа:
• Записать прямой n—разрядный код | x |
• Инвертировать 0 в 1
• Прибавить 1
Пример №1.
Определить восьмиразрядный дополнительный код числа -24.
Решение:
24=16+8=110002

Ответ: 11101000
Пример №2.
Дан восьмиразрядный код числа 10011000. Определить значение числа.
Решение:
В старшем разряде 1, значит число меньше 0.
Прямой алгоритм
• Инвертировать 0 в 1;
• Прибавить 1 к двоичному числу;
• Перевести в десятичную систему счисления.
Число 10011000 инвертируем, получим 01100111,
прибавим 1, получим 1101000, переведем в десятичную систему счисления = 104
Обратный алгоритм
• Вычесть 1 из двоичного числа;
• Инвертировать 0 в 1;
• Перевести
в десятичную систему счисления.
10011000 – 1 = 10010111, инвертируем = 1101000,
переводим в десятичную систему счисления = 104
Ответ: 104
Представление вещественных чисел
Экспоненциальная форма вещественного числа

Нормализованная запись вещественного числа – это запись в виде:

где p – целое число, g – система счисления, m – дробь, целая часть которой содержит одну значащую цифру,

Информатика. 10 класса. Босова Л.Л. Оглавление
§13. Представление чисел в компьютере
Самым первым видом данных, с которыми начали работать компьютеры, были числа. ЭВМ первого поколения могли производить только математические расчёты (вычисления).
Из курса информатики основной школы вы помните, что компьютеры работают с целыми и вещественными числами. Их представление в памяти осуществляется разными способами.
13.1. Представление целых чисел
Во многих задачах, решаемых на компьютере, обрабатываются целочисленные данные. Прежде всего, это задачи экономического характера, при решении которых данными служат количества акций, сотрудников, деталей, транспортных средств и др. Целые числа используются для обозначения даты и времени, для нумерации различных объектов: элементов массивов, записей в базах данных, машинных адресов и т. д. По своей природе множество целых чисел дискретно, т. к. состоит из отдельных элементов.
И хотя любое целое число можно рассматривать как вещественное, но с нулевой дробной частью, предусмотрены специальные способы представления целых чисел. Это обеспечивает: эффективное расходование памяти, повышение быстродействия, повышение точности вычислений за счёт введения операции деления нацело с остатком.
Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда.
Беззнаковое представление можно использовать только для неотрицательных целых чисел.
Для получения компьютерного представления беззнакового целого числа в n-разрядной ячейке памяти достаточно перевести его в двоичную систему счисления и, при необходимости, дополнить полученный результат слева нулями до n-разрядов.
Например, десятичные числа 130 и 39 в восьмиразрядном представлении будут иметь вид:
Понятно, что существуют ограничения на числа, которые могут быть записаны в n-разрядную ячейку памяти. Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2n-1. Минимальное число соответствует n нулям, хранящимся в n разрядах памяти, и равно нулю. Далее приведены диапазоны значений для беззнаковых целых n-разрядных чисел:

При знаковом представлении целых чисел старший разряд ячейки отводится под знак (0 — для положительных, 1 — для отрицательных чисел), а остальные разряды — под цифры числа.
Представление числа в привычной для человека форме «знак-величина», при которой старший разряд ячейки отводится под знак, а остальные разряды — под цифры числа, называется прямым кодом.
Например, прямые коды чисел 48 и -52 для восьмиразрядной ячейки равны:
Минимальное отрицательное число, которое можно записать в знаковом представлении в n разрядах, равно 2n-1. Максимальное положительное число, которое можно записать в знаковом представлении в n разрядах, равно 2n-1 — 1. Ниже приведены диапазоны значений для знаковых представлений целых чисел в ячейках с различной разрядностью:

В математике множество целых чисел бесконечно.
Компьютер работает с ограниченным множеством целых чисел.
Прямой код положительного числа отличается от прямого кода равного по абсолютной величине отрицательного числа только содержимым знакового разряда.
В прямом коде числа можно хранить, но выполнение арифметических операций над числами в прямом коде затруднено — оно требует более сложной архитектуры центрального процессора, «умеющего» выполнять не только сложение, но и вычитание, а также «знающего» особый алгоритм обработки не имеющего «веса» знакового разряда. Этих трудностей позволяет избежать использование дополнительного кода.
Чтобы понять сущность дополнительного кода, рассмотрим работу реверсивного счётчика, последовательность показаний которого можно представить в виде замкнутого кольца из чисел (рис. 3.5).

Рис. 3.5. Реверсивный счётчик
При возрастании показаний счётчика до максимального, например до 999, следующими его состояниями должны быть 1000, 1001, 1002 и т. д. Но для изображения старшей единицы в счётчике не хватает разряда, происходит переполнение разрядной сетки. Поэтому мы увидим 000, 001, 002 и т. д.
При убывании показаний счётчика после состояния 000 будут идти 999, 998, 997 и т. д. Но после достижения нуля последовательное вычитание единицы должно давать -1, -2, -3 и т. д.
Будем рассматривать числа 999, 998, 997 как коды чисел -1, -2, -3 и проверим на их примере соотношение: у + (-у) = 0:
1 + 999 = 1000;
2 + 998 = 1000;
3 + 997 = 1000.
С учётом того что единица переполнения теряется, мы, сложив число и код противоположного ему числа, получаем ноль!
Вот ещё несколько примеров:
5-2 = 5 + [-2] = 5 + 998 = 1003;
7-5 = 7 + [-5] = 7 + 995 = 1002.
Для устранения неоднозначности в кольце будем считать половину состояний (0-499) кодами нуля и положительных чисел, а оставшуюся половину (500-999) — кодами отрицательных чисел.
Таким образом, дополнительный код положительного числа совпадает с этим числом, а для отрицательного числа он равен дополнению его величины до числа qn, возникающего при переполнении разрядной сетки. Здесь q — основание системы счисления, n — число разрядов в разрядной сетке.
Рассмотрим алгоритм получения дополнительного n-разрядного кода отрицательного числа:
1) модуль числа представить прямым кодом в n двоичных разрядах;
2) значения всех разрядов инвертировать (все нули заменить единицами, а единицы — нулями);
3) к полученному представлению, рассматриваемому как n-разрядное неотрицательное двоичное число, прибавить единицу.
Пример 1. Найдём 16-разрядный дополнительный код отрицательного числа -201710.

Использование дополнительного кода позволяет свести операцию вычитания чисел к операции поразрядного сложения кодов этих чисел.
Пример 2. Как известно, 48 — 2017 = -1969.
Выполним эту операцию в 16-разрядных машинных кодах.
Нам потребуются прямой код числа 48 и дополнительный код числа -2017.

Рассмотрим полученный результат. Это отрицательное число (об этом говорит 1 в знаковом разряде), представленное в дополнительном коде. Перейдём к прямому коду модуля соответствующего числа, по которому сможем восстановить десятичное представление результата.
Прямой код можно получить из дополнительного кода, если применить к нему операцию инвертирования и прибавить единицу.

Получаем: -111101100012 = -1969.
13.2. Представление вещественных чисел
В математике множество вещественных чисел непрерывно, бесконечно и не ограничено.
Попробуйте обосновать это утверждение.
Вещественные числа записываются в естественной или в экспоненциальной форме.
В жизни мы чаще пользуемся естественной формой записи чисел, при которой: число представляется последовательностью десятичных цифр со знаком плюс или минус, знак плюс может опускаться, для разделения целой и дробной частей числа используется запятая.
Например: 12,34; 0,0056; -708,9.
В экспоненциальной форме вещественное число а представляется как а = ± m • qp, где m — мантисса числа, q — основание системы счисления, р — порядок числа.
Например, длину некоторого отрезка, равного 47,8 см, можно записать так:
1) 478 • 10-1 см;
2) 47,8 • 100 см;
3) 4,78 • 101 см;
4) 0,478 • 102 см;
5) 0,000478 • 105 см.
Такое многообразие вариантов записи в экспоненциальной форме одного и того же числа не всегда удобно. Для однозначного представления вещественных чисел в компьютере используется нормализованная форма.
Нормализованная запись отличного от нуля вещественного числа1) — это запись вида а = ± m • qp, где р — целое число (положительное, отрицательное или ноль), m — дробь, целая часть которой содержит одну значащую (ненулевую) цифру, т. е. 1 ? m < q.
1) Стандарт IEEE 754.
Примеры нормализации чисел:
1) 31,415926 = 3,1415926 • 101;
2) 1000 = 1,0 • 103;
3) 0,123456789 = 1,23456789 • 10-1;
4) 0,00001078 = 1,078 • 108-5;
5) 1000,00012 = 1,00000012 • 10211;
6) AB,CDEF16 = A,BCDEF16 • 10161.
Диапазон вещественных чисел в памяти компьютера очень широк, но, тем не менее, ограничен. Множество вещественных чисел, которые могут быть представлены в компьютере, конечно.

Поясним это на примере калькулятора, который производит вычисления в десятичной системе счисления. Пусть это будет калькулятор с десятью знакоместами на дисплее:
- 6 знакомест отводится под мантиссу (одно знакоместо отводится под знак мантиссы, четыре — под цифры мантиссы, одно — под точку, разделяющую целую и дробную части мантиссы);
- одно знакоместо отводится под символ «Е»;
- три знакоместа отводятся под порядок (одно — под знак порядка, два — под цифры порядка).
У калькуляторов первая значащая цифра, с которой и начинается мантисса, изображается перед точкой.
Число 12,34 в таком калькуляторе будет представлено как +1.234Е+01.
Число 12,35 будет представлено как + 1.235Е+01.
Как известно, между числами 12,34 и 12,35 находится бесконечное множество вещественных чисел, например: 12,341; 12,3412; 12,34123 и т. д.
Каждое из этих чисел в нашем калькуляторе будет представлено как + 1.234Е+01. Для последних разрядов у нас просто не хватает знакомест! Аналогичная ситуация имеет место и в компьютерном представлении вещественных чисел, независимо от того, ячейки какой разрядности там использованы.
Получается, что точно мы можем представить в компьютере лишь некоторую конечную часть множества вещественных чисел, а остальные числа — лишь приближённо.
Таким образом, множество вещественных чисел, представляемых в компьютере, дискретно, конечно и ограничено.
САМОЕ ГЛАВНОЕ
В математике множество целых чисел дискретно, бесконечно и не ограничено.
Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда. В любом случае компьютерное представление целых чисел дискретно, конечно и ограничено.
В математике множество вещественных чисел непрерывно, бесконечно и не ограничено.
Для компьютерного представления вещественных чисел используется нормализованная запись вещественного числа а = ± m • qp, где q — основание системы счисления, р — целое число (положительное, отрицательное или ноль), m — дробь, целая часть которой содержит одну значащую (ненулевую) цифру, т. е. 1 ? m < q.
Компьютерное представление вещественных чисел дискретно, конечно и ограничено.
Вопросы и задания
1. Представьте в восьмиразрядном формате прямые коды десятичных чисел: 1) 64; 2) 58; 3) 72; 4) -96.
2. Можно ли числа 4316, 1010102, 12910 и -5210 сохранить в однобайтовом формате?
3. Как определяется диапазон представления в компьютере целых чисел без знака? Со знаком?
4. Почему множество целых чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?
5. Представьте в восьмиразрядном формате дополнительные коды двоичных чисел: 1) +1010; 2) -1001; 3) -11; 4) -11011.
6. Найдите десятичные эквиваленты чисел, представленных в прямом коде: 1) 00000100; 2) 00001001; 3) 10000011; 4) 10000110.
*7. Найдите десятичные эквиваленты чисел, представленных в дополнительном коде: 1) 00000100; 2) 11111001.
8. Для хранения целого числа со знаком в компьютере используется два байта. Сколько единиц содержит внутреннее представление числа -101, записанного
9. Вычислите с помощью калькулятора (приложение Windows) в режиме «Программист» следующие примеры: 1) 1110111012 — 11011101102; 2) 11011010012 — 110001001002.
10. Запишите десятичные числа в нормализованной форме: 1) 217,934; 2) 75321; 3) 10,0101; 4) 200450.
11. Сравните следующие числа: 1) 318,4785 • 109 и 3,184785 • 1011; 2) 218,4785 • 10-3 и 1847,85 • 10-4.
12. Выполните операцию сложения: 1) 0,397621 • 103 + 0,2379 • 101; 2) 0,251452 • 10-3 + 0,125111 • 10-2.
13. Чем ограничивается диапазон представимых в памяти компьютера вещественных чисел?
14. Почему множество вещественных чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?
*15. Попытайтесь самостоятельно сформулировать основные принципы представления данных в компьютере.
§ 12. Арифметические операции в позиционных системах счисления
§ 13. Представление чисел в компьютере
§ 14. Кодирование текстовой информации
Представление положительных и отрицательных чисел в памяти компьютера. Прямой и дополнительный код числа
Прямой код
Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.
Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:
0 0001101 – положительное число
1 0001101 – отрицательное число
Количество значений, которые можно поместить в семиразрядной ячейке со знаком в дополнительном разряде равно 256. Это совпадает с количеством значений, которые можно поместить в восьмиразрядную ячейку без указания знака. Однако диапазон значений уже другой, ему принадлежат значения от -128 до 127 включительно (при переводе в десятичную систему счисления).
При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.
Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.
Дополнительный код
В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.
Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.
Далее следует прибавить единицу к получившемуся инверсией числу:
1 1110011 + 1 = 1 1110100
В итоге и получается число, которое принято называть дополнительным кодом числа.
Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.
Операция сложения положительного числа и отрицательного числа, представленного в прямом коде
- Прямой код числа 5: 0 000 0101
Прямой код числа -7: 1 000 0111 - Два исходных числа сравниваются. В разряд знака результата записывается знак большего исходного числа.
- Если числа имеют разные знаки, то вместо операции сложения используется операция вычитания из большего по модулю значения меньшего. При этом первый (знаковый) разряд в операции не участвует.
_ 000 0111 000 0101 ------------- 000 0010 - После выполнения операции учитывается первый разряд. Результат операции 1 000 0010, или -210.
Операция сложения положительного числа и отрицательного числа, представленного в дополнительном коде
- Прямой код числа 5: 0 000 0101
Прямой код числа -7: 1 000 0111 - Формирование дополнительного кода числа -7.
Прямой код : 1 000 0111
Инверсия : 1 111 1000
Добавление единицы: 1 111 1001 - Операция сложения.
0 000 0101 + 1 111 1001 -------------- 1 111 1110 - Проверка результата путем преобразования к прямому коду.
Дополнительный код: 1 111 1110
Вычитание единицы : 1 111 1101
Инверсия : 1 000 0010 (или -210)
Все операции над числами в памяти компьютера выполняются не над самими числами, а над их машинными кодами.
Рассмотрим получение машинного кода целого положительного числа.
Предположим, что мы имеем дело с шестнадцатиразрядной сеткой. Вычислим диапазон целых чисел, которые можно представить.
Amin=0
для целого положительного числа, а
Amax
вычислим по формуле:
Amax = 216 – 1;Amax = 65535.
Пример (1)
Запиши машинный код целого положительного числа (547) в шестнадцатиразрядной сетке.
1. Переведём число в двоичную систему счисления:
2. Дополним недостающие разряды незначащими нулями для заполнения сетки:
3. Машинный код числа принято представлять в шестнадцатеричной системе счисления, так людям его удобнее воспринимать:
KA =0223
.
Такой код принято называть прямым кодом числа и обозначать
[KA]ПК
.
Рассмотрим получение машинного кода целого отрицательного числа.
Предположим, что мы имеем дело с шестнадцатиразрядной сеткой. Один из разрядов сетки, а именно самый старший разряд, будет отведён под хранение знака. Таким образом, для хранения самого числа у нас остаётся (15) разрядов. Вычислим диапазон целых чисел, которые можно представить.
Amin=−215=−32768
для целого положительного числа, а
Amax
вычислим по формуле:
Amax = 215 – 1;Amax = 32767.
Обрати внимание: если мы сложим
Amin
и
Amax
, то получим (65535). То есть диапазон представляемых чисел не изменился.
Целые отрицательные числа хранятся в памяти в виде машинного кода дополнения к модулю исходного числа. Делается это для того, чтобы заменить операцию вычитания операцией сложения.
Для получения дополнительного кода используется следующий алгоритм:
1. получить двоичное представление модуля отрицательного числа.
2. Инвертировать все разряды полученного двоичного числа.
3. Прибавить к инвертированному числу (1).
Пример (2)
Получи дополнительный код числа (B = -125) в восьмиразрядной сетке.
1. Получим двоичное представление модуля отрицательного числа:
2. Инвертируем все разряды полученного двоичного числа ((0) заменим (1), а (1) — (0)).
3.
[KB]ОК=100000102
— это представление числа называется обратным кодом числа.
4. Прибавим к инвертированному числу (1).
— это и есть дополнительный код числа (B).
Ответ:
[KB]ДК=100000112=8216.
Обрати внимание!
Если сложить прямой и обратный коды отрицательного числа, мы получим (2k), где (k) равно количеству разрядов. А в самой (k)-разрядной сетке это число будет равно (0).
Пример (3)
Докажи верность высказывания: дополнительный код отрицательного числа — это дополнение модуля этого числа до (2k), где (k) равно количеству разрядов, или до (0) в (k)-разрядной арифметике.
Для доказательства воспользуемся числами, представленными в восьмиразрядной сетке.
1. Получим дополнительный код числа (C = -56).
Получим двоичное представление модуля отрицательного числа:
2. Инвертируем все разряды полученного двоичного числа ((0) заменим (1), а (1) — (0)).
3.
[KC]ОК=110001112
— это представление числа называется обратным кодом числа.
4. Прибавим к инвертированному числу (1).
— это дополнительный код числа (C).
5. Сложим прямой и дополнительный коды числа (C).
|
(0) |
(0) |
(1) |
(1) |
(1) |
(0) |
(0) |
(0) |
|
|
(+) |
(1) |
(1) |
(0) |
(0) |
(1) |
(0) |
(0) |
(0) |
|
(1) |
(0) |
(0) |
(0) |
(0) |
(0) |
(0) |
(0) |
(0) |
Если пользоваться восьмиразрядной сеткой, мы получили значение, равное (0); единица, вышедшая за разрядную сетку, называется «переполнением». Переведя полученное число в десятичную систему счисления, мы убедимся, что получили
28
. Что и требовалось доказать.
Обрати внимание!
Таким образом, мы можем получать дополнительный код вычитанием из переполненной разрядной сетки модуля заданного отрицательного числа.
Пример (4)
Получи дополнительный код числа (B = -125) в восьмиразрядной сетке.
1. Получим дополнение заданного числа до полной разрядной сетки:
2. Запишем полученное число в восьмиразрядной сетке, указав в старшем бите его знак:
Пример (5)
Запиши машинный код целого отрицательного числа (547) в шестнадцатиразрядной сетке.
1. Переведём число в двоичную систему счисления:
2. Дополним недостающие разряды незначащими нулями для заполнения сетки:
.
3. Инвертируем все разряды полученного двоичного числа ((0) заменим (1), а (1) — (0)):
.
4. Прибавим к инвертированному числу (1).
— это дополнительный код числа (A).
5. Машинный код числа принято представлять в шестнадцатеричной системе счисления, так людям удобнее его воспринимать:
[KA]ДК=FDDD
.
Обрати внимание!
Выводы:
• для положительного целого числа дополнительный код совпадает с прямым кодом числа.
• Для отрицательного целого числа дополнительный код является дополнением модуля этого числа до (2k), где (k) равно количеству разрядов.
• Сложение дополнительного кода отрицательного числа с модулем этого числа в (k)-разрядной арифметике даёт значение, равное нулю.