Как найти внутреннюю энергию при ударе

При неупругом ударе выделяется количество теплоты, равное

Q = W₀ – W.

Найдем энергии W₀ и W. За нулевую высоту примем высоту поверхности, по которой двигается брусок.
По условию массы тел равны (два одинаковых тела) и равны начальные скорости υ₁ = υ₂.

Полная механическая энергия тел в начальном состоянии
[ W_{0} =frac{mcdot upsilon _{1}^{2} }{2} +frac{mcdot upsilon _{2}^{2} }{2} =mcdot upsilon _{1}^{2}. ]
Полная механическая энергия тел в конечном состоянии
[ W=frac{2mcdot upsilon ^{2} }{2} =mcdot upsilon ^{2}, ;;; (1) ]
где υ — скорость тел после столкновения.

Так как удар неупругий, то выполняется закон сохранения импульса. Воспользуемся им для нахождения скорости υ тел после столкновения (рис. 1):
[ mcdot vec{upsilon }_1 +mcdot vec{upsilon }_2 =2mcdot vec{upsilon }, ]

0Х: m⋅υ₁ = 2m⋅υ_х,     0Y: m⋅υ₂ = 2m⋅υ_y.

Тогда
[ upsilon^{2} =upsilon _{x}^{2} +upsilon _{y}^{2} =left(frac{upsilon _{1} }{2} right)^{2} +left(frac{upsilon _{2} }{2} right)^{2} =frac{upsilon _{1}^{2} }{2}. ]
После подстановки в уравнение (1) получаем
[ W=frac{mcdot upsilon _{1}^{2} }{2}. ]
Количество теплоты, которое выделится при неупругом ударе шаров, будет равно
[ Q=mcdot upsilon _{1}^{2} -frac{mcdot upsilon _{1}^{2} }{2} =frac{mcdot upsilon _{1}^{2} }{2}. ]
Часть кинетической энергии, которая переходит во внутреннюю энергию, равна
[ frac{Q}{W_{0} } cdot 100% =frac{mcdot upsilon _{1}^{2} }{2mcdot upsilon _{1}^{2} } cdot 100% =50%. ]

Таким образом,
полная механическая энергия системы
тел, на которые действуют лишь
консервативные силы, остается постоянной
(закон сохранения механической энергии).

Для замкнутой
системы, т.е. системы, на тела которой
не действуют никакие внешние силы
,
т.е. полная механическая энергия замкнутой
системы тел, между которыми действуют
только консервативные силы, остается
постоянной.

Если в замкнутой
системе, кроме консервативных сил,
действуют также неконсервативные силы
(силы трения), то полная механическая
энергия системы не сохраняется:

.

Проинтегрировав
это выражение, получим, что работа
неконсервативных сил равна изменению
полной механической энергии системы:

.

Силы трения,
как правило, совершают отрицательную
работу. Поэтому наличие сил трения в
замкнутой системе приводит к уменьшению
ее полной механической энергии со
временем. Действие сил трения приводит
к превращению механической энергии в
другие, немеханические виды энергии.
Всякий раз, когда «исчезает» энергия
одного вида появляется эквивалентное
количество энергии другого вида. Энергия
никогда не исчезает и не появляется
снова, она лишь превращается из одного
вида в другой. В этом и заключается закон
сохранения энергии в его общем физическом
смысле.

При соударении
тел друг с другом они претерпевают
деформации. При этом кинетическая
энергия, которой обладали тела перед
ударом, частично или полностью переходит
в потенциальную энергию упругой
деформации или в так называемую внутреннюю
энергию тел. Увеличение внутренней
энергии тел сопровождается повышением
температуры. Существуют два предельных
вида удара: абсолютно упругий и абсолютно
неупругий. Абсолютно упругим ударом
называется такой удар, при котором
механическая энергия тел не переходит
в другие немеханические виды энергии.
При таком ударе кинетическая энергия
переходит полностью или частично в
потенциальную энергию упругой деформации.
Затем тела возвращаются к первоначальной
форме, отталкивая друг друга. Потенциальная
энергия упругой деформации снова
переходит в кинетическую энергию, и
тела разлетаются со скоростями, величина
и направление которых определяются
сохранением полной энергии и сохранением
полного импульса системы.

Абсолютно
неупругий удар характеризуется тем,
что потенциальная энергия деформации
не возникает, кинетическая энергия тел
полностью или частично превращается
во внутреннюю энергию. После удара
столкнувшиеся тела либо движутся с
одинаковой скоростью, либо покоятся.

При абсолютно
неупругом ударе выполняется лишь закон
сохранения импульса. Закон сохранения
механической энергии не соблюдается –
имеет место закон сохранения суммарной
энергии различных видов – механической
и внутренней.

Рассмотрим
абсолютно неупругий удар двух частиц,
образующих замкнутую систему, движущихся
вдоль оси x(рис.3.5)

Пусть m₁иm₂— массы частиц,и— скорости частиц до удара,— скорость частиц после удара.

x

m₁
m₂

а)

x

m₁
m₂

б)

Рис.3.5

Запишем закон
сохранения импульса:

;

.
(3.28)

Модуль скорости
частиц после удара для рис. 3.5,аравен

,

для рис. 3.5,б

.

Выясним, как
изменится полная энергия шаров при
абсолютно неупругом ударе. Кинетическая
энергия до удара:

,

после удара:

.

Подставим в это
выражение общую скорость движения
частиц (3.28) для случая, изображенного
на рис. 3.5,б

.

Найдем изменение
кинетической энергии:

;

.
(3.29)

Уменьшение
кинетической энергии при неупругом
ударе означает, что механическая энергия
системы при этом ударе не остается
постоянной, она частично или полностью
превращается в тепловую энергию
движущихся молекул.

Рассмотрим абсолютно
упругий центральный удар двух однородных
шаров (рис.3.6). Удар называется центральным,
если шары до удара движутся вдоль прямой,
проходящей через их центр. Предполагается,
что шары образуют замкнутую систему
тел, что внешние силы, приложенные к
шарам, уравновешивают друг друга. Кроме
того, вращение шаров отсутствует.

x

m₁
m₂

Рис.3.6

Обозначим
m₁
и m₂
— массы шаров,
и
— скорости шаров до удара,
и
— скорости шаров после удара. Положим,
что скорости шаров как до удара, так и
после удара направлены вдоль положительного
направления оси x.

Запишем уравнение
закона сохранения импульса и энергии:

;
(3.30)

. (3.31)

Спроектируем
уравнение закона сохранения импульса
(3.30) на ось x:

и
преобразуем его к виду

.
(3.32)

Из закона
сохранения энергии (3.31) следует:

.
(3.33)

Разделим уравнение
(3.33) на (3.32), получим

.
(3.34)

Для
нахождения скорости u₁
умножим (3.34) на m₂
и полученное соотношение сложим с
уравнением (3.32):

,

получим

,

откуда

. (3.35)

Для
определения скорости u₂
умножим (3.34) на m₁
и полученное соотношение вычтем из
уравнения (3.32):

,

получим

,

откуда

. (3.36)

При
m₁=m₂
из (3.35) и (3.36) следует, что u₁=₂,
а u₂=₁.

При изучении такой науки как физика, рассматриваются тепловые, механические, световые, электрические и многие другие сложные явления. С определенными механическими явлениями мы уже знакомы. Кроме этого, мы знаем, что в природе есть два вида механической энергии: кинетическая и потенциальная.

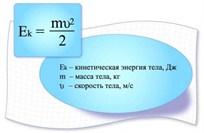
Любое тело, которое находится не в состоянии покоя, обладает кинетической энергией. К примеру, летящая птица, самолет, текущая вода – все эти тела наделены кинетической энергией. Кинетическая энергия тела напрямую зависит от его некоторых параметров – его массы и скорости передвижения.

Потенциальную энергию тела, возможно определить взаимным положением взаимодействующих тел либо его отдельных частей. К примеру, поднятый над землей камень, или пружина, находящаяся в растянутом либо сжатом состоянии наделены потенциальной энергией.

Потенциальная и Кинетическая энергия являются двумя видами механической энергии, они могут переходить друг в друга.

Каким образом происходит преобразование одного вида энергии в другой?

Рассмотрим небольшой пример. Шар из свинца, который покоится на свинцовой плите, поднимем вверх, на определенную высоту и отпустим вниз. При приближении шара к земле, его скорость увеличивается, а высота подъема сокращается. Таким образом, делаем вывод: кинетическая энергия шара увеличивается, в тоже время как его потенциальная энергия уменьшается. На этом примере мы видим, как потенциальная энергия нашего шара переходит в кинетическую энергию. После момента столкновения шара с плитой он остановится. А значит, его потенциальная и кинетическая энергия будут равны нулю. Может ли это обозначать что механическая энергия, которой обладает шар, исчезла в никуда? Очевидно, нет.

Механическая энергия преобразовалась в абсолютно другую форму энергии. В какую жу другую форму энергии она превратилась? Рассмотрим снова свинцовый шар и плиту, однако, уже после удара. Можно заметить, что шар приобрел немного сплюснутую форму, а на плите возникла небольшая впадина. Свинцовый шар и плита деформировались. Сразу после столкновения измерим температуру шара и плиты. Можно заметить, что они нагрелись.

Таким образом, мы видим, что после удара шара о плиту состояние двух тел изменилось – они нагрелись и деформировались. Однако, при изменении состояния тела, изменяется и энергия его частиц, то из чего состоит тело. В самом деле, мы знаем, что при увеличении температуры тела  средняя скорость передвижения молекул увеличивается. А значит, увеличивается и их кинетическая энергия. Но кроме этой энергии, молекулы обладают еще и потенциальной. Ведь они взаимодействуют друг с другом: сближаются, а при еще большем приближении – отталкиваются. При деформации тела, изменяется и двустороннее расположение его молекул, а значит, изменяется и его потенциальная энергия.

Мы пришли к тому, что при ударе кинетическая и потенциальная энергия свинца изменилась. Таким образом, механическая энергия, которой наделен шар изначально, не исчезла. Она была преобразована в энергию молекул.

Делаем вывод: Кинетическая энергия всех молекул, которые образуют тело, а также потенциальная энергия их взаимодействия образуют внутреннюю энергию тела.

При изучении тепловых явлений учитывается только энергия молекул, т.к. только она, главным образом, изменяется в этих явлениях.

Когда тело переходит в состояние покоя, механическое движение останавливается, однако, увеличивается хаотичное (тепловое) передвижение его молекул. Механическая энергия становится внутренней энергией тела.

Хотите узнать больше о внутренней энергии тела? Зарегистрируйтесь на нашем сайте и получите один бесплатный урок с нашим репетитором!

 Остались вопросы? Не знаете, как сделать домашнее задание?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

2017-10-05   

Горизонтально летящая пуля массы $m$ насквозь пробивает первоначально покоившийся шар массы $M$ и вылетает из него со скоростью, вдвое меньшей первоначальной. Какая доля кинетической энергии пули превратилась во внутреннюю энергию?

Решение:

Обозначим скорость пули до столкновения с шаром через $v$, а приобретаемую шаром скорость через $V$. По условию скорость пули на вылете из шара равна $v/2$, поэтому уравнение закона сохранения импульса в проекции на горизонтальное направление принимает вид

$mv = MV + mv/2$. (1)

Из этого уравнения сразу можно получить приобретаемую шаром скорость $V$:

$V = mv/2M$. (2)

Приращение внутренней энергии, т. е. выделяющееся при неупругом взаимодействии пули с шаром количество теплоты $Q$, можно найти с помощью закона сохранения энергии:

$frac{mv^{2}}{2} = frac{MV^{2}}{2} + frac{m(v/2)^{2}}{2} + Q$. (3)

Подставляя сюда $V$ из (2), находим

$Q = frac{mv^{2}}{8} left ( 3 — frac{m}{M} right )$. (4)

Так как начальная кинетическая энергия пули $E_{0} = mv^{2}/2$, то для искомого отношения $Q/E_{0}$ из (4) получаем

$frac{Q}{E_{0}} = frac{1}{4} left ( 3 — frac{m}{M} right )$. (5)

Но можно ли считать, что полученная формула дает ответ на поставленный вопрос? Она выражает искомую величину через приведенные в условии данные, но ставить точку рано, полученный результат нужно еще исследовать. Очевидно, что отношение $Q/E_{0}$ должно быть положительным, поэтому напрашивается вывод, что формула (5) применима при $m/M < 3$. Пусть, например, отношение $m/M = 2$. Тогда формула (5) дает для $Q/E_{0}$ значение 1/4. Казалось бы, все в порядке, поскольку $Q/E_{0}$ получилось положительным и меньшим единицы. И тем не менее этот результат не имеет смысла при приведенных в условии задачи данных. Действительно, посмотрим на формулу (2). Из нее следует, что при $m/M = 2$ скорость $V = v$: пробитый пулей насквозь шар летит со скоростью, вдвое превышающей скорость пули $v/2$! Получилась явная физическая бессмыслица. Уже в процессе решения после получения формулы (2) следовало бы обратить внимание на то, что, пробив шар насквозь, пуля может иметь скорость $v/2$ только при выполнении условия $v/2 > V$, т. е. при

$m/M < 1$. (6)

Только в совокупности с условием (6) формула (5) дает ответ на поставленный в данной задаче вопрос. Теперь ясно, что в зависимости от отношения масс $m/M$ во внутреннюю энергию может превратиться от половины (при $m rightarrow M$) до трех четвертей (при $m rightarrow 0$) первоначальной кинетической энергии.

Теперь подумаем о том, имеет ли какой-нибудь смысл формула (5) при $1 leq m/M leq 3$. Если $m = m$, то из формулы (2) следует, что $V = v/2$, т. е. шар и пуля имеют одинаковую скорость. Столкнувшиеся тела летят вместе, т. е. пуля застревает в шаре. В этом случае говорят об абсолютно неупругом ударе. Конечно, не следует думать, что абсолютно неупругий удар возможен только при $m=M$: здесь так получилось, потому что в условии задана конечная скорость, равная, $v/2$. Если же выполняется строгое неравенство $1 < m/M < 3$, то после столкновения шар летит впереди пули со скоростью $V$, определяемой формулой (2): $v/2 < V < 3v/2$. При таком неупругом ударе во внутреннюю энергию переходит до половины первоначальной кинетической энергии. Наконец, если $n/M=3$, то, как видно из (4), $Q = 0$, т. е. тепло вообще не выделяется: при ударе сохраняется механическая энергия. Это случай абсолютно упругого удара.