Преподаватель который помогает студентам и школьникам в учёбе.
Определение видимости в начертательной геометрии с примерами
Определение видимости:
Точки, расположенные на одной проецирующей прямой, называются конкурирующими.
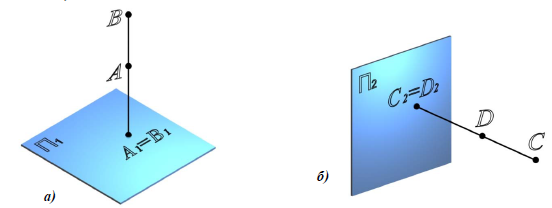
Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).
Рис. 7.1. Конкурирующие точки:
а — относительно горизонтальной плоскости проекций;
б — относительно фронтальной плоскости проекций
Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 7.1,б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C- видима, D — невидима).
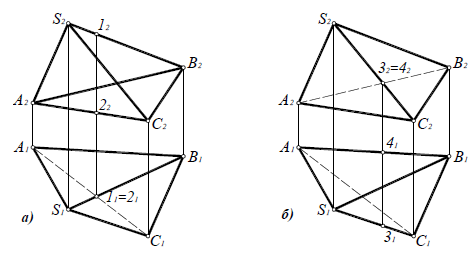
Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).
Рис. 6.17. Определение видимости ребер тетраэдра на комплексном чертеже:
а — относительно горизонтальной плоскости проекций;
б — относительно фронтальной плоскости проекций
Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П1, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П1, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П1.
- Заказать чертежи
Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П2.
- Конструктивное отображение пространства
- Чертежи точки, отрезка прямой
- Чертежи плоскости
- Взаимное положение двух плоскостей, прямой линии и плоскости
- Пересечение поверхностей вращения плоскостью
- Виды, разрезы, сечения
- Геометрические тела
- Комплексный чертеж
Определение видимостиОпределение видимости геометрических фигур на плоскости проекций выполняют с использованием конкурирующих точек.
Определение видимости рассмотрим на примерах: Определение видимости
Конкурирующие точки находим в пересечении проекций прямой с проекциями треугольника ABC — это точки 1 и 2 их проекции 1` и 2` на плоскость H совпадают. — имеется готовый эпюр пересечения прямой с плоскостью заданной следами Определение видимости
Конкурирующие точки находим в пересечении проекций прямой с проекциями плоскости α — для этого проводим в плоскости произвольную прямую f, чтобы имело место пересечение фронтальных проекций заданной прямой n и прямой f. + |

Рис. 2.6.
2.2.2. Пересекающиеся прямые.
Если прямые пересекаются, то точки пересечения одноименных проекций прямых лежат на одной лини связи (рис. 2.6, б).
{( m ∩ n) = К} → {(К′ К″ ) х}
2.2.3. Скрещивающиеся прямые.
Рис.2.7.
Прямые а и b не параллельны и не пересекаются. Следовательно, прямые а и b являются скрещивающимися прямыми (рис. 2.7).
Точки, у которых совпадает одна пара одноименных проекций (а другие проекции не совпадают),

называются конкурирующими точками.
Следствие: две точки, принадлежащие проецирующей прямой, являются конкурирующими точками.
Рис.2.8
Точка А выше чем точка В , поэтому на горизонтальной проекции точка А видима, точка В – невидима (рис. 2.8).
Точка С ближе к нам, чем точка D, поэтому на фронтальной проекции точка C — будет видима, точка D — невидима.
Понятием конкурирующих точек следует пользоваться при решении вопроса о том, какая из двух скрещивающихся прямых проходит выше другой или впереди другой в месте кажущегося пересечения.
Рассматривая скрещивающиеся прямые c и d (рис. 2.7), устанавливаем, что на фронтальной и горизонтальной проекции видна прямая d.
2.3. Определение натуральной величины отрезка прямой общего положения и углов его наклона к плоскостям проекций.
Настоящая задача является первой из группы метрических задач. Выделяя на рис. 2.9 треугольники ABA1 и АВВ1 видим, что в обоих случаях отрезок AВ является гипотенузой этих прямоугольных треугольников.
17

Рис.2.9.
Любой из этих треугольников мы можем построить на комплексном чертеже, т.к. имеются отрезки, конгруентные катетам этих треугольников (рис. 2.10).
Напомним, что две фигуры называются конгруентными, если одна из них может быть переведена в другую при помощи движения.
Для треугольника АВВ1:
[АВ1] = [А′ В′]; [ВB1] = [∆z] = [zB — zA];
Для треугольника ABA1:
[А1 В] = [А″ В″]; [AA1] = [∆y] = [yB — yA];
Приняв проекции отрезка за один из катетов и разность координат концов другой проекции отрезка за второй (рис. 2.10) строим конгруэнтные треугольники.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
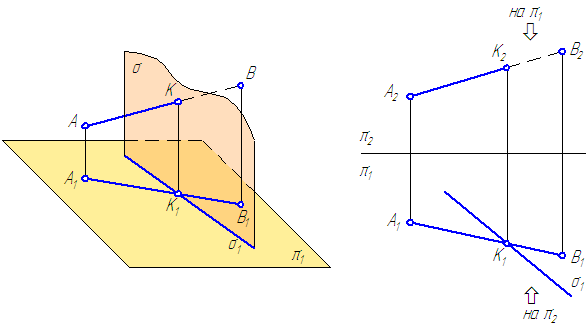
Определение видимости на чертеже.
В начертательной геометрии плоскости считаются непрозрачными, поэтому необходимо на проекциях определить видимость.
Для определения видимости на чертеже используем метод конкурирующих точек, сущность которого заключается в выборе двух скрещивающихся прямых.
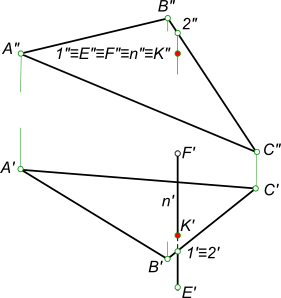
Для определения видимости на фронтальной плоскости проекций V поступают так. Выбираем две скрещивающиеся прямые В²С² и М²N², фронтальные проекции которых пересекаются в точках 1 и 3. По горизонтальной проекции определяем, что проекция точки 3¢, лежащая на проекции прямой M¢N¢, будет закрывать проекцию точки 1¢, лежащую на проекции прямой В¢С¢, т. к она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на фронтальной плоскости проекций проекция М²N² будет закрывать проекцию В²С². Границей видимости является проекция точки пересечения К².
Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые А¢С¢ и M¢N¢, горизонтальные проекции которых пересекаются в точках 4¢ и 5¢. По фронтальной проекции определяем, что проекция точки 5², лежащая на проекции прямой М²N², будет закрывать проекцию точки 4², лежащую на проекции прямой А²С², т. к. она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на горизонтальной плоскости проекций проекция M¢N¢ будет закрывать проекцию А¢С¢. Границей видимости является проекция точки пересечения К¢.
Задача 3. Построение линии пересечения двух плоскостей, одна из которых занимает частное положение.
Даны две плоскости: плоскость ∆АВС – плоскость общего положения, плоскость ∆DЕК – плоскость частного положения, которая расположена перпендикулярно фронтальной плоскости проекций (рис. 3).
Рис. 3. Построение линии пересечения двух плоскостей, одна из которых занимает
частное положение
Фронтальная проекция ∆DЕК совпадает с фронтальным следом плоскости и фронтальной проекцией линии пересечения треугольников.
(KL) ‑ линия пересечения двух треугольников. Проекции этой линии пересечения – фронтальную и горизонтальную строят исходя из свойства принадлежности точек K и L сторонам (АВ) и (ВС), соответственно. Видимость треугольников на горизонтальной плоскости проекций определяем методом конкурирующих точек, рассмотренном в задаче 2.
Задача 4. Построение линии пересечения двух плоскостей общего положения.
Даны две плоскости общего положения, заданные треугольниками АВС и DЕК. Построить линию пересечения двух треугольников, определить видимость треугольников на проекциях.
Прямая линия, получаемая при взаимном пересечении двух плоскостей, определяется двумя точками, каждая из которых одновременно принадлежит обеим плоскостям. Общие точки определяются решением основной позиционной задачи начертательной геометрии – построение точки пересечения прямой с плоскостью (см. рис. 2).
Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (проецирующие плоскости). Решение задачи приведено на рис. 4.
Алгоритм решения задачи:
1. Определяют первую точку линии пересечения двух треугольников – точку М.
1.1. Фронтально-проецирующая плоскость a проведена через сторону DК и задана на чертеже фронтальным следом aV.
1.2. Плоскость a пересекает плоскость треугольника АВС по прямой (1,2), на чертеже строят две проекции этой прямой.
1.3. Прямая (1,2) пересекает сторону DК в точке М, строят две проекции точки М² и М¢.
2. Определяют вторую точку искомой линии пересечения двух треугольников – точку N.
2.1. Горизонтально-проецирующая плоскость b проведена через сторону АВ и задана на чертеже горизонтальным следом bН.
2.2. Плоскость b пересекает плоскость треугольника DЕК по прямой (3,4), на чертеже строят две проекции этой прямой.
2.3. Прямая (3,4) пересекает АВ в точке N, строят две проекции точки N² и N¢.
Плоскости треугольников АВС и DЕК пересекаются по прямой MN.
Рис. 4. Построение линии пересечения двух треугольников
3. Видимость плоских фигур на проекциях определяют методом конкурирующих точек.
Для определения видимости на фронтальной плоскости проекций V выбираем две скрещивающиеся прямые D²K² и A²B², фронтальные проекции которых пересекаются в точках 1² и 5². По горизонтальной проекции определяем, что проекция точки 5¢, лежащая на проекции прямой D¢K¢, будет закрывать проекцию точки 1¢, лежащую на проекции прямой А¢В¢, т. к. она будет ближе к наблюдателю. Следовательно, на фронтальной плоскости проекция D²K² будет закрывать проекцию A²B². Границей видимости является проекция линии пересечения M²N².
Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые А¢В¢ и D¢Е¢, горизонтальные проекции которых пересекаются в точках 3¢ и 6¢. По фронтальной проекции определяем, что проекция точки 3², лежащая на проекции прямой D²Е², будет закрывать проекцию точки 6², лежащую на проекции прямой A²B², т.к. она будет ближе к наблюдателю. Следовательно, на горизонтальной плоскости проекция D¢Е¢ будет закрывать проекцию А¢В¢. Границей видимости является проекция линии пересечения N¢M¢.
Задача 5. Построить две проекции линии пересечения плоскости a ‑ общего положения, заданной следами и плоскости b ‑ общего положения, заданной параллельными прямыми а и b.
Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (плоскости уровня), пересекающие заданные плоскости по прямым, недостающие проекции которых легко строятся и пересекаются в пределах чертежа.
Графическое решение задачи приведено на рис. 5.
Рис. 5. Построение линии пересечения двух плоскостей
Вспомогательная горизонтальная плоскость-посредник γ задана следом γV и пересекает плоскость a по горизонтали, проходящей через точку 3, а плоскость b по горизонтали (1, 2). Горизонтальные проекции этих горизонталей пересекаются в точке К. Строят фронтальную проекцию точки К, используя свойство принадлежности точки прямой линии. Точка К принадлежит обеим плоскостям a и b. Вторая точка N, общая для двух плоскостей a и b, определяется второй вспомогательной плоскостью-посредником частного положения δ (на чертеже задана следом δV). Искомая прямая (КN) является линией пересечения двух плоскостей a и b.
ПРИЛОЖЕНИЕ 1
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Гордон В.О., Семенцов-Огиевский М. А. Курс начертательной геометрии. Учеб. пособие. М.: Высшая школа. 2007.272 с.
2. Самохвалов Ю. И. Начертательная геометрия. Учебное пособие. Екатеринбург: Изд-во УГГУ. 2011. 121 с.
3. Самохвалов Ю. И., Шангина Е. И. Начертательная геометрия. Инженерная графика. Учебно-методическое пособие. Екатеринбург: Изд-во УГГУ. 2011. 96 с.
Определение видимости в начертательной геометрии с примерами
Определение видимости:
Точки, расположенные на одной проецирующей прямой, называются конкурирующими.
Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).
Рис. 7.1. Конкурирующие точки:
а — относительно горизонтальной плоскости проекций;
б — относительно фронтальной плоскости проекций
Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 7.1,б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C- видима, D — невидима).
Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).
Рис. 6.17. Определение видимости ребер тетраэдра на комплексном чертеже:
а — относительно горизонтальной плоскости проекций;
б — относительно фронтальной плоскости проекций
Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П1, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П1, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П1.
Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П2.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Конструктивное отображение пространства
- Чертежи точки, отрезка прямой
- Чертежи плоскости
- Взаимное положение двух плоскостей, прямой линии и плоскости
- Пересечение поверхностей вращения плоскостью
- Виды, разрезы, сечения
- Геометрические тела
- Комплексный чертеж
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Построить линию пересечения треугольников. Определить видимость их на проекциях.
Пример решения задачи на рис. 2.
Чтобы построить линию пересечения двух плоскостей, нужно найти две общие для них точки. Такими точками являются точки пересечения сторон одного треугольника с плоскостью другого. Задача сводится, таким образом, к первой основной позиционной задаче — найти точку пересечения прямой с плоскостью. Эта задача решается с помощью вспомогательной плоскости — посредника по следующему алгоритму (рис. 3).
- Через заданную прямую l проводим вспомогательную проецирующую плоскость М: 1 l.
- Строим линию m пересечения вспомогательной и заданной плоскостей: m =.
- Находим искомую точку К пересечения прямой l с плоскостью как результат пересечения заданной прямой l с построенной линией пересечения m: К=l =lm.
Для нахождения точки пересечения стороны (BС) АBС с плоскостью DЕF заключаем (ВС) во фронтально проецирующую плоскость . Так как 2, то проецируется в П2 в виде прямой (вырожденная проекция 2), а так как проходит через прямую (ВС), то (В2С2)=2.
Строим линию пересечения и DEF. Она определяется двумя точками пересечения со сторонами DEF: 1=(DF), 2= (DE). Построив проекции этих точек сначала на П2 как результат пересечения 2 с (D2F2) и (D2E2), а затем на П1 по принадлежности 11(D1F1), 21(D1E1), соединяем их одноименные проекции и получаем проекции линии пересечения m=(DEF), при этом m2 =2.
Находим точку М пересечения стороны (BС) с плоскостью DEF как результат пересечения (BС)m, сначала на П1, а затем по принадлежности (ВС) на П2.
Аналогичным образом находим вторую точку искомой линии пересечения: N=(FE)IIABC
Соединив одноименные проекции точек М и N, получаем искомую линию пересечения АВС и DEF.
Видимость треугольников определяем методом конкурирующих точек. Для определения видимости на П2 берем пару фронтально конкурирующих точек (лежащих на одном перпендикуляре к П2), одна из которых принадлежит стороне АВС, а другая – стороне DEF. В качестве одной из точек возьмем уже построенную на чертеже точку 1(DF), а вторую точку — 5 на стороне (ВС). При этом 12=52. Строим горизонтальную проекцию точки 5 по принадлежности (ВС) и определяем, какая из точек ближе к наблюдателю при взгляде на П2. Очевидно, это точка 5. Следовательно, точка 5 видима, а точка 1 заслоняется точкой 5 и на П2 невидима. Т. е. сторона (DF) располагается за плоскостью ABC и ее участок (1,8) на П2 является невидимым. Видимость остальных сторон ABC и DEF на фронтальной проекции определяется, исходя из следующих положений: 1) если одна из скрещивающихся прямых, проекции которых пересекаются, видима, то другая — невидима и наоборот; 2) точка пересечения прямой с плоскостью является точкой изменения видимости прямой.
Аналогично с помощью горизонтально конкурирующих точек 6(DE) и 7(ВС) определяем видимость треугольников на П1.
http://www.evkova.org/-opredelenie-vidimosti
http://www.zaochnik.com.ua/nachertatelnaya_geometriya/postroit_liniyu_peresecheniya_treugolnikov_opredelit_vidimost_na_proektsiyah/
3.1. Способы задания плоскости на ортогональных чертежах
Положение плоскости в пространстве определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, взятой вне прямой;
- двумя пересекающимися прямыми;
- двумя параллельными прямыми;
- плоской фигурой.
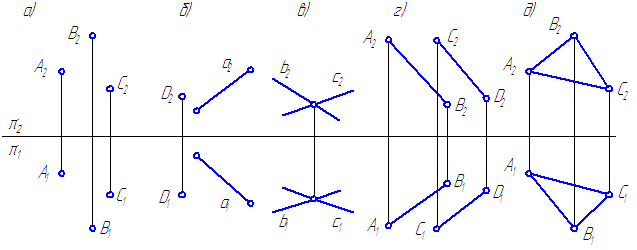
В соответствии с этим на эпюре плоскость может быть задана:
- проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
- проекциями точки и прямой (Рисунок 3.1,б);
- проекциями двух пересекающихся прямых (Рисунок 3.1,в);
- проекциями двух параллельных прямых (Рисунок 3.1,г);
- плоской фигурой (Рисунок 3.1,д);
- следами плоскости;
- линией наибольшего ската плоскости.
Рисунок 3.1 – Способы задания плоскостей
Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.
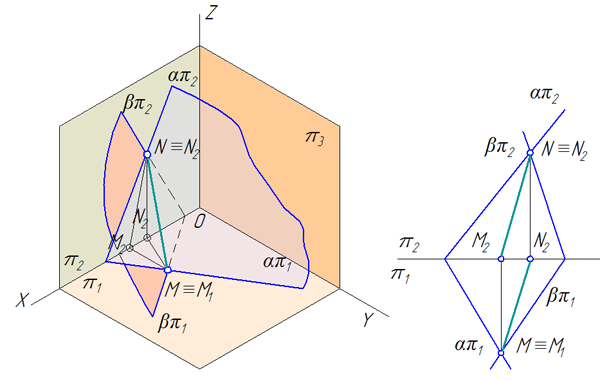
Плоскость общего положения может иметь три следа: горизонтальный – απ1, фронтальный – απ2 и профильный – απ3, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π1, фронтальной π2 и профильной π3 (Рисунок 3.2).
Рисунок 3.2 – Следы плоскости общего положения
3.2. Плоскости частного положения
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости: все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).
Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).
Рисунок 3.4 – Эпюры плоскостей частного положения
3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).
Рисунок 3.5 – Принадлежность точки плоскости
α = m // n D ∈ n ⇒ D ∈ α
Рисунок 3.6 – Принадлежность прямой плоскости
left.begin{array}{l}alpha=mparallel n,\Dinalpha\Cinalpha\end{array}right} Longrightarrow CDinalpha
Упражнение
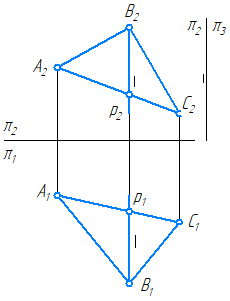
Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С.
Рисунок 3.7 – Решение задачи
Решение:
- ABCD – плоский четырехугольник, задающий плоскость.
- Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
- Согласно признаку пересекающихся прямых, построим фронтальную проекцию точки пересечения этих прямых — K: A2C2 ∩ B2D2=K2.
- Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD: на проекции диагонали B1D1 строим К1.
- Через А1К1 проводим проекцию диагонали А1С1.
- Точку С1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А1К1.
3.4. Главные линии плоскости
В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).
Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π1) (Рисунок 3.8, а; 3.9).
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π2) (Рисунок 3.8, б; 3.10).
Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π3) (Рисунок 3.8, в; 3.11).
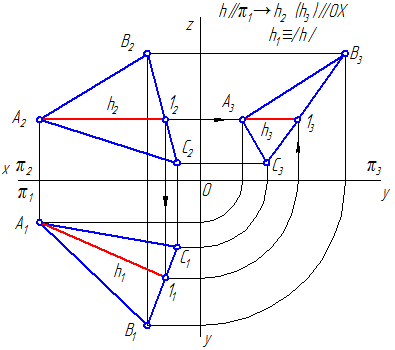
Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником
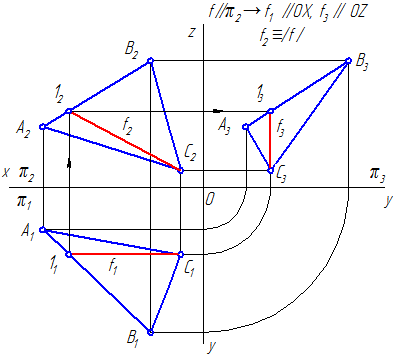
Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником
Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником
Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами
Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами
Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами
3.5. Взаимное положение прямой и плоскости
Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.
3.5.1. Параллельность прямой плоскости
Признак параллельности прямой плоскости: прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).
alpha=mcap n\left.begin{array}{l}a_2parallel m_2\a_1parallel m_1\end{array}right} Rightarrow aparallelalpha
Рисунок 3.12 – Параллельность прямой плоскости
3.5.2. Пересечение прямой с плоскостью
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:
- Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
- Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
- Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.
Рисунок 3.13 – Построение точки встречи прямой с плоскостью
Упражнение
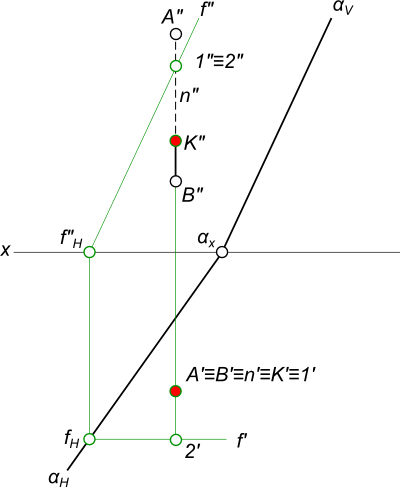
Заданы: прямая АВ общего положения, плоскость σ⊥π1. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.
Решение:
-
- Точка К должна принадлежать прямой АВ ⇒ К1∈А1В и заданной плоскости σ ⇒ К1∈σ, следовательно, К1 находится в точке пересечения проекций А1В1 и σ1;
- Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ1 (горизонтальный след плоскости);
- Фронтальную проекцию точки К находим посредством линии проекционной связи: К2∈А2В2.
Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения
Упражнение
Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).
Требуется построить точку пересечения прямой EF с плоскостью σ.
Рисунок 3.15 – Пересечение прямой с плоскостью
Решение:
- Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
- Если α⊥π1, то на плоскость проекций π1 плоскость α проецируется в прямую (горизонтальный след плоскости απ1 или α1), совпадающую с E1F1;
- Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено ниже);
- Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K.
Алгоритм решения задачи (Рисунок 3.15, б): Через EF проведем вспомогательную плоскость α:
- left.begin{array}{l}alpha perp pi_1\alphain EF\end{array}right} Longrightarrow alpha_1in E_1F_1
- alphacapsigma=(1-2)left.begin{array}{l}|alpha_1cap A_1C_1=1_1longrightarrow 1_2\|alpha_1cap A_1B_1=2_1longrightarrow 2_2\end{array}right.
- (1_2-2_2)cap E_2F_2=K_2\left.begin{array}{l}Kin EF\Kin (1-2)Rightarrow Kinsigma\end{array}right}Longrightarrow K=EFcap (sigma =triangle ABC)
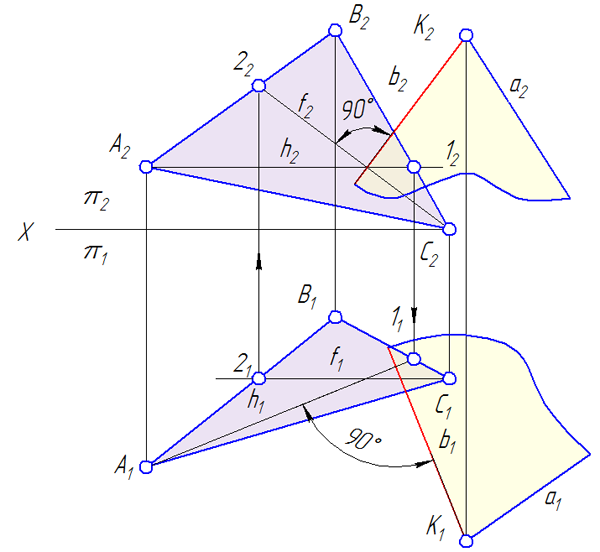
3.6. Определение видимости методом конкурирующих точек
При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π1 или π2.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π2 (рис. 3.15)
Выберем точки, конкурирующие на π2 – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π2.
Направление взгляда на π2 показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π2, видно, что точка 41 располагается ближе к наблюдателю, чем 31.
41∈E1F1 ⇒ 4∈EF ⇒ на π2 будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π1.
Для определения видимости выберем точки, конкурирующие на π1 – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π1.
Направление взгляда на π1 показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π1, видно, что точка 22 располагается ближе к наблюдателю, чем 52.
22∈А2В2 ⇒ 2∈АВ ⇒ на π1 будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.
3.7. Перпендикулярность прямой плоскости
Признак перпендикулярности прямой плоскости: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.
Рисунок 3.16 – Задание прямой, перпендикулярной плоскости
Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)
Теорема доказывается через теорему о проецировании прямого угла в частном случае.
Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).
Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.
- Построим горизонталь и фронталь в плоскости σ=ΔАВС : σ=ΔАВС : A-1∈σ; A-1//π1; С-2∈σ; С-2//π2.
- Восстановим из точки K перпендикуляр к заданной плоскости: p1⊥h1 и p2⊥f2, или p1⊥απ1 и p2⊥απ2.
3.8. Взаимное положение двух плоскостей
3.8.1. Параллельность плоскостей
Две плоскости могут быть параллельными и пересекающимися между собой.
Признак параллельности двух плоскостей: две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Упражнение
Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).
Через точку F провести плоскость β, параллельную плоскости α.
Рисунок 3.17 – Построение плоскости, параллельной заданной
Решение: В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.
- Через точку F проводим прямую m, параллельную, например, АВ.
- Через точку F, или же через любую точку, принадлежащую m, проводим прямую n, параллельную, например, ВС, причём m∩n=F.
- β = m∩n и β//α по определению.
3.8.2. Пересечение плоскостей
Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.
Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.
Упражнение
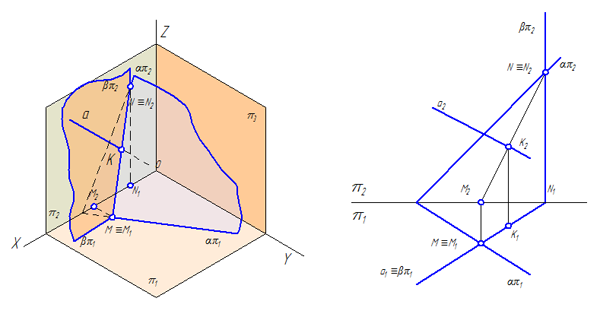
Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей.
Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами
Порядок построения линии пересечения плоскостей:
- Найти точку пересечения горизонтальных следов — это точка М (её проекции М1 и М2, при этом М1=М, т.к. М – точка частного положения, принадлежащая плоскости π1).
- Найти точку пересечения фронтальных следов — это точка N (её проекции N1 и N2, при этом N2=N, т.к. N – точка частного положения, принадлежащая плоскости π2).
- Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М1N1 и М2N2.
МN – линия пересечения плоскостей.
Упражнение
Задана плоскость σ = ΔАВС, плоскость α – горизонтально- проецирующая (α⊥π1) ⇒α1 – горизонтальный след плоскости (Рисунок 3.19). Построить линию пересечения этих плоскостей.
Решение:
Так как плоскость α пересекает стороны АВ и АС треугольника АВС, то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.
Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L, то есть K1 и L1 , на пересечении горизонтального следа (α1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС: А1В1 и A1C1. После чего посредством линий проекционной связи находим фронтальные проекции этих точек K2 и L2 на фронтальных проекциях прямых АВ и АС. Соединим одноимённые проекции: K1 и L1; K2 и L2. Линия пересечения заданных плоскостей построена.
Алгоритм решения задачи:
left.begin{array}{l}ABcapsigma=K\ACcapsigma=L\end{array}right} left.begin{array}{l}Rightarrow A_1B_1capsigma_1=K_1 rightarrow K_2\Rightarrow A_1C_1cap sigma_1=L_1 rightarrow L_2\end{array}right.
KL – линия пересечения ΔАВС и σ (α∩σ = KL).
Рисунок 3.19 – Пересечение плоскостей общего и частного положения
Упражнение
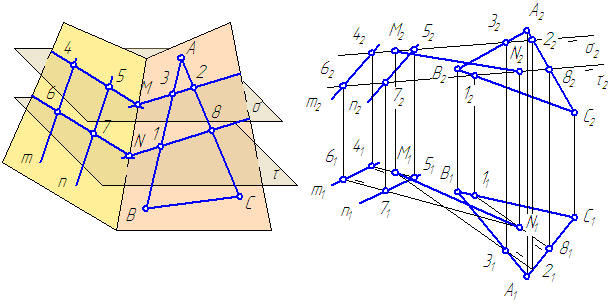
Заданы плоскости α = m//n и плоскость σ = ΔАВС (Рисунок 3.20). Построить линию пересечения заданных плоскостей. Решение:
- Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
- В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π2; τ⊥π2.
- Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:
— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7); — результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).
- Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях σ и β, то есть на прямой пересечения этих плоскостей;
- Аналогично находим точку N, общую для плоскостей σ и β.
- Соединив точки M и N, построим прямую пересечения плоскостей σ и β.
Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)
Алгоритм решения задачи:
left.begin{array}{l}alphacapsigma=(4-5)\betacapsigma=(3-2)\end{array}right}\left.begin{array}{l}alphacaptau=(6-7)\betacaptau=(1-8)\end{array}right}left.begin{array}{l}(4_1-5_1)cap(3_1-2_1)=M_1rightarrow M_2\(6_1-7_1)cap(1_1-8_1)=N_1rightarrow N_2\end{array}right}rightarrow\left.begin{array}{l}M_1N_1\M_2N_2\end{array}right}Rightarrowalphacapbeta=MN
Упражнение
Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).
Рисунок 3.21 Решение задачи на пересечение плоскостей
Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π2, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π2 (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.
3.8.3. Взаимно перпендикулярные плоскости
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Упражнение
Задана плоскость σ⊥π2 и прямая общего положения – DE (Рисунок 3.22)
Требуется построить через DE плоскость τ⊥σ.
Решение.
Проведём перпендикуляр CD к плоскости σ – C2D2⊥σ2 (на основании теоремы о проецировании прямого угла).
Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости
По теореме о проецировании прямого угла C1D1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.
Упражнение
Задана плоскость α = ΔАВС и точка K вне плоскости α. Требуется построить плоскость β⊥α, проходящую через точку K. Алгоритм решения (Рисунок 3.23):
- Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС;
- Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости: если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b2⊥f2; b1⊥h1;
- Задаём плоскость β любым способом, например, β = a∩b, таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.
Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС
3.9. Задачи для самостоятельного решения
1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.
Постройте фронтальную проекцию точки К.
Рисунок 3.24
2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).
Рисунок 3.25
3. Постройте проекции квадрата, принадлежащего плоскости α⊥π2, если его диагональ MN //π2 (Рисунок 3.26).
Рисунок 3.26
4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).
Рисунок 3.27
5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.
Рисунок 3.28
6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π1.
7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π1.