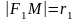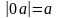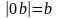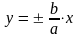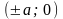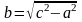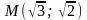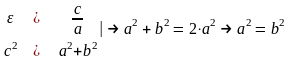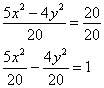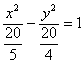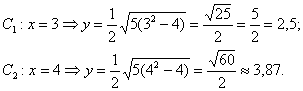Как найти вид уравнения гиперболы - AvtoShod.ru - решение различных проблем

Елена Борисовна Калюжная

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Каноническое уравнение гиперболы имеет следующий вид:
$frac{x^2}{a^2} — frac{y^2}{b^2} = 1$, где $a, b$ — положительные действительные числа.

Для того чтобы составить каноническое уравнение гиперболы, нужно привести квадратное уравнение к каноническому виду.

Вывод канонического уравнения гиперболы

уравнения гиперболы» />

Рисунок 1. Рис. 1.Вывод канонического уравнения гиперболы

Рассмотрим гиперболу с фокусами $F_1$ и $F_2$, находящимися на оси $OX$, причём точка $O$ лежит в центе между фокусами.

Следовательно координаты $F_1(-c; 0)$, а $F_2(c; 0)$, где $c$ — расстояние до фокуса гиперболы.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Рассмотрим произвольную точку $M$, принадлежащую гиперболе.

Отрезки $r_1 =|F_1M|$ и $r_2 =|F_2M|$ называются фокальными радиусами точки $M$ гиперболы.

Из определения гиперболы следует, что $|r_1 -r_2| =2a$, следовательно $r_1 – r_2=±2a$, причём $r_1 = sqrt{(x + c)^2 + y^2}$, а $r_2 = sqrt{(x — c)^2 + y^2}$.

Соответственно, уравнение $r_1 – r_2=±2a$ иначе можно записать как $sqrt{(x + c)^2 + y^2} — sqrt{(x — c)^2 + y^2} = ±2a$ (1).

Умножим выражение (1) на $frac{$sqrt{(x + c)^2 + y^2} + sqrt{(x — c)^2 + y^2}}{±2a}$, получается:, получается:

$frac{(x + c)^2 + y^2 — (x — c)^2 – y^2}{±2a} = sqrt{(x + c)^2 + y^2} + sqrt{(x — c)^2 + y^2}$

Упростим: $frac{2cx}{±a} = sqrt{(x + c)^2 + y^2} + sqrt{(x — c)^2 + y^2}$ (2)

Сложим уравнения (1) и (2), получим:

$±(frac{cx}{a}) + a = sqrt{(x + c)^2 + y^2}$ (3)

Возведём (3) в квадрат:

$frac{c^2 x^2}{a^2} + 2xc + a^2 = (x^2 +2x c + c^2 + y^2)$

$frac{c^2 – a^2}{a^2} cdot x^2 – y^2 = c^2 – a^2$

Пусть $b^2 = c^2 – a^2$, так как $c > 0$ и, следовательно $frac{b^2}{a^2}x^2 – y^2 = b^2$

«Каноническое уравнение гиперболы» 👇

Получаем уравнение:
$frac{x^2}{a^2} — frac{y^2}{b^2} = 1$ (4), являющееся каноническим уравнением гиперболы с центром в начале координат.

Каноническое уравнение параболы и гиперболы немного похожи между собой.

Уравнение параболы выглядит следующим образом:

$y^2 = px$, где число $p$ должно быть больше нуля; это число называется фокальным параметром.

Каноническое уравнение гиперболы примеры решения

Пример 1

Ниже небольшая инструкция о том, как найти каноническое уравнение гиперболы.

Приведём уравнение $5x^2 — 4y^2 = 20$ к каноническому виду гиперболического уравнения, для этого разделим всё уравнение на $20$:

$frac{5x^2}{4} — frac{y^2}{5} = 1$

Запишем знаменатели в виде степеней:

$frac{x^2}{2^2} — frac{y^2}{sqrt{5}^2} = 1$

Теперь вы знаете, как написать каноническое уравнение гиперболы. Дальше мы расскажем о том, как строить гиперболу по каноническому уравнению.

Построение гиперболы по каноническому уравнению

Теперь давайте рассмотрим, как построить гиперболу по каноническому уравнению.

Рисунок 2. Рис. 2. Построение гиперболы по каноническому уравнению

Для начала необходимо построить асимптоты для данной гиперболы, их формулы определяются из уравнения $y = ±frac{bcdot x}{a}$.
Для нашего канонического уравнения гиперболы они будут выглядеть так: $y = ±frac{sqrt{5}} {2}cdot x$
Теперь найдём вершины гиперболы, они расположены на оси абсисс в точках $(0; a)$ и $(0; -a)$, назовём их точками $A_1, A_2$.
Вершины нашей гиперболы находятся в точках $(2; 0)$ и $(-2; 0)$.

Далее необходимо найти две-три точки, принадлежащие любой из двух ветвей гиперболы, если гипербола без смещения – точки на второй ветви будут симметричны им относительно осей гиперболы.
Выразим $y$ из канонического уравнения нашей гиперболы:

$y = ±frac{1}{2} sqrt{5 x^2 — 4}$

Найдём точки для положительной части гиперболы:

при $x = 3, y =2.5$,
а при $x = 3, y ≈3,87$.

Теперь можно отложить все эти точки и построить график гиперболы.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.

Определение и функция гиперболы
Алгоритм построения гиперболы
- Пример 1
- Пример 2

Определение и функция гиперболы

Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:

Здесь:

x – независимая переменная;
k ≠ 0;
при k > 0 гипербола расположена в I и III четвертях координатной плоскости;
при k < 0 график находится во II и IV четвертях.

На рисунке ниже изображен пример гиперболы.

Линии графика (зеленым цветом) называются его ветвями.
Оси абсцисс и ординат (Ox и Oy) являются асимптотами гиперболы, т.е. ветви бесконечно к ним приближаются, но никогда их не коснутся и не пересекут.
Ось симметрии (синим цветом) – это прямая:
- y = x (при k > 0)
- y = -x (при k < 0)

Смещение асимптот

Допустим у нас есть функция, заданная формулой:

В этом случае:

x = a – это вертикальная асимптота графика (при a ≠ 0) вместо оси Oy;
y = b – горизонтальная асимптота (при b ≠ 0) вместо оси Ox.

Канонический вид уравнения гиперболы (координатные оси совпадают с осями графика):

Алгоритм построения гиперболы

Пример 1

Дана функция y = ⁴/_x. Построим ее график.

Решение

Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.

Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.


x	y	Расчет y
0,5	8	⁴ / _0,5 = 8
1	4	⁴ / ₁ = 4
2	2	⁴ / ₂ = 2
4	1	⁴ / ₄ = 1
8	0,5	⁴ / ₈ = 0,5

Теперь отмечаем найденные точки на координатной плоскости и соединяем их плавной линией, которая будет стремиться к осям координат. В итоге получится ветвь гиперболы, расположенная в первой четверти.

Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y.


x	y	Расчет y
-0,5	-8	⁴ / _-0,5 = -8
-1	-4	⁴ / _-1 = -4
-2	-2	⁴ / _-2 = -4
-4	-1	⁴ / _-4 = -1
-8	-0,5	⁴ / _-8 = -0,5

Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено.

Пример 2

Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже:

Решение

Так как k < 0, график будет располагаться во второй и четвертой четвертях.

Теперь определяемся с асимптотами, в нашем случае это x = 3 и y = 4 (см. информацию выше про их смещение).

Составим таблицу соответствия значений x и y.


x_{II четв.}	y_{II четв.}	x_{IV четв.}	y_{IV четв.}
-1	4,5	3,5	0
1	5	4	2
2	6	5	3
2,5	8	7	3.5

Остается только нанести рассчитанные точки на координатную плоскость и соединить их плавными линиями.

Источник

Гиперболой
называется геометрическое место точек,
для которых разность
расстояний от двух фиксированных точек
(называемых фокусами) есть величина
постоянная. Причем указанная разность
берется по абсолютному значению и
необходимо, что бы она была меньше
расстояния между фокусами и не равна
нулю. (См. Рис.23)

Рис.23

На
рисунке:

—

— левый фокальный радиус;

—

—
правый фокальный радиус;

—
(- с; 0) – координаты левого фокуса (точки
F₁);

—
(с; 0) — координаты правого фокуса (точки
F₂);

—

— действительная
полуось
гиперболы;

—

— мнимая
полуось гиперболы;

—
точка (а; 0) – правая вершина гиперболы;

—
точка (- а; 0) – левая вершина гиперболы;

—
прямые

— асимптоты гиперболы.

Названия
полуосей не случайны: точки

гиперболе принадлежат, а точки

—
гиперболе не принадлежат (потому и ось
– мнимая), но мнимая полуось, хотя и не
является частью гиперболы, вполне
определяет ее форму, поскольку именно
между асимптотами гиперболы и располагаются
ветви ее.

Каноническое уравнение гиперболы

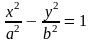
(смотри
замечание о каноничности уравнения).

Связь между полуосями и координатами фокусов гиперболы

При
этом важным является выражение,
связывающее действительную, мнимую
полуось и координату фокуса (сравните
с формой аналогичной связи для параметров
эллипса)

Эксцентриситет
гиперболы

Пример 19 (о нахождении уравнения гиперболы)

Эксцентриситет
гиперболы равен

.
Найти каноническое уравнение гиперболы,
если точка

гиперболе принадлежит.

Решение

Прежде
всего, что ищем конкретно? – Ищем значения
a
и b
в каноническом уравнении гиперболы.
Неизвестных величин две, следовательно,
и уравнений для их нахождения должно
быть два.

Первое
уравнение получим из того факта, что
нам известен эксцентриситет гиперболы
и известна связь
между полуосями и координатами фокуса
гиперболы:

Это
первое равенство, а второе получим,
используя тот факт, что точка М гиперболе
принадлежит, т.е., ее координаты обращают
каноническое уравнение гиперболы в
тождество:

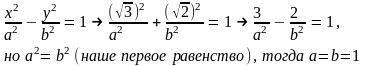
и,
окончательно, получаем

Ответ

Искомая
гипербола описывается каноническим
уравнением

x²
— y²
= 1.

Пример 20 (прямая и гипербола)

Через
точку М(0; — 1) и правую вершину гиперболы

3∙x²
— 4∙y²
= 12

проведена
прямая. Найти вторую точку пересечения
прямой с гиперболой.

Решение

Задачу
будем решать в два шага:

—
найдем уравнение прямой;

—
найдем координату точки пересечения
прямой и гиперболы.

Шаг
1

Для
нахождения уравнения прямой, проходящей
через точку М(0; — 1) и правую вершину
гиперболы необходимо знать координаты
правой вершины гиперболы. Найдем вторую
точку из уравнения гиперболы, приведя
данное уравнение к каноническому
виду,
зная при этом, что в каноническом
уравнении важно все: равно выражение
именно
единице, а в самом выражении – значения
действительной и мнимой полуоси – это
знаменатели дробей, в которых числители
x²
и y².

Откуда
в уравнении гиперболы a
= 2, b
=

,
или координаты правой вершины М₂(2;
0). А вот теперь ищем уравнение
прямой, проходящей через две данные
точки
М и М₂

Шаг
2

Ищем
координаты точек пересечения найденной
прямой и данной гиперболы. Эти координаты
удовлетворяют обоим уравнениям, т.е.
являются решением системы уравнений

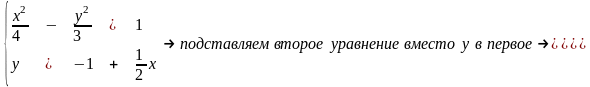
Решаем
полученное уравнение и находим, что x₁
= — 4, x₂
= 2.

Подставляем
найденные x₁
и x₂
во второе уравнение системы и находим
координаты точек пересечения прямой с
гиперболой N₁(-
4; -3) и N₂(2;
0).

Не
трудно убедиться (проверьте самостоятельно)
что точка М гиперболе не принадлежит,
а значит, точек пересечения будет две.

Ответ

Точки
пересечения прямой и гиперболы — N₁(-
4; -3) и N₂(2;
0).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).

Математическая гипербола.

Функция заданная формулой (y=frac{k}{x}), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac{k}{x}) называют гиперболой. Где х является независимой переменной, а у — зависимой.

Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k<0, то ветви гиперболы находятся во 2 и 4 четверти.
гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти

гипербола, где k<0 ветви гиперболы находятся во 2 и 4 четверти

2.Асимптоты гиперболы. Чтобы найти асимптоты гиперболы необходимо,иногда, уравнение гиперболы упростить. Рассмотрим на примере:
Пример №1:
$$y=frac{1}{x}$$
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х не равен 0.
$$yneqcolor{red} {frac{1}{x}}+0$$
(frac{1}{x}) дробь отбрасываем, для того чтобы найти вторую асимптоту.
Остается простое число
y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.

Пример №2:
$$y=frac{1}{x+2}-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота

Находим вторую асимптоту.

$$y=color{red} {frac{1}{x+2}}-1$$

Дробь (color{red} {frac{1}{x+2}}) отбрасываем
Остается y≠ -1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):

Пример №3:

$$begin{align*}
&y=frac{2+x}{1+x} \\
&y=frac{color{red} {1+1}+x}{1+x} \\
&y=frac{1}{1+x}+frac{1+x}{1+x}\\
&y=frac{1}{1+x}+1\\
&y=frac{1}{color{red} {1+x}}+1
end{align*}$$

Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.

Находим вторую асимптоту.

$$y=color{red}{frac{1}{1+x}}+1$$

(color{red}{frac{1}{1+x}}) Дробь убираем.

Остается y≠1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:

$$y=frac{1}{x}$$

Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.

4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:

$$y=frac{1}{x}$$

Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.

Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.

$$f(-x)=frac{1}{-x}=-frac{1}{x}=-f(x)$$

6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:

$$y=frac{-1}{x-1}-1$$

а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.

Находим вторую асимптоту.

$$y=color{red} {frac{-1}{x-1}}-1$$

Дробь (color{red} {frac{-1}{x-1}}) удаляем.

Остается y≠ -1 это вторая асимптота.

б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.

в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5

г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).

д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).

е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k<0 функция возрастающая.

8. Для более точного построения взять несколько дополнительных точек. Пример смотреть в пункте №6.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
реклама

Источник

3.4.1. Каноническое уравнение и построение гиперболы

Общая структура изложения материала будет напоминать предыдущий параграф. Начнём с общего понятия гиперболы и задачи на её построение.

Каноническое уравнение гиперболы имеет вид , где – положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие , то

есть, значение «а» может быть и меньше, чем «бэ».
Надо сказать, довольно неожиданно… – уравнение «школьной» гиперболы и

близко не напоминает каноническую запись. Но эта загадка нас ещё подождёт, а пока раскинем на экране своего воображения график функции …. Какие мысли?

У гиперболы две симметричные ветви.

У гиперболы две асимптоты.

Неплохой прогресс! Данными свойствами обладает любая гипербола, и сейчас вы с неподдельным восхищением заглянем в декольте этой линии:

Задача 99

Построить гиперболу, заданную уравнением

Решение: на первом шаге приведём данное уравнение к каноническому виду . Пожалуйста, запомните типовой порядок действий. Справа необходимо получить «единицу», поэтому

обе части исходного уравнения делим на 20:

Здесь можно сократить обе дроби, но технически грамотнее сделать каждую из них трёхэтажной (см. Приложение Школьные

материалы):

и только после этого провести сокращение:

Выделяем квадраты в знаменателях:

Готово.

Почему преобразования лучше проводить именно так? Ведь дроби левой части можно сразу сократить и получить .

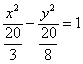
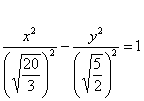
Дело в том, что в рассматриваемом примере немного повезло: число 20 делится и на 4 и на 5. В общем случае получится что-нибудь вроде и без 3-го этажа не обойтись: .

Воспользуемся плодом наших трудов – каноническим уравнением :

Как построить гиперболу?

Существует два подхода к построению гиперболы – геометрический и алгебраический. С практической точки зрения вычерчивание с помощью циркуля я бы

даже сказал утопично, поэтому гораздо выгоднее вновь привлечь на помощь нехитрые расчёты.

Целесообразно придерживаться следующего алгоритма (читайте и смотрите на чертёж ниже):

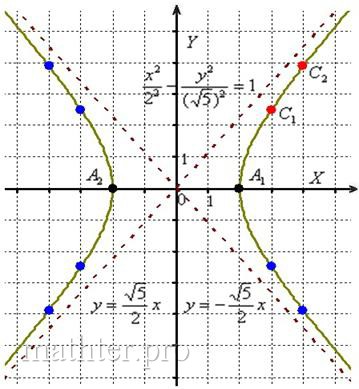
1) Сначала находим асимптоты. Если гипербола задана каноническим уравнением , то её асимптотами являются прямые . В нашем случае: . Данный пункт

обязателен! Это принципиальная особенность чертежа, и будет грубой ошибкой, если ветви гиперболы «вылезут» за свои асимптоты.

2) Теперь находим две вершины гиперболы, которые расположены на оси абсцисс в точках . Выводится элементарно: если , то каноническое уравнение превращается в , откуда и следует,

что . Наша гипербола имеет вершины

3) Ищем дополнительные точки. Обычно хватает двух-трёх. В каноническом положении гипербола симметрична относительно начала

координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Методика точно такая же, как и при построении эллипса. Из канонического уравнения на черновике выражаем:

и уравнение распадается на две функции:
– определяет верхние дуги гиперболы (то, что нам надо);
– определяет нижние дуги гиперболы.

Напрашивается нахождение точек с абсциссами :

4) Изобразим асимптоты , вершины , дополнительные и

симметричные им точки в других координатных четвертях. Аккуратно соединим соответствующие точки у каждой ветви гиперболы:
Техническая трудность может возникнуть с иррациональным угловым коэффициентом , но это вполне преодолимая проблема.