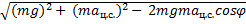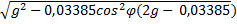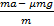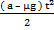Дано:
Решение:
а) Найдем ось вращения на полюсе ((⋅) А). Земля вертится вокруг своей оси, которая проходит через полюса земли. Проведем ось Y по этой оси. На тело будут действовать силы: сила тяжести Fт; сила
реакции опоры N Земли. Ускорение в (⋅) А равно нулю, т.к. она находится на оси вращения.
II закон Ньютона в векторном виде:
или в проекциях на ось Y:
Подставляя получим:
б) Определим вес тела на экваторе ((⋅ )В). При нахождении веса тела на экваторе ((⋅) В) на тело действуют реакция опоры N, сила тяжести Fт = mg, а также центростремительная сила F = mg, где a центростремительное ускорение, приобретаемое телом за счет вращения Земли вокруг оси.
Ось вращения направлена перпендикулярно плоскости вращения и проходит через (⋅) O. II-ой закон Ньютона в векторном виде:
В проекциях на ось Y:
Итак,
Ускорение а тела при вращение Земли вокруг оси определим следующим образом:
где Т — период обращения Земли вокруг оси;
Rз — радиус Земли. Т=24 ч=86400 с. Подставляя в формулу для вычисления N, получим:
Ответ:
Вес тела P=N=9,766 Н≈9,77 Н.
Решение задач повышенной сложности на движение в НСО
Пример задачи
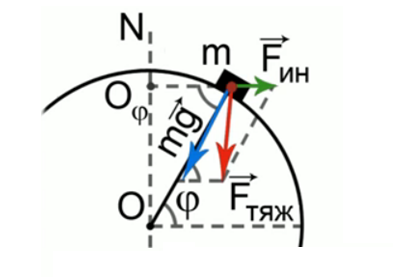
Найти вес тела на широте φ (рис. 1).
Рис. 1. Пример решения задачи
Pφ – ? 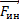
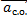
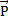
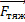
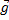
ac.o. = aц.с. = 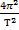
Fтяж =
Fтяж = m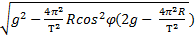
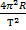
Fтяж = m
Мы привыкли, что вес тела – mg, но Земля совершает свое движение вокруг своей оси и является неинерциальной системой отсчета.
Рассмотрим тело, которое находится на поверхности Земли на широте φ. Широта определяется направлением на эту точку земной поверхности, и угол, который она составляет с экваториальной плоскостью, как раз и является широтой места.
На тело в неинерциальной системе отсчета кроме силы гравитационного притяжения 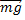
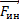
Подставляя выражение для центростремительного ускорения, получаем силу тяжести, в формуле которой мы видим ускорение точек земной поверхности на экваторе – аэ. При вычислении получим аэ = 0,03385 м/с2, и, подставляя в выражение для силы тяжести, мы можем определить ее в любой точке поверхности для необходимых широты и массы тел.
Для контроля найдем силу тяжести тела массой 10 кг на экваторе, на широте 600 и на полюсе, сравним полученные значения.
Ответ: при φ = 00Fтяж1 = 94,62 (H),
φ =600 Fтяж2 = 96,33 (H),
φ = 900Fтяж3 = 98 (H).
Естественно, самое маленькое значение будет на экваторе, самое большое – на полюсе.
Задача 1
Грузы массой 2 кг и 8 кг подвешены к концам нити, перекинутой через блок, который поднимается вертикально с ускорением 5 м/с2. Найти силу натяжения нити.
Сложности при решении этой задачи связаны с тем, что ранее говорилось о применении законов Ньютона только в инерциальных системах отсчета и рассматривалось движение этих грузов относительно Земли. Относительно Земли ускорение грузов разное, поэтому задача и стала для многих сложной.
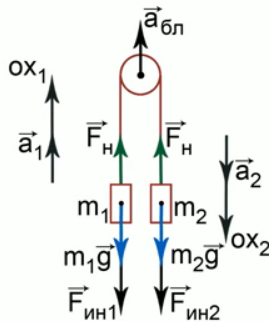
Решать такие задачи необходимо в системе отсчета «Блок» (рис. 2), которая является неинерциальной, и в этой системе отсчета ко всем силам, которые обычно приложены к телам, добавляется сила инерции.
К примеру, когда автобус резко тормозит, нас толкает вниз сила инерции. Здесь при движении блока наверх к каждому из тел добавляется сила, противоположная ускорению блока и направленная вниз.
Рис. 2. Система отсчета «Блок»
Эйнштейн доказал, что эта сила инерции в принципе неотличима от силы гравитационного притяжения. В данном случае на первое тело действует сила натяжения нити 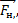
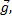
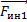
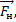
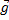
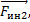
У нас система связанных тел, для каждого из тел ось необходимо направить в свою сторону по ускорению. Очевидно, что первое тело, которое легче, будет двигаться относительно блока вверх, а второе тело будет двигаться вниз. Поэтому ось ох1направляем вверх, ох2 направляем вниз.
Запишем краткое условие задачи и решение.
Ответ: Fн = 48 H.
Уравнение в проекции на ось ох1 будет иметь вид -m1g — m1абл + Fн = m1а.
На ось ох2 будет m2g + m2абл — Fн = m2а.
Решение системы уравнений достигается сложением, при сложении сразу убираем противоположные значения силы натяжения и получаем выражение, из которого можем записать ускорение и вычислить его. Далее его значение можно подставить в любое из уравнений и определить силу натяжения.
Задача 2
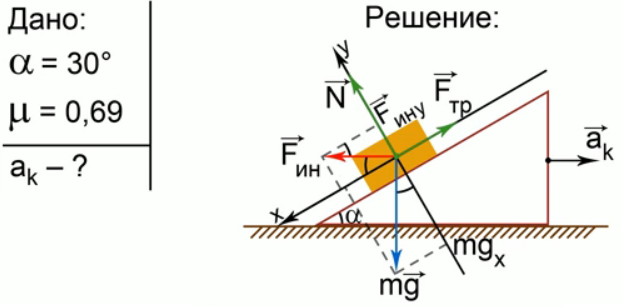
На наклонной поверхности клина с углом 300 покоится брусок при коэффициенте трения 0,69. С каким минимальным ускорением нужно перемещать по горизонтали клин, чтобы брусок стал скользить вниз по его поверхности?
Выполняем краткое условие задачи, рисунок и решение (рис. 3).
Рис. 3. Решение задачи 2
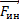
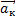
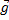
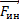
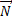
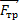
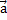
по ох: mgsinα + maкcosα — Fтр ≥ 0
по оу: -mgcosα + maкsinα + N = 0
N = mgcosα — maкsinα Fтр = μN = μmgcosα — μmaкsinα
mgsinα + maкcosα — μmgcosα + μmaкsinα ≥ 0
aк ≥ 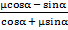
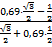
Ответ: aк ≥ 0,8 м/с2.
Сила, которая заставляет брусок проскальзывать, – это mgsinα, но sinα = 0,5 при μ = 0,69, мы видим, что сила трения больше силы, составляющей mg. Решаем задачу в системе отсчета «Клин». К тем силам, которые обычно приложены к бруску, – сила реакции опоры 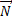
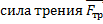
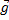
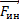
По оси у mg будет со знаком минус, так как она направлена против оси у. Уравнение по оси у необходимо, чтобы выразить силу реакции опоры 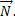
При нахождении максимального ускорения его необходимо направить в противоположную сторону.
Задача 3
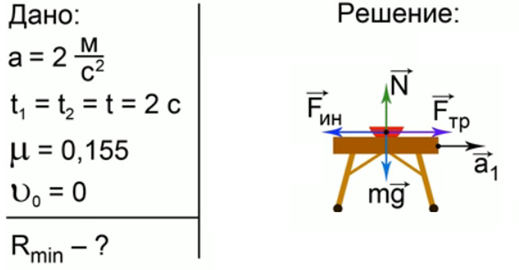
В центре круглого стола поместили маленькое блюдечко. Коэффициент трения между ним и столом μ = 0,155. Стол двигали прямолинейно с ускорением 2 м/ с2 в течение 2 с, а затем остановили с тем же по величине ускорением. При каком минимальном радиусе стола блюдечко с него не упадет?
Запишем краткое условие задачи, схему и решение (рис. 4).
Рис. 4. Решение задачи 3
Fин = ma = 2m; Fтр = μmg = 1,55m
1. t = t1
a1 = 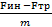
a1 = a — μg V1 = ( a — μg ) t S1 =
2. t = t2
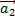
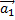
V02 = V1 V2 = 0
S2 = 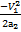
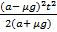
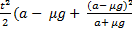
S = 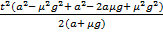
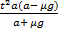
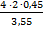
Ответ: Rmin = 1,01 м.
Начальная скорость блюдечка равна нулю, оно лежит в центре стола. Когда стол начинает двигаться с ускорением, он становится неинерциальной системой отсчета и ко всем силам, которые были приложены к блюдечку, добавляется сила инерции, направленная против ускорения стола и равная по величине произведению массы на ускорение блюдечка. Сила трения сразу будет мешать блюдечку двигаться. При подстановке известных величин мы видим, что сила трения меньше силы инерции, блюдечко начинает двигаться по поверхности стола.
Первое условие задачи – стол движется с ускорением, в этом случае сила инерции направлена в противоположную сторону силы трения, но больше нее. Определим ускорение, с которым движется блюдечко, по второму закону Ньютона. За это время скорость блюдечка увеличивается с этим ускорением и достигает значения V1, а путь – S1.
При втором промежутке времени ускорение стола меняется на противоположное, соответственно, и сила инерции принимает противоположное направление, в данном случае она будет совпадать с силой трения, то есть и сила инерции, и сила трения тормозят движение блюдечка. Начальная скорость к моменту торможения будет равна V1, а конечная скорость в результате торможения будет равна нулю. Поэтому за время торможения блюдечко пройдет путь S2, так как ускорение у нас отрицательное, то знак минус уйдет из выражения.
Общий путь, который пройдет блюдечко, составляет сумму двух полученных выражений S1 и S2. Проведя алгебраические преобразования и подставляя числовые значения, мы получим, что блюдечко пройдет путь 1,01 метра, то есть радиус стола от центра до края должен быть не меньше этого значения, иначе блюдечко соскользнет.
Заключение
Как мы увидели на примерах решения задач, при учете сил инерции второй закон Ньютона будет справедлив для любой системы отсчета и ряд задач лучше решается в неинерциальной системе отсчета.
ПОЧЕМУ ВЕС ТЕЛА РАЗЛИЧЕН НА ПОЛЮСЕ И НА ЭКВАТОРЕ?
Вес тела зависит от широты местности.
Если тело, вес которого в Киото 1 кГ (1кГ = 9,8 Н), взвесить на антарктической станции «Сёва», окажется, что здесь его вес увеличился на 29 Г, составив, таким образом, 1 кГ 29 Г. То же тело в столице южно-американской страны Эквадор городе Кито будет весить 997,5 Г.
Другой пример. Тело, весящее в Кито 1 кГ, будет весить в Антарктиде 1005,4 Г. Разница в весе равна 0,5 %. Если принять, что 1 Г золота стоит 4500 иен, то стоимость бруска весом 1 кГ на Южном полюсе увеличится на 24 000 иен. Итак, вес тела изменяется в зависимости от широты местности. Однако такие изменения можно обнаружить только с помощью пружинных весов, так как обычные рычажные весы для этой цели непригодны..
Рычажные и пружинные весы.
Издавна о весе тела судили по тому, насколько тяжело удержать его на ладони пли приподнять с земли. Впоследствии, когда появилась необходимость взвешивать драгоценные металлы и зерно, были изобретены весы. Рисунок на египетском папирусе, относящийся к 1400 г. до н. э., изображает весы, предназначенные для очень точных измерений (рис. 1.1).
Рисунок 1.1. Изображение рычажных весов на древнеегипетском папирусе
Весы — это прибор, с помощью которого вес тела сравнивается с весом гири — противовеса. Поэтому, чтобы измерить вес тела па рычажных весах, необходимо на чашу весов положить гири, вес которых уравновесил бы вес тела. Так как при перемещении в различные точки земной поверхности вес тела и гири изменяется одинаково, то при таком способе взвешивания нельзя заметить изменении веса тела. В повседневной жизни используется простой, по менее точный метод измерения веса с помощью пружинных весов. Под действием приложенной силы пружина растягивается, и по степени растяжения можно судить о величине этой силы, в данном случае — о весе тела. Измеренный таким образом вес есть не что иное, как сила тяжести, действующая на тело. Следовательно, если вес тела, измеренный с помощью пружинных весов, в различных точках земной поверхности окажется различным, то это означает, что сила тяжести в этих точках различна.
Центробежная сила.
Значение силы тяжести зависит от широты местности. На малых широтах, с приближением к экватору, сила тяжести уменьшается. Заметное различие в весе тела на экваторе и на полюсах объясняется, в основном, собственным вращением Земли.
Рис. 1.2. Вращение тела вокруг своей оси
Каждая точка вращающегося тела испытывает действие силы, направленной от оси вращения и перпендикулярной к этой оси. Эту силу называют центробежной. Действие центробежной силы иллюстрируется на рис. 1.2. Шарик, подвешенный к нитке, вращается вокруг оси, а нить подвеса при этом отклоняется на некоторый угол от вертикали. При увеличении скорости вращения угол отклонения также увеличивается. Величина центробежной силы пропорциональна расстоянию вращающегося тела от оси вращения. Земной шар, изображенный на том же рисунке, вращается вокруг своей оси. Расстояние от оси вращения до поверхности Земли на экваторе совпадает с радиусом Земли, а при увеличении широты местности убывает.
Земное притяжение и центробежная сила.
Вес тела, определяющийся, главным образом, действующей на него силой земного притяжения (силой гравитации), на экваторе из-за влияния центробежной силы уменьшается. Так как ось вращения Земли проходит через Северный и Южный полюсы, в этих точках земной поверхности центробежная сила равна нулю и вес тела обусловлен исключительно силой притяжения Земли. Центробежная сила на экваторе составляет 1/300 часть силы притяжения и направлена от центра Земли. Если считать, что на полюсах и экваторе сила земного притяжения одинакова, то вес тела на экваторе будет на 1/300 часть меньше его веса на полюсах, т. е. предмет, который на полюсе весит 1 кГ, на экваторе будет весить 997 Г.
В каком бы месте мы не измеряли вес тела, нам никогда не удастся раздельно измерить силу земного притяжения и центробежную силу. Таким образом, измеряемая сила тяжести является суммой сил земного притяжения и центробежной силы к поэтому на экваторе из-за центробежной силы вес тела па 1/300 часть меньше, чем на полюсах.
Форма Земли.
Как уже отмечалось, вес тела в Кито отличается от его веса на полярной станции «Сёна» на 0,5 %. А так как эта станция достаточно далека от полюса (69° южной широты), то различие в весе тела в Кито и на Южном полюсе должно быть еще большим. Такая разница в весе не может быть объяснена только наличием центробежной силы. За счет чего же возникает эта разница? Самое простое объяснение состоит в том, что Земля не является идеальной сферой. И действительно, ее радиус па экваторе равен 6378,14 км, а на полюсе — 6356,76 км. Разница составляет 1/300 часть радиуса Земли. Таким образом, Земля представляет собой слегка сплющенную на полюсах сферу, точнее говоря, эллипсоид вращения.
0,5 %-е различие в весе.
В произвольном масштабе на рис. 1.3 изображено поперечное сечение Земли. Незаштрихованная часть является идеальной окружностью. Если бы Земля была идеальной сферой, то сила тяжести была бы обратно пропорциональна квадрату расстояния от ее центра.
Рис. 1.3. Сила земного притяжения и форма Земли.
Из рис. 1.3 видно, что расстояние от точки Е на экваторе до центра больше, чем от точки N на Северном полюсе до центра, поэтому сила земного притяжения, обусловленная не заштрихованной частью сечения Земли, на полюсе больше, чем на экваторе. В то же время вклад заштрихованной части сечения больше на экваторе. Два вышеуказанных фактора почти компенсируют действие друг друга, однако, как показали расчеты математика Клеро, проведенные для эллипсоида вращения, вес тела на экваторе, с учетом действия центробежной силы, меньше на 1/200 веса тела на полюсе. Это соотношение действительно подтверждается результатами взвешивания тела на полюсе и на экваторе. Таким образом, центробежная сила и не сферическая форма Земли позволяют объяснить наблюдаемую разницу в весе тела па полюсе и на экваторе.
Равновесие трех сил.
Итак, теперь мы знаем, чем вызвано отличие в весе тела па полюсе и на экваторе. Остается ответить на вопрос: каким будет вес тела в точке, не лежащей ни на полюсе, ни на экваторе, а допустим, в Киото? В этом случае направления силы земного притяжения и центробежной силы не лежат на одной прямой и складываются согласно правилу параллелограмма.
Чтобы представить себе сложение сил, проведем мысленно опыт, используя изображенное на рис. 1.4 приспособление, предназначенное для поднятия груза М. К концам нити, перекинутой через два блока, подвешены грузы М1 и М2, а в произвольной точке между ними закреплен груз М. Если вес М меньше суммы весов М1 и М2, тело А1, достигнув определенной высоты, остановится: наступит состояние равновесия.
Силы F1, F2, F, действующие на грузы, пропорциональны весам соответствующих грузов,
Рис.1.4. Равновесие трех сил.
В левой части рис. 1.4 эти силы вынесены отдельно, так что их величина и направление остаются неизменными. Если F1 и F2 — стороны параллелограмма, F’ — его диагональ, то F и F’ равны друг другу по величине и противоположны по направлению, а поэтому три вышеупомянутые силы находятся в равновесии, в чем мы могли убедиться на опыте.
Сложение и разложение силы на составляющие.
Рассмотренные нами силы F и F’ уравновешивают друг друга, причем действие силы F’ эквивалентно действию двух сил F1 и F2. Сила, действие которой равно действию двух каких-либо сил, называется их результирующей или равнодействующей. Из сказанного следует, что равнодействующей двух сил является диагональ параллелограмма, каждая сторона которого соответствует одной из сил. Таким образом, равнодействующей двух сил является диагональ параллелограмма, построенного на складываемых силах, выходящая из точки приложения этих сил. Поэтому, если на двух силах построить параллелограмм, то диагональ, проведенная из точки их приложения, будет результирующей складываемых сил. Параллелограмм, с помощью которого находят результирующую двух сил, называется параллелограммом сил, а способ ее определения правилом параллелограмма сил.
Если требуется найти равнодействующую более чем двух cил, необходимо последовательно применить правило параллелограмма.

Рис. 1.5. Результирующая двух равных по величине сил F и F2 — притяжения и центробежной силы.
Рис. 1.6. Разложение силы F на две взаимно перпендикулярные составляющие F и F2
В случае, когда силы F1 и F2 равны по величине, их результирующая F’ как показано на рис. 1.5, будет биссектрисой угла между ними. Разложение силы на составляющие является операцией, обратной сложению. На рис. 1.6 показано изложение одной силы F на две взаимно перпендикулярные вставляющие F1 и F2.
Сложение силы земного притяжения и центробежной силы. Зная правило сложения сил, легко найти сумму силы земного притяжения и центробежной силы.
Прежде всего, снова рассмотрим вращательное движение шарика, подвешенного на нитке.

Рис. 1.7. Результирующая силы тяжести и центробежной силы.
Рис. 1.8. Результирующая силы земного притяжения и центробежной силы.
Как видно из рис. 1.7, результирующая силы тяжести и центробежной силы равна и противоположно направлена силе натяжения нити. Сила натяжения нити в зависимости от приложенного усилия может быть разной, но численное ее значение и направление всегда таковы, что уравновешивают это усилие. Таким образом можно определить угол отклонения нити в зависимости от скорости вращения, при условии, что вращение происходит вокруг оси, перпендикулярной к поверхности Земли, т.е. когда сила тяжести и центробежная сила направлены перпендикулярно друг другу. Точно так же можно найти равнодействующую силы земного притяжения и центробежной силы. В этом случае, как показано на рис. 1.8, сила земного притяжения направлена к центру Земли, а центробежная сила — перпендикулярна к оси вращения. Как уже говорилось ранее, центробежная сила очень мала по сравнению с силой земного притяжения, однако на 35,01° северной широты, что соответствует широте Киото, центробежная сила составляет 0,3 % силы тяжести. Это приводит к тому, что направление силы тяжести в этой точке будет на 0,1° отклоняться от линии, соединяющей точку с центром Земли. В повседневной жизни этим отклонением обычно пренебрегают и определяют горизонтальную поверхность как поверхность, перпендикулярную к линии отвеса, т.е. к линии, вдоль которой действует сила тяжести.
Хотя вносимая центробежной силой разница в весе равна лишь 1/300, тем не менее вес стокилограммовой штанги за счет нее уменьшается на 300 Г.
Исследование 1 ЦЕНТРОБЕЖНАЯ СИЛА
Движение по окружности.
Мы уже говорили, что на вращающееся тело действует центробежная сила. Но возникает вопрос: какова природа этой силы? До сих пор, рассматривая вращательное движение, мы обходились без ее определения. Теперь попытаемся восполнить этот пробел. Для этого рассмотрим, как это показано на рис. 1.9, движение тела массой m по окружности радиуса r с постоянной скоростью v. Нам достаточно знать, что измеряемый обычно в килограммах вес тела пропорционален массе.
Рис. 1.9. Что такое центробежная сила?
a=V2/r=r ω2
f=ma=mV2/r=mrω 2
ω=2π/Т =V/r
T=2πr/V
Здесь а-ускорение; f-центробежная сила; ω-угловая скорость; Т-период вращения; r-радиус; V-скорость; m-масса
Ускорение а тела, движущегося по окружности, направлено по радиусу к центру окружности, причем величина его пропорциональна квадрату скорости v2 и обратно пропорциональна радиусу r. Чтобы создать такое ускорение, к телу необходимо приложить силу, равную произведению ускорения на его массу. Это следует из соотношения, которое называется вторым законом Ньютона. Направление силы совпадает с направлением ускорения, благодаря чему сила называется центростремительной.
Если в формуле для силы использовать в качестве единицы длины метр, а единицы времени — секунду, то сила будет выражаться в ньютонах. Один ньютон — это сила, которая сообщает телу массой в 1 кг ускорение 1 м/с2. Сокращенно ньютон обозначают буквой Н.
В качестве величины, дающей представление о скорости тела при движении по окружности, используется угловая скорость.
Эта величина показывает, на какой угол повернулось тело при вращении за единицу времени, причем в качестве единицы угла используется радиан. Угол, опирающийся на дугу, равную по длине радиусу ее окружности, называют углом в один радиан. Таким образом, 360° соответствуют 2 π радиан, где п равно 3,14.
Теперь попытаемся ответить на вопрос, что увидит наблюдатель, вращающийся вместе с исследуемым телом вокруг одной оси с той же угловой скоростью, что и исследуемое тело. С его точки зрения, тело будет выглядеть покоящимся, то есть все действующие на него силы будут находиться в равновесии. При вращении тела пружина растягивается и, следовательно, на него действует упругая сила пружины (см. рис. 1.9). Но с точки зрения вращающегося наблюдателя силу растяжения пружины должна уравновешивать сила, направленная от центра. Эту силу называют центробежной, а действие ее проявляется только во вращающейся системе координат.
Центробежная сила и вес.
Человек на земной поверхности вращается вместе с земным шаром вокруг его оси и, естественно, испытывает на себе действие центробежной силы. Поэтому, интересуясь величиной силы тяжести на поверхности Земли, необходимо всегда принимать во внимание центробежную силу.
Экваториальный радиус Земли равен 6378,14 км, период ее вращения 23 ч 58 мин 4 с. Используя эти значения, получим для центробежной силы, действующей на тело массой 1 кг, величину 0,03 Н. Так как ускорение силы тяжести равно 9,8 м/с2, а следовательно, сила тяжести, действующая на массу в 1 кг, равна 9,8 Н, то отношение центробежной силы на экваторе к силе тяжести равно 1/300. Ввиду малости центробежной силы число 1/300 можно считать отношением центробежной силы к силе земного притяжения.
Известно, что из-за действия центробежной силы поверхность жидкости всегда перпендикулярна к направлению результирующей силы земного притяжения и центробежной силы. В результате этого небесные тела—сгустки жидкой и газообразной материи — при вращении приобретают форму сплюснутого эллипсоида вращения. Такая форма обусловлена в конечном счете наличием центробежной силы.
Сплюснутую форму Земли и других планет можно попытаться объяснить, если предположить, что в начале своего образования они находились в жидком состоянии и вращались с большей скоростью. Однако на вопрос о том, действительно ли планеты в начальном этапе своего образования находились и жидком состоянии, точного ответа дать невозможно.
Исследование 2 ИЗМЕРЕНИЕ СИЛЫ ТЯЖЕСТИ И ЕЕ АНОМАЛИИ
Ускорение силы тяжести.
Как и любую другую силу, силу тяжести можно измерить. Однако на практике обычно измеряют ее ускорение. Для этой цели издавна используется метод маятника, основанный на том, что период колебаний маятника пропорционален квадратному корню из отношения его длины к ускорению силы тяжести. Длина маятника должна быть Большой по сравнению с амплитудой его отклонений от положения равновесия. Тогда выполняется условие малости его колебаний, на основании которого получена формула для периода. Однако измерить его длину с большой точностью трудно. Точность 10-8 при измерении 1 м означает, что абсолютная ошибка соизмерима с длиной волны видимого света.
Существует прямой и намного более точный метод определения ускорения силы тяжести, заключающийся в измерении времени падения тела в вакууме. Путь, пройденный телом, измеряют с помощью лазерного луча, время — с помощью атомных часов. Зная соотношение, связывающее высоту и время падения, можно измерить ускорение силы тяжести с точностью до 10-9. Кроме того, с этой целью используется пружинный гравиметр. С его помощью значение силы тяжести измеряется с точностью до 10-8—10-9. В несколько усовершенствованном варианте прибор используют на кораблях для определения ускорения силы тяжести g на морской поверхности.
В табл. 1.1 представлены значения g, полученные этим методом в разных точках земной поверхности. Существует также метод измерения g, в основе которого лежит эффект Мейсснера. Кроме того, значение g можно найти, используя искусственные спутники Земли.
В геофизике в качестве единицы измерения ускорения принят 1 гал, равный 1 см/с2. Первоначально единица была на звана «галилео»; в настоящее время употребляется сокращенное название этой единицы «гал». Миллигал равен одной тысячной гала.
1Эффект этот заключается в следующем. Если над сверхпроводящим кольцом, по которому циркулирует незатухающий ток, поместить сверхпроводящий шарик из ниобия, он повиснет над кольцом без всякой поддержки. Такая «магнитная подушка» возникает благодаря тому, что ток, циркулирующий в кольце, создает магнитное поле, приводящее к появлению в поверхностном слое сверхпроводящего шарика индуцированных незатухающих токов.
Направление их таково, что возникает сила отталкивания наведенного тока и тока в кольце. Шарик повисает в воздухе на высоте, определяемой равенством силы отталкивания и веса шарика.
| Пункт на поверхности Земли | Геометрическая широта | Высота над уровнем моря | Ускорение силы тяжести, гал |
|---|---|---|---|
| Хельсинки | 60°11′ северной широты | 20,6 | 981,90 |
| Париж | 48°50′ » | 65,9 | 980,83 |
| Саппоро | 43°04′ » | 15 | 980,48 |
| Вашингтон | 38°54′ » | -0,2 | 980,10 |
| Токио | 35°39′ » | 28,0 | 979,76 |
| Киото | 35°01′ | 59,9 | 979,71 |
| Кагосима | 31°34′ » | 4,2 | 979,47 |
| Дели | 28°36′ » | 208,8 | 979,12 |
| Мехико | 19°20′ » | 2268,5 | 977.93 |
| Панама | 8°58′ » | 9 | 978,23 |
| Кито | 0°13′ южной широты | 2815,1 | 977,26 |
| Антарктическая станция «Сева» | 69°00′ » | 14 | 982,53 |
Ускорение силы тяжести зависит от высоты над уровнем моря. Так, в Кито, расположенном на 0°13′ южной широты, g = 977,26 гал. Это меньше стандартного значения g на экваторе, равного 978,04 гал. Подобное различие объясняется тем, что Кито расположен в Андах на высоте 2815 м над уровнем моря.
Аномалии силы тяжести.
Полезную информацию можно получить, сравнивая значения g в разных точках, расположенных на одной широте, предварительно приведя их к стандартным, отвечающим 0 м над уровнем моря. Отклонения g от стандартного значения называются аномалиями силы тяжести. Эти аномалии возникают по многим причинам. Часто они являются первым признаком залежей полезных ископаемых или месторождений нефти.
Наблюдение за движением искусственного спутника, происходящим под действием силы тяжести, показывает, что ее значение изменяется в широких пределах. Это частично объясняется тем, что вся мантия Земли охвачена медленными вихрями мощных течений. Там, где поднимающееся из недр течение расползается в стороны, разогретые участки коры растягиваются, из-за чего значение g в таких местах будет на несколько миллигал ниже.
Наблюдения, проведенные со спутников, показали, что форма Земли отличается от эллипсоида вращения.
Измерения g в различных точках планеты проводятся в рамках международного сотрудничества, однако некоторые страны предпочитают замалчивать точные значения g на своей территории. Дело в том, что эти сведения чрезвычайно важны для наведения межконтинентальных баллистических ракет на цель, точность попадания которых составляет 100 м.
Рейтинг:
(голосов: 0)

1. Konstruktor
Добрый день!
У Вас в данной статье в расчётах веса тела на экваторе и на полюсах точно нет ошибки?
Добавление комментариев доступно только зарегистрированным пользователям
1. Плотность планеты
Рассмотрим, как выразить ускорение свободного падения на поверхности планеты и первую космическую скорость для этой планеты через ее радиус R и среднюю плотность ρ. (Средняя плотность планеты равна отношению массы планеты к ее объему.)
? 1. Выразите массу планеты M через ее радиус R и среднюю плотность ρ.
? 2. Чему равно ускорение свободного падения g на поверхности планеты радиусом R, имеющей среднюю плотность ρ?
Подсказка. Воспользуйтесь формулой (8) из в § 14, заменив массу и радиус Земли на массу и радиус данной планеты.
? 3. Вблизи поверхности планеты-гиганта Юпитер (на рисунке 18.1 Юпитер изображен в одном масштабе с Землей) ускорение свободного падения в 2,6 раза больше, чем вблизи поверхности Земли. Радиус Юпитера примерно в 11 раз больше радиуса Земли. Какова средняя плотность Юпитера?
? 4. На планете радиусом 3400 км камень падает с обрыва высотой 200 м в течение 10 с. Чему равна средняя плотность планеты? Считайте, что сопротивлением атмосферы планеты можно пренебречь.
? 5. Чему равна первая космическая скорость для планеты радиусом R со средней плотностью ρ?
Подсказка. Воспользуйтесь формулой (10) из § 14, заменив радиус Земли и ускорение свободного падения на поверхности Земли на массу данной планеты и ускорение свободного падения на ее поверхности.
А сейчас мы получим несколько неожиданный результат.
? 6. Чему равен период T обращения спутника по низкой круговой орбите вокруг планеты радиусом R со средней плотностью ρ? (В таком случае радиус орбиты можно считать равным радиусу планеты.)
Итак, период обращения спутника на низкой круговой орбите зависит только от средней плотности планеты!
? 7. Астронавты облетели три планеты А, Б и В на низких круговых орбитах с выключенным двигателем. Время облета каждой из планет составило: TА = 55 мин, TБ = 106 мин, TВ = 72 мин. У какой из этих планет наибольшая средняя плотность? У каких из этих планет средняя плотность больше средней плотности Земли? Напомним, что период обращения искусственного спутника Земли на низкой орбите 85 мин.
2. Учет вращения планеты вокруг своей оси
Геостационарная орбита
Телевизионные программы передают в разные точки Земли с помощью спутников связи (рис. 18.2), которые движутся по круговым орбитам.
Сигнал со спутника принимает укрепленная на стене или крыше дома спутниковая антенна. Она направлена постоянно на одну и ту же точку небосвода, поэтому спутник связи должен постоянно «висеть» над одной и той же точкой поверхности Земли.
? 8. Чему равен период одного оборота спутника связи?
Орбиту, по которой движется спутник, находящийся постоянно над одной и той же точкой поверхности Земли, называют геостационарной. Она лежит в экваториальной плоскости Земли (так называют плоскость, в которой лежит экватор).
? 9. Выразите радиус rгс геостационарной орбиты через ускорение свободного падения g вблизи поверхности Земли, радиус Земли и продолжительность суток T.
Подсказка. Запишите уравнение второго закона Ньютона для спутника связи, выразив в нем гравитационную постоянную G через g, MЗем, Rзем.
? 10. Чему равен радиус геостационарной орбиты? На какой высоте над поверхностью Земли находится эта орбита?
Выполнив это задание, вы оцените уровень современной техники: спутниковая антенна устойчиво принимает сигнал с расстояния в десятки тысяч километров!
Вес тела на полюсе и на экваторе
Вследствие вращения планеты вокруг своей оси (его называют суточным) вес одного и того же тела на экваторе планеты меньше, чем на ее полюсе. Выясним, от чего зависит разность значений веса на экваторе и на полюсе.
Пусть тело покоится на поверхности шарообразной планеты вблизи ее полюса. В этом случае вес тела
PП = mg, (1)
где g – ускорение свободного падения.
Чтобы найти вес тела на поверхности планеты вблизи экватора, надо учесть суточное вращение планеты.
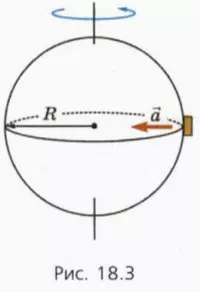
Вследствие этого вращения находящееся на экваторе тело равномерно движется по окружности относительно инерциальной системы отсчета, связанной с удаленными звездами (рис. 18.3). Радиус окружности равен радиусу планеты R, а период обращения T равен продолжительности суток.
Вследствие суточного вращения планеты находящееся на ее экваторе тело движется относительно инерциальная центростремительным ускорением
Это ускорение направлено к центру планеты, то есть вниз. А если тело движется с ускорением 
PЭ = m(g – a).
? 11. Чему равно уменьшение веса тела массой m на экваторе шарообразной планеты радиусом R по сравнению с его весом на полюсе, если период обращения планеты равен T?
? 12. С помощью каких весов можно обнаружить уменьшение веса тела на экваторе – рычажных, в которых используются гири, или пружинных, когда вес тела измеряют по удлинению пружины?
? 13. Каково обусловленное суточным вращением Земли уменьшение веса корабля массой 40000 т при переходе его из приполярной области в экваториальные воды? Уменьшается ли при этом масса корабля?
? 14. На сколько процентов уменьшается вес тела вследствие суточного вращения Земли при перемещении его с полюса Земли на экватор?
Существует еще одна причина уменьшения веса тела на экваторе Земли по сравнению с весом на полюсе.
Дело в том, что Земля немного сплюснута у полюсов – расстояние между Северным и Южным полюсами (по прямой сквозь Землю) примерно на 43 км меньше, чем расстояние между диаметрально противоположными точками экватора Земли. Вследствие этого на полюсе находящаяся на уровне моря точка расположена примерно на 21,5 км ближе к центру Земли, чем точка на экваторе.
Общее уменьшение веса, обусловленное суточным вращением и сплюснутостью Земли, составляет примерно 0,5 %.
? 15. Каким должен быть период обращения шарообразной планеты массой M и радиусом r вокруг своей оси, чтобы находящиеся на ее экваторе тела находились в состоянии невесомости?
? 16. При какой продолжительности земных суток тела на земном экваторе были бы в состоянии невесомости?
Дополнительные вопросы и задания
17. Сорвавшийся с обрыва на некоторой планете камень падал с высоты h в течение времени t. Радиус планеты равен R. Чему равна масса планеты M?
18. Высадившийся на планету радиусом R астронавт бросает камешки с начальной скоростью v0 под разными углами к горизонту. Чему равна средняя плотность планеты, если все камешки упали на расстоянии от космонавта, не превышающем l?
19. Космонавты высадились на экваторе шарообразной малой планеты. Средняя плотность планеты ρ, радиус R, продолжительность суток T.
а) Чему равна скорость точек поверхности планеты на экваторе?
б) Чему равна первая космическая скорость для этой планеты?
в) С какой скоростью космонавты могут ехать на гусеничном вездеходе вдоль экватора по направлению суточного вращения планеты, не отрываясь от ее поверхности?
20. Над находящейся на экваторе Земли африканской деревней 2 раза в сутки – в полдень и в полночь – пролетают одновременно два искусственных спутника, А и Б. Орбиты спутников лежат в экваториальной плоскости, спутник А движется на восток, а Б – на запад.
а) Какой спутник движется в направлении суточного вращения Земли, а какой – в противоположном?
б) Чему равен период обращения каждого спутника?
в) Каковы радиусы орбит спутников?
21. Космический корабль массой 10 т должен постоянно находиться в точке, где силы притяжения со стороны Земли и Луны уравновешивают друг друга. Примите, что Землю можно считать неподвижной, а расстояние от Земли до Луны постоянным.
а) Как направлена сила тяги двигателя корабля?
б) Выразите расстояние r от Земли до корабля через массу Земли MЗем массу Луны MЛ и расстояние RЗЛ от Земли до Луны.
в) Чему равна сила тяги двигателя корабля?
|
Физика. Рассчитайте вес собственного тела на экваторе планеты Земля?Всеми любимый 5 лет назад
Здравствуйте, недавно нашел интересную задачу в интернете, но решить так и не получилось, помогите пожалуйста. Михаил Белодедов 5 лет назад Г. Незнайкина совершенно правильно вычисляет вес тела на основе ускорения свободного падения на экваторе. Но задача-то как раз про то, как определить это ускорение. Для этого надо из чего-то исходить. Если исходить из величины g = 9,83 м/с2 на северном полюсе, то на экваторе из этого числа нужно вычесть центростремительное ускорение, возникающее в результате вращения Земли a = R*w2 = 0,04 м/с2. То есть около 9,79 м/с2. комментировать
в избранное
ссылка
отблагодарить Незнайкина 5 лет назад Не поняла в чем проблема. Вес тела равен массе тела умноженное на ускорение свободного падения,который на экваторе равен 9,78 м/с^2 на экваторе. Если Ваша масса допустим 80 кг, то вес Вашего тела Р=80*9,78=782,4 Н комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |