Как найти весь путь без времени - AvtoShod.ru - решение различных проблем

Существует формула, с помощью которой можно посчитать путь, пройденный телом, когда нам известны его начальная скорость, ускорение и конечная скорость.

Сокращенно эту формулу называют «путь без времени». Так ее называют потому, что в правой ее части время t движения отсутствует (рис. 1).

Рис.1. Так выглядит формула, по которой можно вычислить путь тела, не зная, сколько времени занимало движение

Формула пути без времени помогает упростить решение некоторых задач кинематики. Особенно, задач, части C.

Однако, не торопитесь на ЕГЭ записывать эту формулу в готовом виде. Сначала в решении задачи нужно записать вывод этой формулы. И только потом ее можно использовать.

Формулу выводят из выражений для равнопеременного движения. Сейчас я помогу вам вывести эту формулу с помощью нескольких простых шагов.

Выводим формулу пути без времени

Для определенности будем считать, что тело движется по прямой все быстрее и быстрее. То есть, скорость тела увеличивается, так как появляется ускорение.

В таком случае векторы ускорения и скорости тела будут сонаправленными (параллельными и направленными в одну и ту же сторону).

Сонаправленные или противоположно направленные векторы называют коллинеарными векторами. Прочитайте подробнее о коллинеарных векторах.

Чтобы вычислить путь тела, когда скорость его увеличивается, нужно использовать две формулы:

[ large begin{cases} S = v_{0} cdot t + displaystylefrac{a}{2} cdot t^{2} \ v = v_{0} + a cdot t end{cases} ]

( large v_{0} left( frac{text{м}}{c} right)) – начальная скорость тела;

( large v left( frac{text{м}}{c} right)) – конечная скорость;

( large a left( frac{text{м}}{c^{2}} right)) – ускорение тела;

( large S left( text{м} right)) – путь, пройденный телом;

(large t left( c right)) – время, за которое тело прошло этот путь.

В формуле для пути S присутствует время t. Получим из нее формулу для пути, в которой время будет отсутствовать.

Что сделать, чтобы получить формулу пути, в которой отсутствует время:

сначала получить выражение для времени t из уравнения для скорости;

затем в формулу пути подставить полученное выражение вместо времени t.

Выражаем время из формулы для скорости

Выпишем формулу, связывающую начальную и конечную скорость тела:

[ large v = v_{0} + a cdot t ]

Избавимся в правой части от начальной скорости, обозначенной символом ( v_{0}). Для этого из обеих частей уравнения вычтем число ( v_{0}). Получим такую запись:

[ large v — v_{0} = a cdot t ]

Теперь, чтобы справа в формуле оставалось только время «t», избавимся от ускорения «a». Для этого разделим обе части уравнения на «a»:

[ large frac{ v — v_{0}}{a} = t ]

Это выражение нам пригодится для дальнейшего вывода формулы «путь без времени».

В формулу пути подставим выражение для времени

Запишем теперь формулу для пути S и полученную формулу для времени t, объединив их в систему:

[ large begin{cases} S = v_{0}cdot t + displaystyle frac{a}{2}cdot t^{2}\ displaystyle frac{v — v_{0}}{a} = t end{cases} ]

В первом уравнении системы будем заменять символ t дробью из второго уравнения. Тогда система из двух уравнений превратится в единственное уравнение. И в этом уравнении не будет символа t времени:

[large S = v_{0} cdot frac{ v — v_{0}}{a} + frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2}]

Осталось теперь упростить полученное выражение. Будем производить упрощение по частям.

Упрощаем выражение, расположенное до знака «плюс» в правой части

Выпишем отдельно все, что располагается до знака «плюс» в правой части уравнения:

[large v_{0} cdot frac{ v — v_{0}}{a} ]

Умножим числитель дроби на число (v_{0}).

Для этого:

сначала числитель обособим скобками;
затем запишем число (v_{0}) перед скобками;
а потом внесем это число внутрь скобок.

В числитель дроби, обособленный с помощью скобок помещаем число (v_{0}):

[large v_{0} cdot frac{ (v — v_{0})}{a} = frac{ v_{0} cdot (v — v_{0})}{a} ]

Теперь необходимо умножить скобку на число (v_{0}). На рисунке 2 указано, как правильно выражение в скобках умножить на число, стоящее за скобками.

Рис. 2. Чтобы умножить скобку на число, нужно умножить каждое слагаемое в скобке на это число

Нужно к каждой скорости в скобках дописать число (v_{0}), умножая его на эти скорости. Получим такое выражение:

[large frac{ v_{0} cdot (v — v_{0})}{a} = frac{ (v_{0} cdot v — v_{0} cdot v_{0})}{a} = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} ]

То есть, вместо первоначальной записи, мы получили такую запись:

[large v_{0} cdot frac{ (v — v_{0})}{a} = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} ]

Возводим в квадрат дробь

После знака «плюс» в правой части уравнения располагается дробь, которую нужно возвести в квадрат. Обратим внимание на эту дробь:

[large left( frac{ v — v_{0}}{a} right)^{2}]

Правильно возвести дробь в степень поможет рисунок 3.

Рис. 3. Дробь возводим в степень, отдельно возводя в эту степень ее числитель и знаменатель

В результате возведения в квадрат дробь приобретет такой вид:

[large left( frac{ v — v_{0}}{a} right)^{2} = frac{ (v — v_{0})^{2}}{a^{2}}]

В числителе этой дроби находится выражение в скобках, которое нужно возвести в квадрат. И нам придется применить одну из формул сокращенного умножения. Запоминать формулы сокращенного умножения удобно в виде, приведенном на рисунке 4.

Рис. 4. Удобный для запоминания вид формул сокращенного умножения

Используем для этого формулу сокращенного умножения, которая содержит знак «минус». Она называется «Квадрат разности». Тогда числитель дроби превратится в такую запись:

[large ( v — v_{0})^{2} = (v^{2} + v^{2}_{0} — 2vv_{0})]

Теперь можем записать полученную дробь:

[large frac{ (v — v_{0})^{2}}{a^{2}} = frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{a^{2}} ]

Упрощаем правую часть, записанную после знака «плюс»

Обратим внимание на все, что располагается в правой части уравнения после знака «плюс»:

[large frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2}]

Мы уже провели некоторые преобразования и можем теперь заменить дробь, возводимую в квадрат более подробной записью:

[large frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2} = frac{a}{2} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{a^{2}}]

Примечание: Когда мы умножаем одну дробь на другую, то можем менять местами знаменатели этих дробей.

Итак, поменяем местами знаменатели дробей:

[large frac{a}{2} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{a^{2}} = frac{a}{a^{2}} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2}]

Теперь видно, что мы можем сократить ускорение и еще немного упростить выражение:

[large frac{a}{a^{2}} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2} = frac{1}{a} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2}]

А перемножив числители и знаменатели двух дробей, получим такую запись:

[large frac{1}{a} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2} = frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]

Теперь, первоначальную дробь можно заменить дробью, полученной в ходе преобразований:

[large frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2} = frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]

Мы закончили преобразовывать выражения, содержащиеся в правой части уравнения после знака «плюс».

Теперь, осталось сложить две дроби в правой части – дробь, записанную до знака «плюс» с дробью, записанной после знака «плюс». А чтобы эти дроби можно было сложить, нужно будет привести их к общему знаменателю.

Приводим к общему знаменателю дроби в правой части уравнения

Вернемся еще раз к первоначальному уравнению:

[large S = v_{0} cdot frac{ v — v_{0}}{a} + frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2}]

Заменим правую часть этого уравнения выражениями, которые мы получили:

[large S = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} + frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]

Сравним знаменатели дробей.

Первая дробь обладает знаменателем «a», а вторая – «2a». Выберем число «2a» в качестве общего знаменателя обеих дробей.

Чтобы первую дробь привести к общему знаменателю «2a», умножим ее на единицу:

[large frac{ (v_{0} cdot v – v^{2}_{0} )}{a} = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot 1]

Примечания:

Нам известно, что если какое-либо число умножить на единицу, то после умножения это число не изменится. Значит, если какое-либо выражение умножить на единицу, то полученное выражение останется равным самому себе. На единицу можно умножать все, что угодно – дроби, выражения в скобках и т. п.
Математики часто применяют прием умножения на единицу. А после этого единицу записывают в виде некоторой дроби. При этом используют правило: Единица – это дробь, у которой числитель и знаменатель равны (одинаковые).

Так как снизу в первой дроби не хватает числа 2, то единицу представим в виде дроби 2/2:

[large frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot 1 = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot frac{2}{2}]

Получим такую дробь:

[large frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot frac{2}{2} = frac{ 2(v_{0} cdot v – v^{2}_{0} )}{2a} ]

Поместим ее в выражение для пути:

[large S = frac{ 2(v_{0} cdot v – v^{2}_{0} )}{2a} + frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]

Дроби с одинаковыми знаменателями складываем

Теперь знаменатели дробей равны. И мы можем записать эти дроби под общим знаменателем:

[large S = frac{ 2(v_{0} cdot v – v^{2}_{0} ) + (v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]

Раскроем скобки в числителе полученного выражения:

[large S = frac{ 2v_{0} v – 2v^{2}_{0} + v^{2} + v^{2}_{0} — 2vv_{0}}{2a}]

Примечание: Обратим внимание на то, что в числителе дважды встречается член (2v_{0} v), обладающий различными знаками. В начале числителя – знаком «плюс», а в конце числителя – знаком «минус». Это означает, что из числа (2v_{0}v) вычитается такое же число (2vv_{0}). В конце концов, это число покидает нашу запись и, она упрощается:

[large S = frac{ – 2v^{2}_{0} + v^{2} + v^{2}_{0}}{2a}]

Перепишем выражение, записав все, что содержит знак «плюс» в начало числителя:

[large S = frac{ v^{2} + v^{2}_{0} – 2v^{2}_{0}}{2a}]

Вычтем подобные члены, содержащие ( v^{2}_{0}):

[large v^{2}_{0} – 2v^{2}_{0} = – v^{2}_{0} ]

В результате получим короткую запись. Именно о ней говорят, когда имеется ввиду формула пути без времени:

[large boxed{ S = frac{ v^{2} — v^{2}_{0}}{2a} }]

Примечания:

Это формула, с помощью которой можно рассчитать путь тела, когда известны его начальная и конечная скорость, а, так же, ускорение.
Видно, что время t в правой части этого выражения отсутствует.
Мы выводили эту формулу для случая, когда тело увеличивало скорость.

Как выглядит формула пути без времени, когда скорость тела уменьшается

Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:

[large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]

Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:

[ large begin{cases} S = v_{0} cdot t — displaystyle frac{a}{2} cdot t^{2} \ v = v_{0} — a cdot t end{cases} ]

Выводы

Пусть нам известны начальная и конечная скорость тела и его ускорение. Тогда путь, пройденный телом, можно рассчитать так:

Когда движение равноускоренное и скорость тела увеличивается: [large boxed{ S = frac{ v^{2} — v^{2}_{0}}{2a} }]
А когда движение равнозамедленное и скорость уменьшается: [large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]

Источник

Как посчитать путь ускоряющегося тела не используя время

Формула пути без времени помогает упростить решение некоторых задач кинематики. Особенно, задач, части C.

Выводим формулу пути без времени

Чтобы вычислить путь тела, когда скорость его увеличивается, нужно использовать две формулы:

( large v_ <0>left( frac<text<м>> right)) – начальная скорость тела;

( large v left( frac<text<м>> right)) – конечная скорость;

( large a left( frac<text<м>>> right)) – ускорение тела;

( large S left( text <м>right)) – путь, пройденный телом;

(large t left( c right)) – время, за которое тело прошло этот путь.

Что сделать, чтобы получить формулу пути, в которой отсутствует время:

сначала получить выражение для времени t из уравнения для скорости;
затем в формулу пути подставить полученное выражение вместо времени t.

Выражаем время из формулы для скорости

Выпишем формулу, связывающую начальную и конечную скорость тела:

[ large v = v_ <0>+ a cdot t ]

Избавимся в правой части от начальной скорости, обозначенной символом ( v_<0>). Для этого из обеих частей уравнения вычтем число ( v_<0>). Получим такую запись:

[ large v — v_ <0>= a cdot t ]

Это выражение нам пригодится для дальнейшего вывода формулы «путь без времени».

В формулу пути подставим выражение для времени

Запишем теперь формулу для пути S и полученную формулу для времени t, объединив их в систему:

Осталось теперь упростить полученное выражение. Будем производить упрощение по частям.

Упрощаем выражение, расположенное до знака «плюс» в правой части

Выпишем отдельно все, что располагается до знака «плюс» в правой части уравнения:

Умножим числитель дроби на число (v_<0>).

сначала числитель обособим скобками;
затем запишем число (v_<0>) перед скобками;
а потом внесем это число внутрь скобок.

В числитель дроби, обособленный с помощью скобок помещаем число (v_<0>):

Теперь необходимо умножить скобку на число (v_<0>). На рисунке 2 указано, как правильно выражение в скобках умножить на число, стоящее за скобками.

Нужно к каждой скорости в скобках дописать число (v_<0>), умножая его на эти скорости. Получим такое выражение:

То есть, вместо первоначальной записи, мы получили такую запись:

Возводим в квадрат дробь

Правильно возвести дробь в степень поможет рисунок 3.

В результате возведения в квадрат дробь приобретет такой вид:

Теперь можем записать полученную дробь:

Упрощаем правую часть, записанную после знака «плюс»

Обратим внимание на все, что располагается в правой части уравнения после знака «плюс»:

Примечание: Когда мы умножаем одну дробь на другую, то можем менять местами знаменатели этих дробей.

Итак, поменяем местами знаменатели дробей:

Теперь видно, что мы можем сократить ускорение и еще немного упростить выражение:

А перемножив числители и знаменатели двух дробей, получим такую запись:

Теперь, первоначальную дробь можно заменить дробью, полученной в ходе преобразований:

Мы закончили преобразовывать выражения, содержащиеся в правой части уравнения после знака «плюс».

Приводим к общему знаменателю дроби в правой части уравнения

Вернемся еще раз к первоначальному уравнению:

Заменим правую часть этого уравнения выражениями, которые мы получили:

Сравним знаменатели дробей.

Чтобы первую дробь привести к общему знаменателю «2a», умножим ее на единицу:

Примечания:

Нам известно, что если какое-либо число умножить на единицу, то после умножения это число не изменится. Значит, если какое-либо выражение умножить на единицу, то полученное выражение останется равным самому себе. На единицу можно умножать все, что угодно – дроби, выражения в скобках и т. п.
Математики часто применяют прием умножения на единицу. А после этого единицу записывают в виде некоторой дроби. При этом используют правило: Единица – это дробь, у которой числитель и знаменатель равны (одинаковые).

Так как снизу в первой дроби не хватает числа 2, то единицу представим в виде дроби 2/2:

Получим такую дробь:

Поместим ее в выражение для пути:

Дроби с одинаковыми знаменателями складываем

Теперь знаменатели дробей равны. И мы можем записать эти дроби под общим знаменателем:

Раскроем скобки в числителе полученного выражения:

Примечание: Обратим внимание на то, что в числителе дважды встречается член (2v_ <0>v), обладающий различными знаками. В начале числителя – знаком «плюс», а в конце числителя – знаком «минус». Это означает, что из числа (2v_<0>v) вычитается такое же число (2vv_<0>). В конце концов, это число покидает нашу запись и, она упрощается:

Перепишем выражение, записав все, что содержит знак «плюс» в начало числителя:

Вычтем подобные члены, содержащие ( v^<2>_<0>):

В результате получим короткую запись. Именно о ней говорят, когда имеется ввиду формула пути без времени:

Примечания:

Это формула, с помощью которой можно рассчитать путь тела, когда известны его начальная и конечная скорость, а, так же, ускорение.
Видно, что время t в правой части этого выражения отсутствует.
Мы выводили эту формулу для случая, когда тело увеличивало скорость.

Как выглядит формула пути без времени, когда скорость тела уменьшается

Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:

Выводы

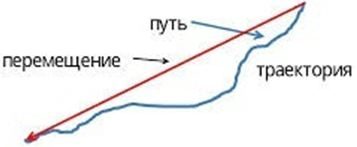
Перемещение и путь при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

Когда тело тормозит, через некоторое время t₁оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:

x ( t ) = x 0 + v 0 t + a t 2 2 . .

Теперь мы можем выделить кинематические характеристики движения тела:

Перемещение тела определяется формулой:

s = v 0 t + a t 2 2 . .

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

x ( t ) = v 0 t + a t 2 2 . . = 5 t − 3 t 2

Кинетическая энергия тела определяется формулой:

Скорость при прямолинейном равноускоренном движении равна:

v = v 0 + a t = 5 − 6 t

Поэтому кинетическая энергия тела равна:

E k = m ( 5 − 6 t ) 2 2 . . = 0 , 2 2 . . ( 5 − 6 t ) 2 = 0 , 1 ( 5 − 6 t ) 2

Следовательно, правильная последовательность цифр в ответе будет: 34.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Определить, какому типу движения соответствует график зависимости координаты тела от времени.
Определить величины, которые характеризуют такое движение.
Определить характер изменения величин, характеризующих это движение.
Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Охарактеризовать движение тела на различных участках графика.
Выделить участки движения, над которыми нужно работать по условию задачи.
Записать исходные данные.
Записать формулу определения искомой величины.
Произвести вычисления.

Решение

Весь график можно поделить на 3 участка:

От t₁ = 0 c до t₂ = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
От t₁ = 10 c до t₂ = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
От t₁ = 30 c до t₂ = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

От t₁ = 20 c до t₂ = 30 с — с равномерным движением.
От t₁ = 30 c до t₂ = 50 с — с равнозамедленным движением.

Для первого участка. Начальный момент времени t₁ = 20 c. Конечный момент времени t₂ = 30 с. Скорость (определяем по графику) — 10 м/с.
Для второго участка. Начальный момент времени t₁ = 30 c. Конечный момент времени t₂ = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Перемещение при равноускоренном движении. Уравнение координаты

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Как, зная тормозной путь, определить начальную скорость автомобиля и как, зная характеристики движения, такие как начальная скорость, ускорение, время, определить перемещение автомобиля? Ответы мы получим после того, как познакомимся с темой сегодняшнего урока: «Перемещение при равноускоренном движении, зависимость координаты от времени при равноускоренном движении».

источники:

Перемещение и путь при равноускоренном прямолинейном движении

http://interneturok.ru/lesson/physics/10-klass/mehanikakinematika/peremeschenie-pri-ravnouskorennom-dvizhenii-uravnenie-koordinaty

Источник

Формула пути

$[ S = frac{a t^{2}}{2} + v_{0} t ]$

Здесь – пройденный путь, – ускорение тела, $v_{0}$ – начальная скорость тела, — время ускоренного движения.

Единица измерения пути – м (метр).

Путь – скалярная величина. Путь – это мера того, какое расстояние преодолело тело в ходе движения. $v_{0}$ – это скорость, с которой тело двигалось к моменту начала ускорения. У этой формулы есть 2 частных случая:

1) Движение равномерное (без ускорения)

Это самый распространённый в задачах, простейший случай. Когда про ускорение ничего не сказано, то под формулой пути имеется в виду именно эта формула.

2) Движение, начатое с неподвижного состояния (без начальной скорости)

$[ S = frac{a t^{2}}{2} ]$

Путь не нужно путать с перемещением – мерой расстояния между конечной и начальной точкой движения.

Примеры решения задач по теме «Путь тела»

Задание	Найти путь, который прошло тело, движущееся с ускорением 1 м/с $^{2}$ в течение 16 с. Начальная скорость была 30 м/с.
Решение	Все исходные данные нам известны. Подставим их в формулу:

(м)

$[ S_{1} = v t ]$

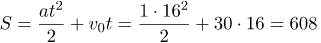
Затем тело замедлялось, пока его скорость не обнулилась ( $t_{1}$ – время замедления):

$[ 0 = v - a t_{1} text{ } rightarrow text{ } t_{1} = frac{v}{a} ]$

Пусть $S_{2}$ – расстояние, пройденное в ходе замедления:

$[ S_{2} = frac{-a t_{1}^{2}}{2} + v t_{1} = frac{-a cdot frac{v^{2}}{a^{2}}}{2} + frac{v^{2}}{a} = frac{v^{2}}{2a} ]$

Затем тело прошло расстояние $S_{1} + S_{2}$ в обратную сторону без начальной скорости с ускорением , за время $t_{2}$ :

Как узнать путь к файлу в Windows

Соавтор(ы): Nicole Levine, MFA. Николь Левин — автор и редактор, пишущий о технологиях для wikiHow. Имеет более 20 лет опыта в написании технической документации и руководстве командами технической поддержки в крупных компаниях, занимающихся веб-хостингом и разработкой программного обеспечения. Получила магистерскую степень по писательскому мастерству в Портлендском государственном университете и преподает композицию, литературное творчество и создание фэнзинов в различных учебных заведениях.

Как посчитать путь ускоряющегося тела не используя время

Формула пути без времени помогает упростить решение некоторых задач кинематики. Особенно, задач, части C.

Выводим формулу пути без времени

Чтобы вычислить путь тела, когда скорость его увеличивается, нужно использовать две формулы:

( large v_ left( frac> right)) – начальная скорость тела;

( large v left( frac> right)) – конечная скорость;

( large a left( frac>> right)) – ускорение тела;

( large S left( text right)) – путь, пройденный телом;

(large t left( c right)) – время, за которое тело прошло этот путь.

сначала получить выражение для времени t из уравнения для скорости;
затем в формулу пути подставить полученное выражение вместо времени t.

Выражаем время из формулы для скорости

Выпишем формулу, связывающую начальную и конечную скорость тела:

[ large v = v_ + a cdot t ]

Избавимся в правой части от начальной скорости, обозначенной символом ( v_). Для этого из обеих частей уравнения вычтем число ( v_). Получим такую запись:

[ large v — v_ = a cdot t ]

Это выражение нам пригодится для дальнейшего вывода формулы «путь без времени».

В формулу пути подставим выражение для времени

Запишем теперь формулу для пути S и полученную формулу для времени t, объединив их в систему:

Осталось теперь упростить полученное выражение. Будем производить упрощение по частям.

Упрощаем выражение, расположенное до знака «плюс» в правой части

Выпишем отдельно все, что располагается до знака «плюс» в правой части уравнения:

Умножим числитель дроби на число (v_).

сначала числитель обособим скобками;
затем запишем число (v_) перед скобками;
а потом внесем это число внутрь скобок.

В числитель дроби, обособленный с помощью скобок помещаем число (v_):

Теперь необходимо умножить скобку на число (v_). На рисунке 2 указано, как правильно выражение в скобках умножить на число, стоящее за скобками.

Нужно к каждой скорости в скобках дописать число (v_), умножая его на эти скорости. Получим такое выражение:

То есть, вместо первоначальной записи, мы получили такую запись:

Возводим в квадрат дробь

Правильно возвести дробь в степень поможет рисунок 3.

В результате возведения в квадрат дробь приобретет такой вид:

Теперь можем записать полученную дробь:

Упрощаем правую часть, записанную после знака «плюс»

Обратим внимание на все, что располагается в правой части уравнения после знака «плюс»:

Примечание: Когда мы умножаем одну дробь на другую, то можем менять местами знаменатели этих дробей.

Итак, поменяем местами знаменатели дробей:

Теперь видно, что мы можем сократить ускорение и еще немного упростить выражение:

А перемножив числители и знаменатели двух дробей, получим такую запись:

Теперь, первоначальную дробь можно заменить дробью, полученной в ходе преобразований:

Мы закончили преобразовывать выражения, содержащиеся в правой части уравнения после знака «плюс».

Приводим к общему знаменателю дроби в правой части уравнения

Вернемся еще раз к первоначальному уравнению:

Заменим правую часть этого уравнения выражениями, которые мы получили:

Сравним знаменатели дробей.

Чтобы первую дробь привести к общему знаменателю «2a», умножим ее на единицу:

Примечания:

Нам известно, что если какое-либо число умножить на единицу, то после умножения это число не изменится. Значит, если какое-либо выражение умножить на единицу, то полученное выражение останется равным самому себе. На единицу можно умножать все, что угодно – дроби, выражения в скобках и т. п.
Математики часто применяют прием умножения на единицу. А после этого единицу записывают в виде некоторой дроби. При этом используют правило: Единица – это дробь, у которой числитель и знаменатель равны (одинаковые).

Так как снизу в первой дроби не хватает числа 2, то единицу представим в виде дроби 2/2:

Получим такую дробь:

Поместим ее в выражение для пути:

Дроби с одинаковыми знаменателями складываем

Теперь знаменатели дробей равны. И мы можем записать эти дроби под общим знаменателем:

Раскроем скобки в числителе полученного выражения:

Примечание: Обратим внимание на то, что в числителе дважды встречается член (2v_ v), обладающий различными знаками. В начале числителя – знаком «плюс», а в конце числителя – знаком «минус». Это означает, что из числа (2v_v) вычитается такое же число (2vv_). В конце концов, это число покидает нашу запись и, она упрощается:

Перепишем выражение, записав все, что содержит знак «плюс» в начало числителя:

Вычтем подобные члены, содержащие ( v^_):

В результате получим короткую запись. Именно о ней говорят, когда имеется ввиду формула пути без времени:

Примечания:

Это формула, с помощью которой можно рассчитать путь тела, когда известны его начальная и конечная скорость, а, так же, ускорение.
Видно, что время t в правой части этого выражения отсутствует.
Мы выводили эту формулу для случая, когда тело увеличивало скорость.

Как выглядит формула пути без времени, когда скорость тела уменьшается

Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:

Выводы

Источник

Задачи на среднюю скорость

Смысл таков: представьте объект передвижения, например автомобиль. Он проходит определённые участки пути с разной скоростью. На весь путь затрачивается какое-то определённое время. Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время То есть формула средней скорости такова:

*В знаменателе суммируем время, а в числителе расстояния пройденные за соответствующие им отрезки времени.

Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть – со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Как уже сказано необходимо весь путь разделить на всё время движения. В условии сказано о трёх участках пути. Формула:

Обозначим весь пусть S. Тогда первую треть пути автомобиль ехал:

Вторую треть пути автомобиль ехал:

Последнюю треть пути автомобиль ехал:

1113

Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

В условии сказано о трёх участках пути. СК будем искать по формуле:

Участки пути нам не даны, но мы можем без труда их вычислить:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км — со скоростью 80 км/ч, а затем 150 км — со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Сказано о трёх участках пути. Формула:

Протяжённость участков дана. Определим время, которое автомобиль затратил на каждый участок: на первый затрачено 120/60 часов, на второй участок 120/80 часов, на третий 150/100 часов. Вычисляем скорость:

1121

Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

*Есть задача про путешественника, который пересёк море. С решением у ребят возникают проблемы. Если вы не видите его, то пройдите регистрацию на сайте! Кнопка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После регистрации войдите на сайт и обновите данную страницу.

Путешественник переплыл море на яхте со средней скоростью 17 км/ч. Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.

В данной рубрике продолжим рассматривать задачи, не пропустите! Успехов вам!

Источник

Как решать задачи на среднюю скорость

В ЕГЭ по матматике профильного уровня встречаются задачи на нахождение средней скорости автомобиля, путешественника, бегуна и т.п. В этой статье мы постараемся разобраться со способами решения данного типа зданий. Попробуйте решить следующие задачи:

Если у Вас возникает недопонимание, или же вы просто не знаете как решать такие задачи, то данная статья предназначена как раз для Вас!

Средняя скорость объекта

Для начала вспомним формулу, по которой решаются все задачи на движение: ( S=vt ) — пройденный путь равняется произведению скорости и времени. Так вот, средняя скорость равна отношению всего пути ко времени, которое было затрачено на прохождение этого пути. Если перевести на математический язык:

Однако, раз возникла нужда вычислить среднюю скорость, то наверняка она была разной на различных промежутках. Например, Вам необходимо прийти в школу. Сначала вы какой-то путь проезжаете на автобусе, а затем идете пешком. Условно, весь ваш путь можно разделить на 2 промежутка, и на обоих Ваша скорость и время его прохождения будет разной. Поэтому, если в задаче дано несколько промежутков, то мы должны найти общий путь, который равен сумме всех промежутков вашего пути (то есть ( S=S_1+S_2+ldots+S_n ) (где ( n ) — количество путей, на которых скорость была постоянной). Аналогично мы должны вычислить и общее время, которое было затрачено на прохождение всего пути. То есть ( t=t_1+t_2+ldots+t_n ) , причем время вычисляем на каждом промежутке! То есть, запишем математически формулу для нахождения времени на n-м промежутке: ( t_n=dfrac )

Решение задач

А теперь, обогатившись некоторой теорией решим первую из предложенных задач:

Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16 км/ч, а последнюю треть – со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.

Решение:

Теперь мы знаем длину всего пути ( ( 3S ) ) и сколько времени автомобиль затратил на прохождение всего пути ( ( t=dfrac<9s> <48>) , значит найти среднюю скорость не составит и труда:

Теперь постарайтесь самостоятельно решить оставшиеся две текстовые задачи на нахождение средней скорости, а если не получается, то посмотрите видео-урок

Ответы к текстовым задачам:

Видео-урок: “Как решать задачу на нахождение средней скорости”:

В данном видео-уроке я покажу, как решаются все три предложенные текстовые задачи на нахождение средней скорости. Также Вы можете сравнить своё решение с моим.

Источник

Текстовые задачи на среднюю скорость.

Чтобы найти среднюю скорость движения, необходимо все расстояние разделить на все время движения.

Задача 1. Первые 105 км автомобиль ехал со скоростью 35 км/ч, следующие 120 км – со скоростью 60 км/ч, а последние 500 км – со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение:

Найдём время движения автомобиля:

1. 105:35=3(ч) — время, за которое автомобиль проехал 105 км со скоростью 35 км/ч.

2. 120:60=2(ч) — время, за которое автомобиль проехал 120 км со скоростью 60 км/ч.

3. 500:100=5(ч) — время, за которое автомобиль проехал 500 км со скоростью 100 км/ч.

4. 3+2+5=10(ч) — время движения автомобиля.

Найдём расстояние, которое проехал автомобиль:

Найдём среднюю скорость автомобиля:

Ответ: средняя скорость автомобиля равна 72,5 км/ч.

Задача 2. Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую – со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение:

Пусть автомобиль проехал Х км.

Найдём время движения автомобиля:

1. Х/110(ч) — время, за которое автомобиль проехал Х/2 км со скоростью 55 км/ч.

2. Х/140(ч) — время, за которое автомобиль проехал Х/2 км со скоростью 70 км/ч.

Найдем среднюю скорость:

Ответ: 61,6 км/ч.

Задачи для самостоятельного решения:

1. Первые 200 км автомобиль ехал со скоростью 50 км/ч, следующие 320 км – со скоростью 80 км/ч, а последние 140 км – со скоростью 35 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

2. Первые 140 км автомобиль ехал со скоростью 70 км/ч, следующие 180 км – со скоростью 60 км/ч, а последние 225 км – со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

3. Первую половину трассы автомобиль проехал со скоростью 65 км/ч, а вторую половину трассы со скоростью 35 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Источник

Как найти среднюю скорость автомобиля на протяжении всего пути формула без пути и времени

Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть — со скоростью 120 км/ч, а последнюю — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть км — весь путь автомобиля, тогда средняя скорость равна:

км/ч.

Первую треть трассы автомобиль ехал со скоростью 120 км/ч, вторую треть — со скоростью 50 км/ч, а последнюю — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть км – весь путь автомобиля, тогда средняя скорость равна:

км/ч.

Примечание: Если внимательно посмотреть, сокращается, поэтому в качестве S можно брать любое число. В данном случае было выбрано число 600, поскольку является наименьшим общим кратным чисел 120, 50 и 75.

Добрый день! На самом деле, без разницы, какое число взять, поскольку, если внимательно посмотреть, S сокращается (так как S и в числителе, и в знаменателе). Число 600 выбрано для удобства, а, именно, потому что оно делится и на 120, и на 50, и на 8.

Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть — со скоростью 90 км/ч, а последнюю — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть 3S км — весь путь автомобиля, тогда средняя скорость равна:

км/ч.

Первую треть трассы автомобиль ехал со скоростью 100 км/ч, вторую треть — со скоростью 75 км/ч, а последнюю — со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

км/ч.

Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть — со скоростью 120 км/ч, а последнюю — со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть 3S км весь путь автомобиля, тогда средняя скорость равна:

км/ч.

Первую треть трассы автомобиль ехал со скоростью 50 км/ч, вторую треть — со скоростью 75 км/ч, а последнюю — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

км/ч.