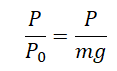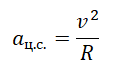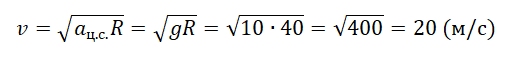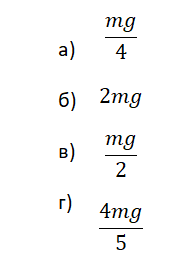Сегодня рассмотрим две силы, которые часто, плохо изучив теорию, путают. Это сила тяжести и вес тела. А затем рассмотрим условие возникновения физического явления невесомость.
Для начала вспомним, что для описания каждой силы используем следующий план:
- Определение силы.
- Точка приложения силы.
- Направление силы.
- Формула, по которой вычисляется модуль силы.
Итак, на все тела, находящиеся в поле тяготения Земли (или других планет) со стороны Земли (других планет) действует сила тяжести (Fmg).
Сила тяжести – это сила, с которой Земля действует на тело. Эта сила приложена к центру тела и направлена по линии отвеса к центру планеты. Формулу для вычисления этой силы вывести довольно легко из закона Всемирного тяготения:
F = GmM/R2 (*),
где G (гравитационная постоянная) = 6,67 · 10-11 Нм2/кг2,
М (масса Земли (планеты)) = 5,9736 · 1024 кг,
R (средний радиус Земли (планеты)) = 6 400 км.
Выражение GM/R2 = const (**), его называют ускорением свободного падения на данной планете. Подставив числа в выражение (**), можно подсчитать, что ускорение свободного падения на Земле
g = GM/R2 = 6,67 · 10-11 Нм2/кг2 · 5,9736 · 1024 кг / (6400×103 м)2 = 9,72751… Н/кг =
= 9,72751… кг м/с 2кг = 9,72751… м/с 2
Учитывая то, что Земля сплюснута у полюсов и её радиус зависит от географической широты, для решения задач используют среднее значение g = 9,8 м/с 2, а в некоторых случаях округляют до g = 10 м/с 2
Зная массу и размеры планеты, можно рассчитать ускорения свободного паления для любой планеты.
Вернёмся к выражению (*), подставляя в него значения, полученные в выражении (**), получим формулу для вычисления силы тяжести
Fmg = GmM/R2 = mg. (***)
Теперь рассмотрим по такому- же плану другую силу – вес тела.
Вес тела (Р) – сила, с которой тело, вследствие земного притяжения (или притяжения других планет) действует на опору или подвес, удерживающие это тело от свободного падения. Внимательно посмотрите на разницу в определениях этих двух сил!
Вес тела не следует путать с массой тела m. Масса тела – это мера инерции тела, скалярная величина, измеряющаяся в килограммах, масса одного и того же тела на разных планетах (т.е. при разных g) const! А вес тела – это сила…. (см. определение выше), измеряется как и все силы в Ньютонах, может меняться в зависимости от движения тела.
Точкой приложения веса тела является точка соприкосновения тела и опоры (подвеса). Направлен вес тела перпендикулярно опоре (вдоль продолжения подвеса). По модулю вес тела равен силе реакции опоры. /Р/ = /N/ (****) и направлен в противоположную сторону. И задача при расчёте веса тела сводится к тому, чтобы рассчитать силу реакции опоры (подвеса) N.
Задача 1.
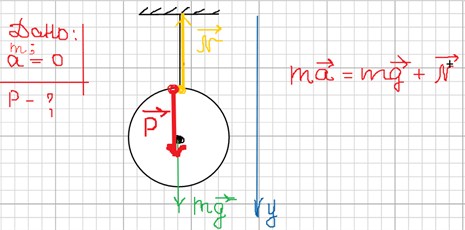
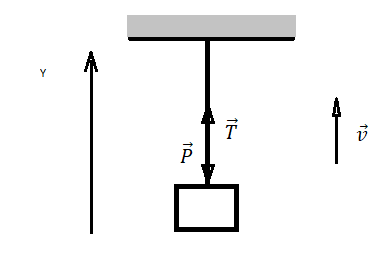
Рассчитаем вес неподвижного тела массой m, закреплённого на подвесе.
Решение.
На рисунке изображено тело, силы, действующие на тело, и записан II закон Ньютона в векторном виде. Запишем это выражение в проекции на ось ОУ, учитывая, что а = 0:
0 = mg – N
N = mg
Учитывая выражение (****), Р = N = mg.
Задача 2.
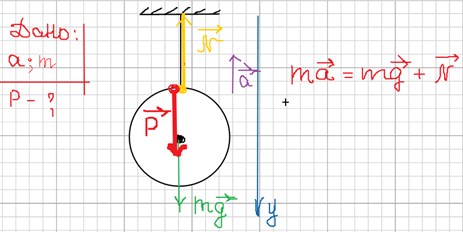
Рассчитаем вес тела массой m, закреплённого на подвесе, если тело поднимают вверх с ускорением а?
Решение.
Запишем II закон Ньютона в проекции на ось ОУ, учитывая знаки:
-ma = mg – N
N = mg + ma
N = m(g + a)
Учитывая выражение (****), Р = N = m(g + a). Как видим, при подъёме вверх с ускорением, вес тела, закрепленного на подвесе, увеличивается на величину ma.
Задача 3.
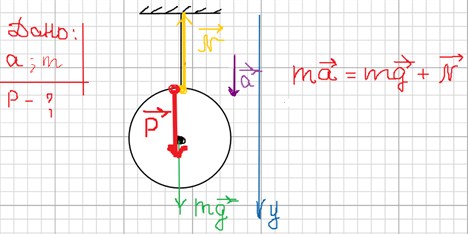
Рассчитаем вес тела массой m, закреплённого на подвесе, если тело опускается вниз с ускорением а?
Решение.
Запишем II закон Ньютона в проекции на ось ОУ, учитывая знаки:
ma = mg – N
N = mg – ma
N = m(g – a)
Учитывая выражение (****), Р = N = m(g – a). Как видим, при движении вниз с ускорением, вес тела, закрепленного на подвесе, уменьшается.
И если /a/ = /g/, то N = m(g – a) = m0 = 0!
Вот это состояние, когда вес тела = 0 и называется невесомостью. Т.е. во время свободного падения тела, тело находится в состоянии невесомости.
Но даже находясь в состоянии невесомости тело будет иметь массу, которая (если тело не разрушать) не меняется!
Надеюсь, прочитав эту статью, Вы будете уверенно различать такие физические величины как масса тела, сила тяжести, вес тела. А также сможете объяснить условие возникновения невесомости.
Остались вопросы? Не знаете, как найти вес тела?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
- Авторы
- Резюме
- Файлы
Иванов Е.М.
Показано, что работа подъема тела в однородном поле тяжести всегда больше величины потенциальной энергии mgh. Величина работы имеет минимум, величина которого зависит от способа подъема тела.
В школьных [1] и вузовских [2-4] курсах физики утверждается, что если тело массы m равномерно поднимать вверх на высоту h с помощью силы F=mg, то сила совершает положительную работу AF=mgh, равную потенциальной энергии П=mgh, а сила тяжести отрицательную работуAP=-mgh [1]. Рассматривается также случай бросания тела вертикально вверх с начальной скоростью V0, обеспечивающей подъем тела на высоту h на основании закона сохранения и превращения энергии: K=П или . Работу бросания считают равной
. В этих безобидных, на первый взгляд, утверждениях, содержится нечто, противоречащее одному из положений физики. В физике используется понятие КОЭФФИЦИЕНТА ПОЛЕЗНОГО ДЕЙСТВИЯ (η ) — КПД. КПД не может быть больше единицы. КПД всегда меньше единицы, поскольку часть энергии превращается тоже в энергию, но не в ту, что нужна, и поэтому теряется для полезного использования. КПД всегда меньше единицы вследствие самой физической природы вещей и явлений. Если же записать КПД для выше приведенных случаев подъема тела на высоту h, то получим:
. Рассмотрим более подробно ряд случаев подъема тела на высоту h.
§ 1. Рассмотрим движение тела, брошенного вертикально вверх с начальной скоростью V0, за счет действия мгновенной силы в виде 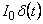
— δ- функция Дирака [7, 8]. Величину I0 будем называть единичным импульсом силы, численно равным количеству движения (импульсу), полученным телом I0=mV0. Дифференциальное уравнение движения (II закон Ньютона) имеет вид:
(1)
при нулевых начальных условиях:
;
(2)
Где x— вертикальная координата, отсчитываемая от поверхности Земли. Для решения задачи воспользуемся двусторонним преобразованием Лапласа [9]
(3)
Для решения этой задачи используется дифференциальное уравнение для односторонней функции где H(t) — единичная (ступенчатая) функция Хевисайда [8, 9]. Тогда производные функции x*(t) имеют вид [9]
;
После соответствующих преобразований, решение получается в следующем виде
(4)
Вычислим работу, совершаемую силами
(5)
Вычисляя интегралы, получим [9]
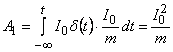
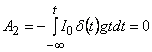
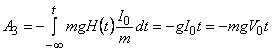
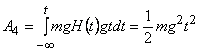
Работа, совершаемая силами, запишется в виде:
(6)
Работа, совершенная единичным импульсом силы I0=mV0 (или начальная энергия, полученная телом) будет равна
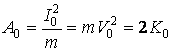
где — начальная кинетическая энергия тела. Время подъема до максимальной высоты
, а максимальная высота подъема
. Подставляя в выражение (6) значение t0, получим конечное значение совершенной работы:
(8)
Поскольку начальная энергия полученная телом A0=2K0, то КПД процесса бросания тела вертикально вверх будет равен
То, что начальная энергия тела A0=2K0 можно объяснить эффектом удвоения массы (силы тяжести) в случае внезапно приложенной нагрузки при бросании [5, 10].
§ 2. Рассмотрим случай движения тела вертикально вверх под действием постоянной вертикальной силы тяги FT. Уравнение движения (II закон Ньютона) запишется в следующем виде
(9)
Если FT=mg, то правая часть тождественно равна нулю, и движения тела вверх не происходит, но в этом случае сила давления тела на опору (например, на поверхность Земли) равна нулю, поскольку сила тяги нейтрализует «тяжелую» массу, и тело находится в квазиневесомом состоянии (состояние левитации). Обозначим силу тяги, равную mg, значком «Л»: FЛ=mg. Если сила тяги больше mg на величину ΔF, то уравнение (9) можно переписать в виде
или
(10)
Таким образом, часть силы тяги FЛ =mg не будет принимать непосредственного участия в работе по подъему тела вверх. Тело будет подниматься вверх только благодаря действию силы ΔF с ускорением . За время t высота подъема будет равна
(11)
Работа подъема составит величину, равную
(12)
Поскольку есть импульс силы, численно равный импульсу (количеству движения), полученному телом
, где V1 — скорость тела в момент времени t, то можно записать
.
Однако чтобы остановить тело на данной высоте h, необходимо еще совершить работу торможения, численно равную кинетической энергии, приобретенной телом ;
(13)
Отдельного разговора заслуживает вопрос о том, что же делает другая часть силы тяги FЛ=mg? Ведь она не принимает участия в подъеме тела на высоту h, она лишь нейтрализует силу тяжести, обеспечивая условия левитации. Можно записать баланс импульсов сил в виде:
(14)
Возведя обе части равенства в квадрат и разделив на 2m, получим баланс энергий (работ):
(15)
Работу, совершаемую силой FT, можно переписать в следующем виде:
(16)
Или, с учетом выражений (11) и (12):
(17)
Первый член в правых частях выражений (15)-(17) представляет собой работу силы левитации в стационарном (неподвижном) состоянии
(18)
Второй член выражает работу, связанную с ускоренным перемещением силы левитации
(19)
Третий член — это обычная работа силы ΔF, обеспечивающей ускоренное движение тела в соответствии со II законом Ньютона:
(20)
Произведение работ . На рис. 1 показана зависимость величины работы левитации AЛ от величины работы AΔ, выраженных в долях потенциальной энергии mgh.
Выражение (17) имеет минимум, равный при
. На графике (рис. 2) показана зависимость работы
, совершаемой силой тяги FT, выраженной в долях потенциальной энергии П=mgh, от величины соотношения ΔF / mg. Если использовать обычную формулу определения работы подъема тела на высоту h с некоторым ускорением a, то будем иметь A=m(g+a)h = (FЛ + ΔF)h . Ее зависимость от величины соотношения ΔF / mg показана на графике (рис. 3). Самое нелепое на этом графике то, что при ΔF=0 совершается работа подъема, равная mgh, хотя, согласно условиям статики, тело должно оставаться неподвижным.
Отрицательная работа, совершаемая силой тяжести при подъеме тела вверх вовсе не равна mgh. Она равна
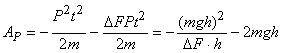
Сумма работ (17) и (21) дает величину , т.е. величину кинетической энергии, приобретенной телом на высоте h.
КПД подъема при без учета работы торможения составляет
.
§3. Тело находится в состоянии левитации (приложена сила тяги ). Для того, чтобы тело двигалось вверх, в начальный момент времени на тело действует направленный вверх единичный импульс силы
. В этом случае дифференциальное уравнение движения запишется в виде
(22)
при нулевых начальных условиях. Решая уравнение с помощью преобразования Лапласа, получим
(23)
Вычисляем работу, совершаемую всеми силами

где , а t1 — время движения до высоты
. Вычисляя интегралы, выделим положительную и отрицательную работы
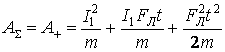
(26)
Преобразуем выражения, входящие в (25)
, где
Тогда суммарную положительную работу (работу подъема) можно записать в виде
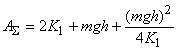
Эта работа имеет минимум, равный при величине
. График зависимости суммарной работы подъема AΣ в зависимости от величины 2K1, выраженных в долях потенциальной энергии П=mgh, показана на графике (рис. 4). Отрицательная работа, совершаемая силой тяжести (27), может быть представлена в виде:
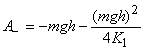
При больших значениях начального импульса ( ) она асимптотически стремится к своему обычному значению
.
Величина энергии, приобретенной в результате ударного нагружения мгновенным импульсом силы I1=mV1, равна . Двойная энергия является результатом удвоения массы при внезапно приложенной нагрузке (в рамках модели материальной точки). В рамках реального упругого тела половина энергии идет на возбуждение упругих колебаний, которые вследствие дисперсии и внутреннего трения с течением времени затухают, переходя во внутреннюю энергию (тело нагревается).
СПИСОК ЛИТЕРАТУР
- Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. средн. шк. — М.: Просвещение, 1990.
- Сивухин Д.В. Общий курс физики. Том I. Механика. — М.: Наука, 1989.
- Детлаф А.А., Яворский Б.М. Курс физики. Учебн. пособие для вузов. — М.: Высш. шк., 1989.
- Матвеев А.Н. Механика и теория относительности: Учебн. пособие для физ. спец. вузов. — М.: Высш. шк., 1986.
- Иванов Е.М. Дополнительные главы классической механики: — Димитровград: ДИТУД УлГТУ, 2004.
- Иванов Е.М. Работа центростремительных и гироскопических //Успехи современного естествознания, № 9, 2004.
- Арсенин В.Я. Математическая физика. — М.: Наука, 1966.
- Арфкен Г. Математические методы в физике. М.: Атомиздат, 1970.
- Б. Ван Дер Поль, Х. Бреммер. Операционное исчисление на основе двустороннего преобразования Лапласа. — М.: Изд. Иностр.Лит. 1952.
- Иванов Е.М. Закон инерции Галилея (I закон Ньютона) //Вестник ДИТУД, № 1, 2003.
Библиографическая ссылка
Иванов Е.М. РАБОТА ПОДЪЕМА ТЕЛА В ОДНОРОДНОМ ПОЛЕ ТЯЖЕСТИ // Современные наукоемкие технологии. – 2005. – № 3.
– С. 9-12;
URL: https://top-technologies.ru/ru/article/view?id=22372 (дата обращения: 28.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
примеры уменьшения веса:
при быстрой езде на велосипеде по небольшим пригоркам велосипедист на вершине пригорка испытывает ощущение лёгкости.
Когда лифт резко начинает движение вниз, находящиеся в лифте люди ощущают, что уменьшается их давление на пол, возникает ощущение свободного падения.
Когда на американских горках проезжают через высшую точку горок, находящиеся в тележке люди испытывают ощущение, будто их «подбрасывает» в воздух.
Когда на качелях раскачиваются до наивысшей точки, ощущается, что на короткий момент тело «зависает» в воздухе.
Изменение веса связано с инерцией — стремлением тела сохранять своё начальное состояние. Поэтому изменение веса всегда противоположно ускорению движения. Когда ускорение движения направлено вверх, вес тела увеличивается. А если ускорение движения направлено вниз, вес тела уменьшается.
Загрузить PDF
Загрузить PDF
Вес — сила, с которой тело действует на опору (или другой вид крепления), возникающая в поле силы тяжести. Масса связана с энергией и импульсом тела и эквивалентна энергии его покоя. Масса не зависит от силы тяжести (точнее от ускорения свободного падения). Поэтому тело, на Земле имеющее массу 20 кг, на Луне будет иметь массу 20 кг, но совсем другой вес (потому что ускорение свободного падения на Луне в 6 раз меньше, чем на Земле).
-
1
Для вычисления веса используйте формулу
. Вес — это сила, с которой тело действует на опору, и его можно рассчитать, зная массу тела. В физике используется формула
.[1]
-
2
Определите массу тела. Так как ускорение свободного падения — это стандартная величина, то необходимо знать массу тела, чтобы найти его вес. Масса должна быть выражена в килограммах.
-
3
Узнайте величину ускорения свободного падения. На Земле, как уже было сказано выше, g = 9,8 м/с2. В других местах Вселенной эта величина меняется.[3]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.[4]
- Ускорение свободного падения на Солнце приблизительно равно 274,0 м/с2 (примерно в 28 раз больше, чем на Земле). Поэтому ваш вес на Солнце будет в 28 раз больше вашего земного веса (если, конечно, вы выживете на Солнце, что еще не факт!).[5]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.[4]
-
4
Подставьте значения в формулу
. Теперь, когда вы знаете массу
и ускорение свободного падения
, подставьте их значения в формулу
. Так вы найдете вес тела (измеряется в ньютонах, Н).
Реклама
-
1
Задача № 1. Найдите вес тела массой 100 кг на поверхности Земли.
-
2
Задача № 2. Найдите вес тела массой 40 кг на поверхности Луны.
-
3
Задача № 3. Найдите массу тела, которое на поверхности Земли весит 549 Н.
Реклама
-
1
Не путайте массу и вес. Самая распространенная ошибка — перепутать вес и массу (что немудрено, ведь в повседневной жизни мы обычно называем массу весом). Но в физике все не так. Запомните, масса — это постоянное свойство объекта, то, сколько в нем вещества (килограммов), где бы он ни находился. Вес — это сила, с которой объект всеми своими килограммами давит на поверхность, и эта сила на разных небесных телах будет различной.
- Масса измеряется в килограммах или граммах. Запомните, что в этих словах, как и в слове «масса», есть буква «м».
-
2
Используйте правильные единицы измерения. В задачах по физике вес или силу измеряют в ньютонах (Н), ускорение свободного падения — в метрах на секунду в квадрате (м/с2), а массу — в килограммах (кг). Если для какой-либо из этих величин вы возьмете не ту единицу измерения, воспользоваться формулой будет нельзя. Если масса в условиях задачи указана в граммах или тоннах, не забудьте перевести ее в килограммы.
Реклама
Приложение: вес, выраженный в кгс
- Ньютон — это единица измерения силы в международной системе единиц СИ. Нередко сила выражается в килограмм-силах, или кгс (в системе единиц МКГСС). Эта единица очень удобна для сравнения весов на Земле и в космосе.
- 1 кгс = 9,8166 Н.
- Разделите вес, выраженный в ньютонах, на 9,80665.
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне.
- Международная система единиц СИ — система единиц физических величин, которая является наиболее широко используемой системой единиц в мире.
Советы
- Самая трудная задача — уяснить разницу между весом и массой, так как в повседневной жизни слова «вес» и «масса» используются как синонимы. Вес — это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу.
- Ускорение свободного падения также может быть выражено в Н/кг. 1 Н/кг = 1 м/с2.
- Плечевые весы измеряют массу (в кг), в то время как весы, работа которых основана на сжатии или расширении пружины, измеряют вес (в кгс).
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне. На нейтронной звезде он будет весить еще больше, но он, вероятно, этого не заметит.
- Единица измерения «Ньютон» применяется намного чаще (чем удобная «кгс»), так как можно найти множество других величин, если сила измеряется в ньютонах.
Реклама
Предупреждения
- Выражение «атомный вес» не имеет ничего общего с весом атома, это масса. В современной науке оно заменено на выражение «атомная масса».
Реклама
Об этой статье
Эту страницу просматривали 113 770 раз.
Была ли эта статья полезной?
Вес тела — сила, с которой тело вследствие притяжения к Земле давит на опору или растягивает подвес.
Вес тела имеет электромагнитную природу (не путать с силой тяжести – она возникает между двумя телами и имеет гравитационную природу!). Обозначается P. Измеряется динамометром. Единица измерения — Н (Ньютон).
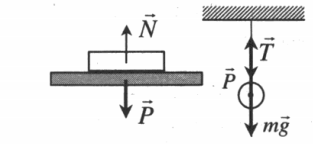
Вес имеет направление, противоположное силе реакции опоры или силе натяжения нити. Точкой приложения веса является точка опоры или подвеса: P↑↓N или P↑↓T.
Согласно III закону Ньютона модуль веса тела определяется одной из следующих формул:
P = T; P = N; P = Fупр.
Если тело и опора или подвес неподвижны, то модули силы реакции опоры, силы натяжения подвеса, а также силы упругости равны модулю силы тяжести. Поэтому в неподвижной системе модуль веса неподвижного тела тоже равен модулю силы тяжести:
P0 = Fтяж = mg
Если тело находится в состоянии невесомости, его вес равен нулю: P = 0. Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.
Пример №1. Гиря массой 1 пуд стоит на полу. Определить вес гири.
Так как гиря покоится, ее вес будет равен модулю силы тяжести. 1 пуд = 16,38 кг. Следовательно:
P = mg = 16,38∙10 = 163,8 (Н)
Перегрузка
Перегрузка — отношение абсолютной величины линейного ускорения, вызванного негравитационными силами, к стандартному ускорению свободного падения на поверхности.
Перегрузка определяется отношением:
Перегрузка возникает, когда система, в которой находится тело, движется с ускорением.
Вес тела в движущейся равноускоренно системе
Вес тела в движущейся системе может быть больше или меньше веса того же тела в системе, которая находится в состоянии покоя:
- Если система движется равноускоренно в направлении ускорения свободного падения, вес тела меньше веса тела в неподвижной системе: при a↑↑g — P < P0.
- Если система движется равноускоренно в направлении, противоположном ускорению свободного падения, вес тела больше веса тела в неподвижной системе: при a↑↓g — P > P0.
- Если система движется с равномерной скоростью (ускорение равно нулю) в любом направлении по отношению к ускорению свободного падения, вес тела равен весу тела в неподвижной системе: при a = 0 — P = P0.
Применение законов Ньютона для определения веса тела
Опора или подвес неподвижны |
|
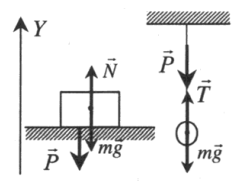 |
Второй закон Ньютона в векторной форме:
N + mg = ma или T + mg = ma Проекция на ось ОУ: N – mg = 0 или T — mg = 0 |
Ускорение опоры направлено вверх |
|
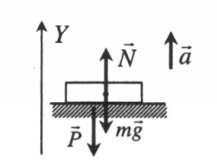 |
Второй закон Ньютона в векторной форме:
N + mg = ma Проекция на ось ОУ: N – mg = ma Вес тела: P = N = ma + mg = m(a + g) |
Ускорение опоры направлено вниз |
|
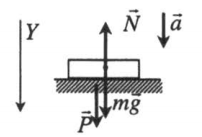 |
Второй закон Ньютона в векторной форме:
N + mg = ma Проекция на ось ОУ: mg – N = ma Вес тела: P = N = mg – ma = m(g – a) |
Вершина выпуклого моста |
|
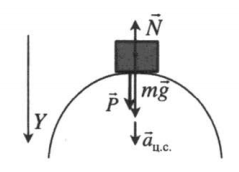 |
Второй закон Ньютона в векторной форме:
N + mg = maц.с. Проекция на ось ОУ: mg – N = m aц.с. Вес тела: P = N = mg – m aц.с. = m(g – aц.с.) |
Нижняя точка вогнутого моста |
|
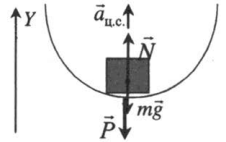 |
Второй закон Ньютона в векторной форме:
N + mg = maц.с. Проекция на ось ОУ: N – mg = maц.с. Вес тела: P = N = maц.с. + mg = m(aц.с. + g) |
Полный оборот на подвесе |
|
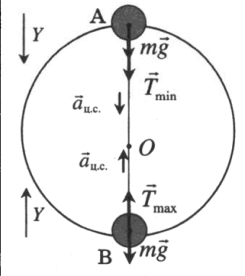 |
Второй закон Ньютона в векторной форме:
T + mg = ma Проекция на ось ОУ в точке А: T + mg = maц.с. Вес тела в точке А: P = T = maц.с. – mg = m (aц.с. – g) Проекция на ось ОУ в точке В: T – mg = maц.с. Вес тела в точке В: P = T = maц.с. + mg = m (aц.с. + g) Важно! Центростремительное ускорение всегда направлено к центру окружности. |
Пример №2. Автомобиль массой 1000 кг едет по выпуклому мосту с радиусом кривизны 40 м. Какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали невесомость?
Вес тела в верхней точке выпуклого моста равен:
P = m(g – aц.с.)
Чтобы пассажиры почувствовали состояние невесомости, вес тела должен быть равен 0:
m(g – aц.с.) = 0
Масса не может быть нулевой, поэтому:
g – aц.с. = 0
g = aц.с
Значит, пассажиры в верхней точке моста почувствуют невесомость, если центростремительное ускорение будет равно ускорению свободного падения. Центростремительное ускорение определяется формулой:
Отсюда скорость автомобиля в верхней точке моста должна быть равна:
Задание EF18133
Алгоритм решения
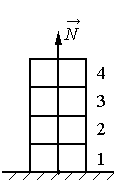
1.Вычислить силу, с которой оставшиеся кирпичи давят на опору.
2.Применить третий закон Ньютона.
3.Определить силу, с которой действует горизонтальная опора на первый кирпич.
Решение
Так как кирпичи покоятся, вес каждого равен:
P = mg
Вес двух кирпичей равен:
2P = 2mg
Опора действует на первый кирпич с такой же силой, с какой на него действует два кирпича, оставшихся после того, как два верхних кирпича убрали.
Следовательно:
N = 2P = 2mg
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17624
Подъёмный кран поднимает груз с постоянным ускорением. На груз со стороны каната действует сила, равная по величине 8⋅103 H. На канат со стороны груза действует сила, которая:
а) 8∙103 Н
б) меньше 8∙103 Н
в) больше 8∙103 Н
г) равна силе тяжести, действующей на груз
Алгоритм решения
1.Сформулировать третий закон Ньютона.
2.Применить закон Ньютона к канату и грузу.
3.На основании закона сделать вывод и определить силу, которая действует на канат со стороны груза.
Решение
Третий закон Ньютона формулируется так:
«Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны».
Математически он записывается так:
FA = –FB
Если на груз со стороны каната действует некоторая сила, то и груз действует на канат с этой силой, которая называется весом этого груза, или силой натяжения нити. Следовательно, груз действует на канат с силой 8∙103 Н.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22586
Мальчик медленно поднимает гирю, действуя на неё с силой 100 Н. Гиря действует на руку мальчика с силой:
а) больше 100 Н, направленной вниз
б) меньше 100 Н, направленной вверх
в) 100 Н, направленной вниз
г) 100 Н, направленной вверх
Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж, иллюстрирующий ситуацию.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций.
5.Вычислить силу, с которой гиря действует на руку мальчика.
Решение
Запишем исходные данные: мальчик поднимает гирю вверх с силой F = 100 Н.
Сделаем рисунок. В данном случае рука мальчика выступает в роли подвеса. Так как мальчик поднимает гирю медленно, можно считать, что он поднимает ее равномерно (равнодействующая всех сил равна нулю). Выберем систему координат, направление оси которой совпадает с направлением движения руки и гири.
На руку (подвес) действуют только две силы. Поэтому второй закон Ньютона выглядит следующим образом:
P + T = 0
Запишем этот же закон в проекции на ось ОУ:
–P + T = 0
Отсюда:
P = T
Следовательно, на руку мальчика действует вес гири, который по модулю равен силе, с которой мальчик действует на эту гирю.
Внимание! Существует второй способ решения задачи через третий закон Ньютона. Согласно ему, тела действуют друг на друга с силами, равными по модулю, но противоположными по направлению.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.6k