Загрузить PDF
Загрузить PDF
В математике существует ряд задач, в которых требуется найти вершину. Например, вершину многогранника, вершину или несколько вершин области системы неравенств, вершину параболы или квадратного уравнения. Эта статья расскажет вам, как найти вершину в разных задачах.
-
1
Теорема Эйлера. Теорема утверждает, что в любом многограннике число его вершин плюс число его граней минус число его ребер всегда равно двум.[1]
- Формула, описывающая теорему Эйлера: F + V — E = 2
- F — число граней.
- V — число вершин.
- E — число ребер.
- Формула, описывающая теорему Эйлера: F + V — E = 2
-
2
Перепишите формулу, чтобы найти число вершин. Если вам дано число граней и число ребер многогранника, вы можете быстро найти число его вершин с помощью формулы Эйлера.
- V = 2 — F + E
-
3
Подставьте данные вам значения в эту формулу. В результате вы получите число вершин многогранника.
- Пример: найдите число вершин многогранника, у которого 6 граней и 12 ребер.
- V = 2 — F + E
- V = 2 — 6 + 12
- V = -4 + 12
- V = 8
Реклама
- Пример: найдите число вершин многогранника, у которого 6 граней и 12 ребер.
-
1
Постройте график решения (области) системы линейных неравенств. В определенных случаях на графике можно увидеть некоторые или все вершины области системы линейных неравенств. В противном случае вам придется найти вершину алгебраически.
- При использовании графического калькулятора вы можете посмотреть весь график и найти координаты вершин.
-
2
Преобразуйте неравенства в уравнения. Для того, чтобы решить систему неравенств (то есть найти «х» и «у»), вам необходимо вместо знаков неравенства поставить знак «равно».
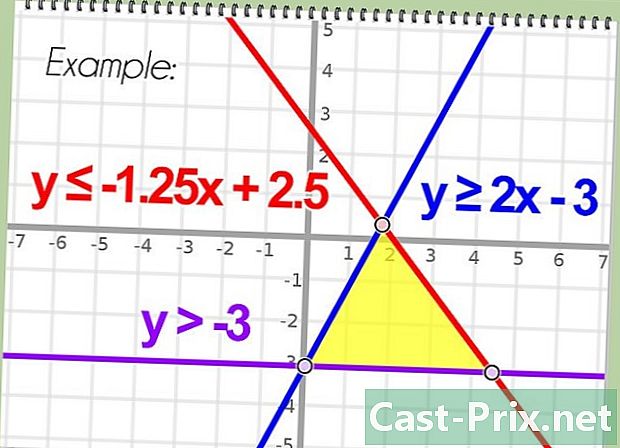
- Пример: дана система неравенств:
- у < х
- у> — х + 4
- Преобразуйте неравенства в уравнения:
- у = х
- у = — х + 4
- Пример: дана система неравенств:
-
3
Теперь выразите любую переменную в одном уравнении и подставьте ее в другое уравнение. В нашем примере подставьте значение «у» из первого уравнения во второе уравнение.
- Пример:
- у = х
- у = — х + 4
- Подставляем у = х в у = — х + 4:
- х = — х + 4
- Пример:
-
4
Найдите одну из переменных. Сейчас у вас есть уравнение только с одной переменной «х», которую легко найти.
- Пример: х = — х + 4
- х + х = 4
- 2x = 4
- 2x/2 = 4/2
- х = 2
- Пример: х = — х + 4
-
5
Найдите другую переменную. Подставьте найденное значение «х» в любое из уравнений и найдите значение «у».
- Пример: у = х
- у = 2
- Пример: у = х
-
6
Найдите вершину. Вершина имеет координаты, равные найденным значениям «х» и «у».
- Пример: вершина области данной системы неравенств есть точка О(2,2).
Реклама
-
1
Разложите уравнение на множители. Есть несколько способов разложения квадратного уравнения на множители. В результате разложения вы получаете два двучлена, которые при перемножении приведут к исходному уравнению.
- Пример: дано квадратное уравнение
- 3×2 — 6x — 45
- Сначала вынесите за скобку общий множитель: 3(x2 — 2x — 15)
- Перемножьте коэффициенты «а» и «с»: 1 * (-15) = -15.
- Найдите два числа, результат умножения которых равен -15, а их сумма равна коэффициенту «b» (b = -2): 3 * (-5) = -15; 3 — 5 = -2.
- Подставьте найденные значения в уравнение ax2 + kx + hx + c: 3(x2 + 3x — 5x — 15).
- Разложите исходное уравнение: f(x) = 3 * (x + 3) * (x — 5)
- Пример: дано квадратное уравнение
-
2
Найдите точку (точки), в которой график функции (в данном случае парабола) пересекает ось абсцисс.[3]
График пересекает ось Х при f(x) = 0.- Пример: 3 * (x + 3) * (x — 5) = 0
- х +3 = 0
- х — 5 = 0
- х = -3; х = 5
- Таким образом, корни уравнения (или точки пересечения с осью Х): А(-3, 0 ) и В(5, 0)
- Пример: 3 * (x + 3) * (x — 5) = 0
-
3
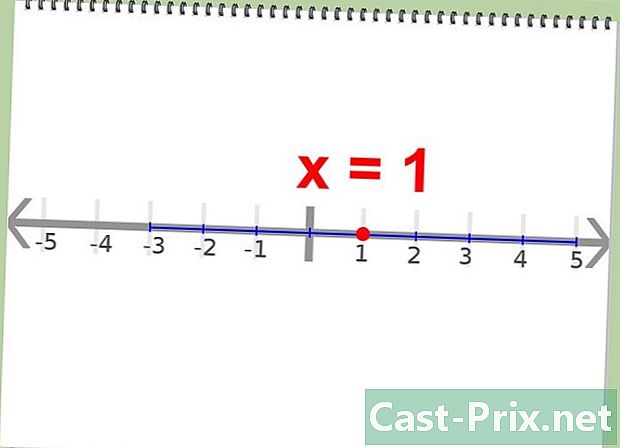
Найдите ось симметрии. Ось симметрии функции проходит через точку, лежащую посередине между двумя корнями. При этом вершина лежит на оси симметрии.
- Пример: х = 1; это значение лежит посередине между -3 и +5.
-
4
Подставьте значение «х» в исходное уравнение и найдите значение «у». Эти значения «х» и «у» — координаты вершины параболы.
- Пример: у = 3×2 — 6x — 45 = 3(1)2 — 6(1) — 45 = -48
-
5
Запишите ответ.
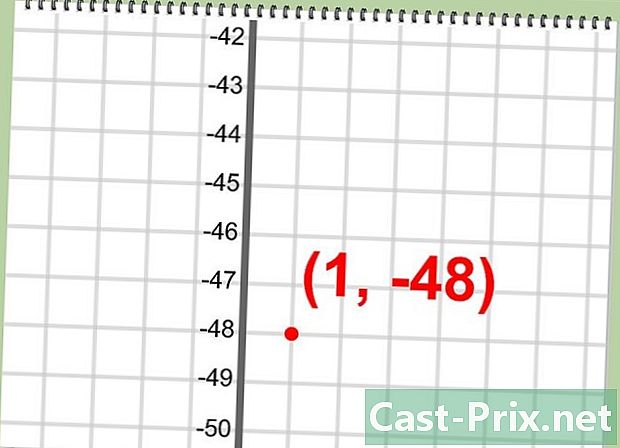
- Пример: вершина данного квадратного уравнения есть точка О(1,-48)
Реклама
-
1
Перепишите исходное уравнение в виде[4]
: y = a(x — h)^2 + k, при этом вершина лежит в точке с координатами (h,k). Для этого нужно дополнить исходное квадратное уравнение до полного квадрата.- Пример: дана квадратичная функция у = — х^2 — 8x — 15.
-
2
Рассмотрите первые два члена. Вынесите за скобку коэффициент первого члена (при этом свободный член игнорируется).
- Пример: -1(х^2 + 8x) — 15.
-
3
Разложите свободный член (-15) на два числа так, чтобы одно из них дополнило выражение в скобках до полного квадрата. Одно из чисел должно быть равно квадрату половины коэффициента второго члена (из выражения в скобках).
- Пример: 8/2 = 4; 4*4 = 16; поэтому
- -1(х^2 + 8x + 16)
- -15 = -16 + 1
- у = -1 (х ^ 2 + 8x + 16) + 1
- Пример: 8/2 = 4; 4*4 = 16; поэтому
-
4
Упростите уравнение. Так как выражение в скобках есть полный квадрат, можно переписать это уравнение в следующем виде (если необходимо, проведите операции сложения или вычитания за скобками):
- Пример: у = -1(х + 4)^2 + 1
-
5
Найдите координаты вершины. Напомним, что координаты вершины функции вида y = a(x — h)^2 + k равны (h,k).
- k = 1
- h = -4
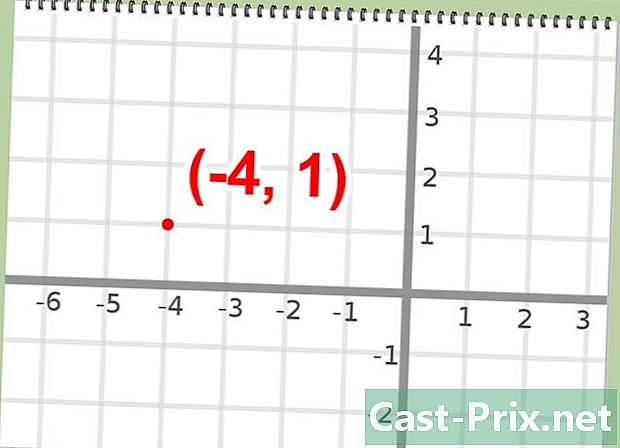
- Таким образом, вершина исходной функции есть точка О(-4,1).
Реклама
-
1
Найдите координату «х» по формуле: x = -b/2a (для функции вида y = ax^2 + bx + c). Подставьте значения «a» и «b» в формулу и найдите координату «х».
- Пример: дана квадратичная функция у = — х^2 — 8x — 15.
- х = -b/2a = -(-8)/(2*(-1)) = 8/(-2) = -4
- х = -4
-
2
Подставьте найденное значение «х» в исходное уравнение. Таким образом вы найдете «у». Эти значения «х» и «у» — координаты вершины параболы.
- Пример: у = — х^2 — 8x — 15 = -(-4 )^2 — 8(-4) — 15 = -(16) -(-32) — 15 = -16 + 32 — 15 = 1
- у = 1
- Пример: у = — х^2 — 8x — 15 = -(-4 )^2 — 8(-4) — 15 = -(16) -(-32) — 15 = -16 + 32 — 15 = 1
-
3
Запишите ответ.
- Пример: вершина исходной функции есть точка О(-4,1).
Реклама
Что вам понадобится
- Калькулятор
- Карандаш
- Бумага
Об этой статье
Эту страницу просматривали 11 682 раза.
Была ли эта статья полезной?
Автор:
Roger Morrison
Дата создания:
27 Сентябрь 2021
Дата обновления:
18 Май 2023
Содержание
- этапы
- Способ 1 Найти количество вершин многогранника
- Способ 2 Найти вершины системы линейных уравнений
- Метод 3 из 3: Найдите вершину притчи с симметрией слабости
- Метод 4 из 4: Найдите вершину притчи, заполнив квадрат
- Метод 5 из 5: Найдите вершину притчи, используя простую формулу
В этой статье: Найти количество вершин многогранника. Найти вершины системы линейных уравнений. Найти вершину параболы, зная ось симметрии.
Многие математические функции воспитывают вершины. У многогранников есть вершины, системы также линейные уравнения, а также притчи (которые являются графическим представлением уравнений второй степени). Расчеты этих конкретных точек различаются в зависимости от математической функции, которая доступна для вас. Здесь мы увидим 5 сценариев
этапы
Способ 1 Найти количество вершин многогранника
-
Взгляните на формулу Эйлера для многогранников. Эта формула устанавливает, что для любого многогранника выпуклыйколичество граней плюс количество вершин минус количество ребер всегда равно 2.
- Написанная в форме уравнения, формула выглядит следующим образом: f + s — a = 2
- е количество лиц
- s количество вершин или углов
- имеет это количество гребней
- Написанная в форме уравнения, формула выглядит следующим образом: f + s — a = 2
-
Управляйте уравнением, чтобы выделить количество вершин («s»). Если вам даны числа граней («f») и ребер («a»), вы, благодаря формуле Эйлера, легко вычислите количество вершин. Вы передаете «F» и «A» на другой стороне уравнения, изменяя их знаки, и вуаля!
- s = 2 — f + a
-
Сделайте цифровое приложение и решите уравнение. Если вам даны «f» и «a», все, что вам нужно сделать, это поместить их в уравнение и выполнить вычисления. Вы получите количество вершин.
- Пример: у вас есть многогранник с 6 гранями и 12 ребрами …
- s = 2 — f + a
- с = 2 — 6 + 12
- с = -4 + 12
- с = 8
- Пример: у вас есть многогранник с 6 гранями и 12 ребрами …
Способ 2 Найти вершины системы линейных уравнений
-
Нарисуйте графики различных линейных неравенств. Таким образом, вы сможете увидеть некоторые или все вершины (здесь они являются точками пересечения), все зависит от уравнений и размера вашего графа. Если вы не видите ни одного из них, они находятся за пределами вашего графика, поэтому вы должны рассчитать их.
- С помощью графического калькулятора вы сможете визуализировать вершины различных кривых (если они есть) и считывать их координаты.
-
Преобразуйте уравнения в уравнения. Чтобы решить систему уравнений, необходимо временно преобразовать уравнения в уравнения, чтобы рассчитать х и там.
- Пример: Либо следующая система уравнений …
- у <х
- у> -х + 4
- Неравенства преобразуются в уравнения:
- у = х
- у = -х + 4
- Пример: Либо следующая система уравнений …
-
Замените одно из неизвестных в другом уравнении. Несмотря на то, что существуют разные способы, мы увидим так называемый метод «замены» х и тампростейшее конечно. Во втором уравнении мы примем там значение, которое имеет в первом. Мы заменяем там, Это равносильно тому, что оба уравнения равны.
- пример:
- у = х
- у = -х + 4
- По замене, у = -х + 4 будет выглядеть так:
- х = -х + 4
- пример:
-
Найдите значение неизвестного. Теперь у вас есть только один неизвестный (х), легко найти здесь по игре сложений, вычитаний, умножений и делений. Это простое уравнение первой степени.
- Пример: х = -х + 4
- х + х = -х + х + 4
- 2x = 4
- 2x / 2 = 4/2
- х = 2
- Пример: х = -х + 4
-
Найдите второго неизвестного. Возьмите только что найденное значение и поместите его в одно из двух уравнений, чтобы определить там.
- Пример: у = х
- у = 2
- Пример: у = х
-
Определите саммит. Вершина тогда имеет для координат ваши два значения, х и там.
- Пример: (2, 2)
Метод 3 из 3: Найдите вершину притчи с симметрией слабости
-
Поместите уравнение в факторы. Напишите уравнение второй степени в факторизованном виде. Есть несколько способов факторизации в соответствии с уравнением, которое мы имеем в начале. Во всяком случае, в конце концов, вы должны иметь уравнение в виде продуктов.
- Пример: (используя разложение)
- f (x) = 3x — 6x — 45
- Поместите 3 в фактор, который дает: 3 (х — 2х — 15)
- Умножьте коэффициенты x («a») и x (постоянная «c»), то есть 1 x -15 = -15
- Найдите два числа, произведение которых равно -15 и сумма равна коэффициенту (б) из х (здесь b = — 2). 3 и — 5 делают сделку, так как 3 x -5 = -15 и 3 + (- 5) = 3 — 5 = — 2
- В уравнении топор + кх + вх + с, замените «k» и «h» на ранее найденные значения, что дает: 3 (x + 3x — 5x — 15)
- Рефакторинг. Тогда получим: f (x) = 3 (x + 3) (x — 5)
- Пример: (используя разложение)
-
Найти точку пересечения параболы с осью X (ось X). Чтобы найти эту точку, нужно решить уравнение: f (x) = 0.
- Пример: 3 (x + 3) (x — 5) = 0
- х +3 = 0
- х — 5 = 0
- х = -3 и х = 5
- Корни уравнения: (-3, 0) и (5, 0)
- Пример: 3 (x + 3) (x — 5) = 0
-
Найдите середину этих точек. Недостаток симметрии притчи пройдет через эту точку, которая находится в середине двух корней. Эта ось является фундаментальной, так как вершина выше ее по определению.
- Пример: середина -3 и 5: х = 1
-
В исходном уравнении заменить х на это значение 1. Вы найдете значение там кто будет хозяином твоей вершины.
- Пример: y = 3x — 6x — 45 = 3 (1) 2 — 6 (1) — 45 = -48
-
Введите координаты вашего саммита. Просто сведи две ценности вместе, х и там, чтобы иметь позицию саммита.
- Пример: (1, -48)
Метод 4 из 4: Найдите вершину притчи, заполнив квадрат
-
Преобразуйте исходное уравнение в вершину. Уравнение в форме «вершины» имеет стиль: у = а (х — ч) + к, в котором вершина параболы имеет для координат (ч, к), Поэтому абсолютно необходимо преобразовать исходное уравнение, для которого оно имеет вид этого типа. Для этого вам нужно, как мы это называем, заполнить квадрат.
- Пример: y = -x — 8x — 15 (формы ax + bx + c)
-
Начните с изоляции имеет. Поместите в коэффициент, только с двумя первыми членами, коэффициент термина во второй степени (будущее имеет). Не трогай постоянное с на данный момент!
- Пример: -1 (х + 8х) — 15
-
Найдите третий термин для скобок. Этот термин не выбран случайным образом: он должен быть таким, чтобы сделать внутри скобок идеальный квадрат (или замечательную идентичность) формы (ax + b). Этот новый термин, который будет добавлен, является квадратом половины коэффициента среднего термина (б).
- пример: б = 8, его половина равна: 8/2 = 4. Возьмем квадрат: 4 x 4 = 16. Таким образом, получим:
- -1 (х + 8х + 16)
- Чтобы уравнение было несбалансированным, то, что было добавлено (или вычтено) внутри скобок, должно быть удалено (или добавлено) наружу.
- у = -1 (х + 8х + 16) — 15 + 16
- пример: б = 8, его половина равна: 8/2 = 4. Возьмем квадрат: 4 x 4 = 16. Таким образом, получим:
-
Выполните расчеты, чтобы упростить уравнение. Напишите в скобках как идеальный квадрат и суммируйте константы.
- Пример: у = -1 (х + 4) + 1
-
Найти координаты вершины из вершины. Помните! нам нужно было уравнение в виде вершины: у = а (х — ч) + к найти координаты напрямую (ч, к) сверху. Тогда достаточно прочитать, а иногда и сделать небольшой расчет, чтобы найти эти два значения (внимание к знакам!)
- к = 1
- h = -4 (-h = 4, поэтому h = — 4)
- Итак, вершина притчи находится в точке с координатами. (-4, 1)
Метод 5 из 5: Найдите вершину притчи, используя простую формулу
-
Найти непосредственно labscisse х сверху. С притчей уравнения у = топор + бх + сLabscisse х Из вершины притчи можно узнать по следующей формуле: х = -б / 2а, Затем просто замените «a» и «b» их соответствующими значениями.
- Пример: y = -x — 8x — 15
- x = -b / 2a = — (-
/ (2 x (-1)) = 8 / (- 2) = -4
- х = -4
-
Затем поместите это значение «x» обратно в исходное уравнение, чтобы найти порядок («y») вершины.
- Пример: y = -x — 8x — 15 = — (- 4) — 8 (-4) — 15 = — (16) — (-32) — 15 = -16 + 32 — 15 = 1
- у = 1
- Пример: y = -x — 8x — 15 = — (- 4) — 8 (-4) — 15 = — (16) — (-32) — 15 = -16 + 32 — 15 = 1
-
Затем введите свой результат, который является координатами вершины. Это координатная точка («х», «у»).
- Пример: (-4, 1)
Обязательно к прочтению

Как убрать разливы нефти
В этой статье: Очистка разливов растительного маслаИспользуйте моющее средство для разливов масляной краски. Удалите разливы нефти на бетоне. Оказание помощи в случае экологических катастроф22. Если в…
Как почистить электрическую зубную щетку
В этой статье: Очистите головку вашей зубной щетки. Очистите ручку зубной щетки. Сохраните чистую зубную щетку. Важно, чтобы вы держали зубную щетку в чистоте, так как ванные комнаты являются гнездом …
Содержание:
- § 1 Многогранные формы (многогранники)
- § 2 Из чего состоит многогранник
- § 3 Классификация многогранников (выпуклые, невыпуклые)
- § 4 Сумма всех плоских углов при вершине многогранника
§ 1 Многогранные формы (многогранники)
Многогранники представляют собой простейшие тела в пространстве, подобно тому, как многоугольники простейшие фигуры на плоскости.
Многогранные формы мы видим ежедневно: книга, комната, многоэтажный дом (с горизонтальной крышей) – это прямоугольные параллелепипеды.
Граненый карандаш, гайка – дают представления о призмах.
— многие архитектурные сооружения или их детали представляют собой пирамиды – такие формы имеют известные египетские пирамиды или башни Кремля.
Ранее были рассмотрены тетраэдр и параллелепипед: тетраэдр – это поверхность, составленная из четырех треугольников, параллелепипед – поверхность, составленная из шести параллелограммов. Каждая из этих поверхностей ограничивает некоторое геометрическое тело, отделяет это тело от остальной части пространства .
§ 2 Из чего состоит многогранник
(определение и элементы многогранника)
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником. Тело, ограниченное многогранником, часто также называют многогранником
Тетраэдр и параллелепипед – примеры многогранников. Октаэдр, представленный на рисунке, так же является многогранником. Он составлен из восьми треугольников.
Обратим внимание, из чего состоит поверхность многогранника. Это многоугольники они называются гранями многогранника. Стороны граней называются ребрами, а концы ребер – вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Плоскость, по обе стороны от которой имеются точки многогранника называется секущей плоскостью, а общая часть многогранника и секущей плоскости – сечением многогранника.
§ 3 Классификация многогранников (выпуклые, невыпуклые)
Многогранники бывают выпуклые и невыпуклые. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
Тетраэдр, параллелепипед, октаэдр – выпуклые многогранники.
Существуют и невыпуклые многогранники, такие как на рисунке.
Поясним сказанное на примере знакомого нам куба. Куб есть выпуклый многогранник.
Его поверхность состоит из шести квадратов: АВСD,AA1B1B, … Они являются его гранями.
Ребрами куба являются стороны этих квадратов: АВ, ВС, СС1…
Вершинами куба являются вершины квадратов А,В,С, D, А1,В1…
У куба шесть граней, двенадцать ребер и восемь вершин.
Ясно, что все грани выпуклого многогранника являются выпуклыми многоугольниками.
§ 4 Сумма всех плоских углов при вершине многогранника
Отметим так же то, что в выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 3600.
Это утверждение поясняет следующая иллюстрация:
тетраэдр «разрезан» вдоль ребер и все его грани с общей вершиной А развернуты так, что оказались расположенными в одной плоскости . Видно, что сумма всех плоских углов при вершине А, т.е. меньше 360°
Список рекомендованной литературы:
- Геометрия. 10 – 11 классы : учебник для общеобразоват. учреждений : базовый и профил. уровни / [ Л. С. Атанасян, В. Ф. Бутузов, С.Б. Кадомцев и др.]. – 22-е изд. – М. : Просвещение, 2013. – 255 с. : ил. – (МГУ — в школе)
- Учебно – методическое пособие в помощь школьному учителю Составитель Яровенко В.А. Поурочные разработки по геометрии к учебному комплекту Л. С. Атанасяна и др. ( М. : Просвещение) 10 класс
- Рабинович Е. М. Задачи и упражнения на готовых чертежах. 10 – 11 классы. Геометрия. – М. : Илекса , 2006 . – 80 с.
- М. Я Выгодский Справочник по элементарной математике М. : АСТ Астрель , 2006. — 509с.
- Аванта+. Энциклопедия для детей. Том 11. Математика 2-е изд., перераб. — М.: Мир энциклопедий Аванта+: Астрель 2007. — 621 с. Ред. коллегия: М. Аксёнова, В. Володин, М. Самсонов
Download Article
Download Article
There are multiple mathematical functions that use vertices. Polyhedrons have vertices, systems of inequalities can have one vertex or multiple vertices, and parabolas or quadratic equations can have a vertex, as well. Finding the vertex[1]
varies depending on the situation, but here’s what you need to know about finding vertices for each scenario.
-
1
Learn Euler’s Formula. Euler’s Formula, as it is used in reference to geometry and graphs, states that for any polyhedron that does not intersect itself, the number of faces plus the number of vertices, minus the number of edges, will always equal two.[2]
- Written out as an equation, the formula looks like: F + V — E = 2
- F refers to the number of faces
- V refers to the number of vertices, or corner points
- E refers to the number of edges
- Written out as an equation, the formula looks like: F + V — E = 2
-
2
Rearrange the formula to find the number of vertices. If you know how many faces and edges the polyhedron has, you can quickly count the number of vertices by using Euler’s Formula. Subtract F from both sides of the equation and add E to both sides, isolating V on one side.[3]
- V = 2 — F + E
Advertisement
-
3
Plug the numbers in and solve. All you need to do at this point is to plug the number of sides and edges into the equation before adding and subtracting like normal. The answer you get should tell you the number of vertices and complete the problem.[4]
- Example: For a polyhedron that has 6 faces and 12 edges…
- V = 2 — F + E
- V = 2 — 6 + 12
- V = -4 + 12
- V = 8
- Example: For a polyhedron that has 6 faces and 12 edges…
Advertisement
-
1
Graph the solutions of the system of linear inequalities. In some instances, graphing the solutions for all inequalities in the system can visually show you where some, if not all, of the vertices lie. When it does not, however, you will need to find the vertex algebraically.[5]
- If using a graphing calculator to graph the inequalities, you can usually scroll over to the vertices and find the coordinates that way.
-
2
Change the inequalities to equations. In order to solve for the system of inequalities, you will need to temporarily change the inequalities to equations, allowing you the ability to find values for x and y.[6]
- Example: For the system of inequalities:
- y < x
- y > -x + 4
- Change the inequalities to:
- y = x
- y = -x + 4
- Example: For the system of inequalities:
-
3
Substitute one variable for the other. While there are a couple of different ways you can solve for x and y, substitution is often the easiest to use. Plug the value of y from one equation into the other equation, effectively «substituting» y in the other equation with additional x values.
- Example: If:
- y = x
- y = -x + 4
- Then y = -x + 4 can be written as:
- x = -x + 4
- Example: If:
-
4
Solve for the first variable. Now that you only have one variable in the equation, you can easily solve for that variable, x, as you would in any other equation: by adding, subtracting, dividing, and multiplying.
- Example: x = -x + 4
- x + x = -x + x + 4
- 2x = 4
- 2x / 2 = 4 / 2
- x = 2
- Example: x = -x + 4
-
5
Solve for the remaining variable. Plug your new value for x into one of the original equations to find the value of y.
- Example: y = x
- y = 2
- Example: y = x
-
6
Determine the vertex. The vertex is simply the coordinate consisting of your new x and y values.[7]
- Example: (2, 2)
Advertisement
-
1
Factor the equation. Rewrite the quadratic equation in its factored form. There are several ways to factor out a quadratic equation, but when done, you should be left with two sets of parentheses that, when multiplied together, equal your original equation.
- Example: (using decomposition)
- 3×2 — 6x — 45
- Factor out the common factor: 3 (x2 — 2x — 15)
- Multiply the a and c terms: 1 * -15 = -15
- Find two numbers with a product that equals -15 and a sum that equals the b value, -2: 3 * -5 = -15; 3 — 5 = -2
- Substitute the two values into the equation ax2 + kx + hx + c: 3(x2 + 3x — 5x — 15)
- Factor the polynomial by grouping: f(x) = 3 * (x + 3) * (x — 5)
- Example: (using decomposition)
-
2
Find the point at which the equation crosses the x-axis.[8]
Whenever the function of x, f(x), equals 0, the parabola will cross the x-axis. This will occur when either set of factors equals 0.- Example: 3 * (x + 3) * (x — 5) = 0
- х +3 = 0
- х — 5 = 0
- х = -3 ; х = 5
- Therefore, the roots are: (-3, 0) and (5, 0)
- Example: 3 * (x + 3) * (x — 5) = 0
-
3
Calculate the midway point. The axis of symmetry for the equation[9]
will lie directly in between the two roots of the equation. You need to know the axis of symmetry since the vertex lies on it.- Example: x = 1; this value lies directly between -3 and 5
-
4
Plug the x value into the original equation. Plug the x value for your axis of symmetry into either equation for your parabola. The y value will be the y value for your vertex.[10]
- Example: y = 3×2 — 6x — 45 = 3(1)2 — 6(1) — 45 = -48
-
5
Write down the vertex point. At this point, your last calculated x and y values should give you the coordinates of your vertex.
- Example: (1, -48)
Advertisement
-
1
Rewrite the original equation in its vertex form. The «vertex» form of an equation is written as y = a(x — h)^2 + k, and the vertex point will be (h, k). Your current quadratic equation will need to be rewritten into this form, and in order to do that, you’ll need to complete the square.[11]
- Example: y = -x^2 — 8x — 15
-
2
Isolate the a value. Factor out the coefficient of the first term, a from the first two terms in the equation. Leave the final term, c, alone for now.[12]
- Example: -1 (x^2 + 8x) — 15
-
3
Find a third term for the parentheses. The third term must complete the set in the parentheses so that the values in parentheses form a perfect square. This new term is the squared value of half the coefficient of the middle term.
- Example: 8 / 2 = 4; 4 * 4 = 16; therefore,
- -1(x^2 + 8x + 16)
- Also keep in mind that what you do to the inside must also be done to the outside:
- y = -1(x^2 + 8x + 16) — 15 + 16
- Example: 8 / 2 = 4; 4 * 4 = 16; therefore,
-
4
Simplify the equation. Since your parentheses now form a perfect square, you can simplify the parenthetical portion to its factored form. Simultaneously, you can do any addition or subtraction needed to the values outside of the parentheses.[13]
- Example: y = -1(x + 4)^2 + 1
-
5
Figure out what the coordinates are based on the vertex equation. Recall that the vertex form of an equation is y = a(x — h)^2 + k, with (h, k) representing the coordinates of the vertex. You now have enough information to plug values into the h and k slots and complete the problem.
- k = 1
- h = -4
- Therefore, the vertex of this equation can be found at: (-4, 1)
Advertisement
-
1
Find the x coordinate of the vertex directly. When the equation of your parabola can be written as y = ax^2 + bx + c, the x of the vertex can be found using the formula x = -b / 2a. Simply plug the a and b values from your equation into this formula to find x.
- Example: y = -x^2 — 8x — 15
- x = -b / 2a = -(-8)/(2*(-1)) = 8/(-2) = -4
- x = -4
-
2
Plug this value into the original equation. By plugging a value for x into the equation, you can solve for y. This y value will be the y coordinate of your vertex.
- Example: y = -x^2 — 8x — 15 = -(-4)^2 — 8(-4) — 15 = -(16) — (-32) — 15 = -16 + 32 — 15 = 1
- y = 1
- Example: y = -x^2 — 8x — 15 = -(-4)^2 — 8(-4) — 15 = -(16) — (-32) — 15 = -16 + 32 — 15 = 1
-
3
Write down your vertex coordinates. The x and y values you have are the coordinates of your vertex point.
- Example: (-4, 1)
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Things You’ll Need
- Calculator
- Pencil
- Paper
References
About This Article
Article SummaryX
To find the vertex of a parabola with axis of symmetry, factor the quadratic equation and find the point at which the equation crosses the x-axis. Next, calculate the midway point, which will lie directly in between the two roots of the equation. Then, plug the x value into either equation for your parabola. Your calculated x and y values are the coordinates of the vertex. For tips on finding a vertex in other mathematical scenarios, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 62,622 times.
Reader Success Stories
-
«So helpful.»
Did this article help you?
На этом уроке мы поговорим о геометрическом теле,
которое называют многогранником. А также узнаем, какими элементами
обладают многогранники.
Как мы уже знаем, геометрия делится на два раздела –
на планиметрию и стереометрию. Планиметрия изучает плоские геометрические
фигуры и их свойства, т.е. фигуры, целиком расположенные в некоторой плоскости.
Стереометрия изучает свойства фигур в пространстве. Пространственные
геометрические фигуры, в отличие от плоских фигур, обладают вместимостью, т.е.
они имеют объем. Такие фигуры называют еще объемными.
Все объемные фигуры можно распределить на две большие
группы – круглые тела (это цилиндр, конус, сфера и шар), их называют телами
вращения, и тела, которые содержат углы, вершины, грани и ребра (это призмы и
пирамиды), такие тела называют многогранниками. Представления о геометрических
телах дают нам окружающие нас предметы.
Многогранники представляют собой простейшие тела в
пространстве, подобно тому, как многоугольники простейшие фигуры на плоскости.
С многогранными формами мы ежедневно встречаемся в жизни – это кубики, с
которыми играют дети, многогранный карандаш, книги, многоэтажные дома,
природные кристаллы, древние египетские пирамиды и т.д.
Ранее, в планиметрии при изучении многоугольников, мы
говорили, что многоугольник – это замкнутая ломаная без самопересечений. Или
иными словами, многоугольником называется часть плоскости, состоящая из простой
замкнутой ломаной и ограниченной ею внутренней области.
При изучении многогранников мы же будем
пользоваться вторым толкованием многоугольника.
Итак, уже само слово «многогранник» указывает на то,
что это тело имеет много граней. Многогранник представляет собой геометрическое
тело, ограниченное конечным числом плоских многоугольников, любые два смежные
из которых не лежат в одной плоскости.
Вы хорошо знакомы с одним из самых простых
многогранников – прямоугольным параллелепипедом. Представление о прямоугольном
параллелепипеде дают, например, спичечный коробок, холодильник, шкаф и другие
тела.
Школьный кабинет также имеет форму прямоугольного
параллелепипеда. Поверхность прямоугольного параллелепипеда состоит из 6
прямоугольников. Частным случаем прямоугольного параллелепипеда является куб.
Напомню, что поверхность куба состоит из шести равных квадратов.
Можно сказать, что многогранник – это
поверхность, составленная из многоугольников и ограничивающая некоторое
геометрическое тело. Это тело также называется многогранником.
На рисунке изображены два многогранника.
Первый из них называют – тетраэдром, второй –
октаэдром. Они составлены соответственно из 4 и 8 треугольников. Что и отражено
в их названиях: в переводе с греческого τετρα – «тетра» – четыре, а οκτώ
– «окто» – восемь.
Обратим внимание, из чего состоит поверхность
многогранника. Давайте рассмотрим, например, прямоугольный параллелепипед ABCDA1B1C1D1.
Как уже говорилось ранее, поверхность прямоугольного
параллелепипеда состоит из 6 прямоугольников. Т.е. его поверхность составлена
из 6 многоугольников. Назовем их: ,
,
,
,
,
. Многоугольники, из которых
составлен многогранник, называют его гранями. Заметим, что никакие две
соседние грани многогранника не лежат в одной плоскости.
Стороны граней ,
,
,
,
,
,
,
,
,
,
,
называются ребрами многогранника.
Концы рёбер ,
,
,
,
,
,
,
– вершины
многогранника.
Отрезок, соединяющий две вершины, не принадлежащие
одной грани, называется диагональю многогранника, например, A1C – называется
диагональю многогранника. В данном случае, диагональ прямоугольного
параллелепипеда.
Многогранники, также как и многоугольники бывают
выпуклыми и невыпуклыми.
Смотрите, если провести плоскость, например, через
грань DD1C1C, то весь многогранник будет лежать по одну сторону от этой
плоскости. Аналогично, если провести плоскости и через остальные его грани,
многогранник всегда будет расположен по одну сторону от этих плоскостей. Такой
многогранник называется выпуклым.
Определение. Многогранник называется выпуклым,
если он лежит по одну сторону от плоскости каждой своей грани.
Если это условие не выполняется, т.е. многогранник
лежит по разные стороны хотя бы от одной плоскости, проходящей через грань, то
многогранник называется невыпуклым.
На рисунке изображен пример невыпуклого многогранника.
Если провести, например, плоскость через указанную грань, то видно, что одна
часть многогранника расположена по одну сторону, а вторая его часть по другую
сторону этой плоскости.
Задание. Сколько граней, рёбер и вершин имеет
каждый из изображенных многогранников?
Итак, как мы уже говорили, поверхность прямоугольного
параллелепипеда составлена из шести прямоугольников. Т.е. она состоит из 6
граней. Теперь посчитаем, сколько же у него ребер. Напомню, что стороны граней
называются ребрами. Назовем их. Это АB, BC, CD, AD, A1B1, B1C1, C1D1, A1D1, AA1, DD1, BB1 и CC1.
Итого, получили, что прямоугольный параллелепипед имеет 12 ребер. Концы этих
ребер называются вершинами. Перечислим их. Это А, B, C, D, A1,
B1, C1, D1. Т.е. у прямоугольного параллелепипеда – 8
вершин.
Следующее геометрическое тело тетраэдр. Его
поверхность состоит из четырех треугольников. Т.е. имеет четыре грани. Его
ребрами будут стороны АB, BC, АC, AD, BD, и CD. Т.е. тетраэдр имеет 6 ребер. Вершины тетраэдра А, B, C и D. Их
4.
И теперь рассмотрим октаэдр. Его поверхность состоит
из 8 треугольников. Т.е. октаэдр имеет 8 граней. Также он имеет 12 ребер и 6
вершин.
Подведем итоги урока. На этом уроке мы узнали, какое
геометрическое тело называют многогранником. Рассмотрели, какими элементами
обладают многогранники. А именно, это грани, ребра и вершины. Узнали, что
прямоугольный параллелепипед имеет 6 граней, 12 ребер и 8 вершин. Познакомились
с интересными многогранниками, которые называются тетраэдр и октаэдр. Узнали,
что тетраэдр имеет 4 грани, 6 ребер и 4 вершины, а октаэдр – 8 граней, 12 ребер
и 6 вершин.




























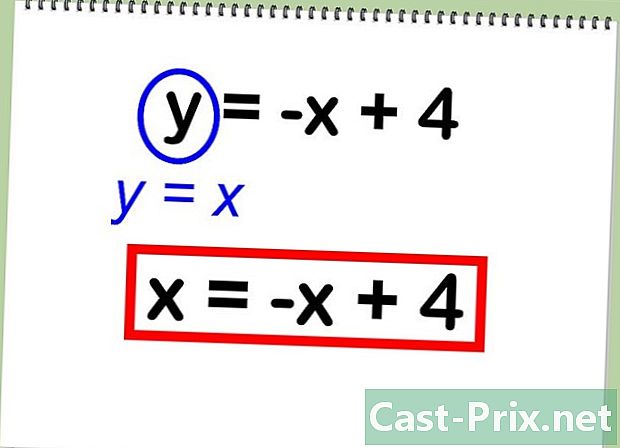



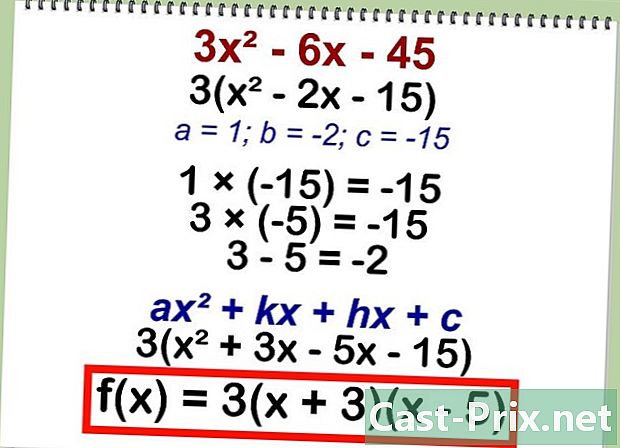





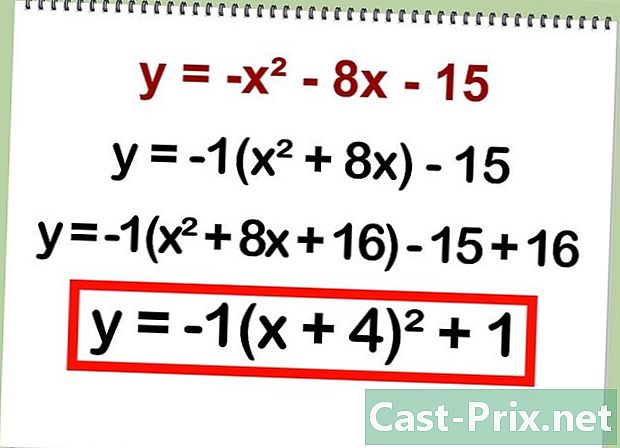


 / (2 x (-1)) = 8 / (- 2) = -4
/ (2 x (-1)) = 8 / (- 2) = -4