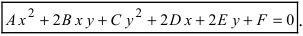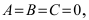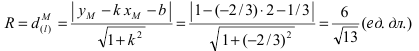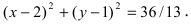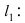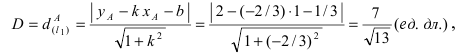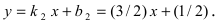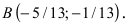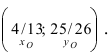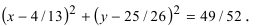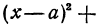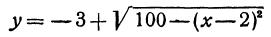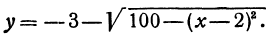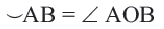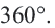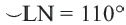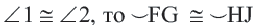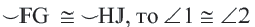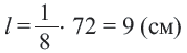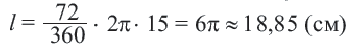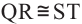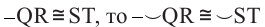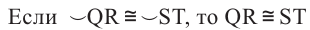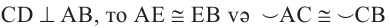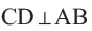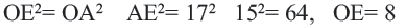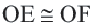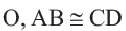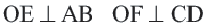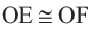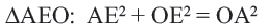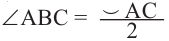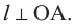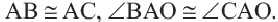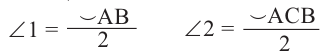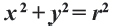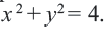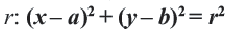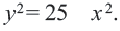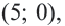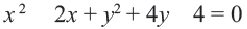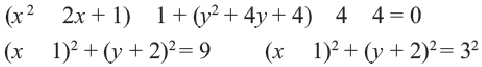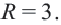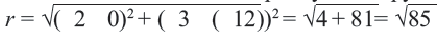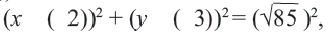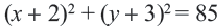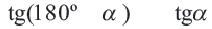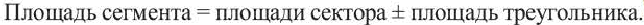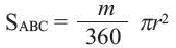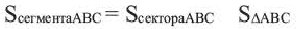Уравнение с двумя переменными и его график. Уравнение окружности
п.1. Понятие уравнения с двумя переменными
Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm) – гипербола.
Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.
Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm<frac1x>) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).
п.2. Обобщенные правила преобразования графика уравнения
Пусть F(x; y) = 0 – исходный график некоторой функции
Симметричное отображение относительно оси OY
Симметричное отображение относительно оси OX
Центральная симметрия относительно начала координат
Параллельный перенос графика на a единиц вправо
Параллельный перенос графика на a единиц влево
Параллельный перенос графика на b единиц вниз
Параллельный перенос графика на b единиц вверх
Сжатие графика к оси OY в a раз
Сжатие графика к оси OX в b раз
F(x; by) = 0
0 Например:
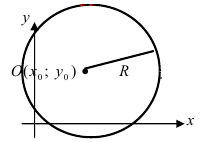
Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm <(x-2)^2+(y-1)^2=9>$$
п.4. Примеры
Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm<7>=-frac<2> + 2 > ) – это прямая
б) xy + 4 = 0
Выразим y из уравнения: ( mathrm> ) – это гипербола
в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm=2> )
г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm<5>> ) – это парабола
Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm<5>=-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.
б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.
в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.
г) |x – 1| + |y – 2| = 4
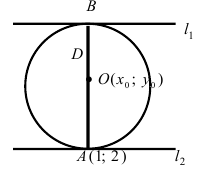
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).
д) (mathrm<frac<|x-1|><2>+2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.
Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.
Как построить окружность?
Как построить окружность?
Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.
Радиусом называется любой отрезок соединяющей точку окружности с ее центром.
Чтобы построить окружность необходимо знать уравнение окружности:
(х – а) 2 + (у – b) 2 = R 2
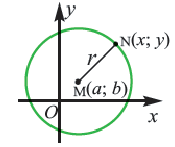
Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.
И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:
Пример №1:
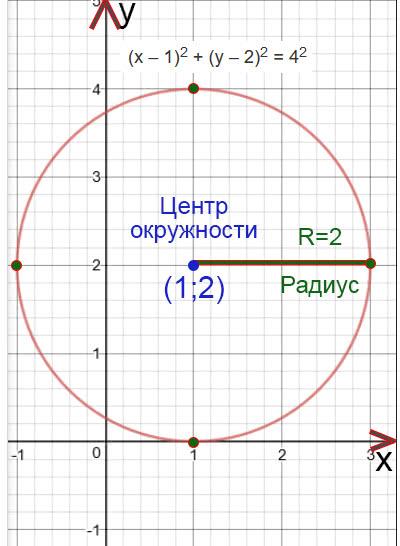
(х – 1) 2 + (у – 2) 2 = 4 2
Найдем центр окружности:
х – 1=0
x=1
Центр окружности будет находится в точке (1;2)
Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2
Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность. 
Пример №2:
х 2 + (у + 1) 2 =1
Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2
Найдем центр окружности:
х=0
Центр окружности будет находится в точке (0;–1)
Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1
Построим окружность. 
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Как строить графики окружности
Как построить окружность?
Как построить окружность?
Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.
Радиусом называется любой отрезок соединяющей точку окружности с ее центром.
Чтобы построить окружность необходимо знать уравнение окружности:
(х – а) 2 + (у – b) 2 = R 2
Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.
И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:
Пример №1:
(х – 1) 2 + (у – 2) 2 = 4 2
Найдем центр окружности:
х – 1=0
x=1
Центр окружности будет находится в точке (1;2)
Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2
Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.
Пример №2:
х 2 + (у + 1) 2 =1
Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2
Найдем центр окружности:
х=0
Центр окружности будет находится в точке (0;–1)
Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1
Построим окружность.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Уравнение с двумя переменными и его график. Уравнение окружности
п.1. Понятие уравнения с двумя переменными
Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm ) – гипербола.
Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.
Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm ) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).
п.2. Обобщенные правила преобразования графика уравнения
Пусть F(x; y) = 0 – исходный график некоторой функции
Симметричное отображение относительно оси OY
Симметричное отображение относительно оси OX
Центральная симметрия относительно начала координат
Параллельный перенос графика на a единиц вправо
Параллельный перенос графика на a единиц влево
Параллельный перенос графика на b единиц вниз
Параллельный перенос графика на b единиц вверх
Сжатие графика к оси OY в a раз
Сжатие графика к оси OX в b раз
F(x; by) = 0
0 Например:
Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm $$
п.4. Примеры
Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm =-frac + 2 > ) – это прямая
б) xy + 4 = 0
Выразим y из уравнения: ( mathrm > ) – это гипербола
в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm =2> )
г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm > ) – это парабола
Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm =-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.
б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.
в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.
г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).
д) (mathrm +2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.
Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.
Окружность
Окружность — это замкнутая кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки. Заданная точка является центром окружности. На Рис.1 точка О — центр окружности.
Основные характеристики окружности
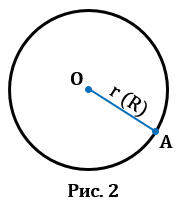
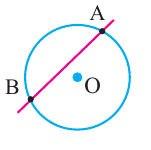
1. Радиус — это отрезок, соединяющий центр с какой-либо точкой окружности. У любой окружности можно провести бесконечно много радиусов, которые будут иметь одну и ту же длину. Обозначают радиус r или R. На Рис.2 представлена окружность с центром в точке О радиусом ОА.
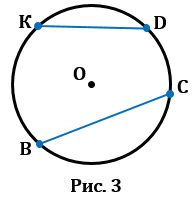
2. Хорда — это отрезок, соединяющий две точки окружности. У любой окружности можно провести бесконечно много хорд. На Рис.3 ВС и KD — хорды окружности с центром в точке О.
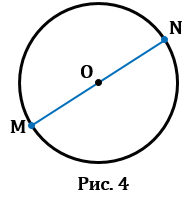
3. Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр (т.е. диаметр — это частный случай хорды). У любой окружности можно провести бесконечно много диаметров, которые будут иметь одну и ту же длину. На Рис.4 МN — диаметр окружности с центром в точке О. Обозначают диаметр d или D. Диаметр в два раза больше радиуса, т.е. d = 2r (D = 2R), откуда r = d : 2 (R = D : 2), следовательно, центр окружности (точка О) является серединой диаметра.
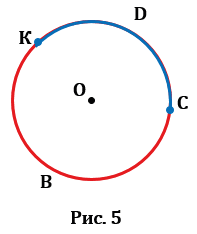
4. Дуга — это часть окружности, ограниченная двумя точками. На Рис.5 KDC и KBC — дуги, ограниченные точками К и С.
Построение окружности
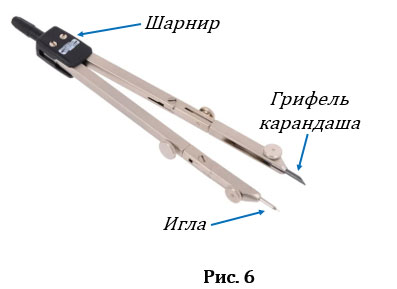
Для того, чтобы построить окружность используют специальный прибор, который называется циркулем (Рис.6). Циркуль состоит из двух частей, соединённых шарниром. Обычно на конце одной из них располагается игла, на конце другой — пишущий предмет, например грифель карандаша.
Выполнение построения:
- отмечаем точку, которая будет центром окружности;
- делаем нужный раствор циркуля (расстояние между иглой и грифелем карандаша), т.е. определяем радиус окружности, которую нам нужно построить (Рис.7);
- ставим иглу циркуля в точку, которая определяет центр окружности;
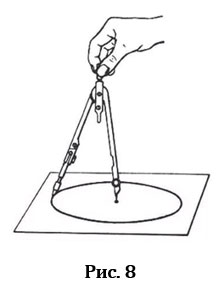
- проводим окружность данного радиуса (Рис.8).
Для того, чтобы построить окружность на местности используют веревку. Сначала отмечаем место, которое будет определять центр окружности, вбиваем в это место колышек, привязываем к нему один конец веревки и отходим, держа другой конец веревки на расстояние равное радиусу окружности, которую мы хотим получить, отмечаем линию окружности (Рис.9).
Часть плоскости, которая ограничена окружностью (выделена черным цветом), называется кругом (выделен голубым цветом) (Рис.10).
Поделись с друзьями в социальных сетях:
http://tutomath.ru/uroki/kak-postroit-okruzhnost.html
http://b4.cooksy.ru/articles/kak-stroit-grafiki-okruzhnosti
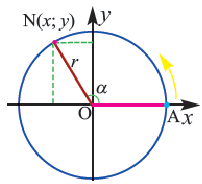
Сегодня поговорим об единичной окружности 🧑🏫
Можно ли найти точку (её координаты) на окружности, зная координаты центра окружности, её радиус и угол поворота?🤔
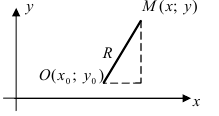
Ну, конечно, можно! Записывай и запоминай общую формулу для нахождения координат точки:
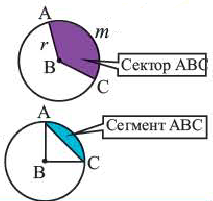
x=x0+r⋅cos δ
y=y0+r⋅sin δ
x0,y0 — координаты центра окружности;
r — радиус окружности;
δ —угол поворота радиуса вектора.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Содержание:
Окружность:
Определение: Кривой второго порядка называется линия, описываемая уравнением 
Замечание: Если коэффициенты 
При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки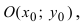 
называемой центром окружности, на расстояние R, которое называется радиусом окружности.
Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:
Рис. 27. Вывод уравнения окружности.
Из рисунка видно, что по теореме Пифагора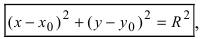 
которое определяет уравнение окружности (Рис. 28): 
Рис. 28. Окружность. 
Если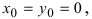 
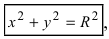
то уравнение принимает вид 
который называется каноническим уравнением окружности.
Пример:
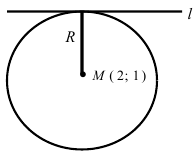
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия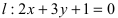 
является касательной к окружности.
Решение:
Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.
В уравнении окружности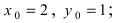 
таким образом оно имеет вид: 
Пример:
Составить уравнение окружности, касающейся двух параллельных прямых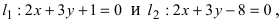 
причем одной из них в т. А (1; 2).
Решение:
Прежде всего определим, на какой из прямых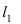 
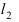
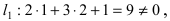
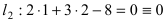
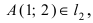
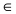
или 
лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых 
следовательно, точка A(1; 2) принадлежит линии 
(в сокращенной форме это предложение пишут так: 
где значок 
означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой 
а радиус окружности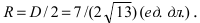 
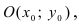
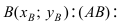
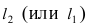
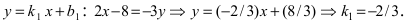
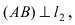
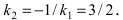
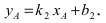
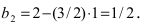
Найдём координаты центра окружности точки 
которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки 
перейдем от общего уравнения прямой 
к уравнению прямой с угловым коэффициентом 
Так как прямая
то её угловой коэффициент 
Прямая (АВ) проходит через известную точку A(1;2), следовательно, 
Отсюда находим 
Таким образом,уравнение прямой (АВ):
Найдем координаты точки B, которая является пересечением прямых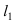 
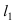
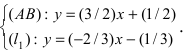
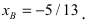
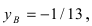
и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых 
и (АВ): (В): 
Подставим выражение для переменной у из второго у равнения в первое, получим 
Подставив это значение во второе уравнение системы, найдем 
т.е. 
Для вычисления координат точки О применим формулы деления отрезка пополам (О):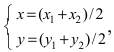 
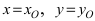
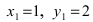
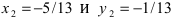
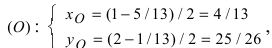
в этой формуле 
(координаты точки О), 
(координаты точки А), 
(координаты точки В), следовательно, 
т.е. координаты точки О 
Таким образом, уравнение искомой окружности имеет вид: 
Окружность в высшей математике
Рассмотрим уравнение
которое получается из уравнения (I), если положить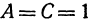 
, 
.
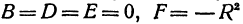
Если в формулу, выражающую расстояние между двумя точками, подставить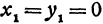 
, 
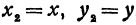
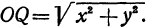
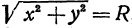
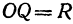
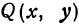
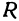
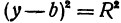
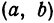
, то получим 
Из уравнения (1) находим, что 
, т. е. 
. Это значит, что все точки 
, координаты которых удовлетворяют уравнению (1), находятся на расстоянии 
от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса 
с центром в начале координат. Аналогично получаем, что уравнение 
определяет окружность радиуса с центром в точке 
.
Пример:
Найдем уравнение окружности с центром в точке 
и радиусом, равным 10.
Решение:
Полагая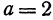
, 
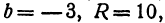
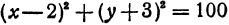
получим 
.
Разрешим это уравнение относительно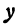 
, будем иметь
и
Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.
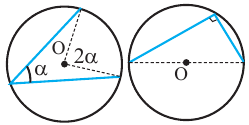
Центральный угол. Градусная мера дуги
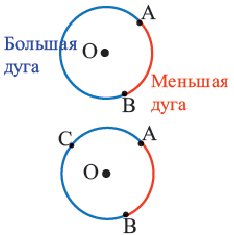
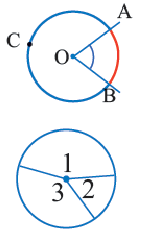
Дуга окружности. Если отметить на окружности точки 
и 
, то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка 
является какой-либо точкой дуги 
, то 
. Если точки и являются концами диаметра, го каждая дуга является полуокружностью.
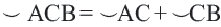
Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла: 
Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна 
Дуги окружности и их величины
Пример: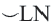 
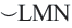
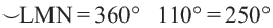
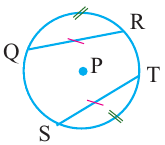
минорная дуга: 
мажорная дуга: 
Конгруэнтные дуги
В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.
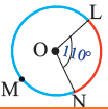
Если 
Если 
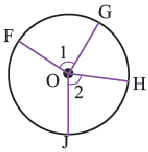
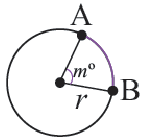
Длина дуги
Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.
Длина дуги в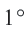 
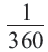
равна 
части длины окружности.
Длина дуги, соответствующей центральному углу с градусной мерой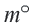 
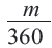
, составляет 
части длины окружности: 
Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)
Пример №1
Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу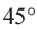 
.
Решение:
Так как центральный угол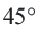 
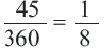
составляет 
часть полного угла, то длина искомой дуги: 
Пример №2
Найдите длину дуги, соответствующей центральному углу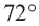 
в окружности радиусом 15 см.
Решение: подставляя значения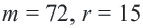 
в формулу длины дуги находим: 
Окружность и хорда
Теорема о конгруэнтных хордах
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.
Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.
1)Если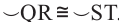 
, то 
2)Если 
Доказательство теоремы 1:
Теорема о серединном перпендикуляре хорд
Теорема 2.
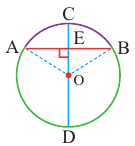
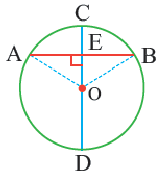
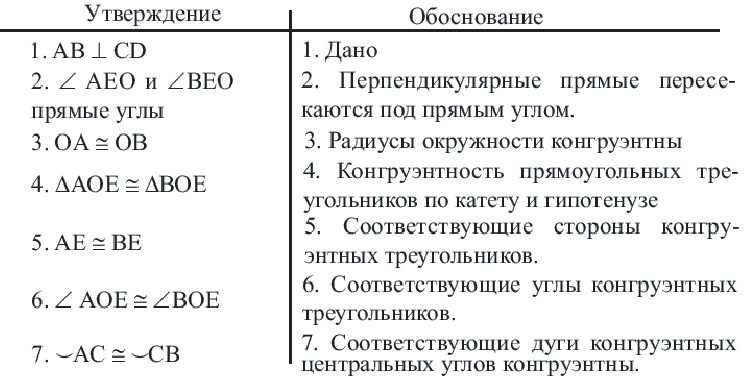
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.
Если 
Доказательство теоремы 2.
Дано: 
— центральный угол, 
Докажите: 
Начертите радиусы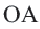 
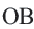
и 
окружности.
Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.
Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.
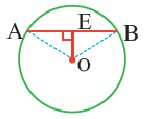
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если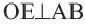 
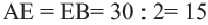
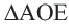
, то 
. Из 
по теореме Пифагора имеем: 
Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности
Теорема 3.
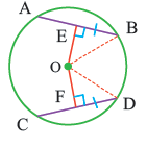
Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.
Если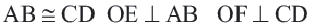 
, то 
Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.
Доказательство теоремы 3
Дано: Окружность с центром 
Докажите: 
Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам. 
и 
— серединные перпендикуляры конгруэнтных хорд 
и 
. 
, так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности 
и 
: 
. Прямоугольные треугольники, 
и 
конгруэнтны (по катету и гипотенузе). Так как и являются соответствующими сторонами данных треугольников, то они конгруэнтны: 
. Теорема доказана.
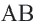
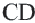
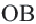
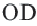
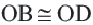
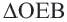
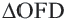
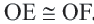
Задача. Хорды 
и 
находятся на одинаковом расстоянии от центра окружности. 
. Если радиус окружности равен 41 единице, то найдите 
.
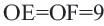
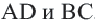
Решение: Так как хорды и находятся на одинаковом расстоянии от центра, то они конгруэнтны: 
Соединим точки 
и 
с точкой 
В прямоугольном треугольнике 
; 
; 
; 
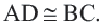
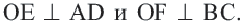
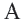
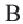
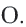
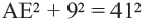
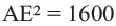
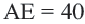
Так как 
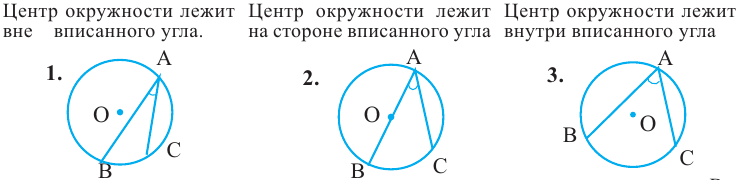
Угол, вписанный в окружность
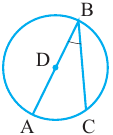
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.
является углом вписанным в окружность с центром 
, а 
дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.
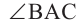
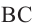
Угол, вписанный в окружность:
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается. 
Доказательство (текстовое):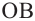 
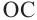
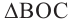
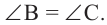
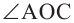
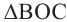
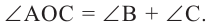
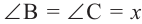
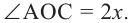
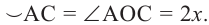
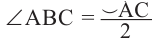
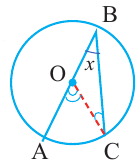
и 
радиусы окружности и 
равнобедренный треугольник. Значит, 
Так как 
является внешним углом 
, 
Если примем, что 
, то 
Так как градусные меры центрального угла и опирающейся на него дуги равны, то 
Следовательно, 
.
Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.
Конгруэнтные углы, вписанные в окружность
Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны.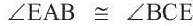 
, 
.
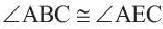
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если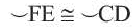 
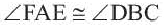
, то 
.
Касательная к окружности
Касательная. Признак касательной
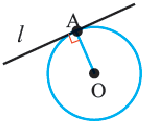
Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Прямая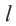 
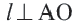
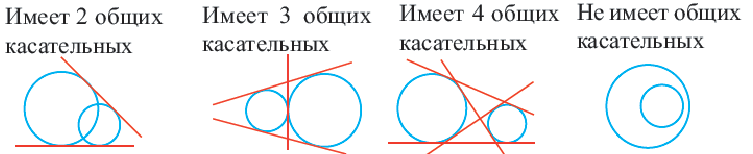
является касательной к окружности. Значит, 
Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.
Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.
Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.
Доказательство теоремы 1. Если прямая 
— касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая 
не перпендикулярна радиусу 
Проведем 
и на прямой выделим отрезок 
Тогда 
так как 
Значит, точка 
также находится на окружности. То есть прямая имеет с окружностью две общие точки, что противоречит условию. Значит, 
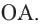
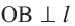
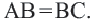
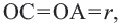
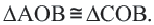
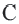
Свойства касательных, проведенных к окружности из одной точки
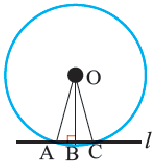
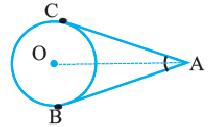
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.
и 
касательные, проведенные из точки 
к окружности с центром 
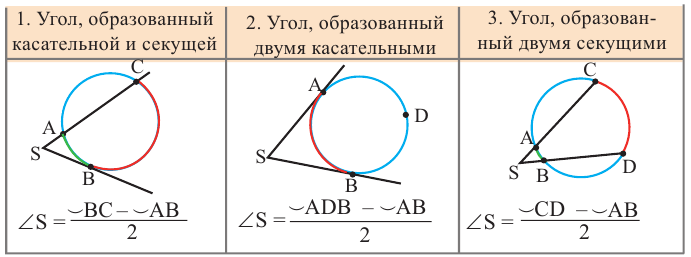
Углы, образованные секущими и касательными
Прямая, имеющая две общие точки с окружностью, называется секущей окружности.
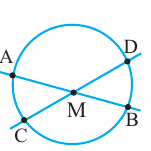
Углы между двумя секущими
Вершина угла находится внутри окружности
Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному. 
Углы между касательной и секущей
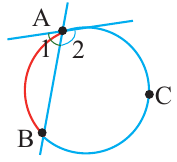
Вершина угла находится на окружности
Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.
Углы, образованные касательной и секущей
Вершина угла находится вне окружности
Теорема 1.
Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.
Отрезки секущих и касательных
Длина отрезков, секущих окружность
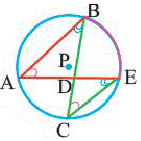
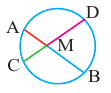
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.
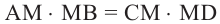
Теорема 2. Если из точки 
провести две прямые, пересекающие окружность соответственно в точках 
и 
, 
и 
то верно равенство 
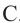
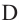
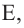
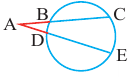
Теорема 3. Если из точки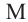 
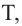
проведены прямая, которая пересекает окружность в точках и и касательная к окружности в точке 
то верно равенство: 
Уравнение окружности
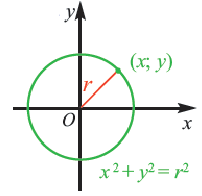
Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом 
и с центром в начале координат. Расстояние между центром окружности 
и ее любой точкой 
равно радиусу окружности.
Расстояние между двумя точками
Упрощение
Возведение обеих частей в квадрат
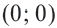
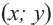
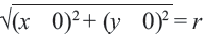
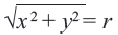
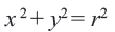
Уравнение окружности с центром в начале координат и радиусом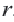 
: 
Например, уравнение окружности с центром в начале координат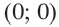 
и радиусом 2 имеет вид: 
По формуле расстояния между центром окружности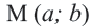 
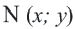
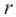
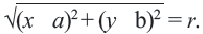
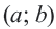
и точки 
на окружности радиуса 
имеем 
Возведя в квадрат обе части, получаем уравнение окружности с центром в точке 
и радиусом 
Например, уравнение окружности с центром в точке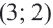 
и радиусом 4 имеет вид: 
Пример №3
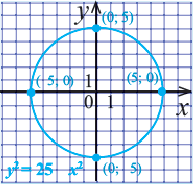
Постройте на координатной плоскости окружность, заданную уравнением 
Решение: Напишем уравнение в виде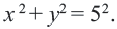 
Как видно, 
Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например,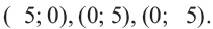 
Проведем окружность через эти точки.
Пример №4
Точка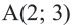 
находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.
Решение: Записав координаты точки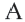 
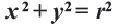
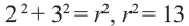
в уравнении 
, получим: 
Уравнение этой окружности: 
Пример №5
Найдем центр и радиус окружности, заданной уравнением 
Решение: 
Центр окружности точка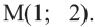 
Радиус 
Пример №6
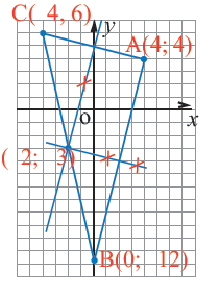
Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках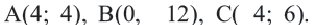 
На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.
Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка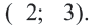 
Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности, 
Уравнение окружности: 
Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.
Координаты точек, находящихся на окружности, и тригонометрические отношения
Если точка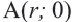 
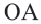
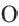
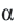
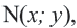
при повороте радиуса 
вокруг точки 
против движения часовой стрелки на угол 
преобразуется в точку 
то 
Для координат точки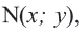 
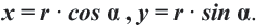
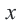
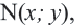
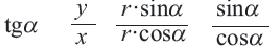
соответствующей углу поворота 
на окружности, верны формулы 
В этих формулах — угол, отсчитываемый от положительной оси 
против движения часовой стрелки. Если точка 
не находится на оси ординат, то 
.
Синусы смежных углов равны, а косинусы взаимно противоположны.
Из этих формул при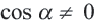 
почленным делением получаем:
С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.
Сектор и сегмент
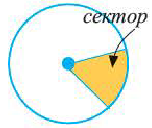
Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.
Например, часть круга, соответствующая центральному углу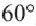 
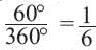
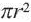
, составляет 
часть всего круга. Так как площадь круга 
, то площадь этого сектора будет 
Сегмент часть круга, ограниченная хордой и соответствующей дугой.
Площадь сектора
Площадь сектора: 
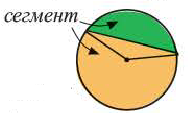
Площадь сегмента: 
Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь 
- Эллипс
- Гипербола
- Парабола
- Многогранник
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
Download Article
Download Article
Finding the center of a circle can help you perform basic geometric tasks like finding the circumference or area. There are several ways to find the center point! You can draw crossed lines, you can draw overlapping circles, or you can use a straightedge and ruler.
Things You Should Know
- Measure out and draw a set of crossed lines inside of a circle to pinpoint the center.
- Sketch two separate sets of overlapping circles to identify the exact center point.
- Draw a square snugly around the circle. Sketch an «X» between all 4 corners of the square to find the circle’s center.
-
1
Draw a circle. Use a compass, or trace any circular object. The size of the circle does not matter. If you’re finding the center of an existing circle, then you don’t need to draw a new circle.
- A geometry compass is a tool specifically designed to draw and measure circles. Buy one in a school or office supply store![1]
- A geometry compass is a tool specifically designed to draw and measure circles. Buy one in a school or office supply store![1]
-
2
Sketch a chord between two points. A chord is a straight line segment that links any two points along the edge of a curve.[2]
Name the chord AB.- Consider using a pencil to sketch your lines. This way, you can erase the marks once you’ve found the center. Draw with a light touch so that it’ll be easier to erase.
Advertisement
-
3
Draw a second chord. This line should be parallel and equal in length to the first chord that you drew. Name this new chord CD.[3]
-
4
Make another line between A and C. This third chord (AC) should stretch through the center of the circle – but you will need to draw one more line to find the exact center point.
-
5
Join B and D. Draw one final chord (BD) across the circle between Point B and Point D. This new line should cross over the third chord (AC) that you drew.
-
6
Find the center. If you have drawn straight and accurate lines, then the center of the circle lies at the intersection of the crossed lines AC and BD.[4]
Mark the center point with a pen or pencil. If you only want the center point marked, then erase the four chords that you drew.
Advertisement
-
1
Draw a chord between two points. Use a ruler or straightedge to draw a straight line inside the circle, from one edge to another. The points that you use don’t matter. Label the two points A and B.
-
2
Use a compass to draw two overlapping circles. The circles should be the exact same size. Make A the center of one circle, and B the center of the other. Space the two circles so that they overlap like a Venn diagram.
- Draw these circles in pencil, not pen. The process will be simpler if you are able to erase these circles later on.
-
3
Draw a vertical line through the two points at which the circles intersect. There will be a point at the top and a point at the bottom of the «Venn diagram» space created between the overlap of the circles. Use a ruler to make sure that the line protrudes straight through these points. Finally, label the two points (C and D) at which this new line crosses the rim of the original circle. This line marks the diameter of the original circle.
-
4
Erase the two overlapping circles. This should clear up your work space for the next step of the process. Now, you should have a circle with two perpendicular lines running through it. Do not erase the center points (A and B) of these circles! You will be drawing two new circles.
-
5
Sketch two new circles. Use your compass to draw two equal circles: one with the point C at its center, and one with the point D. These circles, too, should overlap like a Venn diagram. Remember: C and D are the points at which the vertical line intersects the main circle.
-
6
Draw a line through the points at which these new circles intersect. This straight, horizontal line should cut through the overlap space of the two new circles. This line is the second diameter of your original circle, and it should be exactly perpendicular to the first diameter line.
-
7
Find the center. The intersection point of the two straight diameter lines is the exact center of the circle! Mark this center point for reference. If you want to clean up the page, feel free to erase the diameter lines and the non-original circles.
Advertisement
-
1
Draw two straight, intersecting tangent lines onto the circle. The lines can be completely random. However, the process will be easier if you make them roughly square or rectangular.[5]
-
2
Translate both of the lines to the other side of the circle. You will end up with four tangent lines forming a parallelogram or a rough rectangle.
-
3
Draw the diagonals of the parallelogram. The point where these diagonal lines intersect is the circle’s center.
-
4
Check the accuracy of the center with a compass. The center should be on target as long as you didn’t slip while translating the lines or when drawing the diagonals. Feel free to erase the parallelogram and diagonal lines.
Advertisement
Practice Problems and Answers
Add New Question
-
Question
How do you find the center of a circle if you’re only given the equation?
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
Expert Answer
-
Question
How do you find the center of the circle if you’re only given the endpoints of the diameter?
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
Expert Answer
-
Question
In the first method, what do I do if the chords are of different lengths?
It’s not easy to construct parallel chords of equal length. In practice, it would be a process of trial and error until you get the chords you need. But the real goal here is to find the center of a circle, and here’s a way to do it without worrying about equal and parallel chords: (1) draw any two or more chords; (2) perpendicularly bisect each chord (using either a compass or a ruler and right triangle; (3) the perpendicular bisectors will intersect at the circle’s center.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
You can also find the center of a circle by mathematically «completing the square.»[6]
This is useful if you are given a circle equation, but you aren’t working with a physical circle. -
Try using graph paper instead of blank or ruled paper. It might help to have the perpendicular lines and boxes for guidance.
-
If you have right angled square, place the corner anywhere along the circumference. Draw the 2 lines that intersect the circumference. Draw a line between those 2 points. Repeat on any other point on the circle. Where the lines intersect is the centrepoint.
Advertisement
-
A straightedge is not the same as a ruler. A straightedge can be any straight and even surface, but a ruler shows measurements. You can turn a straightedge into a functional ruler by marking it with inch or centimeter increments.
-
In order to find the true center of a circle, you must use a geometric compass and a straightedge.
Advertisement
Things You’ll Need
- Pencil
- Paper
- Straightedge
- Geometric compass
- Grid paper
References
About This Article
Article SummaryX
To find the center of a circle, start by drawing a straight line between 2 points on the circle. Don’t worry about trying to draw the straight line so it’s in the center — anywhere on the circle will do. Then, draw a second straight line that’s parallel to the first line on the opposite side of the circle. Next, draw a diagonal line from the first end of the first line to the opposite end of the second line. Repeat with the other two ends so that you’ve drawn an “X.” The point where the lines intersect is the center of the circle! If you want to learn how to draw overlapping circles to find the center, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 756,712 times.
Reader Success Stories
-
«I had a circular piece of wood that was a circular tabletop that I wanted to use for something else. I needed to…» more
Did this article help you?
Как найти координаты точки в окружности
Под окружностью понимают фигуру, которая состоит из множества точек плоскости, равноудаленных от ее центра. Расстояние от центра до точек окружности называется радиусом.
Вам понадобится
- — простой карандаш;
- — тетрадь;
- — транспортир;
- — циркуль;
- — ручка.
Инструкция
Прежде чем найти координаты той либо иной точки окружности, постройте заданную окружность. При ее построении вам могут встретиться множество новых понятий. Так хорда – это отрезок, который соединяет две точки окружности, причем хорда, проходящая через центр окружности — максимальная (она носит название диаметра). Кроме того, к окружности может быть проведена касательная, которая представляет собой прямую, перпендикулярно расположенную к радиусу окружности, который проведен к точке пересечения касательной и рассматриваемой геометрической фигуры.
Если по условию задания известно, что построенную вами окружность пересекает другая окружность (она меньше по размерам), изобразите это графически: на рисунке должно быть изображено, что две эти окружности пересекаются, то есть имеют ряд общих точек. Центр первой окружности обозначьте точкой 1 (ее координаты (X1,Y1)), а ее радиус — R1. Таким образом, центр второй окружности должен быть обозначен точкой 2 (координаты этой точки (X2,Y2)), а радиус — R2. В точках пересечения фигур поставьте точки 3 (X3,Y3) и 4 (X4,Y4). Центральная точка пересечения должна быть обозначена 0: ее координаты (X,Y).
Для того чтобы найти координаты пресечения данных окружностей, а следовательно и точку, принадлежащую и первой, и второй из них, вам придется решить квадратное уравнение. Рассмотрите два образовавшихся треугольника (?103 и ?203) и проанализируйте их показатели. Гипотенузы этих треугольников — R1 и R2 соответственно. Зная значение гипотенуз, найдите отрезок D, соединяющий центр первой окружности с центром второй. Выбранный метод расчета напрямую зависит от того, какими получились анализируемые вами треугольники. Если они прямоугольные, то квадрат длины гипотенузы каждого из них будет равен сумме квадратов катетов данного треугольника. К тому же, длину катета можно найти по формуле: a = ccos ?, где с – длина гипотенузы, а cos? – косинус прилежащего угла. Найдя значение катетов, определите координаты интересующей вас точки.
Видео по теме
Обратите внимание
Будьте внимательны, рассчитывая значения катетов: не допустите ошибку.
Полезный совет
Не забудьте: один из углов прямоугольного треугольника прямой, то есть равен 90о.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.