Формула нахождения вершины параболы
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Парабола – это геометрическое множество точек, равноудалённых от точки F, не лежащей на параболе, и прямой $d$, не проходящей через точку $F$.
Что значит вершина параболы
Определение 2
Вершина параболы – это точка, ближайшая к директрисе параболы. Она является центром отрезка, ограниченного точкой фокуса параболы $F$ и директрисой $d$.
Производная в вершине квадратичной параболы равна нулю.
Каноническое уравнение параболы $y^2 = 2px$ справедливо для параболы, вершина которой находится в центре осей.
Для того, чтобы определить, принадлежит ли точка графику заданной параболы, необходимо подставить её координаты в формулу $y = ax^2 + bx + c$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Если равенство выполняется — точка принадлежит графику.
Как найти вершины параболы, задающейся квадратичной функцией
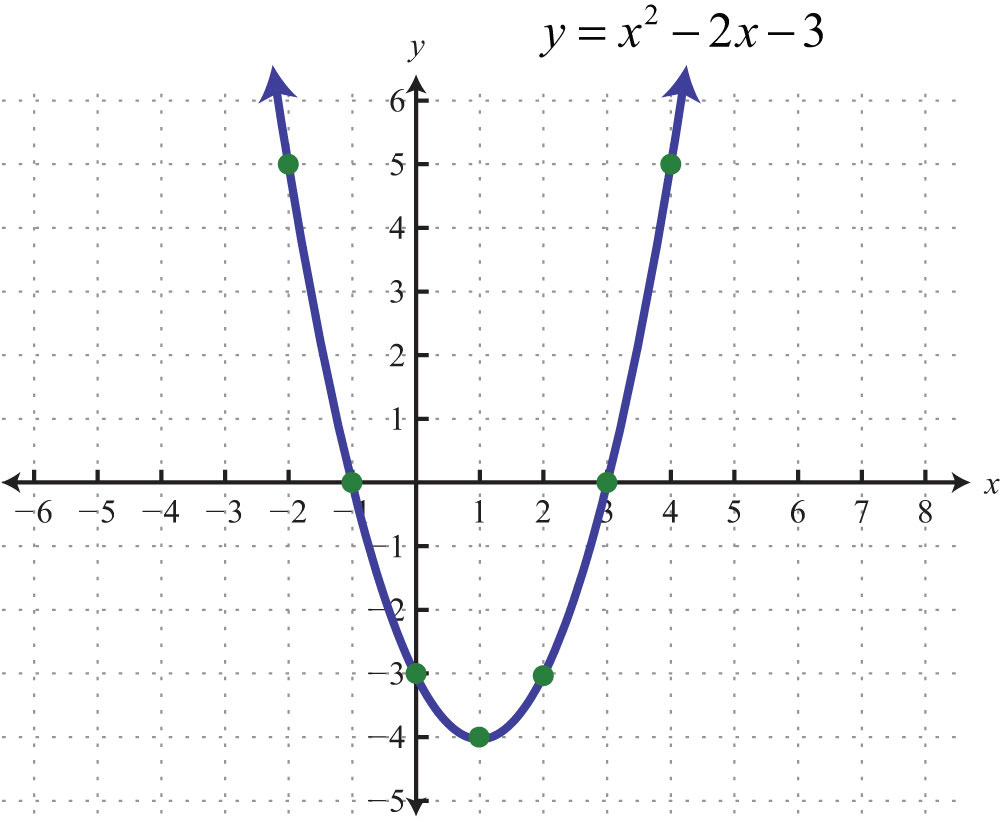
Рисунок 1. Пример уравнения и графика квадратичной параболы
Довольно часто парабола задаётся квадратичной функцией вида $y = ax^2 + bx + c$, вершина такой параболы находится в произвольной точке.
Какой-то единой формулы для нахождения сразу обеих координат вершины параболы нет, но при этом определить координаты вершины параболы по уравнению довольно просто.
Алгоритм для нахождения вершины параболы такой:
- Запишите коэффициенты $a, b, c$ из уравнения. Если коэффициент $a$ при $y$ положительный, то ветви параболы будут смотреть вверх, а если отрицательный, то вниз.
- Найдите абсциссу вершины параболы ($x$ вершины) по формуле $x = — frac{b}{2a}$, для этого воспользуйтесь коэффициентами $a, b, c$ из уравнения.
- Подставьте найденный $x$ в уравнение параболы и вычислите ординату вершины параболы $y$.
- Запишите полученные координаты x и y вершины параболы в форме точки $(x; y)$.
Пример 1
Рассмотрим уравнение параболы $y = x^2 – 5x + 7$
- Коэффициенты этой параболы $a = 1$, $b = -5$, $c = 7$.
- Для вычисления x вершины параболы подставьте $a = 1$ и $b = -5$ в формулу $x = — frac{b}{2a}= frac{5}{2}=2.5$
- Подставьте найденный $x$ в исходное уравнение:
- $y = 2,5^2 – 5 cdot 2.5 + 7$
- $y = 0,75$
- Координаты вершины этой параболы $(2.5;0.75)$.
Вершина кубической параболы
Чтобы найти вершины (точки локальных минимумов и максимумов) кубической параболы, необходимо найти её производную, приравнять её к нулю и затем вычислить $x$ и $y$.
Если же необходимо найти точку перегиба кубической параболы, необходимо найти вторую производную и также приравнять её к нулю.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 04.12.2022
Понятие вершины параболы
Парабола – это геометрическое множество точек, которые равноудалены от точки F, и которая не является частью параболы и прямой, а также не проходит через центр отрезка.
Вершина параболы — это некая точка, которая расположена ближе всего в директрисе параболы. Данная точка является центром любого отрезка, который ограничен точками фокуса параболы и директрисой.
Формула
Каноническое уравнение параболы выглядит следующим образом:
[y^{2}=2 p x]
Где: [p] — параметр параболы; [x] — ось данной параболы.
Данное уравнение будет справедливо только для параболы, вершина которой проходит через центр осей.
Чтобы определить принадлежность точки к графику заданной параболы, нужно точку подставить в уравнение:
[y=a x^{2}+b x+c]
где:
- a, b, c — заданные коэффициенты;
- х — ось координатной прямой.
Определение вершины кубической параболы
Определение
Кубическая парабола – плоская алгебраическая кривая третьего порядка.
Ее каноническое уравнение в прямоугольной декартовой системе координат имеет вид у = ах3, где а ≠ 0.
Для кубической параболы характерен центр симметрии в самом начале координат. Данная точка является точкой перегиба кривой. Касательная к кубической параболе, в этой же точке именуется как ось абсцисс.
Для того, чтобы определить точки вершин кубической параболы, нужно вычислить ее производную. Точки вершин, иначе еще называют точками минимума и максимума.
После того, как определится производная, нужно ее значение приравнять к нулевому. Затем можно приступать к вычислению значений x и y.
Определение вершин параболы, которая задана квадратичной функцией
Квадратичная функция вида: [y=a x^{2}+b x+c] очень часто используется для того, чтобы задать значения параболы.
Вершина такой функции, всегда находится в произвольной точке.
В технических науках не существует единой формулы, чтобы вычислить сразу две вершины параболы. Однако, довольно легко определяются координаты вершины, по уже упомянутому уравнению.
Нет времени решать самому?
Наши эксперты помогут!
Алгоритм решения задач по определению точек вершин параболы
- Необходимо выписать коэффициенты a, b, c по условию заданного уравнения. При условии, что коэффициент а будет иметь положительное значение, можно сделать вывод: ветви параболы направлены вверх. Следовательно, если значение отрицательное, то ветви будут направлены вниз.
- Вторым действием определяется абсцисса вершины параболы.
(x) по следующей формуле [x=-frac{b}{2 a}], для этого необходимо применить коэффициенты a, b, c из заданного по заданию уравнения. - Найденное значение x нужно подставить в уравнение, решить его, и тем самым будет выполнен окончательный расчет.
- В ответ записать найденные координаты вершин параболы x и y.
Пример решения уравнения параболы
Рассмотрим подробно на примере, решение задач данной категории.
Запишем данное уравнение следующего вида: [y=x^{2}-5 x+7].
Воспользуемся алгоритмом решения, и выполним следующие действия:
- Зададим коэффициенты параболы. Они равны следующим значениям: a=1, b=-5, с=7.
- Чтобы вычислить вершину x параболы, нужно известные коэффициенты a=1, b=-5 подставить в формулу: [x=-frac{b}{2 a}=frac{-5}{2}=2,5].
- Вычисленное значение х, нужно подставить в исходное уравнение: [y=2,5^{2}-5 cdot 2,5+7=0,75]
- Координаты вершины параболы будут равняться следующим значения: (0,75 и 2,5).
Кубической
называется функция, заданная
формулой где а ≠ 0
I.
Частным случаем кубической функции является функция , здесь
a = 1, b
= c = d
= 0.
Графиком
кубической функции y
= x3
является кубическая парабола с вершиной в точке (0;0),
проходящая через точки (1;1), (-1;-1), (2;8), (-2;-8) (запомнить
эти точки), располагается в I
и III четвертях.
1) Область определения функции — множество всех
действительных чисел: D(y)=(−; +
).
2) Область значений функции – множество всех действительных
чисел: Е(y) = (−; +
).
3) y(-x) = (-x)3
= — x3 = — y(x). Значит, кубическая функция является нечётной, её график
симметричен относительно начала координат, т.е. точки (0;0).
4) Функция возрастает при х (−
; +
).
II.
Кубическая функция , здесь
a ≠ 0

кубической функции y
= ax3
является кубическая парабола с вершиной в точке (0;0),
проходящая через точки (1;1a),
(-1;-1a), (2;8a),
(-2;-8a)), располагается в I
и III четвертях, если a>0,
и во II и IV четвертях, если a<0.
1) Область определения функции — множество всех
действительных чисел: D(y)=(−; +
).
2) Область значений функции – множество всех действительных
чисел: Е(y) = (−; +
).
3) y(-x) = a(-x)3
= — ax3 = — y(x). Значит, кубическая функция является нечётной, её график
симметричен относительно начала координат, т.е. точки (0;0).
4) При a>0
функция возрастает при х (−
; +
).
При a<0,
функция убывает при х (−
; +
).
III.
Кубическая функция
Графиком
кубической функции является
кубическая парабола с вершиной в точке (m;0).
График функции получается
из графика функции смещением
вдоль оси Ox на m
единиц .
1) Область определения функции — множество всех
действительных чисел: D(y)=(−; +
)
.
2) Область значений функции – множество всех действительных
чисел: Е(y) = (−; +
).
3) y(-x) = a(-x — m)3 = — a(x + m)3 ≠
y(x) ≠ — y(x). Значит, данная
кубическая функция не является ни чётной, ни нечётной.
4) При a>0
функция возрастает при х (−
; +
).
При a<0,
функция убывает при х (−
; +
).
IV.
Кубическая функция
Графиком
кубической функции является
кубическая парабола с вершиной в точке (0; n).
График функции получается
из графика функции смещением
вдоль оси Oy на n
единиц .
1) Область определения функции — множество всех
действительных чисел: D(y)=(−; +
)
.
2) Область значений функции – множество всех действительных
чисел: Е(y) = (−; +
).
3) y(-x) = a(-x)3 + n = — ax3 + n ≠
y(x) ≠ — y(x). Значит,
данная кубическая функция не является ни чётной, ни нечётной.
4) При a>0
функция возрастает при х (−
; +
).
При a<0,
функция убывает при х (−
; +
).
V.
Кубическая функция

кубической функции является
кубическая парабола с вершиной в точке (m;
n). График функции получается
из графика функции смещением
вдоль оси Оx на
m единиц,
а вдоль оси Oy на n
единиц .
1) Область определения функции — множество всех действительных
чисел: D(y)=(−; +
)
.
2) Область значений функции – множество всех действительных
чисел: Е(y) = (−; +
).
3) y(-x) = a(-x)3 + n = — ax3 + n ≠
y(x) ≠ — y(x). Значит,
данная кубическая функция не является ни чётной, ни нечётной.
4) При a>0
функция возрастает при х (−
; +
).
При a<0,
функция убывает при х (−
; +
).
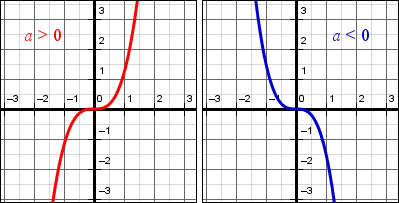
Кубическая парабола задается функцией y=x3
График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции 
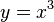
Перечислим основные свойства функции
1.Область определения – любое действительное число:.
2.Область значений – любое действительное число:.
3.Функция является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием .
Производная кубической функции 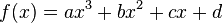
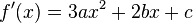





Как построить график кубических функций вида (y = a (x − h)3 + k). В этой статье мы покажем как построить график кубических функций путем построения точек. Общая формула кубической функции:
где (a, b, c) и (d) являются действительными числами и (a) не равно нулю.
Построим график кубических функций путем построения точек.
Пример 1. Постройте график (y = x^3 + 3) на промежутке (-3 ≤ x ≤ 3).
Решение.
- Выберем произвольные точки (x ) и посчитаем соответсвующие им значения (y):
- Построим точки из таблицы и плавно соединим их:
Пример 2. Постройте график (y = x^3-9x + 5) на промежутке (-4 ≤ x ≤ 4):
Решение. Строим график аналогично первому примеру:
1) когда (x = 1.6, ;y≈ –5.3)
2) когда (y = 12, ;x ≈ –0.8 ) или ( x ≈ –2.5)
Теперь выведем правила построения графиков кубических функций вида (y = a (x − h)^3 + k).
- Если (k > 0), то график сдвигается на (k) единиц вверх; если (k < 0), то график сдвигается на (k) единиц вниз.
- Если (h > 0),то график сдвигается на (h) единиц вправо; если (h < 0), то график смещается на (h) единиц влево.
- Если (a < 0), график переворачивается.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!