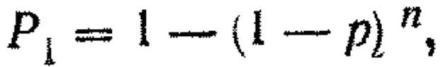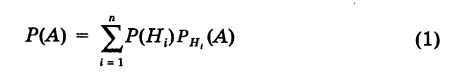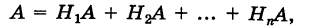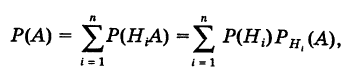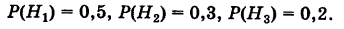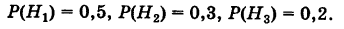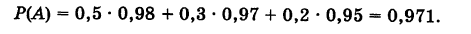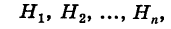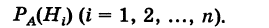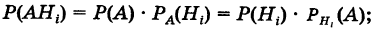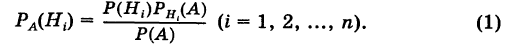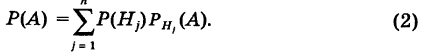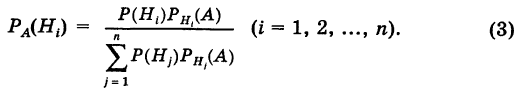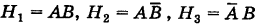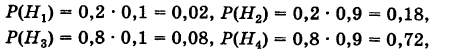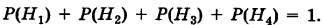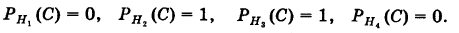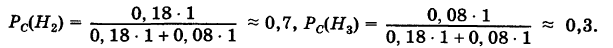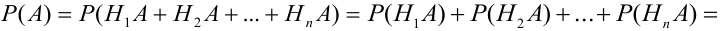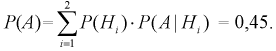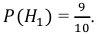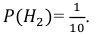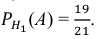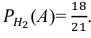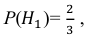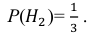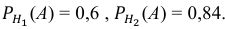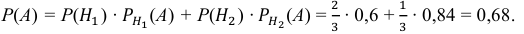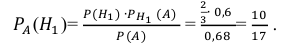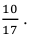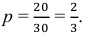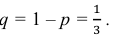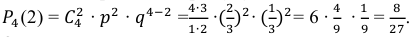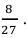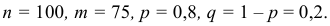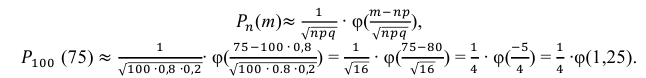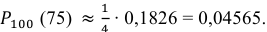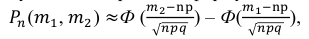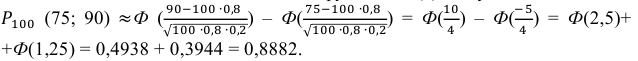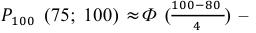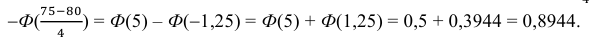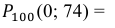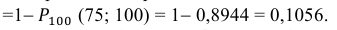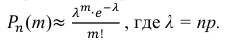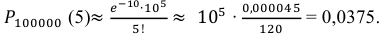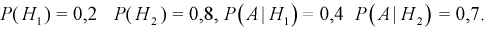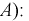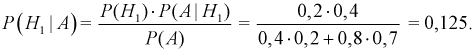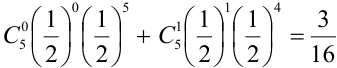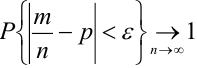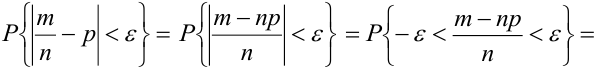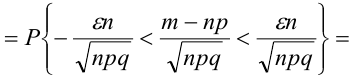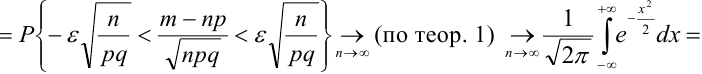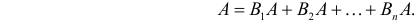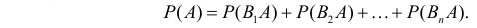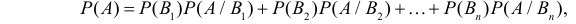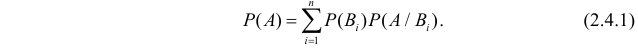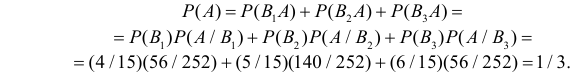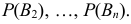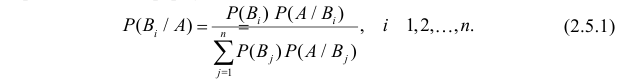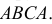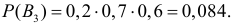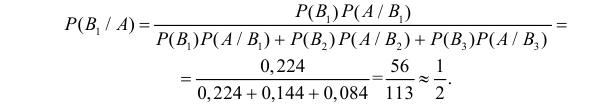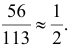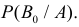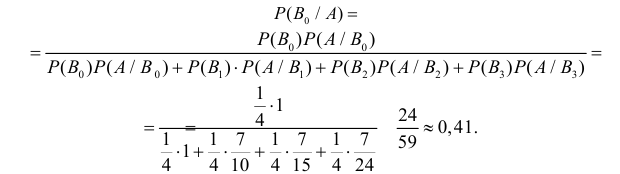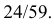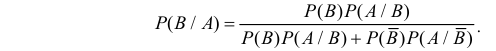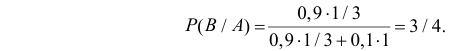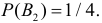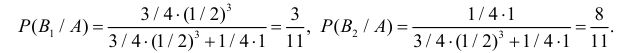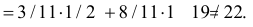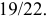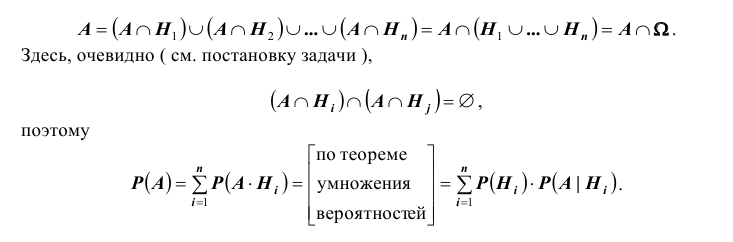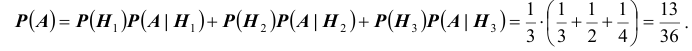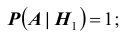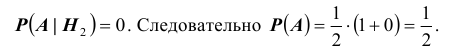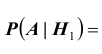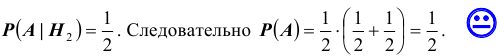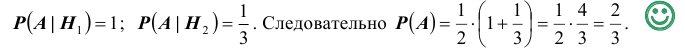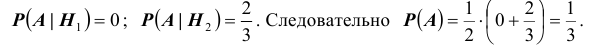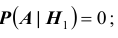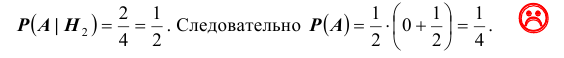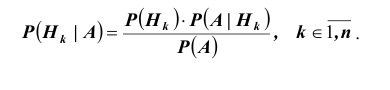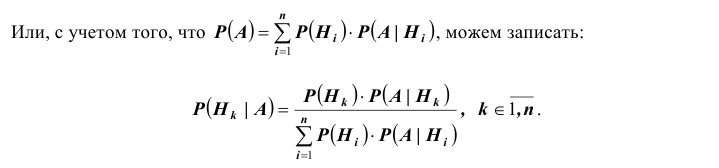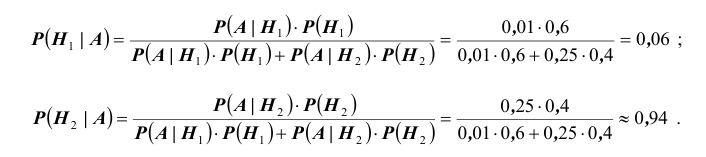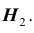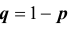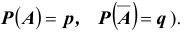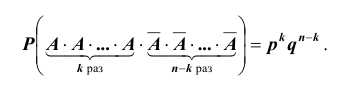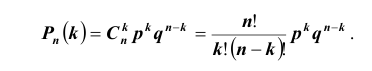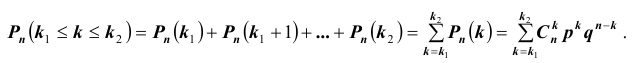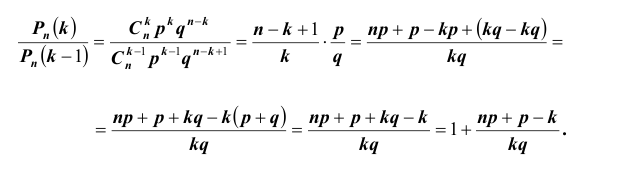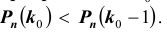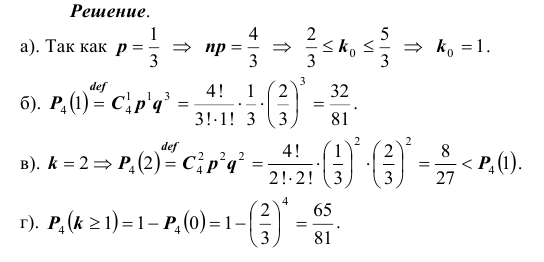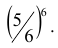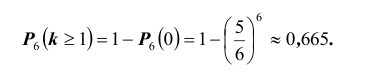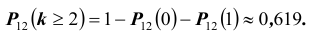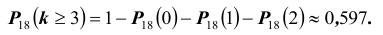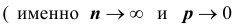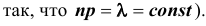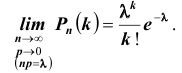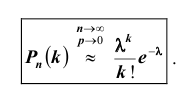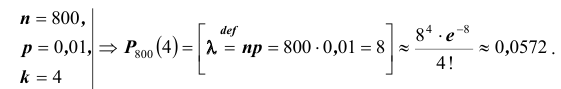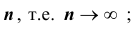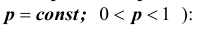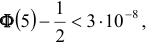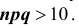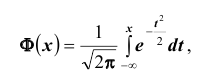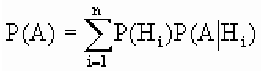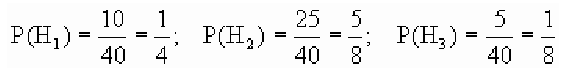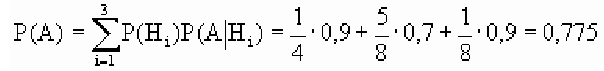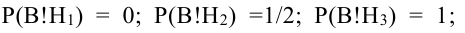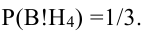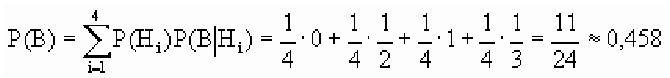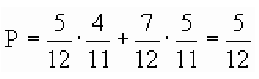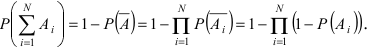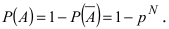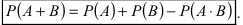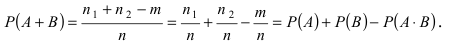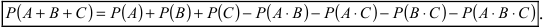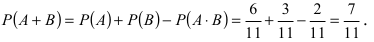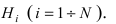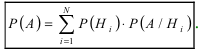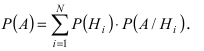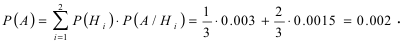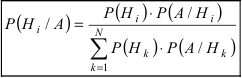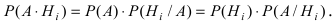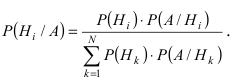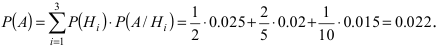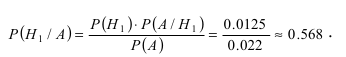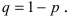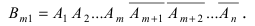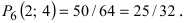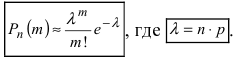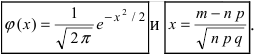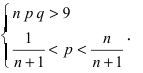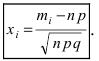Вероятность
попадания, показывая степень объективной
возможности попадания в цель, уже
является некоторым критерием, определяющим
действительность данной стрельбы.
Однако сама по себе вероятность
попадания не дает ответа на целый ряд
практических вопросов, знание которых
необходимо для эффективного использования
оружия. Так, вероятность попадания не
отвечает на вопрос о том, сколько в
среднем можно ожидать попаданий в цель,
если при данной вероятности попадания
по ней будет израсходовано определенное
количество боеприпасов, или какова
вероятность попасть в цель хотя бы одним
снарядом, или какой процент пораженных
фигур можно рассчитывать при стрельбе
данным количеством патронов по групповой
цели.
Решение подобных
вопросов связано с понятиями о вероятности
поражения цели и математическом
ожидании числа попаданий в цель.
Математическое
ожидание числа попаданий
В
практике стрельбы часто надо знать, на
какое количество попаданий в среднем
можно рассчитывать, если в данных
условиях по цели будет произведено
определенное количество выстрелов.
Из
главы «Сведения из теории вероятностей»
известно, что среднее ожидаемое значение
какой-либо случайной величины называется
математическим
ожиданием данной величины.
Математическое ожидание определяется
как сумма парных произведений частных
значений данной величины на соответствующую
ей вероятность:
МОЖ(Х)
= Х1·Р1
+ Х2·Р2+
…+Хn
·Pn.
Таким
образом, математическое ожидание числа
попаданий при одном выстреле (a1)
найдется из выражения:
МОЖ
(числа попаданий) =а1
= 1
· Рф
+0
· q,
где
а1
–
математическое ожидание числа попаданий
при одном выстреле;
Рф
– вероятность попадания в фигуру;
q
– вероятность промаха, равная (1-Рф).
Так
как второй член произведения равен
нулю, можно записать: а1=Рф,
т. е. При одном выстреле математическое
ожидание числа попаданий численно
равно вероятности попадания.
Необходимо
помнить, что это равенство только
численное, т. к. математическое
ожидание числа попаданий в отличие от
вероятности попадания есть именованное
число. Оно может быть целым, дробным,
большим чем единица и вообще любым
именованным числом, в то время как
вероятность попадания отвлеченное
число, которое не бывает меньше нуля и
больше единицы.
Математическое
ожидание числа попаданий при нескольких
выстрелах определяется на основе
одной из теорем теории вероятностей,
которая читается следующим образом.
Математическое
ожидание суммы событий равно сумме
математических ожиданий этих событий:
an=a1
+ а2
+ а3
+ . . . +аn.
Пример.
Определить математическое ожидание
числа попаданий в танк, двигающийся на
огневую позицию противотанкового
орудия, если по нему будет произведено
3 выстрела со следующими вероятностями
попадания: 0,3; 0,6; 0,9.
Решение.
1. Математическое ожидание числа попаданий
при каждом выстреле численно равно
вероятности попадания.
А)
При первом выстреле: а1
= р1=0,3
попадания.
Б)
При втором выстреле: а2=р2
=0,6
попадания.
В)При
третьем выстреле: а3=р3=0,9
попадания.
-
На основе
вышеприведенной теоремы определим
математическое ожидание числа попаданий
при трех выстрелах:
аз=а1
+ а2
+ а3=0,3+0,6+0,9=1,8
попаданий.
Если
вероятность попадания от выстрела к
выстрелу не изменяется, то математические
ожидания числа попаданий при каждом
выстреле будут равными между собой. В
этом случае можно записать: аn
=n·a1
или, учитывая, что a1
= Р, аn
= n·
Р,
где
n
– число предполагаемых выстрелов.
Математическое
ожидание числа попаданий есть среднее
возможное число попаданий, которое
может быть получено при большом числе
выстрелов в возможно одинаковых условиях.
Пример.
Определить, сколько в среднем можно
ожидать попаданий при стрельбе короткими
очередями по поясной мишени из автомата
Калашникова (АК74) на дальность 200 м,
если СТП совпадает с серединой нижнего
обреза цели и по цели будет израсходовано
9 патронов.
Решение.
1. Определим вероятность попадания в
фигуру
Вц=Вб
=0,11 м.
;
;
.
;
;
Pб=Ф(2,27)=0,874.
Рф=Рв·Рб;
Рф=0,5·0,874=0,437.
Кф
в
данном случае применять не следует, так
как фигурные очертания цели выходят
за пределы эллипса рассеивания.
-
Определим среднее
ожидаемое число попаданий.
An
= n·р;
аn=9·0,437=3,933;
аn≈
4
попадания.
Найденный
ответ «≈4 попадания» необходимо понимать
следующим образом. При каждой отдельной
стрельбе может быть различное число
попаданий: от нуля (все промахи) до 9
попаданий. Однако, при большом числе
аналогичных стрельб в среднем на каждые
9 выстрелов будет приходиться 4
попадания.
Формула
аn
=n
·р
применима для определения математического
ожидания числа попаданий в цель при
стрельбе как одиночными выстрелами,
так и очередями (залпами) при условии,
что вероятность попадания р
от
выстрела к выстрелу не изменяется.
При
стрельбе очередями, когда вероятность
попадания первых (Р1)
и последующих (Рпосл.)
снарядов (пуль) неодинакова, математическое
ожидание числа попаданий можно определить
по формуле:
Аn
=n1·P1+
nпосл.·Pпосл.,
где
n1
– число первых снарядов (пуль);
P1
–
вероятность попадания каждого из первых
снарядов (пуль);
nпосл.
– число последующих снарядов в очереди;
Рпосл.
– вероятность попадания последующих
снарядов очереди.
Пример.
Определить математическое ожидание
числа попаданий при стрельбе тремя
очередями, если общее число всех выстрелов
равно 12, а вероятность попадания для
каждого первого Р1
=0,2,
а для каждого последующего Рпосл.
=0,1.
Решение.
Аn=n1
· P1
+
nпосл.·
Рпосл.
= 3·0,2+9·0,1 = 1,5
попадания.
Вероятность
поражения цели (надежность стрельбы)
Математическое
ожидание числа попаданий, являясь
определенным показателем эффективности
стрельбы, не дает, однако, ответа на
вопрос о том, как часто может быть получен
данный результат, то есть не отвечает
на вопрос о том, какова вероятность
того, что при
первой же стрельбе будет
получено 5, 4, 3, 2 или хотя бы одно попадание
в цель.
При
стрельбе по живой цели достаточно
получить хотя бы одно попадание, чтобы
вывести ее из строя; поэтому вероятность
попасть хотя бы один раз при заданном
числе выстрелов называется вероятностью
поражения живой цели или надежностью
стрельбы.
Из
определения вероятности поражения цели
(надежности стрельбы) видно, что
вероятность поражения будет определяться
по формуле вероятности появления события
хотя бы один раз, выведенной в главе
«Сведения из теории вероятностей»:
Р1=1-(1-р)n,
где
Р1
– вероятность поражения цели (надежность
стрельбы) или вероятность появления
события хотя бы один раз;
р
– вероятность попадания при одном
выстреле;
n
– число выстрелов.
Пример.
Пулеметчик ПКМ ведет огонь по грудной
мишени на расстоянии 400 метров
очередями в 5 патронов. Какова вероятность
того, что цель будет поражена первой
очередью? Стрельба ведется легкой
пулей, СТП совпадает с центром цели.
Решение.
1. Определим вероятность попадания в
грудную мишень (по приведенным размерам
цели).
Рв=0,517.
;
Рб=0,401.
Рф=0,517·
0,401 = 0,207; Рф,=0,207.
-
Определим
вероятность поражения цели при стрельбе
5-ю патронами
Р1=1-(1-р)п;
р1
= 1- (1-0,207)5=1-
0,7935=0,687.
Таким образом, при
стрельбе в данных условиях вероятность
поразить цель первой (так же как и
любой последующей) очередью в 5 патронов
равна 0,69.
Найденная
вероятность, отвечая на вопрос о том,
как часто может быть выполнена поставленная
задача, характеризует степень надежности
данной стрельбы. Поэтому вероятность
попасть хотя бы один раз в данных
условиях, кроме вероятности поражения,
называют еще надежностью
стрельбы.
Из
анализа формулы видно, что вероятность
поражения цели (надежность стрельбы)
зависит от вероятности попадания и от
числа выстрелов. При одном выстреле
вероятность поражения равна вероятности
попадания Р1=р.
Чем больше вероятность попадания и
число выстрелов, тем надежнее стрельба.
Для
повышения надежности стрельбы по
одиночным целям в боевых условиях
используют оба эти направления: или
стремятся повысить вероятности
попадания (например, огонь снайперов),
или увеличивают количество патронов
(применение сосредоточенного огня
нескольких огневых средств).
Рассмотренная
нами формула Р1
=(1-р)n
применима для определения вероятности
поражения не только одиночными выстрелами,
но и очередями (залпами) при условии,
если вероятность попадания р
от выстрела к выстрелу не изменяется.
В
предыдущей главе было отмечено, что при
стрельбе очередями рассеивание
последующих снарядов в очереди может
быть больше рассеивания первых и,
кроме того, между СТП первых и последующих
снарядов может быть некоторый разрыв.
В
таких случаях вероятность попадания
каждого последующего снаряда (пули)
будет отличаться от вероятности попадания
первого снаряда (пули) в каждой очереди
выстрелов.
Порядок определения
вероятности поражения цели в этом случае
может быть следующим.
Пример.
Стрельба ведется из автомата Калашникова
по грудной фигуре на дальность 300 м.
Определить вероятность поражения цели
при стрельбе двумя очередями по три
выстрела в каждой, если средняя точка
попадания первых и последующих пуль
совпадает с центром цели.
Решение.
По таблицам стрельбы (ТС № 63 ГРАУ)
находим:
-
при
стрельбе одиночными выстрелами Вв=0,10
м, Вб=0,10
м; -
при
стрельбе очередями Вв=0,17
м; Вб=0,17
м.
Высота
цели 2у1=0,42
м, ширина 2z1
=0,42 м (приведенные размеры цели).
-
Определим
вероятность поражения цели первыми
(двумя) выстрелами очередей.
а) Находим вероятность
попадания в цель
;
;
рв=0,843.
;
;
рб=0,843.
Рф
= Рв
· Рб ; Рф =0,843 ·0,843=0,71
или 71%.
б)
Находим вероятность поражения цели
первыми пулями очередей
Р1посл.-(1-рпосл.)n=1-(1-0,71)2
= 0,916.
-
Определим
вероятность поражения цели последующими
(четырьмя) выстрелами.
а) Находим вероятность
попадания в цель
;
Рв=0,593.
;
Рб=0,593.
Рпосл.=0,593·0,593=0,353.
б) Находим вероятность
поражения
РI
посл.
= 1-(1-рпосл.)n
=1-(1-0,353)4
= 0,825.
-
Определим
вероятность поражения цели с учетом и
первых, и последующих выстрелов.
Вероятность
непоражения
цели только первыми выстрелами равна
1-РI,1
=1-0,916=0,084
и только последующими выстрелами 1-
РI
посл.
=1 – 0,825= =0,175.
Вероятность
того, что цель не будет поражена при
всех шести выстрелах, равна (1-РI,1)·(
1-
РI
посл.)
= 0,084·0,175 = 0,015.
Вероятность
поражения цели при стрельбе очередями
(РI
оч.)с
учетом первых и последующих выстрелов
равна РI
оч.
=1-0,015=0,985.
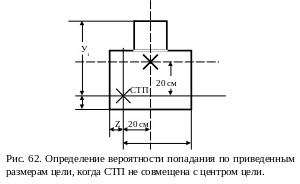
Пример.
Все условия задачи те же, что и в предыдущем
примере, но средняя точка попадания
последующих выстрелов левее центра
цели на 20 см и ниже его на 20 см (рис. 62).
Решение.
1. Вероятность поражения цели первыми
(двумя) выстрелами РI,1
=0,916 (как в предыдущем примере).
-
Определим
вероятность поражения цели последующими
(четырьмя) выстрелами.
а) Находим вероятность
попадания.
Hа
рис. 62 видно, что у1=0,41
м; у2=0,01
м; z1=0,41
м; z2
= 0,01 м.
;
;
.
;
;
.
Рв=Рв1+Рв2;
Рв=0,448+0,016=0,464.
;
;
.
;
;
.
Рб=
Рб1+Рб2;
Рб=0,448+0,016=0,464.
Рпосл.=Рв+Рб;
Рпосл.=0,464·0,464≈0,215.
б)
Находим вероятность поражения цели
последующими выстрелами
Pi,
поcл.
=1 – (1- Рпосл.)n
; Pi
поcл.=1-(1-0,215)4=0,62.
в)
Находим вероятность поражения цели
при стрельбе обеими очередями Р1,
оч.
= 1 – (1 – 0,916)· (1 – 0,62) =1 –0,084·0,38=0,968.
Если
стрельба ведется несколькими
одинаковыми очередями, порядок
определения вероятности поражения
целей может быть еще и такой:
1.
Определить вероятность поражения
цели при стрельбе одной очередью
(вышеописанным способом).
2. Определить
вероятность поражения цели при стрельбе
заданным числом очередей по формуле:
рi,оч.
=
1 — (1 — Р1,оч.)n,
где
Р1,
оч.
– вероятность поражения цели одной
очередью;
n
– число таких очередей.
Решим этим способом
ту же задачу, что и в первом примере.
-
Вероятность
поражения цели последующими двумя
выстреламиочереди равна: Р1,
посл.
=1-(1- 0,353)2=1-
0,6472=1-
0,418=0,582. -
Вероятность
поражения при стрельбе одной
очередью равна:
Р1,
оч.
= 1-(1-0,916)·(1-0,582) =1- 0,084 · 0,418 = 0,965.
Вероятность
поражения цели двумя очередями равна
Р1,
оч.=
1- (1-0,965) 2=1-0,012=0,988.
Как
видим, вероятность поражения цели такая
же, как и в первом примере. Поэтому
гораздо удобнее производить расчеты
вероятности поражения цели при
стрельбе несколькими очередями по
приведенной формуле.
Для
определения вероятности поражения
одиночных целей при условии, что
вероятность попадания от выстрела к
выстрелу не меняется, можно пользоваться
приложением № 1.
Данная
таблица представляет собой рассчитанную
формулу Р1
= 1-(1-р)п
для различной величины вероятности
попадания и числа выстрелов.
После
того, как будет найдена вероятность
попадания в мишень, например, р=0,28,
вероятность поражения находится по
таблице следующим образом: в
вертикальном столбце находим значение
вероятности попадания р=0,28,
а в горизонтальной строчке против числа,
соответствующего числу выстрелов
n,
находим вероятность поражения цели
(надежность стрельбы), например, при
пяти выстрелах – 0,81.
Пользование
этой таблицей облегчает решение целого
ряда задач. Однако она не оказывает
помощи в решении задач при большом числе
выстрелов. Для облегчения решения этой
задачи пользуются зависимостью между
математическим ожиданием числа попаданий
и вероятностью поражения цели.
Зависимость
между математическим ожиданием числа
попаданий и вероятностью поражения
(надежностью стрельбы)
Анализируя
формулы для определения математического
ожидания числа попаданий (аn
= n
· р)
и для определения вероятности поражения
(Рi
=1-(1-р)n),
можно увидеть, что обе эти величины
зависят от вероятности попадания и
числа выстрелов. Вполне естественно,
что эти две величины связаны между собой
определенной зависимостью: чем больше
математическое ожидание числа попаданий,
тем больше вероятность поражения
цели. (Исключение представляет случай,
когда вероятность попадания равна
нулю или единице).
Это положение
позволяет составить специальные таблицы
для перехода от математического
ожидания числа попаданий к вероятности
поражения.
Однако
составление и пользование такими
таблицами осложняется тем, что характер
зависимости между математическим
ожиданием числа попаданий и вероятностью
поражения изменяется с изменением
вероятности попадания. Например, при
вероятности попадания, равной единице,
увеличение количества выстрелов будет
систематически увеличивать математическое
ожидание числа попаданий. Однако
вероятность поражения P1
все
время будет оставаться равной единице.
Для
перехода от вероятности поражения к
математическому ожиданию числа
попаданий можно пользоваться приложением
№ 1, составленным для вероятности
попадания, равной 0,1. (Практически этим
приложением можно пользоваться при
вероятности попадания, не превышающей
0,3 – 0,4).
Наличие
такого приложения значительно облегчает
решение задач по определению вероятности
поражения цели, т. к. вместо решения
формулы
Pi
=1-
(1-р)n
, где приходится возводить дробное число
в «n-ную»
степень, можно решить формулу аn=
n·р
и по приложению № 1 определить значение
вероятности поражения.
Решение
вышеприведенного примера с помощью
таблицы выглядело бы следующим
образом.
После
определения вероятности попадания в
фигуру Рф
= 0,28 надо определить математическое
ожидание числа попаданий при 5 выстрелах.
Аn
=n·р;
аn
=5·0,28= 1,4
попадания.
По
данному значению ап
= 1,4 попадания по приложению №1 определяем,
что вероятность поражения равна 0,772.
Небольшое расхождение в значении
вероятности поражения (Р1),
рассчитанной по формуле и определенной
по таблице, получается в результате
того, что таблица рассчитана для
вероятности попадания, равной 0,1, а в
нашем примере вероятность попадания
равна 0,28.
Таким
образом, наличие приложения № 2 позволяет
быстро переходить от вероятности
поражения к математическому ожиданию
числа попадания и обратно, что особенно
удобно при определении процента
пораженных фигур групповой цели и
при определении количества патронов,
необходимых для выполнения той или
иной огневой задачи.
Математическое
ожидание числа пораженных фигур групповой
цели
Степень
наносимого поражения при стрельбе по
групповым целям определяется числом
(процентом) пораженных фигур, входящих
в данную цель. Считают, что огонь на
уничтожение групповой цели соответствует
поражению 80 % фигур цели, огонь на
подавление соответствует поражению
50% фигур цели. Решая огневую задачу,
необходимо иметь представление о том,
каково может быть поражение цели при
израсходовании данного количества
патронов.
Для
определения процента пораженных фигур
при стрельбе по широким целям из
пулеметов применяется рассмотренная
выше таблица № 1, показывающая зависимость
между математическим ожиданием числа
попаданий в одну фигуру и вероятностью
поражения этой фигуры.
Сущность решения
задачи сводится к следующему.
Пусть
на фронте АВ
имеется
несколько перебегающих фигур. Требуется
определить средний процент пораженных
фигур групповой цели, если по цели будет
израсходовано n
патронов.
Для решения этой
задачи прежде всего необходимо определить
вероятность попадания в одну из фигур
данной групповой цели:
.
Зная
вероятность попадания в одну фигуру и
число патронов n,
по формуле Р1
= 1- (1- р)n
определим вероятность поражения одной
фигуры.
Так
как при определении вероятности попадания
и поражения этой фигуры мы не задавались
определенным положением этой фигуры,
то, следовательно, она будет иметь
приведенную вероятность поражения на
любом участке обстреливаемого фронта.
Отсюда понятно, что сколько бы подобных
фигур не было на данном фронте, все они
будут иметь одинаковую вероятность
поражения P1.
Так
как P1
показывает вероятность поражения фигуры
при данной стрельбе, то вполне естественно,
что при этой стрельбе процент пораженных
фигур будет равен вероятности поражения
одной фигуры, выраженной также в
процентах.
Таким образом, для
определения процента пораженных фигур
групповой цели необходимо:
а) Определить
вероятность попадания в одну фигуру.
Б)
По найденной вероятности попадания и
числу патронов, по формуле Р1=1-(1-р)n
определить вероятность поражения одной
фигуры цели. Вероятность поражения
одной фигуры цели численно равна
проценту пораженных фигур.
Пример.
На удалении 500 м от пулемета на фронте
20 м замечена группа перебегающих солдат
противника. Какой можно ожидать процент
пораженных фигур, если по цели будет
израсходовано 40 патронов? Огонь ведется
пулей обр. 1908г. Ось рассеивания проходит
через середину высоты фигур.
Решение.
1. Определим вероятность попадания в
одну фигуру.
Вв=0,19
м; так как стрельба ведется с рассеиванием
по фронту, то для определения входного
числа необходимо Вв
увеличить в 1,75 раза.
;
;
Рв=
Ф(2,27) = 0,874;
.
-
Определим
вероятность поражения одной фигуры,
если по цели израсходовано 40 патронов.
Р1
= 1(1- р)n;
P1
= 1- (1- 0,017)40=0,51;
Р1=51%.
Таким образом, при
стрельбе в данных условиях мы можем в
среднем ожидать 51% пораженных фигур.
Эту
же задачу проще решать используя
приложение № 2, которое по математическому
ожиданию числа попаданий в 1 фигуру дает
значение вероятности поражения данной
фигуры; последняя, как мы видели выше,
численно равна проценту пораженных
фигур групповой цели.
Решение
вышеприведенной задачи по приложению
№ 2 осуществляется следующим образом.
После определения
вероятности попадания в одну фигуру
групповой цели необходимо найти
математическое ожидание числа попаданий
в эту фигуру при 40 выстрелах,
аn
= n·р;
аn
= 40 ·0,017 = 0,68
попадания.
Затем
по таблице найдем, что данному числу ап
=0,68 попаданий соответствует вероятность
поражения, равная 0,51. Это и есть ожидаемый
процент пораженных фигур.
Так решается вопрос
о поражении групповых и одиночных целей
при заданном числе выстрелов.
Вероятность поражения цели
117. При стрельбе из стрелкового оружия по одиночным живым целям и из гранатометов по одиночным бронированным целям одно попадание обычно дает поражение цели. Поэтому под вероятностью поражения одиночной цели понимается вероятность получения хотя бы одного попадания при заданном числе выстрелов.
118. Вероятность поражения цели при одном выстреле (Pi) численно равна вероятности попадания в цель (р). Расчет вероятности поражения цели при этом условии сводится к определению вероятности попадания в цель.
Пример. Определить вероятность поражения снайпера противника (грудная фигура) с первого выстрела из снайперской винтовки обр, 1891/30 г. на расстояние 500 м; расстояние до цели определено глазомерно.
Решение. 1. По таблицам находим: Bв = 0,08 м; В6 = 0,08 м; из приложения 4 (табл. 7 в 6) ошибка в подготовке стрельбы по высоте
Ев = 0,36 м, приведенные размеры цели: высота 0,45 м, ширина 0,45 м.
2. Определяем суммарную (приведенную) ошибку в подготовке стрельбы по высоте:
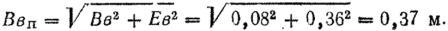
3. Определяем вероятность попадания в цель:
а) в полосу, равную приведенной высоте цели:
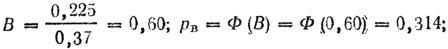
б) в полосу, равную приведенной ширине цели:
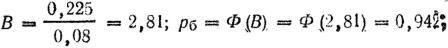
в) в цель:
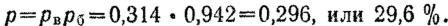
Так как при попадании пули в снайпера будет наверняка получено его поражение, найденное значение вероятности попадания и есть вероятность поражения цели с первого выстрела, т е. р = Pi = 29,6%.
119. Вероятность поражения цели (Pi) при нескольких одиночных выстрелах, одной очередью или несколькими очередями, когда вероятность попадания для всех выстрелов одинакова, равна единице минус вероятность промаха в степени, равной количеству выстрелов (n), т. е.
Пример. Определить вероятность поражения реактивного противотанкового ружья при стрельбе из пулемета Калашникова одной очередью в 5 выстрелов на расстояние 600 м; ветер боковой; расстояние до цели определено глазомерно.
Решение. 1, По таблицам находим: Bв Сум = 0,44 м, Вб сум = 0,61 м; из приложения 4 (табл. 7 и 6) срединная ошибка по высоте .Ев = 0,63 м, по боковому направлению Ен = 0,43 м, коэффициент фигурности 0,72.
2. Определяем суммарную (приведенную) ошибку в подготовке стрельбы по высоте:
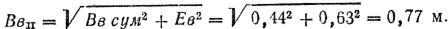
3. Определяем суммарную (приведенную) ошибку в подготовке стрельбы по боковому направлению:
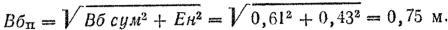
4. Определяем вероятность попадания в цель:
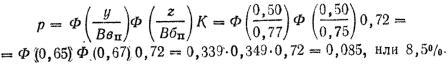
5. Определяем вероятность поражения цели очередью в 5 выстрелов:
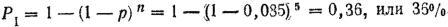
Найденная таким образом вероятность поражения цели характеризует надежность стрельбы, т. е. показывает, в скольких случаях нз ста в среднем цель в данных условиях будет поражена не менее чем при одном попадании. По условиям примера при большом числе подобных стрельб в среднем на каждые 100 стрельб в 36 стрельбах будет получено не менее одного попадания в цель, в 64 стрельбах цель не будет поражена.
Стрельба считается достаточно надежной, если вероятность поражения цели не менее 80%.
120. Вероятность поражения цели при нескольких выстрелах одной очередью или несколькими очередями, когда вероятность попадания первых и последующих пуль (очередей) изменяется от выстрела (очереди) к выстрелу (очереди), равна единице минус вероятность промахов первых и последующих пуль очереди (очередей):
а) для одной очереди:
б) для нескольких очередей (вероятность попадания от очереди к очереди не изменяется):
в) когда осуществляется ввод корректур (вероятность попадания от очереди к очереди изменяется):
где
п — общее количество выстрелов;
к — количество очередей;
S1, S2, Si — количество выстрелов в очереди;
Р1, Р2, Рк — вероятность попадания при одном выстреле первой, второй и т. д. очереди.
Пример. Определить вероятность поражения пулемета из автомата Калашникова (АКМ) одной очередью в 3 выстрела при стрельбе стоя из окопа на расстояние 300 м; ошибок в подготовке стрельбы нет (средняя траектория пройдет через середину цели).
Решение. 1, По таблицам находим: Вв|= 0,12 м, Вб1 — 0,11 м, Вв сумпос — 0,23 м, Вб сумпос= 0,33 м; из приложения 4 (табл. 6) приведенные размеры цели равны: высота 0,48 м, ширина 0,65 м.
2. Определяем вероятность попадания для первой пули очереди
3. Определяем вероятность попадания для последующей пули очереди:
4. Определяем вероятность поражения цели очередью в 3 выстрела:
Если вероятность попадания от выстрела к выстрелу не изменяется, вероятность поражения цели может быть определена по таблице вероятностей поражения цели (приложение 4, табл. 4), рассчитанной для различной величины вероятности попадания (р) и числа выстрелов (п).
Пример. Определить вероятность поражения противотанкового гранатомета при стрельбе из ручного пулемета Калашникова одной очередью в 5 выстрелов, если вероятность попадания равна 0,30.
Решение. По табл. 4 приложения 4 в вертикальной графе, обозначенной буквой р находим значение вероятности попадания, равное 0,30; в горизонтальной строчке против числа, соответствующего числу выстрелов (n), равному 5, находим вероятность поражения цели; она равна p1=0,83, или 83%.
При определении вероятности поражения целей матическим огнем по формулам, указанным в ст. 119 и 120, получаются завышенные результаты (на 3 — 7%). Поэтому при более точных подсчетах вероятностей поражения цели пользуются специальными формулами, учитывающими коэффициент зависимости выстрелов.
Содержание:
Формула полной вероятности:
Пусть событие А может произойти в результате появления одного и только одного события
События этой группы обычно называются гипотезами.
Теорема: Вероятность события А равна сумме парных произведений вероятностей всех гипотез, образующих полную группу, на соответствующие условные вероятности данного события А, т. е.
(формула полной вероятности), причем здесь
Доказательство. Так как
причем, ввиду несовместности событий 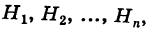
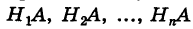
что и требовалось доказать.
Пример:
В магазин для продажи поступает продукция трех фабрик, относительные доли которых есть: I — 50%, II — 30%, III — 20%. Для продукции фабрик брак соответственно составляет: I — 2%, II — 3%, III — 5%. Какова вероятность того, что изделие этой продукции, случайно приобретенное в магазине, окажется доброкачественным (событие А)?
Решение:
Здесь возможны следующие три гипотезы: 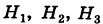
Соответствующие условные вероятности события А равны
По формуле полной вероятности имеем
Формула Бейеса:
Пример:
Имеется полная группа несовместных гипотез
вероятности которых 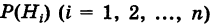
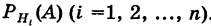
Например, очевидно, следует отбросить гипотезы, отрицающие появление события А. Вообще, проблема состоит в том, что, имея новую информацию, мы должны переоценить вероятности наших гипотез.
Иными словами, нам нужно определить условные вероятности
На основании теоремы умножения вероятностей имеем
отсюда
Для нахождения вероятности Р(А) можно использовать формулу полной вероятности
Отсюда имеем формулу вероятностей гипотез после опыта (<формулу Бейеса)
Пример:
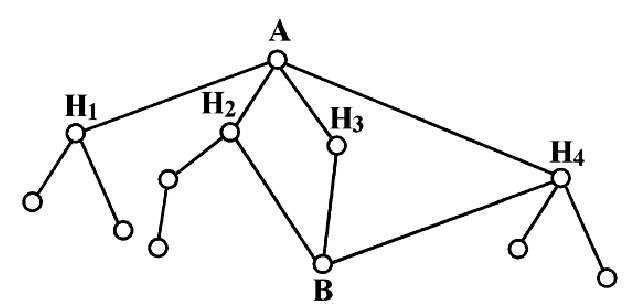
Вероятность поражения самолета при одиночном выстреле для 1-го ракетного расчета (событие А) равна 0,2, а для 2-го (событие В) — 0,1. Каждое из орудий производит по одному выстрелу, причем зарегистрировано одно попадание в самолет (событие С). Какова вероятность, что удачный выстрел принадлежит первому расчету?
Решение:
До опыта возможны четыре гипотезы: 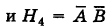
Вероятности их, при независимом действии расчетов, соответственно равны
причем
Условные вероятности для наблюдаемого события С при данных гипотезах будут
Следовательно, гипотезы 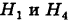
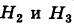
Таким образом, с вероятностью приблизительно 0,7 можно утверждать, что удачный выстрел принадлежит 1-му расчету,
Формула полной вероятности
Пусть событие А еще не произошло, но вскоре должно произойти. Событие А может протекать в различных условиях, относительно характера которых сделано 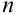
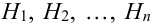
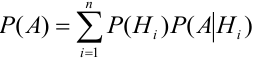
Доказательство.
По условию теоремы гипотезы 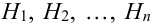
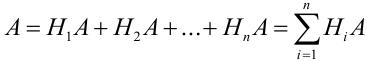
Т.к. гипотезы несовместны, то и комбинации 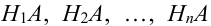
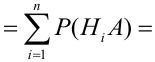
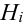
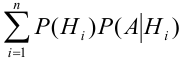
Пример:
Имеется пять урн:
2 урны состава 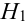
1 урна состава 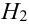
2 урны состава 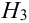
Наудачу выбирается урна, и из нее наудачу выбирается шар. Чему равна вероятность события А = {будет вынут белый шар}?
Решение.
Событие А еще не произошло. Шар может быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 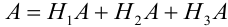
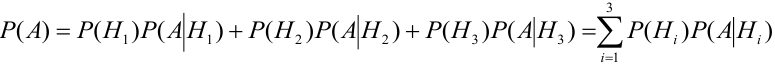
Найдем отдельно вероятности событий:
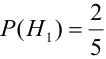
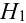
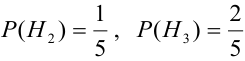
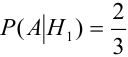
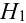
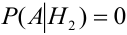
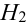
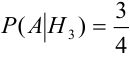
Подставим найденные вероятности в формулу (*): 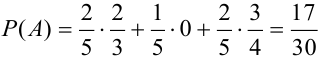
Формула полной вероятности и решение задач
Пример:
В двух одинаковых коробках имеется по 100 резисторов. В 1-й — 60 резисторов по 100 КОм, во 2-й 30 — резисторов по 100 КОм. Определить вероятность того, что взятый наугад из какой-либо коробки резистор будет 100 КОм.
Решение:
Пусть событие 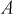
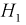
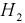
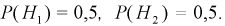
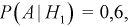
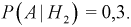
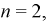
Пример №1
В первой коробке находится 20 деталей, из них 18 стандартных, во второй коробке – 10 деталей, из них 9 стандартных. Из второй коробки наудачу взята одна деталь и переложена в первую коробку.
Какова вероятность того, что деталь, наудачу извлечённая после этого из первой коробки, окажется стандартной?
Решение. Обозначим события:
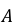
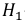
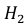
Событие А может наступить при условии наступления одного из событий 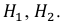
Вероятность того, что из второй коробки извлечена нестандартная деталь
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена стандартная деталь,
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена нестандартная деталь,
Искомая вероятность того, что из первой коробки будет извлечена стандартная деталь, по формуле полной вероятности равна:
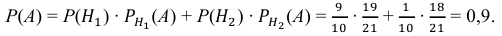
Ответ: 0,9.
Пример №2
Два станка производят одинаковые детали, которые поступают на общий конвейер. Производительность первого станка в два раза больше производительности второго станка. Первый производит 60 % деталей высшего сорта, а второй – 84 %. Наудачу взятая с конвейера деталь оказалась высшего сорта. Какова вероятность того, что эта деталь произведена на первом станке?
Решение. Обозначим события:
А – деталь, взятая с конвейера, оказалась высшего сорта.
Это событие наступит с одним из двух событий (гипотез):
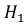
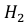
Поскольку производительность первого станка в два раза больше производительности второго станка, вероятности гипотез равны:
Условные вероятности события А даны:
По формуле полной вероятности находим:
По формуле Байеса найдём условную вероятность того, что взятая наудачу деталь высшего сорта произведена на первом станке:
Ответ:
Пример №3
В ящике 20 белых и 10 чёрных шаров. Поочерёдно извлекают 4 шара, причём каждый извлечённый шар возвращают в ящик перед извлечением следующего. Какова вероятность того, что среди четырёх извлечённых шаров окажется два белых?
Решение. Вероятность извлечения белого шара одна и та же во всех четырёх испытаниях, так как каждый извлечённый шар возвращается в ящик:
Тогда вероятность извлечения чёрного шара во всех четырёх испытаниях равна
Используя формулу Бернулли, находим вероятность того, что из четырёх извлечённых шаров два шара будут белыми:
Ответ:
Пример №4
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена 75 раз?
Решение. По условию задачи
Так как n – достаточно большое число, воспользуемся локальной формулой Лапласа:
В таблице значений функции 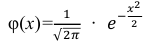
0,1826.
Следовательно,
Ответ: 0,04565.
Пример №5
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена
а) не менее 75 раз и не более 90 раз?
б) не менее 75 раз?
в) не более 74 раз?
Решение.
Воспользуемся интегральной формулой Лапласа:
где 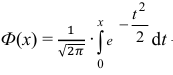
а) По условию задачи 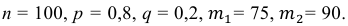
б) Требование того, чтобы событие наступило не менее 75 раз, означает следующее: число появлений события может быть равно либо 75, либо 76, … , либо 100.
Тогда следует принять 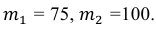
в) Событие «мишень поражена не более 74 раз» и событие «мишень поражена не менее 75 раз» являются противоположными. Поэтому сумма их вероятностей равна 1. Следовательно, искомая вероятность
Ответ: а) 0,8882; б) 0,8944; в) 0,1056.
Пример №6
Учебник издан тиражом 100000 экземпляров.
Вероятность того, что один учебник сброшюрован неправильно, равна 0,0001. Какова вероятность того, что тираж содержит 5 бракованных книг?
Решение. По условию задачи n = 100000, p = 0,0001.
События «из n книг ровно m книг сброшюрованы неправильно», где m = 0,1,2, … ,100000, являются независимыми. Так как число n велико, а вероятность p мала, вероятность 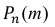
В рассматриваемой задаче 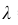
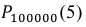
Ответ: 0,0375.
Формула Байеса (Бейеса)
Пусть событие А произошло, причем А могло протекать в различных условиях, относительно характера которых было сделано 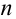
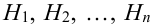
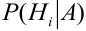
Решение:
По условию теоремы гипотезы 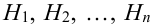
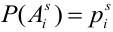
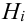
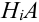
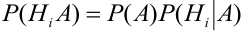
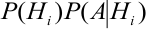
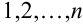
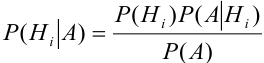
Выразим Р(А) с помощью формулы полной вероятности:
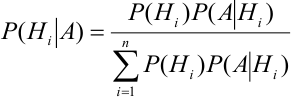
Пример №7
Имеется пять урн:
2 урны состава 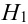
2 урны состава 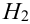
1 урна состава 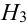
Из одной наудачу выбранной урны взят шар. Он оказался белым (событие А). Чему равна после опыта вероятность события, что шар вынут из урны третьего состава.
Решение.
Событие А произошло. Шар мог быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 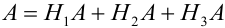
Найдем вероятности событий:
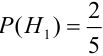
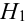
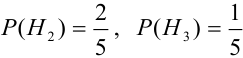
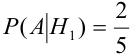
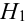
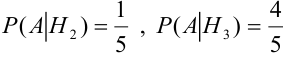
По формуле Байеса найдем условную вероятность 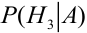
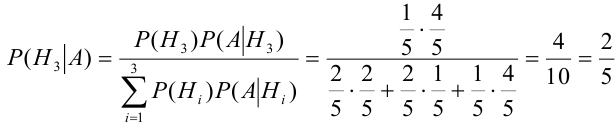
Пример №8
Вероятность дождливого дня в городе равна 0,2. Известно, что вероятность выиграть футбольный матч команде этого города в дождливый день равна 0,4, а в сухой — 0,7. Известно, что команда выиграла матч. Определить, что в этот день шел дождь.
Решение:
Событие 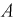
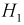
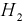
Чтобы ответить на вопрос, пересмотрим вероятность 1-й гипотезы с учетом результата опыта-появилось событие 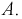
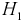
Из полученного результата видим, что с учетом события 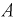
Независимые испытания
Под испытанием станем понимать осуществление определенного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства 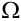
Определение 26. Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.
В каждом испытании вероятность появления события А одинакова.
Ряд задач связан с экспериментом, в котором проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Рассматривается последовательность п независимых испытаний, под которой будем понимать дискретное новое пространство 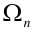
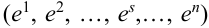
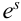

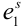
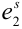
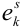
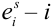



Пример №9
Пусть испытание состоит в подбрасывании игральной кости. Пространство элементарных событий 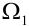
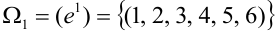
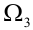
Обычно исходы обозначали большими заглавными буквами. Переобозначим! Пусть происходит 



Обозначим событие 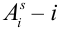



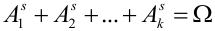
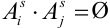
Обозначим вероятность 
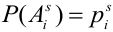
Пусть при первом испытании произошло событие под номером 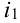
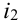

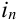

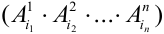
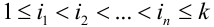
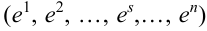
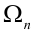
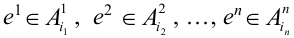
Испытания — независимые, следовательно, по теореме 4, имеет место равенство:
В случае, когда вероятности событий 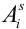
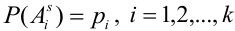
В силу несовместности и единственной возможности исходов, очевидно, что 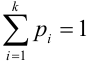
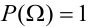
Теорема. Если данные 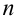
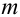
Теорема. Для того, чтобы 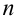
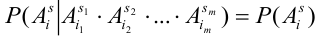
для любой группы чисел 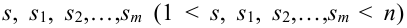
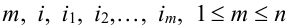
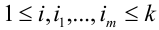
Формулы Бернулли
Пусть проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Схема независимых испытаний является математической моделью серии испытаний, повторяющихся при неизменных условиях. Такая схема называется полиномиальной.
Простейшим классом повторяющихся независимых испытаний является последовательность независимых испытаний с двумя исходами (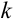
Определение 27. Независимые испытания при двух исходах называются испытаниями Бернулли.
Пример №10
Определить вероятность того, что в результате проведения 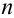

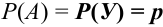
Решение.
Искомую вероятность обозначим 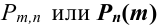
Событие А в данных испытаниях может появиться ровно 
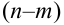
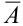
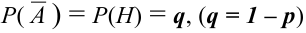
Сначала найдем вероятность того, что события У наступают при определенных 

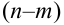
По условию данные события — независимые, следовательно, по теореме 4 для произведения независимых событий можем записать, что
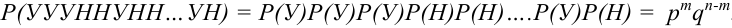
Число успехов и неудач задано. Можно менять только их расположения в цепочках, которое однозначно определяется выбором из 

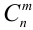
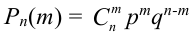
В данной задаче мы доказали теорему Бернулли.
Теорема Бернулли. Если 


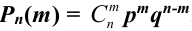
Следствие. 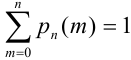

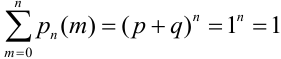
Пример №11
Пусть монета брошена 5 раз. Требуется найти вероятность того, что выпало ровно 3 орла.
Решение.
В каждом из 5 независимых испытаниях (
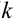
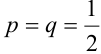

По формуле Бернулли 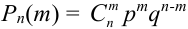
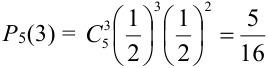
Замечания.
Замечание 1. Вероятность 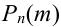
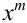
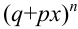
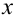
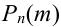
Замечание 2. Рассмотрим схему испытаний с произвольным количеством исходов. Пусть каждое из 
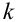
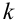
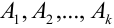
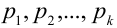

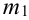
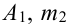
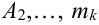
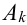

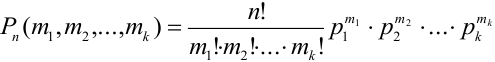
Эта совокупность вероятностей является коэффициентом при 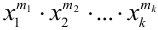
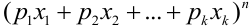
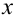
Например. При 

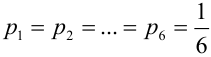
Если различать только «6» и «не 6», то получим схему Бернулли с двумя исходами (
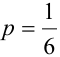
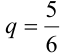
Замечание 3. При вычислении вероятности события, состоящего в том, что число успехов m лежит, например, между а и b, приходится находить числовые значения сумм вероятностей вида: 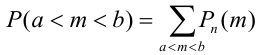
Например, вероятность того, что событие наступит а) менее 



a) 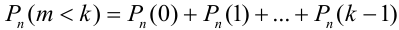
b) 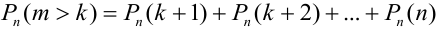
c) 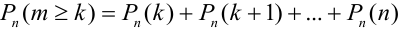
d) 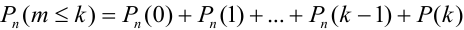
В некоторых случаях удобнее перейти к противоположному событию, например, 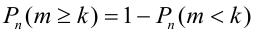
Пример №12
Пусть монета брошена 5 раз. Требуется найти вероятность того, что 1) менее двух раз выпал орел, 2) не менее двух раз выпал орел.
Решение.
Два исхода (
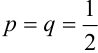
1) Орел выпал менее двух раз, значит, не выпал или выпал раз.
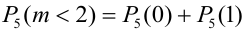
2) Орел выпал не менее двух раз, т.е. выпал два раза или три или четыре или пять:
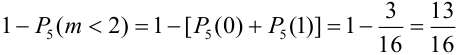
Замечание 4. В примере на формулу Бернулли вычисления проводятся очень легко, однако часто приходится вычислять вероятности при очень больших значениях n и m, например, при n = 1000, m = 500. Также затруднения при вычислении возникают при малых значениях р или q.
В этих случаях удается заменить формулу Бернулли какой-нибудь приближенной асимптотической формулой. Существуют три предельные теоремы, содержащие такие формулы.
Предельные теоремы в схеме Бернулли
Теорема Пуассона (асимптотическая формула для случая малых значений р)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, причем 

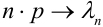
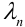
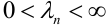
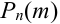

Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при 
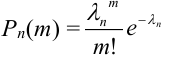
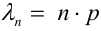
2. Формулой пользуются при больших n и малых р. Например, при n > 100, 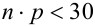
3. Теорема имеет место и в том случае, когда вероятность события А в каждом испытании равна нулю. В этом случае 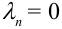
4. Существуют таблицы значений данной вероятности (стр. 410, 411 в задачнике Ефимова -Демидовича).
Пример №13
Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более пулями, если число выстрелов равно 5000.
Решение.
Считаем каждый выстрел за испытание и попадание в цель за событие. Количество испытаний n = 5000 (велико), р = 0,001 (мало). По формуле Бернулли считать сложно. Поэтому применим формулу Пуассона.
Найдем среднее число попаданий: 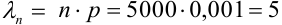
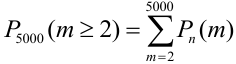
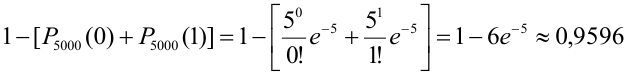
По точной формуле (формуле Бернулли) 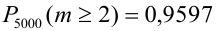
Локальная предельная теорема Муавра — Лапласа (асимптотическая формула для случая больших значений n и m)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, (0 < р < 1), то вероятность 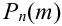

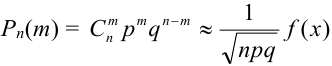
где 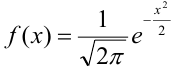
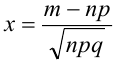
Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при 
2. Формулой пользуются при больших n и m. Например, при п > 100, 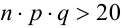
3. Из того, что 
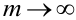
4. Существуют таблицы значений функции 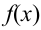
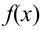
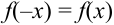
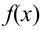
Пример №14
Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение.
Количество испытаний n = 243, количество успехов m = 70, вероятность успеха р = 0,25, вероятность неудачи q = 1 — 0,25 = 0,75.
По формуле Бернулли считать сложно. Так как n и m велики, поэтому применим формулу Муавра — Лапласа.
Найдем сначала х и 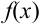
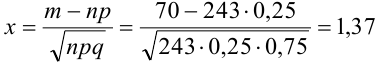
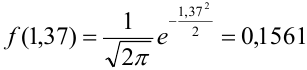
Можно было не считать значение 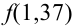
Подставим найденное значение 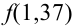
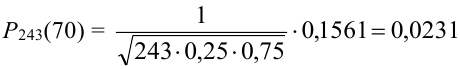
Предельная интегральная теорема Муавра — Лапласа (асимптотическая формула для случая, когда число успехов m лежит в некоторых пределах)
Теорема 1. Если m — число наступлений события А в n независимых испытаниях, в каждом из которых вероятность этого события равна р (0 < р < 1), то равномерно относительно а и b 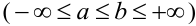
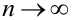
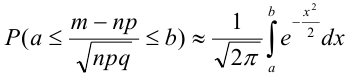
В некоторых источниках 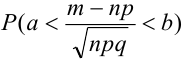
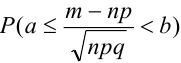
Ранее вывели, что 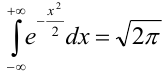
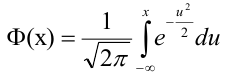
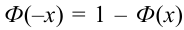
Либо, функция Лапласа может быть в виде: 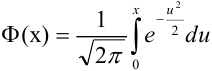
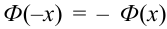
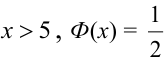
Теорема 2. (Теорема Муавра-Лапласа) Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие А наступит не менее 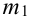
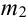
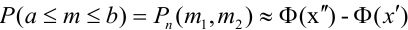
где Ф(х) — функция Лапласа, значения 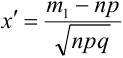
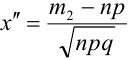
Теорема 3. (Закон больших чисел или теорема Бернулли).
При неограниченном увеличении числа однородных независимых опытов частота события будет сколь угодно мало отличаться от вероятности события в отдельном опыте.
Иначе, вероятность того, что отклонение относительной частоты наступления события 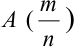
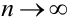
Доказательство.
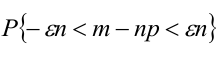
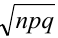
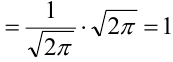
Пример №15
Вероятность появления события А в каждом из 100 независимых испытаний постоянна и равна 0,8. Найти вероятность того, что событие появиться не менее 75 раз и не более 90 раз.
Решение.
Количество испытаний n = 100, вероятность успеха р = 0,8, вероятность неудачи q = 1 — 0,8 = 0,2 , 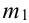
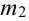
Найдем 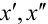
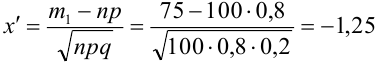
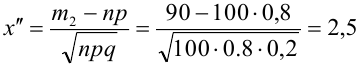
По теореме 2:
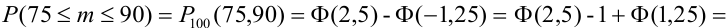
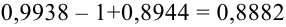
Наивероятнейшее число появления события в независимых испытаниях
Определение 28. Число 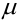
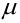
Наивероятнейшее число 
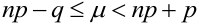
причем 1) если (np — q) -дробное, то существует одно 

Пример №16
Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержат испытание и вероятность этого числа.
Решение.
Количество испытаний n = 15, вероятность успеха р = 0,9, вероятность неудачи q = 0,1.
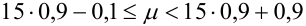
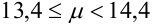
Т.к. 

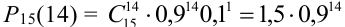
Всё о формуле полной вероятности
Пусть событие 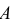
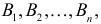
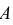
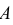
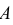
В силу несовместимости событий можно записать
Используя теорему умножения вероятностей, получаем формулу
которая и называется формулой полной вероятности.
Обычно ее записывают кратко:
Пример №17
Имеется две коробки деталей, в каждой из которых по 10 деталей. В первой коробке среди деталей две низкого сорта, а во второй четыре низкосортных детали. Из первой коробки для нужд производства взяли наугад половину деталей, а оставшиеся высыпали во вторую коробку. Через некоторое время из второй коробки взяли наугад деталь. Какова вероятность того, что это деталь низкого сорта?
Решение. Обозначим через A событие, состоящее в выборе из второй коробки детали низкого сорта. Возможность этого выбора зависит от того, какие именно детали были добавлены во вторую коробку. На этот счет можно выдвинуть следующие предположения: B1 – во вторую коробку добавили пять годных деталей; B2 – добавили одну деталь низкого сорта и четыре доброкачественные; B3 – добавили две детали низкого сорта и три доброкачественные. Пять деталей во вторую коробку можно переложить 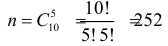
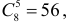
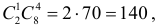
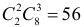
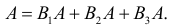

Ответ. 1/ 3.
Всё о Формуле Байеса
Пусть событие A может наступить только при появлении одного из несовместных событий 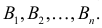

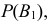
Проделан опыт, в результате которого событие A произошло. Тогда вероятности событий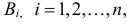
Формулы Байеса позволяют переоценивать вероятности гипотез (событий 
Пример №18
По каналу связи передается одна из последовательностей букв 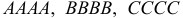
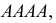
Решение. Для краткости записи формулы обозначим 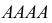
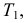
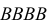
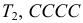
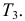
Ответ. 8/9.
Пример №19
Три стрелка производят по одному выстрелу в одну и ту же мишень. Вероятности попадания в мишень при одном выстреле для этих стрелков соответственно равны 0,8; 0,7; 0,6. Какова вероятность того, что третий стрелок промахнулся, если в мишени оказалось две пробоины?
Решение. Обозначим через А событие, состоящее в появлении двух пробоин в мишени. В отношении двух пробоин могут быть три предположения: В1 – попали первый и второй стрелки, а третий не попал, вероятность чего равна 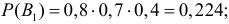
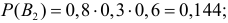
Заметим, что 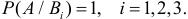
Ответ.
Пример №20
В партии из 10 изделий с равными шансами может оказаться от нуля до трех бракованных. Наугад взяли и проверили три изделия. Они оказались годными. Какова вероятность того, что остальные изделия в партии тоже годные?
Решение. Насчет содержания в партии бракованных изделий по условиям задачи может быть четыре предположения 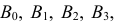
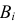
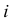
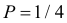
Заметим, что 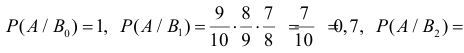
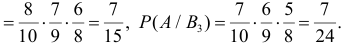
Ответ.
Пример №21
Вероятность того, событие B произойдет в течение часа, равна 0,9. Оказалось, что в течение первых 40 мин. событие B не произошло. Какова вероятность того, что это событие появится в оставшиеся 20 мин. времени?
Решение. В отношении события 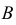
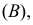
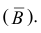
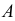
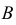
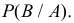
В задаче по умолчанию предполагается, что событие 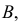
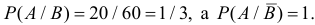
Ответ. 3/4.
Пример №22
В кошельке лежат четыре монеты. Три монеты обычных, а у четвертой на той и другой стороне изображен герб. Наугад взяли монету и подбросили три раза. Все три раза выпал герб. Какова вероятность того, что и при четвертом подбрасывании выпадет герб?
Решение. Обозначим через B1 – выбор монеты с одним гербом, через B2 – выбор монеты с двумя гербами. Априорные вероятности этих событий равны: 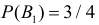
Обозначим через A – выпадение трех гербов подряд. Апостериорные вероятности по формулам Байеса равны:
Тогда по формуле полной вероятности (2.4.1):
P(выпадения герба в четвертый раз)
Ответ.
Подробное объяснение формулы полной вероятности
Постановка задачи: Пусть 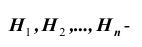
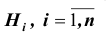


Требуется найти вероятность события A.
Выведем формулу решения этой задачи. Имеем
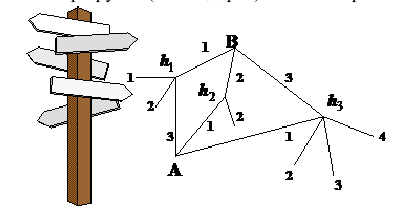
маршрутов (схема дорог). Какова вероятность того, что он попадет в пункт А ?
Решение. Как видим из схемы дорог, путь туриста обязательно проходит через один из пунктов 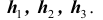
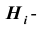
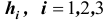
Заметим, что события (гипотезы)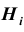
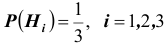
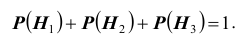
видеть (см. схему), что 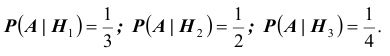
Пример №23 (о мудреце и властелине).
Властелин, разгневавшись на мудреца, приказал отрубить ему голову. Но затем, смягчившись, дал мудрецу возможность попытаться спастись. Итак, властелин взял 2 белых и 2 черных шара и предложил мудрецу распределить их по своему усмотрению по двум одинаковым урнам. После чего, палач сначала наугад выберет одну из урн, а затем также наугад, не глядя, вытащит из неё один шар. Мудрец будет помилован, если вытянутый шар оказался белым. Какую стратегию распределения шаров по урнам должен
выбрать мудрец, чтобы быть помилованным? Какова максимальная вероятность спастись мудрецу? Какая стратегия наименее выгодна для него?
Решение. Выдвинем гипотезы (предположения) 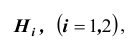
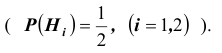
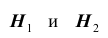
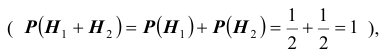
палачом вытянут белый шар. Далее, рассмотрим следующие варианты распределения мудрецом шаров по
урнам:
1). В первой урне 2 белых, а во второй 2 черных шара. Тогда
2 Хотим заметить, что далеко не всегда властелины были глупыми людьми, не знающими математики. Так, например, Наполеон был немного математиком, интересовался, в частности, геометрией. Он вёл дискуссии с Лагранжем и Лапласом, когда ещё не был правителем Франции.
Как-то в одной из таких дискуссий Лаплас резко оборвал Бонапарта: «Менее всего мы хотим от Вас, генерал, урока геометрии». В дальнейшем Лаплас стал его главным военным инженером. Наполеону приписывают теорему: «Если на сторонах произвольного треугольника во внешнюю сторону построены равносторонние треугольники, то их центры образуют равносторонний треугольник» — это так называемый вешний треугольник Наполеона.Так же ему приписывают один из знаменитых палиндромов (читается в обе стороны одинаково): «ABLE WAS I ERE I SAW ELBA» — я был силён, пока не увидел Эльбу.
2). В первой и во второй урнах по 1 белому и 1 черному шару. Тогда
3). В первой урне 1 белый, а во второй 1 белый и 2 черных шара. Тогда
4). В первой урне 1 черный, а во второй 2 белых и 1 черный шары. Тогда
5). Первая урна оказалась пустой, т.е. все шары во второй урне. Тогда
Как видим, наиболее предпочтительной является 3-я стратегия, ей соответствует вероятность быть помилованным равная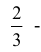
Вероятность гипотез. Формула Байеса
Постановка задачи: Пусть 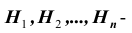
и пусть событие A может произойти лишь совместно с каким — либо одним из этих событий (гипотез) — ситуация аналогичная той, которая была ранее. И пусть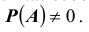
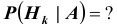
По теореме об умножении вероятностей
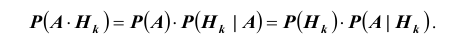
Полученная формула называется формулой Байеса (Бейеса) для переоценки гипотез. Другими словами: вероятность 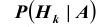
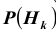
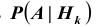
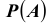
Пример №24
При обследовании больного имеется подозрение (т.е. делаются предположения или, что то же самое, выдвигаются гипотезы)
на одно из двух заболеваний 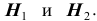
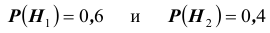
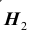
Решение. Во — первых, очевидно, что события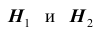
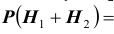
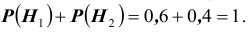
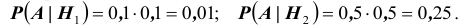
Как видим, при данных результатах обследования следует предполагать болезнь
Повторение испытаний
Формула Бернулли (схема повторения опытов)
Опыты называются независимыми , если вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты. Независимые опыты могут проводиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления какого — либо события A во всех опытах одна и та же, во втором случае — она меняется от опыта к опыту. Ниже мы воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми. Итак, пусть производится n независимых опытов в одинаковых условиях, в каждом из которых некоторое событие A может произойти с одной и той же вероятностью 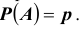
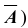
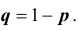
Итак, еще раз: схемой Бернулли называется последовательность n независимых испытаний, проводимых при одних и тех же условиях, в каждом из которых событие A либо происходит с постоянной вероятностью p , не зависящей от номера испытания, либо не происходит с вероятностью
Ставятся задачи:
Задача №1. Найти вероятность 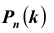
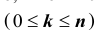
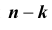
Задача № 2. Найти вероятность 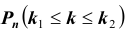
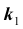
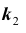
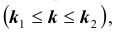
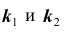
Задача № 3. Найти наивероятнейшее число 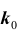
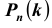
Решение №1.
Вероятность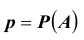
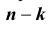
Таких несовместных событий столько, сколько сочетаний из n элементов по k элементов в каждом. Поэтому по теореме о вероятности суммы несовместных событий получим формулу, называемую формулой Бернулли:
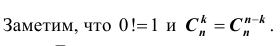
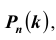
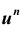
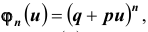
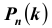
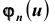
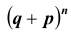
которую называют биномиальным законом распределения вероятностей события A в n испытаниях схемы Бернулли.
Заметим, что вероятность хотя бы одного появления события A в n испытаниях схемы Бернулли равна: 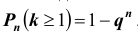
следующим вопросом: честное ли пари вам предлагают, если вы выиграете в том случае, когда при 24-х кратном бросании двух игральных костей хотя бы один раз одновременно появятся две шестёрки? Ответ дайте в конце пары.
(РЕШЕНИЕ. Вероятность одновременного выпадения двух шестерок при одном подбрасывании равна 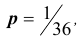
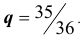
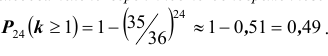
Другие примеры на применение формулы Бернулли, рассмотрим немного позднее, а именно после того, как решим задачи № 2 и № 3
Решение № 2.
Нетрудно показать, что вероятность 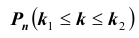
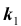
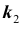
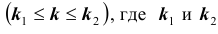
Решение № 3
Важной является задача № 3 о наивероятнейшем числе 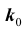
Рассмотрим отношение:
Из полученного следует, что:
1) если 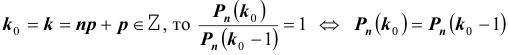
два максимума;
2) если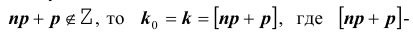
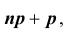
Пример №25
При некоторых условиях стрельбы вероятность p попадания в цель при одном выстреле равна
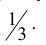
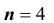
- а). Каково наивероятнейшее число попаданий в цель?
- б). Какова его вероятность?
- в). Какова вероятность двух попаданий?
- г). Какова вероятность хотя бы одного попадания?
Пример №26
Некто Сэмюэль Пепайс обратился к Исааку Ньютону с вопросом: какое из событий наиболее вероятно —
- появление по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей;
- хотя бы двух «шестерок» при подбрасывании 12-ти;
- хотя бы трех «шестерок» при подбрасывании 18-ти?
Решение.
Вероятность q непоявления «шестерки» при одном подбрасывании, как известно, равна 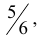
5 . Таким образом, вероятность появления по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей может быть найдена по формуле:
Событие «хотя бы две» противоположно событию «либо ни разу, либо один раз», т.е.
Событие «хотя бы три» противоположно событию «либо ни разу, либо один раз, либо два раза», т.е.
Таким образом, как видим, предпочтительнее первая стратегия – таким и был ответ Ньютона.
Замечу, что при больших значениях числа n испытаний в схеме Бернулли формула для подсчета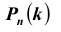
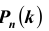
ТЕОРЕМА Пуассона 3. Пусть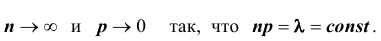
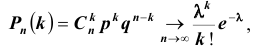
Доказательство
Что и требовалось доказать.
При доказательстве можно воспользоваться приближенной формулой Стирлинга.
Следствие: при указанных выше условиях, т.е. при 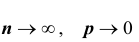
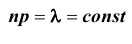
Пример №27
Телефонная станция обслуживает 800 абонентов. Для каждого абонента вероятность того, что в течении часа он позвонит на станцию равна p =0,01. Найти вероятность того, что четыре абонента позвонят на станцию в течении часа.
Решение
Теорема Муавра — Лапласа (локальная)
Остановлюсь еще на двух предельных теоремах в схеме Бернулли — локальной теореме Муавра — Лапласа (её доказательство получим как частный случай закона больших чисел — предельной теоремы Ляпунова, доказательство которой нам ещё предстоит провести) и интегральной теореме Муавра — Лапласа. Итак:
причем, во-первых, погрешность этой формулы есть величина порядка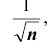
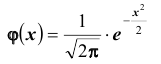
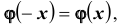
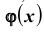
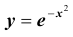
интегральная приближенная формула Лапласа ( при больших
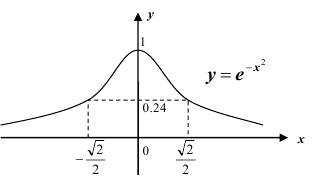
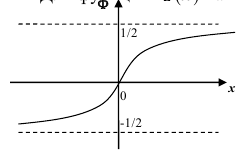
Для функции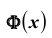
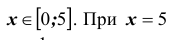
равносильно условию 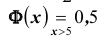
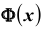
Замечание: если функция Лапласа записана в виде 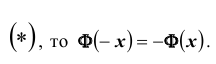
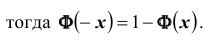
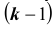
Формула полной вероятности и сложные задачи
В данном разделе мы рассмотрим более сложные задачи, имеющие большое практическое значение. Эти задачи встречается на практике в случае, если имеются несколько возможных сценариев развития событий (несколько вероятных гипотез). Известны как величины вероятности реализации каждого из сценариев, так и вероятность наступления интересующего нас события для любого из этих сценариев, а нас интересует, какова полная (совокупная) вероятность наступления интересующего нас события.
Предположим, что в результате опыта может произойти одно из n несовместных событий (гипотез) 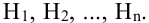
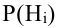
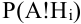
Пример №28
Из 40 деталей 10 изготовлены в первом цехе, 25 — во втором, а остальные — в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех — с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?
Решение:
Обозначим событие А = {выбрана деталь отличного качества}, Hi= {выбранная деталь изготовлена в i цехе}, i = 1, 2, 3. Тогда
По условию задачи 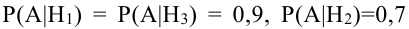
Пример №29
На рисунке изображена схема дорог. Найти вероятность того, что турист, вышедший из пункта А, попадет в пункт В, если на развилке он наугад выбирает любую дорогу (кроме обратной).
Решение:
Обозначим Нi = {приход туриста в пункт Hi}, i = 1, 2, 3, 4. Поскольку, выйдя из пункта А, он выбирает любую дорогу наугад, то 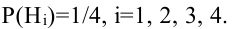
Исходя из схемы дорог, определяем, что
Таким образом, по формуле полной вероятности
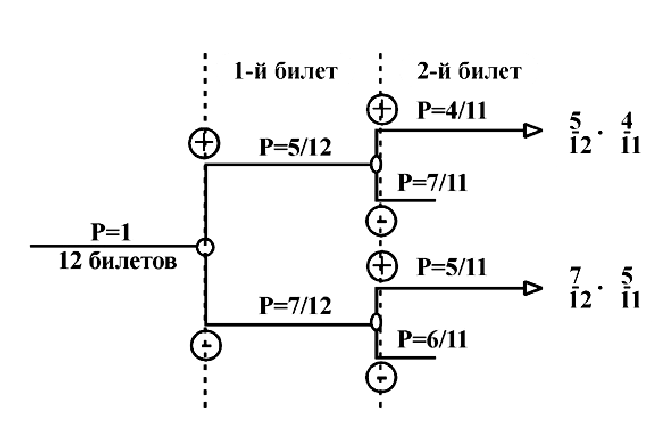
Пример №30
Из двенадцати лотерейных билетов пять выигрышных. Билеты вытягиваются по одному без возвращения. Какова вероятность того, что во второй раз вытянут выигрышный билет?
Решение:
Как обычно, вдоль каждой ветви «дерева вероятностей» значения вероятностей перемножаются, а затем значения на концах нужных веток между собой складываются. В результате получаем ответ:
Случайные события независимые в совокупности
Следует различать попарно независимые случайные события и случайные события независимые в совокупности.
Определение: События называются попарно независимыми событиями, если любые два из них независимы.
Определение: События 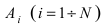
Замечание: Из определений видно, что из попарной независимости еще не следует, что эти события независимы в совокупности. Это означает, что условие независимости в совокупности является более сильным, чем условие попарной независимости случайных событий.
Теорема: Вероятность наступления хотя бы одного из событий 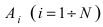
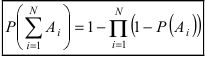
Доказательство: Обозначим через А событие, состоящее в том, что наступит хотя бы одно из событий 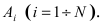
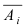
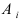
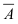
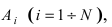
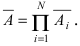
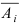
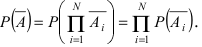
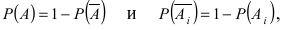
Пример №31
Пусть прибор содержит N последовательно соединенных блоков. Определить вероятность того, что цепь будет разорвана, если вероятность работы каждого блока равна р и она не зависит от работы других блоков.
Решение:
Пусть А — событие, которое состоит в том, что данная цепь разорвана. Это событие происходит, если выходит из строя хотя бы один из блоков, так как блоки включены последовательно. Противоположное событие состоит в том, что все блоки работают, т.е. 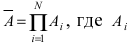
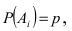
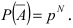
Теорема сложения вероятностей для совместных событий
Если случайные события одновременно появляются в условиях опыта, то имеет место следующая теорема.
Теорема: Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их произведения:
Доказательство: Пусть в результате опыта возможно n равно возможных, несовместных, элементарных исходов. При этом в 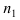
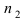
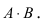
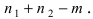
Замечание: Методом математической индукции вышеприведенная теорема может быть обобщена на любое число совместных событий, например, в случае 3 совместных событий А, В и С теорема принимает вид:
Пример №32
Найти вероятность того, что взятое наугад число из чисел от 10 до 20 делится или на 2, или на 3.
Решение:
Всего равновозможных, элементарных исходов 11 (числа от 10 включительно до 20 включительно). В 6 случаях (10, 12, 14, 16, 18, 20) число кратно 2; в 3 случаях (12, 15, 18) число кратно 3; в 2 случаях (12, 18) число кратно и 2, и 3. Пусть событие А состоит в том, что наугад взятое число кратно 2, а событие В состоит в том, что наугад взятое число кратно 3. Сложное событие С состоит в том, что наугад взятое число делится или на 2, или на 3, т.е. С = А + В. Следовательно, вероятность этого события равна:
Все вышерассмотренные теоремы объединяются в теории вероятностей общим названием “основные теоремы теории вероятностей”.
Формула полной вероятности и события
Формула полной вероятности является следствием основных теорем теории вероятностей: теорем сложения и умножения вероятностей событий.
Пусть некоторое случайное событие А наступает с одним и только с одним из несовместных событий
Определение: События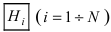
Теорема: Формула полной вероятности определяет вероятность случайного
события л, как сумму произведений вероятности каждой гипотезы 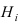
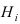
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 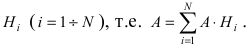
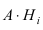
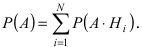
Пример №33
Пусть на сборку поступают детали с двух автоматических станков. Первый станок дает в среднем 0.3 % брака, а второй — 0.15 % брака. Производительность второго станка в два раза выше, чем первого станка. Найти вероятность того, что наугад взятая деталь окажется бракованной.
Решение:
Пусть событие А состоит в том, что наугад взятая деталь окажется бракованной. Тогда гипотеза 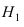
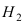
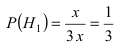
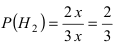
Вероятности события А при условии реализации первой и второй гипотез равны: 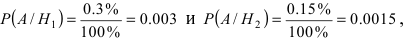
Формула вероятностей гипотез (формула Байеса)
Ниже будет получена формула, которая является следствием основных теорем теории вероятностей и формулы полной вероятности. Эта формула применяется для решения задач следующего типа. Пусть проводится эксперимент, в результате которого может появиться или не появиться событие л, которое наступает с одним и только с одним из несовместных событий 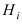
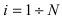
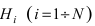
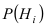
Теорема: Вероятность гипотезы 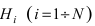
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 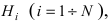
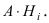
Следовательно, 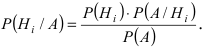
Пример №34
Однотипные пластмассовые детали изготавливаются на 3 прессах. Первый пресс выпускает 50 % всех деталей, второй — 40 %, третий — 10 % . При этом с первого пресса сходит в среднем 0.025 нестандартных деталей, со второго — 0.02 и с третьего — 0.015. Все детали поступают на сборку. Взятая наудачу деталь оказалась нестандартной. Какова вероятность того, что она изготовлена на первом прессе.
Решение:
Событие А состоит в том, что наудачу взятая деталь изготовлена на первом прессе. Гипотеза 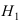
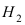
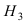
По условию задачи 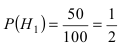
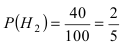
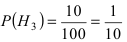
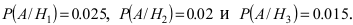
Используя формулу Байеса, получим
Независимые испытания и формула Бернулли
Пусть испытания повторяются n раз, причем событие А появляется в каждом опыте с одной и той же вероятностью р или не появляется с одной и той же вероятностью
Определение: Испытания называются независимыми, если вероятность события А не зависит от того, какие события появились в предыдущих опытах, или появятся в последующих экспериментах.
Пример:
Независимы ли следующие испытания: а) многократное бросание кубика; б) извлечение карты из колоды без ее возвращения в колоду (выяснить самостоятельно).
Формула Бернулли
Теорема: Пусть проводится серия из n независимых испытаний, в каждом из которых событие А появляется с постоянной вероятностью 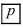
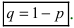
Доказательство: Пусть 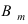
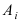
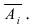
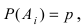
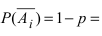
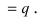
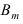
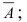
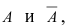
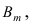
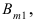
Воспользуемся теоремой умножения вероятностей для независимых событий, получим: 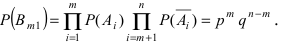
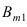
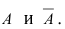
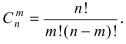
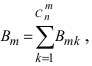
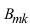
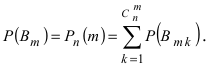
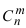
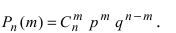

Пример №35
Монета подбрасывается 6 раз. Определить вероятность того, что герб выпадет а) 5 раз; б) от 2 до 4 раз.
Решение:
Вероятность выпадения герба не изменяется от опыта к опыту и равна 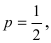
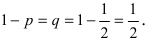
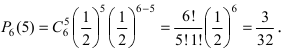
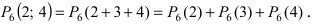
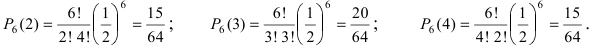
При больших значениях чисел m и n применение формулы Бернулли затруднительно, так как вычисление коэффициентов 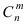
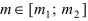
Формула Пуассона
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А мала (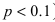
Формулы Муавра-Лапласа
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А р>0.1, то при больших значениях чисел m и n применяют дифференциальную формулу Муавра-Лапласа: 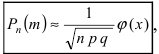
Замечание: В общем случае дифференциальная формула Муавра-Лапласа применяется при выполнении неравенств
Если при проведении серии испытаний по схеме Бернулли числа m и n принимают большие значения, причем число m принимает значения от 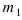
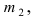
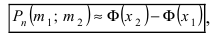
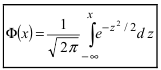
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Теоремы сложения и умножения вероятностей
Решение задач про вероятность попаданий при выстрелах
Полезная страница? Сохрани или расскажи друзьям
Общая постановка задачи следующая:
Вероятность попадания в цель при одном выстреле равна $p$. Производится $n$ выстрелов. Найти вероятность того, что цель будет поражена в точности $k$ раз (будет $k$ попаданий).
Применяем формулу Бернулли и получаем:
$$
P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k} = C_n^k cdot p^k cdot q^{n-k}. qquad (1)
$$
Здесь $C_n^k$ — число сочетаний из $n$ по $k$.
Если в задаче речь идет о нескольких стрелках с разными вероятностями попадания в цель, теорию, примеры решения и калькулятор вы можете найти здесь.
Видеоурок и шаблон Excel
Посмотрите наш ролик о решении задач о выстрелах в схеме Бернулли, узнайте, как использовать Excel для решения типовых задач.
Расчетный файл Эксель из видео можно бесплатно скачать и использовать для решения своих задач.
Примеры решений задач о попаданиях в цель в серии выстрелов
Рассмотрим несколько типовых примеров.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,705. Найти вероятность того, что при этом будет ровно 5 попаданий.
Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах по мишени), всего производится $n=7$ выстрелов, вероятность попадания при каждом $p=0,705$, вероятность промаха $q=1-p=1-0,705=0,295$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$
P_7(5)=C_{7}^5 cdot 0,705^5 cdot 0,295^2 = 21cdot 0,705^5 cdot 0,295^2= 0,318.
$$
Пример 2. Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится четыре независимых выстрела. Найти вероятность того, что будет хотя бы одно попадание в мишень.
Изучаем задачу и выписываем параметры: $n=4$ (выстрела), $p=0,4$ (вероятность попадания), $k ge 1$ (будет хотя бы одно попадание). Используем формулу для вероятности противоположного события (нет ни одного попадания):
$$
P_4(k ge 1) = 1-P_4(k lt 1) = 1-P_4(0)=
$$
$$
=1-C_{4}^0 cdot 0,4^0 cdot 0,6^4 =1- 0,6^4=1- 0,13=0,87.
$$
Вероятность попасть хотя бы один раз из четырех равна 0,87 или 87%.
Пример 3. Вероятность поражения мишени стрелком равна 0,3. Найти вероятность того, что при 6 выстрелах мишень будет поражена от трех до шести раз.
В отличие от предыдущих задач, здесь нужно найти вероятность того, что число попаданий будет находится в некотором интервале (а не равно в точности какому-то числу). Но формула используется прежняя.
Найдем вероятность того, что мишень будет поражена от трех до шести раз, то есть будет или 3, или 4, или 5, или 6 попаданий. Данные вероятности вычислим по формуле (1):
$$
P_6(3)=C_{6}^3 cdot 0,3^3cdot 0,7^3 = 0,185.
$$
$$
P_6(4)=C_{6}^4 cdot 0,3^4cdot 0,7^2 = 0,06.
$$
$$
P_6(5)=C_{6}^5 cdot 0,3^5cdot 0,7^1 = 0,01.
$$
$$
P_6(6)=C_{6}^6 cdot 0,3^6cdot 0,7^0 = 0,001.
$$
Так как события несовместные, искомая вероятность может быть найдена по формуле сложения вероятностей:
$$
P_6(3 le k le 6 )=P_6(3)+P_6(4)+P_6(5)+P_6(6)=$$
$$ = 0,185+0,06+0,01+0,001=0,256.$$
Пример 4. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.
Обозначим вероятность попадания в цель при одном выстреле. Введем событие:
$A = $ (Из четырех выстрелов хотя бы один попадет в цель),
а также противоположное ему событие, которое можно записать как:
$overline{A} = $ (Все 4 выстрела будут мимо цели, ни одного попадания).
Запишем формулу для вероятности события $A$. Выпишем известные значения: $n=4$, $P(A)=0,9984$. Подставляем в формулу (1) и получаем:
$$
P(A)=1-P(overline{A})=1-P_4(0)=1-C_{4}^0 cdot p^0 cdot (1-p)^4=1-(1-p)^4=0,9984.
$$
Решаем получившееся уравнение:
$$
1-(1-p)^4=0,9984,\
(1-p)^4=0,0016,\
1-p=0,2,\
p=0,8.
$$
Итак, вероятность попадания в цель при одном выстреле равна 0,8.
Лучшее спасибо — порекомендовать эту страницу
Полезные ссылки
- Решения разных задач о стрелках и выстрелах
- Примеры контрольных по теории вероятностей
- Заказать контрольную по теории вероятностей
Найдите готовые задачи в решебнике:
Содержание:
- Примеры с решением
- Частота, или статистическая вероятность, события
Каждая наука, развивающая общую теорию какого-либо круга явлений, содержит ряд основных понятий, на которых она базируется. Таковы, например, в геометрии понятия точки, прямой, линии; в механике— понятия силы, массы, скорости, ускорения и т. д. Естественно, что не все основные понятия могут быть строго определены, так как определить понятие — это значит свести его к другим, более известным.
Очевидно, процесс определения одних понятий через другие должен где-то заканчиваться, дойдя до самых первичных понятий, к которым сводятся все остальные и которые сами строго не определяются, а только поясняются.
Такие основные понятия существуют и в теории вероятностей. В качестве первого из них введем понятие события.
Под «событием» в теории вероятностей понимается всякий факт, который в результате опыта может произойти или не произойти.
Приведем несколько примеров событий:
- А — появление герба при бросании монеты;
- В— появление трех гербов при трехкратном бросании монеты;
- С — попадание в цель при выстреле;
- D—появление туза при вынимании карты из колоды;
- Е— обнаружение объекта при одном цикле обзора радиолокационной станции;
- F— обрыв нити в течение часа работы ткацкого станка.
Рассматривая вышеперечисленные события, мы видим, что каждое из них обладает какой-то степенью возможности: одни — большей, другие — меньшей, причем для некоторых из этих событий мы сразу же можем решить, какое из них более, а какое менее возможно. Например, сразу видно, что событие А более возможно, чем В и D. Относительно событий С, Е и F аналогичных выводов сразу сделать нельзя; для этого следовало бы несколько уточнить условия опыта. Так или иначе ясно, что каждое из таких событий обладает той или иной степенью возможности. Чтобы количественно сравнивать между собой события по степени их возможности, очевидно, нужно с каждым событием связать определенное число, которое тем больше, чем более возможно событие. Такое числи мы назовем вероятностью события.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Таким образом, мы ввели в рассмотрение второе основное понятие теории вероятностей — понятие вероятности события. Вероят-ность события есть численная мера степени объективной возможности этого сооытия.
- Заметим, что уже при самом введении понятия вероятности события мы связываем с этим понятием определенный практический смысл, а именно: на основании опыта мы считаем более вероятными те события, которые происходят чаще; менее вероятными —те события, которые происходят реже; мало вероятными—те, которые почти никогда не происходят. Таким образом, понятие вероятности события в самой своей основе связано с опытным, практическим понятием частоты события.
Сравнивая между собой различные события по степени их возможности, мы должны установить какую-то единицу измерения. В качестве такой единицы измерения естественно принять вероятность достоверного события, т. е. такого события, которое в результате опыта непременно должно произойти. Пример достоверного события — выпадение не более 6 очков при бросании одной игральной кости.
Если приписать достоверному событию вероятность, равную единице, то все другие события — возможные, но не достоверные — будут характеризоваться вероятностями, меньшими единицы, составляющими какую-то долю единицы.
Противоположностью по отношению к достоверному событию является невозможное событие, т. е. такое событие, которое в данном опыте не может произойти. Пример невозможного события — появление 12 очков при бросании одной игральной кости. Естественно приписать невозможному событию вероятность, равную нулю.
Таким образом, установлены единица измерения вероятностей— вероятность достоверного события — и диапазон изменения вероятностей любых событий — числа от 0 до 1.
Непосредственный подсчет вероятностей
Существует целый класс опытов, для которых вероятности их возможных исходов легко оценить непосредственно из условий самого опыта. Для этого нужно, чтобы различные исходы опыта обладали симметрией и в силу этого были объективно одинаково возможными.
Рассмотрим, например, опыт, состоящий в бросании игральной кости, т. е. симметричного кубика, на гранях которого нанесено различное число очков: от 1 до 6.
Возможно вам будут полезны данные страницы:
В силу симметрии кубика есть основания считать все шесть возможных исходов опыта одинаково возможными. Именно это дает нам право предполагать, что при многократном бросании кости все шесть граней будут выпадать примерно одинаково часто. Эго предположение для правильно выполненной кости действительно оправдывается па опыте; при многократном бросании кости каждая ее грань появляется примерно в одной шестой доле всех случаев бросания, причем отклонение этой доли от 

Для всякого опыта, в котором возможные исходы симметричны и одинаково возможны, можно применить аналогичный прием, который называется непосредственным подсчетом вероятностей.
Симметричность возможных исходов опыта обычно наблюдается только в искусственно организованных опытах, типа азартных игр. Так как первоначальное развитие теория вероятностей получила именно на схемах азартных игр, то прием непосредственного подсчета вероятностей, исторически возникший вместе с возникновением математической теории случайных явлений, долгое время считался основным и был положен в основу так называемой «классической» теории вероятностей. При этом опыты, не обладающие симметрией возможных исходов, искусственно сводились к «классической» схеме.
- Несмотря на ограниченную сферу практических применений этой схемы, она все же представляет известный интерес, так как именно на опытах, обладающих симметрией возможных исходов, и на событиях, связанных с такими опытами, легче всего познакомиться с основными свойствами вероятностей. Такого рода событиями, допускающими непосредственный подсчет вероятностей, мы и займемся в первую очередь.
Предварительно введем некоторые вспомогательные понятия.
1. Полная группа событий.
Говорят, что несколько событий в данном опыте образуют полную группу событий, если в результате опыта непременно должно появиться хотя бы одно из них.
Примеры событий, образующих полную группу:
- выпадение герба и выпадение цифры при бросании монеты;
- попадание и промах при выстреле;
- появление 1,2, 3, 4, 5, 6 очков при бросании игральной кости;
- появление белого- шара и появление черного шара при вынимании одного шара из урны, в которой 2 белых и 3 черных шара;
- ни одной опечатки, одна, две, три и более трех опечаток при проверке страницы напечатанного текста;
- хотя бы одно попадание и хотя бы один промах при двух выстрелах.
2. Несовместные события.
Цесколько событий называются несовместными в данном опыте, если никакие не могут появиться вместе.
Примеры несовместных событий:
- выпадение герба и выпадение цифры при бросании монеты;
- попадание и промах при одном выстреле;
- появление 1, 3, 4 очков при одном бросании игральной кости;
- ровно один отказ, ровно два отказа, ровно три отказа технического устройства за десять часов работы.
3. Равновозможные события.
Несколько событий в данном опыте называются равновозможными, если по условиям Симметрии есть основание считать, что ни одно из этих событий не является объективно более возможным, чем другое.
Примеры равновозможных событий:
- выпадение герба и выпадение цифры при бросании монеты;
- появление 1, 3, 4, 5 очков при бросании игральной кости;
- появление карты бубновой, червонной, трефовой масти при вынимании карты из колоды;
- появление шара с № 1, 2, 3 при вынимании одного шара из урны» содержащей 10 перенумерованных шаров.
Существуют группы событий, обладающие всеми тремя свойствами: они образуют полную группу, несовместны и равновозможны; например: появление герба и цифры при бросании монеты; появление 1, 2, 3, 4, 5, 6 очков при бросании игральной кости. События, образующие такую группу, называются случаями (иначе «шансами»).
Если какой-либо опыт по своей структуре обладает симметрией возможных исходов, то случаи представляют собой исчерпывающую систему равновозможных и исключающих друг друга исходов опыта. Про такой опыт говорят, что он «сводится к схеме случаев» (иначе — к «схеме урн»).
Схема случаев по преимуществу имеет место в искусственно организованных опытах, в которых заранее и сознательно обеспечена одинаковая возможность исходов опыта (как, например, в азартных играх). Для таких опытов возможен непосредственный подсчет вероятностей, основанный на оценке доли так называемых «благоприятных» случаев в общем числе случаев.
Случай называется благоприятным (или «благоприятствующим») некоторому событию, если появление этого случая влечет за собой появление данного события.
Например, при бросании игральной кости возможны шесть случаев: появление 1, 2, 3, 4, 5, 6 очков. Из них событию А—появлению четного числа очков—благоприятны три случая: 2, 4. 6 и не благоприятны остальные три.
Если опыт сводится к схеме, случаев, то вероятность события А в данном опыте можно оценить по относительной доле благоприятных случаев. Вероятность события А вычисляется как отношение числа благоприятных случаев к общему числу случаев:




Так как число благоприятных случаев всегда заключено между 


Примеры с решением
Пример 1.
В урне находится 2 белых и 3 черных шара. Из урны наугад вынимается один шар. Требуется найти вероятность того, что этот шар будет белым.
Решение:
Обозначим А событие, состоящее в появлении белого шара. Общее число случаев 

Пример 2.
В урне а белых и 
Решение:
Обозначим В событие, состоящее в появлении двух белых шаров. Подсчитаем общее число возможных случаев n и число случаев m, благоприятных событию В:
следовательно,
Пример 3.
В партии из 


Решение:
Общее число случаев, очевидно, равно 

события
Частота, или статистическая вероятность, события
Формула (2.2.1) для непосредственного подсчета вероятностей применима только, когда опыт, в результате которого может появиться интересующее нас событие, обладает симметрией возможных исходов (сводится к схеме случаев). Очевидно, что далеко не всякий опыт может быть сведен к схеме случаев, и существует обширный класс событий, вероятности которых нельзя вычислить по формуле (2.2.1).
Рассмотрим, например, неправильно выполненную, несимметричную игральную кость. Выпадение определенной грани уже не будет характеризоваться вероятностью 
Очевидно, что вероятности таких событий, как «попадание в цель при выстреле», «выход из строя радиолампы в течение одного часа работы» или «пробивание брони осколком снаряда», также не могут быть вычислены по формуле (2.2.1), так как соответствующие опыты к схеме случаев не сводятся. Вместе с тем ясно, что каждое из перечисленных событий обладает определенной степенью объективной возможности, которую в принципе можно измерить численно и которая при повторении подобных опытов будет отражаться в относительной частоте соответствующих событий. Поэтому мы будем считать, что каждое событие, связанное с массой однородных опытов,—сводящееся к схеме случаев или нет, — имеет определенную вероятность, заключенную между нулем и единицей.
Для событий, сводящихся к схеме случаев, эта вероятность может быть вычислена непосредственно по формуле (2.2.1). Для событий, не сводящихся к схеме случаев, применяются другие способы определения вероятностей. Все эти способы корнями своими уходят в опыт, в эксперимент, и для того чтобы составить представление об этих способах, необходимо уяснить себе понятие частоты события и специфику той органической связи, которая существует между вероятностью и частотой.
(если произведена серия из п опытов, в каждом из которых могло появиться или не появиться некоторое событие А, то частотой события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу произведенных опытов.
Частоту события часто называют его статистической вероятностью (в отличие от ранее введенной «математической» вероятности).
Условимся обозначать частоту (статистическую вероятность) события 
где 

При небольшом числе опытов частота события носит в значительной мере случайный характер и может заметно изменяться от одной группы опытов к другой. Например, при каких-то десяти бросаниях монеты вполне возможно, что герб появится только два раза (частота появления герба будет равна 0,2); при других десяти бросаниях мы вполне можем получить 8 гербов (частота 0,8). Однако при увеличении числа опытов частота события все более теряет свой случайный характер; случайные обстоятельства, свойственные каждому отдельному опыту, в массе взаимно погашаются, и частота проявляет тенденцию стабилизироваться, приближаясь с незначительными колебаниями к некоторой средней, постоянной величине. Например, при многократном бросании монеты частота появления герба будет лишь незначительно уклоняться от 
- Это свойство «устойчивости частот», многократно проверенное экспериментально и подтверждающееся всем опытом практической деятельности человечества, есть одна из наиболее характерных закономерностей, наблюдаемых в случайных явлениях.
Математическую формулировку этой закономерности впервые дал Я. Бернулли в своей теореме, которая представляет собой простейшую форму закона больших чисел. Я. Бернулли доказал, что при неограниченном увеличении числа однородных независимых опытов с практической достоверностью можно утверждать, что частота события будет сколь угодно мало отличаться от его вероятности в отдельном опыте.
Связь между частотой события и его вероятностью — глубокая, органическая связь. Эти два понятия по существу неразделимы. Действительно, когда мы оцениваем степень возможности какого-либо события, мы неизбежно связываем эту оценку с большей или меньшей частотой появления аналогичных событий на практике. Характеризуя вероятность события каким-то числом, мы не можем придать этому числу иного реального значения и иного практического смысла, чем относительная частота появления данного события при большом числе опытов. Численная оценка степени возможности события посредством вероятности имеет практический смысл именно потому, что более вероятные события происходят в среднем чаще, чем менее вероятные. И если практика определенно указывает на то, что при увеличении числа опытов частота события имеет тенденцию выравниваться, приближаясь сквозь ряд случайных уклонений к некоторому постоянному числу, естественно предположить, что это число и есть вероятность события.
Пример 6.
Происходит бой («дуэль») между двумя j-частниками (ле-нательными аппаратами, ганками, кораблями) А и В. У стороны А в запасе два выстрела, у стороны В — один. Начинает стрельбу А: он делает, по £ один выстрел и поражает его с вероятностью 0,2. Если В не поражен, о:: отвечает противнику выстрелом н поражает его с вероятностью 0,3. Если А этим выстрелом не поражен, то он делает по В свой последний выстрел, которым поражает его с вероятностью 0,4. Найти вероятность того, что в бою будет поражен: а) участник А, б) участник В.
Решение:
Рассмотрим события:
А — поражение участника А,
В — поражение участника В.
Для выполнения события А необходимо совмещение (Произведение) двул событий: 1) А не поразил В первым выстрелом и 2) В поразил А своим ответным выстрелом. По теореме умножения вероятностей получим




По теореме сложения вероятностей



1) первый выстрел стороны А не должен поразить 5;
2) ответный выстрел стороны В не должен поразить А;
3) последний (второй) выстрел стороны А должен поразить В.
По теореме умножения вероятностей

Пример 7.
Цель, по которой ведется стрельба, состоит нз трех различных по уязвимости частей. Для поражения цели достаточно одного попадания в первую часть, или двух попаданий во вторую, или трех попаданий в третью. Если снаряд попал в цель, то вероятность ему попасть в ту или другую часть пропорциональна площади этой части. На проекции цели на плоскость, перпендикулярную направлению стрельбы, первая, вторая и третья части занимают относительные площади 0,1, 0,2 н 0,7. Известно, что в цель попало ровно два снаряда. Найти вероятность того, что цель будет поражена.
Решение:
Обозначим 

Вероятность того, что хотя бы один снаряд попадет в первую часть, может быть вычислена через вероятность противоположного события (нн один нз двух снарядов не попадет в первую часть) и равна 1 — 0.92. Вероятность того, что оба снаряда попадут во вторую часть, равна 0,22. Следовательно,

Пример 8.
Для условий предыдущего примера найти вероятность поражения цели, если известно, что в псе попало три снаряда.
Решение:
Решим задачу двумя способами: через прямое и противоположное событие.
Прямое событие — пораженно цел:: при трех попаданиях — распадается на четыре несовместных варианта:




Вероятность первого варианта находим аналогично предыдущему примеру:
Найдем вероятность второго варианта. Три попавших снаряда могут распределиться по второй н третьей частям нужным образом (два во вторую и один — в третью) тремя способами 





Пример 9.
Монета бросается 6 раз. Найти вероятность того, что выпадет больше гербов, чем цифр.
Решение:
Для нахождения вероятности интересующего нас события A (выпадет больше гербов, чем цифр) можно было бы перечислить все возможные его варианты, например:


и т. д.
Однако проще будет применить другой прием. Перечислим все возможные исходы опыта:
А — выпадет больше гербов, чем цифр,
В — выпадет больше цифр, чем гербов,
С — выпадет одинаковое число цифр и гербов.
События А, В, С несовместны и образуют полную группу. Следовательно,







Пример 10.
Прибор состоит из четырех узлов: 







Решение:
Рассмотрим совокупность узлов 

А — безотказная работа прибора,
В — безотказная работа обобщенного узла В,
С—безотказная работа обобщенного узла С.
Очевидно,
откуда





Имеем:
аналогично
откуда

Лекции:
- Свойства определенного интеграла
- Комбинаторика
- Однородные дифференциальные уравнения
- Простейшие задачи аналитической геометрии
- Линейные преобразования
- Средняя скорость изменения, мгновенная скорость изменения
- Перпендикулярные прямые
- Найти угол между векторами: пример решения
- Как найти длину
- Экстремум функции двух переменных