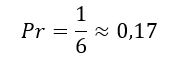Как найти вероятность питон

Привет, Хабр! Я очень долго собирался с мыслями, чтобы попробовать опубликовать свою статью в вашем сообществе, это дебют, поэтому буду рад услышать в комментариях обратную связь по поводу содержимого материала. Тематика сегодняшнего сообщения – это разбор базовых понятий в теории вероятностей с помощью языка программирования Python.

Прежде чем приступить к изложению базовых понятий немного расскажу о себе, о профессиональном опыте, чтобы вы могли иметь представление об авторе. Я окончил Уральский Федеральный Университет по направлению бизнес-информатика и сейчас работаю младшим научным сотрудником в Институте экономики Уральской Академии наук (г. Екатеринбург). В основном направление, по которому я обучался, опиралось на моделировании бизнес процессов. Было конечно немного статистики и теории вероятностей, но по мере своего профессионального роста знаний, полученных в университете, мне оказалось недостаточно, поэтому сейчас я вспоминаю изученный материал и постепенно изучаю новый. В качестве такого своеобразного отчёта о проделанной работе принял решение публиковать небольшие статьи здесь. Надеюсь для новичков, которым собственно я и являюсь по сегодняшний день данный материал будет полезен.

За основу для изучения взял оксфордский учебник на английском языке «Bayesian Statistics for Beginners» (автор Therese M и Ruth M.Mickey). Если у вас есть какие-то базовые знания по математике, которые вы хотите углубить или вспомнить данная книга как раз для вас. Мне очень понравилось её необычное изложение в форме интервью, достаточно простой английский (для уровня B1-B2). Думаю, если вы часто читаете документацию на английском языке или ещё лучше научную литературу, учебник можно осилить практически без словаря. Сама книга – цветная, читать формулы – одно удовольствие. В общем зарекомендовал как мог.

Далее расскажу об опыте изучения литературы, потому что считаю для кого-то это очень важным. Чтение книги я разбил в три этапа.

1.     Обзорное чтение (сюда включается перевод терминов, слов, выражений)

2.     Конспектирование (очень полезный инструмент для осознания материала)

3.     Публикация в Хабре (рефлексия, принятие материала, разработка программного кода для лучшего понимания алгоритмов в теории вероятности)

4.     Получение обратной связи от участников сообщества.

На изучение книги ушло около 4 месяцев (с ноября 2021 года по март 2022 года). Думаю, после этого короткого введения можно начать описывать обзор прочитанного. Ах, чуть не забыл в начале каждой статьи я буду публиковать примерный её содержательный план, к которому буду придерживаться. План описывался мной с помощью карт MindMap. Если вам плохо видно, можно скачать .png версию вот тут (https://cloud.mail.ru/public/Hhja/58V3Wqx1G). Итак, начинаем…

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ

После небольшой вводной информации приступаю к описанию материала. Если говорить научным языком, то следующий материал будет посвящён методам. Здесь я расскажу о том, что такое пространство элементарных событий («sample space») и случайных величин («outcome»); приведу понятие эксперимента и то, как я его понимаю; вероятность («probability»), интерпретация вероятности и дискретных случайных величин. Ещё раз напоминаю, что предложенный препринт не является точной копией книги, поэтому, если у вас будет желание, можете перечитать первую главу и расширить представление о предмете статьи. Начинаем разбор полётов!

Пожалуй, одним из основополагающих понятий, благодаря которому можно понять, что речь идёт о теории вероятностей, а не о другой области исследования является выборка («sample») (1) и пространство элементарных событий («sample space») (2). Я воспринимаю (1) как некоторый список сущностей (или событий), которые может захватить глаз человека и представить его на бумаге. Есть второй вариант интерпретации определения (1) – это могут быть выдуманные значения (числа, символы), которые можно представить на бумаге. Эти данные являются исходными значениями для эксперимента (о нём будет сказано чуть позже). Выборку мы получаем из пространства элементарных событий (2). По сути своей это абстрактное понятие, определяющее множество выборок в пространстве.

Чуть выше мы затронули понятие эксперимента. Поскольку выше было определено, что выборка может быть, как выдуманной, так и нет, то соответственно, эксперимент я воспринимаю как некий процесс манипуляции либо с настоящими данными, либо с вымышленными. В качестве примера можно привести программный код на языке Python.

Вот пример проведения эксперимента с выдуманными данными:

import random

data = []
while len(data) != 5:
    data.append(random.randint(1, 10))
print(data)

Данный пример определяет любое событие в пространстве элементарных событий. В нашем случае пространство элементарных событий – это случайное число в промежутке от 1 до 10 (random.randint(1, 10)), которое добавляет эти значения в список data, пока его длина (len) не будет равняться 5.

Ниже представлен пример с неслучайными данными. Давайте представим, что мы с вами работаем в некоторой фирме и для того, чтобы провести эксперимент, требуется узнать возраст людей (клиентов) по их имени. Вот код.

birth_date ={'Bob': 10, 'Alice':16, 'Ann':15}
print(birth_date)

Он представляет собой словарь, в качестве ключа выступает имя человека, а значения – его возраст.

Представленное событие не является выдуманным (исходя из условия задачи), поскольку в первой задаче мы не знали какое число нам достанется для помещения его в список, а во втором значения данные заранее известны.

После того, как мы получили данные, необходимо их оценить. Оценка может быть либо экспериментальная (её ещё называют «грубой»), либо теоретической.  Логично понимать, что экспериментальная получена в результате проведения эксперимента, а теоретическая без проведения эксперимента.

В качестве примера можно привести всеми известную задачу подбрасывания кубика, у которого на каждой грани написаны цифры от 1 до 6. И нам необходимо определить вероятность выпадения числа на каждой грани.

Вот пример теоретического определения вероятности:

Допустим кубик подбрасывается бесконечное количество раз, тогда в теории вероятность выпадения каждого числа стремится к

 Проблема в том, что на практике мы не можем подбрасывать кубик бесконечное количество раз. Это утомительно и не нужно, поэтому мы проводим реальный эксперимент с ограничениями.

Пример практического определения вероятности:

Например, нам нужно подбросить кубик 10 раз. Для этого я написал функцию, которая носит название «кубик».

def kubik(n: int) -> list:
    """
    
    :param n: Количество подбрасываний
    :return:  Список слкучайных подюрасываний кубика
    """
    data = []
    while len(data) <n:
        data.append(random.randint(1,6))
    return data

Она при помощи метода (random.randint(1,6)) определяет количество выпаданий случайной грани от 1 до 6. Результат случайного числа он описывает в переменную data. Если мы выполним 10 подбрасываний, то результатом будет являться список из этих значений. Значения в списке могут быть любыми.

В моём случае список получил значения [2, 1, 6, 2, 5, 5, 4, 4, 5, 6]

Чтобы получить вероятность выпадения каждой грани, необходимо определить количество граней в выборке. Я реализовал это при помощи следующей функции:

def count_rate(kub_data: list):
    """
    Возвращает частоту выпадания значений кубика,
    согласно полученным данным
    :param kub_data: данные эксперимента
    :return:
    """
    kub_rate = {}
    for i in kub_data:
        if i in kub_rate:
            continue
        else:
            kub_rate[i] = kub_data.count(i)
    for i in range(1, 7):
        if i not in kub_rate:
            kub_rate[i] = 0
    return kub_rate

Результатом функции служит словарь, который считает количество выпадений от 1 до 6. Пример реализует два цикла, первый цикл считает текущие случайные значения в полученной выборке, но поскольку у нас некоторые значения могут не выпасть, то мы их добавляем в конец словаря.

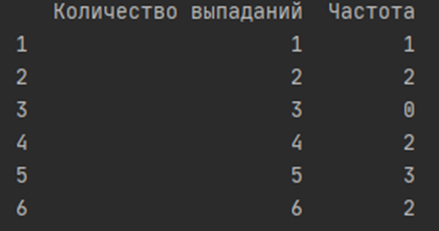
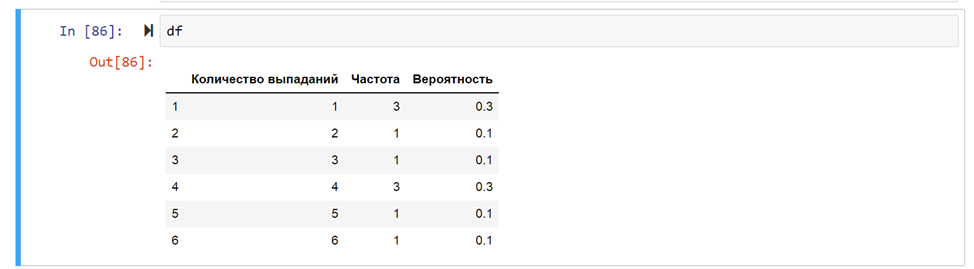
Таким образом получается словарь, содержащий следующие данные: {2: 2, 1: 1, 6: 2, 5: 3, 4: 2, 3: 0}

Данные, конечно, я получил, но мне не нравится формат их вывода. Поэтому необходимо их отсортировать:

def sort_rate(counted_rate: dict):
    """
    Возвращает отсортированную частоту по ключу
    :param counted_rate: Наша неотсортированная частота
    :return:
    """
    sorted_rate = {}
    for key in sorted(counted_rate.keys()):
        sorted_rate[key] = counted_rate[key]
    return sorted_rate

Для сортировки хорошо подойдёт метод sorted. В официальной документации написано, что она возвращает отсортированный список, полученный из итерируемого объекта, который передан как аргумент. В моём случае итерируемый объект – это наш словарь, который мы сортируем по ключу (sorted(counted_rate.keys())).

Вот результат разработанной функции: {1: 1, 2: 2, 3: 0, 4: 2, 5: 3, 6: 2}

Следующий шаг, преобразование данного словаря в dataframe. DataFrame представляет собой табличную структуру представления данных для удобного их структурирования. Для преобразования служит библиотека pandas (ссылка на официальную документацию (для тех, кто не знает): https://pandas.pydata.org/docs/ ). Она очень популярна в Python сообществе, имеет очень много интересных плюшек, о плюсах можно много говорить, об этом много написано в том числе на Хабре, поэтому перечислять их не буду. Вот реализация функции:

def crate_dataframe(sorted_date: dict):
    """
    Создание и преобразование данных в Pandas dataframe
    :param sorted_date: dict
    :return: pd.Dataframe
    """
    df = pd.DataFrame(sorted_date, index=[0])
    df = df.T
    df = df.rename(columns={0: 'Частота'})
    df.insert(0, 'Количество выпаданий', range(1, 1 + len(df)))
    return df

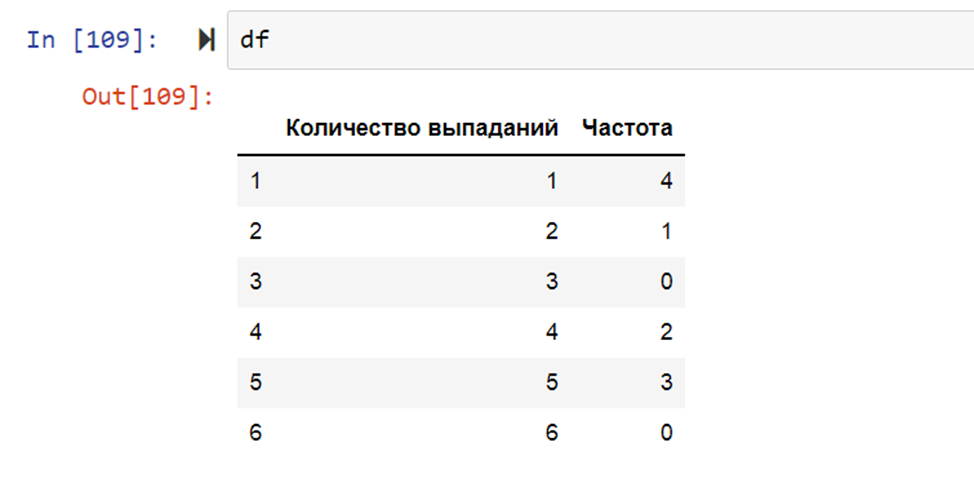
         Результатом вывода функции служит Dataframe. Поскольку я выполнял программу в рабочем окружении Pycharm, то выводом служит такой такой набор данных:

Есть более интересные способы отображения информации, например, в Jupyter Notebook.

Сейчас будьте внимательны, там будут другие данные

Данная функция добавляет название столбцам, присваивает индекс к каждому значению и на выходе получается таблица.

Теперь самое время определить вероятности. Для того, чтобы это сделать, нужно ещё раз убедиться, что мы подбрасывали кубик ровно 10 раз и затем полученное значение разделить на частоту. Ниже опишу общую формулу:

А вот сам код:

def probability_solving(dataframe: pd.DataFrame):
    """
    Вычисление вероятности полученных результатов
    :param dataframe:
    :return:
    """
    sum_rate = dataframe['Частота'].sum()
    probability = []
    for i in dataframe['Частота']:
        probability.append(i / sum_rate)
    dataframe['Вероятность'] = probability
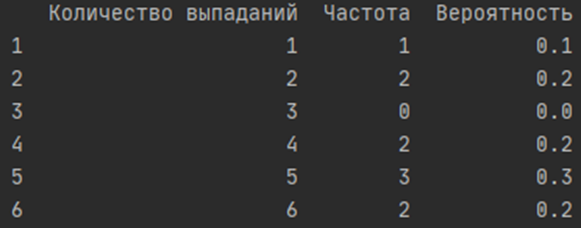
    return dataframe

Суммарное количество бросков описывается переменной   sum_rate, для вычисления вероятности служит цикл, который берёт значения из столбца Частота (dataframe[‘Частота’]) и вычисляет её вероятность, путём создания нового столбца (dataframe[‘Вероятность’]).

Если тестировать функцию в Pycharm, то результат будет такой:

Если в Jupyter Notebook, то такой:

Сейчас будьте внимательны, там будут другие данные

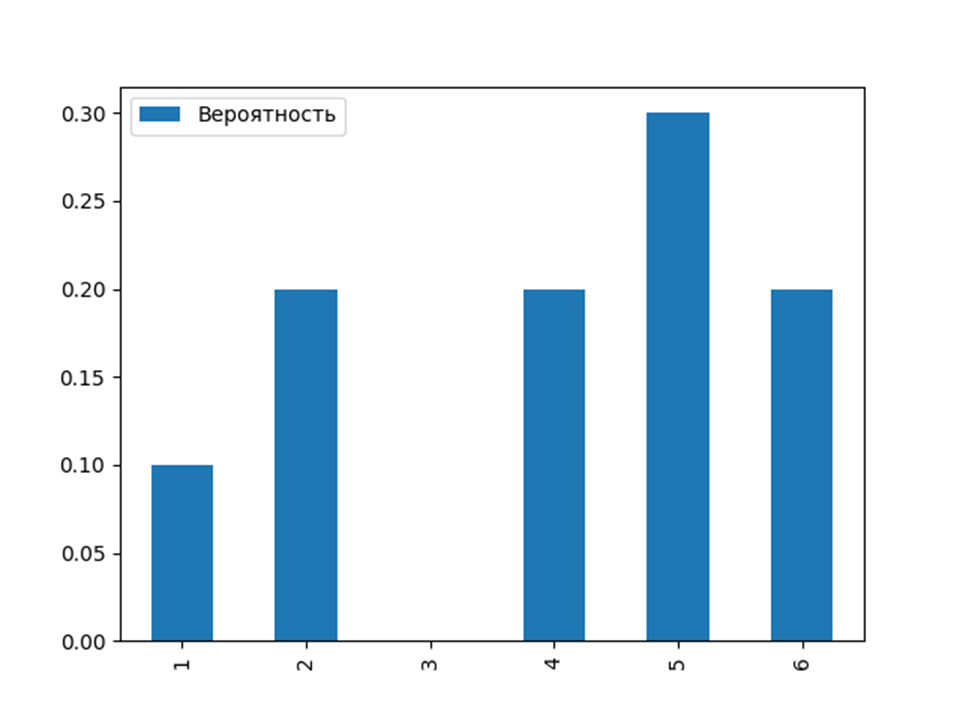
После того как мы получили результат, его можно описать. В качестве результата описания можно построить гистограмму, которая описывает плотность распределения случайных вероятностей исходя из нашей задачи. Для составления графиков вполне подойдёт matplotlib (https://matplotlib.org/ ). Её тоже много где используют и статьи по её использованию в различных задачах тоже можно встретить на Хабре. График можно получить путём импорта библиотеки и написания всего двух строчек

import matplotlib.pyplot as plt
a = proba['Вероятность'].plot(kind='bar', legend=True)
a.figure.savefig('Вероятность.png')

Вторая строчка описывает гистограмму дискретного случайного события (о нём будет сказано далее по тексту), третья строчка сохраняет график на ПК. В результате был получен график распределения вероятностей. Задача решена!

Выше я упомянул о дискретном случайном распределении. Сейчас самое время немного уделить этому внимание. Насколько мне известно в математике существует два вида распределения: непрерывное и прерывающееся. Вот как раз прерывающиеся является дискретным. Задача с кубиком описывает прерывающееся распределение, потому что мы не можем получить значение 1,1 или 1,2 (если конечно не обозначим их на гранях). Зачастую они описываются с помощью гистограмм. Непрерывное распределение описывает линейный график, у которого могут быть выпуклости, вогнутости, экстремумы и т.д.

Ниже описана гистограмма распределения вероятности

Заключение и выводы

На данный момент — это всё, о чём я хотел рассказать в текущей теме, посвящённой вероятностям. Я знаю, что эту тему можно освящать и расширять бесконечно, поэтому ждите следующие статьи.  Признаюсь, когда я всё это описывал мне было самому интересно рефлексировать по данной теме. Считаю третий этап по публикации на Хабре почти выполнен, осталось дождаться рецензирования статьи модераторами. Очень надеюсь, что её одобрят. Всего доброго и до новых встреч.

Теория вероятности не сложная, по крайней мере, на уровне, необходимом для начала работы в науке о данных. Возможно, прошло какое-то время с тех пор, как вы познакомились с этой темой, и, если ваши знания немного ослабли, эта статья поможет вам вернуться в русло. 

Быстрый поиск в Google выявляет 4 основные математические темы, на которых основана вся область:

• Линейная алгебра
• Анализ
• Статистика
• Вероятность

Сегодня я расскажу о двух важнейших концепциях из теории вероятности: сочетаниях и перестановках. 

Начнем с базового определения самой вероятности: 

Вероятность — степень (относительная мера, количественная оценка) возможности наступления некоторого события. В теории вероятностей вероятность принимает значения от 0 до 1. Значение 1 соответствует достоверному событию, невозможное событие имеет вероятность 0. Чем выше значение, тем больше вероятность события.

Вероятность как область научного знания важна, потому что неопределенность и случайность встречаются повсеместно, соответственно, знание о вероятности помогает принимать более информированные решения и осмыслять неопределенности. 

Перед погружением в перестановки и сочетания, нужно понять еще один термин — факториал. 

Что такое факториал? 

Хороший вопрос. Согласно Википедии: 

Факториал — функция, определённая на множестве неотрицательных целых чисел. Факториал натурального числа n определяется как произведение всех натуральных чисел от 1 до n включительно.

Факториал вычисляется по следующей формуле: 

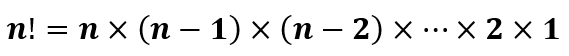
Вот пример:

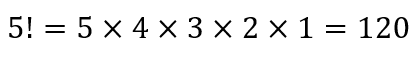
Теперь вы, возможно, задумались, как вычислять факториалы в Python. Во многих библиотеках есть готовые функции, но создать собственную функцию тоже очень легко, и именно это мы и сделаем. 

Вот простая рекурсивная функция, которая справится с задачей: 

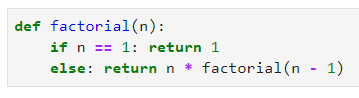
Теперь можно использовать эту функцию для проверки примера выше: 

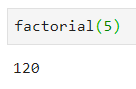
Хорошо, но где факториалы используются в реальном мире? 

Скажем, в гонке участвуют пять человек, и вы хотите узнать количество способов, по которым эти пятеро могут финишировать первыми, вторыми или третьими. Можно взять листок бумаги и просто записать все возможные варианты, но зачем? Что если участников 100? 

Вот как эта задача решается с помощью факториалов: 

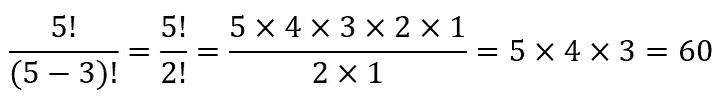
Это называется перестановка. 

Перестановки

И снова начнем с определения: 

В математике перестановка — это упорядочение членов набора в последовательность или, если последовательность уже определена, перестановка (изменение порядка) ее элементов. 

Существует два способа вычисления перестановок. Выбор способа зависит от того, разрешается повторение или нет. Давайте рассмотрим на примере.

У вас есть веб-сайт, на котором могут регистрироваться пользователи. Им нужно вводить пароль длиной строго в 8 символов, которые не должны повторяться. Сперва нужно определить, сколько букв и цифр в английском алфавите:

• количество букв: 26
• количество цифр: 10

То есть всего 36. Тогда n = 36, а r = 8, потому что пароль должен быть длиной в 8 символов. Зная это, мы легко можем рассчитать количество уникальных паролей, используя формулу: 

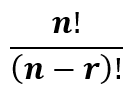
Если вы поспешили и посчитали вручную: 

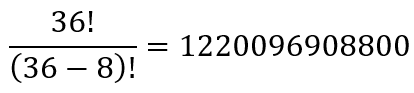
В Python это тривиальная задача:

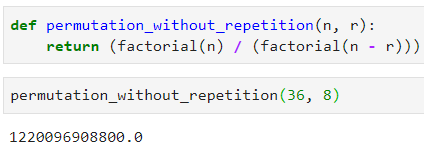
Здорово, но я хочу разрешить пользователям повторно использовать символы. Нет проблем, в данном случае это перестановки с повторениями, формула еще проще: 

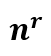
Мы уже знаем, что n (36) и r (8), так что вот решение:

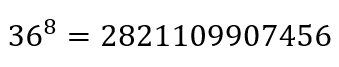
И снова реализация на Python тривиальна:

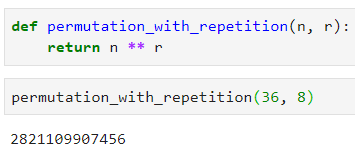
Это действительно большое число. Попробуйте произнести его вслух! 

Сочетания

Далее на повестке дня — сочетания. Вам наверняка любопытно, что это такое и в чем их отличие от перестановок. Начнем с определения: 

Сочетание— это выбор значений из набора, в котором (в отличие от перестановок) порядок выбора не имеет значения. 

Чтобы понять это определение, разберем следующий пример: группа людей, выбранных в команду — это та же самая группа, независимо от порядка участников. Вот и вся идея сочетаний. Если выбрать 5 членов команды, можно упорядочить их по имени, росту или другому параметру, но команда останется прежней — порядок не имеет значения. 

Давайте запишем это формулой. Количество сочетаний C набора из n объектов, взятых по r, рассчитывается так:

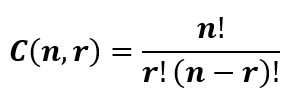
С этим уравнением мы можем решить следующую задачу: сколькими способами можно выбрать в футбольную команду 5 человек из 10? 

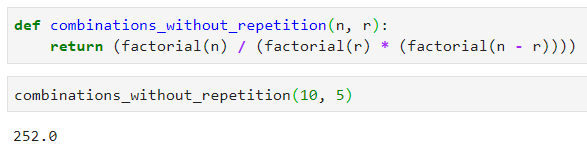
Группа будет той же, порядок значения не имеет. Значит, n = 10, а r = 5:

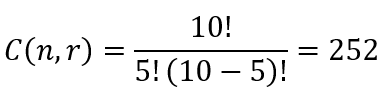
И это можно легко сделано в Python:

Великолепно! Но интересно, существует ли версия сочетаний с повторениями? Да! 

Представьте, что готовите сэндвич и по какой-то причине вам нужно использовать только 4 ингредиента из 10. Однако ингредиенты не должны быть уникальны, например, можно положить 3 куска сыра и 1 кусок салями. Как это здорово, я тоже обожаю сыр, вот спасибо!

Но как сформулировать эту идею математически? Ответ снова прост:

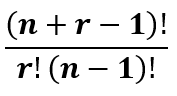
Давайте применим формулу к примеру выше. n снова равно 10 (потому что 10 возможных ингредиентов), а r = 4 (потому что выбрать можно только 4):

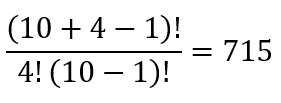
Используем Python для проверки:

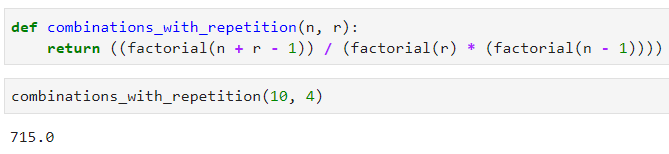
 Превосходно. 

И напоследок 

Сочетания и перестановки математически просты, однако сложность заключается в том, как представить в такой форме реальные проблемы. Иногда бывает трудно выделить значения n и r в повседневной жизни. Я не могу решить для вас подобные задачи, но надеюсь, что данная статья поможет вам разобраться. 

Читайте также:

• Как организовать код в Python
• Превращаем сценарии Python в инструменты МО
• Создаем чат-бот в Python с помощью nltk

Перевод статьи Dario Radečić: Essential Probability in Python: Permutations and Combinations