Глава 6
Двумерная случайная величина
В главе рассматривается новый вопрос о зависимости между случайными величинами.
6.1Двумерная случайная величина, ее функция распределения
Определение. Двумерной случайной величиной называется упорядоченная пара (X, Y )
одномерных случайных величин X и Y . При этом предполагаются определенными вероятности произведения событий X < x и Y < y для любых вещественных x, y. Одномерные случайные величины X, Y называются компонентами двумерной случайной величины
(X, Y ).
Двумерную случайную величину называют также случайным двумерным вектором, случайной двумерной точкой, системой двух случайных величин.
Примеры реальных двумерных случайных величин.
1.Два размера детали в массовом производстве.
2.Величина сигнала в управляющем устройстве в два момента времени.
3.Абсцисса и ордината точки попадания сигнала.
4.Количество бракованных деталей в двух выборках из партии изделий.
Определение. Функцией распределения FXY (x, y) двумерной случайной величины
(X, Y ) называется вероятность произведения двух событий X < x, Y < y, определенная для любых вещественных x, y:
FXY (x, y) = P (X < x, Y < y).
Здесь произведение событий под знаком вероятности обозначено через запятую. Функцию FXY (x, y) будем называть двумерной функцией распределения. Свойства двумерной функции распределения.
1.FXY (−∞, y) = 0; FXY (x, −∞) = 0, так как X < −∞ и Y < −∞ — невозможные события и произведение невозможного события с любым другим событием есть также невозможное событие.
45
2. FXY (+∞, +∞) = 1, так как оба события X < +∞, Y < +∞ являются достоверными.
3. FXY (x, +∞) = FX (x); FXY (+∞, y) = FY (y), так как Y < +∞ — достоверное событие,
его произведение с событием X < x есть событие X < x; FXY (x, +∞) = P (X < x, Y < +∞) =
4.FXY (x, y) не убывает по каждому из своих аргументов при фиксированном другом аргументе.
Замечание. Для того, чтобы из двумерной функции распределения получить законы распределения компонентов, достаточно устремить один из аргументов к +∞.
Обратное неверно, т.е. из одномерных функций распределения компонент в общем случае нельзя получить функцию распределения двумерной случайной величины. Таким образом, двумерная функция распределения несет существенно больше информации, чем две одномерные функции распределения компонент X и Y . Рассматривая случайные величины X, Y порознь, а не в системе, нельзя получить сведения о их зависимости.
Будем различать дискретные и непрерывные двумерные случайные величины.
6.2Дискретная двумерная случайная величина, ее таблица распределения
Определение. Двумерная случайная величина называется дискретной, если множество ее значений (x, y) — конечное или счетное.
Примеры реальных дискретных случайных величин.
1.(X, Y ), где X — число деталей, изготовленных за смену на первом станке, Y — на втором.
2.(X, Y ), где X — число клиентов, поступивших за время T в первую систему массового обслуживания, Y — во вторую.
Закон распределения вероятностей двумерной дискретной случайной величины (X, Y ) можно задать формулой
P (X = xi, Y = yk) = pik (i = 1, . . . , m; k = 1, . . . , n).
Это вероятности совмещения событий X = xi, Y = yk. Так как события, означающие одновременное выполнение равенств X = xi, Y = yk (1, . . . , m; k = 1, . . . , n) являются попарно несовместными и образуют полную группу, то
mn
XX
pik = 1.
i=1 k=1
В случае конечности чисел m и n закон распределения дискретной двумерной случайной величины можно оформить в виде таблицы распределения:
|
XY |
y1 |
y2 |
… |
yn |
|
x1 |
p11 |
p12 |
… |
p1n |
|
… |
… |
… |
… |
… |
|
xm |
pm1 |
pm2 |
… |
pmn |
46
Формулы согласованности для дискретной случайной величины имеют вид:
|
n |
|
|
pi• = |
Xk |
|
pik, |
|
|
=1 |
|
|
m |
|
|
p•k = |
Xi |
|
pik. |
|
|
=1 |
Здесь
pi• = P (X = xi), i = 1, . . . , m; p•k = P (Y = yk), k = 1, . . . , n
— одномерные законы распределения компонент случайной величины. Формулы согласованности позволяют из закона распределения двумерной случайной величины получить одномерные законы распределения ее компонент, которые, таким образом, не произвольные, а согласованы друг с другом.
Функция распределения дискретной двумерной случайной величины по аналогии с одномерным случаем может быть записана в виде
<x y <y
Здесь суммирование распространяется на те значения i и k, для которых xi < x, yk < y. Пример. Задана таблица распределения дискретной двумерной случайной величины.
Требуется найти одномерные законы распределения компонент.
|
XY |
y1 |
y2 |
y3 |
pi• |
|||||||||
|
x1 |
1 |
1 |
1 |
7 |
|||||||||
|
12 |
6 |
3 |
12 |
||||||||||
|
x2 |
1 |
1 |
1 |
5 |
|||||||||
|
6 |
6 |
12 |
12 |
||||||||||
|
p•k |
1 |
1 |
5 |
1 |
|||||||||
|
4 |
3 |
12 |
Применим формулы согласованности. Согласно этим формулам суммы вероятностей pik по строкам таблицы дают pi•, а по столбцам — p•k. Эти суммы записаны в дополнительном столбце справа и в дополнительной строке внизу.
|
1 |
1 |
1 |
7 |
1 |
1 |
1 |
5 |
|||||||||||||||||||||||||||||||
|
p1• = |
+ |
+ |
= |
; p2• = |
+ |
+ |
= |
; |
||||||||||||||||||||||||||||||
|
12 |
6 |
3 |
12 |
6 |
6 |
12 |
12 |
|||||||||||||||||||||||||||||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
5 |
||||||||||||||||||||||||||||||
|
p•1 = |
+ |
= |
; p•2 = |
+ |
= |
; p•3 |
= |
+ |
= |
. |
||||||||||||||||||||||||||||
|
12 |
6 |
4 |
6 |
6 |
3 |
3 |
12 |
12 |
47
6.3Непрерывная двумерная случайная величина. Плотность вероятности
Определение. Двумерная случайная величина называется непрерывной, если существует неотрицательная функция fXY (x, y), называемая двумерной плотностью вероятности, такая, что вероятность попадания случайной величины (X, Y ) в область D равна двойному интегралу от плотности по области D:
ZZ
P ((X, Y ) D) = fXY (x, y)dxdy.
D
Из приведенной формулы следует выражение для функции распределения двумерной непрерывной случайной величины:
|
x |
y |
|
|
FXY (x, y) = P (−∞ < X < x, −∞ < Y < y) = Z |
Z |
fXY (x, y)dxdy. |
−∞ −∞
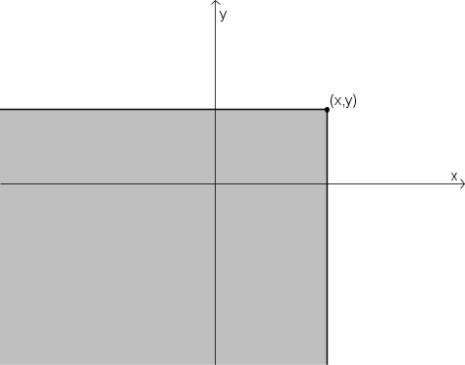
Это есть вероятность попадания случайной точки (X, Y ) в «юго-западный»квадрант с вершиной в точке (x, y).
Рис. 6.1: «Юго-западный» квадрант с вершиной в точке (x, y)
Из формулы, определяющей связь между двумерной плотностью вероятности и функцией распределения следует, что FXY (x, y) непрерывна на всей плоскости xOy.
Свойства двумерной плотности вероятности.
1. Определена на всей плоскости xOy.
48
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Двумерная непрерывная случайная величина
- Краткая теория
- Примеры решения задач
Краткая теория
Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Непрерывной называют двумерную величину, составляющие которой непрерывны.
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Функция распределения двумерной случайной величины и ее свойства
Функцией распределения двумерной случайной величины
называют функцию
, определяющую для каждой
пары чисел
вероятность того, что
примет значение, меньшее
, и при этом
примет значение, меньшее
.
Свойство 1.
Значения
функции распределения удовлетворяют двойному неравенству:
Свойство 2.
есть неубывающая функция по каждому аргументу,
то есть:
если
если
Свойство 3.
Имеют место предельные соотношения:
1)
2)
3)
4)
Свойство 4.
При
функция распределения системы становится
функцией распределения составляющей
:
При
функция распределения системы становится
функцией распределения составляющей
:
Плотность распределения двумерной случайной величины и ее свойства
Плотностью совместного распределения вероятностей
двумерной непрерывной случайной величины
называют вторую смешанную частную производную
от функции распределения:
Зная
плотность совместного распределения
можно найти функцию распределения
по формуле:
Свойство 1.
Двумерная
плотность вероятности неотрицательна:
Свойство 2.
Двойной
несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Безусловные и условные законы распределения составляющих
Пусть
известна плотность совместного распределения вероятностей системы двух
случайных величин. Найдем плотности распределения каждой из составляющих.
Аналогично
находится плотность распределения составляющей
:
Итак,
плотность распределения одной из составляющих равна несобственному интегралу с
бесконечными пределами от плотности совместного распределения системы, причем
переменная интегрирования соответствует другой составляющей.
Пусть
— непрерывная двумерная случайная величина.
Условной
вероятностью
распределения составляющих
при данном значении
называют отношение плотности совместного
распределения
системы
к плотности распределения
составляющей
:
Аналогично
определяется условная плотность составляющей
при данном значении
:
Если
известна плотность совместного распределения
, то условные плотности
составляющих могут быть найдены по формулам:
Эти
формулы можно записать в виде:
Аналогично
определяется условная плотность составляющей
при данном значении
:
То есть
умножая закон распределения одной из составляющих на условный закон
распределения другой составляющей, найдем закон распределения системы случайных
величин.
Смежные темы решебника:
- Двумерная дискретная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Примеры решения задач
Пример 1
Найти
плотность совместного распределения f(x,y) системы случайных величин (X,Y) по
известной функции распределения:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
По определению плотности совместно
распределения:
Искомая плотность совместного распределения:
Пример 2
Найти
функцию распределения системы случайных величин F(x,y) по известной плотности
совместного распределения f(x,y):
Решение
Воспользуемся
формулой:
В нашем
случае:
Ответ:
Пример 3
Двумерная
случайная величина (X,Y) имеет равномерное распределение вероятностей в
треугольнике ABC. Определить функции плотности распределения
компонент этой случайной величины f(x), f(y), их математические
ожидания M(X), M(Y), дисперсии D(X), D(Y),
коэффициент корреляции rxy. Выяснить, являются ли
случайные величины X и Y независимыми?
A(0;0),B(-1;1),C(1;1)
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
где
– площадь треугольника
Разделим
область
на две равные части вдоль оси
, тогда из условия:
или
Тогда
плотность двумерной случайной величины
:
Вычислим
плотность составляющей
:
при
:
Откуда
плотность составляющей
:
Вычислим
плотность составляющей
:
при
Плотность
составляющей
:
Найдем
условную плотность составляющей
:
при
Следовательно,
случайные величины
и
зависимы
Найдем
математическое ожидание случайной величины
:
Найдем
дисперсию случайной величины
:
Найдем
математическое ожидание случайной величины
:
Найдем
дисперсию случайной величины
:
Найдем
математическое ожидание двумерной случайной величины
:
Тогда
ковариация:
Значит
коэффициент корреляции:
Следовательно,
случайные величины
и
– зависимые, но некоррелированные
Пример 4
Двумерная
случайная величина (X,Y) имеет плотность
распределения:
Найти
вероятность попадания значения (X,Y) в область x1≤x≤x2,
y1≤y≤y2, вероятность попадания значения X в
интервал x1≤x≤x2, математическое ожидание M[X] и
условное математическое ожидание M[Y⁄X=x].
a=8, b=2, x1=6, x2=9, y1=0, y2=4
Решение
Найдем
вероятность попадания в область
по формуле:
При
вычислении интеграла учитывается та часть области
, где
, т.е.
Плотность
вероятности для составляющей
имеет вид:
Если
или
, то
и
. При
находим:
Таким
образом, плотность имеет вид:
Тогда:
Условное математическое ожидание
определяется с
помощью условной плотности распределения
составляющей
Получаем:
Искомое
математическое ожидание:
- Краткая теория
- Примеры решения задач
Двумерная непрерывная случайная величина
Ранее мы разобрали примеры решений задач для одномерной непрерывной случайной величины. Перейдем к более сложному случаю — двумерной непрерывной случайной величине $(X,Y)$ (или двумерному вектору). Кратко выпишем основы теории.
Спасибо за ваши закладки и рекомендации
Система непрерывных случайных величин: теория
Двумерная непрерывная СВ задается своей функцией распределения $F(x,y)=P(Xlt x, Ylt y)$, свойства которой аналогичны свойствам одномерной ФР. Эта функция должна быть непрерывна, дифференцируема и иметь вторую смешанную производную, которая будет как раз плотностью распределения вероятностей системы непрерывных случайных величин:
$$
f(x,y)= frac{partial ^2}{partial x partial y} F(x,y)
$$
Зная плотность совместного распределения, можно найти одномерные плотности для $X$ и $Y$:
$$
f(x)= int_{-infty}^{infty} f(x,y) dy, quad f(y)= int_{-infty}^{infty} f(x,y) dx.
$$
Вероятность попадания случайного вектора в прямоугольную область можно вычислить как двойной интеграл от плотности (по этой области) или через функцию распределения:
$$P(x_1 le X le x_2, y_1 le Y le y_2) = F(x_2, y_2)-F(x_1, y_2)-F(x_2, y_1)+F(x_1, y_1).$$
Как и для случая дискретных двумерных СВ вводится понятие условного закона распределения, плотности которых можно найти так:
$$
f(x|y)=f_y(x)= frac{f(x,y)}{f(y)}, quad f(y|x)=f_x(y)= frac{f(x,y)}{f(x)} $$
Если для всех значений $(x,y)$ выполняется равенство
$$f(x,y) =f(x)cdot f(y),$$
то случайные величины $X, Y$ называются независимыми (их условные плотности распределения совпадают с безусловными). Для независимых случайных величин выполняется аналогичное равенство для функций распределений:
$$F(x,y) =F(x)cdot F(y).$$
Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:
$$
cov (X,Y)=M(XY)-M(X)M(Y)= int_{-infty}^{infty}int_{-infty}^{infty} (x-M(X))(y-M(Y)) f(x,y) dxdy, \
r_{XY} = frac{cov(X,Y)}{sqrt{D(X)D(Y)}}.
$$
В этом разделе мы приведем примеры задач с полным решением, где используются непрерывные двумерные случайные величины (системы случайных величин).
Примеры решений
Задача 1. Дана плотность распределения вероятностей системы
$$
f(x)=
left{
begin{array}{l}
C, mbox{ в треугольнике} O(0,0), A(4,0), B(4,1)\
0, mbox{ в остальных точках} \
end{array}
right.
$$
Найти:
$C, rho_1(x), rho_2(y), m_x, m_y, D_x, D_y, cov(X,Y), r_{xy}, F(2,10), M[X|Y=1/2]$.
Задача 2. Дана плотность распределения $f(x,y)$ системы $X,Y$ двух непрерывных случайных величин в треугольнике АВС.
1.1. Найдите константу с.
1.2. Найдите $f_X(x), f_Y(y)$ — плотности распределения с.в. Х и с.в. Y.
Выясните, зависимы или нет с.в. Х и Y. Сформулируйте критерий независимости системы непрерывных случайных величин.
1.3. Найдите математическое ожидание и дисперсию с.в. Х и с.в. Y. Поясните смысл найденных характеристик.
1.4. Найдите коэффициент корреляции с.в. Х и Y. Являются ли случайные величины коррелированными? Сформулируйте свойства коэффициента корреляции.
1.5. Запишите уравнение регрессии с.в. Y на Х и постройте линию регрессии в треугольнике АВС.
1.6. Запишите уравнение линейной среднеквадратичной регрессии с.в. Y на Х и постройте эту прямую в треугольнике АВС. $$ f(x,y)=csqrt{xy}, quad A(0;0), B(-1;-1), C(-1;0) $$
Задача 3. Интегральная функция распределения случайного вектора (X,Y):
$$
F(x)=
left{
begin{array}{l}
0, mbox{ при } x le 0 mbox{ или } yle 0\
(1-e^{-2x})(1-e^{-3y}), mbox{ при } x gt 0 mbox{ и } ygt 0\
end{array}
right.
$$
Найти центр рассеивания случайного вектора.
Задача 4. Плотность совместного распределения непрерывной двумерной случайной величины (Х, У)
$$f(x,y)=C e^{-x^2-2xy-4y^2}$$
Найти:
а) постоянный множитель С;
б) плотности распределения составляющих;
в) условные плотности распределения составляющих.
Задача 5. Задана двумерная плотность вероятности системы двух случайных величин: $f(x,y)=1/2 sin(x+y)$ в квадрате $0 le x le pi/2$, $0 le y le pi/2$, вне квадрата $f(x,y)=0$. Найти функцию распределения системы (X,Y).
Задача 6. Определить плотность вероятности, математические ожидания и корреляционную матрицу системы случайных величин $(X,Y)$, заданных в интервалах $0 le x le pi/2$, $0 le y le pi/2$, если функция распределения системы $F(x,y)=sin x sin y$.
Задача 7. Плотность вероятности системы случайных величин равна
$$f(x,y) = c(R-sqrt{x^2+y^2}), quad x^2+y^2 lt R^2.$$
Определить:
А) постоянную $c$;
Б) вероятность попадания в круг радиуса $alt R$, если центры обоих кругов совпадают с началом координат.
Задача 8. Совместная плотность вероятности системы двух случайных величин X и Y
$$f(x,y)=frac{c}{36+9x^2+4y^2+x^2y^2}.$$
Найти величину $с$; определить законы распределения $F_1(x)$, $F_2(y)$, $f_1(x)$, $f_2(y)$, $f(x/y)$; построить графики $F_1(x)$, $F_2(y)$; вычислить моменты $m_x$, $m_y$, $D_x$, $D_y$, $K_{xy}$.
Мы отлично умеем решать задачи по теории вероятностей
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Пусть дана двумерная случайная величина $(X,Y)$.
Определение 1
Законом распределения двумерной случайной величины $(X,Y)$ — называется множество возможных пар чисел $(x_i, y_j)$ (где $x_i epsilon X, y_j epsilon Y$) и их вероятностей $p_{ij}$.
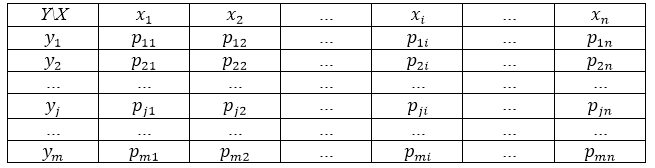
Чаще всего закон распределения двумерной случайной величины записывается в виде таблицы (Таблица 1).
Рисунок 1. Закон распределения двумерной случайной величины.
Вспомним теперь теорему о сложении вероятностей независимых событий.
Вероятность суммы конечного числа независимых событий ${ A}_1$, ${ A}_2$, … ,$ { A}_n$ вычисляется по формуле:
[Pleft(sumlimits^n_{i=1}{{ A}_n}right)=sumlimits^n_{i=1}{P({ A}_n)}]
Пользуясь этой формулой можно получить законы распределения для каждой компоненты двумерной случайной величины, то есть:
Отсюда будет следовать, что сумма всех вероятностей двумерной системы имеет следующий вид:
Рассмотрим подробно (поэтапно) задачу, связанную с понятием закона распределения двумерной случайной величины.
Пример 1
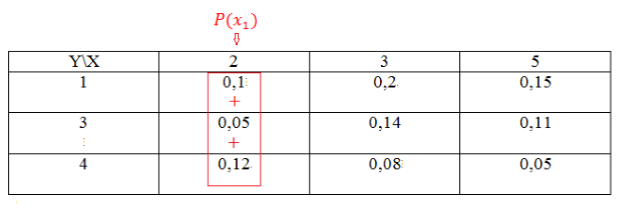
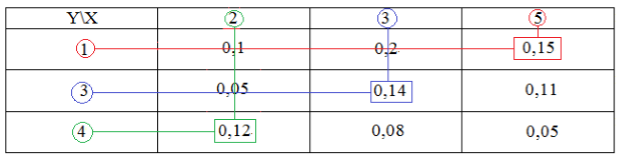
Закон распределения двумерной случайной величины задан следующей таблицей:
Рисунок 2.
Найти законы распределения случайных величин $X, Y$, $X+Y$ и проверить в каждом случае выполнение равенства полной суммы вероятностей единице.
- Найдем сначала распределение случайной величины $X$. Случайная величина $X$ может принимать значения $x_1=2,$ $x_2=3$, $x_3=5$. Для нахождения распределения будем пользоваться теоремой 1.
Найдем вначале сумму вероятностей $x_1$ следующим образом:
Рисунок 3.
[Pleft(x_1right)=0,1+0,05+0,12=0,27]
Аналогично найдем $Pleft(x_2right)$ и $Pleft(x_3right)$:
[Pleft(x_2right)=0,2+0,14+0,08=0,42] [Pleft(x_3right)=0,15+0,11+0,05=0,31]
Значит, закон распределения величины $X$ имеет следующий вид:
Рисунок 4.
Проверим выполнение равенства полной суммы вероятностей:
[0,27+0,42+0,31=1-верно.]
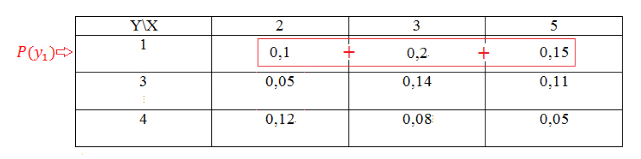
- Найдем теперь распределение случайной величины $Y$. Случайная величина $Y$ может принимать значения $x_1=1,$ $x_2=3$, $x_3=4$. Для нахождения распределения будем пользоваться теоремой 1.
Найдем вначале сумму вероятностей $y_1$ следующим образом:
Рисунок 5.
[Pleft(y_1right)=0,1+0,2+0,15=0,45]
Аналогично найдем $Pleft(y_2right)$ и $Pleft(y_3right)$:
[Pleft(y_2right)=0,05+0,14+0,11=0,3] [Pleft(y_3right)=0,12+0,08+0,05=0,25]
Значит, закон распределения величины $X$ имеет следующий вид:
Рисунок 6.
Проверим выполнение равенства полной суммы вероятностей:
[0,45+0,3+0,25=1-верно.]
- Осталось найти закон распределения случайной величины $X+Y$.
Обозначим её для удобства через $Z$: $Z=X+Y$.
Вначале найдем, какие значения может принимать данная величина. Для этого будем попарно складывать значения величин $X$ и $Y$. Получим следующие значения: 3, 4, 6, 5, 6, 8, 6, 7, 9. Теперь, отбрасывая совпавшие величины, получим, что случайная величина $X+Y$ может принимать значения $z_1=3, z_2=4, z_3=5, z_4=6, z_5=7, z_6=8, z_7=9. $
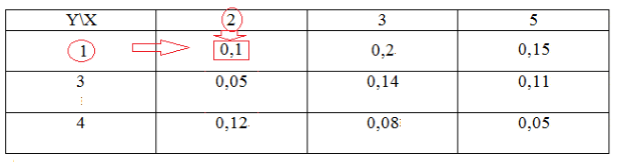
Найдем для начала $P(z_1)$. Так как значение $z_1$ единично, то оно находится следующим образом:
Рисунок 7.
[Pleft(z_1right)=0,1]
Аналогично находятся се вероятности, кроме $P(z_4)$:
[Pleft(z_2right)=0,2, Pleft(z_3right)=0,05, Pleft(z_5right)=0,08, Pleft(z_6right)=0,11, Pleft(z_7right)=0,05]
Найдем теперь $P(z_4)$ следующим образом:
Рисунок 8.
[Pleft(z_4right)=0,12+0,14+0,15=0,41]
Значит, закон распределения величины $Z$ имеет следующий вид:
Рисунок 9.
Проверим выполнение равенства полной суммы вероятностей:
[0,1+0,2+0,05+0,41+0,08+0,11+0,05=1-верно.]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме