Как найти вероятность безотказной работы на интервале

Вероятность
безотказной работы– вероятность
того, что в определённых условиях
эксплуатации, в пределах заданной
наработки (t) отказ объекта
не возникает. ОбозначаетсяP(t).

Если
задано время t, в течение
которого необходимо определить
вероятность безотказной работы, Т –
время работы системы до первого отказа,
тогда вероятность безотказной работы
– это вероятность того, чтоT≥t. Чем большеt,
тем меньше вероятность безотказной
работы.

Вероятность
безотказной работы можно определить
через статистическую формулу:
.

где
– теория,– эксперимент,— количество испытуемых образцов,— число отказавших образцов за времяt.

Вероятность
отказа..
Всегда справедливо:.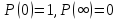

T– случайная величина, промежуток времени
между произвольными двумя соседними
отказами. Ее функция распределенияF(t) =P(T<t),
то есть вероятность того, что система
не откажет за времяt

3. Частота отказов устройств, её вероятностный и статистический смысл

Частота
отказов– отношение числа отказавших
образцов, объектов в единицу времени к
числу образцов первоначально установленных
на испытании, при условии, что отказавшие
образцы не восстанавливаются и не
заменяются исправными. Обозначается..
График выглядит так:

Вероятностное
определение
– число отказавших образцов= число оставшихся образцов в момент
времени (+)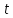
минус.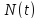

++.
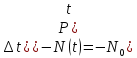
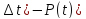
При достаточно большом числе изделий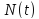при:..
Удобная характеристика, но только для
невосстанавливаемых систем.

4. Интенсивность отказов элементов и устройств, ее вероятностный и статистический смысл

Интенсивность
отказов– отношение числа отказавших
образцов в единицу времени к среднему
числу образцов, исправно работающих в
данный отрезок времени, при условии,
что данные образцы не восстанавливаются.
Обозначается.,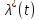
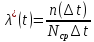
где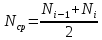– среднее число исправно работающих
образцов в интервале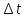,– число отказов вi-ом
интервале.

Принимаем:
на интервале определяем как число
первоначально поставленных элементов
умножить на вероятность безотказной
работы...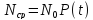
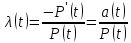
Интенсивность отказов – условная
плотность вероятности возникновения
отказов невосстанавливаемой системы,
определяемая для рассматриваемого
момента времени, при условии, что отказ
до этого не возникал.,
откуда.

5. Средняя наработка до отказа. Средняя наработка между отказами

Средняя
наработка до отказа– математическое
ожидание наработки объекта до первого
отказа. ОбозначаетсяT.

Если
время есть непрерывная случайная
величина:
.
Из аследует, что,.
C учетом этого, получаем:,
тут,
поэтому получаем.

Если
время разделено на небольшие интервалы:
,
где– образцы вначале, отказ каждого элемента
фиксируется.

Выберем
интервал испытаний и через заданные
постоянные промежутки времени
определим значение:,
где— число образцов, отказавших в этом
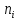
интервале,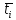– среднее времяi-го
интервала,– время, в течение которого отказали
всеобразцов.

,
где– наработка между отказами,– число отказавших образцов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #

  21.04.2019172.03 Кб3ЧМ.doc

• #
• #
• #
• #
• #
• #
• #
• #

Как вычисляется среднее время до отказа и вероятность безотказной работы?

Понятиям MTTF (Mean Time To Failure — среднее время до отказа) и другим терминам теории надежности посвящено большое количество статей, в том числе на Хабре (см., например, тут). Вместе с тем, редкие публикации «для широкого круга читателей» затрагивают вопросы математической статистики, и уж тем более они не дают ответа на вопрос о принципах расчета надежности электронной аппаратуры по известным характеристикам ее составных элементов.

В последнее время мне довольно много приходится работать с расчетами надежности и рисков, и в этой статье я постараюсь восполнить этот пробел, отталкиваясь от своего предыдущего материала (из цикла о машинном обучении) о пуассоновском случайном процессе и подкрепляя текст вычислениями в Mathcad Express, повторить которые вы сможете скачав этот редактор (подробно о нем тут, обратите внимание, что нужна последняя версия 3.1, как и для цикла по machine learning). Сами маткадовские расчеты лежат здесь (вместе с XPS- копией).

1. Теория: основные характеристики отказоустойчивости
Вроде бы, из самого определения (Mean Time To Failure) понятен его смысл: сколько (конечно, в среднем, поскольку подход вероятностный) прослужит изделие. Но на практике такой параметр не очень полезен. Действительно, информация о том, что среднее время до отказа жесткого диска составляет полмиллиона часов, может поставить в тупик. Гораздо информативнее другой параметр: вероятность поломки или вероятность безотказной работы (ВБР) за определенный период (например, за год).

Для того чтобы разобраться в том, как связаны эти параметры, и как, зная MTTF, вычислить ВБР и вероятности отказа, вспомним некоторые сведения из математической статистики.

Ключевое понятие теории надежности — это понятие отказа, измеряемое, соответственно, интервальным показателем
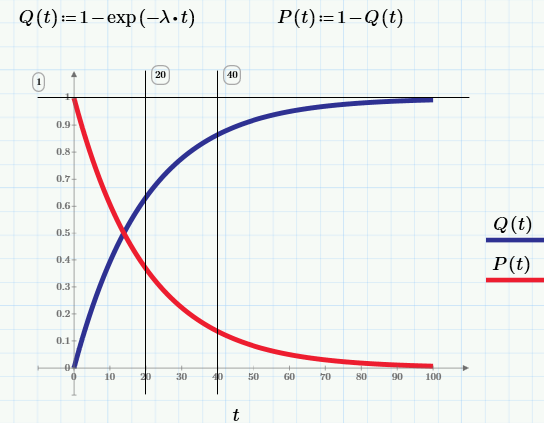
Q(t) = вероятность того, что изделие откажет к моменту времени t.
Соотвественно, вероятность безотказной работы (ВБР, в английской терминологии «reliability»):
P(t) = вероятность того, что изделие проработает без отказа от момента t₀=0 до момента времени t.
По определению, в момент t₀=0 изделие находится в работоспособном состоянии, т.е. Q(0)=0, а P(0)=1.

Оба параметра — это интервальные характеристики отказоустойчивости, т.к. речь идет о вероятности отказа (или наоборот, безотказной работы) на интервале (0,t). Если отказ рассматривать, как случайное событие, то, очевидно, что Q(t) — это, по определению, его функция распределения. А точечную характеристику можно определить, как
p(t)=dQ(t)/dt = плотность вероятности, т.е. значение p(t)dt равно вероятности, что отказ произойдет в малой окрестности dt момента времени t.

И, наконец, самая важная (с практической точки зрения) характеристика: λ(t)=p(t)/P(t)=интенсивность отказов.
Это (внимание!) условная плотность вероятности, т.е. плотность вероятности возникновения отказа в момент времени t при условии, что до этого рассматриваемого момента времени t изделие работало безотказно.

Измерить параметр λ(t) экспериментально можно путём испытания партии изделий. Если к моменту времени t работоспособность сохранило N изделий, то за оценку λ(t) можно принять процент отказов в единицу времени, происходящих в окрестности t. Точнее, если в период от t до t+dt откажет n изделий, то интенсивность отказов будет примерно равна
λ(t)=n/(N*dt).

Именно эта λ-характеристика (в пренебрежении ее зависимостью от времени) и приводится чаще всего в паспортных данных различных электронных компонент и самых разных изделий. Только сразу возникает вопрос: а как вычислить вероятность безотказной работы и при чем здесь среднее время до отказа (MTTF).

А вот при чем.

2. Экспоненциальное распределение
В терминологии, которую мы только что использовали, пока не было никаких предположений о свойствах случайной величины — момента времени, в который происходит отказ изделия. Давайте теперь конкретизируем функцию распределения значения отказа, выбрав в качестве нее экспоненциальную функцию с единственным параметром λ=const (смысл которого будет ясен через несколько предложений).

Дифференцируя Q(t), получим выражение для плотности вероятности экспоненциального распределения:
,
а из него – функцию интенсивности отказов: λ(t)=p(t)/P(t)=const=λ.

Что мы получили? Что для экспоненциального распределения интенсивность отказов – есть величина постоянная, причем совпадающая с параметром распределения. Этот параметр и является главным показателем отказоустойчивости и его часто так и называют λ-характеристикой.

Мало того, если теперь посчитать среднее время до первого отказа – тот самый параметр MTTF (Mean Time To Failure), то мы получим, что он равен MTTF=1/ λ.

Все это замечательные свойства экспоненциального распределения. Почему мы выбрали в качестве для описания отказов именно его? Да потому что это наиболее простая модель – модель пуассоновского потока событий, которая уже была нами рассмотрена в статье про анализ конверсии сайта. Поэтому-то в теории надежности наиболее часто используется показательное (экспоненциальное) распределение, для которого, как мы выяснили:

• надежность элементов можно оценить одним числом, т.к. λ=const;
• по известной λ довольно просто оценить остальные показатели надежности (например, ВБР для любого времени t);
• λ обладает хорошей наглядностью
• λ нетрудно измерить экспериментально

Но это еще не все, потому, что для экспоненциального распределения особенно легко делать расчет систем, состоящих из множества элементов. Но об этом – в следующей статье (продолжение следует).

Как решать задачи о прохождении тока через электрические схемы

В предыдущих статьях мы разобрали популярные учебные задачи по теории вероятностей: задачи про подбрасывания игральных кубиков и монеток, задачи про стрелков и станки.

В этой статье мы рассмотрим задачи вида
«задана схема электрической цепи с надежностью элементов (или вероятностями выхода из строя), найти вероятность работы цепи (или вероятность разрыва цепи)».

Задачи могут иметь чуть разные формулировки, но принцип решения для них одинаков, и его мы изучим, чтобы суметь решать такие задачи со схемами любой сложности.

Далее:

• Базовые события, обозначения и формулы
• Последовательно или параллельно?
• Усложняем схему цепи
• Примеры решений
• На закуску: схема с мостиком
• Полезные ссылки
• Решебник

Базовые события, обозначения и формулы

Самое первое, с чего мы начнем — формализация задачи (и решение любой своей задачи рекомендую начинать с этого). А именно, мы введем основные события:

$X$ = (Цепь работает) = (Цепь пропускает ток) и противоположное ему:

$overline{X}$ =(Цепь не пропускает ток) = (Произошел разрыв в цепи).

$A_i$ = (Элемент i работает, пропускает ток) и $overline{A_i}$ =(Элемент i отказал, не пропускает ток), $i=1,2,…,n$.

Обычно в условии задачи известны вероятности работы элементов (надежности): $p(A_i)=p_i$ или вероятности отказа $p(overline{A_i})=q_i=1-p_i$, $i=1,2,…,n$.

Также напомним основные формулы (из темы действий с событиями, формулы сложения и умножения вероятностей), которые пригодятся в решении этого типа задач.

Для независимых в совокупности событий (а отказы/работа элементов цепи — именно такие):

$$
P(A cdot B) = P(A) cdot P(B); quad(1)
$$
$$
P(A+B) = P(A)+P(B)-P(A)cdot P(B); quad(2)
$$
$$
P(A_1+A_2+…+A_n)=1-P(overline{A_1})cdot P(overline{A_2})cdot … cdot P(overline{A_n}). quad(3)
$$

Последовательно или параллельно?

Еще немного времени посвятим теории, вспомним о том, как могут соединяться элементы в цепи.

Последовательное соединение

Элементы цепи «нанизаны» на провод один за другим (следуют один за другим, отсюда и «последовательно»). Если откажет один любой — ток в цепи прервётся. Или, иначе говоря, цепь работает тогда и только тогда, когда ВСЕ элементы работают. В терминах теории вероятностей получаем произведение событий: $X=A_1 cdot A_2 cdot A_3$, а вероятность работы цепи равна

$$
P(X)=P(A_1 cdot A_2 cdot A_3)= P(A_1) cdot P(A_2) cdot P(A_3) =p_1 cdot p_2 cdot p_3.
$$

Если в цепи последовательно соединены не три, а больше независимо работающих элементов, формула легко обобщается и получаем:

$$
P(X) = p_1 cdot p_2 cdot …cdot p_n; qquad P(overline{X})=1-p_1 cdot p_2 cdot …cdot p_n. quad(4)
$$

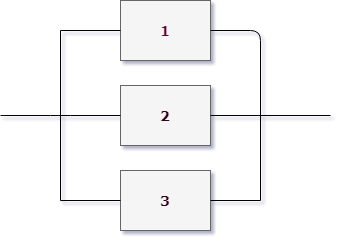
Параллельное соединение

Тут тоже сама схема дает нам подсказку, когда мы видим, что элементы в схеме расположены как бы на параллельных проводах, речь идет о параллельном соединении.

В этом случае если откажет, скажем, элемент 1, ток может пройти через 2. Если откажут 1 и 2, ток пройдет через 3. И только если ВСЕ элементы откажут, цепь разорвется.

Еще говорят, цепь работает, если работает хотя бы один элемент в ней, в терминах теории вероятностей — это сумма событий: $X=A_1+A_2+A_3$.

Используем формулу (3) чтобы записать вероятность работы такой цепи:

$$
P(A_1+A_2+A_3)=1-P(overline{A_1})cdot P(overline{A_2}) cdot P(overline{A_3})=1-q_1 cdot q_2 cdot q_3.
$$

И обобщим на случай $n$ параллельных элементов в цепи:

$$
P(X) = 1-q_1 cdot q_2 cdot …cdot q_n; qquad P(overline{X})=q_1 cdot q_2 cdot …cdot q_n. quad(5)
$$

Важно запомнить правило

Последовательному соединению соответствует произведение событий,
параллельному соединению — сумма событий.

Усложняем схему цепи

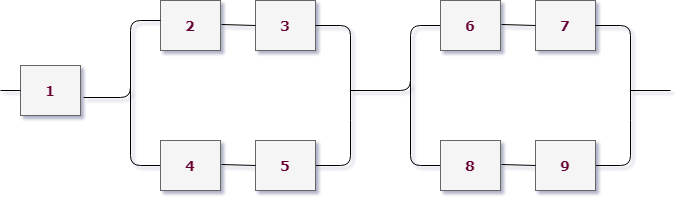
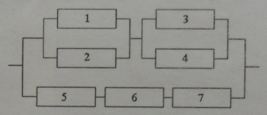
И все это была присказка к настоящему решению задач. Конечно, даже если у вас простая контрольная, схема с «тремя лампочками подряд» вряд ли попадется. Давайте посмотрим на типовые электрические схемы, для которых надо находить надежность в задачах:

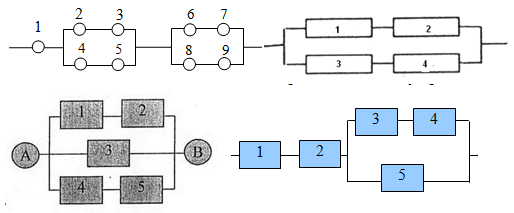
Как для таких схем выписывать вероятности? Нам нужно научиться делать декомпозицию: выделять уровни схемы и определять тип соединения на каждом уровне.

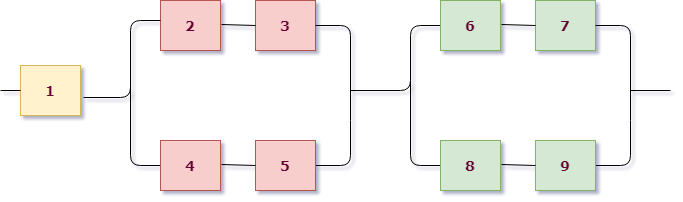
Возьмем для примера левую верхнюю схему:

Работаем с первым уровнем схемы. Нужно мысленно выделить крупные части, которые между собой соединены одинаково (параллельно или последовательно). В данном случае видно три группы элементов, соединенных последовательно. Выделим для наглядности цветом:

То есть тип схемы на первом уровне — последовательный:

Как мы уже знаем, если соединение последовательное, нужно перемножать события, то есть

$$
X=X_1 cdot X_2 cdot X_3,
$$

$X_1$ — работает первая группа элементов,
$X_2$ — работает вторая группа элементов,
$X_3$ — работает третья группа элементов.

Теперь смотрим на каждую группу. В первой группе всего один элемент, то есть она работает, когда работает первый элемент цепи ($X_1=A_1$). Мы дошли до элемента, разбор этой группы закончен.

А вот дальше интереснее. Рассмотрим поближе вторую группу:

В ней сразу выделим цветом подгруппы элементов. Видно, что вторая группа имеет уже параллельную структуру из розовых и фиолетовых элементов (они «висят» на параллельных линиях, это второй уровень вложенности схемы). А вот внутри розовые соединены последовательно (розовая группа работает — $A_4 cdot A_5$), фиолетовые элементы также между собой последовательно (фиолетовая группа работает — $A_2 cdot A_3$). Это уже третий уровень вложенности и он заканчивается отдельными элементами, значит, разбор окончен.

Так как розовая и фиолетовая группа соединены параллельно, речь идет о сумме этих событий, то есть вторая группа работает если:

$$X_2 = A_2 cdot A_3 + A_4 cdot A_5.$$

Абсолютно аналогично разбирается третья подгруппа (она совпадает по структуре со второй):

$$X_3 = A_6 cdot A_7 + A_8 cdot A_9.$$

Сводим все в одну формулу и выпишем искомое событие (Цепь работает исправно):

$$
X=X_1 cdot X_2 cdot X_3 = A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right).
$$

Теперь переходим ко второму этапу решения задачи. Не забываем, что мы решаем задачу по теории вероятностей и надо определить вероятность того, что ток проходит в цепи. Будем использовать формулы (1)-(3).

Так как вероятность произведения для независимых событий равна произведению вероятностей, получим:

$$
P(X)= P left( A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right) right) =\
= P (A_1) cdot P left ( A_2 cdot A_3 + A_4 cdot A_5 right ) cdot P left( A_6 cdot A_7 + A_8 cdot A_9right) =
$$

Для множителей с суммой событий внутри используем формулу (2):

$$
= P (A_1) cdot left[ P(A_2 cdot A_3) + P(A_4 cdot A_5) — P(A_2 cdot A_3 cdot A_4 cdot A_5) right] cdot left[ P(A_6 cdot A_7) + P(A_8 cdot A_9) — P(A_6 cdot A_7 cdot A_8 cdot A_9)right] =
$$

И снова раскрываем вероятности произведений:

$$
= P (A_1) cdot left[ P(A_2) cdot P(A_3) + P(A_4) cdot P(A_5) — P(A_2) cdot P(A_3) cdot P(A_4) cdot P(A_5) right] cdot left[ P(A_6) cdot P(A_7) + P(A_8) cdot P(A_9) — P(A_6) cdot P(A_7) cdot P(A_8) cdot P(A_9)right].
$$

Перейдем к более компактной записи, положив $p_i=P(A_i)$:

$$
P(X)= p_1 cdot left[ p_2 cdot p_3 + p_4 cdot p_5 — p_2 cdot p_3 cdot p_4 cdot p_5 right] cdot left[ p_6 cdot p_7 + p_8 cdot p_9 — p_6 cdot p_7 cdot p_8 cdot p_9right].
$$

Если заданы надежности отдельных элементов $p_i$, подставляя их в формулу, можно найти вероятность работы схемы.

Алгоритм разбора схемы

• Выделяем в схеме основу: группы элементов, соединенные ТОЛЬКО последовательно или ТОЛЬКО параллельно между собой. Это верхний уровень. Записываем событие $X$ = (Цепь работает) как произведение или сумму соответственно.
• Каждую полученную группу анализируем также: ищем в ней подгруппы, соединенные только последовательно или только параллельно. Записываем событие соответственно типу соединения.
• Продолжаем до тех пор, пока не опустимся на уровень элементов (событий $A_i$).
• Подставляем все выражения в исходную формулу, получаем итоговую запись события $X$.
• Пользуясь формулами (1)-(3) выписываем вероятность события $P=P(X)$.
• Подставляем числовые значения $p_i, q_i$ и находим численное значение надежности схемы $P$.
• Если необходимо, находим вероятность отказа цепи $1-P$.

Примеры решений

Отработаем несколько раз этот алгоритм на примерах, чтобы он закрепился.

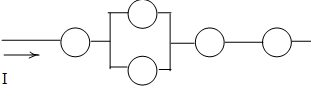
Пример 1. Дана схема включения элементов. Вероятность безотказной работы каждого элемента в течение времени Т равна р. Элементы работают независимо и включены в цепь по приведенной схеме. Пусть событие $А_i$ означает безотказную работу за время Т элемента с номером $i$ ($i=1,2,3,…$), а событие $В$ – безотказную работу цепи. Требуется:
1) Написать формулу, выражающую событие $В$ через все события $А_i$.
2) Найти вероятность события $B$.
3) Вычислить $Р(В)$ при $р=0,6$.

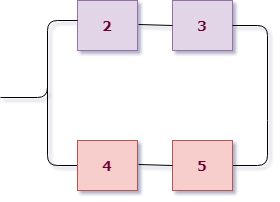
Приступим к разбору схемы. Можно увидеть, что на первом уровне мы имеем три группы, соединенные последовательно: (1), (2,3) и (4,5,6) элементы. Выделим их цветом для наглядности:

Значит, исходное событие можно представить в виде произведения трех событий $B=B_1 cdot B_2 cdot B_3$, где $B_i$ — работает $i$-aя группа элементов.

Первая группа элементов состоит из одного элемента, то есть $B_1=A_1$.

Вторая группа элементов состоит из двух элементов, соединенных параллельно (см. розовые), поэтому $B_2=A_2+A_3$.

Третья группа элементов (см. зеленые) состоит из трех элементов, ее можно представить как параллельное соединение двух подгрупп: (4 и 5, соединены последовательно) и (6), поэтому $B_3=A_4 cdot A_5 + A_6$.

Подставляем все и получаем выражение для события $B$

$$
B=B_1 cdot B_2 cdot B_3 = A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6).
$$

Теперь выразим вероятность безотказной работы цепи за время T. Сначала применим формулу (1), чтобы раскрыть произведение:

$$
P(B)=P left( A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6) right) = P(A_1) cdot P left( A_2+A_3 right) cdot P left( A_4 cdot A_5 + A_6 right) =
$$

Раскроем вторую вероятность по формуле (3), а третью по формуле (2), получим:

$$= P(A_1) cdot left(1 — P(overline{A_2}) cdot P(overline{A_3}) right) cdot left( P(A_4) cdot P(A_5) + P(A_6) — P(A_4) cdot P(A_5) cdot P(A_6) right).$$

Подставляем $P(A_i)=p$ и получим:

$$
p(B)=pcdot(1-(1-p)cdot(1-p))cdot(pcdot p + p -p cdot p cdot p) = pcdotleft(1-(1-p)^2right)cdot left(p+p^2-p^3right).
$$

Осталось только найти значение при $p=0,6$:

$$
p(B)= 0,6cdotleft(1-(1-0,6)^2right)cdot left(0,6+0,6^2-0,6^3right) approx 0,375.
$$

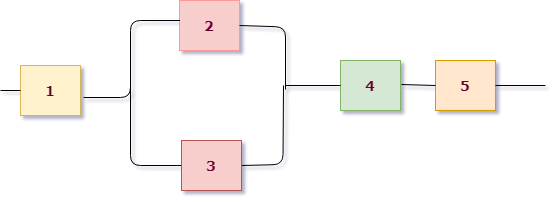
Пример 2. Найти вероятность обрыва цепи, если вероятность отказа каждого элемента равна 0,2, а отказы элементов – независимые события.

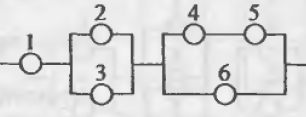
Пронумеруем элементы и сразу раскрасим схему, чтобы выделить ее структуру.

Это опять последовательная схема, но розовая группа состоит из двух элементов, соединенных параллельно, поэтому можем сразу выписать:

$$
X= A_1 cdot (A_2+A_3) cdot A_4 cdot A_5.
$$

Найдем вероятность этого события (работы цепи):

$$
P(X)= P left( A_1 cdot (A_2+A_3) cdot A_4 cdot A_5 right)= P(A_1) cdot P(A_2+A_3) cdot P(A_4) cdot P(A_5)= \
= P(A_1) cdot left( 1- P(overline{A_2}) cdot P(overline{A_3}) right) cdot P(A_4) cdot P(A_5).
$$

Вероятности отказа элементов цепи равна 0,2, вероятность работы элементов — 0,8, поэтому

$$
P(X)= 0,8 cdot left( 1- 0,2 cdot 0,2 right) cdot 0,8 cdot 0,8 = 0,492.
$$

Но в задаче требовалось найти вероятность обрыва цепи, это противоположное событие:

$$
P(overline{X}) = 1- P(X) = 1-0,492 = 0,508.
$$

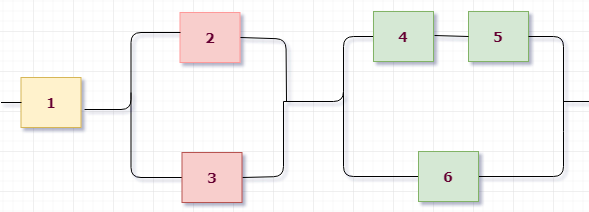
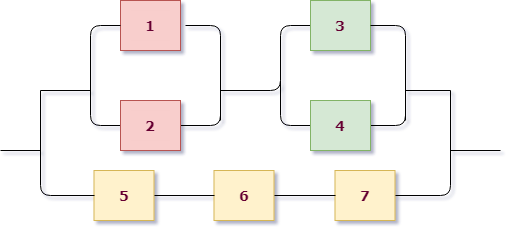
Пример 3. Найти вероятность безотказной работы функциональной цепи, состоящей из независимо работающих элементов, если вероятность надежной работы элементов равна $p_1=p_2=p_3=p_4=0,8$, $p_5=p_6=p_7=0,9$.

Приступим к решению, сразу раскрасив схему. В этот раз схема на первом уровне имеет параллельное соединение: верхняя розово-зеленая группа и нижняя желтая находятся на параллельных линиях. Поэтому $X=X_1+X_2$, где $X_1$ — работает розово-зеленая линия, $X_2$ — работает желтая.

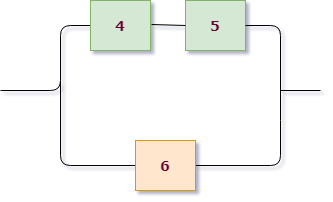
Для желтой группы, состоящей из трех последовательно расположенных элементов, сразу выписываем $X_2=A_5 cdot A_6 cdot A_7$.

Теперь рассмотрим верхнюю группу. Она состоит из двух подгрупп, связанных последовательно: розовой и зеленой. При этом каждая из них состоит из двух параллельно соединенных элементов. Записываем: розовая группа работает = $A_1+A_2$, зеленая группа работает = $A_3+A_4$, значит ток проходит через розово-зеленую группу $X_1 =(A_1+A_2) cdot (A_3+A_4)$.

Объединяем рассуждения и выписываем событие, соответствующее безотказной работе цепи:

$$
X=X_1+X_2 = (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7.
$$

Следующий шаг: выразить вероятность этого события. Во всех предыдущих примерах схема на первом уровне была последовательной, и событие выражалось как произведение. В этом случае схема на первом уровне параллельна, событие выглядит как сумма других событий, что немного усложняет выкладки. Для суммы событий можно использовать формулу (2) или (3), выбирая наиболее удобную в каждом конкретном случае.

В данном случае слагаемых всего два, поэтому возьмем формулу (2):

$$
P(X)= P left( (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7 right) = \
= P left( (A_1+A_2) cdot (A_3+A_4) right) + P left( A_5 cdot A_6 cdot A_7 right) — P left( (A_1+A_2) cdot (A_3+A_4) cdot A_5 cdot A_6 cdot A_7 right)
$$

Раскрываем все произведения по формуле (1):

$$
= P (A_1+A_2) cdot P(A_3+A_4) + P(A_5) cdot P(A_6) cdot P(A_7) — P (A_1+A_2) cdot P(A_3+A_4) cdot P(A_5) cdot P(A_6) cdot P(A_7) =
$$

По формуле (3) расписываем $P(A_1+A_2)=1-P(overline{A_1}) cdot P(overline{A_2}) = 1-q_1cdot q_2$ и $P(A_3+A_4)=1-P(overline{A_3}) cdot P(overline{A_4})= 1-q_3cdot q_4$.

Итого:

$$
P(X)= (1-q_1cdot q_2) cdot (1-q_3cdot q_4) + p_5 cdot p_6 cdot p_7 — \- (1-q_1cdot q_2) cdot (1-q_3cdot q_4) cdot p_5 cdot p_6 cdot p_7.
$$

Подставляем значения надежности элементов:

$$
P(X)= (1-0,2^2)^2 + 0,9^3 — (1-0,2^2)^2 cdot 0,9^3 approx 0,9788.
$$

Еще: другие уроки о решении задач по вероятности

На закуску: схема с мостиком

Для 99% учебных задач вам хватит той теории и примеров, что приведены выше: подробно изучите их и приступайте к своим примерам по аналогии. Но есть такие схемы, для которых нельзя выделить единую структуру на верхнем уровне — параллельную или последовательную, и весь алгоритм решения рушится.

Речь идет о схемах смешанного типа, еще их часто называют схемами с мостиком (мостиковые схемы). Типичная схема имеет такой вид:

Видно, что как ни крути, схему нельзя отнести ни к последовательным, ни к параллельным. Элемент №5 (мостик) «портит» тип схемы. Если его убрать (разорвать этот участок цепи), получим обычную параллельную структуру, а если предположить, что через этот участок всегда идет ток — последовательную (конкретные схемы изобразим ниже).

Поэтому для решения задачи о вычислении надежности подобной электросхемы используют формулу полной вероятности в форме теоремы разложения (см. подробнее тут, стр. 118)

Надежность цепи с избыточностью равна произведению вероятности безотказной работы $i$-го элемента цепи на вероятность безотказной работы оставшейся цепи (места подключения $i$-го элемента замкнуты накоротко) плюс произведение вероятности отказа того же $i$-го элемента на вероятность безотказной работы оставшейся цеии (места подключения $i$-го элемента разомкнуты).

То есть, для выделенного на схеме элемента-мостика рассматриваем две гипотезы:
$H_1$ = (Элемент 5 не пропускает ток), $P(H_1)=1- p_5 = q_5$;
$H_2$ = (Элемент 5 пропускает ток), $P(H_2)=p_5$.

Далее вычисляем надежность схемы при условии верности каждой из гипотез. Для наглядности нарисуем обе схемы:

Рассмотрим левую схему, верную при гипотезе $H_1$, через нее проходит ток, если $X|H_1 = A_1cdot A_3+ A_2cdot A_4$, вероятность

$$
P(X|H_1) = P(A_1cdot A_3+ A_2cdot A_4)= P(A_1cdot A_3)+ P(A_2cdot A_4) — P(A_1cdot A_3 cdot A_2cdot A_4)=\
=p_1 cdot p_3 + p_2 cdot p_4 — p_1 cdot p_2 cdot p_3 cdot p_4.
$$

Рассмотрим правую схему, верную при гипотезе $H_2$, и выпишем для нее аналогично событие и вероятность прохода тока:

$$
X|H_2 = (A_1+A_2)cdot (A_3+A_4),\
P(X|H_2) =P( (A_1+A_2)cdot (A_3+A_4)) = P(A_1+A_2)cdot P(A_3+A_4)=\ = (1-P(overline{A_1}) cdot P(overline{A_2})) cdot (1-P(overline{A_3}) cdot P(overline{A_4})) = (1-q_1cdot q_2) cdot (1-q_3cdot q_4).
$$

Тогда по формуле полной вероятности, надежность схемы равна:

$$
P(X)=P(X|H_1)cdot P(H_1) + P(X|H_2)cdot P(H_2) = \
= q_5 (p_1 cdot p_3 + p_2 cdot p_4 — p_1 cdot p_2 cdot p_3 cdot p_4) + p_5 (1-q_1cdot q_2) cdot (1-q_3cdot q_4).
$$

Аналогичным образом можно разбирать более сложные схемы (в которые более одного мостика), применяя на каждом этапе формулу полной вероятности (как бы вкладывая одну в другую).

Полезные ссылки по ТВ

Решебник по вероятности

А здесь вы найдете разные задачи по теории вероятностей с полными решениями (вводите часть текста для поиска своей задачи):