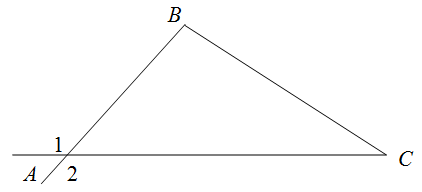
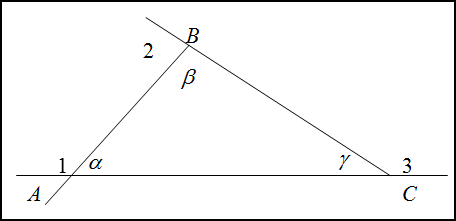
Как найти величину внешнего угла в треугольнике - AvtoShod.ru

Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?

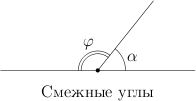
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна $180^{circ}$ .

Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом alpha . Если угол alpha острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:

$sin left( 180^{circ} - alpha right) = sin alpha;$
$cos left( 180^{circ} - alpha right) = - cos alpha;$
$tg , left( 180^{circ} - alpha right) = - , tg , alpha.$

Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.

Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

1. В треугольнике ABC угол равен $90^{circ}$ , $cos A = genfrac{}{}{}{0}{displaystyle 4}{displaystyle sqrt{17}}$ . Найдите тангенс внешнего угла при вершине .

Пусть varphi — внешний угол при вершине .

$cos varphi = - cos A = - genfrac{}{}{}{0}{displaystyle 4}{displaystyle sqrt{17}}.$

Зная , найдем по формуле:

$genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos^2 varphi}= 1 + tg^2 , varphi.$

Получим: $tg , varphi= - genfrac{}{}{}{0}{displaystyle 1}{displaystyle 4} = - 0,25.$

2. В треугольнике ABC угол равен $90^{circ}$ , . Найдите синус внешнего угла при вершине .

Задача решается за четыре секунды. Поскольку сумма углов и равна $90^{circ}$ , . Тогда и синус внешнего угла при вершине также равен 0,1 .

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Внешний угол треугольника. Синус и косинус внешнего угла» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Основные определения

Прежде чем рассмотреть определение внешнего угла треугольника, напомним несколько основных определений из начального курса геометрии, а именно:

угла и треугольника;
смежных углов;
параллельных прямых.

Угол и треугольник являются геометрическими фигурами. Угол состоит из точки (вершины) и двух лучей (сторон угла), которые исходят из данной точки. Треугольник представляет собой три точки (вершины), соединённые отрезками (сторонами). Треугольник имеет три угла.

Определение 1

Смежными называют два угла, имеющие одну общую сторону, а другие две стороны являются продолжениями друг друга.

На рисунке ниже смежными углами являются углы $ADB$ и $BDC$. $angle ADB + angle BDC = angle ADC = 180^{circ}$.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Рисунок 1. Смежные углы. Автор24 — интернет-биржа студенческих работ

Параллельными называются две непересекающиеся прямые на одной плоскости. Секущей по отношению к двум прямым называется прямая, которая пересекает две прямые в двух точках. Если две прямые параллельны, то в случае пересечения пары этих прямых секущей, получившиеся в результате этого действа накрест лежащие углы равны, а сумма односторонних углов равна $180^{circ}$.

Теорема о сумме углов треугольника

Понятие внешнего угла треугольника встречается в теореме о сумме углов треугольника, которая звучит следующим образом:

Сумма углов треугольника равна $180^{circ}$.

«Внешний угол треугольника: определение и свойство» 👇

Приведём её доказательство.

Пусть дан произвольный $triangle ABC$. Нужно доказать, что $angle A + angle B + angle C=180^{circ}$.

Рисунок 2. Теорема о сумме углов треугольника. Автор24 — интернет-биржа студенческих работ

Проведём прямую $b$ через вершину $B$, которая будет параллельна стороне $AC$.

Рисунок 3. Теорема о сумме углов треугольника. Автор24 — интернет-биржа студенческих работ

Видим, что углы 1 и 5 — накрест лежащие углы при пересечении параллельных прямых $b$ и $AC$ секущей $AB$. Углы 3 и 4 также являются накрест лежащими углами при пересечении тех же параллельных прмяых секущей $BC$. Делаем вывод, что: $angle 5 = angle 1, angle 4 = angle 3$.

Очевидно, глядя на рисунок, что сумма углов 2, 4 и 5 равна $180^{circ}$. Отсюда следует, что $angle 1 +angle 2 +angle 3 = 180^{circ}$ или $angle A + angle B + angle C=180^{circ}$. Ч.т.д.

Внешний угол треугольника

В доказательстве теоремы о сумме углов треугольника есть два примера внешнего угла треугольника. Это углы 4 и 5. Дадим определение:

Определение 2

Внешний угол треугольника — это угол, являющийся смежным с каким-нибудь углом данного треугольника.

Имеем теорему:

Теорема 2

Внешний угол треугольника равен сумме двух углов данного треугольника, не являющихся смежным с внешним углом.

Докажем эту теорему.

Рассмотрим следующий рисунок:

Рисунок 4. Внешний угол треугольника. Автор24 — интернет-биржа студенческих работ

Мы видим, что угол 4 является внешним углом, смежным с 2 углом треугольника. Очевидно, что $angle 4 +angle 2 = 180^{circ}$. По теореме о сумме углов:

$(angle 1 +angle 3)+angle 2=180^{circ}$. Отсюда следует, $angle 4 = angle 1 +angle 3$. Ч.т.д.

Рассмотрим пример задачи на данную тему.

Пример 1

Задача. $triangle ABC$ — равнобедренный. $AC$ — основание этого треугольника. $AC$=37 см, внешний угол при $B$ равняется $60^{circ}$. Нужно найти расстояние от точки $C$ до прямой $AB$.

Решение. Сделаем рисунок:

Рисунок 5. Треугольник. Автор24 — интернет-биржа студенческих работ

На рисунке прямая, обозначающая расстояние от точки $C$ до прямой $AB$ обозначена как $CD$. В математике такое расстояние называют высотой. По определению высоты треугольника, прямая высоты перпендикулярна той стороне, на которую опущена. То есть $angle ADC = 90^{circ}$.

По теореме о внешнем угле треугольника находим $angle B$: $angle B=180-60=120^{circ}$. По теореме о сумме углов треугольника получается, что $angle A + angle C = 180-120=60$. Так как треугольник равнобедренный, углы у основания равны по $30^{circ}$.

Рассмотрим $triangle ADC$. Из вышеуказанного следует, что он прямоугольный. Из свойства прямоугольных треугольников известно, что катет такого треугольника, который лежит против угла $30^{circ}$, равен половине гипотенузы. В нашем случае, $СD$ является катетом против угла $30^{circ}$, а $AC$ — гипотенуза. Поэтому справедливо утверждать, что $CD=37/2=18,5$ см.

Ответ: 18,5 см.

Таким образом, в данной статье мы получили полное представление о том, что такое внешний угол треугольника и разобрали сопутствующие теоремы.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

В данной публикации мы рассмотрим одну из основных теорем в геометрии 7 класса – о внешнем угле треугольника. Также разберем примеры решения задач, чтобы закрепить представленный материал.

Определение внешнего угла

Для начала вспомним, что такое внешний угол. Допустим у нас есть треугольник:

Смежный с внутренним углом (λ) треугольника угол при той же вершине является внешним. На нашем рисунке он обозначен буквой γ.

При этом:

сумма данных углов равна 180 градусам, т.е. γ + λ = 180° (свойство внешнего угла);
0 и 0.

Формулировка теоремы

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

γ = α + β

Из данной теоремы следует, что внешний угол треугольника больше любого из несмежных с ним внутренних углов.

Примеры задач

Задание 1
Дан треугольник, в котором известны значения двух углов – 45° и 58°. Найдите внешний угол, смежный с неизвестным углом треугольника.

Решение
Воспользовавшись формулой теоремы получаем: 45° + 58° = 103°.

Задание 1
Внешний угол треугольника равен 115°, а один из несмежных с ним внутренних углов – 28°. Вычислите значения оставшихся углов треугольника.

Решение
Для удобства будем использовать обозначения, указанные на рисунках выше. Известный внутренний угол примем за α.

Исходя из теоремы: β = γ – α = 115° – 28° = 87°.

Угол λ является смежным с внешним, а значит вычисляется по следующей формуле (следует из свойства внешнего угла): λ = 180° – γ = 180° – 115° = 65°.

Источник

Содержание:

Определение внешнего угла треугольника
Свойства внешних углов треугольника
Примеры решения задач

Определение внешнего угла треугольника

Определение

Углы, смежные с углами треугольника, называются внешними.

Например, для $angle A$, внешними будут углы $angle 1$ и $angle 2$ (см. рис.)

Свойства внешних углов треугольника

Сумма внешних углов треугольника, взятых по одному при каждой вершине, равна $360^{circ}$.
Сумма внешнего и внутреннего угла при одной вершине равна $180^{circ}$.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

$$angle 1=angle B+angle C$$

Примеры решения задач

Пример

Задание. В треугольнике $Delta M N K$, внешний угол $angle M$ равен $120^{circ}$,
а угол $angle N=65^{circ}$. Найти угол $angle K$.

Решение. По теореме о внешнем угле
$angle M=angle N+angle K$. Подставляя в это равенство исходные данные, получим

$$120^{circ}=65^{circ}+angle K$$

Выразим $angle K : angle K=120^{circ}-65^{circ} Rightarrow angle K=55^{circ}$

Ответ. $angle K=55^{circ}$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Внешние углы при двух вершинах треугольник равны $70^{circ}$ и $150^{circ}$.
Найти внутренний угол при третьей вершине.

Решение. Обозначим внешние углы $angle 1, angle 2, angle 3$, а соответствующие им
внутренние — $alpha, beta, gamma$.

По условию $angle 1=150^{circ}$ и $angle 2=70^{circ}$. По свойству внешних углов, их сумма,
взятых по одному при каждой вершине, равна $360^{circ}$. То есть

$$angle 1+angle 2+angle 3=360^{circ}$$

Выразим из этого равенства неизвестный угол $angle 3$

$$angle 3=360^{circ}-angle 1-angle 2$$

$$angle 3=360^{circ}-150^{circ}-70^{circ}$$

$$angle 3=140^{circ}$$

Тогда искомый внутренний угол можно найти из условия, что сумма внутреннего и внешнего углов равна
$180^{circ}$, то есть $gamma+angle 3=180^{circ}$, тогда:

$$gamma=180^{circ}-angle 3$$

$$gamma=180^{circ}-140^{circ}=40^{circ}$$

Ответ. $gamma=40^{circ}$

Читать дальше: что такое медиана треугольника.

Источник

Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых
задачах ЕГЭ требуется найти синус,
косинус или тангенс внешнего
угла
треугольника. А что такое внешний
угол треугольника?

Давайте
вспомним сначала, что такое смежные
углы.
Вот они, на рисунке. У смежных углов
одна сторона общая, а две другие лежат
на одной прямой. Сумма смежных углов
равна

Возьмем
треугольник и продолжим одну из его
сторон. Внешний угол

при
вершине

—
это угол, смежный с углом

. Если
угол

острый, то смежный с ним угол —
тупой, и наоборот.

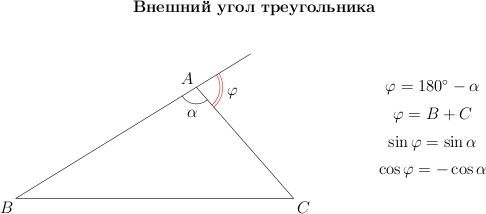
Обратите
внимание, что:

Запомните
эти важные соотношения. Сейчас мы берем
их без доказательств. В разделе
«Тригонометрия», в теме «Тригонометрический
круг»,
мы вернемся к ним.

Легко
доказать, что внешний
угол треугольника равен сумме двух
внутренних углов, не смежных с ним.

1.
В треугольнике

угол

равен

,

.
Найдите тангенс внешнего угла при
вершине

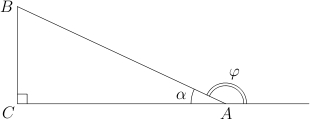
Пусть

—
внешний угол при вершине

.
Имеем:

Зная

,
найдем

по формуле

Получим:

2.
В треугольнике

угол

равен

,

.
Найдите синус внешнего угла при вершине

.

Задача
решается за четыре секунды. Поскольку
сумма углов

равна
,

.
Тогда и синус внешнего угла при
вершине

также равен

.

Высота в прямоугольном треугольнике

Вспомним,
что высота
треугольника —
это перпендикуляр, опущенный из его
вершины на противоположную сторону.

В
прямоугольном треугольнике катеты
являются высотами друг к другу. Главный
интерес представляет высота, проведённая
к гипотенузе.

Один
из типов экзаменационных задач В6 в
банке заданий ФИПИ — такие, где
в прямоугольном треугольнике высота
проведена из вершины прямого угла.
Посмотрим, что получается:

Высота
проведена к гипотенузе

.
Она делит треугольник

на два
прямоугольных треугольника —

и
.
Смотрим внимательно на рисунок
и находим на нем равные
углы.
Это и есть ключ к задачам по геометрии,
в которых высота опущена на гипотенузу.

Мы помним,
что сумма двух острых углов прямоугольного
треугольника равна

.
Значит,

,
то есть угол

равен
углу

.
Аналогично, угол

.

Иными
словами, каждый из трех углов
треугольника

равен
одному из углов треугольника

и треугольника

.
Треугольники

называются подобными.
Давайте нарисуем их рядом друг
с другом.

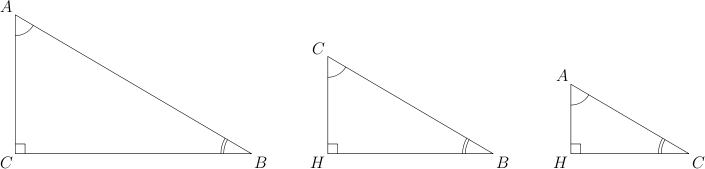
Они
отличаются только размерами. Стороны
подобных треугольников пропорциональны.
Что это значит?

Возьмем
треугольники

и
.
Стороны треугольника

длиннее,
чем стороны треугольника

,
в некоторое число

раз:

При
решении задач нам пригодится равенство
углов треугольников

и
,
а также пропорциональность их сторон.
Обратите также внимание, что площадь
треугольника

можно
записать двумя разными способами: как
половину произведения катетов и как
половину произведения гипотенузы
на проведенную к ней высоту.

1.
В треугольнике

угол

равен

,

—
высота,

,

.
Найдите

.

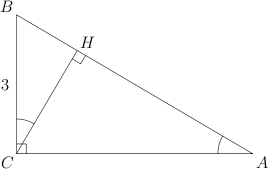
Рассмотрим
треугольник

.
В нем известны косинус угла

и противолежащий катет

.
Зная синус угла
,
мы могли бы найти гипотенузу

.
Так давайте найдем

:

(поскольку
значение синуса острого угла положительно).
Тогда:

Рассмотрим
прямоугольный треугольник

,

.
Имеем:

Отсюда,
поскольку

:

и
тогда

Ответ:

.

2.
В треугольнике

угол

равен

,

,

.
Найдите высоту

Сделайте
чертеж и рассмотрите прямоугольный
треугольник

Ответ:

.

3.
В треугольнике

угол

равен

,

,

.
К гипотенузе проведена высота

.
Найдите

Это
чуть более сложная задача. Ведь вам
неизвестны катеты

и
.

Зато
можно записать теорему Пифагора:

Нам
известно также, что

Решая
эту систему из двух уравнений, найдем:

Запишем
площадь треугольника

двумя
способами:

и найдем

.

Найти
высоту, проведенную из вершины прямого
угла, можно было и другим способом.
Мы выбрали самый короткий путь —
составили и решили систему уравнений.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
30.03.201540.15 Mб22спицын мартыненко.djvu
#
#
#
#
#
#
#
#

Источник

Внешний угол треугольника. Синус и косинус внешнего угла

Основные определения

Теорема о сумме углов треугольника

Внешний угол треугольника

Определение внешнего угла

Формулировка теоремы

Примеры задач

Определение внешнего угла треугольника

Свойства внешних углов треугольника

Примеры решения задач

Внешний угол треугольника. Синус и косинус внешнего угла

Высота в прямоугольном треугольнике

Не пропустите также: