Содержание:
- Определение и формула напряженности магнитного поля
- Закон Био-Савара-Лапласа
- Единицы измерения
- Примеры решения задач
Определение и формула напряженности магнитного поля
Определение
Напряженностью магнитного поля $bar{H}$ называют
векторную физическую величину, направленную по касательной к силовым линиям поля, являющуюся характеристикой магнитного поля, равную:
$$bar{H}=frac{bar{B}}{mu_{0}}-bar{J}(1)$$
где $bar{B}$ – вектор магнитной индукции,
$mu_{0}=4 pi cdot 10^{-7}$ Гн/м(Н/А2)- магнитная постоянная,
$bar{j}$ – вектор намагниченности среды в исследуемой точке поля.
Для магнитного поля в вакууме напряженность магнитного поля определяется выражением:
$$bar{H}=frac{bar{B}}{mu_{0}}$$
В изотропной среде формула (1) преобразуется к виду:
$$bar{H}=frac{bar{B}}{mu_{0} mu}$$
где $mu$ – скалярная величина, называемая
относительной магнитной проницаемостью среды (или просто магнитной проницаемостью). В изотропной среде векторы напряженности
магнитного поля и магнитной индукции совпадают по направлению.
Иногда напряженность магнитного поля $d bar{H}$ определяют как
векторную величину, направленную по касательной к силовой линии поля, по модулю равной отношению силы (dF), с которой поле
воздействует на единичный элемент тока (dl), который расположен перпендикулярно полю в вакууме, к магнитной постоянной:
$$d H=frac{d F}{mu_{0} I d l}$$
Закон Био-Савара-Лапласа
Это важнейший в электромагнетизме закон. Он определяет вектор напряженности $d bar{H}$
в произвольной точке магнитного поля, которое создает в вакууме элементарный проводник длинны dl с постоянным током I:
$$d bar{H}=frac{1}{4 pi} frac{I}{r^{3}} d bar{l} times bar{r}(5)$$
где $d bar{l}$ – вектор элемента проводника, который по модулю равен длине
проводника, направление совпадает с направлением тока; $bar{r}$ – радиус–вектор,
который проводят от рассматриваемого элементарного проводника к точке рассмотрения поля;
$r=|bar{r}|$ .
Вектор $d bar{H}$ – перпендикулярен плоскости, в которой находятся
векторы $d bar{l}$ и
$bar{r}$, и направлен так, что из его конца вращение вектора
$d bar{l}$ по кратчайшему пути до совмещения с вектором
$bar{r}$ происходило по часовой стрелке. Для нахождения направления вектора
$d bar{H}$ можно использовать правило буравчика (Буравчик (винт) вращаем так,
чтобы его поступательное движение совпадало с направлением тока, тогда направление, по которому вращается ручка винта, совпадает с направлением
вектора напряженности поля, которое создает рассматриваемый ток).
Закон Био-Савара-Лапласа дает возможность вычислять величину полной напряженности магнитного поля, которое создает ток, текущий по проводнику любой формы.
Для нахождения полной напряженности магнитного поля, которое создает в исследуемой точке ток I, который течет по проводнику l, следует
векторно суммировать все элементарные напряженности $d bar{H}$, порождаемые
элементами проводника и найденные по формуле (4).
Единицы измерения
Основной единицей измерения момента силы в системе СИ является: [H]=А/м
Примеры решения задач
Пример
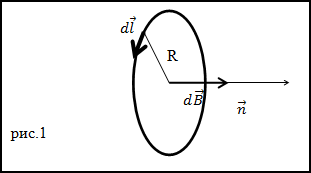
Задание. Чему равна напряженность (H) в центре кругового витка (R — радиус витка) с током I.
Решение. Каждый элементарный ток витка магнитное поле в центре окружности, напряженность которого направлена по
положительной нормали к плоскости контура витка (рис.1). Поэтому, если элементарную напряженность поля найти по закону Био-Савара –
Лапласа, то векторное сложение элементарных полей можно будет заменить на алгебраическое.
В соответствии с законом Био-Савара – Лапласа dH равно:
$$d bar{H}=frac{1}{4 pi} frac{I}{r^{3}} d bar{l} times bar{r}(1.1)$$
Применяя выражение (1.1) к нашему случаю, получим:
$$d H=frac{1}{4 pi} frac{I d l}{R^{2}}(1.2)$$
Возьмем интеграл по контуру, получим:
$$H=oint_{L} frac{1}{4 pi} frac{I d l}{R^{2}}=frac{1}{4 pi} I cdot frac{2 pi R}{R^{2}}=frac{I}{2 R}$$
Ответ. $H=frac{I}{2 R}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова напряженность магнитного поля, которую создает электрон, движущийся прямолинейно и равномерно со
скоростью v? Если точка, в которой исследуется поле, находится на расстоянии r от электрона на перпендикуляре к вектору скорости,
если перпендикуляр провести через мгновенное положение частицы.
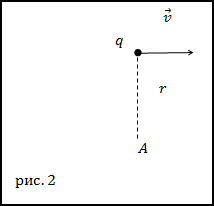
Решение. Сделаем рисунок.
Напряженность магнитного поля будем искать, применяя закон Био – Савара – Лапласа:
$$d bar{H}=frac{1}{4 pi} frac{I}{r^{3}} d bar{l} times bar{r}(2.1)$$
Учтем, что:
$$I d l=S j d l(2.2)$$
Если все заряды одинаковы (q), то плотность тока равна:
$$bar{j}=q n bar{v}(2.3)$$
заряд отрицательный, следовательно, направления векторов
$bar{j}$ и
$bar{v}$ противоположны. n – концентрация зарядов. Подставим формулу (2.3)
в (2.2), результат в (2.1) получаем:
$$d bar{H}=frac{1}{4 pi} frac{S q n d l}{r^{3}} bar{v} times bar{r}(2.4)$$
где dN=Sdln — количество заряженных частиц в отрезке dl. В таком случае, напряженность поля, которое создает один заряд:
$$bar{H}=frac{d bar{H}}{d N}=frac{1}{4 pi} frac{q}{r^{3}} bar{v} times bar{r}(2.4)$$
По условию задачи $bar{v} perp bar{r}$ , значит модуль напряжённости магнитного поля в точке А (рис.2) будет равен:
$$H=frac{1}{4 pi} frac{q v}{r^{2}}$$
Ответ. $H=frac{1}{4 pi} frac{q v}{r^{2}}$
Читать дальше: Формула напряженности электрического поля.
Magnetic field is defined as the region around a magnet which influences the other magnets. i.e. If we place a test magnet near a powerful magnet it experiences some force due to the powerful magnet the region close to the powerful magnet is called the magnetic field of the magnet. It is similar to the electric field of the charged particle and is represented by the magnetic field lines. The denser the magnetic field lines the higher the strength of the magnetic field.
Let’s learn about magnetic field lines formula, derivation, and others in detail in this article.
What is a Magnetic Field?
The region around any magnet or moving electric charge in which other magnets or moving charge experiences magnetic force is called the magnetic field of the magnet or moving charge.
Electromagnets, permanent magnets, and moving electric charges all produce the magnetic field. The magnetic field of these is explained by the magnetic field lines such as the electric field is explained using the electric field line.
Magnetic Field is the region around a magnetic material or a moving electric charge within which the force of magnetism acts. Magnetic field and Electric field are related to each other and a varying electric field produces a magnetic field similarly a varying magnetic field produces an electric field.
The magnetic field by a bar magnet is shown in the following image.
A magnetic field is represented by the symbol B or H.
Unit of Magnetic Field
Magnetic field is measured in Tesla and other units of measurement of the magnetic field are, (Newton-Second) / Coulomb.
Magnetic Field Strength Formula
The magnetic field around any electromagnet can easily be calculated using the formula,
where,
μ0 is the Permeability of Free Space
I is the Magnitude of Electric Current
r is the Distance in Meters
In terms of the number of turns per unit length of a solenoid, the formula for its magnetic field is given,
B = μ0nI
where,
μ0 is the Permeability of Free Space
n is the Number of Turns per unit length of Solenoid
I is the Magnitude of Electric Current
History of Magnetic Field
The history of the magnetic field is very old and as early as the Vedic age people in India know about the magnetic field of the Earth. But the real work in this field began in the late 13th century by French scholars who observed natural magnets with some iron needles and name their endpoints where the magnetic field interacts as the poles.
Then another major breakthrough happens when in 1785 Coulomb verifies that Earth has a magnetic field. After that Hans Christian Oersted a Danish physicist discovered that moving charge produces the magnetic field.
After that in 1831, famous English scientist Faraday demonstrated that a changing magnetic field generates an electric field. This effect came to be known as electromagnetic induction.
Next James Clerk Maxwell was the one who pioneer the field of electromagnetics with Maxwell’s equation which provides a relationship between electric current and magnetism.
Representation of Magnetic Field
The magnetic field around any magnetic material can easily be shown by two categories which are,
- Magnetic Field Vector
- Magnetic Field Lines
Magnetic Field Vector
We can represent a magnetic field with the help of the vector and these vectors are called magnetic field vectors. These vectors are drawn around the magnetic material and the direction of the magnetic field at any point is defined by the direction of the magnetic field vector at that point. The strength of the magnetic field can also be explained by magnetic field vector, the higher the magnetic field vector the higher the is the strength of the magnetic field.
Magnetic Field Lines
Magnetic field of the magnetic material can also be easily represented by magnetic field lines. These lines start from the North pole of the magnetic and end at the south pole of the material forming a complete closed loop. The direction of the magnetic field at any point is defined by the direction of the tangent at that point. The strength of the magnetic field is also explained by magnetic field lines, the denser the magnetic field line the higher the is the strength of the magnetic field.
The image given below shows the magnetic field lines around a bar magnet if similar poles are taken together and if the opposite poles are taken together.
Properties of Magnetic Field Lines
The important properties of the Magnetic Field Lines are,
- Magnetic field lines never intersect each other
- Strength of the magnetic field line at any point is directly proportional to the density of magnetic field lines at that point.
- Magnetic field lines always form a closed loop by starting from the North pole and ending at the south pole.
- Direction of the magnetic field at any point is defined by the direction of the tangent at that point.
Magnetic Field Intensity
The force experienced by the magnetic charge inside the magnetic field of the other magnet is defined as the magnetic field intensity. Vector H is used to represent the magnetic field intensity.
It is given by the formula
H = B/μ – M
where,
B is the magnetic flux density
M is the magnetization
μ is the magnetic permeability
SI unit for measuring the magnetic field intensity is Tesla. One tesla is defined as the magnetic field generating one newton of force per ampere of current per metre of conductor. It can also be measured in ampere/meter.
How does a Magnetic Field Originate?
A moving charge produces an electric field as well as the magnetic field. Both fields are perpendicular to each other thus we can say that moving charges produce a magnetic field.
In the general magnetic field is generated in two ways,
- Magnetic Field created by a Current-Carrying Conductor
- Magnetic field by the motion of Electrons around the Nuclei of Atoms
Let’s learn about these two in brief in this article.
Magnetic Field created by a Current-Carrying Conductor
A moving electric charge produces an electric field. Thus we can say that any conductor which allows current to flow produces an electric field which is true. Current flowing through a conductor produces a magnetic field but the field is very weak to be detected by us.
The value of the magnetic field by the current-carrying conductor is given by the formula,
B = (µoI)/(2πr)
where,
B is the magnetic field strength
µo is the permeability of the free space
I is the current passing through the conductor
r is the distance of the point where the magnetic field is calculated
Note: The value of µo = 4 π×10-7 Tm/A
Fleming Right Hand Rule is used to find the direction of the magnetic field produced by a current-carrying conductor.
For more detail, Magnetic Field due to Current Carrying Conductor
Magnetic Field by Motion of Electrons around the Nuclei of Atoms
We know that electrons revolve around the nucleus in a circular orbit called the shell. These revolving electrons produce the magnetic field.
So the question might arise that why we do not experience a magnetic field around every matter as every matter is made up of atoms. The answer is that the magnetic field by the various atoms cancels out each other generally and is aligned in some special cases in all those cases where the magnetic field is aligned we experience the magnetic force of the matter.
- The material in which the magnetic field of the various atoms cancels out is called Diamagnetic material.
- The material in which the magnetic field of the various atoms aligned themselves naturally and these materials are magnetic in nature is called Paramagnetic material.
- The material which arranges its magnetic field in the presence of an external magnetic field is called paramagnetic material.
Related Resources
- Electromagnetic Induction
- Faraday’s Law of Electromagnetic Induction
- Lenz’s Law
Solved Example on Magnetic Field Strength
Example 1: Find the MFS of a 2 m long solenoid of 2000 loops carrying a current of 1600 A.
Solution:
B = μ0nI
n = 2000/2
= 1000
Now,
B = (4π x 10−7 T m/A)(1000 m−1)(1600 A)
= 2.01 T
Example 2: Find the MFS of a 5 m long solenoid of 800 loops carrying a current of 1700 A.
Solution:
B = μ0NI
n = 800/5
= 160
Now,
B = (4π x 10−7 T m/A)(160 m-1)(1700 A)
= 0.314 T
Example 3: Find the MFS of a 12 m long solenoid of 700 loops carrying a current of 800 A.
Solution:
B = μ0NI
n = 700/12
= 58.33
B = (4π x 10−7 T m/A)(58.33 m-1)(800 A)
= 0.05864 T
FAQs on Magnetic Field Strength
Q1: What is the Magnetic Field?
Answer:
The region around a magnet, moving charge or electromagnet in which other charges experience the magnetic forces is called the Magnetic Field.
Q2: What is the Magnetic Flux Density?
Answer:
The amount of magnetic flux passing through an area perpendicular to the direction of magnetic flux is called the magnetic flux density. Magnetic Flux density is denoted by the symbol B and SI unit for measuring magnetic Flux Density is Tesla.
Q3: What is the Magnetic Field Intensity?
Answer:
Magnetic Field Intensity also called Magnetic Field Strength is defined as the ratio of the MMF required for creating a fixed magnetic flux density (B) in a particular material per unit length of that material.
Q4: What is the SI Unit of Magnetic Field Strength?
Answer:
The SI unit of magnetic field strength is Tesla.
Q5: What is the Strength of the Magnetic Field known as?
Answer:
The strength of the magnetic field is also known as magnetic field intensity or simply magnetic intensity.
Q6: What are Magnetic Flux Lines?
Answer:
The magnetic flux lines are defined as the magnetic field line passing through a particular area.
Q7: What is the cause of the Earth’s Magnetic Field?
Answer:
The Earth has a strong magnetic field which is formed by the revolution of the hot molten core of the Earth which is mostly formed by iron.
Q8: Are there magnetic fields in space?
Answer:
Yes, magnetic fields are present in space. We have found instances of magnetic field radiation from the centre of the milky way galaxy also Interstellar dust clouds are discovered which have magnetic fields.
Напряженность магнитного поля
Напряженность магнитного поля можно определить с помощью силы, которая действует на помещенный в поле пробный магнит.
Так как магнитные полюсы не существуют по отдельности, на северный и южный полюсы пробного магнита действуют противоположно направленные силы, и возникает момент пары сил.
Этот момент характеризует величину напряженности поля в данном месте.
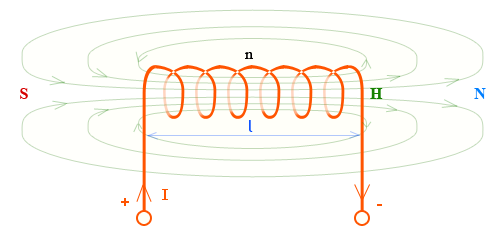
В магнитном поле цилиндрической катушки он прямо пропорционален числу витков и силе тока и обратно пропорционален длине катушки.
Направление вектора напряженности магнитного поля в каждой точке совпадает с направлением силовых линий. Внутри катушки (магнита) он направлен от южного полюса к северному,
вне катушки — от северного к южному.
Единица СИ напряженности магнитного поля
Единица СИ напряженности магнитного поля:
[ [H] = frac{Ампер}{Метр} ]
Эрстед — Единица напряженности магнитного поля
Единица напряженности магнитного поля Эрстед не принадлежит к системе СИ.
[ 1 Эрстед = frac{1000}{4π} frac{Ампер}{метр} ]
[ 1 frac{Ампер}{метр} = frac{4π}{1000} Эрстед ]
Напряженность магнитного поля в цилиндрической катушке
Напряженность магнитного поля в цилиндрической катушке
Если
| H | напряженность магнитного поля внутри цилиндрической катушки, | Ампер/метр |
|---|---|---|
| I | сила тока в катушке, | Ампер |
| n | число витков, | Ампер |
| l | длина катушки (т. е. силовых линий в области однородного поля), | метр |
то напряженность магнитного поля определяется формулой
[ H = frac{I n}{l} ]
Напряженность магнитного поля вокруг прямолинейного проводника
Напряженность Н магнитного поля прямолинейного проводника постоянна вдоль круговой силовой линии.
Если
| H | напряженность магнитного поля прямолинейного проводника, | Ампер/метр |
|---|---|---|
| I | сила тока в проводнике, | Ампер |
| r | расстояние от проводника в плоскости, перпендикулярной проводнику, | метр |
то напряженность магнитного поля определяется формулой
[ H = frac{I}{2πr} ]
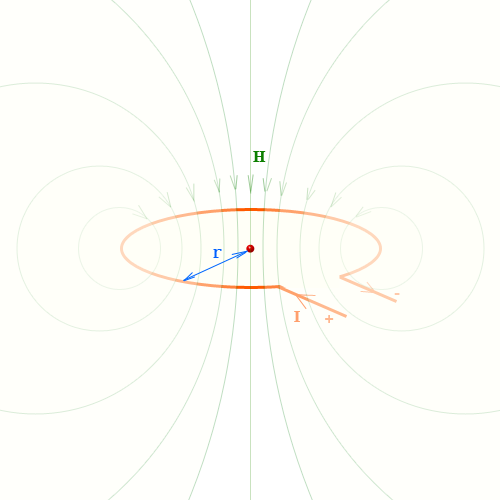
Напряженность магнитного поля в центре витка с током
Напряженность магнитного поля в центре витка с током
Если
| H | напряженность магнитного поля в центре витка с током, | Ампер/метр |
|---|---|---|
| I | сила тока в витке, | Ампер |
| r | радиус витка, | метр |
то напряженность магнитного поля определяется формулой
[ H = frac{I}{2r} ]
Напряженность магнитного поля |
стр. 645 |
|---|
Напряженность магнитного поля
Опыт показывает,
что магнитное поле, создаваемое
проводником с током в вакууме и в
какой-либо среде, будет различным. Это
объясняется тем, что в среде протекают
свои микротоки, которые обусловлены
движением электронов в атомах и молекулах.
Эти микротоки создают свое магнитное
поле. Вектор магнитной индукции
характеризует результирующее поле,
создаваемое всеми микро- и макротоками.
При одном и том же токе в проводнике и
прочих равных условиях величина вектора
В в различных средах будет разной.
Для характеристики
магнитного поля, создаваемого самим
макротоком, вводится вспомогательный
вектор напряженности магнитного поля,
не зависящий от свойств среды. Между
векторами индукции В и напряженности
Н существует зависимость: В = 0Н
= В0.
(В гауссовой системе
В = μН, в вакууме μ = 1 и В = Н).
— относительная
магнитная проницаемость среды, показывает,
во сколько раз индукция магнитного поля
в среде отличается от индукции в вакууме
(В0)
0
= 410-7
Н/м2
(Гн/м) – магнитная постоянная.
Закон Био-Савара-Лапласа
Магнитное поле
проводника с током зависит не только
от величины тока, но и от формы контура
с током. Так же как и в электростатике
для поля распределенных зарядов, можно
полагать, что результирующее поле Н
проводника с током – это векторная
сумма полей dH,
созданных отдельными элементами тока.
Только, в отличие от электростатики,
измерить и изучить поле отдельного
элемента тока невозможно, так как любой
постоянный ток течет по замкнутому
контуру.
Для линейных
проводников, толщина которых мала по
сравнению с расстоянием, на котором
определяется напряженность магнитного
поля, по закону Био-Савара-Лапласа
напряженность магнитного поля,
создаваемого элементом тока на расстоянии
r
от него, обратно пропорциональна квадрату
расстояния и прямо пропорциональна
величине элемента тока и синусу угла
между направлением тока и направлением
на точку, в которой определяется
напряженность
к – коэффициент
пропорциональности, зависит от выбора
системы единиц, в системе СГС к = 1, в СИ
к =
.

перпендикулярен плоскости, проходящей
через элемент тока и точку, в которой
определяется напряженность. Направление
его определяется по правилу буравчика
(или правого винта): если поступательное
движение буравчика совпадает с
направлением тока, то рукоятка описывает
окружности, касательные к которым
совпадают с направлением напряженности
(направлены по направлению движения
рукоятки).
На рисунке показано
сечение проводника, крестиком отмечено,
что ток направлен от нас. Линии
напряженности представляют собой
концентрические окружности.
Полная напряженность
магнитного поля, создаваемого проводником
с током, равна геометрической сумме
напряженностей, создаваемых всеми
элементами тока, и определяется с помощью
интегрирования.
Закон Био-Савара-Лапласа
был установлен для постоянного тока в
проводниках – тока проводимости.
Справедливость этого закона была
подтверждена и для других форм движения
электрических зарядов (конвекционные
токи, токи в вакууме). В случае распределенных
по объему токов выражение для элемента
тока можно записать idl
= jdsdl
=jdV.
Соседние файлы в папке физика механика лекции
- #
- #
- #
- #
Виталий Викторович Карабут
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Любой электрический ток окружает магнитное поле. Нетривиальным является вопрос о локализации собственной энергии тока, – находится она в проводнике, где перемещаются заряды, или в магнитом поле (веществе, которое окружает ток)?
Ответ на заданный вопрос получают при исследовании переменных магнитных полей или электромагнитных волн. В электромагнитной волне магнитные поля, переменные в пространстве и времени, могут существовать при отсутствии токов. Мы знаем, что электромагнитные волны переносят энергию, следовательно, можно сделать вывод о том, что энергия локализуется в магнитном поле.
Объемная плотность энергии магнитного поля
Допустим, что у нас имеется замкнутая тороидальная катушка. Индуктивность этой катушки:
$L=mu mu_{0}frac{N^{2}S}{l}left( 1 right)$, где:
- $mu $ – магнитная проницаемость вещества;
- $mu_{0}$ – магнитная постоянная;
- $N$ -количество витков;
- $l$ – длина катушки;
- $S$ – площадь поперечного сечения.
Собственную энергию тока, текущего в катушке найдем как:
$W=frac{LI^{2}}{2}=mu mu_{0}frac{N^{2}S}{l}frac{I^{2}}{2}left( 2 right)$
где величина $frac{NI}{l}=H$ – напряженность магнитного поля внутри тороида, значит формулу (2) представим в виде:
$W=mu mu_{0}frac{H^{2}V}{2}left( 3 right)$.
где $V=Sl$ — объем катушки.
Выражение (3) говорит нам о том, что если магнитное поле можно считать однородным, то его энергия прямо пропорциональна объему, который это поле занимает.
Следовательно, объемную плотность энергии магнитного поля определим как:
$w=mu mu_{0}frac{H^{2}}{2}left( 4 right)$
В случае неоднородности магнитного поля для вычисления его энергии, проводят его разбиение на малые элементы с объемом $dV$ (элементы такого размера, что в нем поле можно считать однородным). Энергия, которую несет каждый элемент поля, будет равна: $wdV$. Полную энергию произвольного магнитного поля можно найти как:
$W=intlimits_V {wdVleft( 5 right),} $
где интегрирование проводят по всему объему, который занимает поле.
«Плотность энергии магнитного поля и напряженность магнитного поля, формулы расчета» 👇
Ограничения применения формулы для вычисления плотности энергии магнитного поля
Все сказанное выше предполагало, что магнитная проницаемость вещества, в котором находится поле, остается неизменной. Вся работа источника тока переходит в энергию магнитного поля. Это абсолютно точно только для вакуума. Формула для объемной плотности энергии магнитного поля в виде (4) является приближенной, так как она не учитывает точно, что поле выполняет работу при намагничивании.
Предположение о неизменности магнитной проницаемости означает, что:
$vec{B}=mu mu_{0}vec{H}left( 6 right)$.
Замечание 1
Данная зависимость точна для многих веществ, парамагнетиков и диамагнетиков и неприменима для ферромагнетиков.
Применяя формулу (6) плотность энергии магнитного поля представим как:
$w=frac{B^{2}}{2mu_{0}}=frac{BH}{2}left( 7 right)$.
Замечание 2
Формулу (7), определяющую плотность энергии магнитного поля, можно использовать и для неоднородных магнитных полей.
Единицей измерения плотности энергии магнитного поля служит джоуль, деленный на кубический метр ( $frac{Дж}{м^{3}}$).
Напряженность магнитного поля
Напряженность магнитного поля является вспомогательной величиной, помогающей в математическом описании магнитного поля.
Вектор напряженности магнитного поля (H ⃗) можно рассматривать как комбинацию принципиально разных физических величин, часть из них относится к полю (слагаемое, содержащее вектор магнитной индукции), часть к веществу, и, следовательно, напряженность магнитного поля физическим смыслом не обладает:
$vec{H}=frac{vec{B}}{mu_{0}}-vec{P}_{m}left( 8 right)$,
где $vec{P}_{m}$ – вектор намагниченности (вектор интенсивности намагничения вещества). Однако вектор напряженности является количественной характеристикой магнитного поля, которая не зависит от магнитных свойств вещества, в котором его рассматривают. Применение $vec{H}$ упрощает количественные описания магнитного поля в веществе.
В однородном магнитном веществе напряженность магнитного поля определим как:
$vec{H}=frac{vec{B}}{mu mu_{0}}left( 9 right)$.
Важность данной физической величины заключается в том, что она не зависит от магнитных свойств вещества, в котором локализовано магнитное поле (в отличии от $vec{B}$).
Напряженность магнитного поля определяют:
- сила тока, создающая магнитное поле;
- геометрия объекта, по которому следует электрический ток (форма тела);
- расположение точки, в которой рассматривается поле относительно источник поля.
Для однородной магнитной среды направления векторов магнитной индукции и напряженности магнитного поля совпадают.
Напряжённость магнитного поля для постоянных токов разной конфигурации можно рассчитать, применяя закон Био-Савара-Лапласа:
$dH=frac{Idlsin propto }{4pi r^{2}}left( 10 right)$, где:
- $Idl$ – элемент тока на проводнике, который создает магнитное поле;
- $vec{r}$ – радиус – вектор, который провели от элемента тока в точку, в которой исследуем поле;
- $propto =hat{dvec{l}vec{r}}$ — угол между соответсвующим вектором и направлением течения тока;
- $dH$ – величина элементарного магнитного поля, которое в рассматриваемой точке создает элемент тока.
Уравнение (10) можно записать в векторной форме:
$dvec{H}=frac{I}{4pi r^{3}}left[ dvec{l}vec{r} right]left(11right)$.
В соответствии с правилами векторных произведений мы получаем, что $dvec{H}$ нормален плоскости, в которой находятся векторы $dvec{l}$ и $vec{r}$.
Вектор напряженности магнитного поля подчиняется принципу суперпозиции, поэтому напряженность магнитного поля, которое создает весь проводник с постоянным током, в рассматриваемой точке равна:
$vec{H}=frac{I}{4pi }int frac{left[ dvec{l}vec{r} right]}{r^{3}}left( 12 right)$.
Закон (11) бы эмпирически получен учеными Ж.Б. Био и Ф. Саваром при исследованиях действия электрических токов на магнитную стрелку. П.С. Лаплас провел анализ результатов экспериментов Био и Савара понял, что напряженность магнитного поля тока является суммой напряженностей полей, которые создают отдельные токи.
Закон полного тока
В некоторых случаях для нахождения напряженности магнитного поля вместо закона Био-Савара-Лапласа применяют закон полного тока, который формулируется в следующем виде:
$oint {H_{l}dl=sum {I_{m}left( 13 right),} }$
где $oint {H_{l}dl} $ — циркуляция вектора напряженности по замкнутому контуру $l$, $sum I_{m}$ — сумма токов (с учетом знака), которые охватывает контур $l$.
Рисунок 1. Контур. Автор24 — интернет-биржа студенческих работ
Так, если контур $l$ на рис.1 охватывает четыре тока, при этом токи $I_1$, $I_2,$ $I_3$ , больше нуля, $I_4$
$oint {H_{l}dl} =I_{1}+I_{2}+I_{3}-I_{4}(14).$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме