Определение.
Центральный угол правильного многоугольника — это угол, под которым сторона многоугольника видна из его центра.

∠AOB — центральный угол правильного восьмиугольника.
Около любого правильного многоугольника можно описать окружность, центр которой совпадает с центром этого многоугольника. Если у многоугольника n сторон, то центральных углов у него также n и все они равны между собой.
Градусная мера всей окружности — 360º, следовательно, градусная мера каждой дуги окружности, на которую окружность разбивают вершины n-угольника, равна
Так как центральный угол равен дуге, на которую от опирается, то и каждый из центральных углов равен 360º:n.
Примеры

равен 360º:3=120º.

равен 360º:4=90º.

равен 360º:6=60º.

равен 360º:8=45º.
Углы правильного многоугольника делятся на :
- центральный угол;
- внутренний угол;
- внешний угол.
Сумма внутреннего и внешнего угла равна (180°).
Сумма внутренних углов правильного многоугольника с (n) сторонами равна:
((n — 2)180°)
Для нахождения внутреннего угла используют формулу:
(alpha = frac{{{{180}^o}(n — 2)}}{n})
(n)— число сторон
Для нахождения внешнего угла используют формулу:
(varphi = frac{{{{360}^o}}}{n})
(n)— число сторон
Для нахождения центрального угла используют формулу:
(beta = frac{{{{360}^o}}}{n})
(n)— число сторон
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
From Wikipedia, the free encyclopedia
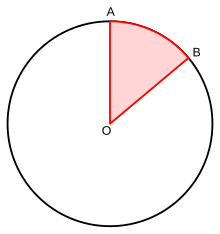
Angle AOB is a central angle
A central angle is an angle whose apex (vertex) is the center O of a circle and whose legs (sides) are radii intersecting the circle in two distinct points A and B. Central angles are subtended by an arc between those two points, and the arc length is the central angle of a circle of radius one (measured in radians).[1] The central angle is also known as the arc’s angular distance. The arc length spanned by a central angle on a sphere is called spherical distance.
The size of a central angle Θ is 0° < Θ < 360° or 0 < Θ < 2π (radians). When defining or drawing a central angle, in addition to specifying the points A and B, one must specify whether the angle being defined is the convex angle (<180°) or the reflex angle (>180°). Equivalently, one must specify whether the movement from point A to point B is clockwise or counterclockwise.
Formulas[edit]
If the intersection points A and B of the legs of the angle with the circle form a diameter, then Θ = 180° is a straight angle. (In radians, Θ = π.)
Let L be the minor arc of the circle between points A and B, and let R be the radius of the circle.[2]
Central angle. Convex. Is subtended by minor arc L
If the central angle Θ is subtended by L, then
Proof (for degrees)
The circumference of a circle with radius R is 2πR, and the minor arc L is the (Θ/360°) proportional part of the whole circumference (see arc). So:
Central angle. Reflex. Is not subtended by L
Proof (for radians)
The circumference of a circle with radius R is 2πR, and the minor arc L is the (Θ/2π) proportional part of the whole circumference (see arc). So
If the central angle Θ is not subtended by the minor arc L, then Θ is a reflex angle and
If a tangent at A and a tangent at B intersect at the exterior point P, then denoting the center as O, the angles ∠BOA (convex) and ∠BPA are supplementary (sum to 180°).
Central angle of a regular polygon[edit]
A regular polygon with n sides has a circumscribed circle upon which all its vertices lie, and the center of the circle is also the center of the polygon. The central angle of the regular polygon is formed at the center by the radii to two adjacent vertices. The measure of this angle is 
See also[edit]
- Inscribed angle
- Great-circle navigation
References[edit]
- ^ Clapham, C.; Nicholson, J. (2009). «Oxford Concise Dictionary of Mathematics, Central Angle» (PDF). Addison-Wesley. p. 122. Retrieved December 30, 2013.
- ^ «Central angle (of a circle)». Math Open Reference. 2009. Retrieved December 30, 2013. interactive
External links[edit]
- «Central angle (of a circle)». Math Open Reference. 2009. Retrieved December 30, 2013. interactive
- «Central Angle Theorem». Math Open Reference. 2009. Retrieved December 30, 2013. interactive
- Inscribed and Central Angles in a Circle
A центральный угол — это угол, вершина (вершина) которого является центром O окружности, а стороны (стороны) равны радиусам, пересекающий круг в двух различных точках A и B. Центральные углы стянуты дугой между этими двумя точками, а длина дуги равна центральный угол окружности радиуса один (измеряется в радианах ). Центральный угол также известен как угловое расстояние.
дуги. Размер центрального угла Θ составляет 0 ° < Θ < 360° or 0 < Θ < 2π (radians). When defining or drawing a central angle, in addition to specifying the points A and B, one must specify whether the angle being defined is the convex angle (<180°) or the reflex angle (>180 °). Равным образом необходимо указать, будет ли движение от точки A к точке B по часовой стрелке или против часовой стрелки.
Содержание
- 1 Формулы
- 2 Центральный угол правильного многоугольника
- 3 См. Также
- 4 Ссылки
- 5 Внешние ссылки
Формулы
Если точки пересечения А и В сторон угла с окружностью образуют диаметр, тогда Θ = 180 ° — это прямой угол. (В радианах Θ = π.)
Пусть L будет вспомогательной дугой окружности между точками A и B, и пусть R будет радиусом окружности круг.
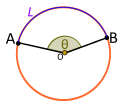 |
| Центральный угол. Выпуклый. Подчиняется малой дугой L |
Если центральный угол Θ ограничен L, то
- 0 ∘ < Θ < 180 ∘, Θ = ( 180 L π R) ∘ = L R. {displaystyle 0^{circ }<Theta <180^{circ },,,,Theta =left({frac {180L}{pi R}}right)^{circ }={frac {L}{R}}.}
- Доказательство (для градусов): длина окружности с радиусом R равна 2πR, а малая дуга L представляет собой (Θ / 360 °) пропорциональную часть всей окружности (см. arc ). Итак:
- L = Θ 360 ∘ ⋅ 2 π R ⇒ Θ = (180 L π R) ∘. { displaystyle L = { frac { Theta} {360 ^ { circ}}} cdot 2 pi R , Rightarrow , Theta = left ({ frac {180L} { pi R} } right) ^ { circ}.}
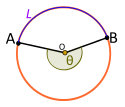 |
| Центральный угол. Рефлекс. Не подтверждается L |
- Доказательство (для радиан): длина окружности окружности с радиусом R равна 2πR, а малая дуга L является (Θ / 2π) пропорциональной частью всей окружности ( см. arc ). Итак,
- L = Θ 2 π ⋅ 2 π R ⇒ Θ = L R. { displaystyle L = { frac { Theta} {2 pi}} cdot 2 pi R , Rightarrow , Theta = { frac {L} {R}}.}
Если центральный угол Θ, а не, под которым проходит вспомогательная дуга L, тогда Θ является углом отражения и
- 180 ∘ < Θ < 360 ∘, Θ = ( 360 − 180 L π R) ∘ = 2 π − L R. {displaystyle 180^{circ }<Theta <360^{circ },,,,Theta =left(360-{frac {180L}{pi R}}right)^{circ }=2pi -{frac {L}{R}}.}
Если касательная в точке A и касательная в точке B пересекаются во внешней точке P, затем обозначая центр как O, углы ∠BOA (выпуклый) и ∠BPA являются дополнительными (в сумме до 180 °).
Центральный угол правильного многоугольника
A правильный многоугольник с n сторонами имеет описанную окружность, на которой лежат все его вершины, и центр окружности также является центром многоугольника. Центральный угол правильного многоугольника образован в центре радиусами двух соседних вершин. Измерение этого угла составляет 2 π / n. { displaystyle 2 pi / n.}
См. также
Ссылки
Внешние ссылки
- «Центральный угол (круга) «. Открытый справочник по математике. 2009. Получено 30 декабря 2013 г. интерактивный
- «Теорема о центральном угле». Открытый справочник по математике. 2009 г. Получено 30 декабря 2013 г. интерактивный
- Вписанные и центральные углы в круге
���������� �������������
�������� �����: �������������, ���������� �������������, �������, ����, ���������, ��������� ����������
�������� ������������� ���������� ����������, ���� � ���� ��� ������� ����� � ��� ���� �����.
������� ����������� �������������� ���������� �����, �������������� �� ���� ��� ������ � ���� ��� ������.
����������� ����� ����������� �������������� ���������� ����, ��� ������� ����� ������� �� ��� ������.
 |
�������� ����������� ��������������.
|
�������
- ����� R — ������ ��������� ������ ����������� �������������� ����������, ����� ������ ��������� ���������� ����� $$r = R cdot cosfrac{pi}{n}$$, � ����� ������� �������������� ����� $$a = 2R cdot sinfrac{pi}{n}$$.
- ������� ����������� �������������� � ������ ������ n � ������ ������� a ���������� $$S = frac{n}{4}a^{2} cdot ctgfrac{pi}{n}$$.
- ������� ����������� �������������� � ������ ������ n, ���������� � ���������� ������� R ���������� $$S = frac{n}{2}R^{2} cdot sinfrac{2pi}{n}$$.
- ������� ����������� �������������� � ������ ������ n, ���������� ������ ���������� ������� r ���������� $$S = nr^{2} cdot tgfrac{pi}{n}$$.

��. �����:
��������� ����������,
��������� ����������,
�������� ����ң���������,
������������ �������� �������������







