Как найти величину центрального угла правильного многоугольника

На этой странице находится вопрос Как найти внутренний и центральный угла правильного двенадцатиугольника?. Здесь же – ответы на него,
и похожие вопросы в категории Геометрия, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.

Угол AOB — это центральный угол

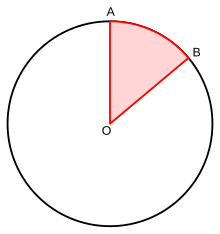
A центральный угол — это угол, вершина (вершина) которого является центром O окружности, а стороны (стороны) равны радиусам, пересекающий круг в двух различных точках A и B. Центральные углы стянуты дугой между этими двумя точками, а длина дуги равна центральный угол окружности радиуса один (измеряется в радианах ). Центральный угол также известен как угловое расстояние.

дуги. Размер центрального угла Θ составляет 0 ° < Θ < 360° or 0 < Θ < 2π (radians). When defining or drawing a central angle, in addition to specifying the points A and B, one must specify whether the angle being defined is the convex angle (<180°) or the reflex angle (>180 °). Равным образом необходимо указать, будет ли движение от точки A к точке B по часовой стрелке или против часовой стрелки.

Содержание

• 1 Формулы
• 2 Центральный угол правильного многоугольника
• 3 См. Также
• 4 Ссылки
• 5 Внешние ссылки

Формулы

Если точки пересечения А и В сторон угла с окружностью образуют диаметр, тогда Θ = 180 ° — это прямой угол. (В радианах Θ = π.)

Пусть L будет вспомогательной дугой окружности между точками A и B, и пусть R будет радиусом окружности круг.

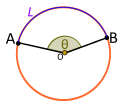Центральный угол. Выпуклый. Подчиняется малой дугой L

Если центральный угол Θ ограничен L, то

0 ∘ < Θ < 180 ∘, Θ = ( 180 L π R) ∘ = L R. {displaystyle 0^{circ }<Theta <180^{circ },,,,Theta =left({frac {180L}{pi R}}right)^{circ }={frac {L}{R}}.}

Доказательство (для градусов): длина окружности с радиусом R равна 2πR, а малая дуга L представляет собой (Θ / 360 °) пропорциональную часть всей окружности (см. arc ). Итак:

L = Θ 360 ∘ ⋅ 2 π R ⇒ Θ = (180 L π R) ∘. { displaystyle L = { frac { Theta} {360 ^ { circ}}} cdot 2 pi R , Rightarrow , Theta = left ({ frac {180L} { pi R} } right) ^ { circ}.}

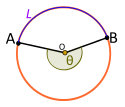Центральный угол. Рефлекс. Не подтверждается L

Доказательство (для радиан): длина окружности окружности с радиусом R равна 2πR, а малая дуга L является (Θ / 2π) пропорциональной частью всей окружности ( см. arc ). Итак,

L = Θ 2 π ⋅ 2 π R ⇒ Θ = L R. { displaystyle L = { frac { Theta} {2 pi}} cdot 2 pi R , Rightarrow , Theta = { frac {L} {R}}.}

Если центральный угол Θ, а не, под которым проходит вспомогательная дуга L, тогда Θ является углом отражения и

180 ∘ < Θ < 360 ∘, Θ = ( 360 − 180 L π R) ∘ = 2 π − L R. {displaystyle 180^{circ }<Theta <360^{circ },,,,Theta =left(360-{frac {180L}{pi R}}right)^{circ }=2pi -{frac {L}{R}}.}

Если касательная в точке A и касательная в точке B пересекаются во внешней точке P, затем обозначая центр как O, углы ∠BOA (выпуклый) и ∠BPA являются дополнительными (в сумме до 180 °).

Центральный угол правильного многоугольника

A правильный многоугольник с n сторонами имеет описанную окружность, на которой лежат все его вершины, и центр окружности также является центром многоугольника. Центральный угол правильного многоугольника образован в центре радиусами двух соседних вершин. Измерение этого угла составляет 2 π / n. { displaystyle 2 pi / n.}

См. также

Ссылки

Внешние ссылки

• «Центральный угол (круга) «. Открытый справочник по математике. 2009. Получено 30 декабря 2013 г. интерактивный
• «Теорема о центральном угле». Открытый справочник по математике. 2009 г. Получено 30 декабря 2013 г. интерактивный
• Вписанные и центральные углы в круге