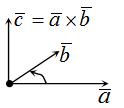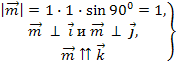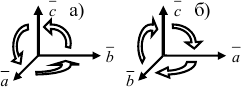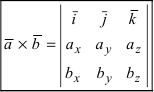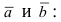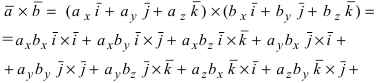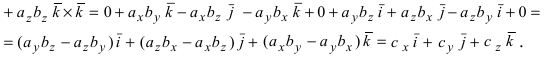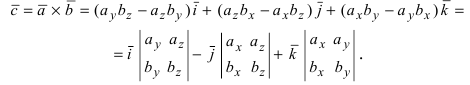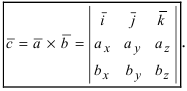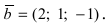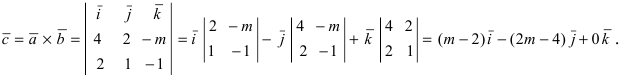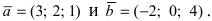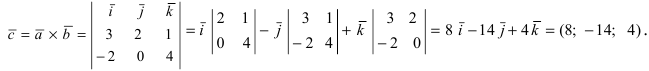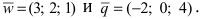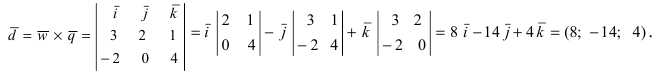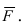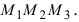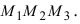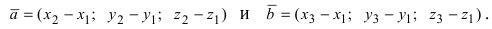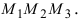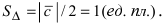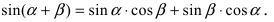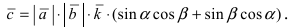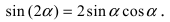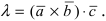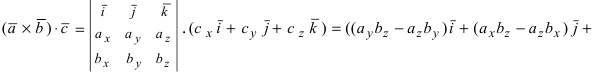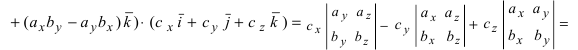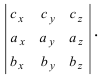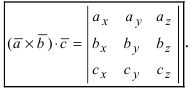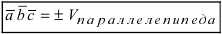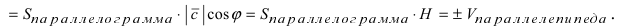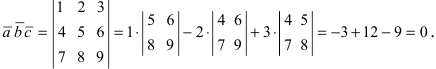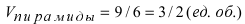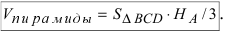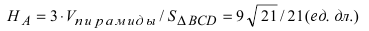Векторное произведение векторов
Определение
| Определение |
|
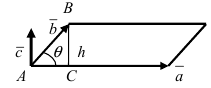
Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $. |
Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.
Формула
| Формула 1 |
|
Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле: $$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$ |
| Формула 2 |
|
В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$ где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $. |
Определитель во второй формуле можно раскрыть по первой строке:
$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 — a_3 b_2) — overline{j} (a_1 b_3 — a_3 b_1) + overline{k} (a_1 b_2 — a_2 b_1) $$
Итого вторая формула приобретает окончательный короткий вид:
$$ overline{a} times overline{b} = (a_2 b_3 — a_3 b_2; a_3 b_1 — a_1 b_3; a_1 b_2 — a_2 b_1) $$
Свойства
- При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
- Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
- $$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$
Примеры решений
| Пример 1 |
|
Найти векторное произведение векторов, заданных координатами $$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$ |
| Решение |
|
Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) — overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} — overline{j} + 3overline{k} $$ Полученный ответ можно записать в удобном виде: $$ overline{a} times overline{b} = (5, -1, 3) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ overline{a} times overline{b} = (5, -1, 3) $$ |
Геометрический смысл
- Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
- Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
- Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.
| Пример 2 |
| Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$ |
| Решение |
|
Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов. Находим определитель: $$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) — overline{j}(2+3) + overline{k}(4+1) = -5overline{i} — 5overline{j} + 5overline{k} $$ Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора: $$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$ По формуле нахождения площади треугольника имеем: $$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$ |
| Ответ |
| $$ S_Delta = 4.33 $$ |
Определение
1.
Векторным произведением двух ненулевых
неколлинеарных векторов
называется вектор
,
такой что:
-
длина
вектора
равна произведению длин этих векторов
на синус угла между ними:
-
вектор
перпендикулярен этим векторам
и
-
векторы
,
образуют базис того же типа, что и
векторы
(правый базис).
Если
же векторы
коллинеарны или хотя бы один из них
нулевой вектор, то их векторное
произведение есть нулевой вектор
Обозначение:
или

Теорема
1.
(О геометрическом смысле векторного
произведения). Длина векторного
произведения двух ненулевых неколлинеарных
векторов равна площади параллелограмма,
построенного на этих векторах.
Доказательство.

Следствие.
Площадь ∆
C
выражается формулой:
Теорема
доказана.
Теорема
2.
Для того, чтобы два вектора
были коллинеарны, необходимо и достаточно,
чтобы их векторное произведение было
нулевым вектором:
Доказательство.
Необходимость.
Пусть
,
тогда согласно определению 1 либо
,
либо
,
либо
,
либо
,
либо
.
Во всех этих случаях вектора
коллинеарны по определению.
Достаточность.
Пусть
,
тогда снова по определению 1
Теорема
доказана.
Следующие
три теоремы сформулируем без доказательства.
Теорема
3.
Векторное произведение антикоммутативно
(антисимметрично):
Теорема
4.
Векторное произведение ассоциативно
относительно скалярного множителя:
Теорема
5.
Векторное произведение дистрибутивно
относительно суммы векторов:
Теорема
6.
Доказательство.
Доказательство
следует из определения 1.
Пусть,
например,
,
тогда имеем:
⟹
⟹
.
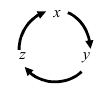
Замечание.
Достаточно запомнить первую формулу,
вторая получается из первой, а третья
– из второй с помощью круговой или
циклической замены векторов

Теорема
7. (О
координатах векторного произведения).
Если в прямоугольном базисе (ортогональном)
(
и
,
то

Доказательство.
Воспользуемся
определением координат вектора и
теоремами 3, 4, 5 и 6:

(см.
определение определителя 3-его порядка)
Теорема
доказана.
Пример.
Вычислить площадь треугольника с
вершинами А(-1,0,-1), В(0,2,-3), С(4,4,1).
Решение.
,

По
следствию из теоремы 1 имеем:
(кв.ед.).
§24. Смешанное произведение векторов
Определение
1.
Смешанным произведением трёх векторов
называется число, равное скалярному
произведению векторного произведения
векторов
на вектор
.
Обозначение.
(
Можно
показать, что
Теорема
1. Абсолютная
величина (модуль) смешанного произведения
трёх неколлинеарных векторов равна
объёму параллелепипеда, построенного
на этих векторах.
Доказательство.

Введём
обозначения:
,
∠(
Тогда
имеем:
(
(1)
По
теореме 1 из §2 имеем:
(2)
Пусть
— высота параллелепипеда (
.
Из
∆
Случай
1:
Случай
2:
В
обоих случаях получаем:
.
(3)

Подставляя
значения (2) и (3) в формулу (1), окончательно
получаем:
(
Итак,
.
(4)
Теорема
доказана.
Следствие
1.
. (5)
Доказательство
следствия.
Следствие
доказано.
Следствие
2. Знак
смешанного произведения тройки
некомпланарных
векторов соответствует
её ориентации,
то есть если тройка правая, то
,
если тройка левая, то
Следствие
3.
Три вектора коллинеарны тогда и только
тогда, когда их смешанное произведение
равно нулю.
Доказательство
следствия.
Если
тройка векторов коллинеарная, то объём
параллелепипеда, построенного на
векторах этой тройки, равно нулю. Обратно,
если VПАР
= 0,
то вектора тройки коллинеарны.
Следствие
доказано.
Замечание.
Из трёх неколлинеарных
векторов
,
можно составить шесть
упорядоченных троек:
причём первые три тройки векторов
образуют правый
базис,
а последние три – левый
базис
(большой, указательный, средний пальцы).
При
перестановке любых двух векторов в
каждой из первых троек получается копия
– либо из трёх последних, поэтому в
результате меняется ориентация
упорядоченных троек векторов.
Если
в упорядоченной тройке векторов
осуществить циклическую перестановку
векторов, то непосредственной проверкой
убедимся, что при этом ориентация
упорядоченной тройки векторов не
меняется.
Из
теоремы 1 следует, что при перестановке
векторов в упорядоченной тройке модуль
скалярного произведения не меняется,
так как во всех случаях он равен объёму
одного и того же параллелепипеда. Так
же от скалярного произведения зависит
ориентации
тройки
векторов.
Следствие
4.
(6)
Пример.
Используя
формулу (6), то есть определение 1
дано
корректно.
Теорема
2.
Теорема
3.
Доказательства
теорем 2 и 3 следуют из свойств определителя
3-го порядка; мы их опускаем (см. теорему
4).
Теорема
4.
Если в ортонормированном базисе
то
(7)
Доказательство.
.
Теорема
доказана.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Векторное и смешанное произведения векторов в векторной алгебре
Векторное произведение
Определение: Тройка векторов
Пример:
Рис. 13. Правая (а) и левая (б) тройки векторов.
Определение: Векторным произведением векторов 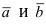
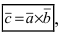
Замечание: Из определения векторного произведения следует, что направление вектора 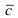
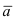
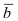
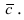
Рис. 14. Площадь параллелограмма, определяющего длину вектора 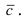
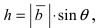
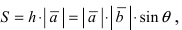
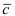
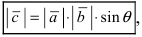
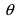
Векторное произведение векторов обладает следующими свойствами:
Замечание: Свойство 4. определяет второе условие коллинеарности векторов.
Формула для векторного произведения векторов через проекции перемножаемых векторов
Теорема: Пусть 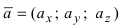
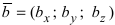
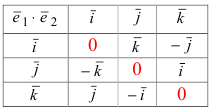
Доказательство: Запишем вектора 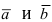
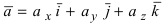
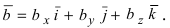
Используя эту таблицу, вычислим векторное произведение векторов
Отсюда следует, что 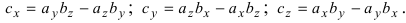
Рис. 15. Циклический переход от одной координаты к другой.
Для нахождения, например проекции 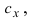
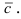
Полученное выражение представляет собой раскрытие определителя III порядка по элементам первой строки, то есть окончательно можно записать, что
Пример:
Найти, при каком значении параметра m вектор 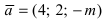
Решение:
Согласно свойству 4. для векторного произведения (пункт 1 Лекция № 6) найдем векторное произведение заданных векторов
Так как вектор 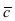
- Заказать решение задач по высшей математике
Пример:
Найти векторное произведение векторов
Решение:
Пример:
Найти векторное произведение векторов
Решение:
Приложения векторного произведения
1. Физика. Пусть точка начала вектора 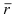
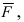
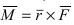
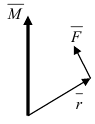
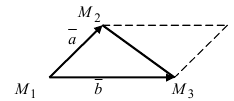
2. Геометрия. Пусть даны три разные точки 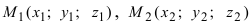
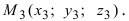
Введем в рассмотрение вектора 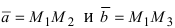
Рис. 17. Площадь треугольника
Проекции этих векторов равны:
Так как площадь треугольника составляет половину от площади параллелограмма, площадь которого равна модулю векторного произведения векторов 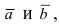
Пример:
Даны три точки 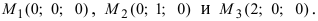
Решение:
Введем в рассмотрение вектора 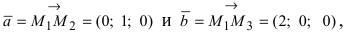
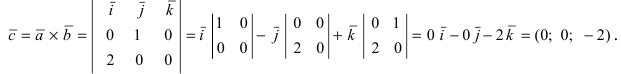
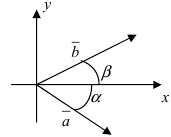
3. Тригонометрия. Выведем формулу для
Пусть в плоской декартовой системе координат даны векторы 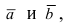
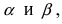
Рис. 18. Синус суммы двух углов.
Проекции векторов равны 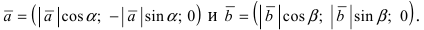
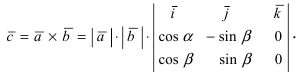
Длина этого вектора равна 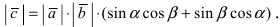
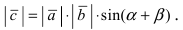
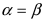
Смешанное произведение векторов
Определение: Смешанным произведением векторов 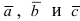
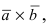
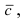
Получим формулу для вычисления смешанного произведения
Обменяв местами первую строку со второй, а затем и с третьей, получим окончательную формулу
Таким образом, смешанное произведение векторов представляет собой определитель III порядка, откуда следуют его свойства:
1. 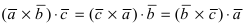
2. Смешанное произведение векторов 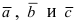
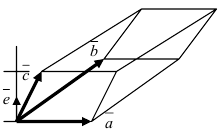
Рис. 19. Объем параллелепипеда, построенного на векторах
Так как
3. Если вектора 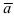
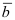
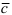
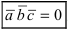
Замечание: Свойство 3. определяет условие компланарности трех векторов, т.е. если 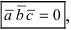
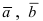
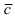
Пример:
Доказать, что вектора 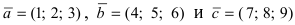
Решение:
Согласно формуле, определяющей смешанное произведение векторов, имеем
Пример:
Даны 4 точки 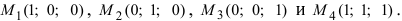
Решение:
Составим векторы 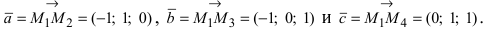
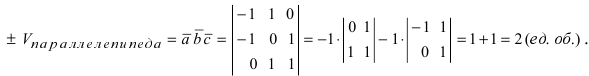
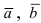
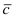
Пример:
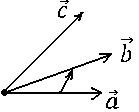
Чему равен объём пирамиды с вершинами А, В, С и D (координаты точек А, В, С и D взять из VIII.). Найти длину высоту, которая опущена из точки А на основание BCD.
Решение:
Объём пирамиды равен 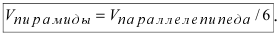
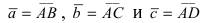
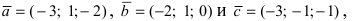
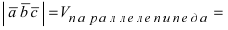
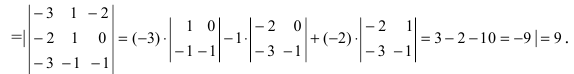
С другой стороны, её объём по формуле из средней школы равен
Вычислим площадь треугольника BCD, лежащего в основании пирамиды: 
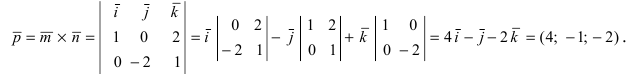
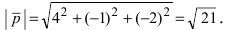
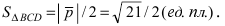
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Матричный метод
- Экстремум функции
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства