Электромагнитная
сила, действующая на заряженную частицу,
складывается из сил, действующих со
стороны электрического и магнитного
полей:
. (3.2)
Силу,
определяемую формулой (3.2), называют
обобщенной силой Лоренца. Учитывая
действие двух полей, электрического и
магнитного, говорят, что на заряженную
частицу действует электромагнитное
поле.
Рассмотрим
движение заряженной частицы в одном
только электрическом поле. При этом
здесь и далее предполагается, что частица
нерелятивистская, т.е. ее
скорость существенно меньше
скорости света. На частицу действует
только электрическая составляющая
обобщенной силы Лоренца
.
Согласно второму закону Ньютона частица
движется с ускорением:
,
(3.3)
которое
направленно вдоль вектора
в случае положительного заряда и против
векторав случае отрицательного заряда.
Разберем
важный случай движения заряженной
частицы в однородном электрическом
поле. В этом случае частица движется
равноускоренно ().
Траектория движения частицы зависит
от направления ее начальной скорости.
Если начальная скорость равна нулю или
направлена вдоль вектора,
движение частицы прямолинейное и
равноускоренное. Если же начальная
скорость частицы направлена под углом
к вектору,
то траекторией движения частицы будет
парабола. Траектории движения заряженной
частицы в однородном электрическом
поле такие же, как и траектории свободно
(без сопротивления воздуха) падающих
тел в гравитационном поле Земли, которое
вблизи поверхности Земли можно считать
однородным.
Пример
3.1. Определить
конечную скорость частицы массой
и зарядом
,
пролетевшей в однородном электрическом
полерасстояние
.
Начальная скорость частицы равна нулю.
Решение.
Так как поле однородно, а начальная
скорость частицы равна нулю, движение
частицы будет прямолинейным равноускоренным.
Запишем уравнения прямолинейного
равноускоренного движения с нулевой
начальной скоростью:

.
Подставим
величину ускорения из уравнения (3.3) и
получим:
.
В
однородном поле
(см. 1.21). Величину
называют ускоряющей разностью потенциалов.
Таким образом, скорость, которую набирает
частица, проходя ускоряющую разность
потенциалов:
.
(3.4)
При
движении в неоднородных электрических
полях ускорение заряженных частиц
переменное, и траектории будут более
сложными. Однако, задачу о нахождении
скорости частицы, прошедшей ускоряющую
разность потенциалов
,
можно решить исходя из закона сохранения
энергии. Энергия движения заряженной
частицы (кинетическая энергия) изменяется
за счет работы электрического поля:
.
Здесь
использована формула (1.5) для работы
электрического поля по перемещению
заряда
.
Если начальная скорость частицы равна
нулю ()
или мала по сравнению с конечной
скоростью, получим:,
откуда следует формула (3.4). Таким образом,
эта формула остается справедливой и в
случае движения заряженной частицы в
неоднородном поле. В этом примере
показаны два способа решения физических
задач. Первый способ основан на
непосредственном применении законов
Ньютона. Если же действующие на тело
силы переменны, бывает более целесообразным
использование второго способа, основанного
на законе сохранения энергии.
Теперь
рассмотрим движение заряженных частиц
в магнитных полях. Изменение кинетической
энергии частицы в магнитном поле могло
бы произойти только за счет работы силы
Лоренца:
.
Но работа силы Лоренца всегда равна
нулю, значит кинетическая энергия
частицы, а вместе с тем и модуль ее
скорости не изменяются. Заряженные
частицы движутся в магнитных полях с
постоянными по модулю скоростями. Если
электрическое поле может быть ускоряющим
по отношению к заряженной частице, то
магнитное поля может быть только
отклоняющим, т. е. изменять лишь направление
ее движения.
Рассмотрим
варианты траекторий движения заряда в
однородном поле.
1.
Вектор магнитной индукции параллелен
или антипараллелен начальной скорости
заряженной частицы. Тогда из формулы
(3.1) следует
.
Следовательно, частица будет двигаться
прямолинейно и равномерно вдоль линий
магнитного поля.
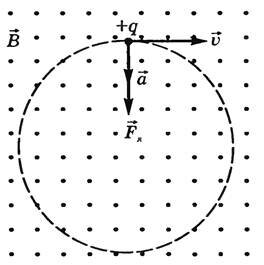
2.
Вектор магнитной индукции
перпендикулярен начальной скорости
частицы (на рис. 3.2 вектор магнитной
индукции направлен за плоскость чертежа).
Второй закон Ньютона для частицы имеет
вид:
или
.
Сила
Лоренца постоянна по величине и направлена
перпендикулярно скорости и вектору
магнитной индукции. Значит, частица
будет двигаться все время в одной
плоскости. Кроме того, из второго закона
Ньютона следует, что и ускорение частицы
будет постоянно по величине и
перпендикулярно скорости. Это возможно
только тогда, когда траектория частицы
– окружность, а ускорение частицы
центростремительное. Подставляя во
второй закон Ньютона величину
центростремительного ускорения
и величину силы Лоренца
,
находим радиус окружности:
.
(3.5)
Отметим,
что период вращения частицы не зависит
от ее скорости:

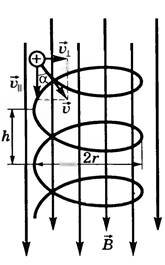
3. В общем случае
вектор магнитной индукции может быть
направлен под некоторым углом
к начальной скорости частицы (рис. 3.3).
Прежде всего, отметим еще раз, что
скорость частицы по модулю остается
постоянной и равной величине начальной
скорости.
Скоростьможно разложить на две составляющие:
параллельную вектору магнитной индукциии перпендикулярную вектору магнитной
индукции.
Ясно,
что если бы частица влетела в магнитное
поле, имея только составляющую
,
то она в точности как в случае 1 двигалась
бы равномерно по направлению вектора
индукции.
Если
бы частица влетела в магнитное поле,
имея одну только составляющую скорости
,
то она оказалась бы в тех же условиях,
что и в случае 2. И, следовательно,
двигалась бы по окружности, радиус
которой определяется опять-таки из
второго закона Ньютона:
.
Таким
образом, результирующее движение частицы
представляет собой одновременно
равномерное движение вдоль вектора
магнитной индукции со скоростью
и равномерное вращение в плоскости,
перпендикулярной вектору магнитной
индукции со скоростью.
Траектория такого движения представляет
собой винтовую линию или спираль (см.
рис. 3.3). Шаг спирали– расстояние, пролетаемое частицей
вдоль вектора индукции за время одного
оборота:
.
Откуда
известны массы мельчайших заряженных
частиц (электрона, протона, ионов)? Каким
образом удается их «взвесить» (ведь, на
весы их не положишь!)? Уравнение (3.5)
показывает, что для определения массы
заряженной частицы нужно знать радиус
ее трека при движении в магнитном поле.
Радиусы треков мельчайших заряженных
частиц определяют с помощью камеры
Вильсона, помещенной в магнитное поле,
или с помощью более совершенной
пузырьковой камеры. Принцип их работы
прост. В камере Вильсона частица движется
в пересыщенном водяном паре и является
ядром конденсации пара. Микрокапельки,
конденсирующиеся при пролете заряженной
частицы, отмечают ее траекторию. В
пузырьковой камере (изобретенной лишь
полвека назад американским физиком Д.
Глейзером) частица движется в перегретой
жидкости, т.е. нагретой выше точки ее
кипения. Это состояние неустойчиво и
при пролете частицы происходит вскипание,
вдоль ее следа образуется цепочка
пузырьков.
Подобную
картину можно наблюдать, бросив в стакан
с пивом крупинку поваренной соли: падая,
она оставляет след из пузырьков газа.
Пузырьковые камеры являются важнейшим
инструментом для регистрации мельчайших
заряженных частиц, являясь по сути,
основными информативными приборами
экспериментальной ядерной физики.
Соседние файлы в папке Методички_Общая физика
- #
- #
- #
- #
- #
- #
- #
- #
Движение заряженных частиц в электрических и магнитных полях
На заряженную частицу в электростатическом поле действует кулоновская сила, которую можно найти, зная напряженность поля в данной точке[~ vec F = q vec E]. Эта сила сообщает ускорение (~ vec a= frac {vec F} {m} =frac {q vec E}{m}), где m — масса заряженной частицы. Как видно, направление ускорения будет совпадать с направлением (~vec E), если заряд частицы положителен (q > 0), и будет противоположно (~vec E), если заряд отрицателен (q<0).
Если электростатическое поле однородное ((~vec E) = const), то ускорение (~vec a ) = const и частица будет совершать равноускоренное движение (разумеется, при отсутствии других сил). Вид траектории частицы зависит от начальных условий. Если вначале заряженная частица покоилась (~(v_0 = 0)) или ее начальная скорость сонаправлена с ускорением (~ (vec v_o upuparrows vec a )), то частица будет совершать равноускоренное прямолинейное движение вдоль поля и ее скорость будет расти. Если (~ vec v_o downarrow uparrow vec a ), то частица будет тормозиться в этом поле.
Если угол между начальной скоростью и ускорением острый О < α < 90° (или тупой), то заряженная частица в таком электростатическом поле будет двигаться по параболе.
Во всех случаях при движении заряженной частицы в электростатическом поле будет изменяться модуль скорости, а следовательно, и кинетическая энергия частицы.
Существенное отличие магнитного поля от электростатического состоит, во-первых, в том, что магнитное поле не действует на покоящуюся заряженную частицу. Магнитное поле действует только на движущиеся в поле заряженные частицы. Во-вторых, сила Лоренца, действующая на заряженные частицы в магнитном поле, всегда перпендикулярна скорости их движения. Поэтому модуль скорости в магнитном поле не изменяется. Не изменяется, следовательно, и кинетическая энергия частицы. Вид траектории заряженной частицы в магнитном поле зависит от угла между скоростью влетающей в поле частицы и магнитной индукцией. Возможны три различных случая.
1. Заряженная частица влетает в магнитное поле со скоростью (~vec v), направленной вдоль поля (~(vec v upuparrows vec B)) или противоположно направлению магнитной индукции поля (~ (vec v downarrow uparrow vec B )). В этих случаях сила Лоренна (~F_L = 0 ) и частица будет продолжать двигаться равномерно прямолинейно.
2. Заряженная частица движется перпендикулярно линиям магнитной индукции (рис. 2), тогда сила Лоренца (~ F_L = qbv ), а следовательно, и сообщаемое ускорение будут постоянны по модулю и перпендикулярны к скорости частицы. В результате частица будет двигаться по окружности, радиус которой можно найти на основании второго закона Ньютона:
(~F_l = ma_c; qBv = frac {mv^2}{R} Rightarrow R =frac {mv}{qB}. )
Отношение (~frac q m ) — называют удельным зарядом частицы.
Рис. 2
Период вращения частицы
(~T = frac {2 pi R}{v} = frac {2 pi m}{qB},)
то есть период вращения не зависит от скорости частицы и радиуса траектории. На этом основано действие циклотрона.
3. Скорость заряженной частицы направлена под углом (~alpha ) к вектору (~vec B) (рис. 3).
Рис. 3
Движение частицы можно представить в виде суперпозиции равномерного прямолинейного движения вдоль поля со скоростью (~ v_{lVert} = v cos alpha ) и движения по окружности с постоянной по модулю скоростью (~ v_{perp} = v sin alpha) в плоскости, перпендикулярной полю. Радиус окружности определяется аналогично предыдущему случаю, только надо заменить (~ v) на (~ v_{perp} = v sin alpha), то есть
(~R = frac {mv sin alpha} {qB}.)
В результате сложения этих движений возникает движение по винтовой линии, ось которой параллельна магнитному полю. Шаг винтовой линии
(~h = v_{lVert} cdot T = v cos alpha cdot T = frac {2 pi mv cos alpha} {qB})
Направление, в котором закручивается спираль, зависит от знака заряда частицы.
Если скорость заряженной частицы составляет угол α с направлением вектора (~vec B) неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, тο R и h уменьшаются с ростом B. На этом основана фокусировка заряженных частиц в магнитном поле.
Если на движущуюся заряженную частицу помимо магнитного поля с индукцией (~vec B) действует одновременно и электростатическое поле с напряженностью (~vec E), то равнодействующая сила, приложенная к частице, равна векторной сумме электрической силы и силы Лоренца[~ vec F_e = vec F_L]. Характер движения и вид траектории зависят в данном случае от соотношения этих сил и от направления электростатического и магнитного полей.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C.326-327.
Что общего между микроволновой печью, электронным микроскопом и старым ЭЛТ-телевизором? Внутри всех этих устройств находится катодно-лучевая трубка, испускающая электроны, которые затем ускоряются электростатическим полем.
Электрические заряды взаимодействуют друг с другом: заряды одинакового знака отталкиваются друг от друга, заряды противоположного знака притягиваются друг к другу. Эти взаимодействия опосредуются электрическим полем. Он создается каждым зарядом, и каждый заряд взаимодействует с ним. Электрическое поле описывается векторной величиной E, — напряженностью электрического поля. Эта величина определяется как отношение силы F, которой поле действует на электрический заряд q, к величине этого заряда: E = F / q .
Поэтому, если электрический заряд q оказывается в электрическом поле, создаваемом другими зарядами, на него действует сила: F = q * E . [2]
Согласно второму закону Ньютона действие силы вызывает движение с ускорением: a = F / m . [3]
Если объединить уравнения (2) и (3), то получим уравнение для ускорения заряженной частицы в электрическом поле: a = q * E / m . [4]
Следует помнить, что в общем случае это ускорение не является постоянным, поскольку величина напряженности электрического поля может зависеть от положения. Это будет иметь место, например, для электрического поля, создаваемого точечным зарядом, напряженность которого уменьшается с квадратом расстояния от заряда.
Рассмотрим пример, когда электрическое поле везде постоянно (так называемое однородное поле). Примерно так обстоит дело внутри плоского конденсатора, т.е. между двумя проводящими заряженными пластинами, расположенными параллельно друг другу.
К двум пластинам прикладывается электрическое напряжение UC, в результате чего пластины заряжаются: верхняя — положительным электрическим зарядом, а нижняя — отрицательным. Линии электрического поля перпендикулярны пластинам и направлены от положительно заряженной пластины к отрицательно заряженной.
Теперь предположим, что электрон падает в область между пластинами со скоростью v0, параллельной поверхности пластин. В самом начале электрон имеет только компонент скорости vx, но электрическое поле заставляет электрон ускоряться. Поскольку электрическое поле, а значит и сила, перпендикулярны компоненту vx, она будет оставаться постоянной, как и в случае горизонтальной проекции в гравитационном поле. Однако компонент vy изменится, потому что в направлении y действует сила Fy = q * E.
Поскольку внутри плоского конденсатора поле однородно, сила будет постоянной. Поэтому ускорение также будет постоянным. Поэтому мы можем определить временную зависимость компонента скорости: vy = a * t .
Используя уравнение (4), мы можем написать, что значение этой составляющей будет: vy = ( q * E * t ) / m . [6]
Обратите внимание, что электрическое поле направленно вниз, но заряд электрона отрицательный. Это означает, что сила действует вверх, поэтому составляющая скорости vy будет направлена вверх.
Зная длину пластин, мы можем определить время t, необходимое электрону для прохождения участка между пластинами: t = l / v0 [7], где где l — длина пластин и, следовательно, x — составляющая положения электрона на выходе из области между пластинами. Наконец, объединив уравнения (6) и (7), мы получим значение компонента vy :
vy = q * E * l / m * v0 .
Эту систему можно использовать для отклонения пути электронов или любых других заряженных частиц. Её также можно использовать в качестве детектора заряженных частиц. Изучая отклонение частицы, мы можем найти отношение ее заряда к массе и, таким образом, определить, с каким типом частицы мы имеем дело.
Теперь рассмотрим систему, которая используется для придания электронам огромных скоростей, так называемую электронную пушку.
Электронная пушка
Первым компонентом электронной пушки является катод (K), который представляет собой кусок проводника (например, вольфрамовой проволоки), нагретый до очень высокой температуры. Катод является источником электронов, которые вырываются из него благодаря так называемой термоэмиссии. Однако скорость электронов, отрывающихся от катода, очень мала.
Второй компонент системы, анод (A), отвечает за их ускорение. В простейшем случае это может быть металлический диск с отверстием. Если к катоду и аноду приложить электрическое напряжение (UA), между ними возникнет электрическое поле. Если электрический потенциал анода выше электрического потенциала катода, тогда электрическое поле будет направлено от анода к катоду. Электроны (e), поскольку они имеют отрицательный заряд, будут притягиваться к аноду. Они достигнут своей максимальной скорости (V) в центре анодного отверстия, потому что электрический потенциал там самый высокий.
В этом случае электрическое поле между катодом и анодом неоднородно, поэтому электрон будет двигаться с неоднородным движением, то есть с переменным ускорением. Однако мы можем определить скорость электрона, пролетающего через отверстие анода, если знаем электрическое напряжение UA, подключенное между катодом и анодом. Электрическое напряжение, или разность потенциалов, умноженная на величину заряда, равна работе, проделанной электрическим полем для ускорения электрического заряда. Если предположить, что скорость электрона непосредственно у катода пренебрежимо мала по сравнению с максимальной скоростью, то эта работа равна кинетической энергии электрона:
e * UA = ( me * v2 ) / 2 , где me — масса электрона, а e — заряд электрона (так называемый элементарный заряд). Из этого мы можем определить значение максимальной скорости электрона:
v = 2 * e * UA / me .
Электронную пушку можно найти во многих устройствах, например, в микроволновой печи, рентгеновской трубке, ламповом усилителе для электрогитары или электронном микроскопе. Значение напряжения UA для ускорения электронов зависит от области применения и может варьироваться от нескольких сотен вольт в случае ламповых усилителей, до значений в диапазоне 2 — 5 кВ в микроволновой печи, и даже до 100 — 300 кВ в трансмиссионном электронном микроскопе.
Использованная литература
- 1. Физическая энциклопедия.- М.: Советская энциклопедия, 1988.
- 2. Иродов И.Е. Основные законы электромагнетизма.- М.: Высшая школа, 1983.
- 3. Матвеев А.Н. Электричество и магнетизм.- М.: Высшая школа, 1983.
13. Электрическое и магнитное поле
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
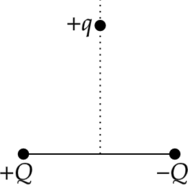
На рисунке изображены три заряда (+q), (+Q) и (-Q). Куда направлено относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) ускорение заряда (+q) в этот момент времени, если на него действуют только заряды (+Q) и (-Q)? Ответ запишите словом (словами).
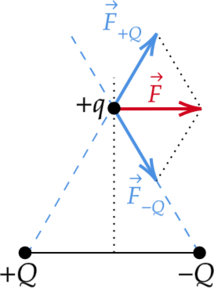
Заряды, имеющие одинаковые знаки, отталкиваются, а заряды, имеющие разные знаки — притягиваются. Исходя из этого, изобразми силы, действующие на заряд (+q) со стороны зарядов (+Q) и (-Q):
Равнодействующая сил, которые действуют на заряд (+q) направлена вправо. Так как вектор ускорения заряда сонаправлен с направлением вектора равнодействующей силы (vec{F}), то он также направлен вправо.
Ответ: ВПРАВО
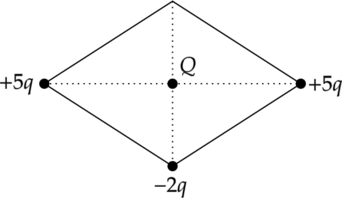
В трёх вершинах ромба расположены точечные заряды (+5q), (-2q) и +(5q) ( (q > 0)). Куда направлена относительно рисунка (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) кулоновская сила ( F), действующая на положительный точечный заряд (Q), помещённый в центр этого ромба (см. рисунок)? Ответ запишите словом (словами).
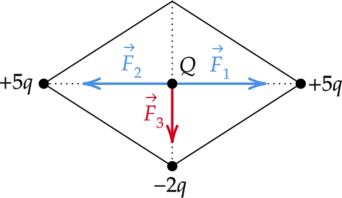
Заряды, имеющие одинаковые знаки, отталкиваются, а заряды, имеющие разные знаки — притягиваются. Исходя из этого, изобразми силы, действующие на заряд (Q) со стороны зарядов (+5q) , (+5q) и (-2q):
Равнодействующая кулоновских сил (vec{F_1}) и (vec{F_2}), действующих на заряд (Q) равна 0, так как левый и правый заряды равны по знаку и по модулю.
Тогда остаётся сила (vec{F_3}), которая направлена вниз, потому что (Q) и (-2q) противоположны по знаку, следовательно, притягиваются. Таким образом, вектор кулоновской силы ( vec{F}) направлен вниз.
Ответ: ВНИЗ
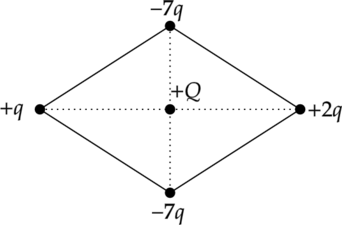
В четырёх вершинах ромба расположены точечные заряды (q, -7q, -2q и -7q) ((q > 0).) Куда направлена относительно рисунка (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) кулоновская сила (F), действующая на положительный точечный заряд (Q), помещённый в центр этого ромба (см. рисунок)? Ответ запишите словом (словами).
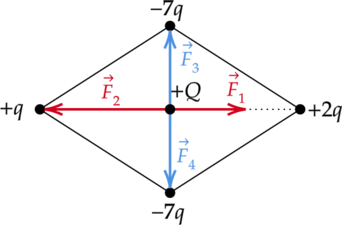
Равнодействующая кулоновских сил (vec{F_3}) и (vec{F_4}), действующих на заряд (Q), равна 0, так как верхний и нижний заряды равны по знаку и по модулю. Сила (vec{F_1}) направлена вправо, так как (Q) и (q) положительны, тогда (vec{F_2}) — влево (одинаковые по знаку заряды отталкиваются).
Но (2q > q), тогда (|vec{F_2}| >| vec{F_1}|) и равнодействующая этих сил сонаправлена с вектором (vec{F_2}), то есть вектор кулоновской силы (F) направлен влево.
Ответ: ВЛЕВО
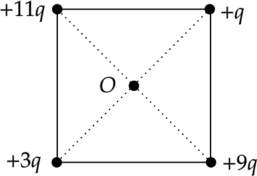
В вершинах квадрата закреплены положительные точечные заряды — так, как показано на рисунке. Как направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор напряжённости электрического поля в центре (O) квадрата? Ответ запишите словом (словами).
По принципу суперпозиции, напряженность поля в точке (O) есть сумма напряженностей полей, создаваемых всеми зарядами по отдельности: [vec{E_{text{общ}}}=vec{E_1}+vec{E_2}+dots+vec{E_n}] Поле отрицательного точечного заряда направлено к заряду, а поле, создаваемое положительным зарядом — от заряда. Поле точечного заряда пропорционально величине заряда (Q) и ослабевает с расстоянием (r). Это выражается зависимостью: [E=dfrac{Q}{r^2}]
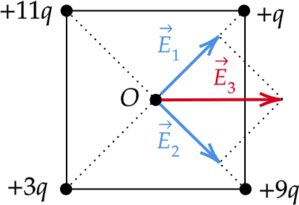
Напряженность поля создаваемого зарядами (q) и (3q) направлено в сторону заряда (q) и по модулю равна: [|E_1|=dfrac{2q}{r^2}] Напряженность поля создаваемого зарядами (11q) и (9q) направлено в сторону заряда (9q) и по модулю равна: [|E_2|=dfrac{2q}{r^2}] Таким образом, вектор (vec{E_3}) напряженности электрического поля в центре (O) квадрата направлен вправо.
Ответ: ВПРАВО
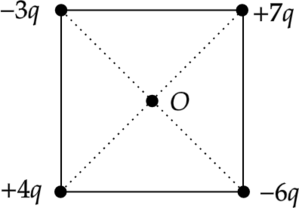
В вершинах квадрата закреплены положительные точечные заряды — так, как показано на рисунке. Как направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор напряжённости электрического поля в центре (O) квадрата? Ответ запишите словом (словами).
По принципу суперпозиции, напряженность поля в точке (O) есть сумма напряженностей полей, создаваемых всеми зарядами по отдельности: [vec{E_{text{общ}}}=vec{E_1}+vec{E_2}+dots+vec{E_n}] Поле отрицательного точечного заряда направлено к заряду, а поле, создаваемое положительным зарядом — от заряда. Поле точечного заряда пропорционально величине заряда (Q) и ослабевает с расстоянием (r). Это выражается зависимостью: [E=dfrac{Q}{r^2}]
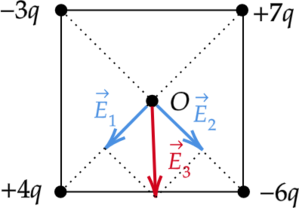
Напряженность поля создаваемого зарядами (+4q) и (+7q) направлено в сторону заряда (+4q) и по модулю равна: [E_1=dfrac{3q}{r^2}] Напряженность поля создаваемого зарядами (-3q) и (-6q) направлено в сторону заряда (-6q) и по модулю равна: [E_2=dfrac{3q}{r^2}] Таким образом, вектор (vec{E_3}) напряженности электрического поля в центре (O) квадрата направлен вниз.
Ответ: ВНИЗ
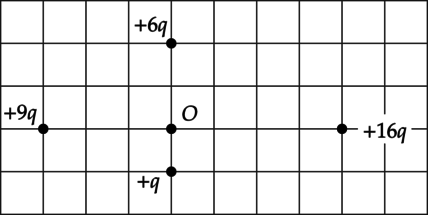
Точечные заряды закреплены так, как показано на рисунке. Как направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор напряжённости электростатического поля в точке (O)? Ответ запишите словом (словами).
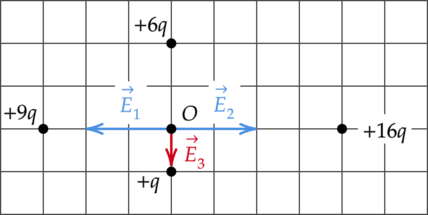
По принципу суперпозиции, напряженность поля в точке (O) есть сумма напряженностей полей, создаваемых всеми зарядами по отдельности: [vec{E_{text{общ}}}=vec{E_1}+vec{E_2}+dots+vec{E_n}] Поле отрицательного точечного заряда направлено к заряду, а поле, создаваемое положительным зарядом — от заряда. Поле точечного заряда пропорционально величине заряда (Q) и ослабевает с расстоянием (r). Это выражается зависимостью: [E=dfrac{Q}{r^2}]
Так как напряженность поля заряда (+3q) в точке (O): [E_1=dfrac{9q}{(3r)^2}=dfrac{q}{r^2}] А напряженность поля заряда (+16q) в точке (O): [E_2=dfrac{16q}{(4r)^2}=dfrac{q}{r^2} ; ; ; Rightarrow ; ; ; E_1=E_2] Тогда результирующая напряженность полей этих зарядов будет равна 0. Поле заряда (+6q) больше поля заряда (+q), так как: [dfrac{6q}{(2r)^2}>dfrac{q}{r^2}] Таким образом, результирующий вектор (vec{E_3}) напряженности электрического поля в точке (O) направлен в сторону (+q), то есть вниз.
Ответ: ВНИЗ
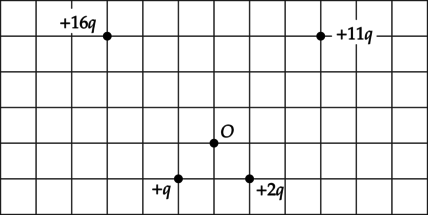
Точечные заряды закреплены так, как показано на рисунке. Как направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор напряжённости электростатического поля в точке (O)? Ответ запишите словом (словами).
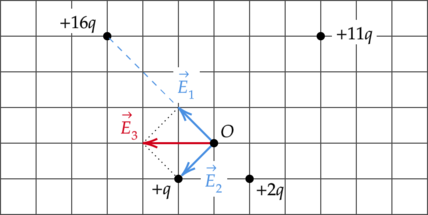
По принципу суперпозиции, напряженность поля в точке (O) есть сумма напряженностей полей, создаваемых всеми зарядами по отдельности: [vec{E_{text{общ}}}=vec{E_1}+vec{E_2}+dots+vec{E_n}] Поле отрицательного точечного заряда направлено к заряду, а поле, создаваемое положительным зарядом — от заряда. Поле точечного заряда пропорционально величине заряда (Q) и ослабевает с расстоянием (r). Это выражается зависимостью: [E=dfrac{Q}{r^2}]
Так как напряженность поля заряда (+2q) в точке (O) равна: [E_{+q}=dfrac{2q}{r^2}] А напряженность поля заряда (+16q) в точке (O): [E_{+16q}=dfrac{16q}{(3r)^2}] Тогда результирующая напряженность полей этих зарядов будет равна: [E_1=dfrac{2q}{r^2}-dfrac{16q}{(3r)^2}=dfrac{2q}{(3r)^2}] Аналогично с результирующим полем зарядов (+11q) и (+q): [E_2=dfrac{11q}{(3r)^2}-dfrac{q}{r^2}=dfrac{2q}{(3r)^2} ; ; ; Rightarrow ; ; ; E_1=E_2] Таким образом, результирующий вектор (vec{E_3}) напряженности электрического поля в точке (O) направлен влево.
Ответ: ВЛЕВО

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Закон Кулона. Силы и ускорения.
В статье рассмотрены задачи, сочетающие законы динамики и взаимодействие зарядов. Здесь встретится и сила упругости, и сила натяжения нити, и нормальное ускорение при движении по окружности. Задачи среднего уровня сложности.
Задача 1. Два одинаковых заряда , соединенных резиновыми шнурами со стенками так, как показано на рисунке, находятся на расстоянии
друг от друга. Расстояние между стенками
, длина каждого недеформированного шнура
. Определить жесткость шнура, массой зарядов пренебречь.
Жесткость шнура равна , где
— сила натяжения шнура,
— удлинение шнура.
Определим, насколько шнур стал длиннее.
К задаче 1.
Определим силу кулоновского взаимодействия зарядов:
Определим силу натяжения шнура, для этого приравняем проекции сил кулоновского взаимодействия и натяжения шнуров:
Найдем косинус угла из геометрических соображений:
Тогда можем подставить все в формулу для жесткости:
Ответ: .
Задача 2. Внутри гладкой сферы диаметром находится маленький заряженный шарик. Какой минимальной величины заряд
нужно поместить в нижней точке сферы, для того чтобы шарик находился в ее верхней точке в устойчивом равновесии? Заряд шарика
, его масса
.
К задаче 2
Минимальная сила, которая может нам понадобиться, это кулонова сила, равная силе тяжести. Тогда
Посмотрим, достаточно ли этого, чтобы равновесие было устойчивым: если шарик отклонится на небольшой угол от вертикали, то кулонова сила может быть разложена на две составляющие, причем раскладывать силу будем, направив ось
по касательной к сфере, а ось
— перпендикулярно касательной. Тогда проекция кулоновой силы на данное направление равна
, а проекция силы тяжести на это же направление равна
. Чтобы шарик возвращался назад в точку равновесия нужно, чтобы проекция кулоновой слы была бы больше проекции силы тяжести. Осталось установить, как соотносятся углы
и
. Посмотрим на рисунок: угол
— центральный, а угол
— вписанный. Поэтому
.
Тогда:
В силу малости углов можно принять ,
. Тогда
Иными словами, устойчивым равновесие будет, если
Ответ:
Задача 3. Два заряженных шарика соединены нитью см. Отношение масс шариков
, заряды по модулю одинаковы
Кл, но противоположны по знаку. Какую минимальную внешнюю силу
надо приложить к шарику массой
, чтобы в процессе движения нить не провисала?
Шарики заряжены одноименно, то есть будут притягиваться. Нужно, чтобы левый шарик «убегал» от правого с определенным ускорением. Нарисуем чертеж:
К задаче 3
Запишем второй закон Ньютона для левого шарика:
Здесь — внешняя сила,
— кулонова сила,
— сила натяжения нити.
Для правого шарика
Чтобы нить не провисала, достаточно чтобы натяжение нити было нулевым, :
Подставим второе в первое:
Подставим ускорение из записанного ранее равенства:
Ответ: 27 мН
Задача 4. Вокруг неподвижного положительного заряда Кл движется по окружности отрицательный заряд. Радиус окружности 1 см. Один оборот заряд совершает за время
с. Найти отношение заряда к массе
для движущегося заряда.
При движении по окружности всегда присутствует нормальное ускорение, поворачивающее вектор скорости. Чтобы его найти, надо бы узнать скорость движения заряда. Мы знаем время прохождения одного оборота, длина же окружности радиуса равна
, поэтому линейная скорость движения заряда равна
.
Нормальное ускорение:
Кулонова сила равна центростремительной:
Запишем иначе:
Ответ: Кл/кг
Задача 5. Шарик массой и зарядом
, подвешенный на непроводящей нити длиной
, вращается вокруг вертикальной оси так, что нить образует с вертикалью угол
. Определить период обращения шарика и силу натяжения нити, если неподвижный точечный заряд
находится: а) в точке подвеса; б) в центре окружности, описываемой шариком; в) на оси вращения, на расстоянии
от шарика внизу.
Первый случай. Заряд – в месте прикрепления нити к потолку, сила кулоновского взаимодействия направлена вдоль нити вниз. Нарисуем картинку и запишем второй закон Ньютона.
К задаче 5 а)
В векторной форме:
Здесь — сила натяжения нити,
— кулонова сила,
— сила, обусловленная наличием нормального ускорения.
Разложим теперь вектора на проекции вдоль координатных осей. Ось абсцисс направим горизонтально вправо, ось ординат – вверх. Тогда:
Определим отсюда силу натяжения нити:
Теперь займемся периодом. Для его определения нужно знать скорость шарика. Распишем второе уравнение, подставив силу натяжения нити и нормальное ускорение:
Так как , то
Второй случай – заряд в центре окружности.
Сила кулоновского взаимодействия направлена вдоль радиуса, наружу. Нарисуем картинку и запишем второй закон Ньютона.
К задаче 5 б)
В векторной форме:
Разложим теперь вектора на проекции вдоль координатных осей. Ось абсцисс направим горизонтально вправо, ось ординат – вверх. Тогда:
Определим отсюда силу натяжения нити:
Тогда первое уравнение:
Определим период. Скорость знаем, длину окружности – тоже. Тогда:
Упростим немного выражение:
Наконец, рассмотрим третий случай, когда заряд находится на оси вращения внизу. Сила кулоновского взаимодействия направлена вдоль линии, проведенной через заряды, вверх и влево.
Нарисуем картинку и запишем второй закон Ньютона.
К задаче 5 в)
В векторной форме:
Разложим теперь вектора на проекции вдоль координатных осей. Ось абсцисс направим горизонтально вправо, ось ординат – вверх. Тогда:
Определим отсюда силу натяжения нити:
Зная скорость, определим период: