Как найти вектор прямой линии

Нормальный вектор прямой, координаты нормального вектора прямой

Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.

Нормальный вектор прямой – определение, примеры, иллюстрации

Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.

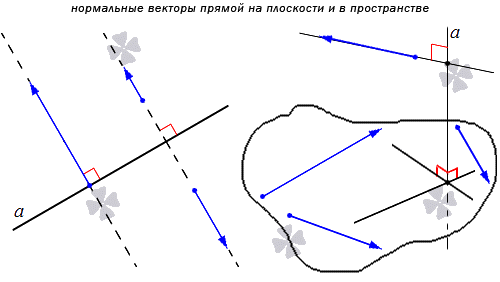
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.

Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.

Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а 1 параллельные, а n → считается нормальным вектором прямой a , также считается нормальным вектором для прямой a 1 . Когда прямая а имеет прямой вектор, тогда вектор t · n → является ненулевым при любом значении параметра t , причем также является нормальным для прямой a .

Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.

Если задана плоскость О х у , то множеством векторов для О х является координатный вектор j → . Он считается ненулевым и принадлежащим координатной оси О у , перпендикулярной О х . Все множество нормальных векторов относительно О х можно записать, как t · j → , t ∈ R , t ≠ 0 .

Прямоугольная система O x y z имеет нормальный вектор i → , относящийся к прямой О z . Вектор j → также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный О z , считается нормальным для O z .

Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой

При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.

Задана прямая вида 2 x + 7 y — 4 = 0 _, найти координаты нормального вектора.

По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2 , 7 .

Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.

Указать нормальный вектор для заданной прямой y — 3 = 0 .

По условию нам дано общее уравнение прямой, значит запишем его таким образом 0 · x + 1 · y — 3 = 0 . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0 , 1 .

Если дано уравнение в отрезках вида x a + y b = 1 или уравнение с угловым коэффициентом y = k · x + b , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.

Найти координаты нормального вектора, если дано уравнение прямой x 1 3 — y = 1 .

Для начала необходимо перейти от уравнения в отрезках x 1 3 — y = 1 к уравнению общего вида. Тогда получим, что x 1 3 — y = 1 ⇔ 3 · x — 1 · y — 1 = 0 .

Отсюда видно, что координаты нормального вектора имеют значение 3 , — 1 .

Ответ: 3 , — 1 .

Если прямая определена каноническим уравнением прямой на плоскости x — x 1 a x = y — y 1 a y или параметрическим x = x 1 + a x · λ y = y 1 + a y · λ , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a → = ( a x , a y ) . Возможность нахождения координат нормального вектора n → возможно, благодаря условию перпендикулярности векторов n → и a → .

Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0

Для решения можно выбирать любой удобный способ.

Найти нормальный вектор заданной прямой x — 2 7 = y + 3 — 2 .

Из прямой x — 2 7 = y + 3 — 2 понятно, что направляющий вектор будет иметь координаты a → = ( 7 , — 2 ) . Нормальный вектор n → = ( n x , n y ) заданной прямой является перпендикулярным a → = ( 7 , — 2 ) .

Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a → = ( 7 , — 2 ) и n → = ( n x , n y ) запишем a → , n → = 7 · n x — 2 · n y = 0 .

Значение n x – произвольное , следует найти n y . Если n x = 1 , отсюда получаем, что 7 · 1 — 2 · n y = 0 ⇔ n y = 7 2 .

Значит, нормальный вектор имеет координаты 1 , 7 2 .

Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем

x — 2 7 = y + 3 — 2 ⇔ 7 · ( y + 3 ) = — 2 · ( x — 2 ) ⇔ 2 x + 7 y — 4 + 7 3 = 0

Полученный результат координат нормального вектора равен 2 , 7 .

Ответ: 2 , 7 или 1 , 7 2 .

Указать координаты нормального вектора прямой x = 1 y = 2 — 3 · λ .

Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:

x = 1 y = 2 — 3 · λ ⇔ x = 1 + 0 · λ y = 2 — 3 · λ ⇔ λ = x — 1 0 λ = y — 2 — 3 ⇔ x — 1 0 = y — 2 — 3 ⇔ ⇔ — 3 · ( x — 1 ) = 0 · ( y — 2 ) ⇔ — 3 · x + 0 · y + 3 = 0

Отсюда видно, что координаты нормального вектора равны — 3 , 0 .

Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат О х у z .

Когда прямая задается при помощи уравнений пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда нормальный вектор плоскости относится к A 2 x + B 2 y + C 2 z + D 2 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда получаем запись векторов в виде n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .

Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрического, имеющего вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , отсюда a x , a y и a z считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a → = ( a x , a y , a z ) . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a → = ( a x , a y , a z ) .

2.2.5. Нормальный вектор прямой

Или вектор нормали.

Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:

Если прямая задана общим уравнением в декартовой системе координат, то вектор является вектором нормали данной прямой.

Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2 работают и в общем аффинном случае.

Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:

И тут всё ещё проще: если координаты направляющего вектора приходилось аккуратно «вытаскивать» из уравнения, то координаты вектора нормали достаточно просто «снять».

Приведу примеры с теми же уравнениями, что и для направляющего вектора:

Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».

Вектор нормали: расчет и пример

Содержание:

В нормальный вектор Он определяет направление, перпендикулярное рассматриваемому геометрическому объекту, который может быть, например, кривой, плоскостью или поверхностью.

Это очень полезная концепция для позиционирования движущейся частицы или какой-либо поверхности в пространстве. На следующем графике можно увидеть, как вектор нормали к произвольной кривой C:

Рассмотрим точку P на кривой C. Точка может представлять движущуюся частицу, которая движется по траектории C. Касательная линия к кривой в точке P нарисована красным.

Обратите внимание, что вектор Т касается C в каждой точке, а вектор N перпендикулярно Т y указывает на центр воображаемого круга, дуга которого является сегментом C. Векторы выделены жирным шрифтом в печатном тексте, чтобы отличать их от других не векторных величин.

Вектор Т он всегда указывает, куда движется частица, следовательно, указывает ее скорость. Вместо вектора N всегда указывает в том направлении, в котором вращается частица, отмечая, таким образом, вогнутость кривой C.

Как получить вектор нормали к плоскости?

Вектор нормали не обязательно является единичным вектором, то есть вектором с модулем 1, но если это так, он называется нормальный единичный вектор.

Во многих приложениях необходимо знать вектор нормали к плоскости вместо кривой. Этот вектор показывает ориентацию указанной плоскости в пространстве. Например, рассмотрим самолет п (желтый) рисунка:

К этой плоскости есть два нормальных вектора: п₁ Y п₂. Использование того или другого будет зависеть от контекста, в котором находится упомянутый самолет. Получить вектор нормали к плоскости очень просто, если вы знаете его уравнение:

ах + по + cz + d = 0, с участием к, б, c Y d вещественные числа.

Ну, нормальный вектор к указанной плоскости задается следующим образом:

N = а я + b j + c k

Здесь вектор N Он выражается через единичные векторы и перпендикулярно друг другу. я, j Y k, направленных по трем направлениям, определяющим пространство X и Zсм. рисунок 2 справа.

Вектор нормали из векторного произведения

Очень простая процедура нахождения вектора нормали использует свойства векторного произведения между двумя векторами.

Как известно, три разные точки, не лежащие на одной прямой, определяют плоскость Р. Теперь можно получить два вектора или Y v которые принадлежат упомянутой плоскости, имеющей эти три точки.

Когда у вас есть векторы, векторный продуктили Икс v — операция, результатом которой, в свою очередь, является вектор, который имеет свойство быть перпендикулярным плоскости, определяемой или Y v.

Известный этот вектор, он обозначается как N, и из него можно будет определить уравнение плоскости благодаря уравнению, указанному в предыдущем разделе:

N = или Икс v

На следующем рисунке показана описанная процедура:

пример

Найти уравнение плоскости, определяемой точками A (2,1,3); В (0,1,1); С (4.2.1).

Решение

Это упражнение иллюстрирует описанную выше процедуру. Имея 3 точки, одна из них выбирается как общее начало двух векторов, которые принадлежат плоскости, определенной этими точками. Например, точка A устанавливается в качестве начала координат и строятся векторы AB Y AC.

Вектор AB — вектор, начало которого — точка A, а конец — точка B. Координаты вектора AB определяются соответственно вычитанием координат B из координат A:

AB = (0-2) я + (1-1) j + (1-3) k = -2я + 0j -2 k

Таким же образом поступаем и находим вектор AC:

AC = (4-2) я + (2-1) j + (1-3) k = 2я + j -2 k

Расчет векторного произведения AB x AC

Существует несколько процедур для нахождения векторного произведения между двумя векторами. В этом примере используется мнемоническая процедура, которая использует следующий рисунок для поиска векторных произведений между единичными векторами. я, j Y k:

Для начала следует помнить, что векторные произведения между параллельными векторами равны нулю, поэтому:

я Икс я = 0; j Икс j = 0; k Икс k = 0

А поскольку векторное произведение — это еще один вектор, перпендикулярный участвующим векторам, двигаясь в направлении красной стрелки, мы имеем:

я Икс j = k ; j Икс k = я; k Икс я = j

Если вам нужно двигаться в направлении, противоположном стрелке, добавьте знак (-):

j Икс я = – k; k Икс j = –я; я Икс k = –j

Всего можно составить 9 векторных произведений с единичными векторами. я, j Y k, из которых 3 будут нулевыми.

AB Икс AC = (-2я + 0j -2 k) х (2я + j -2 k)= -4(я Икс я) -2(я Икс j)+4 (я Икс k)+0 (j Икс я) + 0 (j Икс j) – 0 (j Икс k) – 4 (k Икс я)-2 (k Икс j) + 4 (k Икс k) = -2k-4j-4j+2я = 2я -8j-2k

Уравнение плоскости

Вектор N был определен с помощью предварительно рассчитанного векторного произведения:

N = 2я -8j-2k

Следовательно, a = 2, b = -8, c = -2, искомая плоскость:

ах + по + cz + d = 0 → 2x-8y-2z + d = 0

Значение d. Это легко сделать, если значения любой из имеющихся точек A, B или C подставить в уравнение плоскости. Выбор C, например:

2,4 — 8,2 — 2,1 + d = 0

Вкратце, искомая карта:

Пытливый читатель может задаться вопросом, был бы такой же результат, если бы вместо выполнения AB Икс AC они бы предпочли произвести AC Икс AB. Ответ: да, плоскость, определяемая этими тремя точками, уникальна и имеет два вектора нормали, как показано на рисунке 2.

Что касается точки, выбранной в качестве исходной точки векторов, нет проблем с выбором любого из двух других.

Ссылки

1. Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB). 31-62.
2. Нахождение нормали к плоскости. Получено с: web.ma.utexas.edu.
3. Ларсон, Р. (1986). Исчисление и аналитическая геометрия. Мак Гроу Хилл. 616-647.
4. Линии и плоскости в R 3. Получено с: math.harvard.edu.
5. Нормальный вектор. Получено с сайта mathworld.wolfram.com.

Выбор темы исследования: как это делается, важность, примеры

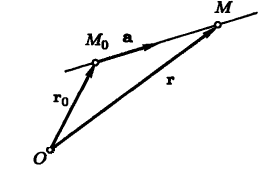
Рассмотрим прямую $L$, заданную точкой $M_0$, лежащей на ней, и направляющим вектором $overline{S}$ с координатами $(l;m)$, при этом вектор $overline{S}$ — ненулевой. Обозначим на прямой произвольную точку $M$ с координатами $(x, y)$, не совпадающую с точкой $M_0$. Радиус-векторы этих точек назовём $overline{r_0}$ и $overline{r}$. Вектор $overline{MM_0}$ при этом будет колинеарен вектору $overline{S}$.

Вектор $overline{r}$ можно выразить через сумму векторов $overline{MM_0}$:

$overline{r} = overline{r_0} + overline{MM_0}left(1right).$

Вектор $overline{MM_0}$ лежит на прямой $L$, поэтому он по условию является параллельным направляющему вектору $overline{S}$ и связан с ним соотношением $overline{MM_0}= toverline{S}left(2right)$, где $t$ — множитель, являющийся скалярной величиной и зависящий от позиции точки $M$ на прямой.

Учитывая равенство $(2)$, формулу $(1)$ можно переписать следующим образом:

Возможны следующие варианты задания уравнения прямой на плоскости:

• Общее уравнение прямой;
• Уравнение с угловым коэффициентом;
• Через параметрические уравнения;
• Каноническое уравнение;
• С помощью двух точек, через которые проходит прямая.

Для каждого из этих вариантов подходит свой способ нахождения направляющего вектора.

Направляющий вектор из канонического уравнения прямой и через две точки

Каноническое уравнение прямой выглядит так:

$frac{x-x_0}{l}= frac{y-y_0}{m}left(4right)$

Из канонического уравнения выразить координаты направляющего вектора проще всего: достаточно выписать знаменатели из уравнения следующим образом:

$overline{S}=(l; m)$.

Уравнение прямой, проходящей через 2 точки, имеет вид, очень похожий на каноническое уравнение:

$frac{x-x_1}{x_2 — x_1}= frac{y-y_1}{y_2-y_1}left(5right)$, где $(x_1; y_1)$ и $(x_2; y_2)$ — координаты точек, через которые проходит прямая.

В этом случае координаты направляющего вектора $overline{S}$ равны $((x_2 – x_1); (y_2-y_1))$.

Направляющий вектор из параметрических уравнений

Параметрические уравнения имеют следующий вид:
$begin{cases} x=x_0 + lt \ y=y_0 + mt end{cases}$

Для того чтобы выразить координаты направляющего вектора из параметрических уравнений, нужно выписать коэффициенты, стоящие перед параметром $t$, т.е. $overline{S}=(l; m)$.

Координаты направляющего вектора из общего уравнения

Общее уравнение имеет следующий вид:

$Ax + By + C = 0left(6right)$

Для того чтобы получить координаты направляющего вектора, нужно от общего уравнения прямой перейти к каноническому.

Сделаем это в общей форме.

Сначала перенесём часть $By + C$ в правую часть:

$Ax = — By – C$

Теперь разделим всё на $A$:

$x=-frac{By}{A} — frac{C}{A}$

А после этого всё уравнение разделим на $B$:

$frac{x}{B}=-frac{y}{A} — frac{C}{AB}$

$frac{x}{B} = frac{y + frac{C}{B}}{-A}left(7right)$

Из вышеизложенного следует, что координаты направляющего вектора $overline{S}$ будут равны $(B; -A)$.

Координаты направляющего вектора из уравнения с угловым коэффициентом

Уравнение с угловым коэффициентом имеет вид:

$y = kx + b$

Для того чтобы получить из него координаты направляющего вектора, необходимо сначала привести его к общему виду, для этого переносим всё в левую часть:

$y — kx – b= 0$

Затем нужно воспользоваться алгоритмом для общего уравнения.

Уравнение с угловым коэффициентом, приведённое к каноническому, выглядит так:

$frac{x}{1}=frac{y-b}{k}$,

то есть координаты направляющего вектора в данном случае будут $overline{S}= (1;k)$.

(схема 27)

         Пусть задан
вектор , параллельный заданной прямой l (без учета направления) и точка M₀, лежащая на данной прямой. Таким образом, прямая l
однозначно определяется в пространстве точкой  M₀(x₀;y₀;z₀) и вектором , называемым для l направляющим.
Обозначим
  и определим его
с точностью до коллинеарности (рис. 2.21).

      Пусть точка M(x;y;z) – текущая точка прямой l,
тогда   текущий вектор прямой имеет координаты . Значит, векторы  и  коллинеарны. По
следствию из теоремы 2.5 данное  условие
можно записать в виде:

    –                                                 (2.43)

канонические уравнения прямой в
пространстве. Равенство нулю одного из знаменателей означает обращение
в нуль соответствующего числителя.

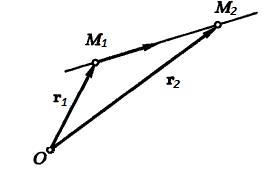
Пусть прямая l проходит через две точки,
одна из которых  – уже введенная в
рассмотрение точка M₀(x₀;y₀;z₀). Другую точку обозначим  M₁(x₁;y₁;z₁). Тогда в качестве направляющего вектора  прямой  можно взять вектор . При этом уравнения (2.43) принимают вид:  

   –                                                                                                                                                    (2.44) 

уравнения прямой в пространстве, проходящей
через две заданные точки.

Все
соотношения (2.43) равны между собой, следовательно, может быть введен
коэффициент пропорциональности t,
называемый параметром прямой:

    – параметрические уравнения прямой.                                                  (2.45) 

Можно записать
частный случай уравнений (2.45) для плоскости: . Они представляют собой параметрические уравнения
прямой линии на плоскости. Проводя аналогичные рассуждения, в качестве
направляющего вектора прямой на плоскости можно взять вектор , параллельный прямой (без учета направления), а точку
M₀(x₀;y₀) – в качестве произвольной точки
прямой. Заметим, что канонические уравнения (2.4) прямой на плоскости
представляют собой частный случай уравнений (2.44).

         Чтобы задать прямую l в пространстве в общем виде
надо рассмотреть её как линию пересечения  двух
плоскостей, которые обозначим через α
и β, и зададим уравнениями соответственно:        . Это
означает, что прямая задается системой, состоящей из уравнений плоскостей α и β:

                                                                                                                                                             (2.46)

–
общее уравнение прямой в пространстве.
Здесь  (в противном случае плоскости параллельны
или совпадают).             

Поставим
задачу – привести общее уравнение (2.46) прямой к  ее каноническим уравнениям (2.43). Решение
состоит из трех этапов.

1.   Отыскание точки  M₀(x₀;y₀;z₀), лежащей на данной прямой.

Координаты
точки  M₀ должны удовлетворять системе (2.46), так как
точка  принадлежит обеим плоскостям  α и β.

Ранг
системы (2.46) равен 2, сама система является совместной неопределенной.
Объявим  базисными  переменными, например, x и y,
тогда z – свободная переменная. Придадим ей конкретное
значение z=z₀. Система примет вид:  при условии, что главный  определитель .  Так как надо знать только одну точку прямой (одно решение системы (2.46)), то
достаточно найти одно ее частное решение. 
Для простоты вычислений можно придать свободной переменной  нулевое значение, то есть z₀=0.  После этого определенную систему уравнений  решают известными методами. Решение
системы  x=x₀; y=y₀
в совокупности со значением свободной переменной представляет собой координаты
искомой точки  M₀(x₀;y₀;z₀).

2.  Рассмотрим нахождение  направляющего вектора  прямой. Так как  перпендикулярен  нормальным векторам  и  плоскостей α и β,
то его можно найти по теореме 2.5 как векторное произведение указанных
векторов:  

.                                                                                                         (2.47)

3. Найденную точку M₀ и вектор  подставляем в
уравнение (2.43). Таким образом, задача о приведении общего уравнения прямой к
каноническому виду решена.

Пример 2.16.
Привести общее уравнение прямой в
пространстве     к
каноническому виду.

Решение. Найдем точку M₀(x₀;y₀;z₀), принадлежащую данной прямой. Достаточно найти одно
частное решение заданной системы, например, при  z₀=0. Решение будет представлять собой координаты точки M₀:  
 

. Используем  метод Крамера – вычислим главный и
вспомогательные определители системы:  .

По формулам (1.6):        

. Следовательно, точка   – искомая точка
заданной прямой.

Найдем направляющий вектор  прямой. Нормальные векторы плоскостей,
пересечением которых задана прямая, есть . Тогда по теореме
2.5: 

.

Подставляя координаты точки M и вектора
 в (2.43), получим искомое каноническое
уравнение прямой l:

Вопросы
для самопроверки

2.2.1. Общее уравнение и направляющий вектор прямой

Ностальгически машем ручкой привычному  и знакомимся с общим уравнением прямой. Поскольку в аналитической геометрии в ходу именно оно:

Общее уравнение прямой имеет вид: , где  – некоторые числа, при этом коэффициенты  одновременно не равны нулю (т.к. теряется смысл).

Оденем в костюм и галстук уравнение с угловым коэффициентом . Сначала перенесём все слагаемые в левую часть:
, слагаемое с «иксом» нужно поставить на первое место:

В принципе, уравнение уже имеет вид , но по правилам математического этикета коэффициент первого слагаемого (в данном случае ) должен быть положительным. Меняем знаки у каждого слагаемого:
, готово.

Запомните эту техническую особенность! Первый коэффициент (чаще всего ) делаем положительным!

По надобности общее уравнение легко привести к «школьному» виду (если  ):

Направляющий вектор прямой

Зададимся вопросом: что достаточно знать, чтобы построить прямую? Две точки. Но об этом детском случае позже, сейчас властвуют палочки со стрелочками. У каждой прямой есть вполне определённый наклон, к которому легко «приспособить» вектор.

Вектор, который параллелен прямой, называется направляющим вектором данной прямой. Очевидно, что у любой прямой бесконечно много направляющих векторов, причём все они будут коллинеарны (сонаправлены или нет – не важно).

Направляющий вектор стандартно обозначается следующим образом: .

Но одного вектора недостаточно для построения прямой, вектор является свободным и не привязан к какой-либо точке плоскости. Поэтому дополнительно нужно знать некоторую точку , которая принадлежит прямой:

2.2.2. Как составить уравнение прямой по точке и направляющему вектору?

2.1. Уравнение прямой с угловым коэффициентом

| Оглавление |



Автор: Aлeксaндр Eмeлин