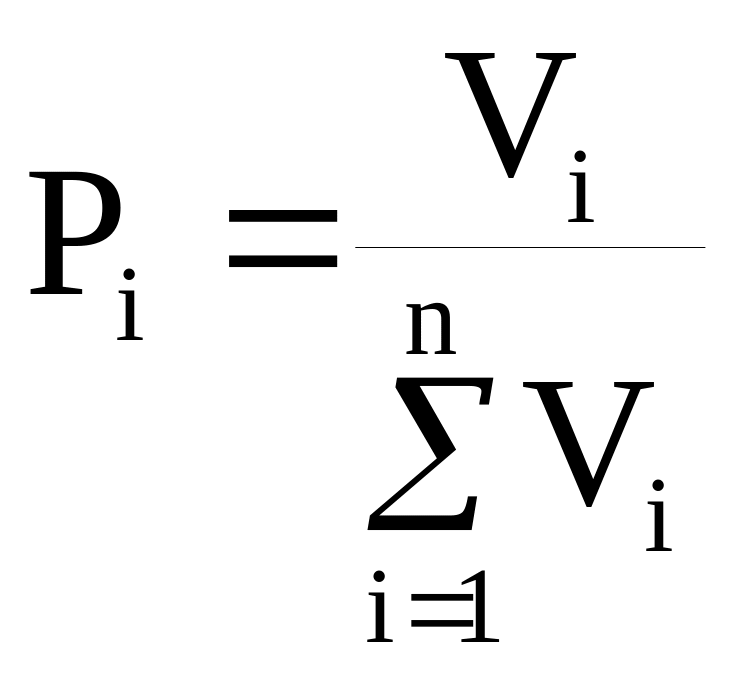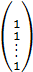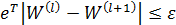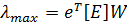Вектор приоритетов.
Проведем
математическую обработку матрицы парных
сравнений в шкале Саати с целью получения
вектора приоритетов сравниваемых
объектов. С математической точки зрения
задача сводится к вычислению главного
собственного вектора, который после
нормализации становится вектором
приоритетов.
Точный
способ вычисления главного собственного
вектора матрицы парных сравнений
заключается в возведении матрицы в
произвольно большие степени и делении
суммы каждой строки на общую сумму
элементов матрицы. Мы воспользуемся
другим, более простым, способом, который
дает хорошее приближение.
|
A1 |
A2 |
… |
An |
Главный собственный вектор |
Ветктор приоритетов |
|
|
A1 |
a11 |
a12 |
… |
a1n |
V1 |
P1 |
|
A2 |
a21 |
a22 |
… |
a2n |
V2 |
P2 |
|
… |
… |
… |
… |
… |
… |
… |
|
An |
an1 |
an2 |
… |
ann |
Vn |
Pn |
Компонента
главного собственного вектора вычисляется
как среднее геометрическое значений в
строке матрицы:
.
Компонента
вектора приоритетов вычисляется как
нормированное значение главного
собственного вектора:
.
Приближенные
значения λmax
для оценки отношения согласованности
можно рассчитать по следующей формуле:
,
где
– сумма элементов i-го
столбца матрицы;
Pj
– вектор приоритетов анализируемой
матрицы.
Пример построения вектора приоритетов.
Пусть
стоит проблема покупки дома. Выделены
следующие факторы, влияющие на решение
этой проблемы: размеры дома, удобство
сообщения, окрестности, возраст дома,
двор, благоустроенность, общее состояние,
финансовые условия покупки. Необходимо
построить вектор приоритетов этих
факторов. Ниже приведена матрица парных
сравнений для рассматриваемых восьми
факторов, заполненная суждениями
эксперта по шкале Саати, на основе
которых и проведены соответствующие
вычисления.
|
общее удовлетворение |
размеры дома |
удобство |
окрестности |
возраст дома |
двор |
благоустроенность |
общее состояние |
финансовые покупки |
главный собственный вектор |
вектор приоритетов |
|
размеры дома |
1 |
5 |
3 |
7 |
6 |
6 |
1/3 |
1/4 |
2.053 |
0.175 |
|
удобство сообщения |
1/5 |
1 |
1/3 |
5 |
3 |
3 |
1/5 |
1/7 |
0.736 |
0.063 |
|
окрестности |
1/3 |
3 |
1 |
6 |
3 |
4 |
6 |
1/5 |
1.746 |
0.149 |
|
возраст дома |
1/7 |
1/5 |
1/6 |
1 |
1/3 |
1/4 |
1/7 |
1/8 |
0.227 |
0.019 |
|
двор |
1/6 |
1/3 |
1/3 |
3 |
1 |
1/2 |
1/5 |
1/6 |
0.418 |
0.036 |
|
благоустроенность |
1/6 |
1/3 |
1/4 |
4 |
2 |
1 |
1/5 |
1/6 |
0.497 |
0.042 |
|
общее состояние |
3 |
5 |
1/6 |
7 |
5 |
5 |
1 |
1/2 |
1.961 |
0.167 |
|
финансовые условия покупки |
4 |
7 |
5 |
8 |
6 |
6 |
2 |
1 |
4.105 |
0.350 |
|
сумма столбца |
9.010 |
21.867 |
10.250 |
41.000 |
26.333 |
25.750 |
10.076 |
2.551 |
11.742 |
1.000 |
λmax=9.863, ИС=0.266, СИ=1.410
(определяем по таблице), ОС=0.189
Следует
отметить, что отношение согласованности
данной матрицы несколько больше
рекомендованного уровня (ОС ≤ 0,1), однако
для задач используемого типа его можно
принять.
В
общем случае уровень согласованности
должен соответствовать тому риску,
который сопутствует работе с
несогласованными данными.
Например, при
сравнении воздействия лекарств на
организм необходимо иметь очень высокий
уровень согласованности.
Порядок выполнения
работы.
-
Орпеделить
из таблицы проблему и список критериев
для своего варианта. Номер проблемы
определяет значение m.
Для определения списка критериев
необходимо из исходного списка указанного
в таблице для данной проблемы вычеркнуть
критерий со значением k.
m
– последняя цифра в номере зачетки;
k
– предпоследняя цифра в номере зачетки.
Если
последняя цифра в номере зачетки равна
нулю, то m=9,
если предпоследняя цифра в номере
зачетки равна нулю, то k=1.
|
m |
Проблема; |
Список |
|
1 |
Покупка
|
|
|
2 |
Выбор
|
|
|
3 |
Оценка
|
|
|
4 |
Выбор
|
|
|
5 |
Отбор
|
|
|
6 |
Внедрение
|
|
|
7 |
Выбор
|
|
|
8 |
Выбор
|
|
|
9 |
Оценка
|
|
-
Построить
матрицу парных сравнений для
рассматриваемых восьми факторов,
заполнив ее экспертными оценками по
шкале Саати. -
Вычислить
главный собственный вектор, вектор
приоритетов, λmax,
ИС, ОС. Если значение ОС будет больше
0,3 скорректировать экспертные оценки.
Контрольная
работа №3.
Метод анализа
иерархий. Рассчет локальных приоритетов.
Синтез приоритетов.
Рассмотрим проблему:
«Выбор и покупка дома с
заданным уровнем качества
или покупка такого дома, который бы
вызывал общее
удовлетворение».
В качестве
альтернативных вариантов рассматриваем
три дома (А, Б, В) со следующими
характеристиками.
Дом А – самый
большой дом (из трех), хорошие окрестности,
интенсивное движение транспорта, налоги
на дом не велики. Двор больше, чем у домов
Б и В. общее состояние не очень хорошее,
нужна основательная починка и проведение
малярных работ. Дом финансируется банком
с высокой процентной ставкой, поэтому
финансовые условия можно считать
неудовлетворительными.
Дом Б – немного
меньше дома А, расположен далеко от
автобусных остановок. Вокруг интенсивное
движение транспорта. В доме отсутствуют
современные удобства, но общее состояние
дома очень хорошее. Кроме того, на дом
можно получить закладную с довольно
низкой процентной ставкой, то есть
финансовые условия вполне удовлетворительные.
Дом В – маленький
и без современных удобств. Окрестности
достаточно привлекательны, но налоги
высокие, однако дом в хорошем состоянии
и достаточно безопасен. Двор больше,
чем у дома Б, однако значитльно меньше,
чем у дома А. Объем восстановительно-ремонтных
работ очень мал. Финансовые условия
намного лучше, чем для дома А, но не так
хороши, как для дома Б.
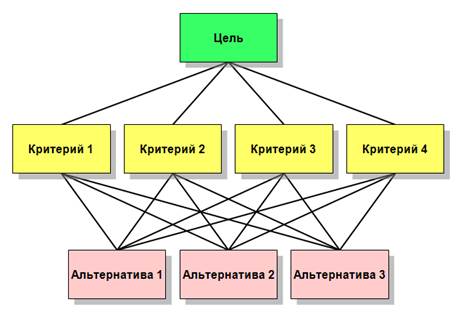
Иерархическая
модель решения проблемы для рассматриваемого
примера имеет следующий вид:
Для того чтобы
принять обоснованное решение на выбор
дома необходимо выполнить следующее.
После построения
иерархической модели проблемы начинаем
первый этап анализа, который состоит в
исследовании степени влияния показателей
свойств качества дома на общее
удовлетворение домом. В формальном виде
этот этап состоит в анализе влияния
факторов второго уровня иерархии на
цель анализа – первый уровень. Этот
этап был выполнен в предыдущей лабораторной
работе. Была представлена матрица парных
сравнений для восьми факторов 1-го
уровня, заполненная суждениями эксперта
по шкале Саати. На основании этих данных
были определены вектор приоритетов,
λmax, ИС, ОС.
На
втором этапе переходим к рассмотрению
влияния факторов третьго уровня на
факторы второго уровня, то есть к анализу
«веса» (предпочтительности) каждого из
рассматриваемых домов (А, Б, В) по отношению
к каждому фактору второго уровня. Для
этого необходимо сформировать и
обработать восемь экспертных матриц
парного сравнения. Сами матрицы и
результаты их обработки в виде векторов
приоритетов и мер согласованности
представлены в таблице.
|
Размеры дома |
А |
Б |
В |
Вектор приоритетов |
Удобство |
А |
Б |
В |
Вектор приоритетов |
|
А |
1 |
6 |
8 |
0.754 |
А |
1 |
5 |
4 |
0.233 |
|
Б |
1/6 |
1 |
4 |
0.181 |
Б |
1/5 |
1 |
1/3 |
0.054 |
|
В |
1/8 |
1/4 |
1 |
0.065 |
В |
1/4 |
3 |
1 |
0.712 |
|
λмах=3.136 ИС=0.068 ОС=0.117 |
λмах=3.247 ИС=0.123 ОС=0.213 |
||||||||
|
окрестности |
А |
Б |
В |
Вектор приоритетов |
возраст дома |
А |
Б |
В |
Вектор приоритетов |
|
А |
1 |
8 |
6 |
0.754 |
А |
1 |
1 |
1 |
0.333 |
|
Б |
1/8 |
1 |
1/4 |
0.065 |
Б |
1 |
1 |
1 |
0.333 |
|
В |
1/6 |
4 |
1 |
0.181 |
В |
1 |
1 |
1 |
0.333 |
|
λмах=3.136 ИС=0.068 ОС=0.117 |
λмах=3.000 ИС=0.000 ОС=0.000 |
||||||||
|
двор |
А |
Б |
В |
Вектор приоритетов |
благоустроенность |
А |
Б |
В |
Вектор приоритетов |
|
А |
1 |
5 |
4 |
0.674 |
А |
1 |
8 |
6 |
0.747 |
|
Б |
1/5 |
1 |
1/3 |
0.101 |
Б |
1/8 |
1 |
1/5 |
0.060 |
|
В |
1/4 |
3 |
1 |
0.226 |
В |
1/6 |
5 |
1 |
0.193 |
|
λмах=3.086 ИС=0.043 ОС=0.074 |
λмах=3.197 ИС=0.099 ОС=0.170 |
||||||||
|
общее состояние |
А |
Б |
В |
Вектор приоритетов |
финансовые покупки |
А |
Б |
В |
Вектор приоритетов |
|
А |
1 |
1/2 |
1/2 |
0.200 |
А |
1 |
1/7 |
1/5 |
0.072 |
|
Б |
2 |
1 |
1 |
0.400 |
Б |
7 |
1 |
3 |
0.649 |
|
В |
2 |
1 |
1 |
0.400 |
В |
5 |
1/3 |
1 |
0.279 |
|
λмах=3.000 ИС=0.000 ОС=0.000 |
λмах=3.065 ИС=0.032 ОС=0.056 |
Анализ векторов
локальных приоритетов показывает, что
дом А лучший по четырем критериям (размер
дома, окрестности, двор и благоустроенность),
дом Б лучший по финансовым условия, а
дом В лучший по удобству сообщения.
На третьем этапе
осуществляется синтез локальных
приоритетов или оценка обобщенных
(глобальных) приоритетов. В нашем примере
речь идет о получении вектора глобальных
приоритетов домов (А, Б, В,) по отношению
к цели верхнего уровня – общего
удовлетворения домом.
Для этого матрицу
локальных приоритетов 2-го уровня,
составленную по результатам анализа,
представленного в приведенной выше
таблицы, умножают на на вектор локальных
приоритетов 1-го уровня, полученный в
примере контрольной работы №2.
Матрица локальных
приоритетов 2-го уровня
.
|
размеры дома |
удобство |
окрестности |
возраст дома |
двор |
благоустроенность |
общее состояние |
финансовые покупки |
|
|
А |
0.754 |
0.233 |
0.754 |
0.333 |
0.674 |
0.747 |
0.200 |
0.072 |
|
Б |
0.181 |
0.054 |
0.065 |
0.333 |
0.101 |
0.060 |
0.400 |
0.649 |
|
В |
0.065 |
0.712 |
0.181 |
0.333 |
0.226 |
0.193 |
0.400 |
0.279 |
Вектор
локальных приоритетов 1-го уровня.
|
размеры дома |
0.175 |
|
удобство |
0.063 |
|
окрестности |
0.149 |
|
возраст дома |
0.019 |
|
двор |
0.036 |
|
благоустроенность |
0.042 |
|
общее состояние |
0.167 |
|
Финансовые |
0.350 |
В
результате получаем обобщенный
(глобальный) вектор проритетов домов
(А, Б, В) по отношению к конечной цели –
покупке дома. Этот вектор имеет вид:
|
Дом |
Вектор приоритетов |
|
А |
0.379 |
|
Б |
0.351 |
|
В |
0.270 |
Таким образом, с
учетом всех рассматриваемых факторов,
предпочтение при покупке отдается дому
А.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Простая математика для решения непростых задач
Время на прочтение
3 мин
Количество просмотров 18K
При рассмотрении статьи, посвященной системе приоритезации обращений в техническую службу АО «Инфовотч», может возникнуть логичный вопрос: каким образом проводился расчет весовых коэффициентов? «Уложить» алгоритм расчета в комментарий к статье с учетом его объема будет, мягко говоря, трудновато. Поэтому, предвидя подобные вопросы, мы решили дополнить предыдущую статью поэтапным рассмотрением алгоритмов расчета данных весовых коэффициентов.
В первую очередь стоит отметить, что весь расчет основывается на инструментарии, используемом в методе анализа иерархий (МАИ). МАИ — математический инструмент принятия управленческих решений экспертным путем. Краткий смысл данного метода, в теории, заключается в представлении проблемы в виде иерархии. Вершиной данной иерархии является наша цель. Нижний уровень содержит альтернативы, промежуточный — критерии оценки данных альтернатив.
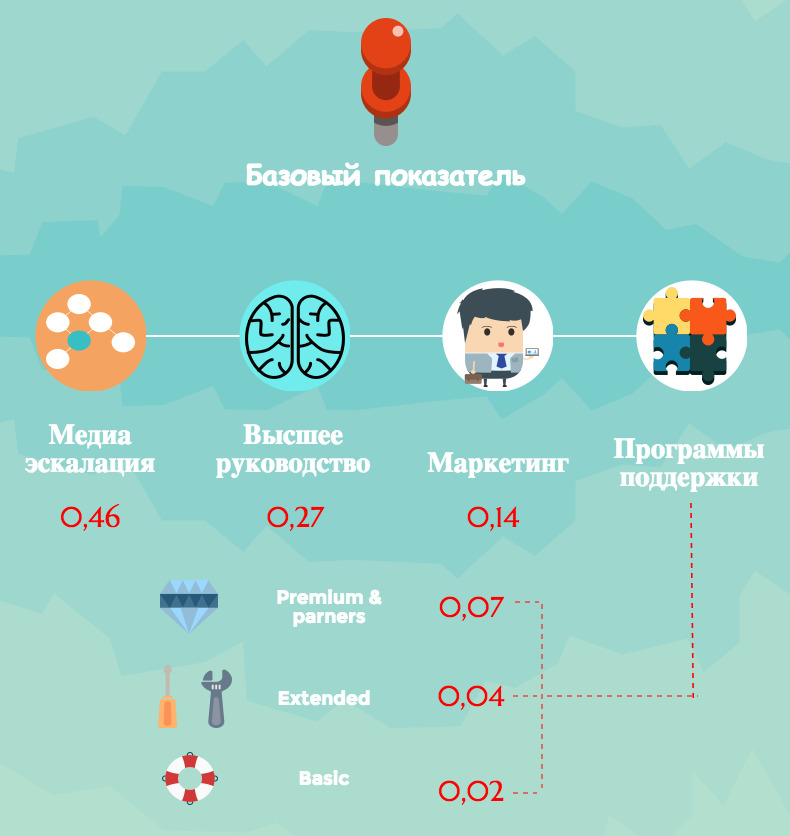
Рисунок 1. Расчетные данные по базовому показателю
Вид иерархии напрямую зависит от задачи, которую мы ставим перед собой при принятии решений. В нашем случае иерархии будут двухуровневые, так как здесь мы не решаем задачу выбора, а используем данный инструмент для расчета весов экспертным путем. В целях упрощения рассмотрения расчетного алгоритма, детально рассмотрим все расчеты на примере определения весов по базовому показателю. Аналогично производится расчет по плавающим показателям.
Рисунок 2. Расчетные данные по базовому показателю
В теории МАИ алгоритм расчета реализуется в пять этапов. Однако мы будем использовать только два этапа, направленные на построение матриц парных сравнений и расчет соответствующего вектора приоритетов, содержащего искомый вес.
Стоит отметить, что представление задачи в виде иерархии на практике является необязательным. Наша иерархия на первом уровне содержит «Базовый показатель», второй уровень иерархии содержит компоненты «Медиа-эскалация», «Высшее руководство», «Маркетинг», а также три программы поддержки.
Следующим этапом является определение приоритетов компонент, которые отражают вес той или иной компоненты в рассматриваемой группе. Также необходимо отметить, что приоритет находится в диапазоне от нуля до единицы. Сумма приоритетов всех компонентов, подчиненных базовому показателю, равна единице. Чтобы рассчитать данные приоритеты, проведем парные сравнения компонент по отношению к базовому показателю. На данном этапе рассчитывается обратно-симметричная матрица по свойству:
где индексы i и j – это номер строки и номер столбца, на пересечении которых стоит элемент.
При сравнении компоненты с самой собой выставляем единицу. Формализация задачи имеет вид:
Матрицы строятся следующим образом. В левом верхнем углу записывается элемент, по отношению к которому проводится сравнение по степени важности. Заглавия столбцов и строк содержат сравниваемые элементы. Для нашей задачи мы строили пять матриц, одну для базового показателя, и четыре по плавающим показателям и их классификационным признакам.
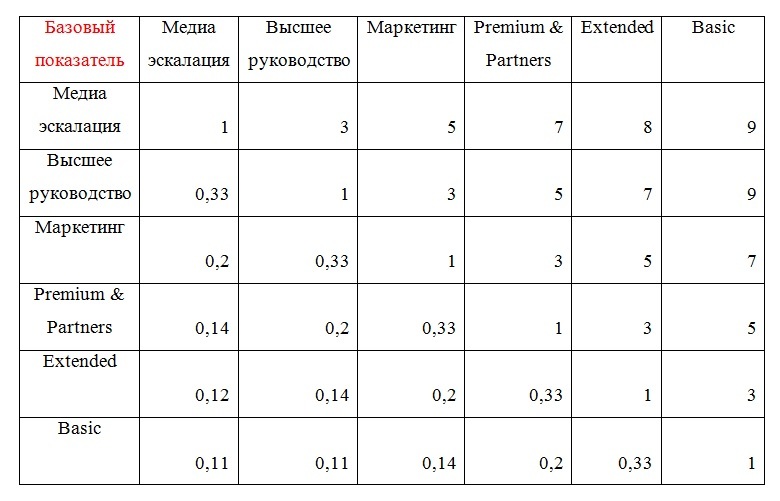
Теперь давайте посмотрим, что представляет матрица для расчета весов по базовому показателю в общем виде.
Таблица 1. Матрица 2 уровня иерархии
Если с диагональю все понятно (как мы уже говорили, при сравнении элемента с самим собой выставляется единица), то откуда брать оценки относительной важности для всех остальных клеток? Для данных целей разработана универсальная шкала относительной важности.
Таблица 2. Шкала относительной важности
Таким образом, эксперт, сравнивая элементы в строках с элементами в столбцах по степени важности с точки зрения базового показателя, постепенно заполнил данную матрицу с использованием свойства обратной симметрии.
Например, из матрицы можно видеть, что «Медиа эскалация» превосходит уровень поддержки «Basic» по отношению к базовому показателю очень сильно, о чем свидетельствует проставленная экспертом интенсивность относительной важности «9».
Стоит отметить, что если между экспертами возникают разногласия, определяется геометрическое среднее разных оценок в качестве общей оценки суждений:
Следующим этапом является синтез приоритетов, который позволяет объединить полученные результаты с целью определения искомых весов.
Для определения относительной ценности каждого элемента нашей матрицы необходимо найти геометрическое среднее и с этой целью перемножить n элементы каждой строки, и из полученного результата извлечь корни n-й степени.
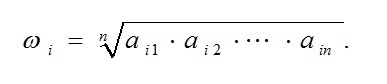
_____________________________________________________________________
Для рассматриваемой матрицы получим (размерность 
Для нормализации полученных чисел определяем нормирующий множитель r.
И каждое из чисел 
В результате получаем вектор приоритетов:

где индекс «2» означает, что вектор приоритетов относится ко второму уровню иерархии.
_____________________________________________________________________
Для рассматриваемого примера нормирующий коэффициент равен:
А вектор приоритетов:
Числа
являются компонентами вектора приоритетов компонент
Подобную процедуру проделываем для всех матриц парных сравнений и получаем результат по всем требуемым весам. В завершении стоит отметить, что данный расчетный алгоритм легко реализуется средствами MS Excel.
- Общая характеристика метода анализа иерархий.
- Этапы применения метода анализа иерархий.
- Основные понятия метода анализа иерархий.
Общая характеристика метода анализа иерархий
Метод Анализа Иерархий (МАИ) – математический инструмент системного подхода к решению проблем принятия решений. МАИ не предписывает лицу, принимающему решение (ЛПР), какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант (альтернативу), который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению. Этот метод разработан американским ученым Томасом Л. Саати в 1970 году, с тех пор он активно развивается и широко используется на практике. Метод анализа иерархий можно применять не только для сравнения объектов, но и для решения более сложных проблем управления, прогнозирования и др.
Основным достоинством метода анализа иерархий является высокая универсальность – метод может применяться для решения самых разнообразных задач: анализа возможных сценариев развития ситуации, распределения ресурсов, составления рейтинга клиентов, принятия кадровых решений и др.
Недостатком метода анализа иерархий является необходимость получения большого объема информации от экспертов. Метод в наибольшей мере подходит для тех случаев, когда основная часть данных основана на предпочтениях лица, принимающего решения, в процессе выбора наилучшего варианта решения из множества существующих альтернатив.
В типичной ситуации принятия решения:
- рассматриваются несколько вариантов решения,
- задан критерий, по которому определяется в какой мере то или иное решение является подходящим,
- известны условия, в которых решается проблема, и причины, влияющие на выбор того или иного решения.
Постановка задачи в процессе применения метода анализа иерархий: Пусть имеется множество альтернатив (вариантов решений): В1, В2, … Вk. Каждая из альтернатив оценивается списком критериев: К1, К2, … Кn. Требуется определить наилучшее решение.
Этапы применения метода анализа иерархий:
1. Предварительное ранжирование критериев, в результате которого они располагаются в порядке убывания важности (значимости).
2. Попарное сравнение критериев по важности по девятибалльной шкале с составлением соответствующей матрицы (таблицы) размера (n х n). Система парных сведений приводит к результату, который может быть представлен в виде обратно симметричной матрицы. Элементом матрицы a(i,j) является интенсивность проявления элемента иерархии i относительно элемента иерархии j, оцениваемая по шкале интенсивности от 1 до 9, где оценки имеют следующий смысл:
- равная важность – 1;
- умеренное превосходство – 3;
- значительное превосходство – 5;
- сильное превосходство – 7;
- очень сильное превосходство – 9;
- в промежуточных случаях ставятся четные оценки: 2, 4, 6, 8 (например, 4 – между умеренным и значительным превосходством).
При этом при проведении попарных сравнений в основном ставятся следующие вопросы при сравнении элементов А и Б:
- какой из них важнее или имеет большее воздействие ?
- какой из них более вероятен?
- какой из них предпочтительнее ?
Затем формируется матрица (схема представлена в Таблице 2). В процессе заполнения матрицы если элемент i важнее элемента j, то клетка (i, j), соответствующая строке i и столбцу j , заполняется целым числом, а клетка (j, i), соответствующая строке j и столбцу i, заполняется обратным числом (дробью).
Например, если К1 умеренно превосходит К4, то в клетку (1;4) (на пересечении первой строки и четвертого столбца) ставится число 3, а в клетку (4;1) (четвертая строка первый столбец) – обратная величина, равная 1/3. Если же элемент j более важен, чем элемент i, то целое число ставится в клетку (j, i), а обратная величина – в клетку (i, j). Если считается, что i, j одинаковы, то в обе клетки ставится единица.
Заполнение таблицы (см.примерная схема в табл.2) проводится построчно с наиболее важного критерия. Сначала проставляют целочисленные оценки, тогда соответствующие им дробные оценки получаются из них автоматически (как обратные к целым числам). Чем важнее критерий, тем больше целочисленных оценок будет в соответствующей ему строке матрицы, и сами оценки имеют большие значения. Так как каждый критерий равен себе по важности, то главная диагональ матрицы всегда будет состоять из единиц. Очевидно, что сумма компонентов равна единице. Каждый компонент НВП представляет собой оценку важности соответствующего критерия (например, 1-й компонент представляет собой оценку важности первого критерия). 

Таблица 1 — Значение показателя случайной согласованности (ПСС)*
| Размер матрицы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ПСС | 0 | 0 | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 |
*Примечание:
Показатель Случайной Согласованности (ПСС) Т.Л.Саати называет Случайный индекс (СИ).
Значения ПСС (СИ) см, например, на с.25 Саати Т.Л. Принятие решений. Метод анализа иерархий. – М.: Радио и связь, 1993, на с. 137 Романов В.Н. Системный анализ для инженеров. – СПб.: СЗГЗТУ, 2006.
Оценки в матрице считаются согласованными, если ОС≤10-15%, в противном случае их надо пересматривать.
5. Проводится попарное сравнение вариантов по каждому критерию аналогично тому, как это делалось для критериев, и заполняются соответствующие таблицы (см.ниже – схема представлена в Таблице 3). Для каждой таблицы проводится проверка согласованности локальных приоритетов путем расчета трех характеристик (см.описание 4-го этапа).
6. Определяется общий критерий (приоритет) для каждого варианта:
К(В1) = оценка В1 по первому критерию х 1й компонент НВП + оценка В1 по второму критерию х 2й компонент НВП + … + оценка В1 по nму критерию х nй компонент НВП (6)
Аналогично подсчитываются К(В2), К(В3) и т.д., при этом в выражении В1 заменяется на В2 , В3 и т.д. соответственно. Заполняется таблица (см.ниже – схема представлена в Таблице 4).
7. Определяется наилучшее решение, для которого значение К максимально.
8. Проверяется достоверность решения:
8.1. расчет обобщенного индекса согласования:
ОИС = ИС1 х 1й компонент НВП + ИС2 х 2й компонент НВП + … + ИСnх nй компонент НВП (7)
8.2. расчет обобщенного отношения согласованности:
ООС = ОИС/ ОПСС (8)
где ОПСС определяется по таблице 1 на уровне ПСС (показателя случайной согласованности) для матриц сравнения вариантов по критериям.
Решение считается достоверным, если ООС≤10-15%, в противном случае нужно корректировать матрицы сравнения вариантов по критериям.
Таблица 2 — Форма таблицы сравнения критериев
| К1 | К2 | …. | Кn | Средние геометрические | НВП(по фор-муле (2)) | |
| К1 | ||||||
| К2 | ||||||
| …. | ||||||
| Кn | ||||||
| ИТОГО | по формуле (1) | |||||
| λmax | по форм. (3) | |||||
| ИС | по форм. (4) | |||||
| ОС | по форм. (5) |
Таблица 3 — Форма таблицы сравнения вариантов по критериям (заполняется по каждому j-му критерию сравнения Kj j=1,n)
| Кj | В1 | В2 | …. | Вk | Средние геометрические | НВП(по фор-муле (2)) |
| В1 | ||||||
| В2 | ||||||
| …. | ||||||
| Вk | ||||||
| ИТОГО | по формуле (1) | |||||
| λmaxj | по форм. (3) | |||||
| ИСj | по форм. (4) | |||||
| ОСj | по форм. (5) |
Таблица 4 — Форма таблицы расчета итоговых значений приоритетов
| К1 | К2 | …. | Кn | Итоговые значения приоритетов (расчет по формуле (6)) | |
| приводятся значения 1-го компонента НВП из таблицы 2 | приводятся значения 2-го компонент НВП из таблицы 2 | приводятся значения n-го компонента НВП из таблицы 2 | |||
| В1 | К(В1)= | ||||
| В2 | К(В2)= | ||||
| …. | … | ||||
| Вk | К(В3)= | ||||
| ИС | приводится зна-чение ИС1 по К1 | приводится зна-чение ИС2 по К2 | … | приводится зна-чение ИСn по Кn | приводится сумма по столбцу |
| ОИС | расч. по форм. (7) | ||||
| ООС | расч. по форм. (8) |
Основные понятия метода анализа иерархий
В соответствии с формулировкой задачи принятия решения структура модели принятия решения в методе анализа иерархий представляет собой схему (граф), которая включает:
- набор альтернативных решений,
- главный критерий рейтингования решений,
- набор групп однотипных факторов, влияющих на рейтинг,
- множество направленных связей, указывающих на влияния решений, критерия и факторов друг на друга.
Структура модели отражает результат анализа ситуации принятия решения. Основные группы понятий метода анализа иерархий:
- Первая группа понятий связана с описанием возможных структур моделей принятия решения. Для вычисления приоритетов альтернативных решений к структуре необходимо добавить информацию о силе влияний решений, критерия и факторов друг на друга.
- Вторая группа понятий связана с описанием данных для моделей принятия решения. После того как сформирована структура и собраны все данные, модель принятия решения готова, т.е. в ней могут быть получены рейтинги приоритетов решений и факторов. Знание приоритетов используется для поддержки принятия решения.
- Третья группа понятий связана с описанием результатов, получаемых в моделях принятия решения. Четвертая группа понятий связана с пояснением того, как организованы вычисления. Знание этих понятий необходимо лишь для понимания математических обоснований метода. Для применения метода знание этих понятий необязательно.
1. Cтруктуры
1.1) Узел – общее название для всех возможных решений (альтернатив), главного критерия (главной цели) рейтингования решений, всех факторов, от которых, так или иначе, зависит рейтинг. Название узла совпадает с названием соответствующего решения, критерия или фактора. Заметим, что с математической точки зрения схема ситуации принятия решения (структура модели), которая строится в методе анализа иерархий, является графом. Таким образом, понятие «узел» вполне оправдано. Ясно также, что решения, критерий и факторы являются «узлами» проблемы принятия решения.
1.2) Уровень – группа всех однотипных (равноправных, однородных, гомогенных и т.п.) узлов. Название уровня отражает назначения, функцию группы узлов в ситуации принятия решения. Каждый узел определяется не только своим названием, но и названием уровня, которому он принадлежит. Ясно, что отдельный уровень образуют альтернативные решения (узлы этого уровня однотипны в том смысле, что они являются решениями; прочие узлы таковыми не являются). Главный критерий рейтингования, как правило, один – это отдельный уровень. На рейтинг оказывают влияние несколько групп факторов – это также уровни.
1.3) Вершина – узел, соответствующий главному критерию (главной цели) отбора альтернатив.
1.4) Связь – указание на наличие влияния одного узла (доминирующего) на другой (подчиненный). На схеме связь изображается стрелкой. Направление связи (и соответствующей стрелки) совпадает с направлением влияния. С точки зрения теории графов связь – дуга направленного графа. Связь от узла-фактора к узлу-решению означает, что предпочтительность (важность, оптимальность) решения оценивается с точки зрения воздействия данного фактора. Связь от вершины к узлу-фактору означает, что важность учета фактора оценивается с точки зрения главного критерия рейтингования альтернатив. Связь от узла-фактора к узлу-фактору означает, что важность учета второго фактора рассматривается с точки зрения первого фактора.
1.5) Кластер – группа узлов одного уровня, подчиненных некоторому узлу другого уровня –вершине кластера (доминирующему узлу). Кластеры образуются при расстановке связей между узлами, т.е. при расстановке связей происходит формирование кластерной структурыAdvice_KlasterStruct. Важность узлов кластера друг относительно друга оценивается в соответствие с тем, какой узел является вершиной кластера.
Кластер определяется: 1) своей вершиной, 2) названием уровня, 3) списком узлов. 1.6) Система (структура модели, схема ситуации принятия решения) – совокупность всех узлов, сгруппированных по уровням, и всех связей между узлами.
С математической точки зрения системы, которыми приходится оперировать в методе анализа иерархий, являются – направленными графами (сетями). Связи образуют пути, ведущие от одних узлов к другим. Все пути так или иначе являются частями основных путей, ведущих от главного критерия рейтингования через факторы к альтернативам, т.е. основные пути, по сути, являются логическими цепочками, ведущими к выбору одной из альтернатив.
Эта система является иерархической (но не является строгой иерархией). Попутно заметим, что даже для простых задач структуры моделей, строящихся с помощью метода анализа иерархий, представляют собой довольно сложные схемы. Однако это свидетельствует лишь о том, что метод позволяет вскрыть реальную сложность задач, которые человеку приходится решать мысленно. Название системы отражает ее назначение, принадлежность к сфере деятельности, в которой принимается решение.
1.7) Иерархия – система, в которой уровни расположены и пронумерованы так, что: 1) нижний уровень содержит рейтингуемые альтернативы, 2) узлы уровней с большими номерами могут доминировать только над узлами уровней с меньшими номерами. Таким образом, в иерархии связи определяют пути одной направленности — от вершины к альтернативам через промежуточные уровни, которые состоят из узлов-факторов. Система представляет собой строгую иерархию, если допустимы связи только между соседними уровнями от верхнего уровня к нижнему.
1.8) Система с обратными связями. Система имеет обратные связи, если при любом способе нумерации уровней в системе есть узлы, доминирующие и над узлами уровней с большими номерами, и над узлами уровней с меньшими номерами, т .е. система имеет обратные связи, если ни при каких перестановках уровней она не сводится к иерархии. Кроме того, понять различия в структуре иерархии и системы с обратными связями можно, рассматривая пути, образованные связями.
Если в системе нет ни одного такого уровня, что по путям, начинающимся в узлах этого уровня, можно попасть в узлы того же уровня, то система является иерархией, т.е. в иерархии любой путь может пересекаться с каждым уровнем лишь однажды. Если в системе имеются такие уровни, что по пути, начинающемуся в одном из узлов этого уровня, можно попасть в один из узлов того же уровня, то система имеет обратные связи. Т.е. в системе с обратными связями обязательно есть пути, пересекающие некоторые уровни хотя бы дважды. Формирование структуры без обратных связей (иерархии) и формирование структуры с обратными связями производятся по определенным правилам.
2. Данные
2.1) Приоритет узла в кластере – положительное число, служащее для количественного выражения важности (веса, значимости, предпочтительности и т.п.) данного узла в кластере относительно остальных узлов кластера в соответствие с критерием, заключенным в вершине кластера. Сумма всех приоритетов узлов кластера равна единице. Поэтому часто приоритеты можно трактовать как вероятности, доли общего ресурса и т.п. в зависимости от рассматриваемого случая.Часто трудно непосредственно определить набор приоритетов (вектор приоритетов) узлов кластера. Тогда используется процедура парных сравнений и метод собственного вектора
2.2) Пaрные сравнения узлов кластера – оценки (качественные или количественные) отношения приоритета одного узла к приоритету другого, т.е. результаты парных сравнений – это оценки важности (предпочтительности, вероятности и т.п.) каждого узла кластера относительно каждого из других по критерию, заключенному в вершине кластера. Результат парного сравнения – оценка отношения «весов» сравниваемых объектов («веса» объектов численно выражают их предпочтительность, оптимальность, значимость и т.п.). Цель парных сравнений – определение приоритетов узлов кластера. Для того, чтобы уточнить, в каком смысле название вершины кластера является критерием для проведения сравнений используется формулировка критерия для парных сравнений. Для проведения парных сравнений задаются параметры: шкала сравнений и способ сравнений. При проведении парного сравнения объектов и достаточно установить только один из результатов (оценка отношения «веса» объекта и весу объекта ) или , так как .
2.3) Шкала сравнений – упорядоченный набор градаций (терминов, чисел и т.п.) для выражения результатов парных сравнений. Шкала сравнений позволяет выражать оценки отношений значений приоритетов узлов, поэтому ее деления – безразмерные величины. Шкалы, использующиеся в методе анализа иерархий, являются шкалами отношений. Т.е. если результату сравнения пары объектов ставится в соответствие значение на шкале, то число — оценка отношения «весов» объектов («веса» объектов численно выражают их предпочтительность, оптимальность, значимость и т.п.)
Шкала является количественной, если результаты парных сравнений выражаются непосредственно с помощью чисел. Шкала является качественной, если результаты парных сравнений выражаются с помощью с градаций-предпочтений. Градациям качественных шкал, использующихся в методе анализа иерархий, соответствуют числа.Т.е. качественные шкалы предоставляют возможность опосредованного оценивания приоритетов через предпочтения.
Дискретная шкала имеет конечных набор градаций (при переходе от одной градации к другой значение парного сравнения изменяется скачком). Дискретной шкале соответствует конечный набор чисел. Дискретные шкалы отличаются по величине наибольшего значения (при количественных сравнениях) или по количеству основных градаций (при качественных сравнениях).
Если число — верхний предел шкалы, то — нижний предел шкалы, т.е. все результаты парных сравнений, выраженные в такой шкале, лежат в пределах от до . Если результату сравнения пары объектов соответствует единица, то значения «весов» объектов оцениваются как равные. Кроме того, для дискретной шкалы — количество градаций для выражения превосходства одного из сравниваемых объектов над другим. При этом дискретная шкала имеет градации . В качестве градаций непрерывной шкалы может использоваться любое из действительных чисел от до .
Непрерывная шкала имеет непрерывный набор градаций (между основными делениями шкалы есть всевозможные промежуточные). Градациям непрерывной шкалы соответствуют числа на отрезке числовой прямой. Непрерывные шкалы отличаются по величине наибольшего значения (при количественных сравнениях) или по количеству основных градаций (при качественных сравнениях). Если «вес» объекта оценивается как превышающий «вес» объекта , результату парного сравнения объектов и соответствует значение на шкале, большее единицы. В противном случае лежит на шкале слева от единицы. В соответствии с этим правилом осуществляется и перевод градаций качественных шкал в числовые значения.
2.4) Способ сравнений определяется набором парных сравнений, необходимых для определения приоритетов узлов кластера. При сравнениях с эталоном (по Стивенсу) выбирается один из узлов кластера, с которым сравниваются все остальные. При проведении классических сравнений (по Саати) каждый узел кластера сравнивается со всеми остальными узлами кластера.
2.5) Сравнения кластеров — процедура оценки важности (приоритетности, силы подчинения) кластеров, имеющих общую вершину.Кластеры сравниваются друг с другом по критерию, заданному названием их вершины. Для проведения сравнений используется та же методика, что и для сравнений узлов в кластере. Фактически при сравнении кластеров, подчиненных одному узлу, производится рейтингование уровней по критерию, определяемому этим узлом.
2.6) Матрица сравнений – таблица числовых значений парных сравнений (для узлов кластера или для кластеров, имеющих общую вершину).
2.7) Индекс согласованности – количественная оценка противоречивости результатов сравнений (для системы в целом, для узлов одного кластера или для кластеров, имеющих общую вершину). Следует иметь в виду, что между достоверностью и непротиворечивостью сравнений нет явной связи. Противоречия в сравнениях возникают из-за субъективных ошибок экспертов. Индекс согласованности не зависит от шкал сравнений, но зависит от количества парных сравнений. Индекс согласованности – положительное число. Чем меньше противоречий в сравнениях, тем меньше значение индекса согласованности. При использовании способа сравнений с эталоном значение индекса согласованности равно нулю.
2.8) Достоверность результата сравнения – количественной оценка, характеризующая степень неточности (размытости) результата сравнения, связанная с компетентностью эксперта, уровнем доверия к данным и т.п. Достоверность сравнения выражается долей единицы (или в процентах). Нулю соответствуют абсолютно недостоверные сравнения, единице (или 100%) – абсолютно достоверные сравнения. На основе значений достоверности сравнений для кластеров, имеющих общую вершину, и значений достоверности парных сравнений в кластерах определяется достоверность данных в масштабах всей системы.
2.9) Относительная согласованность матрицы сравнений– отношение индекса согласованности к среднестатистическому значению индекса согласованности при случайном выборе коэффициентов матрицы сравнений. Относительная согласованность для системы в целом характеризует взвешенное среднее значение относительной согласованности по всем матрицам сравнений. Данные можно считать практически непротиворечивыми (достаточно согласованными), если значение относительной согласованности меньше чем 0,1. Это заключение справедливо как для данных кластера, так и для данных в масштабе всей системы.
2.10) Идеальные сравнения – наиболее близкие к имеющимся непротиворечивые результаты сравнений. Идеальным сравнениям соответствуют нулевой индекс согласованности и, соответственно, нулевое значение относительной согласованности. Знание идеальных сравнений используется при проведении процедуры согласования для кластеров, позволяющей скорректировать сравнения для уменьшения их противоречивости.
2.11) Наиболее противоречивые сравнения – это результаты нескольких парных сравнений узлов одного кластера или кластеров, имеющих общую вершину, вносящие наибольший вклад в значение относительной согласованности.
3. Результаты
3.1) Итоговый вектор приоритетов – рейтинг альтернатив. Каждой альтернативе (каждому возможному решению) ставится в соответствие положительное число – приоритет. Приоритет количественно выражает важность (предпочтительность, вероятность, оптимальность и т.п.) альтернативы в соответствии с главным критерием. Сумма приоритетов всех альтернатив равна единице. Вследствие этого часто допустимо отождествление приоритетов с вероятностями. Для поддержки принятия решения в основном с помощью итогового вектора приоритетов производится интерпретация результатов применения метода. Например, принимается решение с наибольшим приоритетом, отвергается решение с наименьшим приоритетом и т.п.
3.2) Вектор приоритетов уровня — рейтинг узлов данного уровня. Вектор приоритетов уровня вычисляется в предположении, что узлы данного уровня являются альтернативами. Все уровни, кроме тех, что содержат альтернативы и главный критерий рейтингования альтернатив, состоят из факторов, влияющих на итоговый вектор приоритетов. Таким образом, приоритеты узлов-факторов количественно характеризуют важность учета каждого фактора относительно других факторов того же уровня. При вычислении вектора приоритетов уровня рассматриваются только такие пути, образованные связями, которые ведут от вершины к узлам данного уровня. Приоритет узла в системе – это соответствующая компонента вектора приоритетов уровня, которому принадлежит данный узел.
3.3) Вектор приоритетов кластера – рейтинг узлов кластера. Вектор приоритетов узлов кластера может задаваться напрямую (без проведения сравнений) или рассчитываться на основе матрицы сравнений.
3.4) Показатели согласованности и достоверности для системы в целом, характеризующие качество данных, использованных для вычисления векторов приоритетов, также являются результатами. Величины этих показателей позволяют оценить степень доверия к результатам, полученным с помощью метода анализа иерархий. Знание показателей согласованности позволяет решать промежуточную задачу выявления участков проблемы, по которым имеется наиболее противоречивая информация. Решение такой задачи позволяет сделать сбор и корректировку данных более целенаправленными.
3.5) Устойчивость вектора приоритетов – качественная характеристика чувствительности значений приоритетов к малым изменениям данных или структуры модели. Очевидно, данные, использующиеся для принятия решений, всегда более или менее неточны. Поэтому чем меньше чувствительность значений приоритетов, тем больше обоснованность использования этих приоритетов для поддержки принятия решения. В зависимости от решаемой задачи определяется понятие «существенное изменение рейтинга» (смена лидера, смена аутсайдера и т.п.). Если при малых изменениях данных или структуры рейтинг изменяется несущественно, то он считается устойчивым.
3.6) Существенные элементы структуры – это узлы или связи между узлами, удаление которых приводит к существенному изменению рейтинга. Очевидно, заранее бывает чрезвычайно сложно определить, какие факторы являются определяющими для принятия решения, а какими можно пренебречь. Часто при принятии решений происходит упрощение ситуации (отбрасывание ряда факторов) или делается попытка учесть максимально возможное количество факторов. Поэтому поиск существенных факторов является важной самостоятельной задачей в процессе подготовки принятия решения.
3.7) Приоритет узла в модели – соответствующая компонента вектора приоритетов уровня, которому принадлежит данный узел. Допустим, в решаемой задаче близость приоритета к единице (к нулю) ассоциируется с предпочтительностью оптимальностью и т.п. Тогда, как правило, узлы с малыми (с большими) приоритетами оказываются несущественными.
3.8) Приоритет кластера в модели. Если некоторый узел является вершиной только одного кластера, то приоритет кластера в модели совпадает с приоритетом его вершины. (В модели, структура которой является строгой иерархией, так определяется приоритет для каждого кластера.) Если некоторый узел является вершиной нескольких кластеров, то для них устанавливаются приоритеты относительно общей вершины. Приоритет каждого из таких кластеров определяется как произведение приоритета относительно вершины на приоритет узла-вершины в модели.
Источники по процедуре применения Метода анализа иерархий
- Саати Т.Л. Принятие решений. Метод анализа иерархий. – М.: Радио и связь, 1993.
- Саати Т.Л. Принятие решений при зависимостях и обратных свя-зях: аналитические сети. – М.: Либроком, 2009.
- Гудков П.А. Методы сравнительного анализа. Учеб. пособие. – Пенза: Изд-во Пенз. гос. ун-та, 2008.
- Романов В.Н. Системный анализ для инженеров. – СПб.: СЗГЗТУ, 2006.
Собственные векторы и собственные значения матриц
Цель лабораторной работы
Знакомство с методами построения матрицы попарных сравнений и расчета ее собственного вектора.
Теоритическая часть
Матрицы парных сравнений
После построения иерархии устанавливается метод сравнения ее элементов. Если принимается метод попарного сравнения, то строится множество матриц парных сравнений. Для этого в иерархии выделяют элементы двух типов: элементы-«родители» и элементы-«потомки». Элементы-«потомки» воздействуют на соответствующие элементы вышестоящего уровня иерархии, являющиеся по отношению к первым элементами-«родителями». Матрицы парных сравнений строятся для всех элементов-«потомков», относящихся к соответствующему элементу-«родителю». Элементами-«родителями» могут являться элементы, принадлежащие любому иерархическому уровню, кроме последнего, на котором расположены, как правило, альтернативы. Парные сравнения проводятся в терминах доминирования одного элемента над другим. Полученные суждения выражаются в целых числах с учетом девятибалльной шкалы.
| Степень значимости | Определение | Объяснение |
| Одинаковая значимость | Два действия вносят одинаковый вклад в достижение цели | |
| Некоторое преобладание значимости одного действия над другим (слабая значимость) | Существуют соображения в пользу предпочтения одного из действий, однако эти соображения недостаточно убедительны | |
| Существенная или сильная значимость | Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность одного из действий | |
| Очевидная или очень сильная значимость | Убедительное свидетельство в пользу одного действия перед другим | |
| Абсолютная значимость | Свидетельства в пользу предпочтения одного действия другому в высшей степени убедительны | |
| 2,4,6,8 | Промежуточные значения между двумя соседними суждениями | Ситуация, когда необходимо компромиссное решение |
| Обратные величины приведенных выше ненулевых величин | Если действию i при сравнении с действием j приписывается одно из определенных выше ненулевых чисел, то действию j при сравнении с действием i приписывается обратное значение | Если согласованность была постулирована при получении N числовых значений для образования матрицы |
Таблица 2.1 — Шкала оценки сравнения альтернатив
Заполнение квадратных матриц парных сравнений осуществляется по следующему правилу. Если элемент Е1 доминирует над элементом Е2 , то клетка матрицы, соответствующая строке Е1 и столбцу Е2, заполняется целым числом, а клетка, соответствующая строке E2 и столбцу Е1, заполняется обратным к нему числом. Если элемент Е2 доминирует над Е1 , то целое число ставится в клетку, соответствующую строке Е2 и столбцу Е1, а дробь проставляется в клетку, соответствующую строке Е1 и столбцу Е2. Если элементы Е1 и Е2 равнопредпочтительны, то в обе позиции матрицы ставятся единицы.
Для получения каждой матрицы эксперт или ЛПР выносит n(n-1)/2 суждений (здесь n — порядок матрицы парных сравнений).
Рассмотрим в общем виде пример формирования матрицы парных сравнений.
Пусть Е1, Е2, . Еn — множество из n элементов (альтернатив) и v1, v2, . vn — соответственно их веса, или интенсивности. Сравним попарно вес, или интенсивность, каждого элемента с весом, или интенсивностью, любого другого элемента множества по отношению к общему для них свойству или цели (по отношению к элементу-«родителю»). В этом случае матрица парных сравнений [Е] имеет вид, изображенный в таблице 2.2.
| [E] = | E1 | E2 | . | En |
| E1 | v1/v1 | v1/v2 | . | v1/vn |
| E2 | v2/v1 | v2/v2 | . | v2/vn |
| . | . | . | . | . |
| En | vn/v1 | vn/v2 | . | vn/vn |
Таблица 2.2 — Общий вид матрицы парных сравнений
Матрица парных сравнений обладает свойством обратной симметрии, т. е.
При проведении попарных сравнений следует отвечать на следующие вопросы: какой из двух сравниваемых элементов важнее или имеет большее воздействие, какой более вероятен и какой предпочтительнее.
При сравнении критериев обычно спрашивают, какой из критериев более важен; при сравнении альтернатив по отношению к критерию — какая из альтернатив более предпочтительна или более вероятна.
Собственные векторы и собственные значения матриц
Ранжирование элементов, анализируемых с использованием матрицы парных сравнений [Е], осуществляется на основании главных собственных векторов, получаемых в результате обработки матриц.
Вычисление главного собственного вектора W положительной квадратной матрицы [Е] проводится на основании равенства
где λmax — максимальное собственное значение матрицы [E].
Для положительной квадратной матрицы [Е] правый собственный вектор W, соответствующий максимальному собственному значению λmax, с точностью до постоянного сомножителя С можно вычислить по формуле
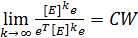
где е T — единичный вектор-строка = (1,1,…,1);
e — единичный вектор-столбец =
k = 1, 2, 3, . — показатель степени;
Вычисления собственного вектора W по выражению (2) производятся до достижения заданной точности:
где l — номер итерации, такой, что l = 1 соответствует k= 1; l = 2, k = 2;
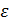
С достаточной для практики точностью можно принять 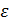
Умножение e T W – можно производить сложением всех элементов W
Максимальное собственное значение вычисляется по формуле:
Индивидуальное задание
Разработать программу, которая запрашивает число альтернатив, после этого, она последовательно задает вопросы о доминировании одной альтернативы, над другой, до тех пор, пока вся матрица не будет заполнена.
Описание разработанной программы:
Программа имеет консольный интерфейс. При запуске требуется ввести размерность матрицы попарных сравнений. В случае ввода недопустимого значения происходит завершение программы. После ввода размерности требуется последовательно ввести оценку для каждой пары альтернатив, располагающейся слева от главной диагонали (остальные значения будут вычислены на основе введённых данных). Если введённое значение недопустимо, пользователь должен повторить ввод для этой пары альтернатив. После ввода всех значений на экран выводится матрица попарных сравнений. Далее в консоль выводится собственный вектор полученной матрицы, после чего программа просит нажать клавишу Escape для завершения программы.
Скриншоты
Исходный код программы
Ответы на контрольные вопросы
1. Матрица парных сравнений — это квадратная матрица, элементами которой являются оценки всех возможных пар альтернатив, которые подвергаются сравнению.
2. В методе парных сравнений существует иерархическая структура. Она изображена на рисунке 4.1. Элементы этой структуры и выступают по отношению друг к другу “родителями” и “потомками” в соответствии с их положением в иерархии.
Рисунок 4.1 — Иерархия в методе анализа альтернатив
3. Для заполнения матрицы ЛПР выносит n(n-1)/2 суждений (здесь n — порядок матрицы парных сравнений). Каждое суждение может принимать значения, указанные в таблице 2.1. С помощью этих суждений и обратных им суждений и происходит заполнение квадратной матрицы парных сравнений.
4. Вычисление главного собственного вектора W производятся по выражению 2.2.
5. Степень значимости отражает отношение двух альтернатив. Если степень значимости больше 1 — первая альтернатива предпочтительнее, если меньше 1 — вторая альтернатива предпочтительнее, если равна 1 — альтернативы имеют одинаковую значимость. Подробно степени значимости описаны в таблице 2.1.
Выводы
В ходе выполнения работы были изучены методы построения матрицы попарных сравнений и расчёта её собственного вектора. Эти методы были реализованы в консольной программе, написаной на ЯП Java. Данная программа запрашивает размерность n матрицы, а также запрашивает ввод n(n-1)/2 степеней значимости альтернатив, а на выходе выдаёт вектор полученной матрицы. Также программа корректно обрабатывает ошибки, связанные со вводом недопустимых данных.
Расчет векторов приоритетов как собственных векторов матриц парных сравнений
Вычисление главного собственного вектора W положительной квадратной матрицы А проводится на основании равенства
где А.тах — максимальное собственное значение матрицы А; Е — единичная матрица того же размера п х п.
Но во многих источниках (как в учебниках, так и в интернет-ресурсах [1] ) для практического отыскания вектора приоритетов рекомендуют приближенную формулу
согласно которой каждую компоненту вектора W находят как среднее гео- метрическое элементов соответствующей строки матрицы А. Заметим, что эта формула точна для матриц размера и=3и служит достаточно точным приближением для матриц А большего размера, если они хорошо согласованы, т.е. с достаточной точностью выполнено свойство однородности aik = = ajs? ask. Однако при плохой согласованности матрицы А формула (11.3) может давать ошибочные результаты уже для п = 4. Убедимся в этом на примере.
Пример: метод средних геометрических для нахождения приоритетов.
Пусть имеются четыре альтернативы х,, х.„ х3, х4, и суждения эксперта о сравнении альтернатив по некоторому критерию представлены в виде матрицы парных сравнений А
Требуется найти вектор приоритетов IT двумя способами:
- а) методом геометрических средних;
- б) через главный собственный вектор матрицы парных сравнений А. Для большей убедительности результатов два значения в матрице парных сравнений А выбраны за пределами 10-балльной шкалы.
Для решения первым способом, применяя соотношение (11.3), получим компоненты приближенного вектора по формуле геометрических средних
Для сопоставления с точным результатом выполним нормировку вектора, разделив каждую из величии Wk на сумму всех четырех компонент. Получим компоненты нормированного приближенного вектора IT: IT, = 0,308, 1Т2 = 0,244, IT., = 0,275,1Т4 = 0,173. Формула (11.3) приводит к выводу об оптимальности альтернативы xv причем ближайшей конкурирующей альтернативой будет х,
Однако при точном нахождении главного собственного вектора, удовлетворяющего уравнению (11.2), компоненты нормированного вектора 1Т с точностью 0,001 оказываются равны IT, = 0,123, W2 = 0,462, VT3 = 0,207, IT, = 0,208. Таким образом, на самом деле оптимальной будет альтернатива х2, а ближайшей конкурирующей (с большим отрывом) — хЛ
Погрешность отыскания приоритетов первых двух альтернатив по формуле (11.3) в этом примере велика: в абсолютном выражении она составила 0,185 и 0,218, а в относительном — в 2,5 и в 2 раза. И главное — выводы на основе формулы (11.3) неверны.
Таким образом, рассмотренный пример приводит к следующему заключению.
Формула (11.3) расчета приоритетов как средних геометрических величин элементов матрицы А парных сравнений для п > 4 при плохой согласованности суждений в матрице А может давать высокие погрешности и неверные выводы относительно оптимальных альтернатив.
Учитывая возможность существенных ошибок при использовании формулы (11.3), приведем метод последовательного сколь угодно точного нахождения нормированного (имеющего сумму компонент, равную единице) главного собственного вектора W.
Наиболее точный и практически эффективный способ отыскания главного собственного вектора W матрицы А — с помощью пакетов прикладных математических программ. В частности, встроенные функции нахождения собственных чисел и векторов имеются во всех основных самых распространенных пакетах (Mathematica, MATLAB, Maple, MathCAD и др.).
При отсутствии доступа к специализированным математическим пакетам (например, при наличии только офисного табличного редактора Excel, не имеющего встроенной функции для поиска собственных чисел и векторов) главный собственный вектор можно найти с помощью последовательных приближений (как правило, за небольшое число шагов) на базе следующей теоремы.
Для положительной квадратной матрицы А нормированный правый собственный вектор W, соответствующий максимальному собственному значению Хтах, можно вычислить по формуле
где е — вектор, состоящий из п единиц; Т — знак транспонирования; k = 1,2,3. показатель степени (число итераций).
С достаточной для практики точностью можно принять ? = 0,01 независимо от порядка матрицы.
Одновременно с главным собственным вектором W можно найти и максимальное собственное значение А,шах, которое требуется для исследования согласованности матрицы парных сравнений А. Максимальное собственное значение вычисляется по формуле:
Собственный вектор матрицы парных сравнений
Автор: Пользователь скрыл имя, 15 Марта 2012 в 18:00, реферат
Краткое описание
.математический инструмент системного подхода к сложным проблемам принятия решений. МАИ не предписывает лицу, принимающему решение, какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант, который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению.
Файлы: 1 файл
1.docx
1.математический инструмент системного подхода к сложным проблемам принятия решений. МАИ не предписывает лицу, принимающему решение, какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант, который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению. Этот метод разработан американским математиком Томасом Саати, который написал о нем книги, разработал программные продукты и в течение 20 лет проводит симпозиумы ISAHP. МАИ широко используется на практике и активно развивается учеными всего мира. В его основе наряду с математикой заложены и психологические аспекты. МАИ позволяет понятным и рациональным образом структурировать сложную проблему принятия решений в виде иерархии, сравнить и выполнить количественную оценку альтернативных вариантов решения. Метод Анализа Иерархий используется во всем мире для принятия решений в разнообразных ситуациях: от управления на межгосударственном уровне до решения отраслевых и частных проблем в бизнесе, промышленности, здравоохранении и образовании. Для компьютерной поддержки МАИ существуют программные продукты, разработанные различными компаниями. Анализ проблемы принятия решений в МАИ начинается с построения иерархической структуры, которая включает цель, критерии, альтернативы и другие рассматриваемые факторы, влияющие на выбор. Эта структура отражает понимание проблемы лицом, принимающим решение. Каждый элемент иерархии может представлять различные аспекты решаемой задачи, причем во внимание могут быть приняты как материальные, так и нематериальные факторы, измеряемые количественные параметры и качественные характеристики, объективные данные и субъективные экспертные оценки . Иными словами, анализ ситуации выбора решения в МАИ напоминает процедуры и методы аргументации, которые используются на интуитивном уровне. Следующим этапом анализа является определение приоритетов, представляющих относительную важность или предпочтительность элементов построенной иерархической структуры, с помощью процедуры парных сравнений. Безразмерные приоритеты позволяют обоснованно сравнивать разнородные факторы, что является отличительной особенностью МАИ. На заключительном этапе анализа выполняется синтез приоритетов на иерархии, в результате которой вычисляются приоритеты альтернативных решений относительно главной цели. Лучшей считается альтернатива с максимальным значением приоритета.
2. Собственный вектор матрицы парных сравнений. Собственный вектор матрицы парных сравнений определяет порядок важности сравниваемых объектов в количественном выражении. Он обеспечивает упорядочение приоритетов (критериев) объектов. Иногда значения собственного вектора матрицы парных сравнений назы- вают вектором приоритетов, а собственное значение является мерой согласованности суждений.
Следующим шагом, после составления матрицы парных сравнений, является вычисление вектора приоритетов. Относительная сила, величина или вероятность каждого отдельного объекта в иерархии определяется оценкой соответствующего ему элемента собственного вектора матрицы приоритетов, нормализованного к единице.
Метод отыскания вектора w основывается на одном из утверждений линейной алгеб-ры — искомый вектор является собственным вектором матрицы парных сравнений, со-ответствующим максимальному собственному числу — λmax. В этом случае отыски-вается λmax, а затем достаточно решить векторное уравнение A*w= λmax *w.
Процедура определения собственных векторов матриц поддается приближе-нию. Например, приближенное вычисление собственного вектора (столбца) методом среднего геометрического измерения расстояний между оцениваемыми объектами может быть осуществлен в следующем порядке:
— перемножаются элементы каждой строки и полученные результаты записы-ваются в столбец;
— извлекается корень n-й степени из каждого элемента найденного столбца;
— складываются элементы этого столбца;
— каждый из этих элементов делится на полученную сумму.
Тем самым получается нормализованный вектор приоритетов.
3. Оценка однородности суждений
В практических задачах количественная (кардинальная) и транзитивная (порядковая) однородность (согласованность) нарушается, поскольку человеческие ощущения нельзя выразить точной формулой. Для улучшения однородности в числовых суждениях, какая бы величина aij ни была взята для сравнения i-го элемента с j-м, aij приписывается значение обратной величины, т. е. аij = 1/aij. Отсюда следует, что если один элемент в а раз предпочтительнее другого, то последний только в 1/а раз предпочтительнее первого.
При нарушении однородности ранг матрицы отличен от единицы и она будет иметь несколько собственных значений. Однако при небольших отклонениях суждений от однородности одно из собственных значений будет существенно больше остальных и приблизительно равно порядку матрицы. Таким образом, для оценки однородности суждений эксперта необходимо использовать отклонение величины максимального собственного значения λmax от порядка матрицы п.
Однородность суждений оценивается индексом однородности (ИО) или отношением однородности (OO) в соответствии со следующими выражениями:
где М(ИО) — среднее значение (математическое ожидание) индекса однородности случайным образом составленной матрицы парных сравнений [E], которое основано на экспериментальных данных (табл. 2.3), полученных в работе [2].
Среднее значение индекса однородности в зависимости от порядка матрицы
В качестве допустимого используется значение OO ≤ 0,10. Если для матрицы парных сравнений отношение однородности OO > 0,10, то это свидетельствует о существенном нарушении логичности суждений, допущенном экспертом при заполнении матрицы, поэтому эксперту предлагается пересмотреть данные, использованные для построения матрицы, чтобы улучшить однородность.
4. Иерархический анализ используется для взвешивания собственных векторов матриц парных сравнений альтернатив весами критериев (элементов), имеющих в иерархии, а также для вычисления суммы по всем соответствующим взвешенным компонентам собственных векторов нижележащего уровня иерархии. Ниже рассматривается алгоритм иерархического синтеза [9] с учетом обозначений, принятых в иерархии на рис.2.1.
На первом шаге определяются векторы приоритетов альтернатив ^^относительно элементов Kj предпоследнего уровня иерархии (i=S).
Здесь через Kj обозначены элементы иерархии (критерии), причем верхний индекс / — указывает уровень иерархии, а нижний индекс j — порядковый номер элемента на уровне. Вычисление множества векторов приоритетов альтернатив Ws относительно S — уровня иерархии осуществляется по итерационному алгоритму, реализованному на основе соотношений (2.5) и (2.6) по исходным данным, зафиксированным в матрицах попарных сравнений. В результате определяется множество векторов:
Ш а г 2. Аналогичным образом обрабатываются матрицы попарных сравнений собственно элементов Данные матрицы построены таким образом, чтобы определить предпочтительность элементов определенного иерархического уровня относительно элементов вышележащего уровня, с которыми они непосредственно связаны. Например, для вычисления векторов приоритетов элементов третьего иерархического уровня (см. рис. 2.1) обрабатываются следующие три матрицы попарных сравнений:
В матрицах через v обозначен вес, или интенсивность, Е -го элемента.
В результате обработки матриц попарных сравнений определяется множество векторов приоритетов элементов:
Полученные значения векторов используются впоследствии при определении векторов
приоритетов альтернатив относительно всех элементов иерархии.
Шаг 3. Осуществляется собственно иерархический синтез, заключающийся в последовательном
определении векторов приоритетов альтернатив относительно элементов Е находящихся на всех
иерархических уровнях, кроме предпоследнего, содержащего элементы Е . Вычисление векторов приоритетов проводится в направлении от нижних уровней к верхним с учетом конкретных связей между элементами, принадлежащими различным уровням. Вычисление проводится путем перемножения соответствующих векторов и матриц.
Общий вид выражения для вычисления векторов приоритетов альтернатив определяется следующим образом:
где — вектор приоритетов альтернатив относительно элемента E1 , определяющий j-й столбец матрицы;
— вектор приоритетов элементов E1, связанных с элементом Ej вышележащего
Ниже приведен конкретный пример по вычислению векторов приоритетов альтернатив относительно элементов третьего (E³ ), второго (Е² ) и первого (Е¹ ) уровней иерархии с учетом конкретных связей между элементами иерархии (см. рис. 2.1).
Определение векторов приоритетов альтернатив для элементов второго уровня осуществляется
Результирующий вектор приоритетов альтернатив относительно корневой вершины иерархии Е¹1
вычисляется следующим образом:
Рассмотренная модификация МАИ может эффективно применяться при решении широкого класса
социально-экономических и управленческих задач.
http://studme.org/269686/informatika/raschet_vektorov_prioritetov_sobstvennyh_vektorov_matrits_parnyh_sravneniy
http://student.zoomru.ru/ecoorg/sobstvennyj-vektor-matricy-parnyh-sravnenij/125322.986300.s1.html
Выбор техники затруднителен практически для всех людей, поскольку любой человек хочет получить наиболее подходящее для себя устройство — особенно в тех случаях, когда гаджет покупается за немалые деньги и должен использоваться в течение нескольких лет. К сожалению, зачастую нет модели, которая опережала бы другие сразу по всем показателям (в том числе и по цене) — какое-то устройство обходит конкурентов по одним показателям, но явно уступает им по другим. Чтобы не полагаться на интуицию и, в случае ошибки, не жалеть о своём выборе в течение длительного времени, мы предлагаем прибегнуть к науке (теории принятия решений) и воспользоваться методом анализа иерархий — математическим инструментом системного подхода к сложным проблемам принятия решения. Не стоит пугаться: он довольно простой (хоть и занимает немало времени). С этой простой инструкцией вам не понадобится получать высшее образование, чтобы использовать этот метод теории принятия решений в реальной жизни.
Я вспомнил о нём в то время, когда планировал приобрести смартфон и не мог определиться между двумя моделями: iPhone 11 и Galaxy S10+. На мой взгляд, первый вариант лучше фронтальной камерой, системой биометрической идентификации пользователя и эксклюзивными фишками для работы с Mac; смартфон от Samsung выделяется автономностью, основной камерой, функционалом операционной системы и, конечно же, более низкой стоимостью. Просто анализируя в голове преимущества и недостатки каждого из устройств, я так и не смог выбрать оптимальный вариант. Но метод анализа иерархий помог окончательно понять, какой смартфон мне больше подходит. Далее в статье я предлагаю рассмотреть пример моей работы — именно на основе неё и будет написана инструкция по использованию данного метода теории принятия решений.
В конце статьи прикреплён Excel-документ со всеми расчётами — при желании, вы можете скачать его и детальнее разобрать пример, либо же просто сделать свой выбор на основе уже написанных формул. Также все расчёты доступны в «Google Таблицах». Сразу стоит отметить, что целью этой инструкции не является реклама конкретного смартфона на фоне его главного конкурента. Также у меня нет задачи доказать, что одна модель объективно лучше другой — статья служит лишь примером, на основе которого вы сможете сделать свой выбор.
1. Определение исходных данных
На первом этапе вы должны определиться, какие устройства будете сравнивать и какие их показатели (характеристики и функции) вам интересны — число гаджетов и критериев неограниченно. В моём случае я выбирал между iPhone 11 и Galaxy S10 по следующим важным для себя показателям:
- Возможности основной камеры.
- Возможности фронтальной камеры.
- Время автономной работы.
- Биометрическая идентификация.
- Наличие функции трекпада (когда вместо сенсорной клавиатуры активируется трекпад, позволяющий передвигать курсор и выделять текст).
- Стоимость.
- Наличие качественных игр.
- Функциональность операционной системы.
- Юзабилити операционной системы (лично моё мнение о том, с какой платформой мне удобнее взаимодействовать).
- Поддержка Apple Watch (умных часов, которые у меня уже есть).
- Синхронизация с Mac (с компьютером, который у меня уже есть).
2. Парное сравнение альтернатив по критериям
Теперь все устройства нужно парно сравнить по каждому из выбранных критериев. Для этого удобнее всего составить таблицы, каждая из которых будет соответствовать одному показателю. В ходе сравнения характеристик каждому устройству необходимо присваивать рейтинг, который рассчитывается следующим образом:
| Рейтинг | Описание | Простое описание по отношению к технике |
| «1» | Одинаковое предпочтение | По конкретному показателю устройства одинаковы |
| «3» | Умеренное предпочтение | По конкретному показателю одного устройство слегка лучше другого |
| «5» | Явное предпочтение | По конкретному показателю одно устройство явно лучше другого |
| «7» | Очевидное предпочтение | По конкретному показателю одно устройство существенно лучше другого |
| «9» | Абсолютное предпочтение | По конкретному показателю одно устройство полностью лучше другого (у второго гаджета нет и шанса в этом сравнении) |
Необходимо использовать вышеописанную шкалу от 1 до 9, но необязательно прибегать только к нечётным цифрам — к примеру, если предпочтение больше умеренного («3»), но меньше явного («5»), то следует присвоить рейтинг «4».
Оценивая характеристики каждого из устройств, необходимо хорошо обдумывать свои предпочтения: от них зависит итоговый результат. На практике всё выглядит следующим образом (для примера, подробно рассмотрим несколько показателей):
Я считаю, что фронтальная камера в iPhone 11 лучше таковой в Galaxy S10+, но не намного — в этом сравнении я присваиваю Айфону рейтинг «3» (умеренное предпочтение) и, как следствие, Самсунгу достаётся обратная оценка — «1/3» (что в таблице Excel записывается как деление с результатом «0,33»). В ячейках главной диагонали, в которых устройства сравниваются сами с собой, следует всегда указывать рейтинг «1».
Время автономной работы, пожалуй, на стороне Galaxy S10+ — но не то, чтобы он работал явно дольше, чем iPhone 11. Поэтому я ему присвоил рейтинг «4», а Айфону присудил обратное число — «1/4» (Excel выполняет деление и записывает «0,25»).
А вот в случае с поддержкой Apple Watch все однозначно: эти умные часы совместимы только с iPhone, поэтому «яблочному» гаджету присваивается «9» (абсолютное предпочтение), а конкуренту прописывается «1/9» (Excel конвертирует в «0,11»).
В итоге матрицы сравнения смартфонов по всем критериям выглядят так, как показано на скриншоте выше.
3. Построение матрицы сравнения критериев
На этом шаге необходимо выполнить то же самое, что было на предыдущем этапе, но теперь в сравнении участвуют только критерии: к примеру, на сколько качественная камера важнее длительного времени автономной работы.
Поскольку в моём случае критериев много, таблица получилась довольно большой. Но это не должно вас пугать, поскольку она строится довольно просто (как и все предыдущие). Главное — обдумывать свои предпочтения.
В качестве примера рассмотрим сравнение биометрических систем идентификации со стоимостью гаджетов.
4. Нормализация матриц альтернатив и нахождение векторов приоритетов
Этот этап — самый муторный. Он отнимает больше всего времени, но отступать не стоит — он почти такой же простой, как и все предыдущие шаги. Чтобы найти вектор приоритетов, необходимо поделить каждым элемент матрицы на сумму всех элементов соответствующего столбца, а затем найти среднее арифметическое из элементов рядков полученных таблиц. Кажется сложным? Пожалуй, да, но на практике всё просто. Разберём на примере нормализации матрицы сравнения фронтальных камер смартфонов.
Первый шаг максимально простой: суммируем все элементы первого столбца, а затем все значения в ячейках второго — результаты удобнее записать ниже.
Далее делим каждый элемент матрицы на сумму значений конкретного столбца.
После этого определяем среднее арифметическое каждой строчки и записываем в отдельную табличку с одним столбцом — она и является вектором приоритетов.
В итоге должны быть найдены векторы приоритетов всех критериев — мои результаты отображены на скриншотах выше.
5. Нормализация матрицы критериев и нахождение весовых коэффициентов
Нормализация матрицы критериев осуществляется точно так же, как нормализация матриц альтернатив: находим сумму элементов в столбце, делим каждый элемент столбца на эту сумму и в получившейся матрице вычисляем среднее арифметическое элементов каждого рядка — эти значения и образуют вектор весовых коэффициентов.
6. Вычисление ранга альтернатив
Это финальный этап — он покажет, какое из устройств (в нашем случае смартфонов) является оптимальным для конкретного человека (в данном случае для меня). Нужно для каждого гаджета найти сумму произведений приоритетов критериев на их весовые коэффициенты. Да, и это звучит непонятно, но всё не так уж и сложно: грубо говоря, для нахождения ранга iPhone 11 надо поочерёдно умножить значения из розовых ячеек, полученных в 4 пункте, на конечные показатели, полученные в 5 пункте, а затем их все суммировать.
Чем больше итоговое значение каждого из устройств, тем этот гаджет больше вам подходит. В идеале, сумма рангов всех гаджетов должна равняться 1, но из-за округлений возможно небольшое отклонение (например, в моём случае сумма равна 0,9908). Как видно по результату, iPhone 11 является более подходящим для меня устройством, чем Galaxy S10+.
Вместо вывода
Я рад, что вспомнил теорию принятия решений и воспользовался методом анализа иерархий для решения интересующей меня задачи. Это один из тех немногих предметов в университете, который пригодился мне в реальной жизни.
На момент написания этой статьи я действительно стою перед выбором смартфона, а вышеописанная работа наконец помогла мне определиться (с выходом обзоров на iPhone 11 я, возможно, изменю рейтинги некоторых показателей, но вряд ли результат существенно поменяется). Надеюсь, благодаря этому топику вы тоже сможете выбирать действительно оптимальные устройства, а также многое другое — применяя метод анализа иерархий, можно делать выбор в различных областях, вплоть до сравнения возможных работ или спутниц жизни (спойлер: финальной девушке лучше не говорить всю правду о том, почему и как вы выбрали именно её😅).
- Эти 7 техноподарков на Новый год хотят все
- Какой MacBook купить на 2020 год
- Исследование: смартфон с какими характеристиками хотят большинство людей
- Почему AirPods — лучшие наушники. Рассказываю на личном опыте
- Какой iPhone купить на 2020 год