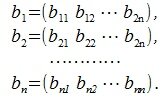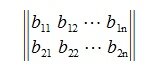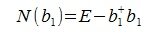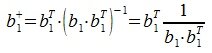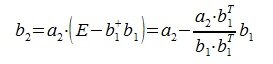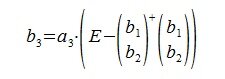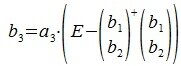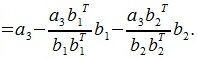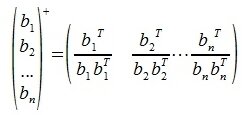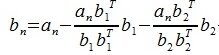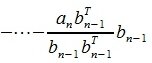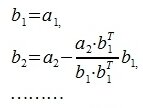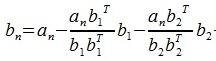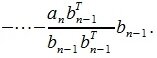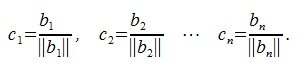Как найти вектор ортогональный трем - AvtoShod.ru

5. Если вектор [math]mathbf[/math] ортогонален подмножеству [math]M[/math] евклидова пространства, то он ортогонален и линейной оболочке этого подмножества, т.e. [math]mathbfperp M

6. Если [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] — ортогональная система векторов, то

Это утверждение является обобщением теоремы Пифагора.

Процесс ортогонализации Грама-Шмидта

Рассмотрим следующую задачу. Дана линейно независимая система [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] векторов конечномерного евклидова пространства. Требуется построить ортогональную систему [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] векторов того же пространства так, чтобы совпадали линейные оболочки:

Решение задачи находится при помощи процесса ортогонализации Грама–Шмидта , выполняемого за [math]k[/math] шагов.

1. Положить [math]mathbf_1=mathbf_1[/math] .

2. Найти [math]mathbf_2=mathbf_2-alpha_<21>cdot mathbf_1[/math] , где [math]alpha_<21>= frac<langle mathbf_2, mathbf_1rangle><langle mathbf_1, mathbf_1 rangle>[/math] .

3. Найти [math]mathbf_3=mathbf_3-alpha_ <31>mathbf_1-alpha_ <32>mathbf_2[/math] , где [math]alpha_<31>=frac<langle mathbf_3,mathbf_1 rangle><langle mathbf_1, mathbf_1rangle>,

4. Найти [math]mathbf_k=mathbf_k-sum_^alpha_mathbf_i[/math] , где [math]alpha_= frac<langle mathbf_k,mathbf_irangle><langle mathbf_i, mathbf_irangle>,

Поясним процесс ортогонализации. Искомый на втором шаге вектор [math]mathbf_2[/math] представлен в виде линейной комбинации [math]mathbf_2=mathbf_2-alpha mathbf_1[/math] . Коэффициент [math]alpha[/math] подберем так, чтобы обеспечить ортогональность векторов [math]mathbf_2[/math] и [math]mathbf_1[/math] . Приравняем нулю скалярное произведение этих векторов [math]langle mathbf_2,mathbf_1rangle= langle mathbf_2,mathbf_1rangle- alpha langle mathbf_1,mathbf_1rangle=0[/math] . Отсюда получаем, что [math]alpha=alpha_<21>[/math] (см. пункт 2 алгоритма). Подбор коэффициентов [math]alpha_[/math] на j-м шаге алгоритма делается так, чтобы искомый вектор [math]mathbf_j[/math] был ортогонален всем ранее найденным векторам [math]mathbf_1, mathbf_2,ldots,mathbf_[/math] .

1. Векторы, найденные в процессе ортогонализации, обладают следующими свойствами:

а) [math]mathbf_j perp operatorname(mathbf_1,mathbf_2,ldots,mathbf_),quad j=2,ldots,k[/math] ;

б) [math]operatorname(mathbf_1)= operatorname(mathbf_1),quad operatorname(mathbf_1,mathbf_2, ldots,mathbf_)= operatorname(mathbf_1,mathbf_2, ldots,mathbf_),quad j=2,ldots,k[/math] .

Первое свойство следует из свойства 4 ортогональных векторов. Второе свойство следует из того, что каждый вектор системы [math]mathbf_1,mathbf_2,ldots,mathbf_[/math] линейно выражается через векторы [math]mathbf_1,mathbf_2, ldots, mathbf_[/math] , и наоборот.

2. В процессе ортогонализации любой вектор [math]mathbf_j[/math] можно заменить на коллинеарный ему ненулевой вектор [math]lambdacdot mathbf_j[/math] . При этом свойства, перечисленные в пункте 1, не нарушаются.

3. Если система [math]mathbf_1,mathbf_2,ldots, mathbf_[/math] векторов линейно зависима, то в процессе ортогонализации будем получать (на некоторых шагах) нулевые векторы. Действительно, если подсистема math]mathbf_1,mathbf_2,ldots, mathbf_[/math] линейно зависима, то [math]mathbf_jin operatorname (mathbf_1,ldots,mathbf_)[/math] . Тогда вектор [math]mathbf_j=mathbf_j-sum_^alpha_ mathbf_i[/math] одновременно удовлетворяет двум условиям [math]mathbf_jperp operatorname(mathbf_1,ldots, mathbf_)[/math] и [math]mathbf_jin operatorname(mathbf_1,ldots,mathbf_)[/math] . Значит, это нулевой вектор [math]mathbf_i=mathbf[/math] .

Поэтому в данном случае формулы вычисления коэффициентов [math]alpha_[/math] на j-м шаге следует записывать в виде:

В остальном процесс ортогонализации остается неизменным.

4. Процесс ортогонализации можно дополнить процессом нормировки, разделив каждый вектор ортогональной системы [math]mathbf_1, mathbf_2,ldots,mathbf_k[/math] на его длину:

В результате получим ортонормированную систему [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] , отвечающую условию [math]operatorname(mathbf_1, ldots, mathbf_k)= operatorname(mathbf_1,ldots,mathbf_k)[/math] . Если исходная система векторов является линейно зависимой, то среди векторов ортогональной системы [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] будут нулевые. Чтобы получить ортонормированную систему, нулевые векторы следует исключить, а остальные векторы нормировать.

Пример 8.18. Даны системы векторов евклидовых пространств:

а) [math]x=begin1\0end!,quad y=begin2\0end!,quad z=begin0\1end[/math] — элементы пространства [math]mathbb^2[/math] со скалярным произведением (8.26):

p_3(x)=x^2[/math] — элементы пространства [math]C[-1;1][/math] со скалярным произведением (8.28):

Провести ортогонализацию данных векторов.

Решение. а) Заметим, что система векторов [math]x,,y,,z[/math] линейно зависимая, так как [math]x[/math] и [math]y[/math] пропорциональны, поэтому используем процесс ортогонализации Грама–Шмидта с учетом пункта 3 замечаний 8.11.

1. Полагаем [math]mathbf=x[/math] .

Проверим условие ортогональности [math]langle mathbf,mathbfrangle= 2cdot1cdot left(-frac<1><2>right)+ 1cdot1+ 0cdotleft(-frac<1><2>right)+0cdot1=0[/math] .

Для получения ортонормированной системы исключаем нулевой вектор [math]mathbf=mathbf[/math] , а остальные нормируем (см. пункт 4 замечаний 8.11):

Таким образом, для системы трех векторов [math]x,,y,,z[/math] построена ортогональная система из трех векторов [math]mathbf,mathbf,mathbf[/math] и ортонормированная система из двух векторов [math]widehat<mathbf>,widehat<mathbf>[/math] . Линейные оболочки этих трех систем совпадают между собой (и со всем пространством [math]mathbb^2[/math] ).

б) 1. Полагаем [math]q_1(x)=p_1(x)=1[/math] .

и находим [math]q_3(x)= x^2-alpha_<31>cdot1-alpha_<32>cdot x=x^2-frac<1><3>[/math] .

Получили ортогональные многочлены [math]q_1(x)=1,

q_3(x)=x^2-frac<1><3>[/math] . Выполним нормировку:

Ортогональные векторы и условие ортогональности

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Ортогональные векторы: определение и условие

Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .

Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a ¯ = < a x × a y >и b ¯ = < b x × b y >записывают следующим образом:

a ¯ × b ¯ = a x × b x + a y × b y = 0

Задача 1. Докажем, что векторы a ¯ = < 1 ; 2 >и b ¯ = < 2 ; — 1 >ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) = 2 — 2 = 0

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Задача 2. Докажем, что векторы a ¯ = < 3 ; — 1 >и b ¯ = < 7 ; 5 >ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 3 × 7 + ( — 1 ) × 5 = 21 — 5 = 16

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Задача 3. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 >и b ¯ = < n ; 1 >будут ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = — 4 n = — 2

Ответ: векторы являются ортогональными при значении n = 2 .

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; — 1 ; 10 >условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .

Задача 4. Докажем, что векторы a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; — 1 ; 10 >являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) + 0 × 10 = 2 — 2 = 0

Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.

Задача 5. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 ; 1 >и b ¯ = < n ; 1 ; — 8 >будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( — 8 ) = 2 n + 4 — 8 = 2 n — 4 2 n — 4 = 0 2 n = 4 n = 2

Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .

источники:

http://mathhelpplanet.com/static.php?p=ortogonalnye-vektory-evklidova-prostranstva

http://zaochnik.com/spravochnik/matematika/vektory/ortogonalnye-vektory-i-uslovie-ortogonalnosti/

Источник

Ортогональные векторы евклидова пространства и их свойства

Два вектора mathbf{u} и mathbf{v} евклидова пространства называются ортогональными (перпендикулярными), если их скалярное произведение равно нулю: langle mathbf{u},mathbf{v}rangle .

Система векторов $mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k$ называется ортогональной, если все ее векторы попарно ортогональны, т.е. $langle mathbf{u}_i, mathbf{v}_jrangle=0$ при ine j . Система векторов $mathbf{v}_1, mathbf{v}_2, ldots,mathbf{v}_k$ называется ортонормированной, если все ее векторы попарно Ортогональны и длина (норма) каждого вектора системы равна единице, т.е.

$langle mathbf{u}_i, mathbf{v}_jrangle=begin{cases}1,&i=j,\0,& ine j. end{cases}$

Говорят, что вектор mathbf{v} ортогонален (перпендикулярен) множеству , если он ортогонален каждому вектору из . Ортогональность векторов обозначается знаком перпендикуляра (perp) .

Свойства ортогональных векторов

1. Нулевой вектор ортогонален каждому вектору пространства.

2. Взаимно ортогональные ненулевые векторы линейно независимы.

В самом деле, пусть векторы $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ попарно ортогональны. Составим из них линейную комбинацию и приравняем ее нулевому вектору:

$lambda_1cdot mathbf{v}_1+lambda_2 mathbf{v}_2+ldots+lambda_k mathbf{v}_k=mathbf{o}.$

Умножим обе части равенства скалярно на вектор $mathbf{v}_1:$

$lambda_1langle mathbf{v}_1,mathbf{v}_1rangle+ lambda_2underbrace{langle mathbf{v}_1,mathbf{v}_2rangle}_{0}+ ldots+ lambda_kunderbrace{langle mathbf{v}_1, mathbf{v}_krangle}_{0}= underbrace{langle mathbf{v}_1,mathbf{o}rangle}_{0}.$

Следовательно, $lambda_1cdot|mathbf{v}_1|^2=0$ . Так как $mathbf{v}_1ne mathbf{o}$ , то lambda_1=o . Аналогично доказываем, что lambda_2=ldots= lambda_k=0 , т.е рассматриваемая линейная комбинация тривиальная. Значит, ортогональная система векторов $mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k$ линейно независима.

3. Если сумма взаимно ортогональных векторов равна нулевому вектору, то каждое из слагаемых равно нулевому вектору.

4. Если вектор mathbf{u} ортогонален каждому вектору системы $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ , то он также ортогонален и любой их линейной комбинации. Другими словами, если $mathbf{u}perp mathbf{v}_i,~ i=1,ldots,k$ , то $mathbf{u}perp operatorname{Lin} (mathbf{v}_1,ldots, mathbf{v}_k)$ .

5. Если вектор mathbf{u} ортогонален подмножеству евклидова пространства, то он ортогонален и линейной оболочке этого подмножества, т.e. mathbf{u}perp M~Rightarrow~ mathbf{u}perp operatorname{Lin}(M) .

6. Если $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ — ортогональная система векторов, то

$|mathbf{v}_1+mathbf{v}_2+ldots+mathbf{v}_k|^2= |mathbf{v}_1|^2+ |mathbf{v}_2|^2+ldots+|mathbf{v}_k|^2.$

Это утверждение является обобщением теоремы Пифагора.

Процесс ортогонализации Грама-Шмидта

Рассмотрим следующую задачу. Дана линейно независимая система $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ векторов конечномерного евклидова пространства. Требуется построить ортогональную систему $mathbf{w}_1,mathbf{w}_2, ldots,mathbf{w}_k$ векторов того же пространства так, чтобы совпадали линейные оболочки:

$operatorname{Lin}(mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k)= operatorname{Lin}(mathbf{w}_1, mathbf{w}_2,ldots,mathbf{w}_k).$

Решение задачи находится при помощи процесса ортогонализации Грама–Шмидта, выполняемого за шагов.

1. Положить $mathbf{w}_1=mathbf{v}_1$ .

2. Найти $mathbf{w}_2=mathbf{v}_2-alpha_{21}cdot mathbf{w}_1$ , где $alpha_{21}= frac{langle mathbf{v}_2, mathbf{w}_1rangle}{langle mathbf{w}_1, mathbf{w}_1 rangle}$ .

3. Найти $mathbf{w}_3=mathbf{v}_3-alpha_{31} mathbf{w}_1-alpha_{32} mathbf{w}_2$ , где $alpha_{31}=frac{langle mathbf{v}_3,mathbf{w}_1 rangle}{langle mathbf{w}_1, mathbf{w}_1rangle},~ alpha_{32}= frac{langle mathbf{v}_3,mathbf{w}_2 rangle}{langle mathbf{w}_2, mathbf{w}_2rangle}$ ; и т.д.

4. Найти $mathbf{w}_k=mathbf{v}_k-sum_{i=1}^{k-1}alpha_{ki}mathbf{w}_i$ , где $alpha_{ki}= frac{langle mathbf{v}_k,mathbf{w}_irangle}{langle mathbf{w}_i, mathbf{w}_irangle},~ i=1,ldots,k-1$ .

Поясним процесс ортогонализации. Искомый на втором шаге вектор $mathbf{w}_2$ представлен в виде линейной комбинации $mathbf{w}_2=mathbf{v}_2-alpha mathbf{w}_1$ . Коэффициент alpha подберем так, чтобы обеспечить ортогональность векторов $mathbf{w}_2$ и $mathbf{w}_1$ . Приравняем нулю скалярное произведение этих векторов $langle mathbf{w}_2,mathbf{w}_1rangle= langle mathbf{v}_2,mathbf{w}_1rangle- alpha langle mathbf{w}_1,mathbf{w}_1rangle=0$ . Отсюда получаем, что $alpha=alpha_{21}$ (см. пункт 2 алгоритма). Подбор коэффициентов $alpha_{ji}$ на j-м шаге алгоритма делается так, чтобы искомый вектор $mathbf{w}_j$ был ортогонален всем ранее найденным векторам $mathbf{w}_1, mathbf{w}_2,ldots,mathbf{w}_{j-1}$ .

Замечания 8.11

1. Векторы, найденные в процессе ортогонализации, обладают следующими свойствами:

а) $mathbf{w}_j perp operatorname{Lin}(mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_{j-1}),quad j=2,ldots,k$ ;

б) $operatorname{Lin}(mathbf{w}_1)= operatorname{Lin}(mathbf{v}_1),quad operatorname{Lin}(mathbf{w}_1,mathbf{w}_2, ldots,mathbf{w}_{j})= operatorname{Lin}(mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_{j}),quad j=2,ldots,k$ .

Первое свойство следует из свойства 4 ортогональных векторов. Второе свойство следует из того, что каждый вектор системы $mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_{j}$ линейно выражается через векторы $mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_{j}$ , и наоборот.

2. В процессе ортогонализации любой вектор $mathbf{w}_j$ можно заменить на коллинеарный ему ненулевой вектор $lambdacdot mathbf{w}_j$ . При этом свойства, перечисленные в пункте 1, не нарушаются.

3. Если система $mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_{k}$ векторов линейно зависима, то в процессе ортогонализации будем получать (на некоторых шагах) нулевые векторы. Действительно, если подсистема $mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_{j}$ линейно зависима, то $mathbf{v}_jin operatorname{Lin} (mathbf{w}_1,ldots,mathbf{w}_{j-1})$ . Тогда вектор $mathbf{w}_j=mathbf{v}_j-sum_{i=1}^{j-1}alpha_{ji} mathbf{w}_i$ одновременно удовлетворяет двум условиям $mathbf{w}_jperp operatorname{Lin}(mathbf{w}_1,ldots, mathbf{w}_{j-1})$ и $mathbf{w}_jin operatorname{Lin}(mathbf{w}_1,ldots,mathbf{w}_{j-1})$ . Значит, это нулевой вектор $mathbf{w}_i=mathbf{o}$ .

Поэтому в данном случае формулы вычисления коэффициентов $alpha_{ji}$ на j-м шаге следует записывать в виде:

$alpha_{j,i}= begin{cases}dfrac{langle mathbf{v}_j,mathbf{w}_irangle}{langle mathbf{w}_i,mathbf{w}_irangle},& mathbf{w}_ine mathbf{o},\ 0,& mathbf{w}_i=mathbf{o}. end{cases}i=1,2,ldots,j-1.$

В остальном процесс ортогонализации остается неизменным.

4. Процесс ортогонализации можно дополнить процессом нормировки, разделив каждый вектор ортогональной системы $mathbf{w}_1, mathbf{w}_2,ldots,mathbf{w}_k$ на его длину:

$mathbf{e}_i=dfrac{1}{|,mathbf{w}_i,|}cdot mathbf{w}_i,quad i=1,2,ldots,k.$

В результате получим ортонормированную систему $mathbf{e}_1,mathbf{e}_2, ldots, mathbf{e}_k$ , отвечающую условию $operatorname{Lin}(mathbf{e}_1, ldots, mathbf{e}_k)= operatorname{Lin}(mathbf{v}_1,ldots,mathbf{v}_k)$ . Если исходная система векторов является линейно зависимой, то среди векторов ортогональной системы $mathbf{w}_1,mathbf{w}_2, ldots,mathbf{w}_k$ будут нулевые. Чтобы получить ортонормированную систему, нулевые векторы следует исключить, а остальные векторы нормировать.

Пример 8.18. Даны системы векторов евклидовых пространств:

а) $x=begin{pmatrix}1\0end{pmatrix}!,quad y=begin{pmatrix}2\0end{pmatrix}!,quad z=begin{pmatrix}0\1end{pmatrix}$ — элементы пространства $mathbb{R}^2$ со скалярным произведением (8.26):

$langle x,yrangle= x^Tcdot! begin{pmatrix}2&1\1&1end{pmatrix}!cdot y= 2cdot x_1cdot y_1+x_1cdot y_2+x_2cdot y_1+x_2cdot y_2,;$

б) p_1(x)=1,~ p_2(x),~ p_3(x)=x^2 — элементы пространства C[-1;1] со скалярным произведением (8.28):

$langle f,grangle= intlimits_{-1}^{1}f(x)g(x),dx,.$

Провести

ортогонализацию данных векторов.

Решение. а) Заметим, что система векторов x,,y,,z линейно зависимая, так как и пропорциональны, поэтому используем процесс ортогонализации Грама–Шмидта с учетом пункта 3 замечаний 8.11.

1. Полагаем mathbf{u}=x .

2. Вычисляем $alpha_{21}=frac{langle y,mathbf{u}rangle}{langle mathbf{u}, mathbf{u}rangle}= frac{2!cdot!2!cdot!1+ 1!cdot!0+ 0!cdot!2+0!cdot!0}{2!cdot!1!cdot!1+ 1!cdot!0+ 0!cdot!1+0!cdot!0}=2$ и находим $mathbf{v}=y-alpha_{21}mathbf{u}= begin{pmatrix}2\0end{pmatrix}-2! begin{pmatrix}1\0end{pmatrix}= begin{pmatrix} 0\0 end{pmatrix}$ . Получили нулевой вектор.

3. Вычисляем $alpha_{31}=frac{langle z,mathbf{u}rangle}{langle mathbf{u}, mathbf{u}rangle}= frac{2!cdot!0!cdot!1+ 0!cdot!0+ 1!cdot!1+1!cdot!0}{2!cdot!1!cdot!1+ 1!cdot!0+0!cdot!1+ 0!cdot!0}=frac{1}{2},;$ $alpha_{32}=0$ согласно пункту 3 замечаний 8.11, так как mathbf{v}=mathbf{o} , и находим

$mathbf{w}=z-alpha_{31}cdot mathbf{u}-alpha_{32}cdot mathbf{v}= begin{pmatrix} 0\1end{pmatrix}-frac{1}{2}cdot! begin{pmatrix}1\0end{pmatrix}- 0cdot! begin{pmatrix}0\0 end{pmatrix}= begin{pmatrix}-1/2\1end{pmatrix}!.$

Проверим условие ортогональности $langle mathbf{u},mathbf{w}rangle= 2cdot1cdot left(-frac{1}{2}right)+ 1cdot1+ 0cdotleft(-frac{1}{2}right)+0cdot1=0$ .

Для получения ортонормированной системы исключаем нулевой вектор mathbf{v}=mathbf{o} , а остальные нормируем (см. пункт 4 замечаний 8.11):

$begin{gathered} |mathbf{u}|= sqrt{langle mathbf{u},mathbf{u} rangle}= sqrt{2},;\[5pt] |mathbf{w}|= sqrt{langle mathbf{w},mathbf{w}rangle}= sqrt{2cdot!left(-frac{1}{2}right)!cdot!left(-frac{1}{2}right)+left(-frac{1}{2}right)!cdot1+ 1cdotleft(-frac{1}{2}right)+ 1cdot1}= sqrt{1/2},;\[5pt] widehat{mathbf{u}}= frac{1}{|mathbf{u}|}cdot mathbf{u}= frac{1}{sqrt{2}}cdot! begin{pmatrix}1\0end{pmatrix}= begin{pmatrix}1/sqrt{2}\ 0end{pmatrix}!,quad widehat{mathbf{w}}= frac{1}{|mathbf{w}|}cdot mathbf{w}= frac{1}{sqrt{1/2}}cdot! begin{pmatrix}-1/2\0end{pmatrix}= begin{pmatrix}-1/sqrt{2}\ sqrt{2}end{pmatrix}!. end{gathered}$

Таким образом, для системы трех векторов x,,y,,z построена ортогональная система из трех векторов mathbf{u},mathbf{v},mathbf{w} и ортонормированная система из двух векторов widehat{mathbf{u}},widehat{mathbf{w}} . Линейные оболочки этих трех систем совпадают между собой (и со всем пространством $mathbb{R}^2$ ).

б) 1. Полагаем q_1(x)=p_1(x)=1 .

2. Вычисляем $alpha_{21}= frac{langle p_2,q_1rangle}{langle q_1,q_1rangle}= Biggl(intlimits_{-1}^{1} xcdot1,dxBiggr):Biggl(intlimits_{-1}^{1}1cdot1,dxBiggr)= left.{frac{1}{2},x^2}right|_{-1}^{1}:2=0$ и находим q_2(x)=x-0!cdot!1=x .

3. Вычисляем

$begin{aligned} alpha_{31}&= frac{langle p_3,q_1rangle}{langle q_1,q_1rangle}= Biggl(intlimits_{-1}^{1} x^2cdot1,dxBiggr):2= left.{frac{1}{3},x^3}right|_{-1}^{1}= frac{2}{3} cdotfrac{1}{2}=frac{1}{3},;\[5pt] alpha_{32}&= frac{langle p_3,q_2rangle}{langle q_2,q_2 rangle}= Biggl(intlimits_{-1}^{1} x^2cdot x,dxBiggr):Biggl(intlimits_{-1}^{1}xcdot x,dxBiggr)= left.{frac{1}{4},x^4}right|_{-1}^{1}:left.{frac{1}{3},x^3}right|_{-1}^{1}=0 end{aligned}$

и находим $q_3(x)= x^2-alpha_{31}cdot1-alpha_{32}cdot x=x^2-frac{1}{3}$ .

Получили ортогональные многочлены $q_1(x)=1,~ q_2(x)=x,~ q_3(x)=x^2-frac{1}{3}$ . Выполним нормировку:

$begin{array}{lll}|q_1(x)|= sqrt{langle q_1(x),q_1(x)rangle}= sqrt{2},;&~ |q_2(x)|= sqrt{langle q_2(x),q_2(x)rangle}= sqrt{dfrac{2}{3}},;&~ |q_3(x)|= sqrt{langle q_3(x),q_3(x) rangle}= dfrac{2}{3}sqrt{dfrac{2}{5}},;\[10pt] widehat{q}_1(x)= dfrac{q_1(x)}{|q_1(x)|}= dfrac{1}{sqrt{2}},;&~ widehat{q}_2(x)= dfrac{q_2(x)}{|q_2(x)|}= sqrt{dfrac{3}{2}}cdot x,;&~ widehat{q}_3(x)= dfrac{q_3(x)}{|q_3(x)|}= dfrac{3}{2}sqrt{dfrac{5}{2}}! left(x^2-dfrac{1}{3}right)!.end{array}$

Получили ортонормированные многочлены (многочлены Лежандра).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Пусть
даны
линейно независимых векторов.
Для построения по этим векторампопарно ортогональных векторовнеобходимо провести следующую процедуру
ортогонализации. Положим вначале.
Затем векторбудем искать в виде.

По
условию ортогональности
.
Следовательно,откуда.
Предположим, что уже построеноортогональных векторов.
Будем искатьв виде

По
условию вектор
должен быть ортогонален,
что даётуравнений для определениянеизвестных.
Выпишем эти уравнения с учётом
ортогональности векторов:

откуда получим

Типовые примеры

1.
В евклидовом пространстве
построить ортонормированный базис по
данному

►Проведём
вначале ортогонализацию, т.е. построим
ортогональный базис
.
Проверим прежде всего, нет ли среди
векторовортогональных. Вычислим:

Откуда
следует, что векторы
иортогональны. Они сразу входят в состав
ортогонального базиса.

Далее
определим
,
пользуясь процедурой ортогонализации.
Ищемв
виде.

Из
условий ортогональности
имеем

Таким
образом
Теперь отнормируем базис,
т.е. переведём его в ортонормированный
базис,
получим

◄

2.
Дополнить
до ортогонального базиса пространства
систему векторов

►Вначале
ортогонализируем
.
Положим.
Исходя из условия ортогональности имеем.

Построим
.
Пусть.
По условиям ортогональности,
откуда имеем

Общее решение
полученной системы есть

ФСР
строится стандартным способом и состоит
из двух линейно независимых решений:

Вектор
ортогонален векторами, следовательно, входит в ортогональный
базис. Вектортакже ортогонален,
но не ортогонален.
Действительно

Проверим
теперь, является ли система векторов
линейно независимой. Для установления
факта зависимости (независимости) этих
векторов вычислим определитель,
составленный из их координат

Неравенство
нулю этого определителя означает, что
однородная система уравнений для
коэффициентов линейной комбинации
рассматриваемых векторов имеет лишь
тривиальное решение. Следовательно,
векторы
линейно независимы и составляют базис
в пространстве.
Остаётся теперь ортогонализировать
вектор.
Следуя стандартной процедуре, ищемв виде

Таким
образом окончательно в качестве
ортогонального базиса в
имеем.◄

Матрица Грамма.Матрицей Грамадля системы векторовназывается симметричная матрица вида

где
.

Утверждение

Скалярное
произведение векторов
и,
заданных в базисе,
вычисляется по формуле

где
— матрица Грама для системы векторов.

Подмножество
евклидова пространства Еⁿ
вида

где
—
линейно независимые векторы, называетсяk-мерным
параллелепипедом,
построенным на векторах
.

Утверждение

Объем
k-мерного
параллелепипеда, построенного на
векторах
,
равен квадратному корню из определителя
матрицы Грама для системы векторов.

4. Ортогональное разложение векторов. Говорят, что векторортогонален к подпространству, если векторортогонален любому вектору из этого подпространства.

Ортогональным
дополнением
к подпространству
из евклидова пространства

называется множество всех векторов
из
,
ортогональных подпространству
.
Обозначается.

Пусть
вектор
представлен в виде,
где,
а
,
тогда вектор
называетсяортогональной
проекцией
вектора
на подпространство,
векторназывается ортогональной составляющей
вектораотносительно подпространства,
число

называется расстоянием от вектора
до подпространства,
а угол между векторамииназывается углом между вектороми подпространством.

Утверждение

Ортогональное
дополнение к подпространству из евклидова
пространства само является подпространством
евклидова пространства
.

Утверждение

Сумма
подпространств
+
является прямой суммой.

Утверждение

Если

–
некоторое подпространство евклидова
пространства
,
то справедливо равенство
+=.

Типовой
пример

Найти
ортогональную проекцию вектора
на подпространство,
порождённое векторами

►Вначале
определим базис данного подпространства.
Проверим, являются ли линейно независимыми
векторы
.
Условие линейной независимости
(зависимости) данных векторовпредставляет собой систему уравнений
относительно коэффициентов.
Найдём решение этой системы с помощью
элементарных преобразований её матрицы:

Как
видно, ранг системы равен 3, определитель
системы отличен от нуля. Следовательно,
однородная система трёх уравнений для
трёх неизвестных имеет лишь тривиальное
решение:
.

Таким
образом векторы
линейно независимы и составляют базис
заданного подпространства. По определению
вектор,
представляющий ортогональную проекциюна подпространство,
принадлежити ортогонален.
Эти условия приводят в итоге к системе
уравнений для координатвекторав базисеподпространства:,
где—
элементы матрицы Грамма. В соответствии
с формулами Крамера решение этой системы
имеет вид

где

—
определитель матрицы Грамма системы
базисных векторов, а
—
определитель, полученный из определителя
Грамма заменой
-го
столбца на столбец из свободных членов

выписанной системы уравнений.

В
рассматриваемой задаче элементы матрицы
Грамма равны

Элементы
столбца свободных членов:
.

Учитывая
это, для определителей

имеем

Откуда

.
Таким образом, для ортогональной прекции
вектора

на подпространство
получим

◄

Пример

Предприятие
выпускает четыре вида продукции
в количествах 50, 80, 20, 120 ед. При этом нормы
расхода сырья составляют соответственно
7; 3,5; 10 и 4 кг. Определить суммарный расход
сырья и его изменение при изменении
выпуска продукциисоответственно на +5, -4, -2, +10 ед.

►Введем
следующие векторы: вектор выпуска
продукции
и вектор расхода сырья.
Тогда суммарный расход сырьяесть скалярное произведение векторови:(кг).

Пусть
— вектор изменения выпуска продукции.
Найдем изменение суммарного расхода
сырья,
используя свойства скалярного произведения
векторов:.

Итак,
(кг).◄

Источник

Ортогональная матрица. Ортогонализация Грамма-Шмидта.

Квадратная матрица 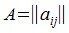||aij|| i=1,2,…n, j=1,2,…n называется ортогональной, если выполняется условие

AA^T=E,

где E — единичная матрица, A^T— транспонированная матрица.

Из условия AA^T=E следует, что A^T является обратной к матрице A:

A^-1=A^T.

Для любой невырожденной квадратной матрицы можно построить ортогональную матрицу. Для построения ортогональной матрицы применяют метод ортогонализации Грамма-Шмидта. Затем нормируют полученные векторы строки. Эти две процедуры вместе называют методом ортонормализации Грамма-Шмидта.

Ортогонализация Грамма-Шмидта

Пусть задана некоторая квадратная матрица, строки которой являются векторы

и пусть эти векторы линейно независимы (т.е. матрица построенная этими векторами строками невырождена). Требуется получить взаимно ортогональные n векторы

Суть метода заключается в следующем:

1. Выбирается некоторая строка (пусть это будет a₁). b₁ выбирается равным a₁.

2. Вектор b₂ получается пректированием a₂ на нуль-пространство b₁.

3. Вектор b₃ получается проектированием a₃ на нуль-пространство матрицы

b_1,b_2

И т.д.

Рассмотрим подробнее процесс ортогонализации.

На первом шаге выбираем b₁=a₁.

На втором шаге вычисляем нуль-пространство b₁:

где E- единичная матрица порядка nxn,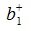-псевдообратная к b₁. Так как b₁ является вектором-строкой (матрицей-строкой), то

Для пректирования a₂ на нуль-пространство b₁ вычисляем

На третьем шаге вычисляем b₃:

Так как векторы b₁ и b₂ ортогональны, то

Следовательно

Для n -го вектора получим:

Таким образом, процедура ортогонализации Грамма-Шмидта имеет следующий вид:

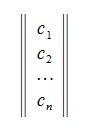
Ортонормализация Грамма-Шмидта

Суть метода ортонормализации Грамма-Шмидта заключается в ортогонализации методом Грамма-Шмидта а затем нормализации полученных векторов строк:

Полученная матрица

является ортогональной матрицей т.к.

Источник

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Так в случае плоской задачи для векторов a = {a_x; a_y} и b = {b_x; b_y}, условие ортогональности запишется следующим образом:

a · b = a_x · b_x + a_y · b_y = 0

Пример 1. Доказать что вектора a = {1; 2} и b = {2; -1} ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 2. Проверить являются ли вектора a = {3; -1} и b = {7; 5} ортогональными.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Пример 3. Найти значение числа n при котором вектора a = {2; 4} и b = {n; 1} будут ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 = 2n + 4
2n + 4 = 0
2n = -4
n = -2

Ответ: вектора a и b будут ортогональны при n = -2.

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = {a_x; a_y; a_z} и b = {b_x; b_y; b_z}, условие ортогональности запишется следующим образом:

a · b = a_x · b_x + a_y · b_y + a_z · b_z = 0

Пример 4. Доказать что вектора a = {1; 2; 0} и b = {2; -1; 10} ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 5. Проверить являются ли вектора a = {2; 3; 1} и b = {3; 1; -9} ортогональными.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 6. Найти значение числа n при котором вектора a = {2; 4; 1} и b = {n; 1; -8} будут ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 — 8 = 2n — 4
2n — 4 = 0
2n = 4
n = 2

Ответ: вектора a и b будут ортогональны при n = 2.

Источник

Процесс ортогонализации Грама-Шмидта

Ортогональные векторы и условие ортогональности

Ортогональные векторы: определение и условие

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Примеры пространственных задач на ортогональность векторов

Ортогональные векторы евклидова пространства и их свойства

Свойства ортогональных векторов

Процесс ортогонализации Грама-Шмидта

Типовые примеры

Матрица Грамма.Матрицей Грамадля системы векторовназывается симметричная матрица вида

4. Ортогональное разложение векторов. Говорят, что векторортогонален к подпро­странству, если векторортогонален любому вектору из этого подпространства.

Ортогональная матрица. Ортогонализация Грамма-Шмидта.

Ортогонализация Грамма-Шмидта

Ортонормализация Грамма-Шмидта

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Примеры пространственных задач на ортогональность векторов

Не пропустите также:

4. Ортогональное разложение векторов. Говорят, что векторортогонален к подпространству, если векторортогонален любому вектору из этого подпространства.