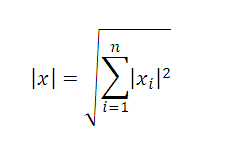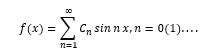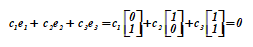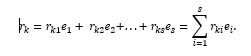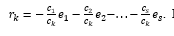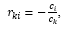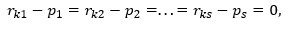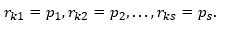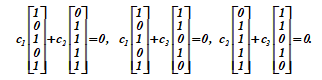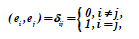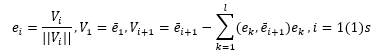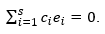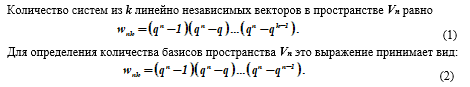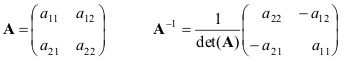Загрузить PDF
Загрузить PDF
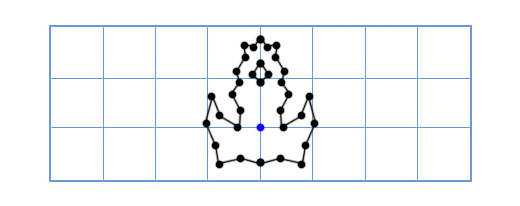
Вектор является геометрическим объектом, он характеризуется направлением и величиной. Его можно представить в виде отрезка с начальной точкой на одном конце и стрелкой на втором, при этом длина отрезка соответствует величине вектора, а стрелка указывает на его направление. Нормирование вектора является стандартной операцией в математике, на практике она используется в компьютерной графике.
-
1
Определим единичный вектор. Единичным вектором вектора A называется такой вектор, направление которого совпадает с направлением вектора A, а длина равна 1. Можно строго доказать, что каждый вектор имеет один и только один соответствующий ему единичный вектор.
-
2
Узнайте, что такое нормирование вектора. Это процедура нахождения единичного вектора для заданного вектора A.
-
3
Определим связанный вектор. В декартовой системе координат связанный вектор выходит из начала координат, то есть для 2-мерного случая из точки (0,0). Это позволяет задавать вектор лишь координатами его конечной точки.
-
4
Освойте запись векторов. Если ограничиться связанными векторами, то в записи A = (x, y) пара координат (x,y) указывает на конечную точку вектора A.
Реклама
-
1
Установите, что известно. Из определения единичного вектора мы знаем, что начальная точка и направление этого вектора совпадают с аналогичными характеристиками вектора A. Кроме того, длина единичного вектора равна 1.
-
2
Определите, что необходимо найти. Требуется найти координаты конечной точки единичного вектора.
Реклама
- Найдите конечную точку единичного вектора для вектора A = (x, y). Единичный вектор и вектор А образуют подобные прямоугольные треугольники, поэтому конечная точка единичного вектора будет иметь координаты (x/c, y/c), где необходимо найти c. Кроме того, длина единичного вектора равна 1. Таким образом, согласно теореме Пифагора имеем: [x^2/c^2 + y^2/c^2]^(1/2) = 1 -> [(x^2 + y^2)/c^2]^(1/2) -> (x^2 + y^2)^(1/2)/c = 1 -> c = (x^2 + y^2)^(1/2). То есть единичный вектор вектора A = (x, y) задается выражением u = (x/(x^2 + y^2)^(1/2), y/(x^2 + y^2)^(1/2)).
- Предположим, что вектор A начинается в начале координат, а его конечная точка расположена в (2,3), то есть A = (2,3). Найдем единичный вектор: u = (x/(x^2 + y^2)^(1/2), y/(x^2 + y^2)^(1/2)) = (2/(2^2 + 3^2)^(1/2), 3/(2^2 + 3^2)^(1/2)) = (2/(13^(1/2)), 3/(13^(1/2))). Таким образом, нормирование вектора A = (2,3) приводит к вектору u = (2/(13^(1/2)), 3/(13^(1/2))).
- Обобщим формулу для нормирования вектора на случай пространства с произвольным числом измерений. Чтобы нормировать вектор A (a, b, c, …), необходимо найти вектор u = (a/z, b/z, c/z, …), где z = (a^2 + b^2 + c^2 …)^(1/2).
Об этой статье
Эту страницу просматривали 29 237 раз.
Была ли эта статья полезной?
Линейная алгебра для разработчиков игр
Эта статья является переводом цикла из четырёх статей «Linear algebra for game developers», написанных David Rosen и посвящённых линейной алгебре и её применению в разработке игр. С оригинальными статьями можно ознакомиться тут: часть 1, часть 2, часть 3 и часть 4. Я не стал публиковать переводы отдельными топиками, а объединил все статьи в одну. Думаю, что так будет удобнее воспринимать материал и работать с ним. Итак приступим.
Зачем нам линейная алгебра?
Одним из направлений в линейной алгебре является изучение векторов. Если в вашей игре применяется позиционирование экранных кнопок, работа с камерой и её направлением, скоростями объектов, то вам придётся иметь дело с векторами. Чем лучше вы понимаете линейную алгебру, тем больший контроль вы получаете над поведением векторов и, следовательно, над вашей игрой.
Что такое вектор?
В играх вектора используются для хранения местоположений, направлений и скоростей. Ниже приведён пример двухмерного вектора: 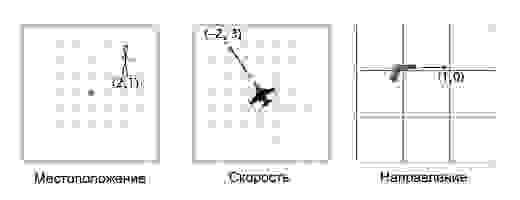
Вектор местоположения (также называемый «радиус-вектором») показывает, что человек стоит в двух метрах восточнее и в одном метре к северу от исходной точки. Вектор скорости показывает, что за единицу времени самолёт перемещается на три километра вверх и на два — влево. Вектор направления говорит нам о том, что пистолет направлен вправо.
Как вы можете заметить, вектор сам по себе всего лишь набор цифр, который обретает тот или иной смысл в зависимости от контекста. К примеру, вектор (1, 0) может быть как направлением для оружия, как показано на картинке, так и координатами строения в одну милю к востоку от вашей текущей позиции. Или скоростью улитки, которая двигается вправо со скоростью в 1 милю в час (прим. переводчика: довольно быстро для улитки, 44 сантиметра в секунду).
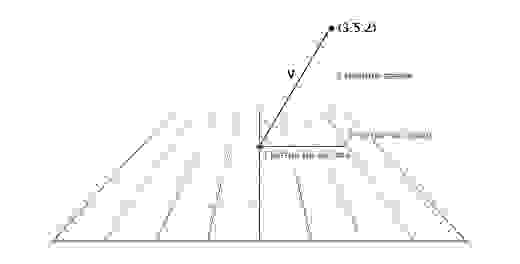
Важно отслеживать единицы измерения. Допустим у нас есть вектор V (3,5,2). Это мало что говорит нам. Три чего, пять чего? В нашей игре Overgrowth расстояния указываются в метрах, а скорости в метрах в секунду. Первое число в этом векторе — это направление на восток, второе — направление вверх, третье — направление на север. Отрицательные числа обозначают противоположные направления, на запад, вниз и на юг. Местоположение, определяемое вектором V (3,5,2), находится в трёх метрах к востоку, в пяти метрах вверху и в двух метрах к северу, как показано на картинке ниже.
Итак, мы изучили основы работы с векторами. Теперь узнаем как вектора использовать.
Сложение векторов
Чтобы сложить вектора, нам надо просто сложить каждую их составляющую друг с другом. Например:
(0, 1, 4) + (3, -2, 5) = (0+3, 1-2, 4+5) = (3, -1, 9)
Зачем нам нужно складывать вектора? Наиболее часто сложение векторов в играх применяется для физического интегрирования. Любой физический объект будет иметь вектора для местоположения, скорости и ускорения. Для каждого кадра (обычно это одна шестидесятая часть секунды), мы должны интегрировать два вектора: добавить скорость к местоположению и ускорение к скорости.
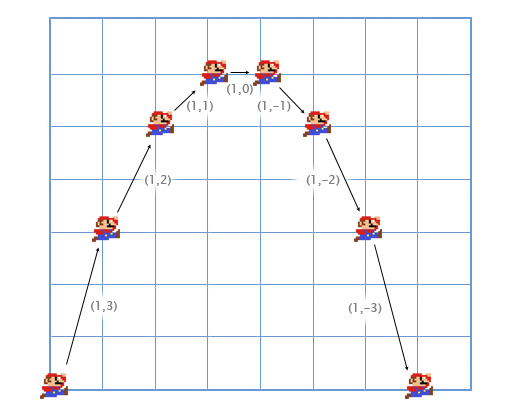
Давайте рассмотрим пример с прыжками Марио. Он начинает с позиции (0, 0). В момент начала прыжка его скорость (1, 3), он быстро двигается вверх и вправо. Его ускорение равно (0, -1), так как гравитация тянет его вниз. На картинке показано, как выглядит его прыжок, разбитый на семь кадров. Чёрным текстом показана его скорость в каждом фрейме.
Давайте рассмотрим первые кадры поподробнее, чтобы понять как всё происходит.
Для первого кадра, мы добавляем скорость Марио (1, 3) к его местоположению (0, 0) и получаем его новые координаты (1, 3). Затем мы складываем ускорение (0, -1) с его скоростью (1, 3) и получаем новое значение скорости Марио (1, 2).
Делаем то-же самое для второго кадра. Добавляем скорость (1, 2) к местоположению (1, 3) и получаем координаты (2, 5). Затем добавляем ускорение (0, -1) к его скорости (1, 2) и получаем новую скорость (1, 1).
Обычно игрок контролирует ускорение игрового персонажа с помощью клавиатуры или геймпада, а игра, в свою очередь, рассчитывает новые значения для скоростей и местоположения, используя физическое сложение (через сложение векторов). Это та-же задача, которая решается в интегральном исчислении, просто мы его сильно упрощаем для нашей игры. Я заметил, что мне намного проще внимательно слушать лекции по интегральному исчислению, думая о практическом его применении, которое мы только что описали.
Вычитание векторов
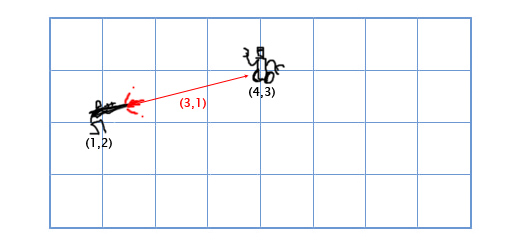
Вычитание рассчитывается по тому-же принципу что и сложение — вычитаем соответствующие компоненты векторов. Вычитание векторов удобно для получения вектора, который показывает из одного местоположения на другое. Например, пусть игрок находится по координатам (1, 2) с лазерным ружьём, а вражеский робот находится по координатам (4, 3). Чтобы определить вектор движения лазерного луча, который поразит робота, нам надо вычесть местоположение игрока из местоположения робота. Получаем:
(4, 3) — (1, 2) = (4-1, 3-2) = (3, 1).
Умножение вектора на скаляр
Когда мы говорим о векторах, мы называем отдельные числа скалярами. Например (3, 4) — вектор, а 5 — это скаляр. В играх, часто бывает нужно умножить вектор на число (скаляр). Например, моделируя простое сопротивление воздуха путём умножения скорости игрока на 0.9 в каждом кадре. Чтобы сделать это, нам надо умножить каждый компонент вектора на скаляр. Если скорость игрока (10, 20), то новая скорость будет:
0.9*(10, 20) = (0.9 * 10, 0.9 * 20) = (9, 18).
Длина вектора
Если у нас есть корабль с вектором скорости V (4, 3), нам также понадобится узнать как быстро он двигается, чтобы посчитать потребность в экранном пространстве или сколько потребуется топлива. Чтобы сделать это, нам понадобится найти длину (модуль) вектора V. Длина вектора обозначается вертикальными линиями, в нашем случае длина вектора V будет обозначаться как |V|.
Мы можем представить V как прямоугольный треугольник со сторонами 4 и 3 и, применяя теорему Пифагора, получить гипотенузу из выражения: x 2 + y 2 = h 2
В нашем случае — длину вектора H с компонентами (x, y) мы получаем из квадратного корня: sqrt(x 2 + y 2 ).
Итак, скорость нашего корабля равна:
|V| = sqrt(4 2 + 3 2 ) = sqrt(25) = 5
Этот подход используется и для трёхмерных векторов. Длина вектора с компонентами (x, y, z) рассчитывается как sqrt(x 2 + y 2 + z 2 )
Расстояние
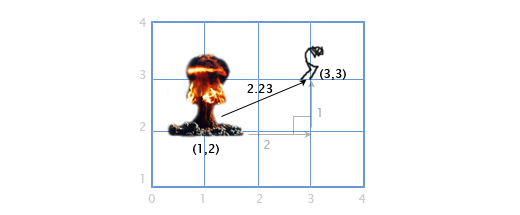
Если игрок P находится в точке (3, 3), а взрыв произошёл в точке E по координатам (1, 2), нам надо определить расстояние между игроком и взрывом, чтобы рассчитать степень ущерба, нанесённого игроку. Это легко сделать, комбинируя две вышеописанных операции: вычитание векторов и их длину.
Мы вычитаем P — E, чтобы получить вектор между ними. А затем определяем длину этого вектора, что и даёт нам искомое расстояние. Порядок следования операндов тут не имеет значения, |E — P| даст тот-же самый результат.
Расстояние = |P — E| = |(3, 3) — (1, 2)| = |(2, 1)| = sqrt(2 2 +1 2 ) = sqrt(5) = 2.23
Нормализация
Когда мы имеем дело с направлениями (в отличие от местоположений и скоростей), важно, чтобы вектор направления имел длину, равную единице. Это сильно упрощает нам жизнь. Например, допустим орудие развёрнуто в направлении (1, 0) и выстреливает снаряд со скоростью 20 метров в секунду. Каков в данном случае вектор скорости для выпущенного снаряда?
Так как вектор направления имеет длину равную единице, мы умножаем направление на скорость снаряда и получаем вектор скорости (20, 0). Если-же вектор направления имеет отличную от единицы длину, мы не сможем сделать этого. Снаряд будет либо слишком быстрым, либо слишком медленным.
Вектор с длиной равной единице называется «нормализованным». Как сделать вектор нормализованным? Довольно просто. Мы делим каждый компонент вектора на его длину. Если, к примеру, мы хотим нормализовать вектор V с компонентами (3, 4), мы просто делим каждый компонент на его длину, то есть на 5, и получаем (3/5, 4/5). Теперь, с помощью теоремы Пифагора, мы убедимся в том, что его длина равна единице:
(3/5) 2 + (4/5) 2 = 9/25 + 16/25 = 25/25 = 1
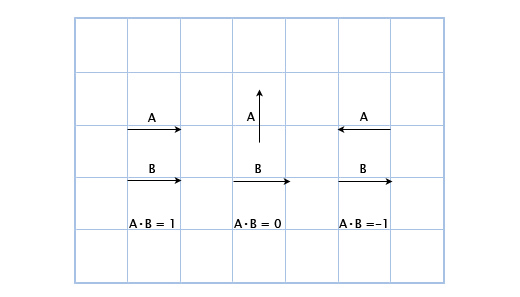
Скалярное произведение векторов
Что такое скалярное произведение (записывается как •)? Чтобы рассчитать скалярное произведение двух векторов, мы должны умножить их компоненты, а затем сложить полученные результаты вместе
(a1, a2) • (b1, b2) = a1b1 + a2b2
Например: (3, 2) • (1, 4) = 3*1 + 2*4 = 11. На первый взгляд это кажется бесполезным, но посмотрим внимательнее на это:
Здесь мы можем увидеть, что если вектора указывают в одном направлении, то их скалярное произведение больше нуля. Когда они перпендикулярны друг другу, то скалярное произведение равно нулю. И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля.
В основном, с помощью скалярного произведения векторов можно рассчитать, сколько их указывает в одном направлении. И хоть это лишь малая часть возможностей скалярного произведения, но уже очень для нас полезная.
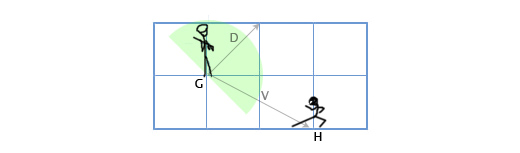
Допустим у нас есть стражник, расположенный в G(1, 3) смотрящий в направлении D(1,1), с углом обзора 180 градусов. Главный герой игры подсматривает за ним с позиции H(3, 2). Как определить, находится-ли главный герой в поле зрения стражника или нет? Сделаем это путём скалярного произведения векторов D и V (вектора, направленного от стражника к главному герою). Мы получим следующее:
V = H — G = (3, 2) — (1, 3) = (3-1, 2-3) = (2, -1)
D•V = (1, 1) • (2, -1) = 1*2 + 1*-1 = 2-1 = 1
Так как единица больше нуля, то главный герой находится в поле зрения стражника.
Мы уже знаем, что скалярное произведение имеет отношение к определению направления векторов. А каково его более точное определение? Математическое выражение скалярного произведения векторов выглядит так:
Где Θ (произносится как «theta») — угол между векторами A и B.
Это позволяет нам найти Θ (угол) с помощью выражения:
Как я говорил ранее, нормализация векторов упрощает нашу жизнь. И если A и B нормализованы, то выражение упрощается следующим образом:
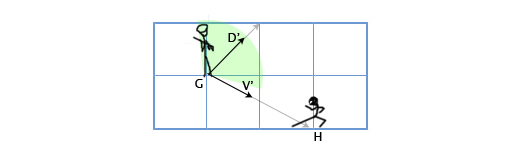
Давайте опять рассмотрим сценарий со стражником. Пусть теперь угол обзора стражника будет равен 120 градусам. Получим нормализованные вектора для направления взгляда стражника (D’) и для направления от стражника к главному герою (V’). Затем определим угол между ними. Если угол более 60 градусов (половина от угла обзора), то главный герой находится вне поля зрения стражника.
D’ = D / |D| = (1, 1) / sqrt(1 2 + 1 2 ) = (1, 1) / sqrt(2) = (0.71, 0.71)
V’ = V / |V| = (2, -1) / sqrt(2 2 + (-1) 2 ) = (2,-1) / sqrt(5) = (0.89, -0.45)
Θ = acos(D’V’) = acos(0.71*0.89 + 0.71*(-0.45)) = acos(0.31) = 72
Угол между центром поля зрения стражника и местоположением главного героя составляет 72 градуса, следовательно стражник его не видит.
Понимаю, что это выглядит довольно сложно, но это потому, что мы всё делаем вручную. В программе это всё довольно просто. Ниже показано как я сделал это в нашей игре Overgrowth с помощью написанных мной С++ библиотек для работы с векторами:
Векторное произведение
Допустим у нас есть корабль с пушками, которые стреляют в правую и в левую стороны по курсу. Допустим, что лодка расположена вдоль вектора направления (2, 1). В каких направлениях теперь стреляют пушки?
Это довольно просто в двухмерной графике. Чтобы повернуть направление на 90 градусов по часовой стрелке, достаточно поменять местами компоненты вектора, а затем поменять знак второму компоненту.
(a, b) превращается в (b, -a). Следовательно у корабля, расположенного вдоль вектора (2, 1), пушки справа по борту будут стрелять в направлении (1, -2), а пушки с левого борта, будут стрелять в противоположном направлении. Меняем знаки у компонент вектора и получаем (-1, 2).
А что если мы хотим рассчитать это всё для трехмерной графики? Рассмотрим пример с кораблём.
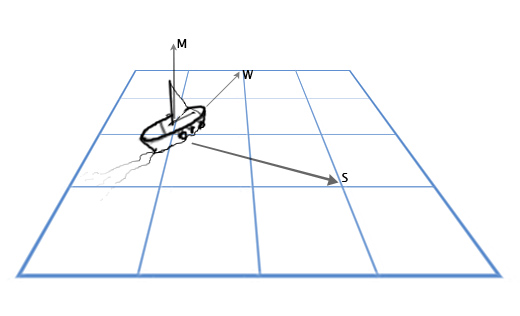
У нас есть вектор мачты M, направленной прямо вверх (0, 1, 0) и направление ветра: север-северо-восток W (1, 0, 2). И мы хотим вычислить вектор направления паруса S, чтобы наилучшим образом «поймать ветер».
Для решения этой задачи мы используем векторное произведение: S = M x W.
Подставим теперь нужные нам значения:
S = MxW = (0, 1, 0) x (1, 0, 2) = ([1*2 — 0*0], [0*1 — 0*2], [0*0 — 1*1]) = (2, 0, -1)
Для расчётов вручную довольно сложно, но для графических и игровых приложений я рекомендую написать функцию, подобную той, что указана ниже и не вдаваться более в детали подобных расчётов.
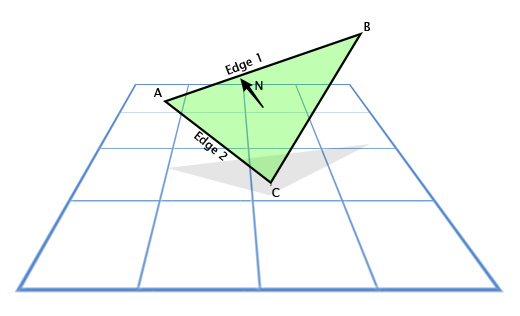
Векторное произведение часто используется в играх, чтобы рассчитать нормали к поверхностям. Направления, в которых «смотрит» та или иная поверхность. Например, рассмотрим треугольник с векторами вершин A, B и С. Как мы найдем направление в котором «смотрит» треугольник, то есть направление перпендикулярное его плоскости? Это кажется сложным, но у нас есть инструмент для решения этой задачи.
Используем вычитание, для определения направления из A в С (C — A), пусть это будет «грань 1» (Edge 1) и направление из A в B (B — A), пусть это будет «грань 2» (Edge 2). А затем применим векторное произведение, чтобы найти вектор, перпендикулярный им обоим, то есть перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».
Вот так это выглядит в коде:
В играх основное выражение освещённости записывается как N • L, где N — это нормаль к освещаемой поверхности, а L — это нормализованный вектор направления света. В результате поверхность выглядит яркой, когда на неё прямо падает свет, и тёмной, когда этого не происходит.
Теперь перейдем к рассмотрению такого важного для разработчиков игр понятия, как «матрица преобразований» (transformation matrix).
Для начала изучим «строительные блоки» матрицы преобразований.
Базисный вектор
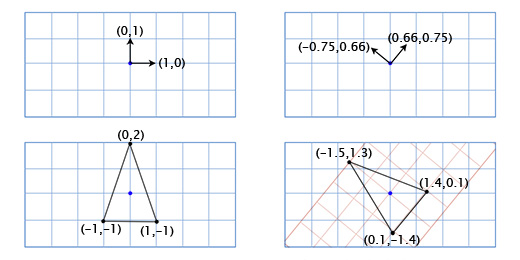
Допустим мы пишем игру Asteroids на очень старом «железе» и нам нужен простой двухмерный космический корабль, который может свободно вращаться в своей плоскости. Модель корабля выглядит так:
Как нам рисовать корабль, когда игрок поворачивает его на произвольный градус, скажем 49 градусов против часовой стрелки. Используя тригонометрию, мы можем написать функцию двухмерного поворота, которая принимает координаты точки и угол поворота, и возвращает координаты смещённой точки:
Применяя эту функцию ко всем трём точкам, мы получим следующую картину:
Операции с синусами и косинусами работают довольно медленно, но так как мы делаем расчёты лишь для трёх точек, это будет нормально работать даже на старом «железе» (прим. переводчика: в случаях, когда предполагается интенсивное использование тригонометрических функций, для ускорения вычислений, в памяти организуют таблицы значений для каждой функции и рассчитывают их во время запуска приложения. Затем при вычислении той или иной тригонометрической функции просто производится обращение к таблице).
Пусть теперь наш корабль выглядит вот так:
Теперь старый подход будет слишком медленным, так как надо будет поворачивать довольно большое количество точек. Одно из элегантных решений данной проблемы будет звучать так — «Что если вместо поворота каждой точки модели корабля, мы повернём координатную решётку нашей модели?»
Как это работает? Давайте посмотрим внимательнее, что собой представляют координаты.
Когда мы говорим о точке с координатами (3, 2), мы говорим, что её местоположение находится в трех шагах от точки отсчёта по координатной оси X, и двух шагах от точки отсчёта по координатной оси Y.
По-умолчанию координатные оси расположены так: вектор координатной оси X (1, 0), вектор координатной оси Y (0, 1). И мы получим расположение: 3(1, 0) + 2(0, 1). Но координатные оси не обязательно должны быть в таком положении. Если мы повернём координатные оси, в это-же время мы повернём все точки в координатной решётке.
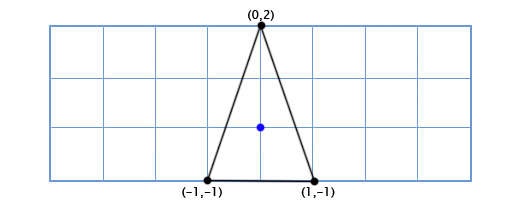
Чтобы получить повернутые оси X и Y мы применим тригонометрические функции, о которых говорили выше. Если мы поворачиваем на 49 градусов, то новая координатная ось X будет получена путём поворота вектора (0, 1) на 49 градусов, а новая координатная ось Y будет получена путём поворота вектора (0, 1) на 49 градусов. Итак вектор новой оси X у нас будет равен (0.66, 0.75), а вектор новой оси Y будет (-0.75, 0.66). Сделаем это вручную для нашей простой модели из трёх точек, чтобы убедиться, что это работает так, как нужно:
Координаты верхней точки (0, 2), что означает, что её новое местоположение находится в 0 на новой (повёрнутой) оси X и 2 на новой оси Y:
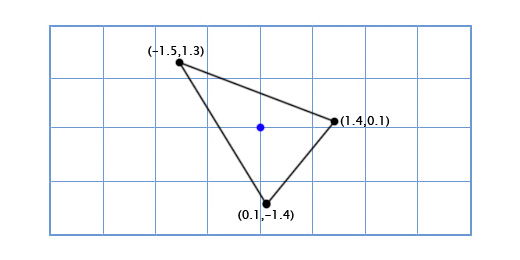
0*(0.66,0.75) + 2*(-0.75, 0.66) = (-1.5, 1.3)
Нижняя левая точка (-1, -1), что означает, что её новое местоположение находится в -1 на повернутой оси X, и -1 на повернутой оси Y:
-1*(0.66,0.75) + -1*(-0.75, 0.66) = (0.1, -1.4)
Нижняя правая точка (1, -1), что означает её новое местоположение находится в 1 на повернутой оси X, и -1 на повернутой оси Y
1*(0.66,0.75) + -1*(-0.75, 0.66) = (1.4, 0.1)
Мы показали, как координаты корабля отображаются в другой координатной сетке с повернутыми осями (или «базисными векторами»). Это удобно в нашем случае, так как избавляет нас от необходимости применять тригонометрические преобразования к каждой из точек модели корабля.
Каждый раз, когда мы изменяем базисные вектора (1, 0) и (0, 1) на (a, b) и (c, d), то новая координата точки (x, y) может быть найдена с помощью выражения:
Обычно базисные вектора равны (1, 0) и (0, 1) и мы просто получаем x(1, 0) + y(0, 1) = (x, y), и нет необходимости заботиться об этом дальше. Однако, важно помнить, что мы можем использовать и другие базисные вектора, когда нам это нужно.
Матрицы
Матрицы похожи на двухмерные вектора. Например, типичная 2×2 матрица, может выглядеть так:
Когда вы умножаете матрицу на вектор, вы суммируете скалярное произведение каждой строки с вектором, на который происходит умножение. Например, если мы умножаем вышеприведённую матрицу на вектор (x, y), то мы получаем:
Будучи записанным по-другому, это выражение выглядит так:
Выглядит знакомо, не так-ли? Это в точности такое-же выражение, которые мы использовали для смены базисных векторов. Это означает, что умножая 2×2 матрицу на двухмерный вектор, мы тем самым меняем базисные вектора. Например, если мы вставим стандартные базисные вектора в (1, 0) и (0, 1) в колонки матрицы, то мы получим:
Это единичная матрица, которая не даёт эффекта, который мы можем ожидать от нейтральных базисных векторов, которые мы указали. Если-же мы повернём базисные вектора на 49-градусов, то мы получим:
Эта матрица будет поворачивать двухмерный вектор на 49 градусов против часовой стрелки. Мы можем сделать код нашей игры Asteriods более элегантным, используя матрицы вроде этой. Например, функция поворота нашего корабля может выглядеть так:
Однако, наш код будет ещё более элегантным, если мы сможем также включить в эту матрицу перемещение корабля в пространстве. Тогда у нас будет единая структура данных, которая будет заключать в себе и применять информацию об ориентации объекта и его местоположении в пространстве.
К счастью есть способ добиться этого, хоть это и выглядит не очень элегантно. Если мы хотим переместиться с помощью вектора (e, f), мы лишь включаем его в нашу матрицу преобразования:
И добавляем дополнительную единицу в конец каждого вектора, определяющего местоположение объекта, например так:
Теперь, когда мы перемножаем их, мы получаем:
(a, c, e) • (x, y, 1) + (b, d, f) • (x, y, 1) + (0, 0, 1) • (x, y, 1)
Что, в свою очередь, может быть записано как:
x(a, b) + y(c, d) + (e, f)
Теперь у нас есть полный механизм трансформации, заключённый в одной матрице. Это важно, если не принимать в расчёт элегантность кода, так как с ней мы теперь можем использовать все стандартные манипуляции с матрицами. Например перемножить матрицы, чтобы добавить нужный эффект, или мы можем инвертировать матрицу, чтобы получить прямо противоположное положение объекта.
Трехмерные матрицы
Матрицы в трехмерном пространстве работают так-же как и в двухмерном. Я приводил примеры с двухмерными векторами и матрицами, так как их просто отобразить с помощью дисплея, показывающего двухмерную картинку. Нам просто надо определить три колонки для базисных векторов, вместо двух. Если базисные вектора это (a,b,c), (d,e,f) and (g,h,i) то наша матрица будет выглядеть так:
Если нам нужно перемещение (j,k,l), то мы добавляем дополнительную колонку и строку, как говорили раньше:
И добавляем единицу [1] в вектор, как здесь:
Вращение в двухмерном пространстве
Так как в нашем случае у нас только одна ось вращения (расположенная на дисплее), единственное, что нам надо знать, это угол. Я говорил об этом ранее, упоминая, что мы можем применять тригонометрические функции для реализации функции двухмерного вращения наподобие этой:
Более элегантно это можно выразить в матричной форме. Чтобы определить матрицу, мы можем применить эту функцию к осям (1, 0) и (0, 1) для угла Θ, а затем включить полученные оси в колонки нашей матрицы. Итак, начнём с координатной оси X (1, 0). Если мы применим к ней нашу функцию, мы получим:
(1*cos(Θ) — 0*sin(Θ), 1*sin(Θ) + 0*cos(Θ)) = (cos(Θ), sin(Θ))
Затем, мы включаем координатную ось Y (0, 1). Получим:
(0*cos(Θ) — 1*sin(Θ), 0*sin(Θ) + 1*cos(Θ)) = (-sin(Θ), cos(Θ))
Включаем полученные координатные оси в матрицу, и получаем двухмерную матрицу вращения:
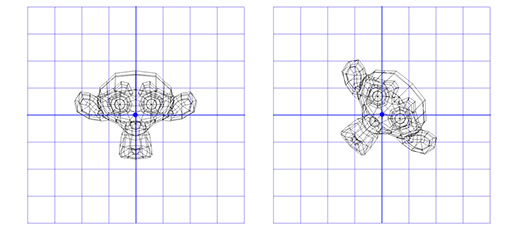
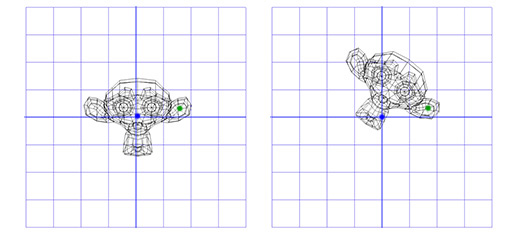
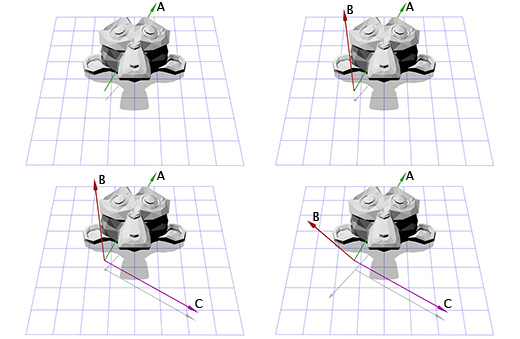
Применим эту матрицу к Сюзанне, мартышке из графического пакета Blender. Угол поворота Θ равен 45 градусов по часовой стрелке.
Как видите — это работает. Но что если нам надо осуществить вращение вокруг точки, отличной от (0, 0)?
Например, мы хотим вращать голову мартышки вокруг точки, расположенной в её ухе:
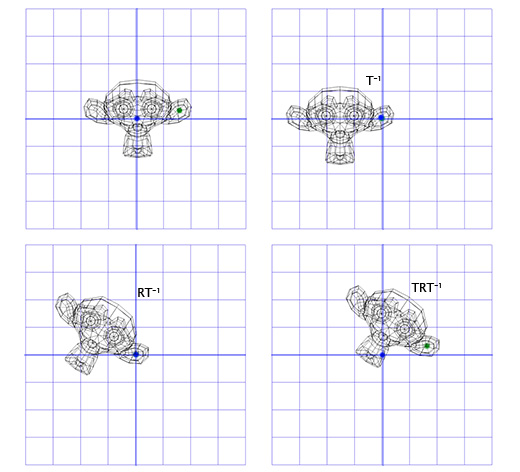
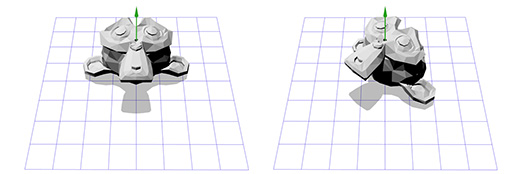
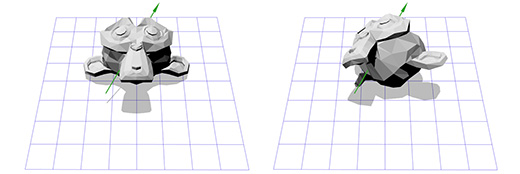
Чтобы сделать это, мы можем начать с создания матрицы перемещения (translation matrix) T, которая перемещает объект из начальной точки в точку вращения в ухе мартышки, и матрицу вращения R, для вращения объекта вокруг начальной точки. Теперь для вращения вокруг точки, расположенной в ухе, мы можем сперва переместить точку в ухе на место начальной точки, с помощью инвертирования матрицы T, записанной как T -1 . Затем, мы вращаем объект вокруг начальной точки, с помощью матрицы R, а затем применяем матрицу T для перемещения точки вращения назад, к своему исходному положению.
Ниже дана иллюстрация к каждому из описанных шагов:
Это важный шаблон, который мы будем применять позднее — применение вращения для двух противоположных трансформаций позволяет нам вращать объект в другом «пространстве». Что очень удобно и полезно.
Теперь рассмотрим трёхмерное вращение.
Трёхмерное вращение
Вращение вокруг оси Z работает по тому-же принципу, что и вращение в двухмерном пространстве. Нам лишь нужно изменить нашу старую матрицу, добавив к ней дополнительную колонку и строку:
Применим эту матрицу к трехмерной версии Сюзанны, мартышки из пакета Blender. Угол поворота Θ пусть будет равен 45 градусов по часовой стрелке.
То-же самое. Вращение только вокруг оси Z ограничивает нас, как насчёт вращения вокруг произвольной оси?
Вращение, определяемое осью и углом (Axis-angle rotation)
Представление вращения, определяемого осью и углом, также известно как вращение в экспоненциальных координатах, параметризованное вращением двух величин. Вектора, определяющего вращение направляющей оси (прямая линия) и угла, описывающего величину поворота вокруг этой оси. Вращение осуществляется согласно правилу правой руки.
Итак, вращение задаётся двумя параметрами (axis, angle), где axis — вектор оси вращения, а angle — угол вращения. Этот приём довольно прост и являет собой отправную точку для множества других операций вращения, с которыми я работаю. Как практически применить вращение, определяемое осью и углом?
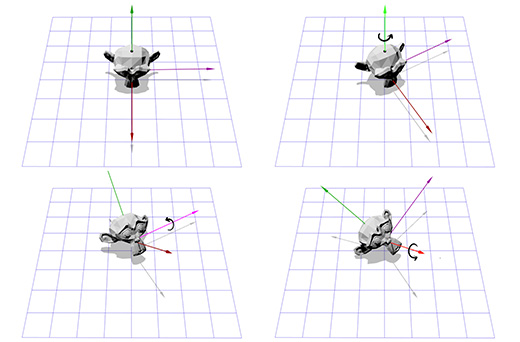
Допустим мы имеем дело с осью вращения, показанной на рисунке ниже:
Мы знаем как вращать объект вокруг оси Z, и мы знаем как вращать объект в других пространствах. Итак, нам лишь надо создать пространство, где наша ось вращения будет являться осью Z. И если эта ось будет осью Z, то что будет являться осями X и Y? Займемся вычислениями сейчас.
Чтобы создать новые оси X и Y нам нужно лишь выбрать два вектора, которые перпендикулярны новой оси Z и перпендикулярны друг другу. Мы уже говорили ранее о векторном умножении, которое берёт два вектора и даёт в итоге перпендикулярный им вектор.
У нас есть один вектор сейчас, это ось вращения, назовём его A. Возьмём теперь случайный другой вектор B, который находится не в том-же направлении, что и вектор A. Пусть это будет (0, 0, 1) к примеру.
Теперь мы имеем ось вращения A и случайный вектор B, мы можем получить нормаль C, через векторное произведение A и B. С перпендикулярен векторам A и B. Теперь мы делаем вектор B перпендикулярным векторам A и C через их векторное произведение. И всё, у нас есть все нужные нам оси координат.
На словах это звучит сложно, но довольно просто выглядит в коде или будучи показанным в картинках.
Ниже показано, как это выглядит в коде:
Тут показана иллюстрация для каждого шага:
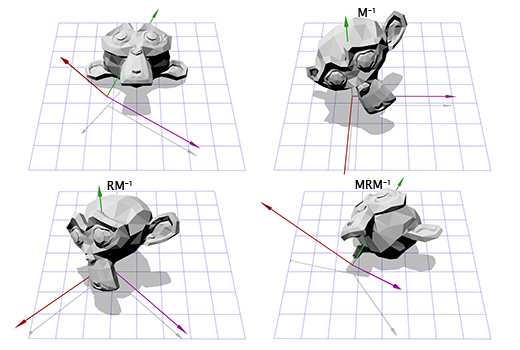
Теперь, имея информацию о новых координатных осях, мы можем составить матрицу M, включив каждую ось как колонку в эту матрицу. Нам надо убедиться, что вектор A является третьей колонкой, чтобы он был нашей новой осью координат Z.
Теперь это похоже на то, что мы делали для поворота в двухмерном пространстве. Мы можем применить инвертированную матрицу M, чтобы переместиться в новую систему координат, затем произвести вращение, согласно матрице R, чтобы повернуть объект вокруг оси Z, затем применить матрицу M, чтобы вернуться в исходное координатное пространство.
Теперь мы можем вращать объект вокруг произвольной оси. В конце концов мы можем просто создать матрицу T = T = M -1 RM и использовать её много раз, без дополнительных усилий с нашей стороны. Есть более эффективные способы конвертирования вращений, определяемых осью и углом во вращения, определяемые матрицами. Просто описанный нами подход показывает многое из того, о чём мы говорили ранее.
Вращение, определяемое осью и углом, возможно, самый интуитивно понятный способ. Применяя его, очень легко инвертировать поворот, поменяв знак у угла, и легко интерполировать, путём интерполяции угла. Однако тут есть серьёзное ограничение, и заключается оно в том, что такое вращение не является суммирующим. То есть вы не можете комбинировать два вращения, определяемых осью и углом в третье.
Вращение, определяемое осью и углом — хороший способ для начала, но оно должно быть преобразовано во что-то другое, чтобы использоваться в более сложных случаях.
Эйлеровские углы
Эйлеровские углы представляют собой другой способ вращения, заключающийся в трёх вложенных вращениях относительно осей X, Y и Z. Вы, возможно, сталкивались с их применением в играх, где камера показывает действие от первого лица, либо от третьего лица.
Допустим вы играете в шутер от первого лица и вы повернулись на 30 градусов влево, а затем посмотрели на 40 градусов вверх. В конце-концов в вас стреляют, попадают, и, в результате удара, камера поворачивается вокруг своей оси на 45 градусов. Ниже показано вращение с помощью углов Эйлера (30, 40, 45).
Углы Эйлера — удобное и простое в управлении средство. Но у этого способа есть два недостатка.
Первый, это вероятность возникновения ситуации под названием «блокировка оси» или «шарнирный замок» (gimbal lock). Представьте, что вы играете в шутер от первого лица, где вы можете посмотреть влево, вправо, вверх и вниз или повернуть камеру вокруг зрительной оси. Теперь представьте, что вы смотрите прямо вверх. В этой ситуации попытка взглянуть налево или направо будет аналогична попытке вращения камеры. Всё что мы можем вы этом случае, это вращать камеру вокруг своей оси, либо посмотреть вниз. Как вы можете представить, это ограничение делает непрактичным применение углов Эйлера в лётных симуляторах.
Второе — интерполяция между двумя эйлеровскими углами вращения не даёт кратчайшего пути между ними.
Например, у вас две интерполяции между двумя одинаковыми вращениями. Первая использует интерполяцию эйлеровского угла, вторая использует сферическую линейную интерполяцию (spherical linear interpolation (SLERP)), чтобы найти кратчайший путь.
Итак, что-же больше подойдет для интерполяции вращений? Может быть матрицы?
Вращение с помощью матриц
Как мы уже говорили ранее, матрицы вращения хранят в себе информацию о трёх осях. Это означает, что интерполяция между двумя матрицами лишь линейно интерполирует каждую ось. В результате это даёт нам эффективный путь, то так-же привносит новые проблемы. Например, тут показаны два вращения и одно интерполированное полу-вращение:
Как вы можете заметить, интерполированное вращение значительно меньше, чем любое из исходных вращений, и две оси более не перпендикулярны друг другу. Это логично, если вдуматься — середина отрезка, соединяющего любые две точки на сфере будет расположена ближе к центру сферы.
Это в свою очередь порождает известный «эффект фантика» (candy wrapper effect), при применении скелетной анимации. Ниже показана демонстрация этого эффекта на примере кролика из нашей игры Overgrowth (прим. переводчика: обратите внимание на середину туловища кролика).
Вращение, основанное на матричных операциях, очень полезно, так как они могут аккумулировать вращения без всяких проблем, вроде блокировки оси (gimbal lock), и может очень эффективно применяться к точкам сцены. Вот почему поддержка вращения на матрицах встроена в графические карты. Для любого типа трёхмерной графики матричный формат вращения — это всегда итоговый применяемый способ.
Однако, как мы уже знаем, матрицы не очень хорошо интерполируются, и они не столь интуитивно понятны.
Итак, остался только один главный формат вращения. Последний, но тем не менее, важный.
Кватернионы
Что-же такое кватернионы? Если очень кратко, то это альтернативный вариант вращения, основанный на оси и угле (axis-angle rotation), который существует в пространстве.
Подобно матрицам они могут аккумулировать вращения, то есть вы можете составлять из них цепочку вращений, без опаски получить блокировку оси (gimbal lock). И в то-же время, в отличие от матриц, они могут хорошо интерполироваться из одного положения в другое.
Являются-ли кватернионы лучшим решением, нежели остальные способы вращений (rotation formats)?
На сегодняшний день они комбинируют все сильные стороны других способов вращений. Но у них есть два слабых места, рассмотрев которые, мы придём к выводу, что кватернионы лучше использовать для промежуточных вращений. Итак, каковы недостатки кватернионов.
Во-первых кватернионы непросто отобразить на трёхмерном пространстве. И мы вынуждены всегда реализовывать вращение более простым способом, а затем конвертировать его. Во-вторых, кватернионы не могут эффективно вращать точки, и мы вынуждены конвертировать их в матрицы, чтобы повернуть значительное количество точек.
Это означает, что вы скорее всего не начнете или не закончите серию вращений с помощью кватернионов. Но с их помощью можно реализовать промежуточные вращения более эффективно, нежели при применении любого другого подхода.
«Внутренняя кухня» механизма кватернионов не очень понятна и не интересна мне. И, возможно, не будет интересна и вам, если только вы не математик. И я советую вам найти библиотеки, которые работают с кватернионами, чтобы облегчить вам решение ваших задач с их помощью.
Математические библиотеки «Bullet» или «Blender» будут хорошим вариантом для начала.
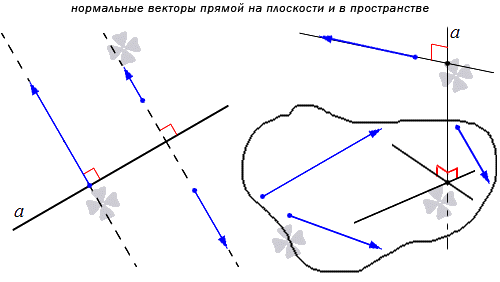
Нормальный вектор прямой, координаты нормального вектора прямой
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а 1 параллельные, а n → считается нормальным вектором прямой a , также считается нормальным вектором для прямой a 1 . Когда прямая а имеет прямой вектор, тогда вектор t · n → является ненулевым при любом значении параметра t , причем также является нормальным для прямой a .
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Если задана плоскость О х у , то множеством векторов для О х является координатный вектор j → . Он считается ненулевым и принадлежащим координатной оси О у , перпендикулярной О х . Все множество нормальных векторов относительно О х можно записать, как t · j → , t ∈ R , t ≠ 0 .
Прямоугольная система O x y z имеет нормальный вектор i → , относящийся к прямой О z . Вектор j → также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный О z , считается нормальным для O z .
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Задана прямая вида 2 x + 7 y — 4 = 0 _, найти координаты нормального вектора.
По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2 , 7 .
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Указать нормальный вектор для заданной прямой y — 3 = 0 .
По условию нам дано общее уравнение прямой, значит запишем его таким образом 0 · x + 1 · y — 3 = 0 . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0 , 1 .
Если дано уравнение в отрезках вида x a + y b = 1 или уравнение с угловым коэффициентом y = k · x + b , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.
Найти координаты нормального вектора, если дано уравнение прямой x 1 3 — y = 1 .
Для начала необходимо перейти от уравнения в отрезках x 1 3 — y = 1 к уравнению общего вида. Тогда получим, что x 1 3 — y = 1 ⇔ 3 · x — 1 · y — 1 = 0 .
Отсюда видно, что координаты нормального вектора имеют значение 3 , — 1 .
Ответ: 3 , — 1 .
Если прямая определена каноническим уравнением прямой на плоскости x — x 1 a x = y — y 1 a y или параметрическим x = x 1 + a x · λ y = y 1 + a y · λ , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a → = ( a x , a y ) . Возможность нахождения координат нормального вектора n → возможно, благодаря условию перпендикулярности векторов n → и a → .
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0
Для решения можно выбирать любой удобный способ.
Найти нормальный вектор заданной прямой x — 2 7 = y + 3 — 2 .
Из прямой x — 2 7 = y + 3 — 2 понятно, что направляющий вектор будет иметь координаты a → = ( 7 , — 2 ) . Нормальный вектор n → = ( n x , n y ) заданной прямой является перпендикулярным a → = ( 7 , — 2 ) .
Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a → = ( 7 , — 2 ) и n → = ( n x , n y ) запишем a → , n → = 7 · n x — 2 · n y = 0 .
Значение n x – произвольное , следует найти n y . Если n x = 1 , отсюда получаем, что 7 · 1 — 2 · n y = 0 ⇔ n y = 7 2 .
Значит, нормальный вектор имеет координаты 1 , 7 2 .
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
x — 2 7 = y + 3 — 2 ⇔ 7 · ( y + 3 ) = — 2 · ( x — 2 ) ⇔ 2 x + 7 y — 4 + 7 3 = 0
Полученный результат координат нормального вектора равен 2 , 7 .
Ответ: 2 , 7 или 1 , 7 2 .
Указать координаты нормального вектора прямой x = 1 y = 2 — 3 · λ .
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
x = 1 y = 2 — 3 · λ ⇔ x = 1 + 0 · λ y = 2 — 3 · λ ⇔ λ = x — 1 0 λ = y — 2 — 3 ⇔ x — 1 0 = y — 2 — 3 ⇔ ⇔ — 3 · ( x — 1 ) = 0 · ( y — 2 ) ⇔ — 3 · x + 0 · y + 3 = 0
Отсюда видно, что координаты нормального вектора равны — 3 , 0 .
Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат О х у z .
Когда прямая задается при помощи уравнений пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда нормальный вектор плоскости относится к A 2 x + B 2 y + C 2 z + D 2 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда получаем запись векторов в виде n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрического, имеющего вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , отсюда a x , a y и a z считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a → = ( a x , a y , a z ) . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a → = ( a x , a y , a z ) .
59. Норма вектора. Нормированное пространство
Определим длину или норму вектора, которую обозначим

Здесь учтена аксиома 40 и берется арифметическое значение корня. Из определения нормы вытекает:
1) |x| > 0 при x ¹ 0 и |x| = 0 только, если x = 0.
Вектор X, длина которого равна единице, называется нормированным. Очевидно, всякий ненулевой вектор можно пронормировать, умножив его на число 

Определим угол между векторами. Углом между векторами назовем угол, косинус которого определяется из соотношения
В силу неравенства Коши – Буняковского |cos j| £ 1, что корректно.
Договоримся считать два вектора евклидового пространства х и у ортогональными, если их скалярное произведение равно нулю. Отсюда следует, что в евклидовом пространстве справедлива теорема Пифагора:
|| x + y ||2 = (x + y, x + y) = (x, x) + 2(x, y) + (y, y) = || x ||2 + || y ||2
Приведем пример условия ортогональности двух векторов X и Y в пространстве An
X1y1 + x2y2 + … + xnyn = 0
Вспомним, что это условие ортогональности двух векторов, которое в векторной алгебре мы получим из скалярного произведения.
В пространстве c(a, b) условие ортогональности имеет вид
Например, векторы x = cos nt и y = sin mt, где m и n – целые, ортогональны при a = — p и b = p
С этим важным примером мы будем часто встречаться в математике.
Теперь введем определение: линейное пространство R называется нормированным, если выполнены следующие два требования:
1. любому элементу x пространства ставится в соответствие или определяется норма 
2. Указанное правило введения нормы подчинено следующим аксиомам:
10 || x || > 0, если x ¹ 0; || x || = 0, если x = 0
30 справедливо равенство || x + y || £ || x || + || y || называемое неравенством Минковского или неравенством треугольника.
Всякое евклидово пространство является нормированным, если в нем норму любого элемента х определить равенством 
Справедливость неравенства Минковского докажем, опираясь на неравенство Коши – Буняковского:
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnyj-vektor-prjamoj-koordinaty-normalnogo-vek/
http://matica.org.ua/metodichki-i-knigi-po-matematike/kurs-lektcii-po-lineinoi-algebre-i-analiticheskoi-geometrii/59-norma-vektora-normirovannoe-prostranstvo
Норма вектораФормулы, примеры, калькулятор нормы вектора Определение 1. Норма вектора ( эвклидова норма, модуль вектора, длина вектора) x=(x1,x2, …xn) Пример 1. Найти норму вектора a = (5,-2,7) Решение. Подставляем координаты вектора, получаем норму вектора Как нормировать векторНормированный вектор – это единичный вектор по направлению. То есть, сохраняется информация только о направлении вектора: Для того чтобы получить нормированный вектор, необходимо каждую координату исходного вектора разделить на норму вектора. Пример 2. Нормировать вектор a = (5,-2,7) Решение. Подставляем координаты вектора, получаем нормированный вектор Проверить правильность вычисления нормы вектора, а также найти нормированный вектор можно с помощью калькулятора. |
Категория: Аналитическая геометрия | Просмотров: 12351 | | Теги: вектор | Рейтинг: 0.0/0 |
При проведении научных и прикладных исследование часто создаются модели, в которых рассматриваются точки и/или векторы определенных пространств. Например, в моделях шифров на эллиптических кривых используются аффинные и проективные пространства. К проективным прибегают тогда, когда необходимо ускорить вычисления, так как в формулах манипулирования с точками эллиптической кривой выводимых в рамках проективного пространства отсутствует операция деления на координату, которую в случае аффинного пространства обойти не удается.
Операция деления как раз одна из самых «дорогих» операций. Дело в том, что в алгебраических полях, а соответственно и в группах операция деления вообще отсутствует и выход из положения (когда не делить нельзя) состоит в том, что операцию деления заменяют умножением, но умножают не на саму координату, а на обращенное ее значение. Из этого следует, что предварительно надо привлекать расширенный алгоритм Евклида НОД и кое что еще. Одним словом, не все так просто как изображают авторы большинства публикаций о ЕСС. Почти все, что по этой теме опубликовано и не только в Интернете мне знакомо. Мало того, что авторы не компетентны и занимаются профанацией, оценщики этих публикаций плюсуют авторов в комментариях, т. е. не видят ни пробелов, ни явных ошибок. Про нормальную же статью пишут, что она уже 100500-я и от нее нулевой эффект. Так все пока на Хабре устроено, анализ публикаций делается огромный, но не качества содержания. Здесь возразить нечего — реклама двигатель бизнеса.
Линейное векторное пространство
Изучение и описание явлений окружающего мира с необходимостью приводит нас к введению и использованию ряда понятий таких как точки, числа, пространства, прямые линии, плоскости, системы координат, векторы, множества и др.
Пусть r<3> = <r1, r2, r3> вектор трехмерного пространства, задает положение одной частицы (точки) относительно начала координат. Если рассматривать N элементов, то описание их положения требует задания 3∙N координат, которые можно рассматривать как координаты некоторого вектора в 3N-мерном пространстве. Если рассматривать непрерывные функции и их совокупности, то приходим к пространствам, размерность которых равна бесконечности. На практике часто ограничиваются использованием лишь подпространства такого бесконечномерного пространства функции координат, обладающего конечным числом измерений.
Пример 1. Ряд Фурье — пример использования пространства функций. Рассмотрим разложение произвольной функции в ряд Фурье
Его можно трактовать как разложение «вектора» f(x) по бесконечному набору «ортогональных» базисных векторов sinпх
Это пример абстрагирования и распространения понятия вектора на бесконечное число измерений. Действительно, известно, что при -π≤x≤π
Существо дальнейшего рассмотрения не пострадает, если мы отвлечемся от размерности абстрактного векторного пространства – будь — то 3, 3N или бесконечность, хотя для практических приложений больший интерес представляет конечномерные поля и векторные пространства.
Набор векторов r1, r2,… будем называть линейным векторным пространством L, если сумма любых двух его элементов тоже находится в этом наборе и если результат умножения элемента на число С также входит в этот набор. Оговоримся сразу, что значения числа С могут быть выбраны из вполне определенного числового множества Fр – поля вычетов по модулю простого числа р, которое считается присоединенным к L.
Пример 2. Набор из 8 векторов, составленных из n =5 -разрядных двоичных чисел
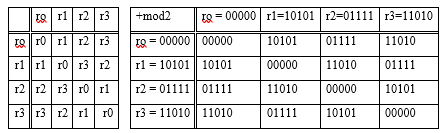
r0 = 00000, r1 = 10101, r2 = 01111, r3 = 11010, r4 = 00101, r5 = 10110, r6 = 01001, r7 = 11100 образует векторное пространство L, если числа С є {0,1}. Этот небольшой пример позволяет убедиться в проявлении свойств векторного пространства, включенных в его определение.
Суммирование этих векторов выполняется поразрядно по модулю два, т. е. без переноса единиц в старший разряд. Отметим, что если все С действительные (в общем случае С принадлежат полю комплексных чисел), то векторное пространство называют действительным.
Формально аксиомы векторного пространства и записываются так:
r1 + r2 = r2 + r1 = r3; r1, r2, r3 є L – коммутативность сложения и замкнутость;
(r1 + r2) + r3 = r1 + (r2 + r3) = r1 + r2 + r3 – ассоциативность сложения;
ri + r0 = r0 + ri = ri; ∀i, ri, r0 є L–существование нейтрального элемента;
ri +(- ri) = r0, для ∀i существует противоположный вектор (-ri) є L;
1∙ ri = ri ∙1 = ri существование единицы для умножения;
α (β∙ri) = (α∙β)∙ri; α, β, 1, 0 – элементы числового поля F, ri є L; умножение на скаляры ассоциативно; результат умножения принадлежит L;
(α + β) ri = α∙ri + β∙ri; для ∀i, ri є L, α, β – скаляры;
а (ri + rj) = ari + arj для всех а, ri, rj є L;
a∙0 = 0, 0∙ri = 0; (-1) ∙ ri = – ri.
Размерность и базис векторного пространства
При изучении векторных пространств представляет интерес выяснение таких вопросов, как число векторов, образующих все пространство; какова размерность пространства; какой наименьший набор векторов путем применения к нему операции суммирования и умножения на число позволяет сформировать все векторы пространства? Эти вопросы основополагающие и их нельзя обойти стороной, так как без ответов на них утрачивается ясность восприятия всего остального, что составляет теорию векторных пространств.
Оказалось, что размерность пространства самым тесным образом связана с линейной зависимостью векторов, и с числом линейно независимых векторов, которые можно выбирать в изучаемом пространстве многими способами.
Линейная независимость векторов
Набор векторов r1, r2, r3 … rр из L называют линейно независимым, если для них соотношение
выполняется только при условии одновременного равенства
.
Все
, k = 1(1)p, принадлежат числовому полю вычетов по модулю два
F = {0, 1}.
Если в некотором векторном пространстве L можно подобрать набор из р векторов, для которых соотношение
выполняется, при условии, что не все
одновременно, т.е. в поле вычетов оказалось возможным выбрать набор
, k =1(1)р, среди которых есть ненулевые, то такие векторы
называются линейно зависимыми.
Пример 3. На плоскости два вектора
= <0, 1>T и
= <1, 0>T являются линейно независимыми, так как в соотношении (T-транспонирование)
невозможно подобрать никакой пары чисел
коэффициентов не равных нулю одновременно, чтобы соотношение было выполнено.
Три вектора
= <0, 1>T,
= <1, 0>T,
= <1, 1>T образуют систему линейно зависимых векторов, так как в соотношении
равенство может быть обеспечено выбором коэффициентов
, не равных нулю одновременно. Более того, вектор
является функцией
и
(их суммой), что указывает на зависимость
от
и
. Доказательство общего случая состоит в следующем.
Пусть хотя бы одно из значений
, k = 1(1)р, например,
, а соотношение выполнено. Это означает, что векторы
, k = 1(1)р, линейно зависимы
Выделим явным образом из суммы вектор rр
Говорят, что вектор rр является л и н е й н о й комбинацией векторов
или rр через остальные векторы выражается линейным образом, т.е. rр линейно зависит от остальных. Он является их функцией.
На плоскости двух измерений любые три вектора линейно зависимы, но любые два неколлинеарных вектора являются независимыми. В трехмерном пространстве любые три некомпланарных вектора линейно независимы, но любые четыре вектора всегда линейно зависимы.
Зависимость/независимость совокупности {
} векторов часто определяют, вычисляя определитель матрицы Грама (ее строки скалярные произведения наших векторов). Если определитель равен нулю, среди векторов имеются зависимые, если определитель отличен от нуля — векторы в матрице независимы.
Определителем Грама (грамианом) системы векторов
в евклидовом пространстве называется определитель матрицы Грама этой системы:
где
— скалярное произведение векторов
и
.
Размерность и базис векторного пространства
Размерность s = d (L) пространства L определяется как наибольшее число векторов в L, образующих линейно независимый набор. Размерность – это не число векторов в L, которое может быть бесконечным и не число компонентов вектора.
Пространства, имеющие конечную размерность s ≠ ∞, называются конечномерными, если
s = ∞, – бесконечномерными.
Ответом на вопрос о минимальном числе и составе векторов, которые обеспечивают порождение всех векторов линейного векторного пространства является следующее утверждение.
Любой набор s линейно независимых векторов в пространстве L образует его б а з и с. Это следует из того, что любой вектор
линейного s-мерного векторного пространства L может быть представлен единственным способом в виде линейной комбинации векторов базиса.
Зафиксируем и обозначим символом
, i = 1(1)s, один из наборов, образующих базис пространства L. Тогда
Числа rki, i = 1(1)s называются координатами вектора
в базисе
, i = 1(1)s, причем rki = (
,
).
Покажем единственность представления
. Очевидно, что набор
,
является зависимым, так как
, i = 1(1)s – базис. Другими словами, существуют такие
не равные одновременно нулю, что
.
При этом пусть
, ибо если
, то хоть одно из
, было бы отлично от нуля и тогда векторы
, i = 1(1)s, были бы линейно зависимы, что невозможно, так как это базис. Следовательно,
Полагая
, будем иметь
Используя прием доказательства «от противного», допустим, что записанное представление
не единственное в этом базисе и существует другое
Тогда запишем отличие представлений, что, естественно, выражается как
Очевидно, что правая и левая части равны, но левая представляет разность вектора с самим собой, т. е. равна нулю. Следовательно, и правая часть равна нулю. Векторы
, i = 1(1)s линейно независимы, поэтому все коэффициенты при них могут быть только нулевыми. Отсюда получаем, что
а это возможно только при
Выбор базиса. Ортонормированность
Векторы называют нормированными, если длина каждого из них равна единице. Этого можно достичь, применяя к произвольным векторам процедуру нормировки.
Векторы называют ортогональными, если они перпендикулярны друг другу. Такие векторы могут быть получены применением к каждому из них процедуры ортогонализации. Если для совокупности векторов выполняются оба свойства, то векторы называются ортонормированными.
Необходимость рассмотрения ортонормированных базисов вызвана потребностями использования быстрых преобразований как одно –, так и многомерных функций. Задачи такой обработки возникают при исследовании кодов, кодирующих информационные сообщения в сетях связи различного назначения, при исследовании изображений, получаемых
посредством автоматических и автоматизированных устройств, в ряде других областей, использующих цифровые представления информации.
Определение. Совокупность n линейно независимых векторов n-мерного векторного
пространства V называется его базисом.
Теорема. Каждый вектор х линейного n-мерного векторного пространства V можно представить, притом единственным образом, в виде линейной комбинации векторов базиса. Векторное пространство V над полем F обладает следующими свойствами:
0·х = 0 (0 в левой части равенства – нейтральный элемент аддитивной группы поля F; 0 в правой части равенства – элемент пространства V, являющийся нейтральным единичным элементом аддитивной группы V, называемый нулевым вектором);
(– 1)·х = –х; –1є F; x є V; –x є V;
Если α·х = 0єV, то при х ≠ 0 всегда α = 0.
Пусть Vn(F) – множество всех последовательностей (х1, х2, …, хn) длины n с компонентами из поля F, т.е. Vn(F) ={x, таких, что х = (х1, х2, …, хn), хi є F;
i =1(1)n }.
Сложение и умножение на скаляр определяются следующим образом:
x + y =(x1 + y1, x2 + y2, …, xn + yn);
α·х = (α·х1, α·х2,…, α·хn), где у = (у1, у2,…, уn),
тогда Vn(F) является векторным пространством над полем F.
Пример 4. В векторном пространстве rо = 00000, r1 = 10101, r2 = 11010, r3 = 10101 над полем F2 = {0,1} определить его размерность и базис.
Решение. Сформируем таблицу сложения векторов линейного векторного пространства
В этом векторном пространстве V= {rо,r1,r2,r3} каждый вектор в качестве противоположного имеет самого себя. Любые два вектора, исключая rо, являются линейно независимыми, в чем легко убедиться
c1·r1 + c2·r2 = 0; c1·r1 + c3·r3 = 0; c2·r2 + c3·r3 = 0;
Каждое из трех соотношений справедливо только при одновременных нулевых значениях пар коэффициентов сi, сj є {0,1}.
При одновременном рассмотрении трех ненулевых векторов один из них всегда является суммой двух других или равен самому себе, а r1+r2+r3=rо.
Таким образом, размерность рассматриваемого линейного векторного пространства равна двум s = 2, d(L) = s = 2, хотя каждый из векторов имеет пять компонентов. Базисом пространства является набор (r1, r2). Можно в качестве базиса использовать пару (r1, r3).
Важным в теоретическом и практическом отношении является вопрос описания векторного пространства. Оказывается, любое множество базисных векторов можно рассматривать как строки некоторой матрицы G, называемой порождающей матрицей векторного пространства. Любой вектор этого пространства может быть представлен как линейная комбинация строк матрицы G ( как, например, здесь).
Если размерность векторного пространства равна k и равна числу строк матрицы G, рангу матрицы G, то очевидно, существует k коэффициентов с q различными значениями для порождения всех возможных линейных комбинаций строк матрицы. При этом векторное пространство L содержит qk векторов.
Множество всех векторов из ℤpn с операциями сложения векторов и умножения вектора на скаляр из ℤp есть линейное векторное пространство.
Определение. Подмножество W векторного пространства V, удовлетворяющее условиям:
Если w1, w2 є W, то w1+ w2 є W,
Для любых α є F и w є W элемент αw є W,
само является векторным пространством над полем F и называется подпространством векторного пространства V.
Пусть V есть векторное пространство над полем F и множество W ⊆ V. Множество W есть подпространство пространства V, если W по отношению к линейным операциям, определенным в V, есть линейное векторное пространство.
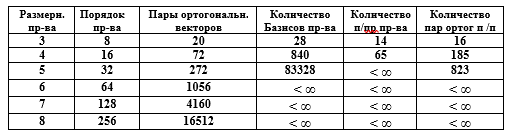
Таблица. Характеристики векторных пространств
Компактность матричного представления векторного пространства очевидна. Например, задание L векторов двоичных 50-разрядных чисел, среди которых 30 векторов образуют базис векторного пространства, требует формирования матрицы G[30,50], а описываемое количество векторов превышает 109, что в поэлементной записи представляется неразумным.
Все базисы любого пространства L разбиваются подгруппой Р невырожденных матриц с det G > 0 на два класса. Один из них (произвольно) называют классом с положительно ориентированными базисами (правыми), другой класс содержит левые базисы.
В этом случае говорят, что в пространстве задана ориентация. После этого любой базис представляет собой упорядоченный набор векторов.
Если нумерацию двух векторов изменить в правом базисе, то базис станет левым. Это связано с тем, что в матрице G поменяются местами две строки, следовательно, определитель detG изменит знак.
Норма и скалярное произведение векторов
После того как решены вопросы о нахождении базиса линейного векторного пространства, о порождении всех элементов этого пространства и о представлении любого элемента и самого векторного пространства через базисные векторы, можно поставить задачу об измерении в этом пространстве расстояний между элементами, углов между векторами, значений компонентов векторов, длины самих векторов.
Действительное или комплексное векторное пространство L называется нормированным векторным пространством, если каждый вектор r в нем может быть сопоставлен действительному числу || r || – модулю вектора, норме. Единичный вектор – это вектор, норма которого равна единице. Нулевой вектор имеет компонентами нули.
Определение. Векторное пространство называется унитарным, если в нем определена бинарная операция, ставящая каждой паре ri, rj векторов из L в соответствие скаляр. В круглых скобках (ri, rj) записывается (обозначается) скалярное или внутреннее произведение ri и rj, причем
1. (ri, rj) = ri ∙ rj;
2. (ri, rj) = (rj ∙ ri)*, где * указывает на комплексное сопряжение или эрмитову симметрию;
3. (сri, rj) = с(ri ∙ rj) – ассоциативный закон;
4. (ri + rj, rk) = (ri ∙ rk)+ (rj ∙ rk)– дистрибутивный закон;
5. (ri, rk) ≥ 0 и из (ri, rj ) = 0 следует ri = 0.
Определение. Положительное значение квадратного корня 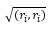
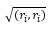
Два вектора ri, rj унитарного векторного пространства L взаимно ортогональны, если их скалярное произведение равно нулю, т.е. (ri, rj) = 0.
При s = 3 в линейном векторном пространстве в качестве базиса удобно выбирать три взаимно перпендикулярных вектора. Такой выбор существенно упрощает ряд зависимостей и вычислений. Этот же принцип ортогональности используется при выборе базиса в пространствах и других размерностей s > 3. Использование введенной операции скалярного произведения векторов обеспечивает возможность такого выбора.
Еще большие преимущества достигаются при выборе в качестве базиса векторного пространства ортогональных нормированных векторов – ортонормированного базиса. Если не оговорено специально, то далее всегда будем считать, что базис еi, i = 1(1)s выбран именно таким образом, т.е.
, где ij — символ Кронекера (1823 — 1891).
В унитарных векторных пространствах такой выбор всегда реализуем. Покажем реализуемость такого выбора.
Определение. Пусть S = {v1, v2,…, vn} есть конечное подмножество векторного пространства V над полем F.
Линейная комбинация векторов из S есть выражение вида а1∙v1 + а2∙v2 +…+ аn∙vn, где каждое аi ∊ F.
Оболочка для множества S (обозначение {S}) есть множество всех линейных комбинаций векторов из S. Оболочка для S есть подпространство пространства V.
Если U есть пространство в V, то U натянуто на S (S стягивает U), если {S}=U.
Множество векторов S линейно зависимо над F, если в F существуют скаляры а1, а2,…, аn, не все нули, для которых а1∙v1+ а2∙v2 +…+ аn∙vn = 0. Если таких скаляров не существует, то множество векторов S линейно независимо над F.
Если векторное пространство V натянуто на линейно независимую систему векторов S (или система S стягивает пространство V), то система S называется базисом для V.
Приведение произвольного базиса к ортонормированному виду
Пусть в пространстве V имеется не ортонормированный базис ē i, i = 1(1)s. Обозначим норму каждого вектора базиса символом
Известно следующее утверждение [11]. Если ē i, i = 1(1)s – произвольная конечная или счетная система линейно независимых векторов в унитарном векторном пространстве, то существует ортонормированная система ē i, i = 1(1)s, порождающая то же самое линейное пространство (многообразие).
В основу процедуры приведения базиса к ортонормированному виду положен процесс ортогонализации Грама — Шмидта, который в свою очередь, реализуется рекуррентными формулами
В развернутом виде алгоритм ортогонализации и нормирования базиса содержит следующие условия:
Делим вектор ē 1, на его норму; получим нормированный вектор ē i=ē 1/(||ē 1 ||);
Формируем V2 = ē 2 — (ē 1, ē 2)e 1 и нормируем его, получим е 2. Ясно, что тогда
(е1, е2) ~ (е1, е2) – (е1, ē 2)( е1, е1) = 0;
Построив V3 = ē 3– (e1, ē 3)e1 – (e2, ē 3) e2 и нормируя его, получим е3.
Для него имеем сразу же (е1, е3) = (е2, е3) = 0.
Продолжая такой процесс, получим ортонормированный набор ē i, i = 1(1)s. Этот набор содержит линейно независимые векторы, поскольку все они взаимно ортогональны.
Убедимся в этом. Пусть выполняется соотношение
Если набор ē i, i = 1(1)s зависимый, то хотя бы один сj коэффициент не равен нулю сj ≠ 0.
Умножив обе части соотношения на еj, получаем
(ej, c1∙e1 ) + (ej, c2∙e2 )+ …+ ( ej, cj∙ej ) +…+ ( ej, cs∙rs ) = 0.
Каждое слагаемое в сумме равно нулю как скалярное произведение ортогональных векторов, кроме (ej ,cj∙ej), которое равно нулю по условию. Но в этом слагаемом
(ej, ej) = 1 ≠ 0, следовательно, нулем может быть только cj.
Таким образом, допущение о том, что cj ≠ 0 неверно и набор является линейно независимым.
Пример 5. Задан базис 3-х мерного векторного пространства:
{<-1, 2 ,3, 0>,<0, 1, 2, 1>,<2,-1,-1,1>}.
Скалярное произведение определено соотношением:
(<x1,x2,x3,x4>,<y1,y2,y3,y4>) = x1∙y1+x2∙y2+x3∙y3+x4∙y4.
Процедурой ортогонализации Грама — Шмидта получаем систему векторов:
а1 = <-1, 2, 3, 0>; a2 = <0, 1, 2, 1>-4<-1, 2, 3,0>/7=<4,-1, 2, 7>/7;
a3 =<2, -1, -1, 1>+½<-1, 2, 3, 0> — <4, -1, 2, 7>/5 =<7, 2, 1, -4>/10.
(a1,a2)= (1+4+9+0) = 14;
a1 E =a1/√14;
a2-(a1E,a2)∙a1E=a2-(8/√14)(a1/√14)=a2 — 4∙a1/7;
Третий вектор читателю предлагается обработать самостоятельно.
Нормированные векторы получают вид:
a1 E =a1/√14;
a2 E =<4, -1, 2, 7>/√70;
a3 E =<7, 2, 1,-4>/√70;
Ниже в примере 6 дается подробный развернутый процесс вычислений получения ортонормированного базиса из простого (взятого наугад).
Пример 6. Привести заданный базис линейного векторного пространства к ортонормированному виду.
Дано: векторы базиса
Подпространства векторных пространств
Структура векторного пространства
Представление объектов (тел) в многомерных пространствах весьма непростая задача. Так, четырехмерный куб в качестве своих граней имеет обычные трехмерные кубы, и в трехмерном пространстве может быть построена развертка четырехмерного куба. В некоторой степени «образность» и наглядность объекта или его частей способствует более успешному его изучению.
Сказанное позволяет предположить, что векторные пространства можно некоторым образом расчленять, выделять в них части, называемые подпространствами. Очевидно, что рассмотрение многомерных и тем более бесконечномерных пространств и объектов в них лишает нас наглядности представлений, что весьма затрудняет исследование объектов в таких
пространствах. Даже, казалось бы, такие простые вопросы, как количественные характеристики элементов многогранников (число вершин, ребер, граней, и т. п.) в этих пространствах решены далеко не полностью.
Конструктивный путь изучения подобных объектов состоит в выделении их элементов (например, ребер, граней) и описании их в пространствах меньшей размерности. Так четырехмерный куб в качестве своих граней имеет обычные трехмерные кубы и в трехмерном пространстве может быть построена развертка четырехмерного куба. В некоторой степени
«образность» и наглядность объекта или его частей способствует более успешному их изучению.
Если L – расширение поля К, то L можно рассматривать как векторное (или линейное) пространство над полем К. Элементы поля L (т. е. векторы) образуют по сложению абелеву группу. Кроме того, каждый «вектор» а є L может быть умножен на «скаляр» r є K, и при этом произведение ra снова принадлежит L (здесь ra – просто произведение в смысле операции поля L элементов r и а этого поля). Выполняются также законы
r∙(a+b) = r∙a+r∙b, (r+s)∙a = r∙a + r∙s, (r∙s)∙a = r∙(s∙a) и 1∙а = а, где r,s є K, a,b є L.
Сказанное позволяет предположить, что векторные пространства можно некоторым образом расчленять, выделять в них части, называемые подпространствами. Очевидно, что основным результатом при таком подходе является сокращение размерности выделяемых подпространств. Пусть в векторном линейном пространстве L выделены подпространства L1 и L2. В качестве базиса L1 выбирается меньший набор еi, i = 1(1)s1, s1 < s, чем в исходном L.
Оставшиеся базисные векторы порождают другое подпространство L2, называемое «ортогональным дополнением» подпространства L1. Будем использовать запись L = L1 + L2. Она означает не то, что все векторы пространства L принадлежат либо L1, либо L2,, а то, что любой вектор из L можно представить в виде суммы вектора из L1 и ортогонального ему вектора из L2.
Разбивается не множество векторов векторного пространства L, а размерность d(L) и набор базисных векторов. Таким образом, подпространством L1 векторного пространства L называется множество L1, его элементов (меньшей размерности), само являющееся векторным пространством относительно введенных в L операций сложения и умножения на число.
Каждое линейное векторное подпространство Li – содержит нулевой вектор и вместе с любыми своими векторами содержит и все их линейные комбинации. Размерность любого линейного подпространства не превосходит размерности самого исходного пространства.
Пример 7. В обычном трехмерном пространстве подпространствами являются все прямые (размерность s =1) линии, плоскости (размерность s = 2), проходящие через начало координат. В пространстве Рn многочленов степени не выше n подпространствами будут, например, все Рk при k < n, так как складывая и умножая на числа многочлены степени, не выше k, снова будут получаться такие же многочлены.
Однако, каждое из пространств Рп содержится в качестве подпространств в пространстве Р всех многочленов с вещественными коэффициентами, а это последнее является подпространством пространства С непрерывных функций.
Матрицы одинакового типа над полем действительных чисел также образуют линейное векторное пространство, так как для них выполняются все аксиомы векторных пространств. Векторное пространство L2 наборов длины n, каждый из которых ортогонален подпространству L1 наборов длины п, образует подпространство L2, называемое нулевым пространством для L1. Другими словами, каждый вектор из L2 ортогонален каждому вектору из L1 и наоборот.
Оба подпространства L1 и L2 являются подпространствами векторного пространства L наборов длины п. В теории кодирования [4] каждое из подпространств L1 и L2 порождает линейный код, двойственный по отношению к коду, порожденному другими подпространства-ми. Если L1 есть (п, k)-код, то L2 — это (п, п – k)-код. Если код является векторным пространством строк некоторой матрицы, то двойственный к нему код — нулевое пространство этой матрицы и наоборот.
Важным вопросом при изучении векторных пространств Vn является установление их структуры (строения). Другими словами, интерес представляют элементы, их совокупности (подпространства размерности 1<k<п ), а также их отношения (упорядоченность, вложенность и т.п.). Будем считать заданным векторное пространство Vn над конечным полем GF(q), образованным q = р r элементами, где р — простое число, r — целое.
Известны следующие результаты.
Количества подпространств векторного пространства
Приведем следующее обоснование. Каждый вектор v1 ≠ 0 из системы k линейно независимых ( v1,v2,…,vk ) векторов может быть выбран qn – 1 способами. Следующий вектор v2 ≠ 0 не может быть выражен линейно через v1, т.е. может быть выбран qn – q способами и т.д.
Последний вектор vk ≠ 0 также линейно не выражается через предыдущие выбранные векторы v1,v2,…,vk и, следовательно, может быть выбран qn – qk – 1 способами. Общее число способов для выбора совокупности векторов v1,v2,…,vk, таким образом, определится как произведение числа выборов отдельных векторов, что и дает формулу (1). Для случая, когда k = п, имеем wп = wn, n и из формулы (I) получаем формулу (2).
Важные обобщающие результаты о размерностях подпространств.
Совокупность всех наборов длины n, ортогональных подпространству V1 наборов длины n, образует подпространство V2 наборов длины n. Это подпространство V2 называется нулевым пространством для V1.
Если вектор ортогонален каждому из векторов, порождающих подпространство V1, то этот вектор принадлежит нулевому пространству для V1.
Примером (V1) может служить множество 7-разрядных векторов порождающей матрицы (7,4)-кода Хемминга, с нулевым подпространством (V2) 7-разрядных векторов, образующих проверочную матрицу этого кода.
Если размерность подпространства (V1) наборов длины n равна k, то размерность нулевого подпространства (V2) равна n — k.
Если V2 — подпространство наборов длины n и V1 — нулевое пространство для V2, то (V2) — нулевое пространство для V1.
Пусть U∩V обозначает совокупность векторов, принадлежащих одновременно U и V, тогда U∩V является подпространством.
Пусть U⊕V обозначает подпространство, состоящее из совокупности всех линейных комбинаций вида au +bv, где u є U, v є V, a b — числа.
Сумма размерностей подпространств U∩V и U⊕V равна сумме размерностей подпространств U и V.
Пусть U2 — нулевое подпространство для U1, а V2 -нулевое пространство для V1. Тогда U2∩V2 является нулевым пространством для U1⊕V1.
Заключение
В работе рассмотрены основные понятия векторных пространств, которые часто используются при построении моделей анализа систем шифрования, кодирования и стеганографических, процессов, протекающих в них. Так в новом американском стандарте шифрования использованы пространства аффинные, а в цифровых подписях на эллиптических кривых и аффинные и
проективные (для ускорения обработки точек кривой).
Об этих пространствах в работе речь не идет (нельзя валить все в одну кучу, да и объем публикации я ограничиваю), но упоминания об этом сделаны не зря. Авторы, пишущие о средствах защиты, об алгоритмах шифров наивно полагают, что понимают детали описываемых явлений, но понимание евклидовых пространств и их свойств без всяких оговорок переносится в другие пространства, с другими свойствами и законами. Читающая аудитория вводится в заблуждение относительно простоты и доступности материала.
Создается ложная картина действительности в области информационной безопасности и специальной техники (технологий и математики).
В общем почин мною сделан, насколько удачно судить читателям.
Литература
1. Авдошин С.М., Набебин А.А. Дискретная математика. Модулярная алгебра, криптография, кодирование. — М.: ДМК Пресс, 2017. -352 с.
2. Акимов О.Е. Дискретная математика.Логика, группы, графы- М.: Лаб.Баз. Зн., 2001. -352 с.
3. Андерсон Д.А. Дискретная математика и комбинаторика.- М.: Вильямс, 2003. -960 с.
4. Берлекэмп Э. Алгебраическая теория кодирования. -М.: Мир,1971.- 478 с.
5. Ваулин А.Е. Дискретная математика в задачах компьютерной безопасности. Ч 1- СПб.: ВКА им. А.Ф. Можайского, 2015. -219 с.
6. Ваулин А.Е. Дискретная математика в задачах компьютерной безопасности. Ч 2- СПб.: ВКА им. А.Ф. Можайского, 2017. -151 с.
7. Горенстейн Д. Конечные простые группы. Введение в их классификацию.-М.: Мир,1985.- 352 с.
7. Грэхем Р., Кнут Д., Пташник О. Конкретная математика.Основание информатики.-М.: Мир,1998.-703 с.
9. Елизаров В.П. Конечные кольца.- М.: Гелиос АРВ,2006. — 304 с.
Иванов Б.Н. Дискретная математика: алгоритмы и программы-М.: Лаб.Баз. Знаний., 2001. -280 с.
10. Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения-М.: Вузовская книга, 2000.-280 с.
11. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров.-М.: Наука, 1973.-832 с.
12. Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т. Т.1 -М.: Мир,1988. — 430 с.
13. Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т. Т.2 -М.: Мир,1988. — 392 с.
14. Ляпин Е.С., АйзенштатА.Я., Лесохин М.М., Упражнения по теории групп.- М.: Наука,1967.-264 с.
15. Муттер В.М. Основы помехоустойчивой телепередачи информации. -Л. Энергоатомиздат,1990.- 288 с.
16. Набебин А.А.Дискретная математика.- М.: Лаб.Баз. Знаний., 2001. -280 с.
17. Новиков Ф.А. Дискретная математика для программистов.- СПб.: Питер, 2000. -304 с.
18. Розенфельд Б.А. Многомерные пространства.-М.: Наука,1966.-648 с.
18. Холл М. Теория групп.-М.: Изд. ИЛ, 1962.- 468 с.
19. Шиханович Ю.А. Группы, кольца, решётки. — СПб.: Кирцидели,2006. — 368 с.
20. Шнеперман Л.Б. Курс алгебры и теории чисел в задачах и упражнениях: В 2-х ч Ч.2.-Мн.: Выш. шк., 1987. -256 с.
21. Шнеперман Л.Б. Сборник задач по алгебре и теории чисел.- Минск: Дизайн ПРО, 2000. -240 с.
Скалярное
произведение вектора самого на себя
называется скалярным квадратом. Эта
величина
определяет
квадрат длины вектора x.
Для обозначения длины (называемой
также нормой вектора)
используется обозначение
Например,
Рис.
16 Норма вектора
Вектор
единичной длины (||x||
= 1) называется нормированным. Ненулевой
вектор (x ≠ 0)
можно нормировать, разделив его на
длину, т.е. x =
||x||
(x/||x||)
= ||x|| e.
Здесь e =x/||x||
— нормированный вектор.
Векторы называются
ортонормированными, если все они
нормированы и попарно ортогональны.
Содержание
1.10. Угол между векторами
Скалярное
произведение определяет и угол φ
между двумя векторами x и y
Если вектора
ортогональны, то cosφ = 0 и φ = π/2, а если
они колинеарны, то cosφ = 1 и φ = 0.
Содержание
1.11. Векторное представление матрицы
Каждую
матрицу A размера I×J можно
представить как набор векторов
Здесь
каждый вектор aj является j-ым
столбцом, а вектор-строка bi является i-ой
строкой матрицы A
Содержание
1.12. Линейно зависимые векторы
Векторы
одинаковой размерности (N)
можно складывать и умножать на число,
также как матрицы. В результате получится
вектор той же размерности. Пусть имеется
несколько векторов одной
размерности x1, x2,…,xK и
столько же чисел α α1,
α2,…,αK.
Вектор
y =
α1x1+
α2x2+…+
αKxK
называется линейной
комбинацией векторов xk.
Если
существуют такие ненулевые числа αk ≠
0, k =
1,…, K,
что y = 0,
то такой набор векторов xk называется линейно
зависимым.
В противном случае векторы называются
линейно независимыми. Например,
векторы x1 =
(2, 2)t и x2 =
(−1, −1)t линейно
зависимы, т.к. x1 +2x2 = 0
Содержание
1.13. Ранг матрицы
Рассмотрим
набор из K векторов x1, x2,…,xK размерности N.
Рангом этой системы векторов называется
максимальное число линейно-независимых
векторов. Например в наборе
имеются
только два линейно независимых вектора,
например x1 и x2,
поэтому ее ранг равен 2.
Очевидно,
что если векторов в наборе больше, чем
их размерность (K>N),
то они обязательно линейно зависимы.
Рангом
матрицы (обозначается
rank(A))
называется ранг системы векторов, из
которых она состоит. Хотя любую матрицу
можно представить двумя способами
(векторы столбцы или строки), это не
влияет на величину ранга, т.к.
rank(A)
= rank(At).
Содержание
1.14. Обратная матрица
Квадратная
матрица A называется
невырожденной, если она имеет
единственную обратную матрицу A-1,
определяемую условиями
AA−1 = A−1A = I.
Обратная матрица
существует не для всех матриц. Необходимым
и достаточным условием невырожденности
является
det(A)
≠ 0 или rank(A)
= N.
Обращение матрицы
— это сложная процедура, для выполнения
которой существуют специальные программы.
Например,
Рис.
17 Обращение матрицы
Приведем формулы
для простейшего случая — матрицы 2×2
Если
матрицы A и B невырождены,
то
(AB)−1 = B−1A−1.
Содержание
1.15. Псевдообратная матрица
Если
матрица A вырождена
и обратная матрица не существует, то в
некоторых случаях можно
использовать псевдообратную матрицу,
которая определяется как такая матрица A+,
что
AA+A = A.
Псевдобратная
матрица — не единственная и ее вид
зависит от способа построения. Например
для прямоугольной матрицы можно
использовать метод
Мура-Пенроуза.
Если число столбцов
меньше числа строк, то
A+=(AtA)−1At
Например,

Рис.
17a Псевдообращение
матрицы
Если же число
столбцов больше числа строк, то
A+=At(AAt)−1
Содержание
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #