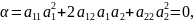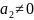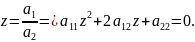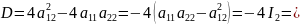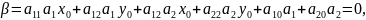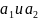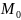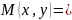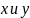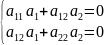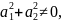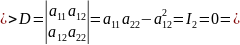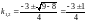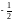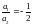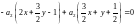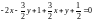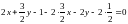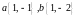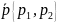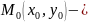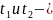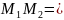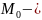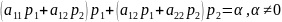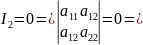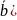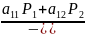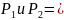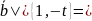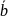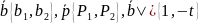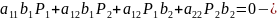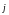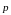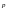Как найти вектор асимптотического направления

Прямая
имеет асимптотическое направление к
ЛВП, когда

координаты
направляющего вектора прямой, тогда
они сразу не могут равняться нулю. Пусть

,
тогда поделим на

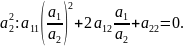
Обозначим

Количество решений квадратного уравнения
зависит от дискриминанта

Линии
эллиптического типа не имеют
асимптотических направлений. Линии
параболического типа имеют одно
асимптотическое направление. Линии
гиперболического типа имеют два
асимптотических направлений.

§6. Асимптоты лвп

Кроме
того, что

должно выполняться, что

.

где

находятся из условия

,
а

координаты некоторой точки, принадлежащей
асимптоте.

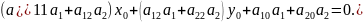
Будем
считать точку

произвольной точкой

будем
определять асимптоту (прямую), если
коэффициенты при

одновременно не равны нулю.

Если
же

,
где

то
система имеет бесчисленное множество
решений

линии параболического типа не имеют
асимптот.

У
линии гиперболического типа две
асимптоты.

У
линий эллиптического типа асимптот
нет, так как нет асимптотических
направлений.

Задача.
Найти векторы асимптотического
направления для ЛВП, заданной уравнением
2х²
+ 3ху
+ у²
– 2х
+ у =
0. Написать уравнение асимптот, если они
существуют.

Решение.1)Находятся
векторы асимптотического направления,
используя уравнение (4). Для этого
составляется квадратное уравнение
2k²
+ 3k
+ 1
= 0. Отсюда

,
или
k₁=
–1,
k₂=
.

Квадратное
уравнение имеет два решения. Поэтому у
данной ЛВП два асимптотических направления
и две асимптоты, так как J₂<0.
Найдем асимптотические направления:

а)

.
Отсюда а₁=
– а₂.

б)

.
Отсюда а₂
=
–2а₁.

2)
Уравнения асимптот можно найти в виде
(6):

а)
,
т.к. а₂
≠
0, то

или х
+ у
– 3 =0.

б)

.

Так
как а₁≠0,
то

или 2х
+ у + 4
=0.

Ответ:

,
x
+ y
– 3
= 0 и 2x
+ y
+
4 = 0.■

§7. Диаметры лвп

Определение.
Диаметром ЛВП сопряженных к вектору

,
называется множество всех середин хорд
ЛВП, параллельных вектору

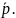
Пусть
дана ЛВП уравнением (*) и вектор

не асимптотического направления

.

Пусть

является серединой хорды, параллельной
вектору

.
Так как

имеет не асимптотическое направление,
то эта хорда пересекается с ЛВП в двух
точках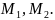

Уравнение
хорды:

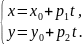
При

;

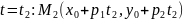
решения
уравнения

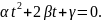
Точка

должна являться серединой отрезка

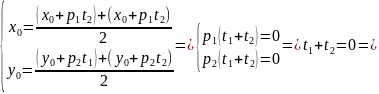
По
теореме Виета

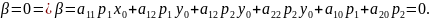
Так
как

произвольная точка, принадлежащая
диаметру, то будем вместе

брать точку

.

Следовательно,
это
уравнение диаметра.

Известно,
что

Рассмотрим
выражение

,
так как

не имеет асимптотического направления.

Следовательно,
коэффициенты в скобках не могут
одновременно равны нулю, тогда уравнение
диаметра является уравнением первой
степени, то есть всегда определяет
прямую линию.

Замечание
1. Если у ЛВП имеется центр

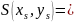
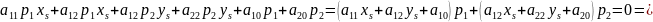
если
ЛВП имеет центр, то любой диаметр проходит
через центр.

Замечание
2. Если у ЛВП являются линий параболического
типа, то

существует

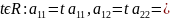
если
взять направляющий вектор диаметра

,
то отношение

и
оно не зависит от

вектор

все диаметры линий параболического
типа параллельны.

Замечание
3. Направляющий вектор диаметра

и вектор

называются сопряженными

с другой стороны

условие
сопряженности двух векторов

относительно ЛВП.

Задача.
Найти диаметр кривой x²
– 2xy
+ 4y²
– 6x+2y
– 7
= 0,
сопряженный: а)
оси Оy,
б)
оси Ох.

Решение.
а)
В качестве вектора

,
сопряженного с искомым диаметром,
можно взять вектор

{0,
1}, то есть

{0,1}.
Уравнение диаметра будем искать в
виде:

p₁
(a₁₁x
+ a₁₂y
+ a₁₀)
+ p₂(a₁₂x
+ a₂₂y
+ a₂₀)
= 0, где

{p₁,
p₂}.

Тогда
учитывая, что p₁
=
0,
p₂
= 1, получим

0(x
– y
– 3)
+ 1 (–
x
+
4y
+ 1)
= 0, то есть уравнение диаметра будет
иметь вид x
– 4y
–
1 = 0 .

б)

{1,
0}, тогда 1(x
– y
– 3)
+ 0 (–x
+
4y
+ 1)
= 0 или x
– y
– 3
= 0.■

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Определение
. Направление, определяемое ненулевым вектором называется асимптотическимнаправлением

относительно линии второго порядка, если любая

прямая этого направления (то есть параллельная вектору ) либо имеет с линией не более одной общей точки, либо содержится в этой линии.

?
Сколько общих точек может быть у линии второго порядка и прямой асимптотического направления относительно этой линии?

В общей теории линий второго порядка доказывается, что если

То ненулевой вектор ( задаёт асимптотическое направление относительно линии

(общий критерий асимптотического направления
).

Для линий второго порядка

если , то нет асимптотических направлений,

если то существует два асимптотических направления,

если то существует только одно асимптотическое направление.

Полезной оказывается следующая лемма (критерий асимптотического направления линии параболического типа
).

Лемма

. Пусть — линия параболического типа.

Ненулевой вектор имеет асимптотическое направление

относительно . (5)

(Задача. Доказать лемму.)

Определение
. Прямая асимптотического направления называется асимптотой

линии второго порядка, если эта прямая либо не пересекается с , либо содержится в ней.

Теорема

. Если имеет асимптотическое направление относительно , то асимптота, параллельная вектору , определяется уравнением

Заполняем таблицу.

ЗАДАЧИ
.

1. Найти векторы асимптотических направлений для следующих линий второго поря дка:

4 — гиперболического типа два асимптотических направления.

Воспользуемся критерием асимптотического направления:

Имеет асимптотическое направление относительно данной линии 4 .

Если =0, то =0, то есть — нулевой. Тогда Поделим на Получаем квадратное уравнение: , где t = . Решаем это квадратное уравнение и находим два решения: t = 4 и t = 1. Тогда асимптотические направления линии .

(Можно рассмотреть два способа, так как линия – параболического типа.)

2. Выясните, имеют ли оси координат асимптотические направления относительно линий второго порядка:

3. Напишите общее уравнение линии второго порядка, для которой

а) ось абсцисс имеет асимптотическое направление;

б) Обе оси координат имеют асимптотические направления;

в) оси координат имеют асимптотические направления и О – центр линии.

4. Напишите уравнения асимптот для линий:

а) ng w:val=»EN-US»/>y=0″> ;

5. Докажите, что если линия второго порядка имеет две непараллельные асимптоты, то их точка пересечения является центром данной линии.

Указание:
Так как есть две непараллельные асимптоты, то существует два асимптотических направления, тогда , а, значит, линия – центральная.

Запишите уравнения асимптот в общем виде и систему для нахождения центра. Всё очевидно.

6.(№920) Напишите уравнение гиперболы, проходящей через точку А(0, -5) и имеющей асимптоты х – 1 = 0 и 2х – y + 1 = 0.

Указание
. Воспользуйтесь утверждением предыдущей задачи.

Домашнее задание
. , №915(в,д,е), №916 (в,г,д), №920 (если не успели);

Шпаргалки;

Силаев, Тимошенко. Практические задания по геометрии,

1 семестр. С.67, вопросы 1-8, с.70, вопросы 1-3 (устно).

ДИАМЕТРЫ ЛИНИИ ВТОРОГО ПОРЯДКА.

СОПРЯЖЕННЫЕ ДИАМЕТРЫ.

Дана аффинная система координат .

Определение.
Диаметром

линии второго порядка, сопряженным вектору не асимптотического направления относительно , называется множество середин всех хорд линии , параллельных вектору .

На лекции доказано, что диаметр – это прямая и получено её уравнение

Рекомендации
: Показать (на эллипсе), как строится (задаём не асимптотическое направление; проводим [две] прямые этого направления, пересекающие линию; находим середины отсекаемых хорд; проводим через середины прямую – это и есть диаметр).

Обсудить:

1. Почему в определении диаметра берётся вектор не асимптотического направления. Если не могут ответить, то попросите построить диаметр, например, для параболы.

2. Любая ли линия второго порядка имеет хотя бы один диаметр? Почему?

3. На лекции доказано, что диаметр – это прямая. Серединой какой хорды является точка М на рисунке?

4. Посмотрите на скобки в уравнении (7). Что они напоминают?

Вывод: 1) каждый центр принадлежит каждому диаметру;

2) если существует прямая центров, то существует единственный диаметр.

5. Какое направление имеют диаметры линии параболического типа? (Асимптотическое)

Доказательство (наверно, на лекции).

Пусть диаметр d, заданный уравнением (7`) сопряжен вектору не асимптотического направления. Тогда его направляющий вектор

(-(), ). Покажем, что этот вектор имеет асимптотическое направление. Воспользуемся критерием вектора асимптотического направления для линии параболического типа (см.(5)). Подставляем и убеждаемся (не забываем, что .

6. Сколько диаметров у параболы? Их взаимное расположение? Сколько диаметров у остальных линий параболического типа? Почему?

7. Как построить общий диаметр некоторых пар линий второго порядка (см. вопросы 30, 31 далее).

8. Заполняем таблицу, обязательно делаем рисунки.

1. . Напишите уравнение множества середин всех хорд, параллельных вектору

2. Напишите уравнение диаметра d, проходящего через точку К(1,-2) для линии .

Этапы решения
:

1-й способ
.

1. Определяем тип (чтобы знать, как ведут себя диаметры этой линии).

В данном случае линия центральная, тогда все диаметры проходят через центр С.

2. Составляем уравнение прямой, проходящей через две точки К и С. Это и есть искомый диаметр.

2-й способ
.

1. Записываем уравнение диаметра d в виде (7`).

2. Подставив в это уравнение координаты точки К, находим зависимость между координатами вектора, сопряженного диаметру d.

3. Задаём этот вектор, учитывая найденную зависимость, и составляем уравнение диаметра d.

В данной задаче вычислять проще вторым способом.

3. . Напишите уравнение диаметра, параллельного оси абсцисс.

4. Найдите середину хорды, отсекаемой линией

на прямой x + 3y – 12 =0.

Указание к решению
: Конечно, можно найти точки пересечения данных прямой и линии , а затем – середину полученного отрезка. Желание сделать так отпадает, если взять, к примеру, прямую с уравнением х +3у – 2009 =0.

Назначение сервиса
. Онлайн-калькулятор предназначен для нахождения минимума функции методом Пауэлла
. Решение оформляется в формате Word
.

Правила ввода функций:

1. Все переменные выражаются через x 1 ,x 2
2. Все математические операции выражаются через общепринятые символы (+,-,*,/,^). Например, x 1 2 +x 1 x 2 , записываем как x1^2+x1*x2 .

Метод Пауэлла
относится к прямым методам (методам нулевого порядка). Этим методом наиболее эффективно осуществляется минимизация функций, близких к квадратичным. На каждой итерации алгоритма поиск осуществляется вдоль системы сопряженных направлений.

Два направления поиска S
i , S
j называются сопряженными
, если S
j T ·H·S
j =0, i≠j, S
i T ·H·S
i =0, i=j.

где H — положительно определенная квадратная матрица.

Обоснование применения сопряженных направлений в алгоритмах оптимизации
. В методе Пауэлла H=▽²f(x
k) — матрица вторых частных производных. Идеи метода Пауэлла относятся к квадратичной функции f(x
).

Основная идея заключается в том, что если на каждом этапе поиска определяется минимум квадратичной функции f(x
) вдоль каждого из p (p < n) — сопряженных направлений и если затем в каждом из направлений делается шаг до минимальной точки, то полное перемещение от начала до шага с номером p сопряжено ко всем поднаправлениям поиска.

Идея использования сопряженных направлений лежит в основе ряда алгоритмов.

Пусть f(x
) — квадратичная функция и процесс минимизации начинается в точке x
0 с начальным направлением S
1 . Для удобства возьмем этот вектор единичным, т.е. (S
1) T ·S
1 =1. Тогда вектор x
1 =x
0 +λ 1 ·S
1 и длина шага λ 1 определяется из условия минимальности функции в данном направлении т.е.

.

Для квадратичной функции

, (1)

и, таким образом, оптимальное значение λ на первом шаге определяется в соответствии с соотношением

, (2)

где H=▽²f(x
k).

Из точки x
1 процесс минимизации должен осуществляться в другом сопряженном направлении S
2 и при этом

(S
2) T ·H·).

В общем случае система n линейно независимых направлений поиска S
1 , S
2 ,…, S
n называется сопряженной
по отношению к некоторой положительно определенной матрице H , если (S
i) T ·H·S
j =0, 0 ≤ i ≠ j ≤ n.

Так как сопряженные направления линейно независимы, то любой вектор в пространстве E n можно выразить через S
1 , S
2 ,…, S
n следующим образом:

где . (3)

Для некоторой матрицы H всегда существует, по крайней мере, одна система из n взаимно сопряженных направлений, так как сами собственные векторы матрицы H представляют собой такую систему.

Отметим, что для квадратичной функции справедливо следующее соотношение, которое потребуется в дальнейшем:

. (4)

Чтобы убедиться в его справедливости, рассмотрим матрицу . Умножение ее справа на H·S
k дает

,

если положить .

Вообще говоря, справедливо общее правило, заключающееся в том, что если используются сопряженные направления для поиска минимума квадратичной функции f(x
), то эта функция может быть минимизирована за n шагов по одному в каждом из сопряженных направлений. Более того, порядок использования сопряженных направлений несущественен.

Покажем, что это действительно так. Пусть f()=b
+H·x
.

В точке минимума ▽f(x
*), и эта точка x
*=-H T ·b
.

Заметим, что ▽ T f(x
k)·S
k =(S
k) T ·▽f(x
k).

Так как x
1 =x
0 +λ 1 ·S
1 , (5)

где λ 1 определяется в соответствии с соотношением (2):

,

затем минимум находится в следующем сопряженном направлении по аналогичным формулам i-1 +λ i ·S
i) в направлении S
i , чтобы получить λ i , что приводит к следующему выражению (на основании (2))

. (7)

Кроме того,

и (S
i) T ·▽f(x
i-1)=(S
i) T ·,

так как все (S
i) T ·H·S
k =0, ∀i≠k, 0 и H -1 ·b
через систему сопряженных векторов S
i следующим образом (по аналогии с (3)):

,

.

Подставив эти выражения в (7), получим

x
n =x
0 -x
0 +H -1 ·b
=H -1 ·b
. (9)

Таким образом, точка x
n , полученная в результате минимизации квад­ратичной функции на n -м шаге, совпадает с точкой минимума квадратичной функции f(x
).

Покажем, что для сопряженных направлений, если f(x
) каждый раз минимизируется в сопряженном направлении S
j в соответствии с формулой (2), то при этом выполняется следующее равенство:

(x
j) T ·▽f(x
l), 1 ≤ j ≤ l-1 ,

при использовании не более чем n направлений, то есть ▽f(x
l) ортогонален использованным сопряженным направлениям.

Для квадратичной функции ▽f( k — произвольная точка, из которой начинается поиск по сопряженным направлениям. Поскольку ▽f( k-1) T дает

.

Первый член в правой части (S
k-1) T ·▽f(x
k)=0, так как градиент в точке x
k ортогонален направлению предыдущего спуска, если точка получена в результате минимизации функции в этом направлении. Кроме того, все остальные слагаемые под знаком суммы исчезают вследствие сопряженности направлений S
k-1 и S
j , и таким образом

(S
j) T ·▽f(x
l)=0, 1≤j≤l-1 . (10)

Алгоритм Пауэлла

Переход из точки x
k 0 в точку x
k n на k -м шаге алгоритма Пауэлла осуществляется в соответствии с формулой:

.

При этом последовательно осуществляется минимизация исходной функции по сопряженным направлениям S
k 1 , … ,S
k n . Результатом минимизации по каждому из сопряженных направлений является система параметров λ 1 k ,…,λ n k , при которых функция минимальна в каждом из сопряженных направлений:

, .

Начальную систему сопряженных направлений можно выбрать параллельной осям системы координат. В конце каждой итерации алгоритма Пауэлла необходимо выбрать новую систему сопряженных направлений, так как если этого не сделать, то получим простой покоординатный поиск. В основе построения новой системы лежит следующая теорема.

Теорема:

Если при начальной точке x
0 поиска в направлении вектора S
минимум функции f(x
) находится к точке x
a , а при начальной точке x
1 ≠x
0 поиск минимума функции f(x
) в том же направлении S
приводит к точке x
b , то при f(x
b)

Доказательство
. Используя ранее полученные результаты (10), можно записать, что в первом случае

S
T ·▽f(x
a)=S
T ·(H·x
a +b
)=0,

аналогично, во втором случае можно записать

S
T ·▽f(x
b)=S
T ·(H·x
b +b
)=0,

Вычитая из первого выражения второе получим, что

S
T ·H·(x
b -x
a)=0,

Следовательно, векторы S
и (x
b -x
a) являются сопряженными.

Эта теорема непосредственно может быть распространена на случай нескольких сопряженных направлений следующим образом. Если, начиная из точки x
0 , точка x
a определяется после использования при минимизации нескольких сопряженных направлений p (pСледующий рисунок служит иллюстрацией теоремы.

Рисунок.

Пусть в начальный момент для двумерной задачи поиск осуществляется из точки x
0 вдоль направлений, параллельных осям координат: S
0 1 и S
0 2 . Последовательно были найдены точки x
0 1 , x
0 2 , x
0 3 (см. рис.).

Таким образом, определили 2 сопряженных направления, в которых следует вести поиск: S
0 2 и (x
0 3 -x
0 1). В системе исходных направлений S
0 1 должно быть заменено на (x
0 3 -x
0 1), представляющее собой полное перемещение из первого минимума. Направления поиска на следующем этапе:

S
1 1 =S
0 2 ,

S
1 2 =x
0 3 -x
0 1 .

Второй этап начинается с минимизации вдоль направления S
1 2 , затем, если необходимо, перемещение в направлении S
1 1 . Но в случае квадратичной функции двух переменных после минимизации по двум сопряженным направлениям будет достигнута точка минимума.

В общем случае, на k -м шаге алгоритма Пауэлла используется n линейно независимых направлений поиска. Поиск начинается с точки x
k 0 и осуществляется по следующему алгоритму:

1. Начиная с точки , в направлениях S
k 1 , … , S
k n . При этом находятся точки x
k 1 , … , x
k n , которые минимизируют исходную функцию в заданных направлениях, причем x
k 1 =x
k 0 +λ 1 ·S
k 1 = x
k 1 +λ 2 ·S
k 2 , …, x
k n =x
k n-1 +λ n ·S
k n .

2. Поиск, осуществляемый на первом этапе, может привести к линейно зависимым направлениям, если, например, в одном из направлений S
i не удается найти меньшего значения функции. Поэтому 2 направления могут стать коллинеарными. Поэтому в системе сопряженных направлений не следует заменять старое направление на новое, если после такой замены направления нового набора становятся линейно зависимыми.

На примере квадратичной функции Пауэллом было показано, что при нормировании направлений поиска в соответствии с соотношением:

(S
k i)·H·S
k i =1, i=1,n
,

определитель матрицы, столбцы которой представляют собой направления поиска, принимает максимальное значение тогда и только тогда, когда S
k i взаимно сопряжены относительно матрицы H . Он пришел к выводу, что направление полного перемещения на k -м шаге должно заменять предыдущее направление только в том случае, когда заменяющий вектор увеличивает определитель матрицы направлений поиска. Так как только тогда новый набор направлений будет более эффективным.

Для такой проверки из точки x
k n делается дополнительный шаг в направлении (x
k n -x
k 0), соответствующий полному перемещению на k -м этапе и получают точку (2x
k n -x
k 0). Для проверки того, что определитель матрицы направлений поиска увеличивается при включении нового направления, делается шаг 3.

3. Обозначим наибольшее уменьшение f( k m .

Обозначим:

f 1 =f(x
k 0), f 2 =f(x
k n), f 3 =f(2x
k n -f 1 =f(x
k 0),

где x
k 0 =x
k-1 n , .

Тогда, если f 3 ≥f 1 и (или) (f 1 -2f 2 +f 3)(f 1 -f 2 -Δ k) 2 ≥0.5*Δ k (f 1 -f 3) 2 , то следует использовать на (k+1) -м этапе те же направления S
k 1 , … , S
k n , что и на k -м этапе, то есть S
k+1 i =S
k i , i=1,n
, и начать поиск из точки x
k+1 0 =x
k n или из точки x
k+1 0 =2x
k n -x
k 0 =x
k n+1 , в зависимости от того, в какой точке функция принимает минимальное значение.

4. Если тест на шаге 3 не прошел, то ищется минимум f(x
) в направлении вектора S
k n+1 , проведенного из x
k 0 в x
k n: S
k n+1 =(x
k n -x
k 0). Точка этого минимума берется в качестве начальной точки на (k+1) -м этапе. А в системе сопряженных направлений сохраняются все, кроме направления S
k m , которое заменяется на новое направление S
k n+1 , но новое направление помещается в последний столбец матрицы направлений. На (k+1) -м этапе будут использоваться направления

= .

5. Критерий останова. Алгоритм прерывается, если изменение по каждой переменной оказывается меньше заданной точности по соответствующей переменной или ||x
k n -x
k 0 ||≤ε.

Пример №1
. Методом Пауэлла найти точку минимума функции 4(x 1 -5) 2 +(x 2 -6) 2 , если задана начальная точка х (0) = (8, 9) Т.

Решение
:

Градиент функции:

Шаг №2. Сделаем шаг вдоль другого направления поиска p 1 = T


f(X 2) = 4((h+8)-5) 2 +((6)-6) 2 → min

f(X 2) = 4h 2 +24h+36 → min

Найдем такой шаг h, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f»(x 2)=0):

8h+24 = 0. Получим шаг: h = -3

Выполнение этого шага приведет в точку:

Шаг №3. Повторно сделаем шаг вдоль направления поиска p 2 = T

f(X 3) = 4(5-5) 2 +((h+6)-6) 2 → min

f(X 3) = h 2 → min

Найдем такой шаг h, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f»(x 3)=0):

2h = 0. Получим шаг: h = 0

Выполнение этого шага приведет в точку:

Шаг №4. Выбираем сопряженное направление: p 2 = x 3 — x 1
p 2 = T — T = [-3;0] T

Пример №2
. Минимизировать функцию f(x) методом сопряженных направлений, заканчивая вычисления при |d(x)/dx| < 10 -3 , i=1,2,..,n.

x 1 4 +2*x 2 4 +x 1 2 *x 2 2 +2*x 1 +x 2

Градиент функции

+ h

-0.5

+ h

-0.7413

+ h

+ 0.09038

+ h

+ 0.02394

+ h

+ 0.000178

+ h

+ 0.000243

=

Ответ: X = [-0.759;-0.4074] T

Итерация №2
.

Проверим критерий остановки:
|▽f(X 6)|
Вычислим значение функции в новой точке f(X 6) = -1.443.

Направление поиска: p 1 = T , p 2 = T

Одно из направлений поиска p 2 = T . Заканчиваем процесс итераций.

Ответ: X = [-0.759;-0.4074] T

СОПРЯЖЕННЫЕ НАПРАВЛЕНИЯ

Пара направлений, исходящих из точки Рповерхности Sи таких, что содержащие их прямые являются сопряженными диаметрами индикатрисы Дюпена поверхности Sвточке Р.
Для того чтобы направления (du
: dv
),
вточке Рповерхности Sбыли С. н., необходимо и достаточно выполнения условия

где L, М
и N —
коэффициенты второй квадратичной формы поверхности S,
вычисленные в точке Р.
Примеры: асимптотические направления, главные направления.

Лит.
: Погорелов А. В., Дифференциальная , 5 изд., М., 1969.
Е. В. Шикин.

Математическая энциклопедия. — М.: Советская энциклопедия
.
И. М. Виноградов
.
1977-1985
.

Смотреть что такое «СОПРЯЖЕННЫЕ НАПРАВЛЕНИЯ» в других словарях:

Раздел геометрии, в к ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в … Математическая энциклопедия


1) Сумма квадратов длин сопряженных полудиаметров эллипса есть величина постоянная, равная сумме квадратов длин его полуосей. 2) Площадь описанного вокруг эллипса параллелограмма, стороны к рого имеют сопряженные направления, постоянна и равна… … Математическая энциклопедия


Направ ление на регулярной поверхности, в к ром кривизна нормального сечения поверхности равна нулю. Для того чтобы направление в точке Рбыло А. н., необходимо и достаточно выполнение условия: где внутренние координаты на поверхности, а L, М и N… … Математическая энциклопедия


Численные методы раздел вычислительной математики, посвященный математич. описанию и исследованию процессов численного решения задач линейной алгебры. Среди задач Л. а. наибольшее значение имеют две: решение системы линейных алгебраич. уравнений… … Математическая энциклопедия


Сеть линий на поверхности, образованная двумя семействами линий такими, что в каждой точке поверхности линии сети различных семейств имеют сопряженные направления. Если координатная сеть является С. с., то коэффициент М второй квадратичной формы… … Математическая энциклопедия


СО 34.21.308-2005: Гидротехника. Основные понятия. Термины и определения
— Терминология СО 34.21.308 2005: Гидротехника. Основные понятия. Термины и определения: 3.10.28 аванпорт: Ограниченная волнозащитными дамбами акватория в верхнем бьефе гидроузла, снабженная причальными устройствами и предназначенная для размещения … Словарь-справочник терминов нормативно-технической документации


I I. История развития железных дорог. Ж. дорога, в том виде, в каком она существует теперь, изобретена не сразу. Три элемента, ее составляющие, рельсовый путь, перевозочные средства и двигательная сила прошли каждый отдельную стадию развития,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона


Заработная плата
— (Wages) Важнейшее средство повышения заинтересованности работников Участие трудящихся в доле вновь созданных материальных и духовных благ Содержание Содержание. > заработная плата — это важнейшее средство повышения заинтересованности… … Энциклопедия инвестора


Диверсификация
— (Diversification) Диверсификация это инвестиционный подход направленный на снижение финансовых рынков Понятие, основные методы и цели диверсификации производства, бизнеса и финансовых рисков на валютных, фондовых и сырьевых рынках Содержание… … Энциклопедия инвестора


XIII. Дела внутренние (1866—1871). 4 го апреля 1866 года, в четвертом часу дня, Император Александр, после обычной прогулки в Летнем саду, садился в коляску, когда неизвестный человек выстрелил в него из пистолета. В эту минуту, стоявший в… … Большая биографическая энциклопедия

Высокая
скорость сходимости метода Ньютона
обусловлена тем, что он минимизирует
квадратичную функцию

Где
А – симметрическая положительно
определенная матрица размера nxn

,
за один шаг. Квазиньютоновские методы
позволяют найти минимум квадратичной
функции за
шагов. На стремлении минимизировать
квадратичную функцию за конечно число
шагов основана идея метода сопряженных
направлений. Точнее говоря, в методах
сопряженных направлений требуется
найти направлениятакие, что последовательностьодномерных минимизаций вдоль этих
направлений приводит к отысканию
минимума функции 2.1, т. е.при любом,
где

Оказывается,
что указаным свойством обладает система
взаимно сопряженных относительно
матрицы А направлений

Пусть
А – симетрическая положительно
определенная матрица размера
.

Определение
2.1. Векторы (направления)
иназываются сопряженными (относительно
матрицы А), если они отличны от нуля и.
Векторы (направления)называются взаимно сопряженными
(относительно матрицы А), если все они
отличны от нуля и.
(2.3)

Лемма
3.1. Пусть векторы являются взаимно
сопряженными. Тогда они линейно
независимы.

Доказательство.
Пусть это неверно, т. е.
при некотором.
Тогда,
что возможно только при,
так как матрица А положительно определена.
Полученное противоречие доказывает
лемму.

Рассмотрим
задачу минимизации на R
n
функции 2.1. Будем решать ее методом 2.2.
Если векторы
,
взаимно сопряжены, то метод 3.2 можно
назвать методом сопряженных направлений.
Однако обычно это название употребляется
лишь для тех методов, в которых именно
стремление добится условия взаимной
сопряженности определяет выбор
направлений.
К выполнению того же самого условия
может привести и реализация совершенно
новой идеи.

Теорема
3.1. Если векторы h
k

в методе 2.2 взаимно сопряжены, k
=0,1,…,
m
-1
,
то для функции f
,
заданой формулой 2.1,

,
(2.4)

где
– линейное подпространство, натянутое
на указанные векторы.

Доказательство.
С учетом 2.2 и определения 2.1 имеем

(2.5)

Используя
это равенство, получаем

(2.6)

Следствие.
Если векторы h
k

в методе 2.2 взаимно сопряженны,
k
=0,1,…,
n
-1
,
то для функции f
,
заданной формулой 2.1, и произвольной
точки

Таким
образом, метод 2.2 позволяет найти точку
минимума квадратичной функции 2.1 не
более чем за n
шагов.

2.2. Метод сопряженных направлений нулевого порядка.

Алгоритм
состоит из последовательности циклов,
k
-й
из которых определяется начальной
точкой t
0
(k
)

и направлениями минимизации p
0
(k
),
p
1
(k
),
…,
p
n
-1
(k
)
.
На нулевом цикле в качестве t
0
(0),

выбирается произвольная точка
,
в качествеp
0
(0),
p
1
(k
),
…,
p
n
-1
(k
)

– направления координатных осей.

Очередной
k
-й
цикл состоит в последовательном решении
одномерных задач

Тем
самым определяется шаг из точки
в точку

где
итаковы, что

После
завершения k
-го
цикланачальная точка и направления
минимизации (k
+1)
-го
цикла определяются по формулам

Критерием
остановки может служить выполнение
неравенства
,
где– заранее выбраное малое положительное
число.

Теорема
3.2. Если векторы
в методе 2.5-2.7 отличны от нуля, то для
функцииf
,
заданой формулой 2.1

Доказательство.
Учитывая следствие из теоремы 3.1,
достаточно показать, что векторы
взаимно сопряжены. Пусть. Предположив, что векторывзаимно сопряжены, докажем, что векторсопряжен с векторами.

Заметим,
что
и, стало быть, точкаt
n
(k
)
,
согласно формулам 2.5, получена из точки
t
n
—
k
(k
)

с помощью последовательности одномерных
минимизаций вдоль направлений
.
Это, в силу теоремы 2.1, означает, что

Аналогично,
точка t
0
(k
)

получена из точки t
n
—
k
+1
(k
)

помощью последовательности одномерных
минимизаций вдоль тех же направлений,
и поэтому

Доказываемое
утверждение теперь непосредственно
следует с леммы 2.2 так как
.

Предположение
теоремы 2.2 о том, что
отличны от нуля, выполняется далеко не
всегда. Система векторовможет при некоторомk

оказатся линейно зависимой (или «почти»
линейно зависимой), в результате чего
метод может не обеспечить отыскание
минимума даже квадратичной функции.

Опишем
модификацию метода 2.5-2.7, приводящую к
эффективному алгоритму минимизации.

После
завершения k
-го
цикла проверяется выполнение неравенств
.
Если хотя бы одно с них выполнено, то
производится остановка. В противном
случае проверяется выполнение неравенства

,
(2.16)

Если
оно выполнено, то направления минимизации
(k
+1)
-го
цикла остаются прежними, т. е.

Если
нет, то направления минимизации (k
+1)
-го
цикла определяется по формулам

В
обоих случаях начальная точка (k
+1)
-го
цикла вычисляется так, же как и в исходном
алгоритме.

Метод
ориентирован на решение задач с
квадратичными целевыми функциями и
основывается на фундаментальных
теоретических результатах. Хотя
используемые в реальных ситуациях
алгоритмы, являющиеся эффективными
для квадратичных целевых функций, могут
плохо работать при более сложных целевых
функциях, тем не менее этот подход
представляется вполне разумным.

Определение
.
Пусть
—
симметрическая матрица порядка
.
Векторы
называются
—
сопряженными, если они линейно независимы
и выполняется условие
при
.

Пример.
Рассмотрим
функцию

В
качестве матрицы

можно взять матрицу Гессе

.

В
качестве одного из направлений выберем

.
Тогда направление
должно удовлетворять равенству

.

Следует
заметить, что сопряженные направления
выбираются неоднозначно. Однако если
добавить условие нормировки, то их
можно определить однозначно:

Утверждение.
Любая квадратичная функция
переменных, имеющая минимум, может быть
минимизирована зашагов, при условии, что поиск ведется
вдоль сопряженных относительно матрицы
Гессе направлений
.

Произвольная
функция может быть достаточно хорошо
представлена в окрестности оптимальной
точки ее квадратичной аппроксимацией.
Поэтому сопряженные направления могут
быть полезны для ее оптимизации. Однако
потребуется более чем
шагов. Для определения сопряженных
направлений применяется способ,
основанный на следующем утверждении.

Утверждение.
Пусть задана квадратичная функция

,
две произвольные точки
и направление
S
..Если
точка
является точкой минимума функции
вдоль направления
S

из точки
,
а— точкой минимума функции вдоль
направления
S

из точки

,
то направление
сопряжено с направлением
S
.

Алгоритм.

Шаг 1.
Задать
начальную точку
и систему

линейно независимых направлений


(они первоначально могут совпадать с
направлениями координатных осей).
Минимизировать
функцию


при последовательном движении по
направлениям; используя какой-либо
одномерный поиск; и полученную ранее
точку минимума взять в качестве исходной.

Шаг 2.
Выполнить
дополнительный шаг

,
соответствующий полному перемещению
на шаге 1. Вычислить точку
(рис 12). Проверить критерий (*) включения
нового направления в систему сопряженных
направлений.

Шаг 3.
Пусть
– наибольшее уменьшение целевой функции
в одном из направлений
:

и
является направлением, соответствующим.

Если выполняются
условия

(*)

то поиск продолжить
вдоль первоначальных направлений

из точки
или
(из той точки, где меньше значение
функции).

Шаг 4.
Если
условия
не выполняются, то минимизировать
функцию
вдоль направления
.
Точку этого минимума взять в качестве
начальной на следующем этапе. На этом
этапе использовать систему направлений

т.е. направление
заменить на,
которое поместить в последний столбец
матрицы направлений.

Шаг 5.
Если

,
то минимум найден. В противном случае
выполнить шаг 1.

Пример.
Щелкнув
по значку, откроется Mathcad
документ метода сопряженных направлений,
в котором можно выполнить вычисления.

Минимизация
функции

методом
сопряженных направлений

Может показаться
нерациональным отбрасывать самое
удачное направление текущей итерации
и устанавливать новое перспективное
направление на последнее место вместо
первого. Однако же нетрудно видеть, что
самое удачное направление скорее всего
исчерпало себя, а новое перспективное
направление только что было использовано
для одномерной оптимизации и применять
его сразу же нет никакого смысла, так
как продвижения просто на будет.

Пауэлл доказал,
что определитель матрицы направлений
принимает максимальное значение тогда
и только тогда, когда направления
,
сопряжены относительно матрицы Гессе.
Он пришел к выводу, что направление
полного перемещения должно заменять
предыдущее только в том случае, когда
это направление увеличивает определитель
матрицы направлений, так как только
тогда новый набор направлений будет
эффективным.

Доказано, что
процедура Пауэлла сходится к точке, в
которой градиент равен нулю, если
целевая функция строго выпукла. Эта
точка является локальным минимумом.
Метод очень чувствителен к способу
построения сопряженных направлений и
поэтому зависит от точности используемого
одномерного поиска. Пауэлл предложил
использовать последовательность
квадратичных интерполяций со специальной
процедурой настройки параметров этого
линейного поиска. Тем не менее численные
исследования показали, что метод
сопряженных направлений Пауэлла не
следует использовать при размерности
свыше 20.

1. Пересечение линии второго порядка и прямой.

   Начать изучение
   

2. Тип линии.

   Начать изучение
   

3. Диаметр линии второго порядка.

   Начать изучение
   

4. Центр линии второго порядка.

   Начать изучение
   

5. Сопряженные направления.

   Начать изучение
   

6. Главные направления.

   Начать изучение
   

7. Касательная к линии второго порядка.

   Начать изучение
   

8. Особые точки.

   Начать изучение
   

Пересечение линии второго порядка и прямой.

Рассмотрим линию второго порядка, заданную общим уравнением
$$
Ax^{2}+2Bxy+Cy^{2}+2Dx+2Ey+F=0label{ref1}
$$
в декартовой системе координат, и исследуем пересечение этой линии с произвольной прямой
$$
x=x_{0}+alpha t, y=y_{0}+beta t.label{ref2}
$$
Значения параметра (t), соответствующие точкам пересечения, должны удовлетворять уравнению, получаемому подстановкой eqref{ref2} в eqref{ref1}:
$$
A(x_{0}+alpha t)^{2}+2B(x_{0}+alpha t)(y_{0}+beta t)+C(y_{0}+beta t)^{2} +\+ 2D(x_{0}+alpha t)+2E(y_{0}+beta t)+F=0.label{ref3}
$$
Раскрывая скобки и приводя подобные члены, мы получим уравнение
$$
Pt^{2}+2Qt+R=0,label{ref4}
$$
в котором
$$
P=Aalpha^{2}+2Balphabeta+Cbeta^{2},label{ref5}
$$
$$
Q=(Ax_{0}+By_{0}+D)alpha+(Bx_{0}+Cy_{0}+E)beta,label{ref6}
$$
или, при другой группировке слагаемых,
$$
Q=(Aalpha+Bbeta)x_{0}+(Balpha+Cbeta)y_{0}+Dalpha+Ebeta.label{ref7}
$$
Свободный член — это значение многочлена при (t=0), то есть
$$
R=Ax_{0}^{2}+2Bx_{0}y_{0}+Cy_{0}^{2}+2Dx_{0}+2Ey_{0}+F=0.label{ref8}
$$

Вообще говоря, уравнение eqref{ref4} квадратное, имеет не больше двух корней, и прямая пересекает линию или в двух точках, или в одной точке (кратные корни), или не пересекает ее (комплексные корни). Но возможны “исключительные” прямые, для которых (P=0), то есть
$$
Aalpha^{2}+2Balphabeta+Cbeta^{2}=0,label{ref9}
$$
и, следовательно, уравнение eqref{ref4} является линейным. В этом случае оно имеет один корень при (Q neq 0), а при (Q=0) либо выполнено тождественно (если и (R=0)), либо не имеет решений. Следовательно, “исключительные” прямые или пересекают линию в единственной точке, или лежат на ней целиком, или не имеют с ней общих точек.

В равенство eqref{ref9} не входят координаты начальной точки прямой. Кроме того, оно остается справедливым, если умножить (alpha) и (beta) на общий ненулевой множитель.

Тип линии.

Выясним, сколько асимптотических направлений может иметь линия второго порядка. Обозначив
$$
delta=begin{vmatrix}
A& B\
B& C
end{vmatrix},nonumber
$$
сформулируем следующее утверждение.

От противного нетрудно проверить, что и обратно число асимптотических направлений определяет знак (delta).

Мы определили асимптотические направления при помощи аналитического условия eqref{ref9}. Поэтому в принципе при изменении системы координат асимптотическое направление могло бы перестать быть асимптотическим, или, наоборот, обыкновенное направление стать асимптотическим. Из геометрического смысла асимптотических направлений видно, что в действительности асимптотические направления не зависят от выбора системы координат.

Используя канонические уравнения, легко проверить, что эллипс не имеет асимптотических направлений, парабола имеет одно, а гипербола — два асимптотических направления (рис. 9.1). Поэтому линии второго порядка называются линиями гиперболического, параболического или эллиптического типа, смотря по тому, имеют они два, одно или не имеют ни одного асимптотического направления.

Для линий гиперболического типа (delta < 0), для параболического типа (delta=0), а для эллиптического (delta > 0).

Диаметр линии второго порядка.

Назовем хордой любой отрезок, концы которого лежат на линии, а остальные точки на ней не лежат. Таким образом, хорда не может иметь асимптотического направления.

Предположим, что рассматриваемая линия второго порядка имеет по крайней мере одну хорду. Этому условию удовлетворяют эллипсы, гиперболы, пары пересекающихся прямых, параболы и пары параллельных прямых.

Фиксируем какое-нибудь неасимптотическое направление и исследуем множество середин хорд, имеющих это направление. Если начальная точка (M_{0}(x_{0}, y_{0})) секущей eqref{ref2} находится в середине хорды, то корни уравнения eqref{ref4} равны по абсолютной величине и отличаются знаком (рис. 9.2). Это будет так в том и только том случае, когда (Q=0). Используя eqref{ref7}, мы получаем, что середины хорд направления ((alpha, beta)^{2}) лежат на прямой
$$
(Aalpha+Bbeta)x+(Balpha+Cbeta)y+Dalpha+Ebeta=0.label{ref10}
$$

Стоит обратить внимание на то, что диаметром называется вся прямая. Это не означает, что середины хорд заполняют ее целиком. Так может быть, но возможно также, что множество середин хорд есть, например, отрезок или луч.

Конечно, остается сомнение, действительно ли уравнение eqref{ref10} определяет прямую: не окажутся ли в нем коэффициенты при переменных оба равными нулю? Допустим, что это так, то есть
$$
Aalpha+Bbeta=0, Balpha+Cbeta=0.nonumber
$$

Умножим первое из этих равенств на (alpha), второе — на (beta) и сложим. Мы получим равенство eqref{ref9}, которое по предположению не имеет места. Следовательно, уравнение eqref{ref10} определяет прямую.

Центр линии второго порядка.

Обозначим левую часть уравнения eqref{ref1} через (boldsymbol{Phi}(x, y)) и введем еще одно понятие.

По-видимому, это определение зависит от выбора системы координат, так как в нем участвует не линия, а многочлен, стоящий в левой части ее уравнения. Допустим, что координаты (x_{0}, y_{0}) точки (O) в некоторой системе координат удовлетворяют уравнению eqref{ref11}. Будут ли ее координаты ((tilde{x}_{0}, tilde{y}_{0})) в другой системе координат удовлетворять равенству того же вида для многочлена (tilde{boldsymbol{Phi}}(tilde{x}, tilde{y})), задающего ту же линию в новой системе координат? Легко видеть, что это так, потому что многочлен (tilde{boldsymbol{Phi}}) так и выбирается, чтобы для координат любой точки выполнялось равенство (tilde{boldsymbol{Phi}}(tilde{x}, tilde{y})=boldsymbol{Phi}(x, y)). Нам остается только выписать это равенство для точек, получаемых из (O) сдвигом на векторы (boldsymbol{a}) и (-boldsymbol{a}).

Ниже мы докажем, что в том случае, когда линия содержит хоть одну точку, центры линии и только они являются ее центрами симметрии. Однако понятие центра несколько более общее: линии, являющиеся пустыми множествами, имеют вполне определенные центры, хотя говорить об их центрах симметрии смысла нет. Например, каждая точка прямой (y=0) является центром линии с уравнением (y^{2}+1=0).

Получим систему уравнений для координат центра. С этой целью напишем подробнее равенство eqref{ref11}. Его левая часть равна
$$
A(x_{0}+alpha)^{2}+2B(x_{0}+alpha)(y_{0}+beta) +\+ C(y_{0}+beta)^{2}+2D(x_{0}+alpha)+2E(y_{0}+beta)+F.nonumber
$$
Правая часть отличается от левой только знаками у (alpha) и (beta). Поэтому при вычитании (boldsymbol{Phi}(x_{0}-alpha, y_{0}-beta)) из (boldsymbol{Phi}(x_{0}+alpha, y_{0}+beta)) уничтожаются все члены, кроме тех, в которые (alpha) и (beta) входят в первой степени, а члены с первыми степенями удвоятся. После упрощений мы получаем
$$
(Ax_{0}+By_{0}+D)alpha+(Bx_{0}+Cy_{0}+E)beta=0.label{ref12}
$$

Но равенство eqref{ref11}, а вместе с ним и равносильное равенство eqref{ref12} имеет место при любых (alpha) и (beta), в частности, при (alpha=1), (beta=0) и при (alpha=0), (beta=1). Отсюда следует, что координаты ((x_{0}, y_{0})) центра должны удовлетворять системе уравнений
$$
left{begin{array}{l}
Ax_{0}+By_{0}+D=0,\
Bx_{0}+Cy_{0}+E=0.
end{array}right.label{ref13}
$$

Легко видеть, что и обратно, если справедливы равенства eqref{ref13}, то, умножая их на произвольные числа (alpha) и (beta) и складывая, мы получим eqref{ref12}, а тем самым и eqref{ref11}.

Исследуем, обязательно ли существуют центры у линии второго порядка, а если они существуют, то сколько их и как они расположены. Система уравнений eqref{ref13} имеет единственное решение тогда и только тогда, когда
$$
delta=begin{vmatrix}
A& B\
B& C
end{vmatrix} neq 0.label{ref14}
$$
Таким образом, условие (delta neq 0) необходимо и достаточно для того, чтобы линия второго порядка имела единственный центр.

Линии второго порядка, имеющие единственный центр, называются центральными.

Полученное условие показывает, что центральными являются линии эллиптического и гиперболического типов.

Условие (delta=0) характеризует нецентральные линии. Это — линии параболического типа. При условии (delta=0) система eqref{ref13} либо не имеет решения, либо равносильна одному из составляющих ее уравнений (ранее мы уже доказывали этот факт). Это значит, что нецентральная линия либо не имеет центра (парабола), либо ее центры заполняют прямую линию (пары параллельных прямых, вещественных и мнимых, и пары совпавших прямых).

Сопряженные направления.

Направление ((alpha’, beta’)), определяемое диаметром, сопряженным направлению ((alpha, beta)), называется сопряженным направлению ((alpha, beta)). Компоненты ((alpha’, beta’)), направляющего вектора диаметра eqref{ref10} согласно доказанному ранее утверждению 6 удовлетворяют условию
$$
(Aalpha+Bbeta)alpha’+(Balpha+Cbeta)beta’=0label{ref15}
$$
или
$$
Aalphaalpha’+B(alpha’beta+alphabeta’)+Cbetabeta’=0label{ref16}
$$
В последнее выражение пары чисел ((alpha, beta)) и ((alpha’, beta’)) входят симметричным образом. Поэтому имеет место следующее утверждение.

Возникает вопрос, при каких условиях направление, сопряженное какому-нибудь направлению ((alpha, beta)) может оказаться асимптотическим. Это легко выяснить. Из равенства eqref{ref15} следует, что в качестве (alpha’) и (beta’) можно выбрать соответственно — (-(Balpha+Cbeta)) и ((Aalpha+Bbeta)). Подставим это в уравнение eqref{ref9} для асимптотических направлений:
$$
A(Balpha+Cbeta)^{2}-2B(Balpha+Cbeta)(Aalpha+Bbeta)+C(Aalpha+Bbeta)^{2}=0.nonumber
$$
После преобразований получаем ((AC-B^{2}) times (Aalpha^{2}+2Balphabeta+Cbeta^{2})=0). Поскольку исходное направление не асимптотическое, это произведение может обратиться в нуль только за счет первого сомножителя. Мы получаем новое утверждение.

Главные направления.

Если диаметр перпендикулярен хордам, которым он сопряжен, то он является осью симметрии рассматриваемой линии.

Если система координат декартова прямоугольная, то для главного направления компоненты ((alpha, beta)) должны быть пропорциональны коэффициентам уравнения eqref{ref10}, то есть должно существовать такое число (lambda), что
$$
Aalpha+Bbeta=lambdaalpha, Balpha+Cbeta=lambdabeta.label{ref17}
$$
Исключая (lambda), мы получаем уравнение для (alpha) и (beta):
$$
(A-C)alphabeta+B(beta^{2}-alpha^{2})=0.label{ref18}
$$

Если положить (alpha=cos varphi), (beta=sin varphi), то уравнение eqref{ref18} превратится в уравнение (2B cos 2varphi = (A-C)sin 2varphi), которое, как мы видели, обязательно имеет решение относительно (varphi). Поэтому имеет место следующее утверждение.

Более подробное исследование уравнения eqref{ref18} показывает, что либо эта пара единственная, либо каждая пара перпендикулярных направлений является главной. Последний случай имеет место, когда (A=C), (B=0). При этом уравнение линии приводится к одному из канонических видов: (x^{2}+y^{2}=a^{2}), (x^{2}+y^{2}=-a^{2}) или (x^{2}+y^{2}=0). В двух последних случаях линия не имеет хорд, и результат лишен геометрического смысла.

Касательная к линии второго порядка.

Как известно, касательной к какой-либо линии называется предельное положение секущей, когда хорда стягивается в точку. Выведем уравнение касательной к линии второго порядка, заданной уравнением eqref{ref1}. Дадим предварительно следующее определение.

Особыми точками являются: точка пересечения пары пересекающихся прямых, единственная точка пары мнимых пересекающихся прямых и каждая точка пары совпавших прямых. В особой точке касательная не определена. Если точка лежит на прямой, входящей в состав линии, то касательная в этой точке совпадает с прямой. Исключив эти случаи, мы фактически ограничиваемся рассмотрением касательных к эллипсам, гиперболам и параболам.

Рассмотрим точку (M_{0}(x_{0, y_{0}})), лежащую на линии (L), и прямую с начальной точкой (M_{0}), заданную уравнением eqref{ref2}. С нашей точки зрения, приведенное выше определение касательной означает, что уравнение eqref{ref4}, определяющее точки пересечения (L) и прямой, имеет два совпадающих корня.

Так как начальная точка принадлежит (L), в уравнении eqref{ref4} (R=0), и один из его корней равен нулю. Корни совпадают, если и второй корень равен нулю, для чего необходимо, чтобы (Q=0). Если при этом окажется, что и (P=0), то прямая принадлежит линии второго порядка. Этот случай мы исключили, и потому уравнение имеет кратный корень (t=0) в том и только том случае, когда (Q=0). Мы рассматриваем равенство (Q=0) как условие, определяющее направляющий вектор касательной:
$$
(Ax_{0}+By_{0}+D)alpha+(Bx_{0}+Cy_{0}+E)beta=0.label{ref19}
$$

Так как (M_{0}) не особая точка, обе скобки здесь одновременно в нуль не обращаются, и условие eqref{ref19} определяет (alpha) и (beta) с точностью до общего множителя. Точка (M(x, y)) лежит на касательной тогда и только тогда, когда вектор (overrightarrow{M_{0}M}) коллинеарен (boldsymbol{a}(alpha, beta)), то есть его координаты (x-x_{0}) и (y-y_{0}) удовлетворяют тому же условию, что и ((alpha, beta)):
$$
(Ax_{0}+By_{0}+D)(x-x_{0})+(Bx_{0}+Cy_{0}+E)(y-y_{0})=0.label{ref20}
$$

Это и есть уравнение касательной к линии (L) в точке (M_{0}), лежащей на линии. Уравнение eqref{ref20} можно записать и иначе, если заметить, что координаты (M_{0}) удовлетворяют уравнению eqref{ref1} и, следовательно,
$$
(Ax_{0}+By_{0}+D)x_{0}+(Bx_{0}+Cy_{0}+E)y_{0}+Dx_{0}+Ey_{0}+F=0.nonumber
$$
Прибавляя это равенство к eqref{ref20} и группируя слагаемые, получим окончательное уравнение
$$
Axx_{0}+B(xy_{0}+x_{0}y)+Cyy_{0}+D(x+x_{0})+E(y+y_{0})+F=0.label{ref21}
$$

Особые точки.

Напомним, что особая точка линии второго порядка — это ее центр, лежащий на линии. Исследуем, при каких условиях линия второго порядка имеет особую точку. Для координат ((x_{0}, y_{0})) особой точки должны быть справедливы равенства
$$
begin{array}{cc}
& Ax_{0}+By_{0}+D=0, Bx_{0}+Cy_{0}+E=0,\
& Ax_{0}^{2}+2Bx_{0}y_{0}+Cy_{0}^{2}+2Dx_{0}+2Ey_{0}+F=0.
end{array}nonumber
$$
Умножим первое из них на (x_{0}), второе на (y_{0}) и вычтем из третьего. Мы получим эквивалентную систему уравнений
$$
left{begin{array}{l}
Ax_{0}+By_{0}+D=0,\
Bx_{0}+Cy_{0}+E=0,\
Dx_{0}+Ey_{0}+F=0.
end{array}right.label{ref22}
$$
Выберем какой-нибудь базис в пространстве и рассмотрим вспомогательные векторы (boldsymbol{p}(A, B, D)), (boldsymbol{q}(B, C, E)) и (boldsymbol{r}(D, E, F)). Равенства eqref{ref22} представляют собой координатную запись векторного равенства
$$
x_{0}boldsymbol{p}+y_{0}boldsymbol{q}=-boldsymbol{r}.label{ref23}
$$
Отсюда следует, что при наличии особой точки векторы (boldsymbol{p}), (boldsymbol{q}) и (boldsymbol{r}) компланарны, и потому
$$
triangle=begin{vmatrix}
A& B& D\
B& C& E\
D& E& F
end{vmatrix}=0.label{ref24}
$$

Если линия центральная, то векторы (boldsymbol{p}) и (boldsymbol{q}) не коллинеарны, и условие компланарности eqref{ref24} равносильно существованию разложения eqref{ref23}, то есть существованию решения системы eqref{ref22}. Мы получили ещё одно утверждение.

Итак, сочетание (delta < 0), (triangle=0) характеризует пары пересекающихся прямых, а (delta > 0), (triangle=0) — пары мнимых пересекающихся прямых.

Рассмотрим нецентральные линии. Для них существует центр, хотя бы не являющийся особой точкой, тогда и только тогда, когда (triangle=0). В этом (и только этом) случае векторы (boldsymbol{p}) и (boldsymbol{q}) коллинеарны. Действительно, так как (delta=0), по предложению 9 § 2 гл. II, если система уравнений eqref{ref13} имеет решение, она равносильна одному из составляющих ее уравнений: либо коэффициенты и свободный член одного из уравнений равны нулю, либо коэффициенты и свободные члены обоих уравнений пропорциональны. Тогда (triangle=0) независимо от (boldsymbol{r}).

Обратно, пусть для нецентральной линии (triangle=0). Докажем, что (boldsymbol{p}) и (boldsymbol{q}) коллинеарны, что равносильно совместности уравнений центра. Действительно, в противном случае (boldsymbol{r}) по ним раскладывается, и согласно eqref{ref23} существует особая точка. Она — центр, (boldsymbol{p}) и (boldsymbol{q}) коллинеарны, и мы получаем противоречие.

Итак, сочетание (delta=triangle=0) характеризует пары параллельных прямых (вещественных, мнимых или совпавших).

Из последних двух утверждений следует, что равенство (triangle=0) является инвариантным: оно не может измениться при переходе к другой системе координат.