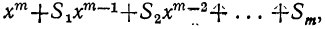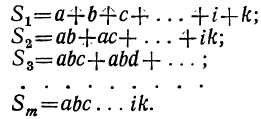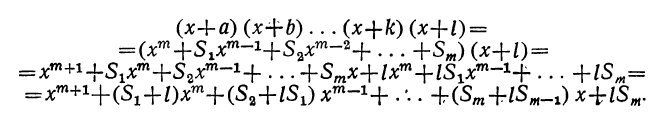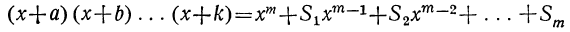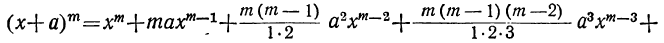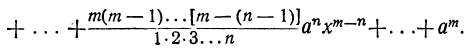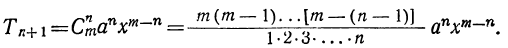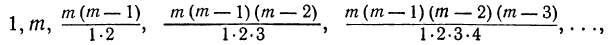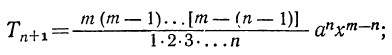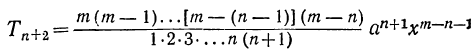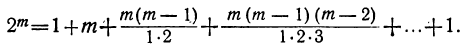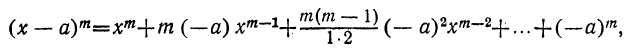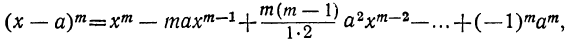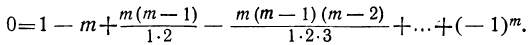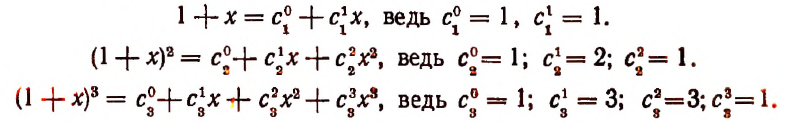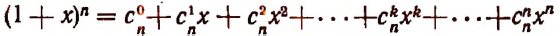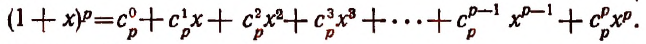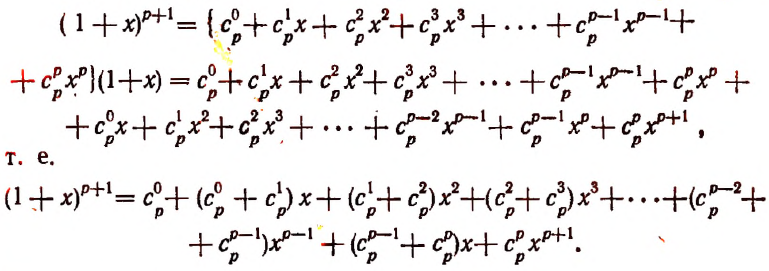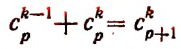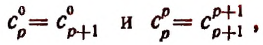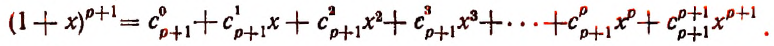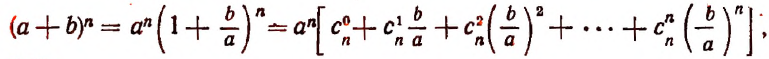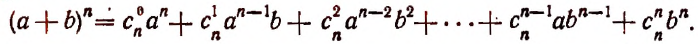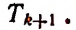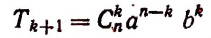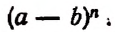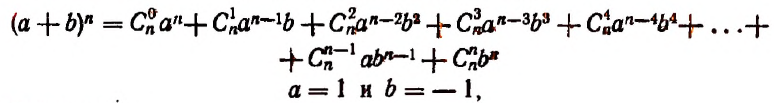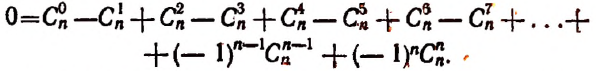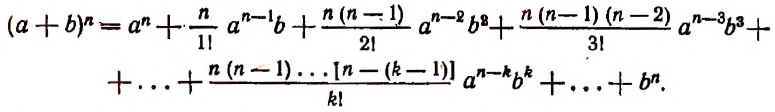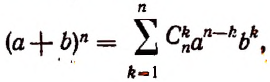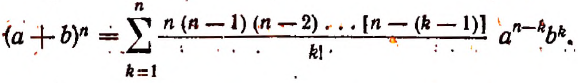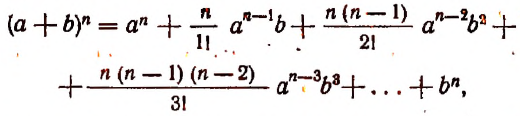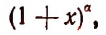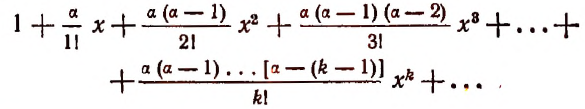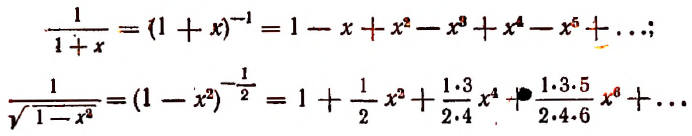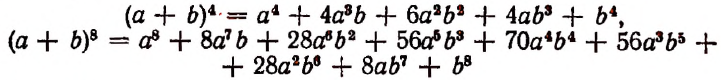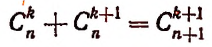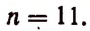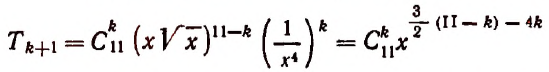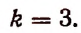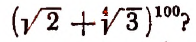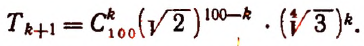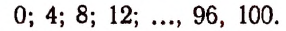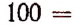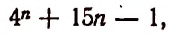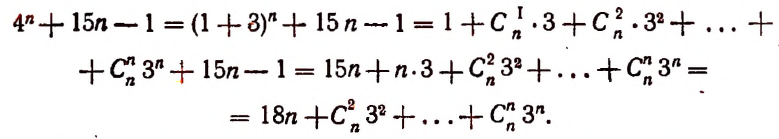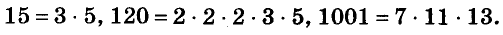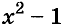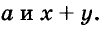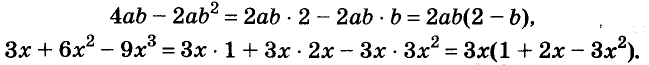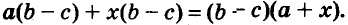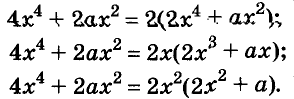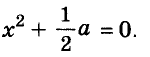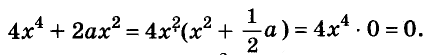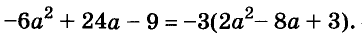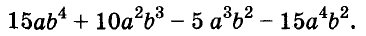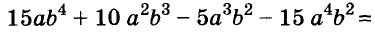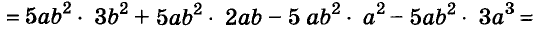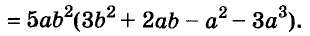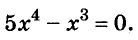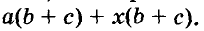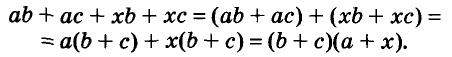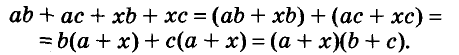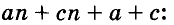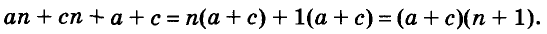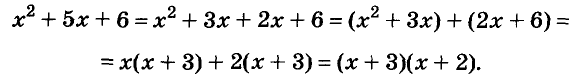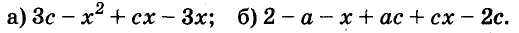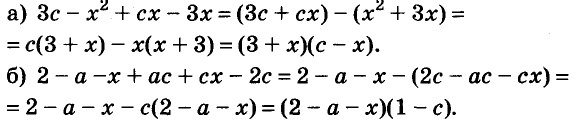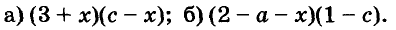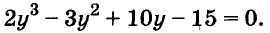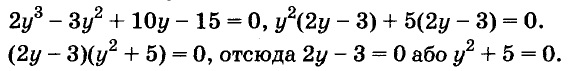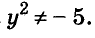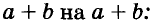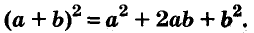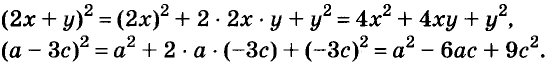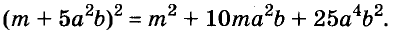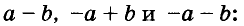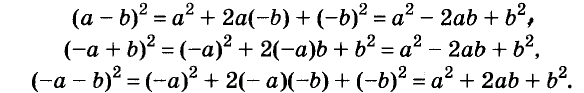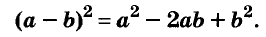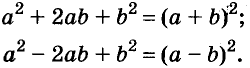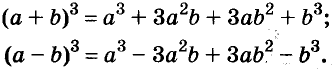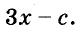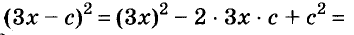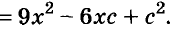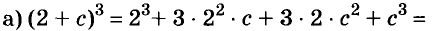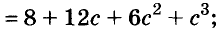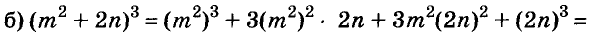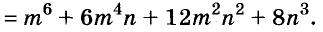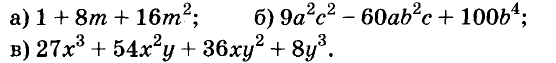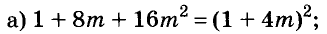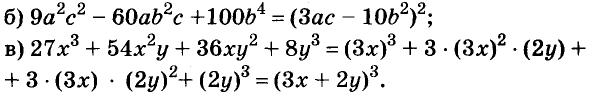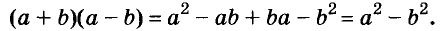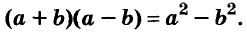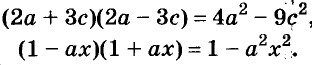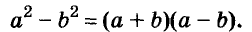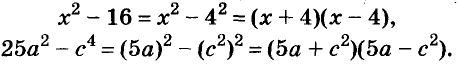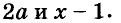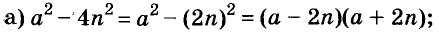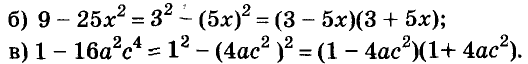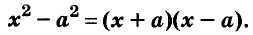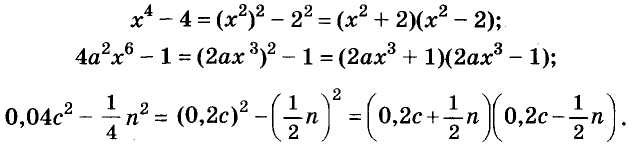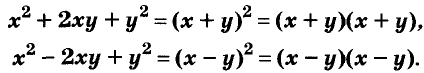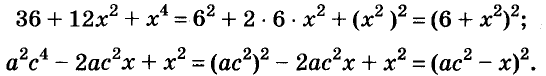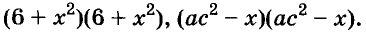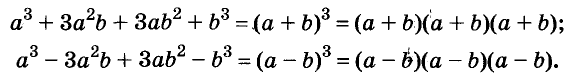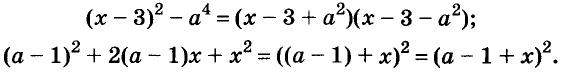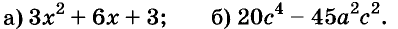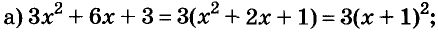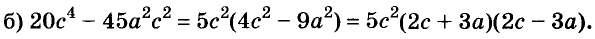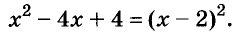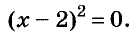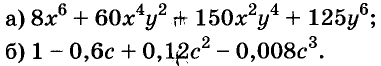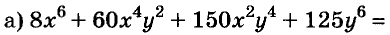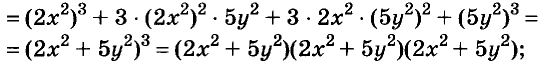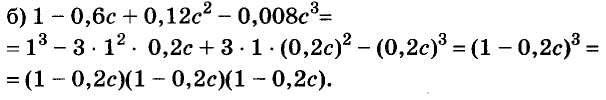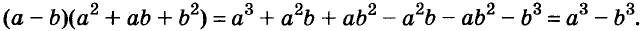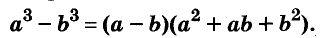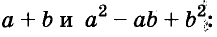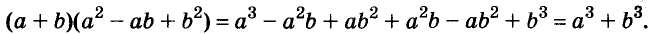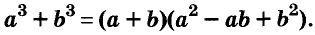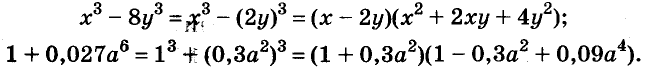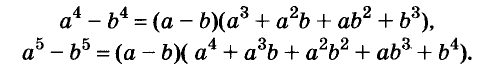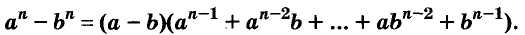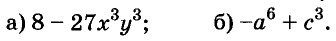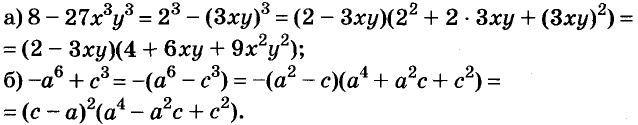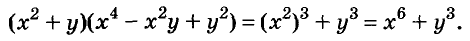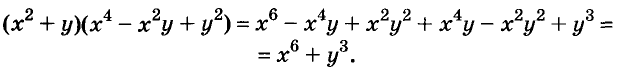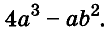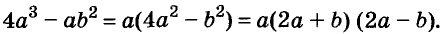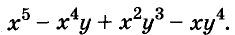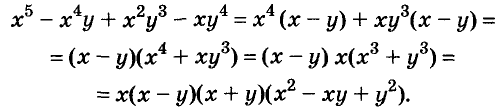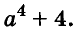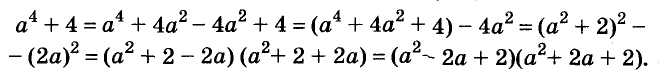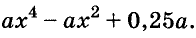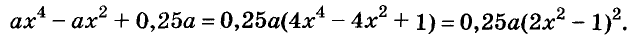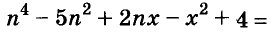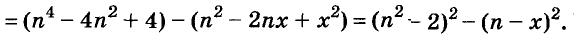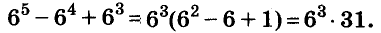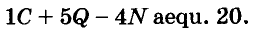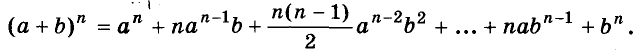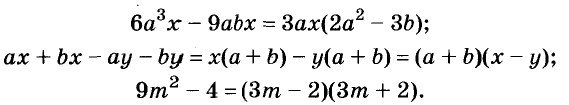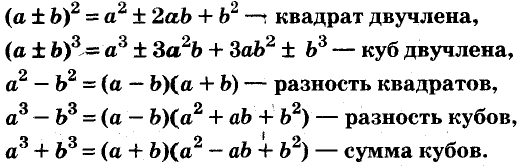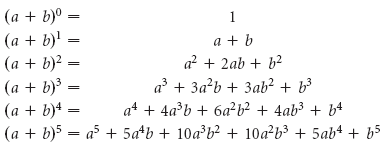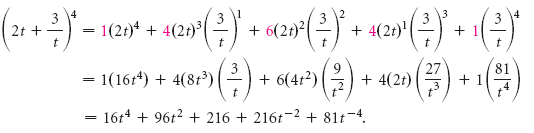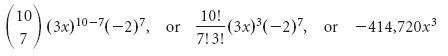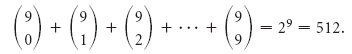Как найти в выражении член в разложении - AvtoShod.ru

Формула бинома Ньютона
- Свойства формулы бинома Ньютона
- Применение формулы бинома к многочлену
Вывод формулы бинома ньютона
Свойства разложения бинома
Свойства биномиальных коэффициентов
Арифметический треугольник, или треугольник паскаля
Примеры с решением на Бином Ньютона
Дополнение к Бином Ньютону

Произведение биномов, отличающихся только вторыми членами. Обыкновенным умножением находим:
(x+α) (x+b)=x²+ax+bx+ab=x²+(a+b) x+ab;
(x+a) (x+b) (x+c) = [x²+(a+b) x+ab] (x+c) =
= x³+(a+b) x2+abx+cx²+(ac+bc) x+abc=
= x³ + (a+b+c) x²+(ab+ac+bc) x+abc.

Подобно этому найдём:
(x+a) (х+b) (х+с) (x+d) = x⁴+(a +b+c+d) x³+
+ (ab+ac+ ad+bc+bd+cd) x²+(abc+abd+acd+bcd) x+abcd.

Рассматривая эти произведения, замечаем, что все они составлены по одному и тому же закону, а именно:

Произведение составляет многочлен, расположенный по убывающим степеням буквы х.

Показатель первого члена равен числу перемножаемых биномов; показатели при х в следующих членах убывают на 1; последний член не содержит х (содержит его в нулевой степени).

Коэффициент первого члена есть 1; коэффициент второго члена есть сумма всех вторых членов перемножаемых биномов; коэффициент третьего члена есть сумма всех произведений вторых членов, взятых по два; коэффициент четвёртого члена есть сумма всех произведений вторых членов, взятых по три. Последний член есть произведение всех вторых членов.

Докажем, что этот закон применим к произведению какого угодно числа биномов. Для этого предварительно убедимся, что если он верен для произведения m биномов:
(x+a) (x+b) (х+с) … (x+k),
то при этом предположении будет верен и для произведения (m+1) биномов:
(x+a) (x+b) (x+c) . .. (x+k) (х+l).

Итак, допустим, что верно следующее равенство:
(x+α) (x+b) (х+с)… (x+k) =
где для краткости мы положим:

Умножим обе части допущенного равенства на бином x+l:

Рассматривая это новое произведение, убеждаемся, что оно подчиняется такому же закону, какой мы предположили верным для m биномов. Действительно, во-первых, этому закону следуют показатели буквы х; во-вторых, ему же следуют и коэффициенты, так как коэффициент второго члена S+l есть сумма всех вторых членов перемножаемых биномов, включая сюда и l; коэффициент третьего члена S₂+lS₁ есть сумма парных произведений всех вторых членов, включая сюда и l, и т. д.; наконец, 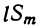есть произведение всех вторых членов: abc… kl.

Мы видели, что закон этот верен для произведения двух, трёх и четырёх биномов; следовательно, по доказанному теперь, он должен быть верен и для произведения 4+1, т. е. для произведения пяти биномов, если же он верен для произведения пяти биномов, то он верен и для произведения 5+1, т. е. для произведения шести биномов, и т. д.

Изложенное рассуждение представляет так называемое „доказательство от m к m+1“. Оно называется также „математической индукцией» (или „совершенной индукцией»). Заметим, что в предыдущих главах этой книги неоднократно представлялся случай применить доказательство от m к m + 1 . Мы этого не делали только ради простоты изложения.

Формула бинома Ньютона

Предположим, что в доказанном нами равенстве

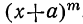
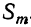
все вторые члены биномов одинаковы, т. е. что a=b=c= … =k. Тогда левая часть будет степень бинома . Посмотрим, во что обратятся коэффициенты S₁, S₂, …, .

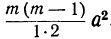
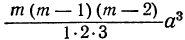
Коэффициент S₁, равный a+b+c+ … +k, обратится в та. Коэффициент S₂, равный ab+ac+ad+ …. обратится в число α², повторённое столько раз, сколько можно составить сочетаний из m элементов по 2, т. е. обратится в . Коэффициент S₃, равный abc+abd+…, обратится в число а³, повторённое столько раз, сколько можно составить сочетаний из т элементов по 3, т. е. и т. д. Наконец, коэффициент , равный abc...k, обратится в . Таким образом, мы получим:

Это равенство известно как формула бинома Ньютона, причём многочлен, стоящий в правой части формулы, называется разложением бинома. Рассмотрим особенности этого многочлена.

Свойства формулы бинома Ньютона

Из этих свойств мы укажем следующие 10:

1) Показатели буквы х уменьшаются на 1 от первого члена к последнему, причём в первом члене показатель х равен показателю степени бинома, а в последнем он есть 0; наоборот, показатели буквы а увеличиваются на 1 от первого члена к последнему, причём в первом члене показатель при а есть 0; а в последнем он равен показателю степени бинома. Вследствие этого сумма показателей при х и а в каждом члене одна и та же, а именно: она равна показателю степени бинома.

2) Число всех членов разложения есть m+1, так как разложение содержит все степени а от 0 до m включительно.

3) Коэффициенты равны: у первого члена — единице, у второго члена — показателю степени бинома, у третьего члена — числу сочетаний из m элементов по 2, у четвёртого члена — числу сочетаний из m элементов по 3; вообще коэффициент (n+1)-ro члена есть число сочетаний из m элементов по n. Наконец, коэффициент последнего члена равен числу сочетаний из т элементов по m, т. е. 1.

Заметим, что эти коэффициенты называются биномиальными.

4) Обозначая каждый член разложения буквой T с цифрой внизу, указывающей номер места этого члена в разложении, т. е. первый член T₁, второй член T₂ и т. д., мы можем написать:

Эта формула выражает общий член разложения, так как из неё мы можем получить все члены (кроме первого), подставляя на место n числа: 1, 2, 3,…. m.

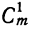
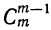
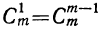
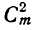
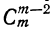
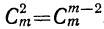
5) Коэффициент первого члена от начала разложения равен единице, коэффициент первого члена от конца тоже равен единице. Коэффициент второго члена от начала есть m, т. е. ; коэффициент второго члена от конца есть ; но так как , то эти коэффициенты одинаковы. Коэффициент третьего члена от начала есть , а третьего члена от конца есть ; но , поэтому и эти коэффициенты одинаковы и т. д. Значит:

Коэффициенты членов, одинаково удалённых от концов разложения, равны между собой.

6) Рассматривая биномиальные коэффициенты:

мы замечаем, что при переходе от одного коэффициента к следующему числители умножаются на числа, всё меньшие и меньшие (на m—1, на m — 2, на m — 3 и т. д.), а знаменатели умножаются на числа, всё большие и большие (на 2, на 3, на 4 и т. д.). Вследствие этого коэффициенты сначала возрастают (пока множители в числителе остаются большими соответственных множителей в знаменателе), а затем убывают. Так как коэффициенты членов, равно отстоящих от концов разложения, одинаковы, то наибольший коэффициент должен находиться посередине разложения. При этом, если число всех членов разложения нечётное (что бывает при чётном показателе бинома), то посередине будет один член с наибольшим коэффициентом; если же число всех членов чётное (что бывает при нечётном показателе бинома), то посередине должны быть два члена с одинаковыми наибольшими коэффициентами. Например:
(х+α)⁴=x⁴+4αx³+6α²x²+4α³x+α⁴;
(x+α)⁵=x⁵+5αx⁴+10α²x3+10α³x²+5α⁴x+α⁵∙

7) Из сравнения двух рядом стоящих членов:

заключаем, что:

Для получения коэффициента следующего члена достаточно умножить коэффициент предыдущего члена на показатель буквы х в этом члене и разделить на число членов, предшествующих определяемому.

Пользуясь этим свойством, можно сразу писать, например, (x+a)⁷=x⁷+7ax⁶+…

Теперь берём 7, умножаем его на 6 и делим на 2, получаем 21: (x+a)⁷=x⁷+7ax⁶+21a²x⁵+… .

Теперь берём 21, умножаем на 5 и делим на 3, получаем 35:
(x+a)⁷ =х⁷+7ax⁶+21a²x⁵+35a³x⁴+….

Теперь уже выписаны члены до середины ряда, остальные получим, основываясь на свойстве пятом:
(х+а)⁷ =х⁷-7αx⁶+21α²x⁵+35α³x⁴+35α⁴x³+21α⁵x²+7α⁶x+α⁷.

Сумма всех биномиальных коэффициентов равна . Действительно, положив в формуле бинома x=a=1, получим:

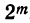
Например, сумма коэффициентов в разложении (х+a)⁷ равна
1+7+21+35+35 +21+7+1 = 128=2⁷.

9) Заменив в формуле бинома а на — а, получим:

т. е.

следовательно, знаки + и — чередуются.

10) Если в последнем равенстве положим x=α =1, то найдём:

Сумма биномиальных коэффициентов, стоящих на нечётных местах, равна сумме биномиальных коэффициентов, стоящих на чётных местах.

Применение формулы бинома к многочлену

Формула бинома Ньютона позволяет возвышать в степень многочлен. Так:
(α+ b+c)⁴ = [(а+b)+с]⁴= (a+b)⁴+4c (а+b)³+6c² (а+b)²+4c³ (a+b)+c⁴.

Разложив (a+b)⁴, (a+b)³, (а+b)², окончательно получим:
(a+b+с)⁴=a⁴+4a³b+ 6a²b²+ 4ab³+ b⁴ +4a³c+12a²bc+
+12ab²c+4b³c+6a²c²+12abc²+6b²c²+ 4ac³ + 4bc³+с⁴.

Вывод формулы бинома ньютона

Очевидно, что

Возникает вопрос, будет ли закономерность, наблюдаемая в этих формулах, обладать общностью, т. е. будет ли справедливой формула

при всяком натуральном значении n?

Воспользуемся методом полной индукции. Допустим, что формула верна для произвольно взятого натурального числа р, т. е. предположим справедливым следующее равенство:

Умножим обе части этого предполагаемого равенства на

Тогда получим:

Пользуясь формулой

и приняв во внимание, что

получим окончательно:

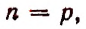
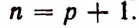
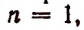
Из предположения, что формула верна при мы пришли к тому, что формула оказалась верной и при Но поскольку, кроме того, формула верна при то она должна быть верна и при любом натуральном значении n.

Теперь легко получить разложение и для

Действительно,

или

Последняя формула и называется формулой бинома Ньютона. Ее правая часть называется разложением степени бинома.

Числа называются биномиальными коэффициентами.

Свойства разложения бинома

В разложении бинома содержится членов на один больше, чем показатель степени бинома.

Все члены разложения имеют относительно букв а и b одно и то же измерение, равное показателю степени бинома. (Измерением одночлена относительно букв а и b называется сумма показателей степеней этих букв, входящих в этот одночлен.)

Поскольку все члены разложения имеют одинаковое измерение относительно букв а и b, то это разложение является однородным многочленом относительно букв а и b (см. стр. 450).

В разложении показатель степени буквы а последовательно понижается на единицу, начиная с показателя n, а показатель степени буквы b последовательно повышается на единицу, начиная с показателя, равного нулю.

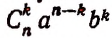
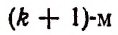
Член разложения является членом разложения и обозначается символом

Формула

называется формулой общего члена разложения, так как, давая букве k целые значения от 0 до n, мы можем получить из нее любой член разложения.

Теперь напишем разложение для выражения

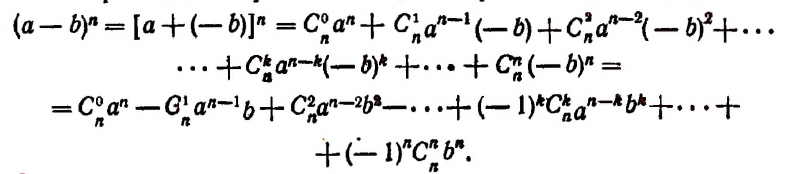
Здесь

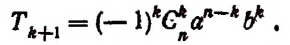
Свойства биномиальных коэффициентов

1. Биномиальные коэффициенты, равноудаленные от начала и конца разложения, равны между собой. Действительно, по первому свойству числа сочетаний имеем:

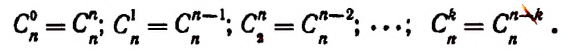
2. Сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома.

Доказательство:

Положим, в формуле бинома

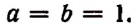
Тогда получим:

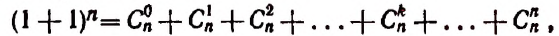
или

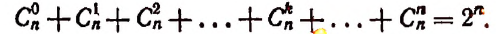
3. Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме, биномиальных коэффициентов, стоящих на нечетных местах.

Доказательство:

Полагая в тождестве

получим:

Перенеся все отрицательные члены в левую часть, получим:

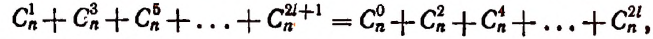
что и требовалось доказать.

Если вместо биномиальных коэффициентов подставить их значения, то формула бином Ньютона примет вид:

Формулу бинома Ньютона принято записывать ради краткости в следующем символическом виде:

или

Читателю может показаться непонятным, почему столь элементарная формула

где n — целое положительное число, носит имя великого ученого Ньютона, тем более что эта формула была известна до Ньютона. Например, ее знал Аль-Каши (XV век) и она встречается в трудах Паскаля. Объясняется это тем, что именно Ньютоном была обобщена эта формула для любого действительного показателя.

Ньютон впервые показал, что выражение

где и — любое действительное число, равняется сумме следующего сходящегося, ряда:

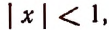
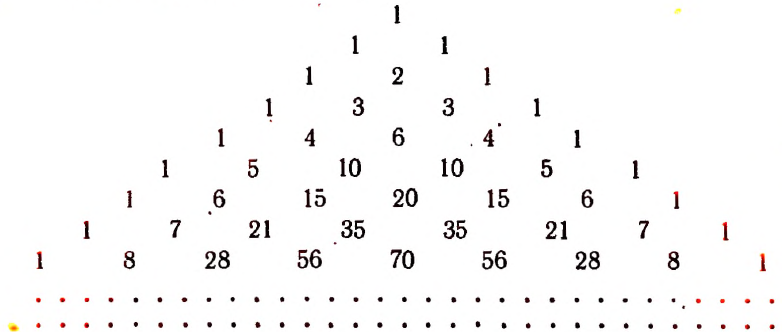
Например, если то

Арифметический треугольник, или треугольник паскаля

Написанная ниже таблица

называется треугольником Паскаля *.

По боковым сторонам этой таблицы стоят единицы, внутри же стоят числа, получающиеся сложением двух соответствующих чисел предыдущей строки. Например, число 21 в 8-й строке получается сложением стоящих над ним чисел 6 и 15.

строка этой таблицы дает биномиальные коэффициенты разложения n-й степени бинома. Например:

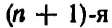
и так далее.

Треугольник Паскаля получается из следующей таблицы:

в силу того, что

(см. стр. 662).

Треугольник Паскаля приведен в книге Паскаля «Трактат об арифметическом треугольнике», изданной после его смерти в 1665 году.

Примеры с решением на Бином Ньютона

1. В разложении 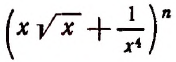коэффициент третьего члена на 44 больше коэффициента второго члена. Найти свободный член, т. е. член разложения, не зависящий от x (членом, не зависящим от х, будет тот, который содержит х в нулевой степени).

Решение:

Отсюда

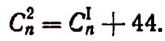
Приравняв показатель степени буквы х к нулю, получим:

Отсюда

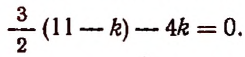
Искомым свободным членом будет четвертый, и он будет равен т. е. 165.

2. Сколько рациональных членов содержится в разложении

Решение:

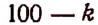
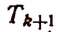
Для рациональности члена разложения необходимо, чтобы число k было кратно четырем. Но тогда будет числом четным и будет числом рациональным.

Число k может принимать целые значения 0, 1, 2….. 100. Среди этих чисел кратными четырем будут

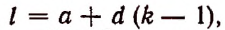
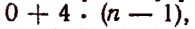
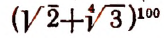
Пользуясь формулой получим: или Следовательно, в разложении рациональных членов будет 26.

3. Доказать, что значение выражения

где n — натуральное число, делится на 9.

Доказательство:

Каждое слагаемое последней суммы делится на 9, следовательно, и вся эта сумма, т. е. значение выражения 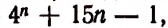делится на 9, что и требовалось доказать.

Дополнение к Бином Ньютону

Смотрите также:

Решение задач по финансовой математике

Решение заданий и задач по предметам:

Математика
Высшая математика
Математический анализ
Линейная алгебра

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Преобразование Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Источник

Квадратный трехчлен. Разложение квадратного трехчлена на множители

Квадратный трехчлен – это многочлен вида (ax^2+bx+c) ((a≠0)).

Почему его называют именно так? Потому что, наибольшая степень у него – квадрат, а состоит он из трех слагаемых ( одночленов ). Вот и получается – квадратный трехчлен.

Примеры не квадратных трехчленов:

(x^3-3x^2-5x+6) — кубический четырёхчлен
(2x+1) — линейный двучлен

Корень квадратного трехчлена:

Значение переменной (x), при котором квадратный трехчлен обращается в ноль, называют его корнем.

Пример:
У трехчлена (x^2-2x+1) корень (1), потому что (1^2-2·1+1=0)
У трехчлена (x^2+2x-3) корни (1) и (-3), потому что (1^2+2-3=0) и ((-3)^2-6-3=9-9=0)

Чтобы найти корни квадратного трехчлена нужно решить соответствующее квадратное уравнение.

Например: если нужно найти корни для квадратного трехчлена (x^2-2x+1), приравняем его к нулю и решим уравнение (x^2-2x+1=0).

Готово. Корень равен (1).

Разложение квадратного трёхчлена на множители:

Квадратный трехчлен (ax^2+bx+c) можно разложить как (a(x-x_1 )(x-x_2)), если дискриминант уравнения (ax^2+bx+c=0) больше нуля (x_1) и (x_2) — корни того же уравнения).

Например, рассмотрим трехчлен (3x^2+13x-10).
У квадратного уравнения (3x^2+13x-10=0) дискриминант равен 289 (больше нуля), а корни равны (-5) и (frac<2><3>). Поэтому (3x^2+13x-10=3(x+5)(x-frac<2><3>)). В верности этого утверждения легко убедится – если мы раскроем скобки , то получим исходный трехчлен.

Квадратный трехчлен (ax^2+bx+c) можно представить как (a(x-x_1)^2), если дискриминант уравнения (ax^2+bx+c=0) равен нулю.

Например, рассмотрим трехчлен (x^2+6x+9).
У квадратного уравнения (x^2+6x+9=0) дискриминант равен (0), а единственный корень равен (-3). Значит, (x^2+6x+9=(x+3)^2) (здесь коэффициент (a=1), поэтому перед скобкой не пишется – незачем). Обратите внимание, что тоже самое преобразование можно сделать и по формулам сокращенного умножения .

Квадратный трехчлен (ax^2+bx+c) не раскладывается на множители, если дискриминант уравнения (ax^2+bx+c=0) меньше нуля.

Например, у трехчленов (x^2+x+4) и (-5x^2+2x-1) – дискриминант меньше нуля. Поэтому разложить их на множители невозможно.

Пример. Разложите на множители (2x^2-11x+12).
Решение:
Найдем корни квадратного уравнения (2x^2-11x+12=0)

Полученный ответ, может быть, записать по-другому: ((2x-3)(x-4)).

Пример. (Задание из ОГЭ) Квадратный трехчлен разложен на множители (5x^2+33x+40=5(x++ 5)(x-a)). Найдите (a).
Решение:
(5x^2+33x+40=0)
(D=33^2-4 cdot 5 cdot 40=1089-800=289=17^2)
(x_1=frac<-33-17><10>=-5)
(x_2=frac<-33+17><10>=-1,6)
(5x^2+33x+40=5(x+5)(x+1,6))
Ответ: (-1,6)

Разложение квадратного трёхчлена на множители

Как разложить на множители квадратный трёхчлен

Квадратный трёхчлен — это многочлен вида ax 2 + bx + c .

В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:

Левая часть этого уравнения является квадратным трёхчленом.

Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.

Полученные корни x₁ и x₂ следует подстáвить в следующее выражение, которое и станет разложением:

Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:

Где левая часть — исходный квадратный трёхчлен.

Пример 1. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:

В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:

Итак, x₁ = 6 , x₂ = 2 . Теперь воспользуемся формулой ax 2 + bx + c = a(x − x₁)(x − x₂). В левой части вместо выражения ax 2 + bx + c напишем свой квадратный трёхчлен x 2 − 8x + 12. А в правой части подставим имеющиеся у нас значения. В данном случае a = 1, x₁ = 6, x₂ = 2

Если a равно единице (как в данном примере), то решение можно записать покороче:

Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.

Раскроем скобки у правой части равенства, то есть в выражении (x − 6)(x − 2) . Если мы всё сделали правильно, то должен получиться квадратный трёхчлен x 2 − 8x + 12

Пример 2. Разложить на множители следующий квадратный трёхчлен:

Приравняем данный квадратный трёхчлен к нулю и решим уравнение:

Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:

Итак, x₁ = 4 , x₂ = 3 . Приравняем квадратный трехчлен 2x 2 − 14x + 24 к выражению a(x − x₁)(x − x₂) , где вместо переменных a , x₁ и x₂ подстáвим соответствующие значения. В данном случае a = 2

Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x 2 − 14x + 24

Как это работает

Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования.

Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:

Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:

Тогда приведённый квадратный трехчлен x 2 + bx + c можно разложить на множители следующим образом. Сначала выразим b из уравнения x₁ + x₂ = −b . Для этого можно умножить обе его части на −1

Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:

Теперь подставим выраженные переменные b и c в квадратный трёхчлен x 2 + bx + c

Раскроем скобки там где это можно:

В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:

Из первых скобок вынесем общий множитель x , из вторых скобок — общий множитель −x₂

Далее замечаем, что выражение ( x − x₁ ) является общим множителем. Вынесем его за скобки:

Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.

Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a

Вспоминаем, что если квадратное уравнение не является приведённым, то есть имеет вид ax 2 + bx + c = 0 , то теорема Виета принимает следующий вид:

Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax 2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a

Далее чтобы квадратный трёхчлен вида ax 2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства и

Для начала выразим b и c . В первом равенстве умножим обе части на a . Затем обе части получившегося равенства умножим на −1

Теперь из второго равенства выразим c . Для этого умножим обе его части на a

Теперь подставим выраженные переменные b и с в квадратный трёхчлен ax 2 + bx + c . Для наглядности каждое преобразование будем выполнять на новой строчке:

Здесь вместо переменных b и c были подставлены выражения −ax₁ − ax₂ и ax₁x₂ , которые мы ранее выразили из теоремы Виета. Теперь раскроем скобки там где это можно:

Теперь из первых скобок вынесем общий множитель ax , а из вторых — общий множитель −ax₂

Далее замечаем, что выражение x − x₁ тоже является общим множителем. Вынесем его за скобки:

Вторые скобки содержат общий множитель a . Вынесем его за скобки. Его можно расположить в самом начале выражения:

Отметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители. Действительно, если не найдены корни квадратного трёхчлена, то нéчего будет подставлять в выражение a(x − x₁)(x − x₂) вместо переменных x₁ и x₂ .

Если квадратный трёхчлен имеет только один корень, то этот корень одновременно подставляется в x₁ и x₂ . Например, квадратный трёхчлен x 2 + 4x + 4 имеет только один корень −2

Тогда значение −2 в процессе разложения на множители будет подставлено вместо x₁ и x₂ . А значение a в данном случае равно единице. Её можно не записывать, поскольку это ничего не даст:

Скобки внутри скобок можно раскрыть. Тогда получим следующее:

При этом если нужно получить короткий ответ, последнее выражение можно записать в виде (x + 2) 2 поскольку выражение (x + 2)(x + 2) это перемножение двух сомножителей, каждый из которых равен (x + 2)

Примеры разложений

Пример 1. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения. В левой части напишем квадратный трёхчлен 3x 2 − 2x − 1 , а в правой части — его разложение в виде a(x − x₁)(x − x₂) , где вместо a , x₁ и x₂ подстáвим соответствующие значения:

Во вторых скобках можно заменить вычитание сложением:

Пример 2. Разложить на множители следующий квадратный трёхчлен:

Упорядочим члены так, чтобы старший коэффициент располагался первым, средний — вторым, свободный член — третьим:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3

Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:

Пример 3. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Пример 4. Найдите значение k , при котором разложение на множители трёхчлена 3x 2 − 8x + k содержит множитель (x − 2)

Если разложение содержит множитель (x − 2) , то один из корней квадратного трёхчлена равен 2 . Пусть корень 2 это значение переменной x₁

Чтобы найти значение k , нужно знать чему равен второй корень. Для его определения воспользуемся теоремой Виета.

В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби , а произведение корней — дроби

Выразим из первого равенства переменную x₂ и сразу подстáвим найденное значение во второе равенство вместо x₂

Теперь из второго равенства выразим k . Так мы найдём его значение.

Пример 5. Разложить на множители следующий квадратный трёхчлен:

Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим . Если поменять местами сомножители, то получится . То есть коэффициент a станет равным

Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Задания для самостоятельного решения

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Как решать квадратные уравнения

О чем эта статья:

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, которое содержит переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.

А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Квадратные уравнения могут иметь два корня, один корень или не иметь корней.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:

если D 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.

Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.

Давайте-ка на примерах — вот у нас есть два уравнения:

x 2 — 2x + 6 = 0
x 2 — x — 1/4 = 0

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.

2x 2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.

Полные и неполные квадратные уравнения

В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.

Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.

Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.

Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Для самых любопытных объясняем откуда появились такие названия:

Если b = 0, то квадратное уравнение принимает вид ax 2 + 0x+c=0 и оно равносильно ax 2 + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax 2 + bx + 0 = 0, иначе его можно написать как ax 2 + bx = 0.
Если b = 0 и c = 0, то квадратное уравнение выглядит так ax 2 = 0.

Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax 2 + c = 0, при b = 0;
ax 2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax 2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.

Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x 2 = 0.

Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:

Как решить уравнение ax 2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:

перенесем c в правую часть: ax 2 = — c,
разделим обе части на a: x 2 = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.

Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:

не имеет корней при — c/а 0.

В двух словах

Пример 1. Найти решение уравнения 8x 2 + 5 = 0.

Перенесем свободный член в правую часть:

Разделим обе части на 8:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.

Как решить уравнение ax 2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0

Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.

Решить линейное уравнение:

0,5x = 0,125,
х = 0,125/0,5

Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена

Если x₁ и x₂ — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x₁) (x − x₂).

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b 2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

вычислить его значение дискриминанта по формуле D = b 2 −4ac;
если дискриминант отрицательный, зафиксировать, что действительных корней нет;
если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.

Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
Найдем корень

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x 2 = 0.

Произведем равносильные преобразования. Умножим обе части на −1

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x 2 — х = 0.

Преобразуем уравнение так, чтобы появились множители

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x 2 — 10 = 39.

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.

Найдем дискриминант по формуле

D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112

Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b 2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней:

2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>

Для удобства вычислений обозначим выражение n 2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n 2 — ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

вычислить D₁= n 2 — ac;
если D₁ 0, значит можно найти два действительных корня по формуле

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.

Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>

Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p>

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

источники:

Разложение квадратного трёхчлена на множители

http://skysmart.ru/articles/mathematic/kak-reshat-kvadratnye-uravneniya

Источник

Содержание:

Разложение многочленов на множители

Разложение многочленов на множители — операция, об-I ратная умножению многочленов. Как вы уже знаете, решая разные задачи, иногда умножают два или более чисел, а иногда — раскладывают данное число на множители. Подобные задачи возникают и при преобразовании целых алгебраических выражений. В этой главе вы узнаете о:

вынесении общего множителя за скобки;
способе группировки;
формулах сокращённого умножения;
применении разных способов разложения многочленов на множители.

Вынесение общего множителя за скобки

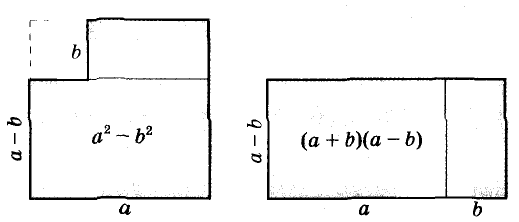
Вы уже умеете раскладывать на множители натуральные числа. Например,

На множители раскладывают и многочлены. Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену. Например, многочлен

Один из способов разложения многочленов на множители — вынесение общего множителя за скобки. Рассмотрим его.

Каждый член многочлена ах + ау имеет общий множитель а. На основании распределительного закона умножения 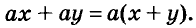Это означает, что данный многочлен ах + ау разложен на два множителя:

Другие примеры:

Чтобы убедиться, правильно ли разложен многочлен на множители, нужно выполнить умножение полученных множителей. Если всё верно, то в результате должен получиться данный многочлен.

Иногда приходится раскладывать на множители и выражения, имеющие общий многочленный множитель. Например, в выражении 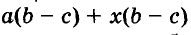общий множитель b — с. Его также можно выносить за скобки:

Один и тот же многочлен можно разложить на множители по-разному. Например,

Как правило, стараются вынести за скобки такой общий множитель, чтобы в скобках осталось простейшее выражение. Поэтому чаще всего в качестве коэффициента общего множителя берут наибольший общий делитель (НОД) коэффициентов всех членов данного многочлена или их модулей. Но не всегда. Все зависит от того, с какой целью раскладывают на множители многочлен.

Пусть, например, надо найти значение выражения 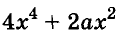при условии, когда

Чтобы использовать условие, это упражнение можно решить так:

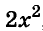
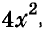
Здесь вынесено за скобки не , а тогда в скобках имеем выражение, значение которого известно из условия.

Пример:

Разложите на множители многочлен

Решение:

или

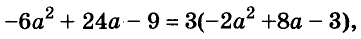
Пример:

Разложите на множители многочлен

Решение:

Пример:

Докажите, что число 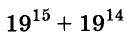делится на 20.

Доказательство:

Последнее произведение делится на 20, поэтому делится на 20 и данная сумма.

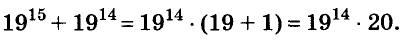
Пример:

Решите уравнение

Решение:

поэтому данное уравнение равносильно уравнению Произведение двух чисел равно нулю тогда, когда хотя бы одно из них равно нулю.

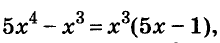
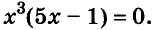
Значит, 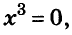отсюда х = 0, или 5х — 1 = 0, отсюда х = 0,2.

Ответ. Уравнение имеет два корня: 0 и 0,2.

Способ группировки

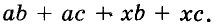
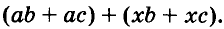
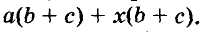
Разложим на множители многочлен Сгруппируем его члены так, чтобы слагаемые в каждой группе имели общий множитель Вынесем из первой группы за скобки общий множитель а, из второй — общий множитель х, получим выражение Слагаемые этого выражения имеют общий множитель b + с, вынесем его за скобки, получим выражение

Указанные преобразования можно записать цепочкой:

Такой способ разложения многочленов на множители называют способом группировки.

Замечание. Раскладывая на множители представленный выше многочлен, можно сгруппировать его члены иначе:

Получили такой же результат.

Разложим на множители многочлен

Записывать сумму а + с в виде 1 (а + с) необязательно, но сначала, чтобы не допускать ошибок, можно писать и так.

Чтобы воспользоваться способом группировки, иногда приходится один член данного многочлена представлять в виде суммы или разности одночленов. Чтобы разложить на множители трёхчлен 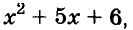• запишем одночлен

Подобные преобразования также можно выполнять, используя тождества.

Пример:

Разложите на множители многочлен:

Решение:

Ответ.

Пример:

Решите уравнение:

Решение:

Разложим левую часть уравнения на множители:

Корнем первого уравнения является у = 1,5, а второе уравнение корней не имеет, так как

Ответ. у = 1,5.

Квадрат двучлена

Решая различные задачи, часто приходится умножать двучлены вида 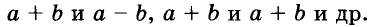Чтобы в таких случаях можно было сразу написать ответ, полезно запомнить тождества, которые называют формулами сокращённого умножения. Рассмотрим некоторые из них.

Умножим двучлен

Следовательно,

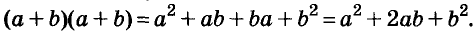
Квадрат двучлена равен квадрату первого его члена плюс удвоенное произведение первого на второй плюс квадрат второго члена.

Доказанное равенство — тождество, его называют формулой квадрата двучлена. Пользуясь ею, можно сразу записать:

Промежуточные преобразования желательно выполнять устно, тем самым сокращается запись:

По формуле квадрата двучлена можно возводить в квадрат любые двучлены, в том числе

Запомните формулу

Формулы квадрата двучлена используют и в «обратном направлении»:

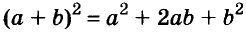
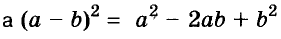
Формулу часто называют формулой квадрата суммы двух выражений, — квадрата разности двух выражений.

Для положительных чисел а и b формулу

можно доказать геометрически, как показано на рисунке 44. Так её доказывали ещё древние греки. Ведь площадь квадрата со стороной а + b равна сумме площадей квадратов а также прямоугольников ab и ab.

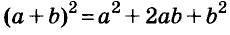
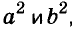
Существуют и другие формулы сокращённого умножения:

Пример:

Возведите в квадрат двучлен

Решение:

Пример:

Упростите выражение

Решение:

Пример:

Представьте в виде многочлена выражение:

Решение:

Пример:

Представьте выражение в виде степени двучлена:

Решение:

Заказать решение задач по высшей математике

Разность квадратов

Умножим сумму переменных а и b на их разность.

Значит,

Это равенство — тождество. Словами его читают так:

Произведение суммы двух выражений и их разности равно разности квадратов этих выражений.

Пользуясь доказанной формулой, можно сразу записать:

Левую и правую части доказанной формулы можно поменять местами. Получим формулу разности квадратов двух выражений:

Разность квадратов двух выражений равна произведению их суммы и разности.

Пример:

Формула разности квадратов очень удобна для разложения многочленов на множители.

Для положительных чисел а и b формулу 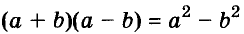можно проиллюстрировать геометрически (рис. 46). Но это тождество верно не только для положительных чисел, но и для любых других чисел и выражений.

Истинность формулы разности квадратов следует из правила умножения многочленов, а это правило — из законов действий сложения и умножения. Законы сложения и умножения чисел — это своеобразные аксиомы, следствиями которых являются алгебраические тождества.

Пример:

Напишите разность квадратов и квадрат разности выражений

Решение:

— разность квадратов; — квадрат разности данных выражений.

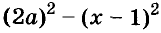
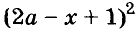
Пример:

Запишите в виде произведения двух двучленов выражение:

Решение:

Пример:

Представьте в виде двучлена выражение:

Решение:

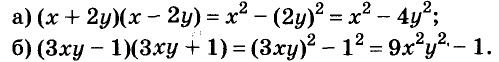
Используя формулу разности квадратов, промежуточные вычисления и преобразования можно выполнять устно, а записывать лишь конечный результат.

Использование формул сокращённого умножения

С помощью формул сокращённого умножения некоторые многочлены можно разложить на множители. Например, двучлен 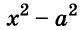можно представить в виде произведения по формуле разности квадратов:

Примеры:

Трёхчлены 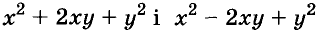раскладывают на множители по формуле квадрата двучлена:

Примеры:

Полученные, выражения можно разложить на множители и записать так:

Многочлен 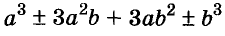можно разложить на множители по формуле куба двучлена:

Раскладывать на множители можно не только многочлены, но и некоторые другие целые выражения.

Например, 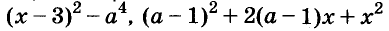— не многочлены, но и их можно представить в виде произведений многочленов:

Пример:

Разложите на множители многочлен:

Решение:

Пример:

Решите уравнение

Решение:

Значит, данное уравнение равносильно такому:

Квадрат числа равен нулю только тогда, когда это число равно 0. А х — 2 = 0, когда х = 2.

Ответ. х = 2.

Пример:

Разложите на множители многочлен:

Решение:

Разность и сумма кубов

Выполним умножение многочленов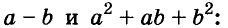

Следовательно, при любых значениях а и b

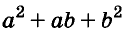
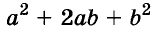
Трёхчлен называют неполным квадратом суммы выражений а и b (от он отличается только коэффициентом среднего члена). Поэтому доказанную формулу словами читают так:

разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Выполним умножение многочленов

Следовательно,

Трёхчлен 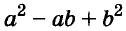называют неполным квадратом разности выражений а и b. Поэтому полученную формулу читаю так:

сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

С помощью доказанных формул можно раскладывать на множители многочлены, являющиеся разностями или суммами кубов.

Примеры:

Формулу «разность кубов» для положительных значений а и b можно проиллюстрировать геометрически, как показано на рисунке 49.

Если умножить на а — b выражения то получим формулы:

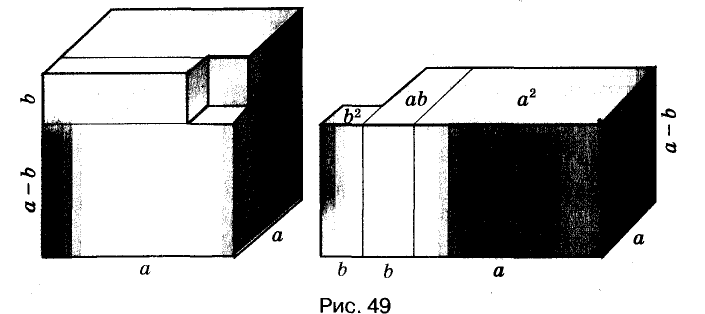
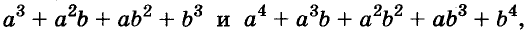
Можно доказать, что для каждого натурального значения n истинна формула:

Формулы «разность квадратов» и «разность кубов» — простейшие случаи этой общей формулы.

Пример:

Разложите на множители двучлен:

Решение:

Пример:

Найдите произведение многочленов: •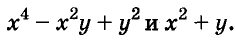

Решение:

Первый способ. По формуле суммы кубов:

Второй способ. По правилу умножения многочленов:

Применение разных способов разложения многочленов на множители

Чтобы разложить многочлен на множители, иногда приходится применять несколько способов.

Пример:

Разложите на множители многочлен

Решение:

Сначала за скобки вынесен общий множитель а, потом выражение в скобках разложено на множители по формуле разности квадратов.

Пример:

Разложите на множители выражение

Решение:

Здесь применены способ группировки, вынесение общего множителя за скобки и формула суммы кубов.

Чтобы разложить на множители более сложные многочлены, приходится применять несколько известных способов или искусственные приёмы.

В этом случае можно использовать такое правило-ориентир:

Вынести общий множитель (если он есть) за скобки.
Проверить, не является ли выражение в скобках разностью квадратов, разностью или суммой кубов.
Если это трёхчлен, то проверить, не является ли он квадратом двучлена.
Если многочлен содержит больше трёх членов, то надо попробовать группировать их и к каждой группе применить п. 1—3.

Иногда удаётся разложить многочлен на множители, прибавляя и вычитая из него одно и то же выражение.

Пример:

Разложите на множители двучлен

Решение:

Прибавим к данному двучлену выражение

Пример:

Разложите на множители выражение

Решение:

Пример:

Представьте многочлен 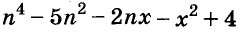в виде разности квадратов двух многочленов.

Решение:

Пример:

Докажите, что число 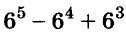делится на 31.

Доказательство:

Последнее произведение делится на 31, поэтому делится на 31 и равное ему данное числовое выражение.

Исторические сведения:

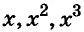
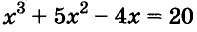
Наибольший вклад в развитие алгебраической символики внёс известный французский математик Ф. Виет, которого называли «отцом алгебры ». Он часто использовал буквенные обозначения. Вместо писал соответственно N,Q,C — первые буквы латинских слов Numerus (число), Quadratus (квадрат), Cubus (куб). Уравнение Ф. Виет записывал так:

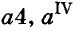
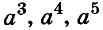
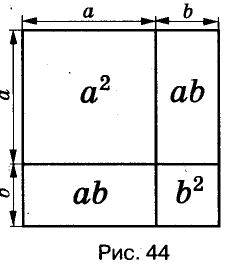
Степени чисел продолжительное время не имели специальных обозначений, четвёртую степень числа а записывали в виде произведения аааа. Позднее такое произведение начали записывать . Записи предложил Р. Декарт.

Формулы сокращённого умножения древним китайским и греческим математикам были известны за много веков до начала нашей эры. Записывали их тогда не с помощью букв, а словами и доказывали геометрически (только для положительных чисел). Пользуясь рисунком, объясняли, что для любых чисел а и b площадь квадрата со стороной а + b равна сумме площадей двух квадратов со сторонами а и b к двух прямоугольников со сторонами а, b. Итак, 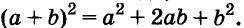Подобным способом обосновали и другие равенства, которые. мы теперь называем формулами сокращённого умножения.

В учебнике рассмотрены простейшие формулы сокращённого умножения.

Формулы квадрата и куба двучлена — простейшие случаи общей формулы бинома Ньютона:

Напомню:

Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену.

Простейшие способы разложения многочленов на множители:

вынесение общего множителя за скобки;
способ группировки;
использование формул сокращённого умножения.

Примеры:

Формулы сокращённого умножения

Разложение многочленов на множители — это преобразование, обратное умножению многочленов. Схематично эти две операции можно изобразить, например, так.

Системы линейных уравнений с двумя переменными
Рациональные выражения
Квадратные корни
Квадратные уравнения
Целые выражения
Одночлены
Многочлены
Формулы сокращенного умножения

Источник

На чтение 17 мин Просмотров 8.9к. Опубликовано 31.07.2020

Содержание

Биноминальное разложение с использованием треугольника Паскаля
Бином Ньютона с использованием треугольника Паскаля
Разложение бинома используя значения факториала
Бином Ньютона с использованием обозначение факториала
Нахождение определенного члена
Нахождение (k + 1) члена
Общее число подмножеств
Полное число подмножеств
Урок и презентация на тему: «Треугольник Паскаля. Бином Ньютона»
Бином Ньютона — формула
Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля
Доказательство формулы бинома Ньютона
Бином Ньютона — применение при решении примеров и задач

Биноминальное разложение с использованием треугольника Паскаля

Рассмотрим следующие выражения со степенями (a + b) n , где a + b есть любой бином, а n — целое число.

Каждое выражение — это полином. Во всех выражениях можно заметить особенности.

1. В каждом выражении на одно слагаемое больше, чем показатель степени n.

2. В каждом слагаемом сумма степеней равна n, т.е. степени, в которую возводится бином.

3. Степени начинаются со степени бинома n и уменьшаются к 0. Последний член не имеет множителя a. Первый член не имеет множителя b, т.е. степени b начинаются с 0 и увеличиваются до n.

4. Коэффициенты начинаются с 1 и увеличиваются на определенные значения до «половины пути», а потом уменьшаются на те же значения обратно к 1.

Давайте рассмотрим коэффициенты подробнее. Предположим, что мы хотим найти значение (a + b) 6 . Согласно особенности, которую мы только что заметили, здесь должно быть 7 членов
a 6 + c₁a 5 b + c₂a 4 b 2 + c₃a 3 b 3 + c₄a 2 b 4 + c₅ab 5 + b 6 .
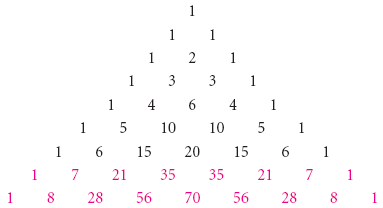
Но как мы можем определить значение каждого коэффициента, c_i? Мы можем сделать это двумя путями. Первый метод включает в себя написание коэффициентов треугольником, как показано ниже. Это известно как Треугольник Паскаля:

Есть много особенностей в треугольнике. Найдите столько, сколько сможете.
Возможно вы нашли путь, как записать следующую строку чисел, используя числа в строке выше. Единицы всегда расположены по сторонам. Каждое оставшееся число это сумма двух чисел, расположенных выше этого числа. Давайте попробуем отыскать значение выражения (a + b) 6 путем добавления следующей строки, используя особенности, которые мы нашли:

Мы видим, что в последней строке

первой и последнее числа 1;
второе число равно 1 + 5, или 6;
третье число это 5 + 10, или 15;
четвертое число это 10 + 10, или 20;
пятое число это 10 + 5, или 15; и
шестое число это 5 + 1, или 6.

Таким образом, выражение (a + b) 6 будет равно
(a + b) 6 = 1a 6 + 6a 5 b + 15a 4 b 2 + 20a 3 b 3 + 15a 2 b 4 + 6ab 5 + 1b 6 .

Для того, чтобы возвести в степень (a + b) 8 , мы дополняем две строки к треугольнику Паскаля:

Тогда
(a + b) 8 = a 8 + 8a 7 b + 28a 6 b 2 + 56a 5 b 3 + 70a 4 b 4 + 56a 3 b 5 + 28a 2 b 6 + 8ab 7 + b 8 .

Мы можем обобщить наши результаты следующим образом.

Бином Ньютона с использованием треугольника Паскаля

Для любого бинома a+ b и любого натурального числа n,
(a + b) n = ca n b 0 + c₁a n-1 b 1 + c₂a n-2 b 2 + . + c_n-1a 1 b n-1 + c_na 0 b n ,
где числа c, c₁, c₂. c_n-1, c_n взяты с (n + 1) ряда треугольника Паскаля.

Пример 1 Возведите в степень: (u — v) 5 .

Решение У нас есть (a + b) n , где a = u, b = -v, и n = 5. Мы используем 6-й ряд треугольника Паскаля:
1 5 10 10 5 1
Тогда у нас есть
(u — v) 5 = [u + (-v)] 5 = 1(u) 5 + 5(u) 4 (-v) 1 + 10(u) 3 (-v) 2 + 10(u) 2 (-v) 3 + 5(u)(-v) 4 + 1(-v) 5 = u 5 — 5u 4 v + 10u 3 v 2 — 10u 2 v 3 + 5uv 4 — v 5 .
Обратите внимание, что знаки членов колеблются между + и -. Когда степень -v есть нечетным числом, знак -.

Пример 2 Возведите в степень: (2t + 3/t) 4 .

Решение У нас есть (a + b) n , где a = 2t, b = 3/t, и n = 4. Мы используем 5-й ряд треугольника Паскаля:
1 4 6 4 1
Тогда мы имеем

Разложение бинома используя значения факториала

Предположим, что мы хотим найти значение (a + b) 11 . Недостаток в использовании треугольника Паскаля в том, что мы должны вычислить все предыдущие строки треугольника, чтобы получить необходимый ряд. Следующий метод позволяет избежать этого. Он также позволяет найти определенную строку — скажем, 8-ю строку — без вычисления всех других строк. Этот метод полезен в вычислениях, статистике и он использует биномиальное обозначение коэффициента .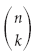
Мы можем сформулировать бином Ньютона следующим образом.

Бином Ньютона с использованием обозначение факториала

Для любого бинома (a + b) и любого натурального числа n,
.

Бином Ньютона может быть доказан методом математической индукции. Она показывает почему 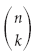называется биноминальным коэффициентом.

Пример 3 Возведите в степень: (x 2 — 2y) 5 .

Решение У нас есть (a + b) n , где a = x 2 , b = -2y, и n = 5. Тогда, используя бином Ньютона, мы имеем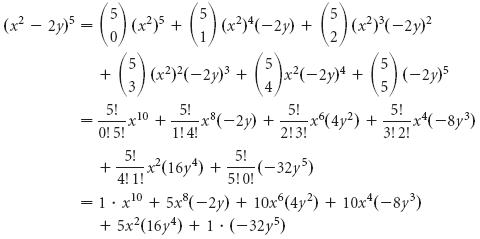

Наконец, (x 2 — 2y) 5 = x 10 — 10x 8 y + 40x 6 y 2 — 80x 4 y 3 + 80x 2 y 4 — 35y 5 .

Пример 4 Возведите в степень: (2/x + 3√ x ) 4 .

Решение У нас есть (a + b) n , где a = 2/x, b = 3√ x , и n = 4. Тогда, используя бином Ньютона, мы получим

Finally (2/x + 3√ x ) 4 = 16/x 4 + 96/x 5/2 + 216/x + 216x 1/2 + 81x 2 .

Нахождение определенного члена

Предположим, что мы хотим определить тот или иной член термин из выражения. Метод, который мы разработали, позволит нам найти этот член без вычисления всех строк треугольника Паскаля или всех предыдущих коэффициентов.

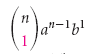
Обратите внимание, что в биноме Ньютона дает нам 1-й член, дает нам 2-й член, дает нам 3-й член и так далее. Это может быть обощено следующим образом.

Нахождение (k + 1) члена

(k + 1) член выражения (a + b) n есть .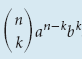

Пример 5 Найдите 5-й член в выражении (2x — 5y) 6 .

Решение Во-первых, отмечаем, что 5 = 4 + 1. Тогда k = 4, a = 2x, b = -5y, и n = 6. Тогда 5-й член выражения будет

Пример 6 Найдите 8-й член в выражении (3x — 2) 10 .

Решение Во-первых, отмечаем, что 8 = 7 + 1. Тогда k = 7, a = 3x, b = -2 и n = 10. Тогда 8-й член выражения будет

Общее число подмножеств

Предположим, что множество имеет n объектов. Число подмножеств, содержащих k элементов есть 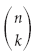. Общее число подмножеств множества есть число подмножеств с 0 элементами, а также число подмножеств с 1 элементом, а также число подмножеств с 2-мя элементами и так далее. Общее число подмножеств множества с n элементами есть
.
Теперь давайте рассмотрим возведение в степень (1 + 1) n :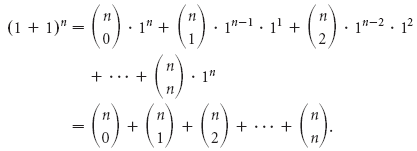
.
Так. общее количество подмножеств (1 + 1) n , или 2 n . Мы доказали следующее.

Полное число подмножеств

Полное число подмножеств множества с n элементами равно 2 n .

Пример 7 Сколько подмножеств имеет множество ?

Решение Множество имеет 5 элементов, тогда число подмножеств равно 2 5 , или 32.

Пример 8 Сеть ресторанов Венди предлагает следующую начинку для гамбургеров:
<кетчуп, горчица, майонез, помидоры, салат, лук, грибы, оливки, сыр>.
Сколько разных видов гамбургеров может предложить Венди, исключая размеры гамбургеров или их количество?

Решение Начинки на каждый гамбургер являются элементами подмножества множества всех возможных начинок, а пустое множество это просто гамбургер. Общее число возможных гамбургеров будет равно

. Таким образом, Венди может предложить 512 различных гамбургеров.

Урок и презентация на тему: «Треугольник Паскаля. Бином Ньютона»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

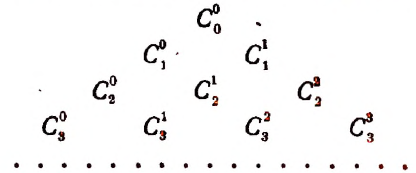
Ребята, на прошлом уроке мы с вами изучали перестановки и размещения. Сегодня мы остановимся на одном из самых замечательных применением формулы перестановок.
Числа $C_n^$ имеют очень красивую и знаменитую запись, которая имеет большое значение. Такая запись называется треугольником Паскаля:
Правило записи треугольника легко запомнить. Каждое число в треугольнике паскаля равно сумме двух чисел, стоящих над ними в предыдущей строке. Давайте распишем несколько строк:
Математически свойство подсчета числа сочетаний без повторений можно записать еще вот так:
Как оказалось треугольника Паскаля находит свое применение и в другой математической задаче. Давайте вспомним несколько правил возведения в квадрат суммы.
Самое первое правило, которое мы с вами выучили, это квадрат суммы: $(a+b)^2=a^2+2ab+b^2$.
Довольно таки легко найти выражение и для следующей степени, используя правила перемножения многочленов:
$(a+b)^3=(a^2+2ab+b^2)(a+b)=a^3+3a^2b+3ab^2+b^3$.
Проделаем эту же операцию и для четвертой степени:
$(a+b)^4=(a^3+3a^2b+3ab^2+b^3)(a+b)=a^4+4a^3b+6a^2b^2+4ab^3+b^4$.

Выпишем для наглядности все наши формулы:
$(a+b)^1=a+b$.
$(a+b)^2=a^2+2ab+b^2$.
$(a+b)^3=(a^2+2ab+b^2)(a+b)=a^3+3a^2b+3ab^2+b^3$.
$(a+b)^4=(a^3+3a^2b+3ab^2+b^3)(a+b)=a^4+4a^3b+6a^2b^2+4ab^3+b^4$.

Давайте проведем небольшой анализ полученных формул.

Обратить внимание: показатель степени в левой части равен сумме показателей степеней в правой части для любого слагаемого.

Для четвертой степени, очевидно, что слева показатель равен 4. В правой части показатель степени при первом слагаемом равен для а четырем, для b нулю и в сумме равен 4.

Для второго слагаемого сумма показателей равна $3+1=4$, для следующего — $2+2=4$ и так до самого конца сумма показателей равна 4.

Ребята, посмотрите внимательно на коэффициенты в правой части. Что он вам напоминает? Правильно, коэффициенты образуют треугольник Паскаля.

Эти два замечательных свойства, замеченных выше, позволяют вычислять сумму двух одночленов в n-ой степени:
$(a+b)^n=C_n^<0>a^n+C_n^<1>a^b+C_n^<2>a^b^2+C_n^<3>a^b^3+. +C_n^a^b^k+. +C_n^ab^+C_n^b^n$.

Давайте попробуем доказать нашу формулу:
Рассмотрим слагаемое, стоящее на месте под номером $k+1$. По написанной выше формуле получаем, вот такое слагаемое: $C_n^a^b^k$.
Нам нужно доказать, что коэффициент при данном одночлене как раз и равен $C_n^$.
Для того, чтобы двучлен возвести в n-ую степень нам нужно этот двучлен умножить на себя n раз, то есть:
Чтобы получить требуемое слагаемое надо выбрать k штук множителей для b. Тогда получается $n-k$ множителей для а. В каком порядке будем выбирать данные множители не важно. Эта задача есть ни что иное как: число сочетаний из n элементов по k без повторений или $C_n^$.
Наша формула доказана.

Полученная нами формула называется «Бином Ньютона».

Коэффициенты, стоящие перед слагаемыми, это биномиальные коэффициенты.

Пример.
Раскрыть скобки:
а) $(y+1)^7$; б) $(z^2-3t)^5$.
Решение.
Применим нашу формулу:
$а(y+1)^7=C_7^<0>y^7+C_7^<1>*y^6*1+C_7^<2>*y^5*1^2+C_7^<3>*y^4*1^3+C_7^<4>*y^3*1^4+$
$+C_7^<5>*y^2*1^5+C_7^<6>*y*1^6+C_7^<7>*1^7$.

Вычислим все коэффициенты:
$C_7^<0>=1$; $C_7^<1>=7$; $C_7^2=frac<7!><2!5!>=21$; $C_7^3=35$; $C_7^4=35$; $C_7^5=21$; $C_7^6=7$; $C_7^7=1$.

В итоге получаем: $(y+1)^7=y^7+7*y^6+21*y^5+35*y^4+35*y^3+21*y^2+7*y+1$.

В конце урока обратим вниманием на еще одно удивительное свойство.
Рассмотрим двучлен: $(x+1)^n$.
Используя Бином Ньютона получим:
При $х=1$ получаем: $(x+1)^n=C_n^<0>x^n+C_n^<1>x^+C_n^<2>x^+C_n^<3>x^+. +C_n^x^<2>+C_n^x+C_n^$.
При $х=1$ получаем: $2^n=C_n^<0>+C_n^<1>+C_n^<2>+C_n^<3>+. +C_n^+C_n^+C_n^$.

Бином Ньютона — формула

С натуральным n формула Бинома Ньютона принимает вид a + b n = C n 0 + a n + C n 1 + a n — 1 · b + C n 2 + a n — 2 · b 2 + . . . + C n n — 1 + a · b n — 1 + C n n · b n , где имеем, что C n k = ( n ) ! ( k ) ! · ( n — k ) ! = n ( n — 1 ) · ( n — 2 ) · . . . · ( n — ( k — 1 ) ) ( k ) ! — биномиальные коэффициенты, где есть n по k , k = 0 , 1 , 2 , … , n , а » ! » является знаком факториала.

В формуле сокращенного умножения a + b 2 = C 2 0 · a 2 + C 2 1 · a 1 · b + C 2 2 · b 2 = a 2 + 2 a b + b 2
просматривается формула бинома Ньютона, так как при n = 2 является его частным случаем.

Первая часть бинома называют разложением ( a + b ) n , а С n k · a n — k · b k — ( k + 1 ) -ым членом разложения, где k = 0 , 1 , 2 , … , n .

Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля

Представление биномиальных коэффициентов для различных n осуществляется при помощи таблицы, которая имеет название арифметического треугольника Паскаля. Общий вид таблицы:

Показатель степени	Биноминальные коэффициенты
	C 0 0
1	C 1 0	C 1 1
2	C 2 0	C 2 1	C 2 2
3	C 3 0	C 3 1	C 3 2	C 3 3
⋮	…	…	…	…	…	…	…	…	…
n	C n 0	C n 1	…	…	…	…	…	C n n — 1	C n n

При натуральных n такой треугольник Паскаля состоит из значений коэффициентов бинома:

Показатель степени	Биноминальные коэффициенты
	1
1	1	1
2	1	2	1
3	1	3	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1
⋮	…	…	…	…	…	…	…	…	…	…	…	…	…
n	C n 0	C n 1	…	…	…	…	…	…	…	…	…	C n n — 1	C n n

Боковые стороны треугольника имеют значение единиц. Внутри располагаются числа, которые получаются при сложении двух чисел соседних сторон. Значения, которые выделены красным, получают как сумму четверки, а синим – шестерки. Правило применимо для всех внутренних чисел, которые входят в состав треугольника. Свойства коэффициентов объясняются при помощи бинома Ньютона.

Доказательство формулы бинома Ньютона

Имеются равенства, которые справедливы для коэффициентов бинома Ньютона:

коэффициента располагаются равноудалено от начала и конца, причем равны, что видно по формуле C n p = C n n — p , где р = 0 , 1 , 2 , … , n ;
C n p = C n p + 1 = C n + 1 p + 1 ;
биномиальные коэффициенты в сумме дают 2 в степени показателя степени бинома, то есть C n 0 + C n 1 + C n 2 + . . . + C n n = 2 n ;
при четном расположении биноминальных коэффициентов их сумма равняется сумме биномиальных коэффициентов, расположенных в нечетных местах.

Равенство вида a + b n = C n 0 + a n + C n 1 + a n — 1 · b + C n 2 + a n — 2 · b 2 + . . . + C n n — 1 + a · b n — 1 + C n n · b n считается справедливым. Докажем его существование.

Для этого необходимо применить метод математической индукции.

Для доказательства необходимо выполнить несколько пунктов:

Проверка справедливости разложения при n = 3 . Имеем, что
a + b 3 = a + b a + b a + b = a 2 + a b + b a + b 2 a + b = = a 2 + 2 a b + b 2 a + b = a 3 + 2 a 2 b + a b 2 + a 2 b + 2 a b + b 3 = = a 3 + 3 a 2 b + 3 a b 2 + b 3 = C 3 0 a 3 + C 3 1 a 2 b + C 3 2 a b 2 + C 3 3 b 3
Если неравенство верно при n — 1 , тогда выражение вида a + b n — 1 = C n — 1 0 · a n — 1 · C n — 1 1 · a n — 2 · b · C n — 1 2 · a n — 3 · b 2 + . . . + C n — 1 n — 2 · a · b n — 2 + C n — 1 n — 1 · b n — 1

Доказательство равенства a + b n — 1 = C n — 1 0 · a n — 1 · C n — 1 1 · a n — 2 · b · C n — 1 2 · a n — 3 · b 2 + . . . + C n — 1 n — 2 · a · b n — 2 + C n — 1 n — 1 · b n — 1 , основываясь на 2 пункте.

Доказательство 1

a + b n = a + b a + b n — 1 = = ( a + b ) C n — 1 0 · a n — 1 · C n — 1 1 · a n — 2 · b · C n — 1 2 · a n — 3 · b 2 + . . . + C n — 1 n — 2 · a · b n — 2 + C n — 1 n — 1 · b n — 1

Необходимо раскрыть скобки, тогда получим a + b n = C n — 1 0 · a n + C n — 1 1 · a n — 1 · b + C n — 1 2 · a n — 2 · b 2 + . . . + C n — 1 n — 2 · a 2 · b n — 2 + + C n — 1 n — 1 · a · b n — 1 + C n — 1 0 · a n — 1 · b + C n — 1 1 · a n — 2 · b 2 + C n — 1 2 · a n — 3 · b 3 + . . . + C n — 1 n — 2 · a · b n — 1 + C n — 1 n — 1 · b n

Производим группировку слагаемых

a + b n = = C n — 1 0 · a n + C n — 1 1 + C n — 1 0 · a n — 1 · b + C n — 1 2 + C n — 1 1 · a n — 2 · b 2 + . . . + + C n — 1 n — 1 + C n — 1 n — 2 · a · b n — 1 + C n — 1 n — 1 · b n

Имеем, что C n — 1 0 = 1 и C n 0 = 1 , тогда C n — 1 0 = C n 0 . Если C n — 1 n — 1 = 1 и C n n = 1 , тогда C n — 1 n — 1 = C n n . При применении свойства сочетаний C n p + C n p + 1 = C n + 1 p + 1 , получаем выражение вида

C n — 1 1 + C n — 1 0 = C n 1 C n — 1 2 + C n — 1 1 = C n 2 ⋮ C n — 1 n — 1 + C n — 1 n — 2 = C n n — 1

Произведем подстановку в полученное равенство. Получим, что

a + b n = = C n — 1 0 · a n + C n — 1 1 + C n — 1 0 · a n — 1 · b + C n — 1 2 + C n — 1 1 · a n — 2 · b 2 + . . . + + C n — 1 n — 1 + C n — 1 n — 2 · a · b n — 1 = C n — 1 n — 1 · b n

После чего можно переходить к биному Ньютона, тогда a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . . + C n n — 1 · a · b n — 1 + C n n · b n .

Формула бинома доказана.

Бином Ньютона — применение при решении примеров и задач

Для полного понятия использования формулы рассмотрим примеры.

Разложить выражение ( a + b ) 5 , используя формулу бинома Ньютона.

Решение

По треугольнику Паскаля с пятой степенью видно, что биноминальные коэффициенты – это 1 , 5 , 10 , 10 , 5 , 1 . То есть, получаем, что a + b 5 = a 5 + 5 a 4 b + 10 a 3 b 2 + 10 a 2 b 3 + 5 a b 4 + b 5 является искомым разложением.

Ответ: a + b 5 = a 5 + 5 a 4 b + 10 a 3 b 2 + 10 a 2 b 3 + 5 a b 4 + b 5

Найти коэффициенты бинома Ньютона для шестого члена разложения выражения вида a + b 10 .

Решение

По условию имеем, что n = 10 , k = 6 — 1 = 5 . Тогда можно перейти к вычислению биномиального коэффициента:

C n k = C 10 5 = ( 10 ) ! ( 5 ) ! · 10 — 5 ! = ( 10 ) ! ( 5 ) ! · ( 5 ) ! = = 10 · 9 · 8 · 7 · 6 ( 5 ) ! = 10 · 9 · 8 · 7 · 6 1 · 2 · 3 · 4 · 5 = 252

Ответ: C n k = C 10 5 = 252

Ниже приведен пример, где используется бином для доказательства делимости выражения с заданным числом.

Доказать, что значение выражения 5 n + 28 · n — 1 , при n , являющимся натуральным числом, делится на 16 без остатка.

Решение

Необходимо представить выражение в виде 5 n = 4 + 1 n и воспользоваться биномом Ньютона. Тогда получим, что

5 n + 28 · n — 1 = 4 + 1 n + 28 · n — 1 = = C n 0 · 4 n + C n 1 · 4 n — 1 · 1 + . . . + C n n — 2 · 4 2 · 1 n — 2 + C n n — 1 · 4 · 1 n — 1 + C n n · 1 n + 28 · n — 1 = = 4 n + C n 1 · 4 n — 1 + . . . + C n n — 2 · 4 2 + n · 4 + 1 + 28 · n — 1 = = 4 n + C n 1 · 4 n — 1 + . . . + C n n — 2 · 4 2 + 32 · n = = 16 · ( 4 n — 2 + C n 1 · 4 n — 3 + . . . + C n n — 2 + 2 · n )

Ответ: Исходя из полученного выражения, видно, что исходное выражение делится на 16 .

Источник

Разложение функций в степенные ряды. Ряд Тейлора

Общая постановка задачи разложения функции в ряд в комплексной области формулируется так же, как и в действительной области. А именно, для заданной функции f(z) , определенной в области и удовлетворяющий в ней него которым дополнительным условиям, требуется найти ряд вида $sum_{n=1}^{infty}u_n(z)$ который бы сходился в области и его сумма в этой области совпадала с f(z) .

Постановка задачи разложения функции в степенной ряд

Для функции f(z) , аналитической в области , найти ряд $sum_{n=0}^{infty}c_n(z-z_0)^n$ , сходящийся к f(z) в круге |z-z_0|<R , принадлежащем области , то есть

$f(z)=sum_{n=0}^{infty}c_n(z-z_0)^n,quad |z-z_0|<R.$

(3.15)

Равенство (3.15) означает, что f(z) является суммой ряда в круге |z-z_0|<R .

Для решения задачи нужно, очевидно, найти коэффициенты ряда по заданной функции f(z) ; найти круг сходимости ряда и установить сходимость ряда именно к f(z) . Последнее, напомним, означает, что для точек круга выполняется неравенство |S_n(z)-f(z)|<varepsilon для любого varepsilon>0 и N(varepsilon,z) .

Все поставленные вопросы решаются с помощью следующей теоремы.

Теорема Тейлора о разложении функции в степенной ряд

Теорема 3.4. Функция, аналитическая в области , в окрестности каждой точки z_0 этой области представляется в виде степенного ряда (3.15), радиус сходимости которого не меньше, чем расстояние от точки z_0 до границы области . Коэффициенты ряда вычисляются по формуле

$c_n=frac{1}{2pi i}ointlimits_{gamma}frac{f(z)}{(z-z_0)^{n+1}},dz,quad n=0,1,2,ldots,$

(3.16)

где gamma — произвольный контур, принадлежащий области и охватывающий точку z_0 , в частности, gamma — окружность |z-z_0|=rho или по формуле

$c_n=frac{1}{n!}f^{(n)}(z_0),quad n=0,1,2,ldots$

(3.17)

На основании теоремы можно сформулировать алгоритм решения поставленной выше задачи и вывод — утверждение.

Алгоритм разложения аналитической функции в степенной ряд

1. Найти производные от данной функции: $f'(z),,f''(z),,ldots,,f^{(n)}(z),,ldots$ .

2. Вычислить значения производных в точке z_0; ; записать коэффициенты по формуле (3.17). Составить ряд по степеням z-z_0 с этими коэффициентами, который соответствует данной функции $f(z)sim sum_{n=0}^{infty}c_n(z-z_0)^n.$

3. Найти область сходимости полученного ряда и записать разложение (3.15).

Если функция не имеет конечных особых точек, то ряд сходится к ней во всей плоскости, R=infty .

Утверждение 3.3

1. Функция, аналитическая в точке z_0 , раскладывается в окрестности этой точки в степенной ряд.

2. На границе круга сходимости ряда есть хотя бы одна особая точка функции, т.е. радиус сходимости круга равен расстоянию от центра разложения z_0 до ближайшей особой точки функции.

3. Степенной ряд в круге сходимости является рядом Тейлора для своей суммы, т.е. коэффициенты ряда вычисляются по формулам (3.16), (3.17).

Примеры разложения функций по степеням z

Пример 3.13. Записать разложения по степеням функций $e^z,,sin z,,cos z,,operatorname{sh}z,,operatorname{ch}z$ .

Решение

Задачу решаем по вышеприведенному алгоритму.

1. Найдем производные:

$begin{aligned}&f_1(z)=e^z,quad f_1^{(n)}(z)=e^z;\[2pt] &f_2(z)=sin z,quad f_2^{(n)}(z)=sin!left(z+nfrac{pi}{2}right)!;\[2pt] &f_3(z)=cos z,quad f_3^{(n)}(z)=cos!left(z+nfrac{pi}{2}right)!;\[2pt] &f_4(z)=operatorname{sh}z,quad f_4^{(n)}(z)=begin{cases}operatorname{sh}z,&text{if}quad n=2k,\ operatorname{ch}z,&text{if}quad n=2k-1;end{cases}\[2pt] &f_5(z)=operatorname{ch}z,quad f_5^{(n)}(z)=begin{cases}operatorname{ch}z,&text{if}quad n=2k,\ operatorname{sh}z,&text{if}quad n=2k-1. end{cases}end{aligned}$

В поставленной задаче z_0=0 . По формуле (3.17) имеем

$begin{aligned}f_1(z)&=e^z,quad c_n=frac{1}{n!};qquad e^zsim sum_{n=0}^{infty} frac{z^n}{n!},;\[2pt] f_2(z)&=sin z,quad c_n=begin{cases}0,&n=2k;\ dfrac{(-1)^{k+1}}{(2k-1)!},&n=2k-1;end{cases} sin zsim sum_{n=1}^{infty}frac{(-1)^{n+1}}{(2n-1)!}z^{2n-1};\[2pt] f_3(z)&=cos z,quad c_n=begin{cases}0,&n=2k-1;\ dfrac{(-1)^k}{(2k)!},& n=2k;end{cases} cos zsim sum_{n=0}^{infty}frac{(-1)^n}{(2n)!}z^{2n};\[2pt] f_4(z)&=operatorname{sh}z,quad c_n= begin{cases}0,&n=2k;\ dfrac{1}{n!},&n=2k-1;end{cases} operatorname{sh}zsim sum_{n=1}^{infty}frac{z^{2n-1}}{(2n-1)!},;\[2pt] f_5(z)&=operatorname{ch}z,quad c_n=begin{cases}0,&n=2k-1;\ dfrac{1}{n!},&n=2k;end{cases} operatorname{ch}zsim sum_{n=1}^{infty}frac{z^{2n}}{(2n)!},.end{aligned}$

3. Нетрудно убедиться, что все составленные ряды сходятся во всей комплексной плоскости, R=infty . В результате получаем формулы, которые ранее были приняты за определения соответствующих функций:

$begin{gathered}e^z= sum_{n=0}^{infty} frac{z^n}{n!},;qquad sin z= sum_{n=1}^{infty}frac{(-1)^{n+1}}{(2n-1)!}z^{2n-1};qquad cos z= sum_{n=0}^{infty}frac{(-1)^n}{(2n)!}z^{2n};\ operatorname{sh}z= sum_{n=1}^{infty}frac{z^{2n-1}}{(2n-1)!},;qquad operatorname{ch}zsim sum_{n=1}^{infty}frac{z^{2n}}{(2n)!},. end{gathered}$

В результате получены так называемые основные разложения.

Пример 3.14. Записать разложения по степеням функций: а) $frac{1}{1-z}$ ; б) $frac{z^2}{z-1}$ .

Решение

Задачу можно решать, пользуясь алгоритмом, а можно использовать формулы (3.13) для суммы членов геометрической профессии. Заданные функции являются аналитическими во всей комплексной плоскости за исключением одной точки z=1 . Для каждого случая получаем:

$mathsf{a)}~frac{1}{1-z}=sum_{n=0}^{infty}z^n,quad |z|<1;$

$mathsf{b)}~frac{z^2}{z-1}=-z^2cdotfrac{1}{1-z}=-z^2cdotsum_{n=0}^{infty}z^n= -sum_{n=0}^{infty}z^{n+2},quad |z|<1;$ заметим, что здесь c_0=0,~c_1=0,~c_n=-1 для ngeqslant2 .

Пример 3.15. Записать разложения по степеням (z-z_0) функций: а) ln z,~z_0=1,~ln1=0 ; б) ln(1+z),~z_0=0,~ln1=0 .

Решение

Разложения записываются для однозначных ветвей многозначного выражения. Выбор ветви определяется заданием функции в точке z_0 .

a) Функция определена во всей комплексной плоскости за исключением z=0 , т.е. в двусвязной области 0<|z|<infty . Чтобы получить односвязную область из , проведем разрез, соединяющий точки z=0 и z=infty . Из условия ln1=0 следует, что точка z_0=1 должна быть внутренней точкой области. Поэтому выбираем разрез, не проходящий через z_0 . например по лучу (-infty;0] . В полученной односвязной области, где -pi<arg z<pi , функция ln z является однозначной аналитической функцией. Далее решаем задачу по алгоритму.

1. Находим производные (формулу устанавливаем по индукции):

$f'(z)=frac{1}{z},quad f''(z)=-frac{1}{z^2},quad f'''(z)=frac{2}{z^3},quad f^{(4)}(z)=frac{-2cdot3}{z^4},quad ldots,quad f^{(n)}(z)=(-1)^{n+1}frac{(n-1)!}{z^n},.$

2. По формуле (3.17):

$f^{(n)}(1)=(-1)^{n+1}(n-1)!,quad c_n=frac{(-1)^{n+1}}{n},~ n=1,2,ldots;qquad ln zsim sum_{n=1}^{infty}frac{(-1)^{n+1}(z-1)^n}{n},.$

3. Находим радиус сходимости ряда: $R=frac{1}{ell}$ , где $ell=lim_{ntoinfty} sqrt[LARGE{n}]{frac{1}{n}}=1,~ R=1$ . В результате получаем

$ln z=sum_{n=1}^{infty}frac{(-1)^{n+1}(z-1)^n}{n},quad |z-1|<1.$

б) Функция ln(1+z) определена всюду в mathbb{C} за исключением z=-1 , т.е. в двусвязной области. В односвязной области, полученной из путем разреза по лучу (-infty;-1] , функция является однозначной , аналитической. Задачу можно решать, как и выше, т.е. по алгоритму, а можно использовать полученный выше результат, введя обозначение 1+z=t . Для , удовлетворяющих неравенству |t-1|<1 имеем разложение $ln t=sum_{n=1}^{infty}frac{(-1)^{n+1}}{n}(t-1)^n$ . Заменяя на (1+z) , получаем результат

$ln(1+z)= sum_{n=1}^{infty}frac{(-1)^{n+1}}{n},z^n,quad |z|<1.$

Разложения основных функция в степенной ряд

Разложения, полученные в результате решения примеров 3.13-3.15, носят название основных (табличных) разложений. Выпишем их:

$begin{aligned} &bold{1)}~ e^z=sum_{n=0}^{infty}frac{z^n}{n!},; qquad bold{2)}~ sin z=sum_{n=1}^{infty}frac{(-1)^{n+1}z^{2n-1}}{(2n-1)!},; qquad bold{3)}~ cos z=sum_{n=0}^{infty}frac{(-1)^{n}z^{2n}}{(2n)!},; \[4pt] &bold{4)}~ operatorname{sh}z=sum_{n=1}^{infty}frac{z^{2n-1}}{(2n-1)!},; qquad bold{5)}~ operatorname{ch}z=sum_{n=0}^{infty}frac{z^{2n}}{(2n)!},;\[4pt] &bold{6)}~ frac{1}{1-z}=sum_{n=0}^{infty}z^n,~ |z|<1;qquad bold{7)}~ln(1+z)=sum_{n=1}^{infty}frac{(-1)^{n+1}}{n},z^n,~|z|<1. end{aligned}$

Основные разложения позволяют при решении примеров на разложение функции в ряд Тейлора не пользоваться сформулированным выше алгоритмом, сложность которого связана с техникой дифференцирования и составления формулы общего члена.

Утверждение 3.4. При разложении функции в ряд Тейлора используются основные (табличные) разложения и действия над рядами. Радиус сходимости ряда может быть получен по виду раскладываемой функции без использования формулы общего члена ряда и формул для нахождения радиуса. Радиус сходимости ряда, полученного при разложении данной функции в окрестности точки z_0 , равен расстоянию от центра разложения — точки z_0 до ближайшей особой точки функции. Если функция является аналитической всюду, то R=infty .

Пример 3.16. Разложить по степеням функции комплексного переменного:

$bold{1)}~operatorname{ch}3z;qquad bold{2)}~ e^{z+2};qquad bold{3)}~ sin^2z;qquad bold{4)}~ ln(3+z).$

Решение

а) Обозначим через и, используя табличное разложение для функции operatorname{ch}t , получим ответ:

$operatorname{ch}3z=operatorname{ch}t= sum_{n=0}^{infty} frac{t^{2n}}{(2n)!}$ , то есть $operatorname{ch}3z= sum_{n=0}^{infty} frac{9^nz^{2n}}{(2n)!},~~ R=infty.$ .

б) Запишем функцию в виде произведения e^2cdot e^z и, используя разложение для e^z , получим ответ:

$e^{z+2}= e^2cdot sum_{n=0}^{infty} frac{z^n}{n!}$ , то есть $e^{z+2}= sum_{n=0}^{infty} frac{e^2}{n!},z^n,~~ R=infty$ .

в) Чтобы воспользоваться одним из основных разложений, применим тригонометрическую формулу — формулу «понижения». Получим:

$sin^2z= frac{1-cos2z}{2}= frac{1}{2}-frac{1}{2}cos2z= frac{1}{2}-frac{1}{2} sum_{n=0}^{infty} frac{(2z)^{2n}(-1)^n}{(2n)!}= frac{1}{2}-frac{1}{2} sum_{n=0}^{infty} frac{2^{2n}(-1)^nz^{2n}}{(2n)!},.$

Заметим, что свободный член разложения в этой записи встречается дважды, поэтому нужно привести подобные члены. Для этого в записи рада отделим слагаемое при n=0 — свободный член:

$frac{1}{2}-frac{1}{2}-frac{1}{2} sum_{n=1}^{infty} frac{2^{2n}(-1)^nz^{2n}}{(2n)!},.$

В результате имеем $sin^2z= sum_{n=1}^{infty} frac{(-1)^{n+1}2^{2n-1}}{(2n)!},z^{2n},~ R=infty$ .

Из этого разложения можно найти значение производной любого порядка функции sin^2z в точке z_0=0 , так как эти значения связаны формулой (3.17) с коэффициентами разложения: $f^{(n)}(z_0)=c_ncdot n!$ . Поэтому, учитывая, что в разложении присутствуют только четные степени, заключаем, что все производные нечетных порядков от sin^2z в точке z_0=0 равны нулю, а производная, например, десятого порядка не равна нулю. Найдем ее, используя равенство $f^{(10)}(0)= c_{10}cdot10!$ , где $c_{10}$ — коэффициент в разложении f(z)=sin^2z при $z^{10}$ , т.е. в записанном выше разложении нужно взять n=5 . Получим

$c_{10}= frac{(-1)^6cdot2^9}{10!},qquad left.{bigl(sin^2z bigr)^{(10)}}right|_{z=0}= 2^9.$

г) Функция определена всюду, кроме z=-3 . В односвязной области, например в плоскости с разрезом по лучу (-infty;-3] , где -pi<arg z<pi , возможно выделение однозначных ветвей многозначного выражения operatorname{Ln}(z+3)= ln|z+3|+ ibigl(arg(z+3)+2kpibigr) (рис. 3.1). Выбираем ту ветвь, для которой f(0)=ln3 , то есть из operatorname{Ln}3= ln3+i(arg3+ 2kpi)=ln3 получаем k=0 . Разложим аналитическую функцию ln(z+3) по степеням в круге |z|<3 ; радиус круга R=3 — расстояние от центра разложения z_0=0 до граничной точки z=-3 .

3.1. Ветви комплексного логарифма

Чтобы воспользоваться основным разложением, преобразуем функцию следующим образом:

$ln(3+z)= ln left[3! left(1+frac{z}{3}right)right]= ln3+ln! left(1+ frac{z}{3}right)!.$

Тогда, обозначая $frac{z}{3}$ через и используя основное разложение для ln(1+t) , получаем $ln(3+z)=ln3+sum_{n=1}^{infty} frac{(-1)^{n+1}}{ncdot 3^n},z^n$ при условии $left|frac{z}{3}right|<1$ , т.е. в круге |z|<3 .

Пример 3.17. Разложить в окрестности точки z_0=0 ветвь функции ln(z^2-z-6) , для которой f(0)=ln6+ipi .

Решение

Функция ln(z^2-z-6)=lnbigl[(z+2)(z-3)bigr] определена всюду в mathbb{C} , кроме точек z_1=-2,~z_2=3 , т.е. в трехсвязной области — плоскости с выколотыми точками z_1 и z_2 . Чтобы получить односвязную область, проведем разрезы по лучам, выходящим из этих точек. Например, луч из точки z_1=-2 выберем параллельным мнимой оси, {operatorname{Re}z=-2,~operatorname{Im}z geqslant0} , а луч из точки z_2=3 — по действительной оси: operatorname{Im}z=0,~ operatorname{Re}zgeqslant3 . В полученной односвязной области (рис. 3.2) каждая ветвь является аналитической функцией и раскладывается в ряд в круге |z|<2 ( R=2 — расстояние от z_0=0 до границы). Здесь ветвь задается условием:

f(0)=ln6+ipi , то есть из operatorname{Ln}(-6)=ln6+i(pi+2kpi)= ln6+ipi при k=0 .

3.2. Ветви комплексного логарифма в односвязной

Далее, чтобы использовать основное разложение, преобразуем функцию:

ln bigl[(z+2)(z-3)bigr]= ln bigl[(z+2)(-1)(3-z)bigr]= ln(z+2)+ln(-1)+ln(3-z).

Для числа ln(-1) в силу выбора ветви берем ln(-1)=ipi~(k=0) , а функции ln(z+2) и ln(3-z) раскладываем в ряды, как в предыдущем примере:

$begin{aligned}&ln(z+2)= ln2+ sum_{n=1}^{infty} frac{(-1)^{n+1}z^n}{2^ncdot n},quad |z|<2;\[2pt] &ln(3-z)= ln3+ ln! left(1-frac{z}{3}right)= ln3+sum_{n=1}^{infty} frac{(-1)^{n+1}}{ncdot3^n}(-z)^n= ln3-sum_{n=1}^{infty} frac{z^n}{ncdot3^n},quad |z|<3. end{aligned}$

В области |z|<2 , принадлежащей выбранной односвязной области, сходятся оба ряда. Используя свойство сложения рядов, получаем окончательный результат:

$ln(z^2-z-6)= ln6+ipi+sum_{n=1}^{infty}! left(frac{(-1)^{n+1}}{2^n}-frac{1}{3^n} right)!cdot frac{1}{n}cdot z^n,quad |z|<2$

При разложении функции в ряд в окрестности точки z_0ne0 , т.е. по степеням (z-z_0) , удобно использовать замену (z-z_0)=t и полученную после замены функцию раскладывать по степеням .

Пример 3.18. Разложить по степеням (z-2) функции: a) sin z ; б) e^z в) ln(1+z) .

Решение

а) Обозначим (z-2) через , и, используя тригонометрическую формулу для функции sin(2+t) , получим: sin(2+t)= sin2cdotcos t+cos2cdotsin t . Здесь sin2 и cos2 — постоянные величины, а для функций cos t и sin t используем основные разложения. В результате получим

$sin z=sin2cdot sum_{n=0}^{infty} frac{(-1)^n(z-2)^{2n}}{(2n)!}+ cos2cdot sum_{n=1}^{infty} frac{(-1)^{n+1}(z-2)^{2n-1}}{(2n-1)!},,$

то есть ряд вида $textstyle{sumlimits_{n=0}^{infty}c_n(z-2)^n}$ , где коэффициент c_n определяется следующим образом: $c_n=frac{(-1)^k}{k!}sin2$ для n=2k и $c_n=frac{(-1)^k}{k!}cos2$ для n=2k-1 .

б) Можно, как и выше, использовать вспомогательную переменную, а можно сделать то же самое, применив простое преобразование: $e^z=e^{z-2+2}=e^2cdot e^{z-2}$ . Здесь e^2 — постоянная величина, функция $e^{z-2}$ раскладывается в ряд как функция e^t по степеням . Получаем ответ:

$e^z=e^2cdot sum_{n=0}^{infty} frac{(z-2)^n}{n!}$ , или $e^z= sum_{n=0}^{infty} frac{e^2}{n!}(z-2)^n,~~ R=infty$ .

в) Обозначая (z-2) через , получаем функцию ln(t+3) . Разложение этой функции по степеням найдено в примере 3.16:

$ln(t+3)=ln3+ sum_{n=1}^{infty} frac{(-1)^{n+1}}{ncdot3^n},t^n,quad |t|<3.$

Возвращаясь к исходной переменной, получаем разложение исходной функции в круге |z-2|<3 (рис. 3.3):

$ln(1+z)=ln3+sum_{n=1}^{infty}frac{(-1)^{n+1}}{ncdot3^n}(z-2)^n,quad |z-2|<3.$

Круг на комплексной плоскости

Пример 3.19. Разложить по степеням функции: $f(z)=frac{1}{1-az};~~ f(z)=frac{1}{a-z};~~ f(z)=frac{1}{(1-z)^2}$ .

Решение

Данные функции являются простейшими рациональными (элементарными) дробями. Для их разложения используется формула суммы членов бесконечно убывающей геометрической прогрессии $frac{1}{1-q}= sum_{n=0}^{infty} q^n,~|q|<1$ . В первом случае формула используется непосредственно, при q=az , во втором — после преобразования $frac{1}{a-z}= frac{1}{a}cdot frac{1}{1-frac{z}{a}}$ получаем $q=frac{z}{a}$ . Разложение заданных функций имеет вид

$frac{1}{1-az}= sum_{n=0}^{infty}a^nz^n,quad |z|<frac{1}{|a|}=R;$

(3.18)

$frac{1}{a-z}= sum_{n=0}^{infty} frac{z^n}{a^{n+1}},quad |z|<|a|=R.$

(3.19)

Соотношения (3.18),(3.19) обобщают формулу $frac{1}{1-z}= sum_{n=0}^{infty}z^n,~ |z|<1$ , которая получается из них при a=1 .

При разложении дроби $frac{1}{(1-z)^2}$ замечаем, что она является производной от $frac{1}{1-z}$ , то есть $left(frac{1}{1-z}right)'=frac{1}{(1-z)^2}$ , поэтому ее разложение можно получить, используя дифференцирование ряда:

$begin{gathered}frac{1}{1-z}= sum_{n=0}^{infty}z^n,quad |z|<1,\[2pt] frac{1}{(1-z)^2}= left(frac{1}{1-z}right)'= sum_{n=0}^{infty}(z^n)'= sum_{n=0}^{infty}nz^{n-1},quad |z|<1. end{gathered}$

Ответ удобнее записать в виде $frac{1}{(1-z)^2}= sum_{n=0}^{infty}(n+1)z^n,~|z|<1$ .

Очевидно, повторяя процедуру дифференцирования, можно получить разложение элементарных дробей вида $frac{1}{(a-z)^k}$ при любом натуральном .

Алгоритм разложения рациональных дробей в ряд Тейлора

Рассмотрим примеры на разложение в ряд Тейлора рациональных дробей

$R(z)= frac{P_m(z)}{Q_n(z)},,$

где P_m(z) и Q_n(z) — многочлены. Первые этапы решения задачи аналогичны этапам интегрирования этих дробей. Приведем полный алгоритм.

1. Если дробь неправильная (mgeqslant n) , следует выделить целую часть дроби многочлен.

2. Правильную рациональную дробь разложить на элементарные дроби:
а) записать дробь в виде суммы элементарных дробей вида $frac{A_k}{(z-a)^k}$ с неопределенными коэффициентами A_k , где — корень знаменателя, — его кратность;
б) найти неопределенные коэффициенты.

3. Разложить элементарные дроби в степенные ряды. Основными приемами при этом являются применение формул (3.13),(3.18),(3.19) и правила дифференцирования ряда (см. пример 3.19)).

При разложении по степеням (z-z_0),~z_0ne0 можно предварительно ввести вспомогательную переменную z-z_0=t .

Пример 3.20. Разложить по степеням функции: а) $frac{2z-1}{z+2}$ ; б) $frac{z^2-z+3}{z+2}$ .

Решение

а) Воспользуемся алгоритмом.

1. Дробь неправильная, поэтому выделяем целую часть: $frac{2z-1}{z+2}= frac{2(z+2)-5}{z+2}=2-frac{5}{z+2}$ .

2. Полученная правильная дробь является элементарной дробью.

3. Записываем разложение элементарной дроби и получаем:

$frac{2z-1}{z+2}= 2-5cdot frac{1}{2}cdot frac{1}{1-left(-frac{z}{2}right)}= 2-frac{5}{2} sum_{n=0}^{infty} frac{(-1)^nz^n}{2^n}= 2-5 sum_{n=0}^{infty} frac{(-1)^nz^n}{2^{n+1}},,quad |z|<2.$

Для разложения дроби $frac{1}{z+2}$ можно было использовать формулу (3.19) при a=-2 .

Для нахождения окончательного ответа нужно сделать преобразование приведения подобных членов, так как в полученном выражении свободный член встречается дважды. Имеем

$2-frac{5}{2}-5 sum_{n=1}^{infty} frac{(-1)^nz^n}{2^{n+1}}$ , то есть $frac{2z-1}{z+2}= 5 sum_{n=1}^{infty} frac{(-1)^{n+1}z^n}{2^{n+1}}-frac{1}{2},,~~|z|<2.$ .

б) Воспользуемся алгоритмом.

1. Дробь неправильная, выделяем целую часть. Можно, как и выше, применить преобразование дроби:

$frac{z^2-z+3}{z+2}= frac{(z+2)^2-5z-1}{z+2}= frac{(z+2)^2-5(z+2)+9}{z+2}= (z+2)-5+frac{9}{z+2}= z-3+frac{9}{z+2},.$

Можно для выделения целой части применить метод деления «углом», или, обозначая i + 2 = t, произвести почленное деление на одночлен (z=t-2)colon

$frac{z^2-z+3}{z+2}= frac{(t-2)^2+(t-2)+3}{t}= frac{t^2-5t+4}{t}= t-5+frac{9}{t}= z-3+frac{9}{z+2},.$

2,3. Записываем разложение заданной функции, используя формулу (3.19) для правильной дроби:

$frac{z^2-z+3}{z+2}= z-3+frac{9}{2} sum_{n=0}^{infty} frac{(-1)^nz^n}{2^n}= z-3+frac{9}{2}-frac{9}{4}z+frac{9}{2} sum_{n=2}^{infty} frac{(-1)^nz^t}{2^n},.$

Окончательный ответ: $frac{z^2-z+3}{z+2}= frac{3}{2}-frac{5}{4}z+9 sum_{n=2}^{infty}frac{(-1)^n}{2^{n+1}},z^n,~ |z|<2$ .

Получен ряд вида $sum_{n=0}^{infty}c_nz^n$ , где $c_0=frac{3}{2},~ c_1=-frac{5}{4},~ c_n=frac{9(-1)^n}{2^{n+1}}~(ngeqslant2)$ . Нетрудно проверить равенство: $c_0=f(0)=frac{3}{2}$ .

Пример 3.21. Функцию $frac{z+2}{z^2-2z-3}$ разложить в ряд Тейлора в окрестности точки z_0 , если а) z_0=0 ; б) z_0=1 .

Решение

а) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Раскладываем ее на элементарные дроби. Для этого представим дробь в виде

$frac{z+2}{(z+1)(z-3)}= frac{A}{z+1}+ frac{B}{z-3},,$

где и — неопределенные коэффициенты, которые находим из тождества

z+2=Acdot(z-3)+Bcdot(z+1).

Полагая последовательно z=-1 и z=3 , получаем $A=-frac{1}{4},~ B=frac{5}{4}$ .

Записываем дробь в виде суммы дробей: $frac{z+2}{(z+1)(z-3)}= -frac{1}{4}cdot frac{1}{z+1}+frac{5}{4}cdot frac{1}{z-3}$ .

3. Раскладываем по степеням г каждую элементарную дробь:

$begin{aligned}frac{1}{1+z}&= frac{1}{1-(-z)}= sum_{n=0}^{infty} (-z)^nz^n,quad |z|<1.\[2pt] frac{1}{z-3}&=-frac{1}{3}cdot frac{1}{1-frac{z}{3}}= -frac{1}{3} sum_{n=0}^{infty}! left(frac{z}{3}right)^n= — sum_{n=0}^{infty} frac{z^n}{3^{n+1}},,quad |z|<3.end{aligned}$

В общей области сходимости — круге |z|<1 — записываем сумму рядов разложение исходной дроби:

$frac{z+2}{z^2-2z-3}= -frac{1}{4} sum_{n=0}^{infty} (-1)^nz^n-frac{5}{4} sum_{n=0}^{infty} frac{z^n}{3^{n+1}}= sum_{n=0}^{infty} frac{z^n}{4}! left((-1)^{n+1}-frac{5}{3^{n+1}}right)!,quad |z|<1.$

б) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Разложение дроби на элементарные получено в предыдущем пункте:

$frac{z+2}{(z+1)(z-3)}= -frac{1}{4}cdot frac{1}{z+1}+frac{5}{4}cdot frac{1}{z-3},.$

3. Раскладываем по степеням (z-1) каждую элементарную дробь:

$begin{aligned}frac{1}{z+1}= frac{1}{z-1+2}= frac{1}{2}cdot frac{1}{1-left(-frac{z-1}{2}right)}= sum_{n=0}^{infty} frac{(-1)^n(z-1)^n}{2^{n+1}},quad |z-1|<2;\[2pt] frac{1}{z-3}= frac{1}{z-1-2}= -frac{1}{2}cdot frac{1}{1-frac{z-1}{2}}= -sum_{n=0}^{infty}frac{(z-1)^n}{2^{n+1}},quad |z-1|<2. end{aligned}$

Записываем разложение исходной дроби в круге |z-1|<2colon

$frac{z+2}{z^2-2z-3}= -frac{1}{4} sum_{n=0}^{infty}frac{(-1)^n(z-1)^n}{2^{n+1}}-frac{5}{4} sum_{n=0}^{infty} frac{(z-1)^n}{2^{n+1}}= sum_{n=0}^{infty} frac{(-1)^{n+1}-5}{2^{n+3}}(z-1)^n.$

При разложении по степеням, (z-1) можно было сделать замену z-1=t в исходной дроби.

Радиусы сходимости в обоих случаях можно определить заранее, до записи» разложения — по виду функции. Ее особыми точками являются точки z_1=-1 и z_2=3 . В первом случае ближайшей к точке z_0=0 является точка z_1 , расстояние между точками равно единице и, следовательно, R=1 ; во втором — обе особые точки удалены от z_0=1 на расстояние, равное двум, и R=2 .

Пример 3.22. Разложить по степеням функции (рациональные дроби): а) $f(z)=frac{2}{z^2-2z+2}$ ; б) $f(z)=frac{z+1}{(z-1)^2(z+2)}$ .

Решение

а) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Раскладываем правильную дробь на элементарные дроби, предварительно разложив знаменатель на множители:

z^2-2z+2=(z-z_1)(z-z_2) , где z_1=1-i и z_2=1+i .

Представим дробь в виде $frac{2}{z^2-2z+2}= frac{2}{(z-z_1)(z-z_2)}= frac{A}{z-z_1}+ frac{B}{z-z_2}$ . Находим коэффициенты и из тождества A(z-z_2)+B(z-z_1)=2 , т.е. из системы

$begin{cases}A+B=0,\Az_2+Bz_1=-2;end{cases}Leftrightarrow begin{cases} B=-A,\ A(z_2-z_1)=-2;end{cases} Leftrightarrow begin{cases}A=dfrac{2}{z_1-z_2}=i,\ B=-i. end{cases}$

Дробь представлена в виде суммы: $frac{2}{z^2-2z+2}= frac{i}{z-(1-i)}+frac{-i}{z-(1+i)}$ .

3. Раскладываем элементарные дроби по степеням

$begin{aligned}frac{1}{z-(1-i)}&= frac{-1}{1-i}cdot frac{1}{1-frac{z}{1-i}}= -frac{1}{1-i} sum_{n=0}^{infty} frac{z^n}{(1-i)^n},quad left|frac{z}{1-i}right|<1 ~Leftrightarrow~ |z|<sqrt{2},;\[2pt] frac{1}{z-(1+i)}&= frac{-1}{1+i}cdot frac{1}{1-frac{z}{1+i}}= -frac{1}{1+i} sum_{n=0}^{infty} frac{z^n}{(1+i)^n};quad left|frac{z}{1+i}right|<1~ Leftrightarrow~ |z|<sqrt{2},.end{aligned}$

Записываем ответ:

$begin{aligned}frac{2}{z^2-2z+2}&= frac{-i}{1-i} sum_{n=0}^{infty} frac{z^n}{(1-i)^n}+ frac{i}{1+i} sum_{n=0}^{infty} frac{z^n}{(1+i)^n}= frac{1-i}{2} sum_{n=0}^{infty} frac{z^n}{(1-i)^n}+ frac{1+i}{2} sum_{n=0}^{infty} frac{z^n}{(1+i)^n}=\ &= frac{1}{2} sum_{n=0}^{infty}! left(frac{1}{(1-i)^{n-1}}+ frac{1}{(1+i)^{n-1}}right)!z^n,quad |z|<sqrt{2},. end{aligned}$

б) Воспользуемся алгоритмом.
1,2. Раскладываем дробь на элементарные:

$frac{z+1}{(z-1)^2(z+2)}= frac{A}{z-1}+ frac{B}{(z-1)^2}+ frac{C}{z+2}$ , где A,,B,,C — неопределенные коэффициенты.

Находим коэффициенты из тождества A(z-1)(z+2)+B(z+2)+C(z-1)^2=z+1 .
Приравнивая коэффициенты при одинаковых степенях , имеем

$begin{cases}A+C=0,A+B-2C=1,\ -2A+2B+C=1;end{cases} Leftrightarrow~ begin{cases} A=1!!not{phantom{|}}, 9,\ B=2!!not{phantom{|}}, 3,\ C=-1!!not{phantom{|}}, 9.end{cases}$

3. Раскладываем элементарные дроби по степеням

$begin{aligned}frac{1}{z-1}&= -frac{1}{1-z}= -sum_{n=0}^{infty}z^n,quad |z|<1;\ frac{1}{(z-1)^2}&= -left(frac{1}{z-1}right)'= sum_{n=0}^{infty}(z^n)'= sum_{n=1}^{infty} (n+1)z^n,quad |z|<1;\ frac{1}{z+2}&= frac{1}{2} sum_{n=0}^{infty} frac{(-1)^nz^n}{2^n},quad |z|<2. end{aligned}$

Для исходной дроби получаем разложение:

$frac{z+1}{(z-1)^2(z+2)}= -frac{1}{9}cdot sum_{n=0}^{infty}z^n+ frac{2}{3}cdot sum_{n=0}^{infty} (n+1)z^n- frac{1}{9}cdot sum_{n=0}^{infty} frac{(-1)^nz^n}{2^{n+1}},,$

или, складывая ряды: $frac{z+1}{(z-1)^2(z+2)}= frac{1}{9} sum_{n=0}^{infty}! left( 6(n+1)-1+frac{(-1)^{n+1}}{2^{n+1}}right)!z^n$ .

Окончательный ответ: $frac{z+1}{(z-1)^2(z+2)}= frac{1}{9} sum_{n=0}^{infty}! left( 6n+5 +frac{(-1)^{n+1}}{2^{n+1}}right)!z^n,~ |z|<1$ .

Пример 3.23. Разложить по степеням функции: а) $frac{4}{4+z^2}$ ; б) $frac{z}{z^2-i}$ .

Решение

Обе дроби правильные; раскладывать на более простые нет необходимости. Используя основные разложения, получаем ответы:

а) $frac{4}{4+z^2}= frac{4}{4}cdot frac{1}{1-left(-frac{z^2}{4}right)}= sum_{n=0}^{infty} frac{(-1)^nz^{2n}}{4^n},~~ left|frac{z^2}{4}right|<1~ Leftrightarrow~ |z|<2$ ;

б) $frac{z}{z^2-i}= frac{z}{-i}cdot frac{1}{1-frac{z^2}{i}}= -sum_{n=0}^{infty} frac{z^{2n+1}}{i^{n+1}},~~ |z|<1$ или $frac{z}{z^2-i}= sum_{n=0}^{infty}(-1)^ni^{n+1} z^{2n+1},~~ |z|<1$ .

Пример 3.24. Используя разложение функции $e^{z^2+z}$ по степеням , найти значение производной седьмого порядка в точке z_0=0 .

Решение

Пример 3.25. Записать разложение функций a) $e^{sin z}$ и б) operatorname{tg}z по степеням до члена, содержащего z^5 .

Решение

а) Применим метод подстановки ряда в ряд, используя основные разложения для функций e^z и sin z . Имеем

$u=sin z,quad u(0)=0,quad u=z-frac{z^3}{3!}+ frac{z^5}{5!}+ldots;$

$e^u=1+u+ frac{1}{2!},u^2+ frac{1}{3!},u^3+ldots$ , или, подставляя:

$begin{gathered}e^{sin z}= 1+ left(z-frac{z^3}{3!}+ ldots right)+ frac{1}{2!}! left(z-frac{z^3}{3!}+ ldots right)^2+ frac{1}{3!}left(z-frac{z^3}{3!}+ ldots right)^3+ frac{1}{4!}! left(z-frac{z^3}{3!}+ ldots right)^4+ frac{1}{5!}! left(z-frac{z^3}{3!}+ ldots right)^5+ ldots=\ =1+z-frac{z^3}{3!}+ frac{z^5}{5!}+ frac{1}{2!}(z+a)^2+ frac{1}{3!}(z+a)^3+ frac{1}{4!}(z+a)^4+ frac{1}{5!}(z+a)^5+ldots, end{gathered}$

где $a=left(-frac{z^3}{3!}+frac{z^5}{5!}-ldotsright)$ . Записывать большее число слагаемых нет необходимости, так как уже у следующего (первого отброшенного) младшая степень равна z^6 .

Возведение в степень рядов, как и перемножение рядов, производится по правилам действий с многочленами, в частности применяется формула бинома Ньютона:

$(z+a)^n= z^n+nz^{n-1}a+ frac{n(n-1)}{2!},z^{n-2}a^2+ldots+a^n.$

Так как младшая степень выражения $a=left(-frac{z^3}{3!}+frac{z^5}{5!}-ldotsright)$ равна трем, следовательно, a^2 — шести, то для записи результата следует взять из первых двух скобок по два слагаемых, а из остальных по одному, т.е.

$e^{sin z}= 1+z-frac{z^3}{3!}+frac{z^5}{5!}+ frac{1}{2!}! left(z^2+2z! left( -frac{z^3}{3!}right)!right)+ frac{1}{3!}! left(z^3+3z^2! left(-frac{z^3}{3!}right)!right)+ frac{1}{4!}z^4+ frac{1}{5!}z^5+ldots$

Приводя подобные члены, получим окончательный ответ:

$e^{sin z}= 1+z+z^2cdot frac{1}{2}+ z^3! left(-frac{1}{3!}+frac{1}{3!}right)+ z^4! left(-2cdot frac{1}{2!}cdot frac{1}{3!}+ frac{1}{4!}right)+ z^5! left(frac{1}{5!}-3cdot frac{1}{3!}cdot frac{1}{3!}+ frac{1}{5!}right)+ldots$

или $e^{sin z}= 1+z+frac{1}{2!}z^2-frac{3}{4!}z^4-frac{1}{15}z^5+ldots$ .

Разложение, очевидно, можно получить, вычисляя коэффициенты разложения по формуле (3.17), что более громоздко.

б) Разложение operatorname{tg}z можно получить, используя формулу (3.17) для коэффициентов либо произведя деление ряда $sin z=z-frac{z^3}{3!}+ frac{z^5}{5!}-ldots$ на ряд $cos z=1-frac{z^2}{2!}+frac{z^4}{4!}-ldots$ методом деления «утлом» или методом неопределенных коэффициентов.

Применим последний прием. Разложение operatorname{tg}z по степеням ищем в виде

$operatorname{tg}z= frac{sin z}{cos z}=c_0+c_1cdot z+c_2cdot z^2+ldots$

По определению деления имеем тождество

$z-frac{z^3}{3!}+ frac{z^5}{5!}-ldots= left(1-frac{z^2}{2!}+ frac{z^4}{4!}- frac{z^6}{6!}+ldots right)! bigl(c_0+ c_1z+c_2z^2+c_3z^3+c_4z^4+c_5z^5+ldots bigr).$

Перемножаем ряды справа и приравниваем коэффициенты полученного ряда известным коэффициентам при соответствующих степенях ряда, записанного слева. Получаем систему уравнений

$c_0=0,quad c_1=1,quad c_2-frac{c_0}{2}=0,quad c_3-frac{c_1}{2}=-frac{1}{3!},quad c_4-frac{c_2}{2!} +frac{c_0}{4!}=0,quad c_5-frac{c_3}{2!}+ frac{c_1}{4!}= frac{1}{5!},,$

из которой находим коэффициенты $c_0=0,~ c_1=1,~ c_2=0,~ c_3=frac{1}{3},~ c_4=0,~ c_5= frac{2}{15}$ .

Ответ получаем в виде $operatorname{tg}z= z+frac{1}{3}z^3+frac{2}{15}z^5+ldots$ . Это разложение справедливо в круге $z<frac{pi}{2}$ , так как $z= frac{pi}{2}$ — ближайшая к z_0=0 особая точка функции тангенса .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Формула бинома Ньютона

Свойства формулы бинома Ньютона

Применение формулы бинома к многочлену

Вывод формулы бинома ньютона

Свойства разложения бинома

Свойства биномиальных коэффициентов

Арифметический треугольник, или треугольник паскаля

Примеры с решением на Бином Ньютона

Дополнение к Бином Ньютону

Квадратный трехчлен. Разложение квадратного трехчлена на множители

Квадратный трехчлен – это многочлен вида (ax^2+bx+c) ((a≠0)).

Корень квадратного трехчлена:

Значение переменной (x), при котором квадратный трехчлен обращается в ноль, называют его корнем.

Чтобы найти корни квадратного трехчлена нужно решить соответствующее квадратное уравнение.

Разложение квадратного трёхчлена на множители:

Квадратный трехчлен (ax^2+bx+c) можно разложить как (a(x-x_1 )(x-x_2)), если дискриминант уравнения (ax^2+bx+c=0) больше нуля (x_1) и (x_2) — корни того же уравнения).

Квадратный трехчлен (ax^2+bx+c) можно представить как (a(x-x_1)^2), если дискриминант уравнения (ax^2+bx+c=0) равен нулю.

Квадратный трехчлен (ax^2+bx+c) не раскладывается на множители, если дискриминант уравнения (ax^2+bx+c=0) меньше нуля.

Разложение квадратного трёхчлена на множители

Как разложить на множители квадратный трёхчлен

Как это работает

Примеры разложений

Задания для самостоятельного решения

Как решать квадратные уравнения

Понятие квадратного уравнения

Приведенные и неприведенные квадратные уравнения

Полные и неполные квадратные уравнения

Решение неполных квадратных уравнений

Как решить уравнение ax 2 = 0

Как решить уравнение ax 2 + с = 0

Как решить уравнение ax 2 + bx = 0

Как разложить квадратное уравнение

Дискриминант: формула корней квадратного уравнения

Алгоритм решения квадратных уравнений по формулам корней

Примеры решения квадратных уравнений

Формула корней для четных вторых коэффициентов

Формула Виета

Упрощаем вид квадратных уравнений

Связь между корнями и коэффициентами

Разложение многочленов на множители

Вынесение общего множителя за скобки

Способ группировки

Квадрат двучлена

Разность квадратов

Использование формул сокращённого умножения

Разность и сумма кубов

Применение разных способов разложения многочленов на множители

Биноминальное разложение с использованием треугольника Паскаля

Бином Ньютона с использованием треугольника Паскаля

Разложение бинома используя значения факториала

Бином Ньютона с использованием обозначение факториала

Нахождение определенного члена

Нахождение (k + 1) члена

Общее число подмножеств

Полное число подмножеств

Урок и презентация на тему: «Треугольник Паскаля. Бином Ньютона»

Бином Ньютона — формула

Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля

Доказательство формулы бинома Ньютона

Бином Ньютона — применение при решении примеров и задач

Разложение функций в степенные ряды. Ряд Тейлора

Постановка задачи разложения функции в степенной ряд

Теорема Тейлора о разложении функции в степенной ряд

Алгоритм разложения аналитической функции в степенной ряд

Примеры разложения функций по степеням z

Разложения основных функция в степенной ряд

Алгоритм разложения рациональных дробей в ряд Тейлора

Не пропустите также: