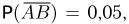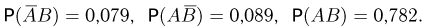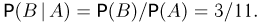Как найти условную вероятность формула - AvtoShod.ru

Лучшее спасибо — порекомендовать эту страницу

Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события $B$ при дополнительном условии, что произошло событие $А$.

Условной вероятностью $P_A(B)=P(B|A)$ (два обозначения) называют вероятность события $В$, вычисленную в предположении, что событие $А$ уже наступило.

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.

$$P(AB)=P(B)cdot P(A|B) = P(A) cdot P(B|A).$$

В частности, отсюда получаем формулы для условной вероятности:

$$P(A|B)=frac{P(AB)}{P(B)}, quad P(B|A)=frac{P(AB)}{P(A)}.$$

Примеры решений на условную вероятность

Пример. В урне находятся 3 белых шара и 2 черных. Из урны вынимается один шар, а затем второй. Событие В – появление белого шара при первом вынимании. Событие А – появление белого шара при втором вынимании.

Решение. Очевидно, что вероятность события А, если событие В произошло, будет
.
Вероятность события А при условии, что событие В не произошло, будет
.

Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).

Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность .

Этот же результат можно получить по формуле
.

Действительно, вероятность появления белого шара при первом испытании
.

Найдем вероятность того, что в первом испытании появится черный шар, а во втором — белый. Общее число исходов — совместного появления двух шаров, безразлично какого цвета, равно числу размещений . Из этого числа исходов событию благоприятствуют исходов. Следовательно, .

Искомая условная вероятность

Результаты совпали.

Пример. В трамвайном парке имеются 15 трамваев маршрута №1 и 10 трамваев маршрута №2. Какова вероятность того, что вторым по счету на линию выйдет трамвай маршрута №1?

Решение. Пусть А — событие, состоящее в том, что на линию вышел трамвай маршрута №1, В — маршрута №2.

Рассмотрим все события, которые могут при этом быть (в условиях нашей задачи): . Из них нас будут интересовать только первое и третье, когда вторым выйдет трамвай маршрута №1.

Так как все эти события совместны, то:

;

отсюда искомая вероятность

Пример. Какова вероятность того, что 2 карты, вынутые из колоды в 36 карт, окажутся одной масти?

Решение. Сначала подсчитаем вероятность того, что две карты окажутся одной определенной масти (например «пики»). Пусть А — появление первой карты такой масти, В — появление второй карты той же масти. Событие В зависит от события А, т.к. его вероятность меняется от того, произошло или нет событие А. Поэтому придется воспользоваться теоремой умножения в ее общей форме:

,
где (после вынимания первой карты осталось 35 карт, из них той же масти, что и первая — 8).

Получаем
.

События, состоящие в том, что будут вынуты две карты масти «пики», масти «треф» и т.д., несовместны друг с другом. Следовательно, для нахождения вероятности их объединения воспользуемся теоремой сложения:
.

Источник

Условная вероятность. Формула Байеса

Условная вероятность является одним из важнейших понятий теории вероятностей.

Условная вероятность — вероятность наступления события А при условии, что событие В произошло.

Вероятность события А, вычисленная в предположении, что событие В уже произошло, обозначается .

Прежде чем привести формулу, позволяющую вычислить условную вероятность, проиллюстрируем это понятие с помощью кругов Эйлера:

Пусть для некоторого эксперимента красный круг обозначает множество всех возможных исходов. Зеленый круг обозначает множество исходов, благоприятствующих событию , синий круг обозначает множество исходов, благоприятствующих событию , область, лежащая в пересечении этих кругов обозначает множество исходов, благоприятствующих обоим событиям и , обозначим его .

Как мы знаем, вероятностью события называется отношение числа благоприятных исходов к числу всех возможных исходов.

То есть вероятность события показывает, какую часть благоприятные исходы составляют от всех возможных исходов.

Если мы вычисляем вероятность события в предположении, что событие уже произошло (то есть условную вероятность), то в этом случае для нас множество исходов, благоприятствующих событию событию окажется множеством всех возможных исходов, а благоприятными исходами будут те исходы, которые при этом еще благоприятствуют событию . То есть нам нужно найти, какую часть число исходов, благоприятствующих событиям и составляет от числа исходов, благоприятствующих событию .

Пусть , где — число исходов, благоприятствующих событию , — число всех возможных исходов. ( В нашей иллюстрации — число элементов множества )

Пусть , где — число исходов, благоприятствующих событиям и , — число всех возможных исходов. ( В нашей иллюстрации — число элементов множества , которое является пересечением множеств и ).

Тогда

Но по определению условной вероятности , следовательно

(1)

Заметим, что аналогично получим формулу для нахождения вероятности наступления события при условии, что событие произошло:

(2)

Очевидно, что

Формулы (1) и (2) для нахождения условной вероятности по сути одна и та же формула, это и есть формула Байеса.

Рассмотрим примеры задач на условную вероятность.

Пример 1. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.

Решение.

В задаче описана следующая ситуация: при производстве посуды часть тарелок имеют дефект. Но контроль качества отбраковывает не все дефектные тарелки, а только 80% из них, остальные (20%) поступают в продажу.

Нам нужно найти вероятность того, что что случайно выбранная при покупке тарелка не имеет дефектов. То есть нас интересует какая часть из всех тарелок, которые поступили в продажу, не имеют дефекта.

Нарисуем дерево вероятностей:

Красными веточками обозначены тарелки, которые поступили в продажу. Это тарелки без дефектов (они составляют 0,9 от всех тарелок) и тарелки с дефектами, которые пропустила система контроля. Их от всех тарелок.

Таким образом, вероятность того, что тарелка поступила в продажу равна . При этом вероятность того, что тарелка не имеет дефектов равна .

Следовательно, вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов равна

Ответ: 0,98.

Пример 2.

40% пакетов с молоком производят на молочном комбинате в Л., а остальные на молокозаводе в С. Известно, что в среднем 3% пакетов, поступивших в продажу протекают, а среди пакетов, изготовленных в Л. протекают в среднем 5%.

а) Найдите вероятность того, что протекающий пакет изготовлен на заводе в С.

б) Найдите вероятность того, что пакет, изготовленный на заводе в С протекает.

Решение. Нам нужно найти вероятность того, что протекающий пакет изготовлен на заводе в С. То есть нам нужно найти, какая часть из всех протекающих пакетов изготовлена на заводе в С. По условию задачи всего протекает 3%, то есть 0,03 часть всех пакетов. Пусть среди пакетов, изготовленных на заводе в С. протекает %.

Нарисуем дерево вероятностей:

Красными веточками обозначены пакеты, которые протекают. При этом на заводе в Л. изготовлено всех протекающих пакетов. На заводе в С. изготовлено от всех протекающих пакетов.

Получаем , отсюда . То есть вероятность того, что пакет, изготовленный на заводе в С. протекает, равна . Получим, что на заводе в С. изготовлено от всех протекающих пакетов. Это число мы могли бы получить, если бы из части всех протекающих пакетов (0,03) вычли бы часть протекающих пакетов, изготовленных на заводе в Л. (0,02). (Мы бы так и поступили, если бы нужно было бы ответить только на п. а) задачи)

Тогда вероятность того, что протекающий пакет изготовлен на заводе в С. равна .

Ответ: а) , б) .

Источник

Полная вероятность и формула Байеса

Зависимые события и условные вероятности
Вероятность совместного появления событий
Формула полной вероятности
Формула Байеса
Примеры

п.1. Зависимые события и условные вероятности

Чтобы вспомнить о сложении и умножении вероятностей и независимых событиях – см. §39 справочника для 9 класса.

Напомним, что два случайных события A и B называют независимыми, если наступление одного из них не изменяет вероятность наступления другого.
Например: при бросании монеты несколько раз каждый следующий бросок совершенно не зависит от предыдущих.

Два случайных события A и B называют зависимыми, если вероятность одного из них зависит от того, произошло или нет другое событие.
Вероятность события B, определенная при условии, что событие A произошло, называется условной вероятностью и обозначается (P(B|A)) или (P_A(B)).
Для условных вероятностей справедливы формулы: $$ P(A|B)=frac{P(Awedge B)}{P(B)}, P(B|A)=frac{P(Awedge B)}{P(A)} $$ где (P(Awedge B)) — вероятность совместного появления событий A и B.

Например:
Рассмотрим урну, в которой находится 3 белых и 3 черных шара.
Мы достаем шары, смотрим на их цвет и не возвращаем их на место. События в последовательности становятся зависимыми.
Пусть событие A=»в 1й раз достаем черный шар»,
Событие B=»во 2й раз достаем белый шар»
Событие C=»во 2й раз достаем черный шар»
После того, как произошло событие A, в урне остается 3 белых и 2 черных шара.
Тогда условная вероятность для события B при условии, что событие A произошло:
(P(B|A)=frac35)
Аналогично, условная вероятность для события C:
(P(B|A)=frac25)

п.2. Вероятность совместного появления событий

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло: $$ P(Awedge B)=P(B)cdot P(A|B)=P(A)cdot P(B|A) $$ Это утверждение также называют теоремой умножения вероятностей.

Например:
Продолжая предыдущий пример, вероятность события ((Awedge B)) – 1й раз достали черный шар и 2й раз белый – равна: $$ P(Awedge B)=P(A)cdot P(B|A)=frac12cdot frac35=0,3 $$ Также, напомним:

Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий: $$ P(Awedge B)=P(A)cdot P(B) $$

Например:
Пусть в урне 3 белых и 3 черных шара. Мы достаем шары, смотрим на их цвет и возвращаем их на место. В последовательности наших действий все события будут независимыми. Каждый раз, вероятность достать белый или черный шар будет равна 1/2. Поэтому, в этом случае вероятность события ((Awedge B)) – 1й раз достали черный шар, а 2й раз белый – равна: $$ P(Awedge B)=P(A)cdot P(B)=frac12cdotfrac12=0,25 $$

п.3. Формула полной вероятности

Чтобы вспомнить о несовместных событиях и полной группе событий – см. §39 справочника для 9 класса.
Например:
При подбрасывании монеты события A=«получить орла» и B=«получить решку» — несовместные, т.к. одновременно произойти не могут.
В то же время, эти несовместные события A и B образуют пространство элементарных событий или полную группу (Omega=left{B;Bright}), т.к. ничего другого, кроме орла или решки, получить нельзя. Сумма вероятностей (P(A)+P(B)=frac12+frac12=1), как и положено для полной группы.

Если событие A может произойти только при выполнении одного из событий (B_1,B_2,…,B_k), которые образуют полную группу событий, то вероятность события A определяется по формуле полной вероятности: $$ P(A)=P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+…+P(B_k)P(A|B_k)=sum_{i=1}^k P(B_i)P(A|B_i) $$

Например:
В 11А и 11Б учится по 35 человек, а в 11В — 30 человек. Будем считать тех, у кого 4 и 5 баллов по алгебре и геометрии, «знатоками математики». Таких учеников в 11А — 10 человек, в 11Б — 7 человек, и в 11В — 3 человека.
Какова вероятность, что произвольно выбранный 11-классник окажется знатоком математики?
Пусть события A=«знаток математики», B_i=«ученик i-го класса», (i=overline{1,3})
Составим таблицу:

i	Класс	К-во учеников	(P(B_i))	К-во знатоков	(P(A\|B_i))	(P(B_i)cdot P(A\|B_i))
1	11A	35	35/100=0,35	10	10/35=2/7	0,1
2	11Б	35	35/100=0,35	7	7/35=1/5	0,07
3	11В	30	30/100=0,3	10	3/30=1/10	0,03
Всего	100	1	20	×	0,2

Получаем полную вероятность (P(A)=sum_{i=1}^3 P(B_i)cdot P(A|B_i)=0,2)
В данном случае ответ можно получить и проще: 20 знатоков на 100 человек дает (P(A)=0,2).

п.4. Формула Байеса

По данному выше определению полной вероятности событие A случается, если происходит одно из событий полной группы (left{B_iright}).
Допустим, что событие A случилось. А какова вероятность, что при этом произошло конкретное событие (B_1inleft{B_iright})? Т.е., нас интересует условная вероятность (P(B_1|A)).
По теореме об умножении вероятностей: $$ P(Awedge B_1)=P(B_1)cdot P(A|B_1)=P(A)cdot P(B_1|A) $$ Откуда: $$ P(B_1|A)=frac{P(B_1)cdot P(A|B_1)}{P(A)} $$ То же самое справедливо для любого события (B_pinleft{B_iright}). Предположение о том, что случилось событие (B_p), называют гипотезой.

Если событие A может произойти только при выполнении одного из событий полной группы (left{B_iright}) и событие A случилось, то вероятность гипотезы, что при этом случилось событие (B_pinleft{B_iright}), определяется формулой Байеса: $$ P(B_p|A)=frac{P(B_p)cdot P(A|B_p)}{P(A)}=frac{P(B_p)cdot P(A|B_p)}{sum_{i=1}^k P(B_i)P(A|B_i)} $$ Вероятность (P(B_p)) называют априорной вероятностью.
Вероятность (P(B_p|A)) называют апостериорной вероятностью. Случившееся событие A может поменять априорную (предварительную) оценку вероятности события (B_p).

Например:
Продолжим задачу с 11-классниками. Какова вероятность того, что произвольно взятый знаток математики учится в 11Б?
Наши события: A=«знаток математики», B₂=«ученик 11Б класса».
Событие A «случилось» — у нас имеется знаток, а событие B₂ — это гипотеза про 11Б.
И ответом на поставленный вопрос является вероятность (P(B_2|A)).
Из нашей таблицы: $$ P(B_2)cdot P(A|B_2)=0,07; P(A)=0,2 $$ Получаем: $$ P(B_2|A)=frac{P(B_2)cdot P(A|B_2)}{P(A)}=frac{0,07}{0,2}=0,35 $$ Т.е. 11Б дает 35% всех знатоков математики в этой школе.
Если сравнить апостериорную вероятность (P(B_2|A)=0,35) с априорной вероятностью (P(B_2)=0,35), они равны. Событие A не повлияло на оценку вклада 11Б в интеллектуальный багаж школы, он находится на среднем уровне.
Теперь найдем вероятность того, что произвольно взятый знаток математики учится в 11А: begin{gather*} P(B_1|A)=frac{P(B_1)cdot P(A|B_1)}{P(A)}=frac{0,1}{0,2}=0,5\ P(B_1|A)gt P(B_1) end{gather*} Вклад 11А по факту (апостериорная вероятность 0,5) оказывается большим, чем ожидалось по количеству учеников (априорная вероятность 0,35). 50% знатоков всей школы – из этого класса.
Наконец, найдем вероятность того, что произвольно взятый знаток математики учится в 11В: begin{gather*} P(B_3|A)=frac{P(B_3)cdot P(A|B_3)}{P(A)}=frac{0,03}{0,2}=0,15\ P(B_3|A)lt P(B_3) end{gather*} Вклад 11В по факту (апостериорная вероятность 0,15) оказывается меньшим, чем ожидалось по количеству учеников (априорная вероятность 0,3). Только 15% знатоков всей школы – из этого класса.

п.5. Примеры

Пример 1. Двигатель работает в трех режимах: нормальном (65% времени), форсированном (25% времени) и холостом. Вероятность поломки в каждом из режимов соответственно равна (p_1=0,1; p_2=0,8; p_3=0,05).
а) найдите вероятность поломки двигателя во время работы;
б) двигатель сломался. Какова вероятность, что он в этот момент работал в форсированном режиме?

а) Пусть событие A=«поломка двигателя», B_i — «работа в i-м режиме», (i=overline{1,3})
Необходимо найти полную вероятность (P(A)).
Составим таблицу:

i	Режим	Часть времени (P(B_i))	Вероятность поломки (P(A\|B_i))	(P(B_i)cdot P(A\|B_i))
1	Нормальный	0,65	0,1	0,065
2	Форсированный	0,25	0,8	0,2
3	Холостой	0,1	0,05	0,005
Всего	1	×	0,27

Вероятность поломки (полная вероятность): $$ P(A)=sum_{i=1}^3 P(B_i)cdot P(A|B_i)=0,27 $$
б) Событие A=«поломка двигателя» произошло. Гипотеза B₂ — «работа в форсированном режиме» при фактической поломке имеет вероятность: $$ P(B_2|A)=frac{P(B_2)cdot P(A|B_2)}{P(A)}=frac{0,2}{0,27}=frac{20}{27}approx 0,741 $$ Апостериорная вероятность (P(B_2|A)approx 0,741) больше априорной вероятности (P(B_2)=0,25).

Ответ: a) 0,27; б) (frac{20}{27}approx 0,741)

Пример 2. В состязании лучников участвуют три стрелка. Вероятность попадания в мишень для каждого из них равна 0,3; 0,5 и 0,7. Один из стрелков стреляет и не попадает. Какова вероятность, что это был:
а) первый стрелок;
б) второй стрелок;
в) третий стрелок;

Пусть событие A=«промах», B_i — «выстрел i-го стрелка», (i=overline{1,3})
Т.к. стрелять мог любой из стрелков (P(B_i)=frac13) для каждого из них.
Чтобы найти вероятность промаха, нужно от 1 отнять вероятность попадания.
Составим таблицу:

i	(P(B_i))	Вероятность промаха (P(A\|B_i))	(P(B_i)cdot P(A\|B_i))
1	(frac13)	1-0,3=0,7	(frac13cdot 0,7=frac{7}{30})
2	(frac13)	1-0,5=0,5	(frac13cdot 0,5=frac{1}{6})
3	(frac13)	1-0,7=0,3	(frac13cdot 0,3=frac{1}{10})
∑	1	×	0,5

Полная вероятность: $$ P(A)=sum_{i=1}^3 P(B_i)cdot P(A|B_i)=frac{7}{30}+frac16+frac{1}{10}=0,5 $$ Промах произошел. Находим апостериорные вероятности для каждого стрелка: begin{gather*} P(B_1|A)=frac{P(B_1)cdot P(A|B_1)}{P(A)}=frac{7/30}{0,5}=frac{7}{15}approx 0,467\ P(B_2|A)=frac{P(B_2)cdot P(A|B_2)}{P(A)}=frac{1/6}{0,5}=frac{2}{3}approx 0,333\ P(B_3|A)=frac{P(B_3)cdot P(A|B_3)}{P(A)}=frac{1/10}{0,5}=frac{1}{5}=0,2\ end{gather*} С точки зрения практической, можно сказать, что «вероятнее всего», это был первый стрелок.

Ответ: a) (frac{7}{15}); б) (frac{1}{3}); в) (frac{1}{5})

Пример 3. Три фрилансера на площадке выполняют заказы в отношении по количеству 3:4:3. Доля успешно выполненных заказов для каждого из них составляет 98%, 95% и 90%.
а) найдите вероятность успешного выполнения заказа на площадке;
б) найдите вероятность неуспеха на площадке;
в) кто из фрилансеров, вероятнее всего, виноват в неуспешной работе?

Пусть событие A=«успех», B_i — «работа i-го фрилансера», (i=overline{1,3})
Составим таблицу успешной деятельности:

i	(P(B_i))	Вероятность успеха (P(A\|B_i))	(P(B_i)cdot P(A\|B_i))
1	0,3	0,98	0,294
2	0,4	0,95	0,38
3	0,3	0,9	0,27
∑	1	×	0,944

Вероятность успешного выполнения (полная вероятность): $$ P(A)=sum_{i=1}^3 P(B_i)cdot P(A|B_i)=0,944 $$ б) Вероятность неуспеха (противоположное событие): $$ P(overline{A})=1-P(A)=1-0,944=0,056 $$ в) Составим таблицу неуспешной деятельности:

i	(P(B_i))	Вероятность неуспеха (P(overline{A}\|B_i))	(P(B_i)cdot P(overline{A}\|B_i))
1	0,3	1-0,98=0,02	0,006
2	0,4	1-0,95=0,05	0,02
3	0,3	1-0,9=0,1	0,03
∑	1	×	0,056

Апостериорные вероятности для каждого из фрилансеров: begin{gather*} P(B_1|overline{A})=frac{P(B_1)cdot P(overline{A}|B_1)}{P(overline{A})}=frac{0,006}{0,056}=frac{3}{28}approx 0,107\ P(B_2|overline{A})=frac{P(B_2)cdot P(overline{A}|B_2)}{P(overline{A})}=frac{0,02}{0,056}=frac{5}{14}approx 0,357\ P(B_3|overline{A})=frac{P(B_3)cdot P(overline{A}|B_3)}{P(overline{A})}=frac{0,03}{0,056}=frac{15}{28}approx 0,536 end{gather*} Наибольшая вероятность неуспеха – у третьего фрилансера.

Ответ: а) 0,944; б) 0,056; в) третий фрилансер.

Пример 4. Докажите, что если полная вероятность события A равна $$ P(A)=sum_{i=1}^k P(B_i)cdot P(A|B_i) $$ то вероятность противоположного события равна (P(overline{A})=1-P(A)).

По условию событие A происходит только при выполнении одного из событий полной группы (left{B_iright}. i=overline{i,k}). Соответственно, противоположное событие (overline{A}) также происходит при выполнении одного из событий (B_i). При этом условная вероятность для противоположного события: $$ P(overline{A}|B_i)=1-P(A|B_i) $$ Заметим также, что для полной группы сумма вероятностей равна 1: begin{gather*} sum_{i=1}^k P(B_i)=1 end{gather*} Получаем: begin{gather*} P(overline{A})=sum_{i=1}^k P(B_i)cdot P(overline{A}|B_i)=sum_{i=1}^k P(B_i)cdot (1-P(A|B_i))=\ =sum_{i=1}^k P(B_i)-sum_{i=1}^k P(B_i)cdot P(A|B_i)=1-P(A) end{gather*} Что и требовалось доказать.

Источник

Одним из основных понятий при аксиоматическом построении теории вероятностей является понятие условной вероятности. Именно условная вероятность оценивает то изменение в степени уверенности о наступлении некоторого события, которое происходит после получения дополнительной информации. С помощью условной вероятности определяется независимость событий, формализующая понятие не связанных между собой опытов. Использование условной вероятности в ряде случаев позволяет существенно упростить решение задачи (формулы умножения вероятностей, полной вероятности и Байеса).

Условная вероятность

Рассмотрим два события А и В. Пусть известно, что событие А наступило, но неизвестно, какой конкретно из элементарных исходов 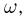составляющих событие А, произошел. Что можно сказать в этом случае о вероятности наступления события В?

Пример:

Событие А — выпадение четного числа очков на игральной кости, событие В — выпадение нечетного числа очков. Поскольку события А и В несовместны, то при наступлении события А событие В уже не может произойти и ему естественно приписать условную вероятность 0.

Пример:

Событие А — выпадение 4 или 6 очков на игральной кости, событие В — выпадение четного числа очков. Так как событие А принадлежит событию В, то при наступлении события А событие В обязательно произойдет, т.е. событие В имеет условную вероятность 1.

Пример:

Событие А — выпадение четного числа очков на игральной кости, событие В — выпадение не менее 5 очков. Если событие А наступило, то произошел один из трех элементарных исходов: выпало 2, 4 или 6 очков. Но из этих трех исходов только один исход (выпадение «шестерки») влечет за собой появление события В. В соответствии с принципом классической вероятности в данном случае естественно определить условную вероятность события В числом 1/3. Заметим, что в этом примере условная вероятность появления события В совпадает с безусловной.

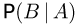
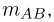
Из приведенных примеров видно, что условная вероятность может как совпадать с безусловной вероятностью, так и быть меньше или больше нее. Саму же условную вероятность события В при условии события А в рамках классической схемы естественно определить как отношение числа исходов благоприятных для

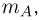
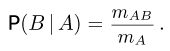
совместного осуществления событий А и В, к числу исходов благоприятных для события А т. е.

Поделим теперь числитель и знаменатель полученного выражения на общее число n элементарных исходов:

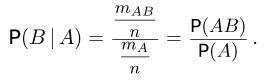
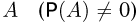
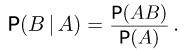
Последняя формула уже может служить общим определением условной вероятности при аксиоматическом подходе. Итак, условной вероятностью события В при условии события называется отношение вероятности пересечения событий А и В к вероятности события А:

Нетрудно видеть, что условная вероятность обладает всеми свойствами безусловной вероятности. Так,

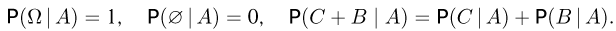
Иногда бывает полезным равенство

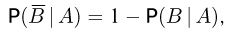
вытекающее из соотношения

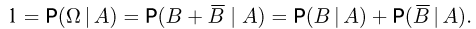
Пример:

При переписи населения Англии и Уэльса в 1891 г. оказалось, что темноволосые отцы и темноволосые сыновья составляют 5% обследованных, темноволосые отцы и светловолосые сыновья — 7,9%, светловолосые отцы и темноволосые сыновья — 8,9%, светловолосые отцы и светловолосые сыновья — 78,2%. Найдем условные вероятности рождения светловолосого сына у темноволосого и светловолосого отцов. Пусть событие А означает, что в случайно выбранной паре отец-сын светловолосым является отец, событие В — светловолосый сын. 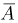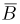Тогда событие — темноволосый отец, событие — темноволосый сын и из результатов переписи следует, что

Поэтому

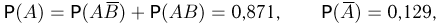
и условная вероятность у темноволосого отца родиться светловолосому сыну

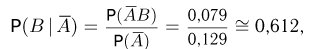
а у светловолосого

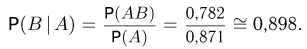
Пример:

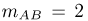
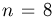
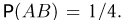
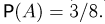
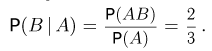
При трехкратном подбрасывании симметричной монеты выпало два «герба» (событие А). Определим условную вероятность того, что при втором подбрасывании выпал «герб» (событие В). В этом случае событие АВ состоит в выпадении двух «гербов», один из которых выпал при втором подбрасывании, т. е. содержит элементарных исходов: «герб»-«герб»-«цифра» и «цифра»-вгерб»-«герб». Поскольку всего у нас элементарных исходов и мы находимся в рамках классической схемы, то Аналогично, событию А благоприятствуют 3 исхода, и Итак, искомая вероятность

Пример:

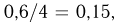
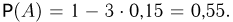
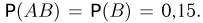
Электрон может быть с вероятностью 0,6 обнаружен на одной из четырех орбит атома, причем с равной вероятностью — на любой из них, и с дополнительной вероятностью 0,4 не обнаружен вообще. На первых трех орбитах электрон не обнаружен (событие /1). Найдем вероятность обнаружить его на четвертой орбите (событие В) при этом условии. Поскольку вероятность обнаружить электрон на каждой орбите равна то вероятность не обнаружить электрон на первых трех орбитах Событие АВ — электрон не обнаружен на первых трех орбитах и обнаружен на четвертой орбите — совпадает просто с событием В — электрон находится на четвертой орбите и имеет вероятность Искомая вероятность, равная условной вероятности события В при условии события А, в этом случае имеет вид

Условные вероятности

Смотрите также:

Предмет теория вероятностей и математическая статистика

Решение заданий и задач по предметам:

Теория вероятностей
Математическая статистика

Дополнительные лекции по теории вероятностей:

Случайные события и их вероятности
Случайные величины
Функции случайных величин
Числовые характеристики случайных величин
Законы больших чисел
Статистические оценки
Статистическая проверка гипотез
Статистическое исследование зависимостей
Теории игр
Вероятность события
Теорема умножения вероятностей
Формула полной вероятности
Теорема о повторении опытов
Нормальный закон распределения
Определение законов распределения случайных величин на основе опытных данных
Системы случайных величин
Нормальный закон распределения для системы случайных величин
Вероятностное пространство
Классическое определение вероятности
Геометрическая вероятность
Схема Бернулли
Многомерные случайные величины
Предельные теоремы теории вероятностей
Оценки неизвестных параметров
Генеральная совокупность

Источник

1. Условная вероятность. Независимые события.

Пусть
ислучайные события из алгебры событий.

Определение.
Вероятностью
события
при условии, что событиенаступило, или просто условной вероятностью
событияназывают выражение

(1)

Проиллюстрируем
это понятие в случае, когда пространство
элементарных событий
конечно. Пусть,
то естьесть число всевозможных исходов опыта.
Пустьk,
m
есть
количество исходов опыта при которых
наступают события
исоответственно (очевидно, что).
Тогдаи по определениюЭто соответствует классическому
определению вероятности для нового
опыта, в котором общее количество исходов
равно(в
стольких случаях наступает событие),
а число случаев, когда еще наступает
событие(то естьинаступают одновременно) равно.

Замечание.
Условная вероятность обладает всеми
свойствами обычной вероятности. Из
формулы (1) следует также, что

(2)

Пример.
Какова вероятность того, что вытащенная
кость домино окажется «дуплем», если
известно, что сумма очков на этой кости
является четным числом?

Решение.

Пусть
событие
состоит в том, что вытащенная кость есть
дупль, а событиесостоит в том, что сумма очков на ней
четна. Из 28 костей домино 16 имеют четную
сумму и на 7 дублях сумма очков четна.
Поэтому

Заметим,
что безусловная вероятность

Определение.
Случайные события
инезависимы, если наступление событияне изменит вероятности наступления
события:

(3)

Замечание.
Если случайные
события
инезависимы, то из формул (1), (2) следует
следующее правило умножения вероятностей:

(4)

В
дальнейшем независимость случайных
событий
ибудет пониматься, как выполнение
равенства (4).

Задача.
Доказать, что если
инезависимы, то независимы также событияи,и,и.

Пример.
Брошены монета и игральная кость. Найти
вероятность того, что выпадет «герб»
или «6».

Решение.

Пусть
иесть случайные события, состоящие в
падении герба и шестерки соответственно.
Пустьесть искомое случайное событие. Очевидно,
что

Появление
герба не влияет на появление шестерки.
Поэтому события
инезависимы и

По
формуле вероятности суммы событий

Замечание.
При решении многих задач на вероятность
мы будем следовать по такому же плану,
как в последнем примере.

Приведем
этот план:

Обозначить буквами
события, рассматриваемые в задаче.
С помощью введенных
обозначений выразить случайное событие,
вероятность которого требуется найти.
Выбрать необходимую
для решения формулу и выполнить
необходимые вычисления.

2. Формула полной вероятности и Байеса.

Пусть
—
пространство элементарных событий с
алгеброй случайных событий.

Определение.
Говорят, что случайные события
образуют полную группу событий, если
они попарно несовместны (то естьи

Такие
случайные события называют также
гипотезами. Заметим, что для полной
группы событий
из аксиом 2, 3 следует, что

Теорема.
Пусть
полная группа событий. Тогда

(5)

Доказательство.

Так
как
полная группа событий, то не трудно
доказать, что

При
этом события
как и событияпопарно несовместны. Из последнего
равенства, аксиомы 3 и формулы (2) следует
(5). Теорема доказана.

Формула
(5) называется формулой
полной вероятности.

Пример.
В первой урне находится три белых и
четыре черных шара, а во второй – пять
белых и два черных. Из первой урны во
вторую перекладывается один шар. Какова
вероятность того, что шар, вынутый наугад
из второй урны, окажется белым?

Решение.

Обозначим
искомое событие через
.
Состав второй урны зависит от того,
какой шар переложили из первой урны.

Обозначим
через
случайные события, состоящие в том, что
из первой урны переложен белый и черный
шары соответственно. Очевидно, чтоисоставляют полную группу событий. Найдем

Если
переложили белый шар (то есть верна
гипотеза
),
то во второй урне окажется 6 белых и 2
черных шара. Поэтому

Аналогично,

По
формуле полной вероятности

В
качестве следствия из формулы полной
вероятности выведем формулу Байеса,
которая в некотором смысле решает
обратную задачу. Пусть
полная группа событий. Допустим, что в
результате некоторого опыта наступило
случайное событие.
Требуется найти вероятности выполнения
гипотезто
есть вычислить