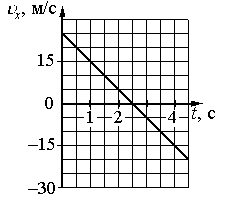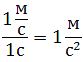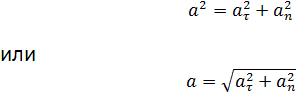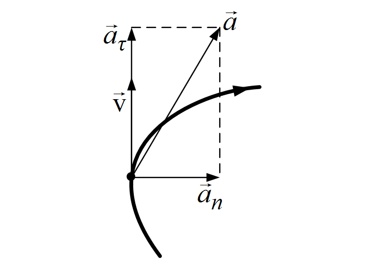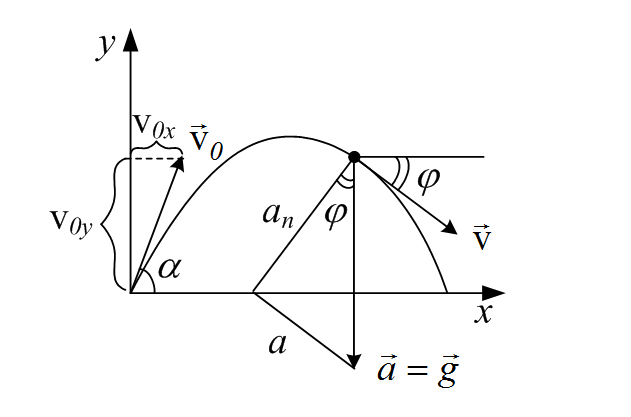Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.
Примеры равноускоренного движения:
- разгон самолета перед взлетом;
- падающая с крыши сосулька;
- торможение лыжника на горном склоне;
- разгоняющийся на склоне сноубордист;
- свободное падение в результате прыжка с парашютом;
- камень брошенный под углом к горизонту;
Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
Равноускоренное движение: формулы
Формула для скорости при равноускоренном движении:
Vк=Vн+at
где: Vк — конечная скорость тела,
Vн — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.
Формула для ускорения при равноускоренном движении:
a=(Vк-Vн)/t
Во время движения тела ускорение остается постоянным.
Задача 1
Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.
Формула расстояния при равноускоренном движении
- Если известны время, скорость начальная и скорость конечная
S = t*(Vн+ Vк)/2
- Если известны время, скорость начальная и ускорение
S = Vнt + at2/2 = t*(Vн + at/2)
где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.
В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:
2аS = Vк2−Vн2
где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.
Задача 2
Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.
Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
- Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
- Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.
Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.
Равноускоренное движение: графически
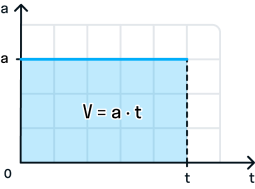
График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.
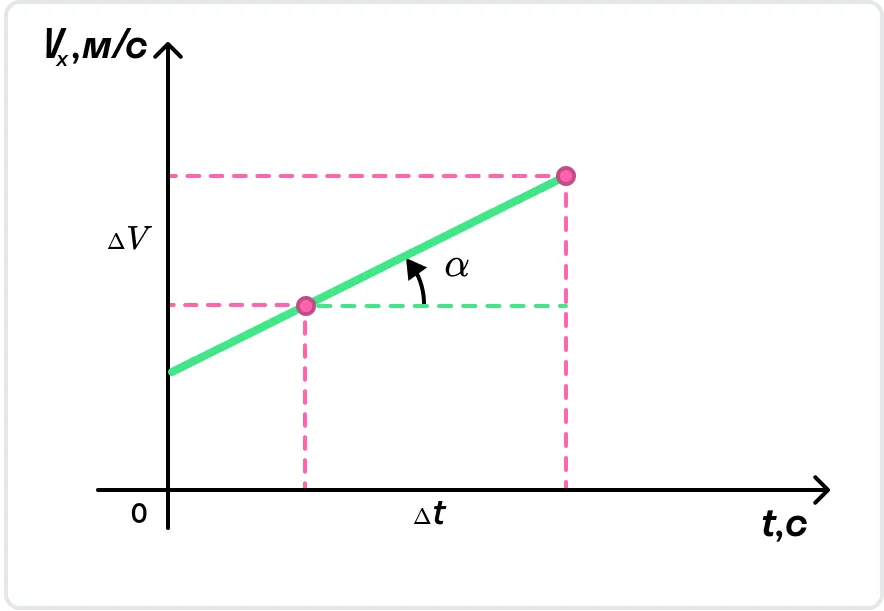
Взаимосвязь скорости, времени и расстояния:
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.
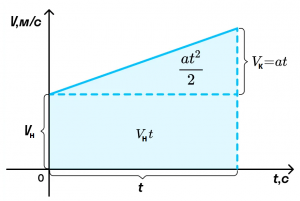
Из графика скорости получим формулу пути при равноускоренном движении тела.
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника Vнt и треугольника at2/2. Получим: S = Vнt + at2/2.
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Задача 3
Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.
Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.
Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = Vк2−Vн2
Получим: а = (Vк2−Vн2 )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = Vнt + at2/2.
Получаем: x(t) = 3t + 1,5t2
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*22 =6+6=12 м.
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.
Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:
- Конвертер единиц измерения расстояния (длины)
- Конвертер единиц измерения скорости
- Конвертер единиц измерения времени
- Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
- Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
- Единица измерения ускорения — метр в секунду в квадрате (м/с2).
- Акселерометр — прибор для измерения ускорения.
Формула ускорения
Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:
v — скорость тела в данный момент времени, v0 — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:
Проекция ускорения
Проекция ускорения на ось ОХ
vx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
- Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
- Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.
При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.
График ускорения
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.
Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
- Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
- Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.
Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.
В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
В момент времени t1 = 1с ускорение a = 2 м/с2. В момент времени t2 = 3 ускорение a = 0 м/с2.
Задание EF18774
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17992
Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?
Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
Ответ: 2,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18202
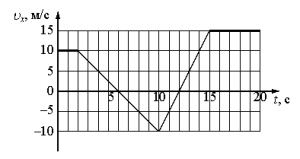
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?
Алгоритм решения
- Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
- Вычислить ускорение движение тела на этом участке.
- Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
- t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Используем для вычислений следующую формулу:
Подставим в нее известные данные и сделаем вычисления:
Этому значению соответствует график «г».
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18027
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.
Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.
Решение
Записываем формулу ускорения:
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:
Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:
Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.9k
Download Article
Download Article
If you’ve ever watched a bright red Ferrari fly ahead of your Honda Civic after a stoplight, you’ve experienced differing rates of acceleration firsthand. Acceleration is the rate of change in the velocity of an object as it moves. You can calculate this rate of acceleration, measured in meters per second, based on the time it takes you to go from one velocity to another, or based on the mass of an object.[1]
-
1
Define Newton’s Second Law of Motion. Newton’s second law of motion states that when the forces acting on an object are unbalanced, the object will accelerate. This acceleration is dependent upon the net forces that act upon the object and the object’s mass.[2]
Using this law, acceleration can be calculated when a known force is acting on an object of known mass.- Newton’s law can be represented by the equation Fnet = m x a, where Fnet is the total force acting on the object, m is the object’s mass, and a is the acceleration of the object.
- When using this equation, keep your units in the metric system. Use kilograms (kg) for mass, newtons (N) for force, and meters per second squared (m/s2) for acceleration.
-
2
Find the mass of your object. To find the mass of an object, simply place it on a balance or scale and find its mass in grams. If you have a very large object, you may need to find a reference that can provide you with the mass.[3]
Larger objects will likely have a mass with the unit of kilograms (kg).- For this equation, you will want to convert the mass into kilograms. If the mass you have is in grams simply divide that mass by 1000 to convert to kilograms.
Advertisement
-
3
Calculate the net force acting on your object. A net force is an unbalanced force. If you have two forces opposing each other and one is larger than the other, you will have a net force in the direction of the larger force.[4]
Acceleration happens when an unbalanced force acts on an object, causing it to change speeds towards the direction the force is pushing or pulling it.- For example: Let’s say you and your big brother are playing tug-of-war. You pull the rope to the left with a force of 5 newtons while your brother pulls the rope in the opposite direction with a force of 7 newtons. The net force on the rope is 2 newtons to the right, in the direction of your brother.
- In order to properly understand the units, know that 1 newton (N) is equal to 1 kilogram X meter/second squared (kg X m/s2).[5]
-
4
Rearrange the equation F = ma to solve for acceleration. You can change this formula around to solve for acceleration by dividing both sides by the mass, so: a = F/m.[6]
To find the acceleration, simply divide the force by the mass of the object being accelerated.- Force is directly proportional to the acceleration, meaning that a greater force will lead to a greater acceleration.
- Mass is inversely proportional to acceleration, meaning that with a greater mass, the acceleration will decrease.
-
5
Use the formula to solve for acceleration. Acceleration is equal to the net force acting on an object divided by the mass of the object. Once you’ve established the values for your variables, do the simple division to find the acceleration of the object.
- For example: A 10 Newton force acts uniformly on a mass of 2 kilograms. What is the object’s acceleration?
- a = F/m = 10/2 = 5 m/s2
Advertisement
-
1
Define the equation for average acceleration. You can calculate the average acceleration of an object over a period of time based on its velocity (its speed traveling in a specific direction), before and after that time. To do this you need to know equation for acceleration: a = Δv / Δt where a is acceleration, Δv is the change in velocity, and Δt is the amount of time it took for that change to occur.[7]
- The unit for acceleration is meters per second per second or m/s2.[8]
- Acceleration is a vector quantity, meaning it has both a magnitude and a direction.[9]
The magnitude is the total amount of acceleration whereas the direction is the way in which the object is moving. If it is slowing down the acceleration will be negative.
- The unit for acceleration is meters per second per second or m/s2.[8]
-
2
Understand the variables. You can further define Δv and Δt: Δv = vf — vi and Δt = tf — ti where vf is the final velocity, vi is the initial velocity, tf is the ending time, and ti is the starting time.[10]
- Because acceleration has a direction, it is important to always subtract the initial velocity from the final velocity. If you reverse them, the direction of your acceleration will be incorrect.
- Unless otherwise stated in the problem, the starting time is usually 0 seconds.
-
3
Use the formula to find acceleration. First write down your equation and all of the given variables. The equation is a = Δv / Δt = (vf — vi)/(tf — ti). Subtract the initial velocity from the final velocity, then divide the result by the time interval. The final result is your average acceleration over that time.
- If the final velocity is less than the initial velocity, acceleration will turn out to be a negative quantity or the rate at which an object slows down.
- Example 1: A race car accelerates uniformly from 18.5 m/s to 46.1 m/s in 2.47 seconds. What is its average acceleration?
- Write the equation: a = Δv / Δt = (vf — vi)/(tf — ti)
- Define the variables: vf = 46.1 m/s, vi = 18.5 m/s, tf = 2.47 s, ti = 0 s.
- Solve: a = (46.1 – 18.5)/2.47 = 11.17 meters/second2.
- Example 2: A biker traveling at 22.4 m/s comes to halt in 2.55 s after applying brakes. Find his deceleration.
- Write the equation: a = Δv / Δt = (vf — vi)/(tf — ti)
- Define the variables: vf = 0 m/s, vi = 22.4 m/s, tf = 2.55 s, ti = 0 s.
- Solve: a = (0 – 22.4)/2.55 = -8.78 meters/second2.
Advertisement
-
1
Understand the Direction of Acceleration. The physics concept of acceleration doesn’t always match how we would use the term in everyday life. Every acceleration has a direction, usually represented as positive if it’s UP or RIGHT, and negative if DOWN or LEFT. See if your answer makes sense based on this breakdown:
Behavior of a Car How is Velocity Changing? Direction of Acceleration Driver moving right (+) hits gas pedal + → ++ (more positive)
positive
Driver moving right (+) hits brakes ++ → + (less positive)
negative
Driver moving left (-) hits gas pedal — → — (more negative)
negative
Driver moving left (-) hits brakes — → — (less negative)
positive
Driver moves at constant velocity remains the same
acceleration is zero
-
2
Understand the Direction of Force. Remember, a force only causes acceleration in the direction of the force. Some problems may try to trick you with irrelevant values.
- Example Problem: A toy boat with mass 10kg is accelerating north at 2 m/s2. A wind blowing due west exerts a force of 100 Newtons on the boat. What is the boat’s new northward acceleration?
- Solution: Because the force is perpendicular to the direction of motion, it does not have an effect on motion in that direction. The boat continues to accelerate north at 2 m/s2.
-
3
Understand Net Force. If more than one force acts on an object, combine them into a net force before you calculate acceleration. For a problem in two dimensions, this looks something like this:
- Example Problem: April is pulling a 400 kg container right with a force of 150 newtons. Bob stand on the left of the container and pushes with a force of 200 newtons. A wind blowing left exerts a force of 10 newtons. What is the acceleration of the container?
- Solution: This problem uses tricky language to try and catch you. Draw a diagram and you’ll see the forces are 150 newtons right, 200 newtons right, and 10 newtons left. If «right» is the positive direction, the net force is 150 + 200 — 10 = 340 newtons. Acceleration = F / m = 340 newtons / 400 kg = 0.85 m/s2.
Advertisement
Calculator, Practice Problems, and Answers
Add New Question
-
Question
How do you solve acceleration word problems?
Sean Alexander is an Academic Tutor specializing in teaching mathematics and physics. Sean is the Owner of Alexander Tutoring, an academic tutoring business that provides personalized studying sessions focused on mathematics and physics. With over 15 years of experience, Sean has worked as a physics and math instructor and tutor for Stanford University, San Francisco State University, and Stanbridge Academy. He holds a BS in Physics from the University of California, Santa Barbara and an MS in Theoretical Physics from San Francisco State University.
Academic Tutor
Expert Answer
-
Question
What is the SI unit for acceleration?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
SI units are standardized units that are used internationally in scientific writing. When describing acceleration, use the SI units meters per seconds squared (m/s^2).
-
Question
How do you calculate acceleration without time?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
If you know that acceleration is constant, you can solve for it without time if you have the initial and final velocity of the object as well as the amount of displacement. Use the formula v^2=u^2+2as where v is the final velocity, u is the initial velocity, a is acceleration, and s is displacement. Solve for a to find acceleration.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
References
About This Article
Article SummaryX
To calculate acceleration, use the equation a = Δv / Δt, where Δv is the change in velocity, and Δt is how long it took for that change to occur. To calculate Δv, use the equation Δv = vf — vi, where vf is final velocity and vi is initial velocity. To caltulate Δt, use the equation Δt = tf — ti, where tf is the ending time and ti is the starting time. Once you’ve calculated Δv and Δt, plug them into the equation a = Δv / Δt to get the acceleration. To learn how to calculate acceleration from a force, read the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,763,841 times.
Reader Success Stories
-
DrDave Alpenschnee
Mar 5, 2018
«I am an Alpine ski instructor, and was interested in how unbalanced forces cause one ski to accelerate more than…» more
Did this article help you?
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
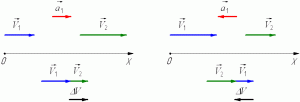
Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
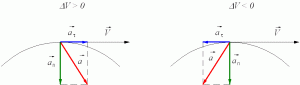
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
v2 > v1
а направление вектора ускорения совпадает с вектором скорости
Если скорость тела по модулю уменьшается, то есть
v2 < v1
то направление вектора ускорения противоположно направлению вектора скорости Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.
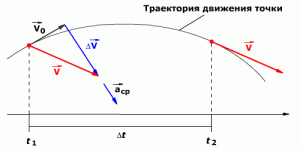
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
Скорость тела в инерциальной системе отсчета может изменяться под действием внешних воздействий на тело. Ускорение является характеристикой этого изменения.
Определение и физический смысл
Ускорение для скорости является тем же самым, что скорость для радиус-вектора: производной по времени.
Мгновенным ускорением называется первая производная по времени от мгновенной скорости:
a→=dv→dtoverrightarrow{a}=frac{doverrightarrow{v}}{dt}
Средним ускорением называется отношение вектора изменения скорости материальной точки, которая состоялась за время Δt,Δt, к величине времени ΔtΔt:
aср→=Δv→Δtoverrightarrow{{{a}_{ср}}}=frac{Delta overrightarrow{v}}{Delta t}
Единицей измерения ускорения в системе СИ является метр, разделенный на секунду в квадрате – м /с2.
Физический смысл ускорения заключается в том, что ускорение — это физическая величина, которая показывает, как со временем меняется скорость тела.
Пример 1
Вычисление ускорения
Координаты материальной точки, движущейся в плоскости xy, определяются формулами:
x=At4+Bt2,x = At^4 + Bt^2, y=Ct3−t,y = Ct^3- t, где A=0,25м/с4A = 0,25 м/с^4; $B = 0,5 м / с2; C=1/3м/с3;C = 1/3 м / с^3; D=1м/с.D = 1 м / с.
Найти вектор ускорения и его модуль.
Решение
Продифференцируем выражения для проекций скорости по времени и получим проекции координаты вектора ускорения в нужный момент времени:
ax=ddt(t3+ t)=3⋅t2+1=3⋅12+1=4ax = frac{d}{dt}({{t}^{3}}+text{ }t)=3cdot {{t}^{2}}+1=3cdot {{1}^{2}}+1=4 м/с2;
ay=ddt(t2+1)=2⋅t=2⋅1=2ay = frac{d}{dt}({{t}^{2}}+1)=2cdot t=2cdot 1=2 м/с2.
Вектор скорости:
a⃗=2⋅(2⋅i⃗+j⃗)vec{a}=2cdot (2cdot vec{i}+vec{j}) м/с2.
Его модуль:
a=ax2+ay2=42+22=25≈4,5a=sqrt{a_{x}^{2}+a_{y}^{2}}=sqrt{4_{{}}^{2}+2_{{}}^{2}}=2sqrt{5}approx 4,5 м/с
Нормальное и тангенциальное ускорения
Рассматривая движение материальной точки по криволинейной траектории, удобно вектор полного ускорения разложить на две взаимно перпендикулярных компоненты: aτa_τ –тангенциальное и ana_n –нормальное ускорение:
Вектор тангенциального ускорения имеет направление вдоль касательной, а нормальное ускорение — вдоль нормали к траектории. Модуль тангенциального ускорения является первой производной по времени от модуля скорости:
Модуль нормального ускорения зависит от радиуса кривизны траектории в данной точке траектории и модуля скорости:
∣a⃗τ∣=aτ=v˙|{vec{a}}_{tau}|={a}_{tau}={dot{v}}
Вектор полного ускорения является векторной суммой тангенциального и нормального ускорений:
a⃗=a⃗τ+a⃗nvec{a}={{vec{a}}_{tau }}+{{vec{a}}_{n}}
Модуль полного ускорения находят по теореме Пифагора:
a=∣a⃗∣=aτ2+an2=v˙2+v4R2a=|{vec{a}}|=sqrt{a_{tau }^{2}+a_{n}^{2}}=sqrt{{{{dot{v}}}^{2}}+frac{{{v}}^{4}}{{{R}^{2}}}}
Движение точки называется ускоренным, если численное значение ее скорости увеличивается со временем, то есть а>0а > 0 движение точки называется замедленным, если численное значение ее скорости уменьшается со временем, то есть а<0а < 0. Если aτ=0a_τ = 0, то материальная точка совершает равномерное движение, а если an=0a_n = 0 – движение по прямой (прямолинейное движение). Величины aτa_τ и ana_n характиризуют скорость изменения в соответствии с численным значением и направлением скорости движущейся материальной точки.
Пример 2
Тело подбросили под углом α к горизонту. Для момента времени, когда вектор скорости будет составлять угол ϕ=30∘phi=30^{circ} с горизонтальной линией. Найти: 1) нормальное, 2) тангенциальное, 3) полное ускорение.
Решение
Полное ускорение– это ускорение свободного падения a=ga=g. Из рисунка получим^
an=gcosϕ=9,8cos30∘≈8,49 /2{{a}_{n}}=gcos phi =9,8cos {{30}^{circ }}approx 8,49text{ }/{{}^{2}},
aτ=gsinϕ=9,8sin30∘≈4,90 /2{{a}_{tau }}=gsin phi =9,8sin {{30}^{circ }}approx 4,90text{ }/{{}^{2}},
a=an2+aτ2=a=sqrt{a_{n}^{2}+a_{tau }^{2}}=
=8,492+4,902≈9,8 /2.=sqrt{{{8,49}^{2}}+{{4,90}^{2}}}approx 9,8text{ }/{{}^{2}}.
Ответ: an≈8,49 /2{{a}_{n}}approx 8,49text{ }/{{}^{2}}, aτ≈4,90 /2{{a}_{tau }}approx 4,90text{ }/{{}^{2}}, a≈9,8 /2.aapprox 9,8text{ }/{{}^{2}}.