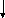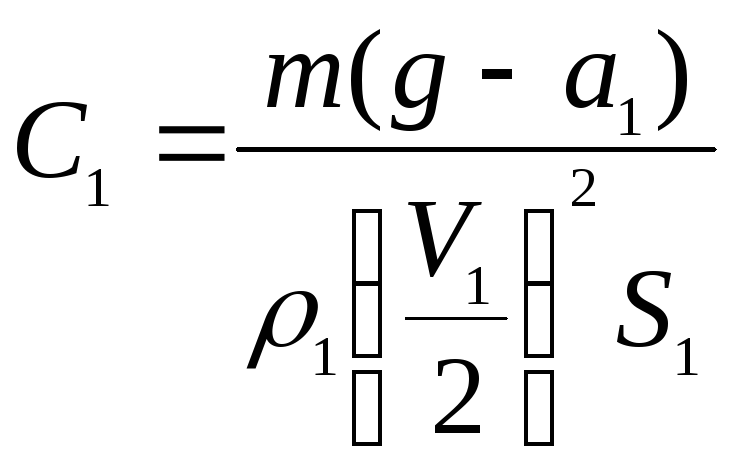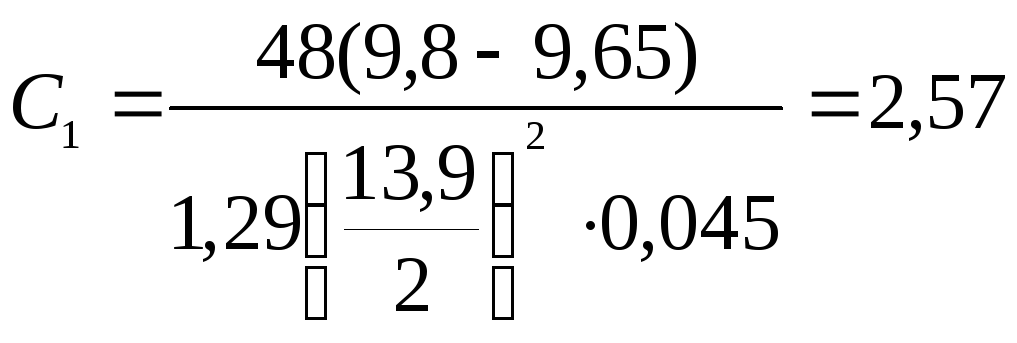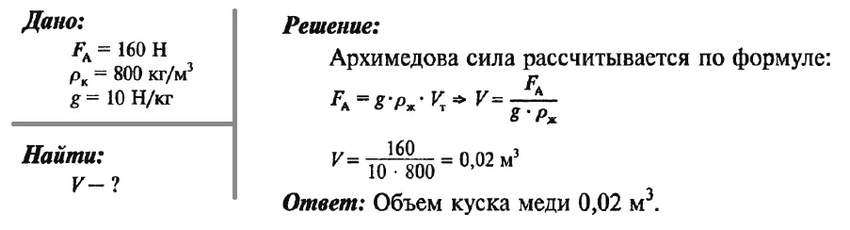Движение тела в жидкости
Основные положения
гидроаэромеханики
Жидкости
являются телами с характерным ближайшим
упорядочением структурной взаимосвязи
молекул. Расстояние между молекулами
жидкости мало, поэтому силы взаимодействия
значительны, что приводит к малой
сжимаемости жидкостей от действия
внешних сил и вызывает появление
значительных сил межмолекулярного
отталкивания.
Молекулы жидкости
колеблются около положения равновесия,
однако эти положения не являются
постоянными. По истечении некоторого
времени, называемого «временем оседлой
жизни», молекула скачком переходит в
новое положение равновесия, равное
среднему расстоянию между соседними
молекулами. Например, для воды это
расстояние составляет:
метра.
Подвижность
молекул объясняет малую вязкость
жидкости. С понижением температуры и
давления подвижность молекул аморфных
тел уменьшается и тела становятся
твердыми.
Силы противодействия
внешней силе, сжимающей жидкость,
определяют упругие свойства жидкости.
Особенностью упругих сил жидкости (сил
давления) является то, что, будучи
векторами, они не имеют определенной
точки приложения. Для характеристики
распределения сил давления вдоль
поверхности введена скалярная
характеристика – давление. Величина
давления измеряется силой, действующей
в направлении нормали на единицу
поверхности:
Паскалем
было
определено, что жидкость или газ передают
производимое на них давление по всем
направлениям одинаково.
В сообщающихся
сосудах, например, давление жидкости
на одной горизонтальной плоскости будет
одинаковым. При этом соотношение высот
столбов установившейся жидкости в
сообщающихся сосудах обратно соотношению
плотностей этих жидкостей:
Давление
в слое жидкости образованное от веса
самой вышерасположенной жидкости
называется гидростатическим и определяется
по формуле:
или, преобразовав,
Разность
гидростатических давлений на верхнюю
и нижнюю поверхности тела обуславливает
появление выталкивающей силы, действующей
со стороны жидкости на погруженное в
нее тело и равной:
где dж
– удельный вес жидкости,
Vт
– объем погруженной части тела.
Движущаяся жидкость
может образовать два вида своего течения
– неразрывное (ламинарное) и разрывное
(турбулентное). Если соотношение скоростей
струй жидкости в потоке остается
постоянным по всему течению, то такое
называется ламинарным в противном
случае -течение турбулентное. Вязкость
— это проявление взаимодействие слоев
жидкости. Силы вязкости направлены
касательно к слоям жидкости. Вязкость
называют еще и внутренним трением
жидкости.
Сила вязкости
изменяется от изменения скорости
жидкости, отнесенной к длине в направлении,
перпендикулярном скорости течения:
где
– коэффициент внутреннего трения или
коэффициент динамической вязкости с
размерностью [кг/м·с];
изменяется в
широких пределах.
Например: для воды
— 0,105 10-2,
для смазочных
масел – 66·10-2,
для глицерина –
139, 3·10-2.
Это различие
объясняется различием связей молекул
— чем сложнее молекула. Тем крепче связи,
тем больше вязкость.
Объем
протекающей
жидкости в выделенном ее сечении (S)
радиуса R
за 1 секунду был определен в 18 веке
Пуазейлем:
.
В случае движения
тела в жидкости с постоянной скоростью,
сила трения со стороны жидкости,
обладающей определенной вязкостью,
находится по формуле Стокса:
где R
– радиус тела, V
– скорость движения.
Определителем
характера движения жидкости (ламинарного
или турбулентного) служит коэффициент,
называемый числом Рейнольдса
(Re):
где V
– скорость течения; D
– диаметр сечения объема жидкости.
Например, если для
течения воды Re
> 2300, то в ней возникает турбулентное
движение, если Re
меньше – ламинарное.
Бернулли
было
установлено, что в стационарном потоке
жидкости полное давление, состоящее из
статистического (p),
динамического (ρ(V)2/2)
и гидростатистического (ρgh)
есть величина постоянная:
Движущаяся
жидкость, обладая кинетической энергией,
образует так называемую силу лобового
сопротивления:
;
S
– площадь поперечного сечения тела в
направлении перпендикулярном вектору
скорости движения потока (миделево
сечения).
Контрольные
вопросы по теории
-
Чем объясняется
свойство текучести жидкости? -
Что такое время
оседлости молекул? -
Что называется
давлением жидкости? -
Напишите формулу
гидростатистического давления. -
Сформулируйте
закон Архимеда и напишите формулу. -
Напишите формулу
лобового сопротивления жидкости. -
Напишите формулу
Стокса величины вязкости жидкости. -
В каком случае
сила давления жидкости на стенку будет
равно силе давления на дно сосуда? -
Сформулируйте
условия плавания тел. -
Почему давление
не векторная величина? -
Напишите уравнение
Бернулли для стационарного потока
жидкости. -
Дайте определение
ламинарного и турбулентного течений
жидкости. -
Каков механизм
подъемной силы крыла? -
Сформулируйте
закон Паскаля. -
Каков принцип
работы гидравлического пресса? -
На поверхности
воды в сосуде плавает лед. Изменится
ли уровень воды, если лед растает? -
Почему возникает
выталкивающая сила в жидкостях и газе? -
Как будут относиться
высоты жидкостей различной плотности
в сообщающихся сосудах? -
Назовите основные
механические свойства жидкости.
Российский
государственный университет физической
культуры,
спорта и туризма
Кафедра
естественно-научных дисциплин
Движение тела в
жидкости и газе
Вычисление глубины
погружения спортсмена при прыжках в
воду
РГР №2
по курсу физики
Вариант №43
Выполнил:
студент I
курса I
потока I
группы
Иванов И.И.
Преподаватель:
доцент (профессор)
кафедры ЕНД
Москва 2010 г.
Содержание:
-
Текст задания.
-
Алгоритм решения.
-
Иллюстрация.
-
Таблица исходных
данных. -
Таблица вычислений.
-
Таблица результатов.
-
Текст задания:
Спортсмен прыгает
в воду с вышки высотой Н=10
м.
Масса тела спортсмена
m.
Коэффициент
обтекаемости тела спортсмена при
погружении в воду C2.
Коэффициент
обтекаемости тела спортсмена при
всплытии
C1.
Плотность тела ρ.
Плотность воздуха
ρ1=1,29
кг/м3.
Плотность воды
ρ2=103
кг/м3.
Коэффициент
вязкости воды j=0,105·10-2
(Па·с).
Ускорение свободного
падения g=9,8
м/с2.
Вычислить:
Глубину погружения
спортсмена в бассейне h1.
Время погружения
t2.
Время всплытия
t3.
Время нахождения
спортсмена под водой t4.
Величину инерционных
перегрузок при входе в воду n.
Импульс силы при
погружении в воду F·t.
Силу сопротивления
воздуха F0.
Коэффициент
обтекания в воздухе C1.
Построить:
График зависимости
глубины погружения h
от массы
тела m
по трём
точкам: m;
m-4;
m+4
(кг).
2. Алгоритм
решения:
2.1. Максимальная
глубина погружения определяется из
условия, что вся потенциальная энергия
тела ПАС
от уровня вышки до уровня погружения
затрачена на работу против силы
динамического (лобового) сопротивления
воды (FЛС),
гидростатической силы выталкивания
(силы Архимеда FАр)
и силы вязкости воды (FВ):
ПАС
= АЛС
+ ААр
+ АВ.
2.2. Сделаем допущение,
что скорость движения тела спортсмена
в воде снижается равнозамедленно под
действием всех приложенных сил, что
допускает расчёт силы динамического
(лобового) сопротивления с использованием
значения квадрата средней скорости
движения.
2.3. Коэффициент
обтекаемости и плотность тела спортсмена
на вдохе примем равными табличным
значениям.
а
Faрх
Fлс
Fв
mg
mg
Fлс
Погружение
Всплытие
H
h1
Faрх
Графическая
интерпретация
условий задачи.
mg
FВ
а
4. Таблица исходных
данных
|
№ |
Параметр |
Обозначение |
Величина |
Единица |
|
1. |
Масса |
m |
48 |
кг |
|
2. |
Высота |
Н |
10 |
м |
|
3. |
Плотность |
ρ |
996 |
кг/м3 |
|
4. |
Плотность |
ρ1 |
1,29 |
кг/м3 |
|
5. |
Плотность |
ρ2 |
1000 |
кг/м3 |
|
6. |
Коэффициент |
C2 |
0,43 |
– |
|
7. |
Коэффициент |
C3 |
0,63 |
– |
|
8. |
Коэффициент |
j |
0,105·10-2 |
Па·с |
|
9. |
Ускорение |
g |
9,8 |
м/с2 |
|
10. |
Время |
t1 |
1,44 |
с |
|
11. |
Обхват |
L |
0,81 |
м |
|
12. |
Площадь |
S1 |
0,045 |
м2 |
5. Таблица
вычислений
|
Параметр |
Формула |
Вычисления |
Результат |
|
1. |
|||
|
1.1. |
|
|
9,65 |
|
1.2. |
|
|
7,2 |
|
1.3. |
|
|
13,9 |
|
1.4. Силу
где |
|
|
2,57 |
|
2. |
|||
|
2.1. |
|
|
934,65 |
|
2.2. |
|
|
0,0177 |
|
Параметр |
Формула |
Вычисления |
Резуль- тат |
|
2.3. |
|
|
472,3 |
|
2.4. |
|
|
5,023 |
|
2.5. |
|
|
0,72 |
|
2.6. |
|
|
1,97 |
|
2.7. |
|
|
667,2 |
|
3. |
|||
|
3.1.
т.к. |
|
|
0,0159 |
|
3.2. |
|
|
25,14 |
|
Параметр |
Формула |
Вычисления |
Резуль- тат |
|
3.3. |
|
|
25,86 |
6. Таблица
результатов
|
№ |
Параметр |
Обозначение |
Величина |
Единица |
|
1. |
Сила |
F0 |
7,2 |
Н |
|
2. |
Коэффициент |
C1 |
2,57 |
– |
|
3. |
Глубина |
h1 |
5,023 |
м |
|
4. |
Время |
t2 |
0,72 |
с |
|
5. |
Время |
t3 |
25,14 |
с |
|
6. |
Время |
t4 |
25,86 |
с |
|
7. |
Инерционные |
n |
1,97 |
|
|
8. |
Импульс |
F·t |
667,2 |
Н·с |
Таблица вариантов
исходных данных РГР №2
|
Параметры |
Номер |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
1. |
Масса |
42 |
44 |
46 |
48 |
50 |
52 |
54 |
56 |
58 |
60 |
|
2. |
Высота |
10 |
10 |
||||||||
|
3. |
Плотность |
996 |
994 |
||||||||
|
4. |
Плотность |
1,29 |
1,29 |
||||||||
|
5. |
Плотность |
1000 |
1000 |
||||||||
|
6. |
Коэффициент |
0,40 |
0,41 |
0,42 |
0,43 |
0,44 |
0,45 |
0,46 |
0,47 |
0,48 |
0,49 |
|
7. |
Коэффициент |
0,60 |
0,61 |
0,62 |
0,63 |
0,64 |
0,65 |
0,66 |
0,67 |
0,68 |
0,69 |
|
8. |
Коэффициент |
0,105·10-2 |
0,105·10-2 |
||||||||
|
9. |
Ускорение |
9,8 |
9,8 |
||||||||
|
10. |
Время |
1,44 |
1,44 |
||||||||
|
11. |
Обхват |
0,75 |
0,77 |
0,79 |
0,81 |
0,83 |
0,85 |
0,88 |
0,90 |
0,91 |
0,93 |
|
12. |
Площадь |
0,045 |
0,045 |
0,053 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
С. Н. Манида
Установлена зависимость силы гидростатического давления (силы Архимеда) от плотности свободного тела, погруженного в жидкость.
1. Закон Архимеда для неподвижных тел
Любое тело, погруженное в жидкость, подвергается сжимающему и выталкивающему действию со стороны жидкости.
Представим такую ситуацию: ученый, владеющий современными приборами и мощным математическим аппаратом, решил вычислить силу, выталкивающую из жидкости погруженное в нее тело.
Он экспериментально установит, что на единицу поверхности тела, погруженного в жидкость с плотностью действует по нормали к поверхности сила гидростатического давления p, зависящая от глубины погружения h по определенному закону (
gh) и не зависящая от ориентации поверхности.
Он сложит векторы сил давления, действующих на различные элементы поверхности тела и направленные по нормали к ним; для этого потребуется вычислить так называемый поверхностный интеграл от некоторой векторной функции по поверхности тела сложной формы. С помощью современного математического аппарата и мощных компьютеров этот интеграл может быть вычислен. Но каково же будет изумление этого ученого, когда окажется, что полученный результат численно равен весу жидкост и в объеме погруженной части тела! Этот результат был получен греческим ученым Архимедом 2200 лет назад, причем в общем виде — для тел любой формы!
Попробуем восстановить ход рассуждений Архимеда и вывести его закон.
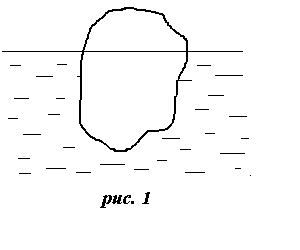
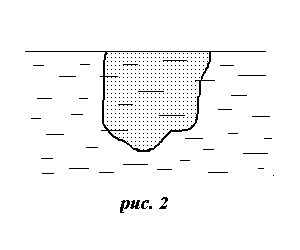
На рис. 1, изображено тело, помещенное в жидкость. На это тело со стороны жидкости действует описанная выше сила гидростатического давления. Для нахождения этой силы вместо вычисления сложных интегралов проведем мысленный эксперимент: уберем тело и рассмотрим жидкость в объеме V, который занимала погруженная часть тела (рис. 2). На эту жидкость действует сила тяжести Vg и сила гидростатического давления F. Выделенный объем находится в равновесии, следовательно, сумма сил, действующих на жидкость в этом объеме, равна нулю: F+
Vg =0.
Отсюда следует выражение для силы гидростатического давления: F=—Vg.
Мы нашли силу, действующую на поверхность жидкости, заполняющей объем V. Но поверхность тела, погруженного в жидкость, совпадает с поверхностью жидкости в нашем мысленном эксперименте, следовательно, найденное выражение и есть «выталкивающая’’ сила — сила Архимеда
F Арх = —Vg. (*)
Это равенство и носит название закон Архимеда.
2. Неприменимость закона Архимеда для случая свободных тел
Казалось бы, решение задач с использованием этого закона не должно вызывать затруднений. Однако неверные решения отдельных задач на закон Архимеда встречаются не только у школьников, но и в ряде задачников.
Дело в том, что при использовании этого (как и любого другого) закона надо всегда помнить, как и для каких ситуаций он выводился. Так, например, мы вычисляли силу гидростатического давления, действующую на поверхность неподвижного объема жидко сти, находящейся в равновесии, т. е. имеющей нулевые скорость и ускорение. Следовательно, и использовать выведенное выражение для силы Архимеда можно только в тех случаях, когда и скорость, и ускорение тела равны нулю.
Покажем, что применение этого закона в других ситуациях абсолютно неправомочно, так как приводит к неверным результатам.
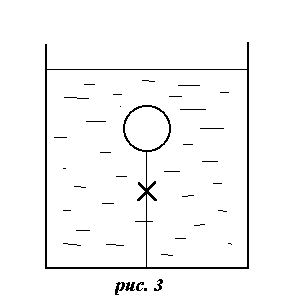
Рассмотрим легкое тело, привязанное ниткой к дну сосуда, заполненного жидкостью (рис. 3). Тело погружено в жидкость и находится в равновесии. На него действуют вниз сила тяжести mg= Vg и сила натяжения нити T, а вверх — сила гидростатического давления
F=FАрх=- Vg, (*)
где — плотность тела,
— плотность жидкости. Условие равновесия тела
—Vg +T+
Vg =0. (1)
Пусть в некоторый момент нить обрывается (т. е. исчезает сила натяжения T), равенство (1) перестает выполняться, и тело начинает двигаться вве рх (всплывать) с некоторым ускорением a, которое можно найти из уравнения движения
F+ V g =
V a. (2)
Предположив, что в этом случае можно использовать закон Архимеда, подставим — Vg в левую часть равенства (2) вместо F. Для ускорения тела получаем выражение
a = — g (—
)/
(3)
Исследуем выражение (3). Ускорение тела направлено против ускорения свободного падения (что абсолютно верно), а его величина неограниченно возрастает при уменьшении плотности тела. Такой результат противоречит как здравому смыслу, так и наблюдениям.
Таким образом, закон Архимеда в форме (*) неприменим к телам, ускорение которых относительно жидкости отлично от нуля (даже при равной нулю скорости).
3. Сила гидростатического давления для случая свободных тел
Точный расчет гидростатического давления на поверхность ускоренно движущегося тела возможен только с применением аппарата математической физики, а ответ представим в аналитическом виде лишь для некоторых частных случаев. Уравнения, описывающие движение тела в жидкости, были впервые получены профессором Петербургского университета Леонардом Эйлером в середине XVIII века. Решение этой задачи для случая тела сферической формы, размеры которого много меньше размеро в сосуда, приведено в Приложении (для читателей, владеющих методами постановки и решения граничных задач математической физики). Полученное там выражение (**) для силы давления отличается от (*):
(4)
и, с учетом (2), ускорение тела имеет вид:
(5)
4. Выводы
Сравнивая выражения (4) и (*) видим, что они совпадают только при =
. Зависимость силы гидростатического давления, действующей на свободное тело, от его плотности
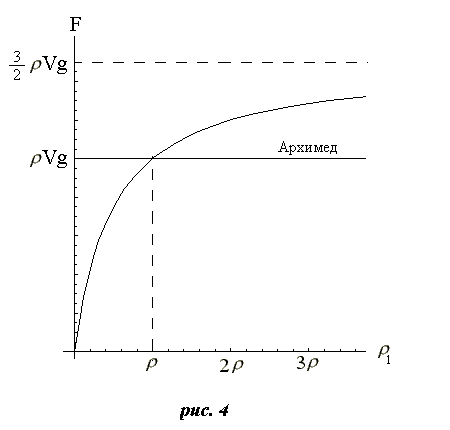
представлена на графике рис. 4 в сравнении со стандартным выражением для силы Архимеда
Vg:
Из графика на рис.4 видно, что для малых плотностей тела сила давления убывает до нуля, а при увеличении плотности эта сила стремится к величине 1,5Vg.
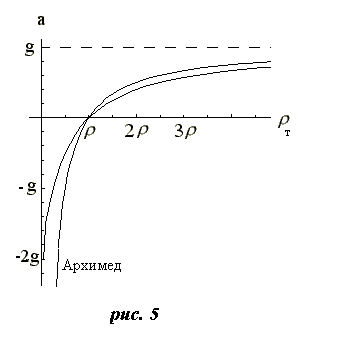
На следующем графике (рис. 5) приведена зависимость ускорения свободного тела в жидкости от его плотности [уравнение (5)]. Для сравнения приведен график ускорения, получающийся непосредственн о из закона Архимеда [уравнение (3)]
Из этого графика видно, что даже бесконечно легкий шарик всплывает с конечным ускорением, равным -2g, а тяжелые тела тонут с ускорением, меньшим, чем это следует из закона Архимеда.
ну, тут все просто: на шарик с одной стороны действует сила тяготения (F=mg), заставляя его опускаться вниз, с другой стороны аржимедова сила (F=pgV) р — плотность жидкости. вот и считаем силу, действующую на шарик: F=g*(pV-m). так же существует формула, по которой вычисляется сила: F=mа, отсюда для шарика в жидкости a=g*(pV-m)/m
а потом, зная силу, из этого вычисляем время. движение равноускоренное. v=at, отсюда t=v/a, далее S=v*v/2a, v=корень(S/2a),
подставляем и вычисляем t=числитель:корень(S/(2g*(pV-m)/m))Знаменатель:g*(pV-m)/m.
к сожалению, нет под рукой таблицы плотностей)))) кто-нибудь, подставьте в формулу значения!!!
Задачи на силу Архимеда с решениями
Формулы, используемые на уроках «Задачи на силу Архимеда», «Сообщающиеся сосуды».
Название величины |
Обозначение |
Единица измерения |
Формула |
Объем тела |
V |
м3 |
Vт = FA / pg |
Плотность жидкости |
p |
кг/м3 |
pж = FA / (Vg) |
Сила Архимеда |
FA |
Н |
FA = pж Vт g |
Постоянная |
g ≈ 10 Н/кг |
Н/кг |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Тело объемом 2 м3 погружено в воду. Найдите архимедову силу, действующую на тело.
Задача № 2.
Определить выталкивающую силу, действующую на деревянный плот объемом 12 м3, погруженный в воду на половину своего объема.
Задача № 3.
Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?
Задача № 4.
Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?
Задача № 5.
Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?
Задача № 6.
Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?
Задача № 7.
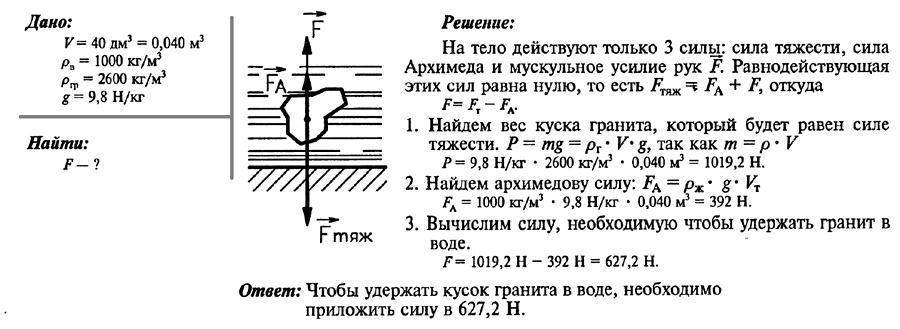
Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм3?
Задача № 8.
Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.
Задача № 9 (повышенной сложности).
Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?
Задача № 10 (повышенной сложности).
Рассчитайте, какой груз сможет поднять шар объемом 1 м3, наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)
Задача № 11.
Деревянный цилиндр плавает на поверхности воды так, что он погружен в воду на 90%. Какая часть цилиндра будет погружена в воду, если поверх воды налить слой масла, полностью закрывающий цилиндр? Плотность масла 800 кг/м3.
Дано: V – объем цилиндра (V = Sh); h – высота цилиндра; S – площадь основания цилиндра; V1 – объем цилиндра, погруженного в масло (V1 = V – V2 = Sh1); h1 – высота части цилиндра, погруженной в масло; V2 – объем цилиндра, погруженного в воду после добавления масла; рв – плотность воды (1000 кг/м3); рм – плотность масла (800 кг/м3)
Найти: (h – h1) / h — ?
Решение. F – сила, выталкивающая цилиндр из воды до добавления масла F = 0,9pвgV
F1 – сила, выталкивающая цилиндр из масла F1 = pмgV1
F2 – сила, выталкивающая цилиндр из воды после добавления масла F2 = pвgV2
Баланс сил: F – F1 = F2
0,9pвgV – pмgV1 = pвgV2 V1 = V – V2 ⇒ 0,9pвV – pм(V – V2) = pвV2
V(0,9pв – pм) = V2(pв – pм) V = Sh; V1 = Sh1 ⇒
Ответ: 1/2 часть цилиндра будет погружена в воду (50%).
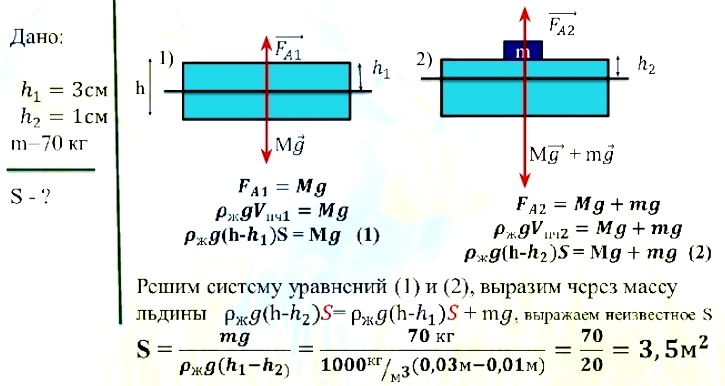
Задача № 12.
Плоская льдина плавает в воде, выступая над уровнем воды на 3 см. Человек массой 70 кг зашел на льдину. В результате, высота выступающей части над льдиной уменьшилась в 3 раза. Найти площадь льдины.
Ответ: 3,5 м3.
Теория для решения задач.
Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = ратм + p*g*h
Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.
Конспект урока «Задачи на силу Архимеда с решениями».
Следующая тема: «Задачи на механическую работу».
Сила Архимеда
Вместе с преподавателем физики разбираемся, в чем измеряется и от чего зависит сила Архимеда. А в конце статьи вспомним известную легенду о том, как был открыт закон Архимеда, и узнаем, действует ли он в условиях невесомости
Как объяснить, почему плавают огромные корабли из стали, которая тяжелее воды? Да еще и перевозят тонны грузов. Это происходит благодаря открытию, сделанному за два с лишним столетия до нашей эры изобретателем и ученым Архимедом.
История сохранила нам немного имен ученых-практиков, чьи изобретения изменили мир. Навсегда забыт гений, который придумал колесо. Но любой современный школьник назовет Архимеда, даже если знает о нем только легенду про мокрого голого философа, бежавшего по улице Сиракуз с криком: «Эврика!», то есть «Нашел!». А ведь ученый заслужил вечную благодарную память человечества благодаря многим изобретениям и открытиям:
- Теория рычага и способы его расчета. На этой основе построены боевые машины для метания тяжелых камней и «коготь Архимеда» — машина для переворачивания римских трирем;
- Шкив и многоступенчатый блок, полиспаст;
- Червячная передача;
- Архимедов винт и насосы, работающие на его принципе;
- Одометр, машина для измерения пройденного пути;
- «Архимедово число»: отношение длины окружности к ее диаметру
- Фокусировка световых лучей при помощи зеркал. По легенде, так были сожжены римские корабли, осаждавшие Сиракузы. Недавно энтузиасты провели экспериментальную проверку и удалось поджечь деревянный баркас.
Однако самое знаменитое открытие — закон Архимеда, основа гидростатики. Удивительно, что он был почти забыт, пока корабли строили из дерева. И только когда они стали железными, а потом стальными, инженеры осознали важность силы Архимеда и стали применять ее формулу при расчетах водных и воздушных судов.
Определение закона Архимеда простыми словами
На тело, погруженное в жидкость или газ, действует подъемная, она же выталкивающая сила (сила Архимеда), равная весу вытесненного объема жидкости или газа.
Вектор силы Архимеда направлен против направления действия силы тяжести. Следствия закона Архимеда:
- В невесомости закон Архимеда не действует.
- Если сила Архимеда меньше силы тяжести, то тело утонет.
- Если силы одинаковы по величине, тело «повисает» в окружающей среде.
- Если сила Архимеда больше силы тяжести, то тело всплывает, пока они не уравновесятся. В воде этот момент наступит на поверхности.
Формула силы Архимеда
Предыдущая формулировка годится только для участка цепи, где отсутствует сам источник электродвижущей силы. В реальности ток течет по замкнутому контуру, где обязательно есть батарея или генератор, имеющий собственное внутреннее сопротивление. Поэтому формула закона Ома для полной цепи выглядит несколько сложнее
Где: FA — сила Архимеда;
ρ — плотность жидкости или газа, в которое погружают тело;
g — ускорение свободного падения, которое зависит от того, на какой планете или спутнике мы находимся. Для поверхности Земли, например, ускорение примерно равно 9,8 м/с2;
V — объем погруженной в среду части тела.
Закон Паскаля
Объяснение закона простыми словами и его формула
подробнее
В чем измеряется сила Архимеда
Единица измерения силы Архимеда в системе СИ — ньютон (Н).
1Н = 1 кг·м/с2
Архимед и наше время
В перечне военных трофеев, взятых римлянами в Сиракузах, есть некий «Планетарий Архимеда» — механическая модель движения планет. Он не сохранился, но есть подозрение, что загадочное устройство, случайно обнаруженное в затонувшем корабле у острова Антикитера, тоже сделано золотыми руками Архимеда. Прямых доказательств этого факта нет, но уже выяснено, что время изготовления приблизительно соответствует годам жизни гениального инженера.
Популярные вопросы и ответы
Отвечает Николай Герасимов, старший преподаватель по физике Домашней школы «ИнтернетУрок».
От чего зависит сила Архимеда?
Например, для определения выталкивающей силы, действующей на камень, лежащий на дне озера, нужно брать весь его объем. Если же определяем силу Архимеда, действующую на мяч, плавающий по этому озеру, то нужно брать лишь объем той части, которая находится под водой. Зависимость выталкивающей силы от ускорения свободного падения позволяет сделать интересный вывод о том, что в невесомости силы Архимеда нет.
Зная, что сила Архимеда зависит от плотности жидкости, можно объяснить следующее явление: куриное яйцо, помещенное в обычную воду, утонет и будет лежать на дне банки. Но стоит добавить в эту банку насыщенный раствор поваренной соли и тем самым изменить плотность воды — и яйцо начинает всплывать.
Как был открыт закон Архимеда?
Открытие закона Архимеда связано с интересной легендой. Древнегреческий царь Герон II приказал ювелирам изготовить золотую корону, что и было вскоре выполнено. Царь заподозрил, что ювелиры его обманули и сделали корону из электрона, сплава золота и серебра. Отличить подделку на глаз не удалось. Для проверки пригласили ученого из Сиракуз по имени Архимед. Достаточно было сравнить объем короны с объемом куска золота такой же массы.
Сложность состояла в определении объема короны, так как она была сложной формы, и вычислить объем по математическим формулам было невозможно. Долгие размышления не увенчались успехом, и Архимед решил сходить отдохнуть в баню. Именно там ученому пришла гениальная идея: погружаясь в воду, тело вытесняет ее в объеме, который равен объему погруженной части тела. «Эврика!» («Нашел!») — закричал Архимед и побежал к царю.
Сравнив объемы воды, вытесненной короной и куском золота такой же массы, он уличил ювелиров в нечестности и алчности. Так Архимедом был открыт закон, который позволяет нам объяснить, почему ходят по морям и океанам огромные корабли, изготовленные из железа, а маленькая металлическая гайка тонет.
Какой буквой обозначают силу Архимеда?
Как и большинство сил, сила Архимеда обозначается буквой F. Это первая буква английского слова force – сила. В индексе пишут букву А или В, которые позволяют отличить силу Архимеда FA или выталкивающую силу FВ от других сил в природе.