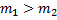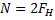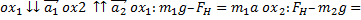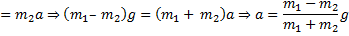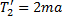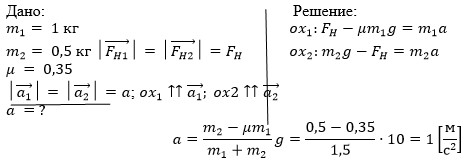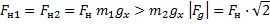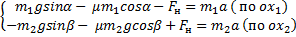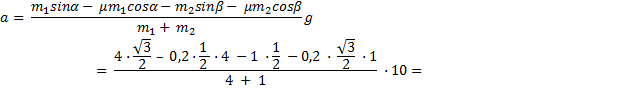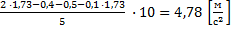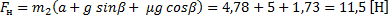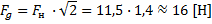Условие задачи:
Через неподвижный блок перекинута нить с грузами массой 3 и 5 кг. С каким ускорением будут двигаться грузы?
Задача №2.2.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=3) кг, (M=5) кг, (a-?)
Решение задачи:
Нарисуем схему к задаче и покажем все силы, действующие на каждый груз – силу тяжести и силу натяжения нити. Понятно, что когда грузы отпустят, то груз (M) станет двигаться вниз, поскольку он тяжелее, а груз (m) – вверх. Грузы будут двигаться с одинаковыми ускорениями, так как нить, соединяющая их, нерастяжима.
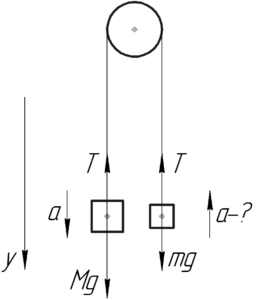
Запишем второй закон Ньютона для обоих грузов в проекции на вертикальную ось (y):
[left{ begin{gathered}
Mg – T = Ma hfill \
mg – T = – ma hfill \
end{gathered} right.]
Вычтем из первого равенства системы второе, тогда получим следующее:
[Mg – mg = Ma + ma]
[gleft( {M – m} right) = aleft( {M + m} right)]
Выразим искомое ускорение:
[a = frac{{gleft( {M – m} right)}}{{M + m}}]
Считаем ответ:
[a = frac{{10 cdot left( {5 – 3} right)}}{{5 + 3}} = 2,5; м/с^2]
Ответ: 2,5 м/с2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.90 На материальную точку массы 1 кг действует две постоянные взаимно перпендикулярные
2.2.2 Три груза массами m1=1 кг, m2=2 кг, m3=3 кг соединены легкими нитями, проходящими
2.2.3 Через неподвижный блок перекинута нить, к концам которой подвешены грузы
§ 41. Блок и наклонная плоскость
Во всех задачах на блоки, которые мы решали ранее, мы не учитывали силу трения. Точнее, сила трения была такой, что ей можно было пренебречь. Сейчас я предлагаю вам рассмотреть задачу, в которой мы все-таки увидим эту силу.
На картинке изображена наклонная плоскость, соединенная с блоком. Масса большого груза составляет 6 килограмм. В результате небольшого толчка этот груз начинает скользить вниз, поднимая при этом небольшой (двухкилограммовый) балласт. Коэффициент трения скольжения равен 0.3, а угол наклона плоскости к горизонту составляет 45 градусов.
Итак, тела будут двигаться с одинаковым ускорением. А значит, мы можем воспользоваться уже хорошо известным нам методом – рассмотреть движение системы тел.
Ускорение системы можно найти при помощи второго закона Ньютона:
vec{a}_{сис}=dfrac{varSigmavec{F}_{вн}}{M}
Какие внешние силы действуют на «гусеницу»? На первое тело действуют сила тяжести, сила реакции опоры и сила трения скольжения. Еще действует сила натяжения нити, но ее мы не учитываем, так как это внутренняя сила. Силу реакции опоры уравновешивает один из компонентов силы тяжести, а другой компонент этой силы тянет тело вниз по наклонной плоскости. Что касается силы трения скольжения, ее величину можно найти по следующей формуле:
F_с=mu_сN=mu_сmgcos45degree
На второе тело действует только сила тяжести. Опять же, на силу натяжения не обращаем никакого внимания.
Направление, в котором движется система, будем считать положительным. Силы, действующие в этом направлении, будем подставлять в уравнение с плюсом. В противном случае – с минусом.
Посмотрим, что у нас получилось:
vec{a}_{сис}=dfrac{varSigmavec{F}_{вн}}{M}=dfrac{m_1gsin45degree-mu_сmgcos45degree-m_2g}{m_1+m_2}
Проведем все необходимые расчеты:
vec{a}_{сис}approxdfrac{41.6thickspaceН-12.5thickspaceН-19.6thickspaceН}{6thickspaceкг+2thickspaceкг}=dfrac{9.5thickspaceН}{8thickspaceкг}approx1.2thickspaceм/с^2
Первый груз движется влево, при работе с наклонной плоскостью мы считаем это направление положительным. Второй груз движется вверх, в направлении, которое мы также условно считаем положительным. Значит:
vec{a}_1=1.2thickspaceм/с^2
vec{a}_2=1.2thickspaceм/с^2
Решение задач на движение системы связанных тел
Общий случай решения
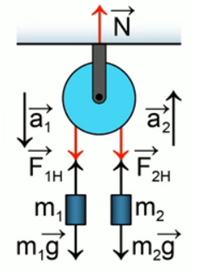
Рассмотрим общий случай. Имеется неподвижный блок, через который перекинута нить, к концам которой подвешены два грузика массой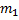 
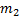
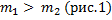
и 
, где 
.
Рис. 1. Схема блока
; 
; 
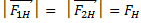
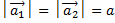
На первый грузик действует сила притяжения к земле и сила натяжения нити, которая направлена вверх. Соответственно, на второй грузик будут действовать те же силы. Величины сил натяжения их будут одинаковы по модулю при условии, что трение в оси блока отсутствует и сам блок невесом, то есть его не нужно раскручивать какой-то парой сил. Сила натяжения – это внутренняя сила, возникающая в системе связанных тел, друг на друга они действуют посредством нити. Ускорение у этих грузиков будет иметь разное направление, так как первый грузик тяжелее, то он будет двигаться вниз, а второй вверх, но величины ускорений будут одинаковы и равны а, при условии, что нить нерастяжима. К блоку приложены три силы – две силы натяжения, которые тянут блок вниз, и сила реакции крепления оси блока, направленная вверх и равная удвоенной силе натяжения, так как центр блока никуда не перемещается и сумма сил, приложенных к нему должна быть равна нулю. При разборе таких задач оси рисовать не обязательно, потому что подразумевается, что для каждого тела можно выбрать свое направление оси. Так как первое тело движется вниз, то ось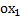 
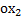
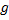
необходимо направить вниз так, как направлено ускорение. Второе тело движется вверх и 
направлено вверх согласно второму ускорению. Записываем второй закон Ньютона для этих тел, при сложении внутренние силы у нас сократятся, и мы получим общий вид для ускорения. Это отношение у нас будет всегда, то есть какое-то числовое значение, умноженное на 
, которое заставляет систему всегда двигаться.
Задача 1
Одинаковые бруски, связанные нитью, движутся под действием внешней силы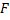 
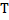
по гладкой горизонтальной поверхности (Рис. 2). Как изменится сила натяжения нити 
, если третий брусок переложить с первого на второй?
1. Увеличится в 2 раза
2. Увеличится в 3 раза
3. Уменьшится в 1,5 раза
4. Уменьшится в 2раза
Рис. 2. Иллюстрация к задаче 1
В этой задаче необходимо найти отношение силы натяжения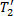 
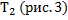
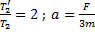
к 
.
; 
; 
Рис. 3. Решение задачи 1
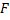
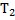
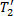
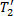
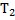
Растянутая нить в этой системе действует на брусок 2, заставляя его двигаться вперед, но она также действует и на брусок 1, пытаясь препятствовать его движению. Эти две силы натяжения равны по величине, и нам как раз необходимо найти эту силу натяжения. В таких задачах необходимо упростить решение следующим образом: считаем, что сила является единственной внешней силой, которая заставляет двигаться систему трех одинаковых брусков, и ускорение остается неизменным, то есть сила заставляет двигаться все три бруска с одинаковым ускорением. Тогда натяжение 
всегда двигает только один брусок и будет равно mа по второму закону Ньютона. будет равно удвоенному произведению массы на ускорение, так как третий брусок находится на втором и нить натяжения должна уже двигать два бруска. В таком случае отношение к будет равно 2. Правильный ответ – первый.
Задача 2
Два тела массой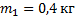 
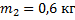
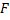
и 
, связанные невесомой нерастяжимой нитью, могут без трения скользить по гладкой горизонтальной поверхности под действием постоянной силы (Рис. 4). Чему равно отношение сил натяжения нити в случаях а и б?
Выбор ответа: 1. 2/3; 2. 1; 3. 3/2; 4. 9/4.
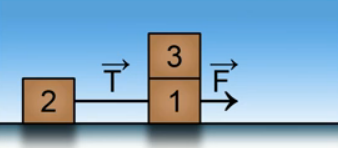
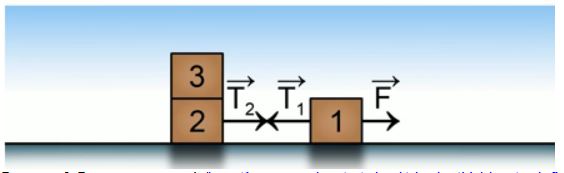
Рис. 4. Иллюстрация к задаче 2
Рис. 5. Решение задачи 2
На бруски действует одна и та же сила, только в разных направлениях, поэтому ускорение в случае «а» и случае «б» будет одним и тем же, так как одна и та же сила вызывает ускорение двух масс. Но в случае «а» эта сила натяжения заставляет двигаться еще и брусок 2, в случае «б» это брусок 1. Тогда отношение этих сил будет равно отношению их масс и мы получим ответ – 1,5. Это третий ответ.
Задача 3
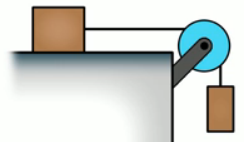
На столе лежит брусок массой 1 кг, к которому привязана нить, перекинутая через неподвижный блок. Ко второму концу нити подвешен груз массой 0,5 кг (Рис. 6). Определить ускорение, с которым движется брусок, если коэффициент трения бруска о стол составляет 0,35.
Рис. 6. Иллюстрация к задаче 3
Записываем краткое условие задачи:
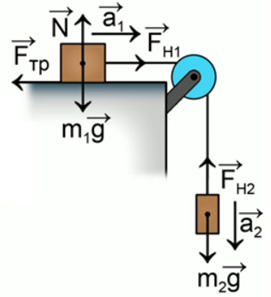
Рис. 7. Решение задачи 3
Необходимо помнить, что силы натяжения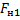 
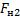
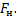
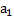
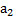
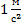
и 
как векторы разные, но величины этих сил одинаковы и равны 
Точно также у нас будут одинаковы и ускорения этих тел, так как они связаны нерастяжимой нитью, хотя направлены они в разные стороны: 
– горизонтально, 
– вертикально. Соответственно, и оси для каждого из тел выбираем свои. Запишем уравнения второго закона Ньютона для каждого из этих тел, при сложении внутренние силы натяжения сократятся, и получим обычное уравнение, подставив в него данные, получим, что ускорение равно 
.
Для решения таких задач можно пользоваться методом, который использовался в прошлом веке: движущей силой в данном случае является результирующая внешних сил, приложенных к телу. Заставляет двигаться эту систему сила тяжести второго тела, но мешает движению сила трения бруска о стол, в этом случае:
, так как движутся оба тела, то движущая масса будет равна сумме масс 
, тогда ускорение будет равно отношению движущей силы на движущую массу 
Так можно сразу прийти к ответу.
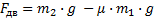
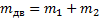
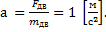
Задача 4
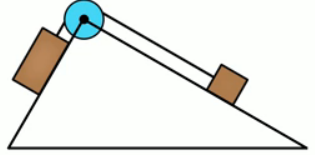
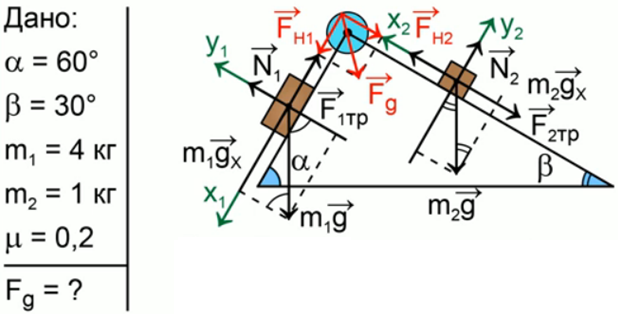
В вершине двух наклонных плоскостей, составляющих с горизонтом углы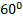 
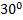
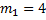
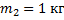
и 
, закреплен блок. По поверхности плоскостей при коэффициенте трения 0,2 движутся бруски 
кг и 
, связанные нитью, перекинутой через блок (Рис. 8). Найти силу давления на ось блока.
Рис. 8. Иллюстрация к задаче 4
Выполним краткую запись условия задачи и поясняющий чертеж (рис. 9):
Рис. 9. Решение задачи 4
Мы помним, что если одна плоскость составляет угол в 600 с горизонтом, а вторая плоскость – 300 с горизонтом, то угол при вершине будет 900, это обычный прямоугольный треугольник. Через блок перекинута нить, к которой подвешены бруски, они тянут вниз с одной и той же силой, и действие сил натяжения Fн1 и Fн2 приводит к тому, что на блок действует их результирующая сила. Но между собой эти силы натяжения будут равны, составляют они между собой прямой угол, поэтому при сложении этих сил получается квадрат вместо обычного параллелограмма. Искомая сила Fд является диагональю квадрата. Мы видим, что для результата нам необходимо найти силу натяжения нити. Проведем анализ: в какую сторону движется система из двух связанных брусков? Более массивный брусок, естественно, перетянет более легкий, брусок 1 будет соскальзывать вниз, а брусок 2 будет двигаться наверх по склону, тогда уравнение второго закона Ньютона для каждого из брусков будет выглядеть: 
Решение системы уравнений для связанных тел выполняется методом сложения, далее преобразовываем и находим ускорение:
= 
Это значение ускорения необходимо подставить в формулу для силы натяжения и найти силу давления на ось блока:
Мы выяснили, что сила давления на ось блока приблизительно равна 16 Н.
Заключение
Мы рассмотрели различные способы решения задач, которые многим из вас пригодятся в дальнейшем, чтобы понять принципы устройства и работы тех машин и механизмов, с которыми придется иметь дело на производстве, в армии, в быту.
2018-03-04 
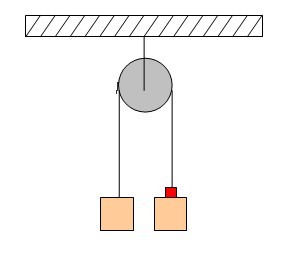
В системе, изображенной на рис., блоки невесомы, а нити — невесомы и нерастяжимы. Найти ускорение подвижного блока.
Решение:
Для подвижного блока и груза $M$ (рис.)
$2T_{1} — Mg = Ma$,
где $T_{1}$ — натяжение нити. Ускорения двух других грузов равны $2a$. Для груза $m$
$T_{2} — T_{1} — mg = m2a$.
Для первого груза
$mg — T_{2} = M2a$.
Решая систему полученных уравнений, найдем
$a = g frac{M — 2m}{5M + 4m}$.
Два тела
массами по 0,2 кг, на одном из которых лежит перегрузок массой 0,05 кг, связаны
невесомой нерастяжимой нитью, переброшенной через неподвижный блок. Определите
ускорения тел, силу давления перегрузка на тела и силу давления на ось блока.
Решение.
Систему
отсчета свяжем с лабораторией и будем считать ее инерциальной. Начало координат
выберем в точке, совпадающей с осью блока, ось OY направим вертикально вниз.
В качестве
физических систем будем поочерёдно рассматривать первое тело, второе тело,
перегрузок и блок. Причем, тела и перегрузок примем за материальные точки, а
блок будем считать абсолютно твердым телом.
Взаимодействием
с воздухом, массой
блока, массой нити и ее деформацией, а также трением в оси
блока пренебрегаем.
Для решения
задачи воспользуемся законами динамики (вторым законом Ньютона и законами для
частных сил). Движущиеся тела m1 , m2 и ∆m
взаимодействуют с
гравитационным полем Земли, т.е. на них действуют силы тяжести m1g , m2g и ∆m , направленные вертикально вниз;
взаимодействие тел m1 и m2 с нитью дает силы упругости T1 и T2 , направленные вертикально вверх;
кроме того, тело m2 взаимодействует с перегрузком ∆m , что дает силу давления перегрузка
на это тело F
и силу реакции N
, действующую со стороны этого тела на перегрузок.
Согласно
второму закону Ньютона, для каждого из движущихся тел получим систему
.
Если спроецировать
векторные величины на ось OY,
получим:
Поскольку нить
невесомая и нерастяжимая, то T1 = T2 = T
и a1 = a2 = a.
Согласно третьему закону
Ньютона F
= N. По условию задачи m1 = m2 = m. С учетом того динамические законы
движения тел можно записать следующим образом
Если решить эту систему
уравнений относительно неизвестных, получим:
Для нахождения силы
давления на ось блока рассмотрим силы, действующие на него. Взаимодействие блока
с нитью дает две силы упругости T’1
и T’2 направленные вертикально
вниз. С учетом того, что нить невесома и нерастяжима, имеем: T’1 = T’2 = T . Откуда найдем силу натяжения
Кроме того, на блок
действует сила реакции оси N’
, на которой этот блок закреплен. Таким образом, N’ + T’1 + T’2 = 0 , откуда N’ = T’1 + T’2 = 2T .
По третьему закону
Ньютона сила давления F’
на ось блока равно по модулю силе реакции оси N’ , т.е.
Численно: a = 1.1 м/с2; F = 0.44 H; F’ = 19 H.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.