Как найти ускорение свободного падения сатурна

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Масса Сатурна.

Масса Сатурна составляет 95,16 масс Земли. Среди всех планет Солнечной системы Сатурн стоит на втором месте по массе.

Масса и плотность Сатурна

Сила тяжести и ускорение свободного падения на Сатурне

Первая космическая скорость и вторая космическая скорость на Сатурне

Масса Солнца, Меркурия, Венеры, Земли, Луны, Марса, Юпитера, Сатурна, Урана, Нептуна

Масса и плотность Сатурна:

Масса Сатурна составляет 5,68 · 10²⁶ кг или, если быть точнее, 5,6834 ⋅ 10²⁶ кг. Она также составляет 95,16 масс Земли.

Среди всех планет Солнечной системы Сатурн стоит на втором месте по массе (после Юпитера).

Масса, как физическая величина, является мерой гравитационных свойств тела (гравитации, притяжения) и мерой его инертности. Соответственно различают гравитационную массу тела и инертную массу тела. В современной физике гравитационная масса и инертная масса считаются равными.

Как следствие проявления гравитационных свойств и действия закона всемирного тяготения два тела притягиваются друг к другу тем сильнее, чем больше их массы. Или чем больше масса тела, тем с большей силой она притягивает другие тела. Гравитационная масса определяет меру такого гравитационного притяжения (силы гравитационного притяжения).

Согласно закону всемирного тяготения сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием r, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния:

F = G · m₁ · m₂ / r² ,

где G – гравитационная постоянная, равная примерно 6,67⋅10⁻¹¹ м³/(кг·с²).

При этом масса тела не зависит от скорости движения тела и остается неизменным при любых процессах.

Масса измеряется в килограммах и относится к одной из семи основных единиц Международной системы единиц (СИ).

Исходя из массы Сатурна, как физической величины рассчитываются и другие параметры планеты: плотность, ускорение свободного падения, сила тяжести, первая космическая скорость, вторая космическая скорость и пр.

Средняя плотность Сатурна (ρ) – 0,687 г/см³ или 687 кг/м³. Для сравнения: средняя плотность Земли (ρ) – 5,5153 г/см³.

Сила тяжести и ускорение свободного падения на Сатурне:

Ускорение свободного падения на экваторе Сатурна (g) равно 10,44 м/с² или 1,064 g Земли. Для сравнения: на Земле ускорение свободного падения составляет  9,81 м/с² и меняется от 9,832 м/с² на полюсах до 9,78 м/с² на экваторе.

Сила тяжести на Сатурне в 1,064 раза больше, чем на Земле, т.е. практически равна земной. Это означает, что человек, весящий 72 кг, будет весить на Сатурне всего 76,6 кг, т.е. около 77 кг. Каждый шаг потребует в 1,064 раз больше усилий, чем на Земле. Если быть точнее, то вес человека на Земле равен 72 кг · 9,81 м/с² = 706,32 Н, а вес на Сатурне равен 72 кг · 10,44 м/с² = 751,68 Н. В то время масса человека на Сатурне (72 кг) будет одинаковой, что и на Земле (72 кг).

Вес – это сила, с которой любое тело, находящееся в поле сил тяжести (как правило, создаваемое каким-либо небесным телом, например, Землёй, Солнцем и т. д.), действует на опору или подвес, препятствующие свободному падению тела. Вес тела, покоящегося в инерциальной системе отсчёта, равен силе тяжести, действующей на тело. Сила тяжести – это сила притяжения тела к небесному телу.

Вес (сила тяжести) рассчитывается по формуле F = m·g ,

где

F – сила тяжести, Н,

m – масса тела, кг,

g – ускорение свободного падения, м/с².

Первая космическая скорость и вторая космическая скорость на Сатурне:

Первая космическая скорость (v₁) на Сатурне равна 25,535 км/с. Для сравнения: первая космическая скорость на Земле равна 7,91 км/с.

Первая космическая скорость (круговая скорость) – это минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.

Первая космическая скорость определяется массой и радиусом небесного тела, а также высотой над его поверхностью.

Первая космическая скорость вычисляется по формулам:

,

,

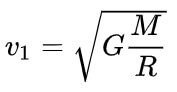
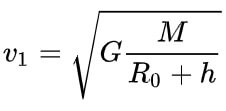
где

М – масса планеты, кг,

R – радиус орбиты, м,

R₀ – радиус планеты, м,

h – высота над поверхностью планеты, м.

Вторая космическая скорость (v₂) на Сатурне равна 35,5 км/с. Она в 3,172 раза больше второй космической скорости на Земле. Для сравнения: вторая космическая скорость на Земле равна 11,19 км/с.

Вторая космическая скорость (параболическая скорость, скорость освобождения, скорость убегания) – это наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него.

Вторая космическая скорость определяется радиусом и массой небесного тела.

Вторая космическая скорость вычисляется по формулам:

,

.

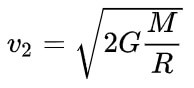
Источник: https://ru.wikipedia.org/wiki/Сатурн, https://nssdc.gsfc.nasa.gov/planetary/factsheet/saturnfact.html

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
1 359

UCHEES.RU — помощь студентам и школьникам

Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.

2020 — 2023 — UCHEES.RU

Массы планет и секреты расчёта ускорений свободного падения.

Аннотация. Ускорения свободного падения на планеты зависят от массы планет.
Массы планет и ускорения свободного падения на них приведены в соответствие.

Annotation. The acceleration of free fall on the planets depends on the mass of the planets. The masses of the planets and the acceleration of free fall on them are brought into line.

Ключевые слова: масса; ускорение свободного падения; гравитационная постоянная; планета

Keywords: mass; acceleration of gravity; gravitational constant; planet

УДК 53
Введение. Продолжая исправлять ошибки, заложенные в закон всемирного тяготения и раскрытые в работе: Массы планет и глобальная ошибка их расчёта

http://www.newtheory.ru/physics/massi-p … t6260.html

, найдена методика, с помощью которой определили ускорения свободного падения на планеты. Для каждой планеты определили, гравитационную постоянную.
Актуальность данной работы обусловлены тем, что выведенные справочные массы планет и ускорения свободного падения на них не соответствуют действительности. При освоении космоса, этот факт может привести к огромным тратам материальных средств и не запланированные потери космических аппаратов. Знания, получаемые с искажёнными данными, наносят вред не одному поколению учащихся, студентов, ученых, заставляя принимать эти данные за истину и искать от них закономерности в космологических параметрах, и делать ошибочные расчёты.
Цели и задачи работы заключаются в том, чтобы опираясь на формулы, найти ускорения свободного падения на планетах в зависимости от массы планет.
Научная новизна работы заключается в том, что удалось по — новому взглянуть на связь и зависимость ускорений свободного падения с массой планет.
Опираясь на работы: [1];[2];[3]; [4];[5];[6];[7]; [8]; [9]; [10]; [11];[12]; [13]; [14]; [15], а также:
Массы планет и глобальная ошибка их расчёта.

http://www.newtheory.ru/physics/massi-p … t6260.html

;
Что не так в ускорениях свободного падения?

http://www.newtheory.ru/physics/chto-ne … t6259.html

, найдены ускорения свободного падения на каждую планету, а так же для каждой планеты определена гравитационная постоянная.

В связи с тем, что закон всемирного тяготения сводиться к одной из сил третьего закона И. Ньютона, а гравитационная постоянная является ликвидатором одной из масс в расчётах и служит частью формулы для нахождения ускорения оставшейся массы. При этом при расчёте масс ускорения искажены, а для расчёта по закону всемирного тяготения, ускорения остались, что приводит к искажению определения силы по массе и ускорению.
Поэтому определение ускорения свободного падения по формуле:
F = GMm/R^2 — (1), приводит к ошибке.
F = GMm/R^2 — (1),
где: F – сила взаимодействия двух тел; М – масса центрального тела; m – масса тела на орбите вокруг центрального тела; R – расстояние между центрами тел; G – гравитационная постоянная.
Для определения ускорения свободного падения в эту формулу подставить массы, найденные по третьему закону И. Ньютона, оставив общепринятую G, проблему не решит, так как это всего лишь подгоночный коэффициент и какие искажения в параметрах этот коэффициент тянет за собой, предстоит ещё выяснить. Зачем нам нужна G, если установлено, что сила взаимодействия по закону всемирного тяготения равна одной из сил третьего закона И.Ньютона?
Поэтому приведём ускорения свободного падения и массы в соответствие.
Массы планет определены в работе:
«Расчётная масса Меркурия: 9,14319849411771 * 10^23 кг
Расчётная масса Венеры: 3,124673087913046 *10 ^24 кг
Масса Земли: 5,9726*10^24 кг
Расчётная масса Марса: 13,86394880873882 *10^24 кг.
Расчётная масса Юпитера: 1,614014900441029 *10^26 кг
Расчётная масса Сатурна: 5,391109952886316 * 10^26 кг
Расчётная масса Урана: 21, 96701058680913 * 10^26 кг
Расчётная масса Нептуна: 53, 99274237341659 *10^26 кг»

Расширение закономерностей и определение массы у планет. — Астрономия — Новая Теория

http://www.newtheory.ru/astronomy/rassh … t6190.html

Ускорения свободного падения для масс планет вычислим, опираясь на работу:
Что не так в ускорениях свободного падения?

http://www.newtheory.ru/physics/chto-ne … t6259.html

и проведя более точные расчёты.
Масса Земли: 5,9726*10^24 кг
9,780327 м/с^2
Проведённые вычисления, привели к знаменателю геометрической прогрессии:1,764.
Если каждый следующий порядок по массе вызывает изменение по ускорению свободного падения на знаменатель геометрической прогрессии:1,764.
То внутри каждого порядка, ускорение свободного падения измениться на 10 единиц, знаменатель геометрической прогрессии: 1,764. А при изменении массы на одну единицу, знаменатель геометрической прогрессии равен 0,1764. При изменении массы на одну десятую, знаменатель геометрической прогрессии равен: 0,01764. При изменении массы на одну сотую, знаменатель геометрической прогрессии равен; 0,001764.
Найдём ускорение свободного падения на массу тела, кратную массе Солнца:
1,9885*10^24 кг
5,9726*10^24 кг — 1,9885*10^24 кг = 3,9841*10^24 кг
3*0,1764 = 0,5292
9 * 0,01764 = 0,15876
8 * 0,001764 = 0,014112
0,5292 + 0,15876 + 0,014112 = 0,701276
9,780327 м/с^2 — 0,702072 м/с^2 = 9,078255 м/с^2
1,9885*10^24 кг — 9,078255 м/с^2
Проверим знаменатель геометрической прогрессии 1,764 .
1,9885*10^24 кг — 9,078255 м/с^2
1,9885*10^25 кг — 16,01404182 м/с^2
1,9885*10^26 кг — 28,24876977048 м/с^2
1,9885*10^27 кг — 49,83082987512672 м/с^2
1,9885*10^28 кг — 87,90158389972353 м/с^2
1,9885*10^29 кг — 155,0583939991123 м/с^2
1,9885*10^30 кг — 273,5230070144341 м/с^2
1,9885*10^23 кг — 5,14640306122449 м/с^2
1,9885*10^22 кг — 2,91746205284835 м/с^2
1,9885*10^21 кг — 1,653890052635119 м/с^2
1,9885*10^20 кг — 0,9375793949178679 м/с^2

Рассчитаем ускорение свободного падения для Меркурия:
Расчётная масса Меркурия: 9,14319849411771 * 10^23 кг

Находим для пробного тела массой: 9,14319849411771 * 10^24 кг, ускорение свободного падения на его поверхность будет равно:
9,14319849411771 * 10^24 кг — 5,9726*10^24 кг = 3,17059849411771*10^24 кг
3*0,1764 = 0,5292
1 * 0,01764 = 0,01764
7 * 0,001764 = 0,012348
0,5292 + 0,01764 + 0,012348 = 0,559188
9,780327 м/с^2 + 0,559188 м/с^2 = 10,339515 м/с^2
9,14319849411771 * 10^24 кг —- 10,339515 м/с^2
Ускорение свободного падения на Меркурий равно: 5,86140306122449 м/с^2
10,339515 м/с^2 / 1,764 = 5,86140306122449 м/с^2
Подставим в формулу(2) и найдём G для Меркурия:
«Гравитационная постоянная G связана с параметрами тел следующей зависимостью:
G = (r(1)^2 *g(1) / M —- (2),
где: r(1) – радиус тела M; g(1) – ускорение свободного падения на тело M;
G = (r(1)^2 *g(1) / M = (2,4397 *10^6 м)^2 * 5,86140306122449 м/с^2 / 9,14319849411771 * 10^23 кг = 3,815718177965394 * 10^-11 м^3/ с^2 кг
G(м) = 3,815718177965394 * 10^-11 м^3/ с^2 кг
Проверочный расчёт показал, что подгоночный коэффициент G искажал ускорения свободного падения на поверхность Меркурия.
Этот коэффициент G просто подгоночный коэффициент, который выдали за гравитационную постоянную.

Находим ускорение свободного падения на поверхность Венеры.
Расчётная масса Венеры: 3,124673087913046 *10 ^24 кг
5,9726*10^24 кг — 3,124673087913046 *10 ^24 кг = 2,847926912086954*10 ^24 кг
2*0,1764 = 0,3528
8 * 0,01764 = 0,14112
4 * 0,001764 = 0,007056
0,3528 + 0,14112 + 0,007056 = 0,500976
9,780327 м/с^2 — 0,500976 м/с^2 = 9,279351 м/с^2
Ускорение свободного падения на поверхность Венеры: 9,279351 м/с^2
Подставим в формулу(2) и найдём G для Венеры:
«Гравитационная постоянная G связана с параметрами тел следующей зависимостью:
G = (r(1)^2 *g(1) / M —- (2),
G = (6,0518 *10^6 м)^2 * 9,279351 м/с^2 / 3,124673087913046 *10 ^24 кг = 108,7632433043935* 10^-12 м^3/ с^2 кг
G(в) =10,87632433043935 *10^-11 м^3/ с^2 кг
Гравитационная постоянная для Венеры, далека от справочной.

Находим ускорение свободного падения на поверхность Марса.
Расчётная масса Марса: 13,86394880873882 *10^24 кг = 1,386394880873882 *10^25 кг.
5,9726*10^24 кг — 1,386394880873882 *10^24 кг = 4,586205119126118*10^24 кг
4*0,1764 = 0,7056
5 * 0,01764 = 0,0882
8 * 0,001764 = 0,014112
0,7056 + 0,0882 + 0,014112 = 0,807912
9,780327 м/с^2 — 0,807912 м/с^2 = 8,972415 м/с^2
Ускорение свободного падения на поверхности Марса: 15,82734006 м/с^2
8,972415 м/с^2 * 1,764 = 15,82734006 м/с^2
Подставим в формулу(2) и найдём G для Марса:
G = (r(1)^2 *g(1) / M —- (2),
G = (3,3962 *10^6 м)^2 * 15,82734006 м/с^2 / 1,386394880873882 *10^25 кг = 131,6762660420172*10^-13 м^3/ с^2 кг
G(мар.) =1,316762660420172*10^-11 м^3/ с^2 кг

Находим ускорение свободного падения на поверхность Юпитера.
Расчётная масса Юпитера: 1,614014900441029 *10^26 кг
5,9726*10^24 кг — 1,614014900441029 *10^24 кг = 4,358585099558971*10^24 кг
4*0,1764 = 0,7056
3 * 0,01764 = 0,05292
5 * 0,001764 = 0,00882
0,7056 + 0,05292 + 0,00882 = 0,76734
9,780327 м/с^2 — 0,76734 м/с^2 = 9,012987 м/с^2
Ускорение свободного падения на поверхности Юпитера: 28,045675595952 м/с^2
9,012987 м/с^2 *1,764 = 15,898909068 *1,764 = 28,045675595952 м/с^2
Находим гравитационную постоянную для Юпитера:
G = (r(1)^2 *g(1) / M —- (2),
G(ю) = (7,1 492 *10^7м)^2 * 28,045675595952 м/с^2 / 1,614014900441029 *10^26 кг =
888,123291602068 *10^-12 м^3/ с^2 кг
G(ю) = 88,8123291602068 *10^-11 м^3/ с^2 кг

Находим ускорение свободного падения на поверхность Сатурна.
Расчётная масса Сатурна: 5,391109952886316 * 10^26 кг
5,9726*10^24 кг — 5,391109952886316 *10^24 кг = 0,581490047113684*10^24 кг
5 * 0,01764 = 0,0882
8 * 0,001764 = 0,014112
0,0882 + 0,014112 = 0,102312
9,780327 м/с^2 — 0,102312 м/с^2 = 9,678015 м/с^2
Ускорение свободного падения на поверхность Сатурна: 30,11504056344 м/с^2
9,678015 м/с^2 * 1,764 = 17,07201846 * 1,764 = 30,11504056344 м/с^2
Находим гравитационную постоянную для Сатурна:
G = (r(1)^2 *g(1) / M —- (2),
G(с) = (6,0 268*10^7м)^2 * 30,11504056344 м/с^2 / 5,391109952886316 * 10^26 кг =
202,8984933928397*10^-12 м^3/ с^2 кг
G(с) = 20,28984933928397*10^-11 м^3/ с^2 кг

Находим ускорение свободного падения на поверхность Урана.
Расчётная масса Урана: 21, 96701058680913 * 10^26 кг = 2,196701058680913 *10^27 кг
5,9726*10^24 кг — 2,196701058680913 *10^24 кг = 3,775898941319087*10^24 кг
3*0,1764 = 0,5292
7 * 0,01764 = 0,12348
7 * 0,001764 = 0,012348
0,5292 + 0,12348 + 0,012348 = 0,665028
9,780327 м/с^2 — 0,665028 м/с^2 = 9,115299 м/с^2
Ускорение свободного падения на поверхность Урана: 50,03416556705146 м/с^2
9,115299 м/с^2 * 1,764 = 16,079387436 *1,764 = 28,364039437104 *1,764 = 50,03416556705146 м/с^2
Находим гравитационную постоянную для Урана:
G = (r(1)^2 *g(1) / M —- (2),
G(у) = (2,5 559 *10^7 м)^2 * 50,03416556705146 м/с^2 / 2,196701058680913 *10^27 кг =
148,7933144290646 *10^-13 м^3/ с^2 кг
G(у) = 1,487933144290646 *10^-11 м^3/ с^2 кг

Находим ускорение свободного падения на поверхность Нептуна.
Расчётная масса Нептуна: 53, 99274237341659 *10^26 кг = 5,399274237341659 *10^27 кг
5,9726*10^24 кг — 5,399274237341659 *10^24 кг = 0,573325762658341*10^24 кг
5 * 0,01764 = 0,0882
7 * 0,001764 = 0,012348
0,0882 + 0,012348 = 0,100548
9,780327 м/с^2 — 0,100548 м/с^2 = 9,679779 м/с^2
Ускорение свободного падения на поверхность Нептуна: 53,13261420590458 м/с^2
9,679779 м/с^2 * 1,764 = 17,075130156 *1,764 = 30,120529595184*1,764 = 53,13261420590458 м/с^2
Находим гравитационную постоянную для Нептуна:
G = (r(1)^2 *g(1) / M —- (2),
G(н) = (2,4 764 *10^7 м)^2 * 53,13261420590458 м/с^2 / 5,399274237341659 *10^27 кг =
60,34862626497043*10^-13 м^3/ с^2 кг
G(н) = 0,6034862626497043*10^-11 м^3/ с^2 кг

Ускорение свободного падения на Меркурий равно: 5,86140306122449 м/с^2
Ускорение свободного падения на поверхность Венеры: 9,279351 м/с^2
Ускорение свободного падения на поверхности Марса: 15,82734006 м/с^2
Ускорение свободного падения на поверхности Юпитера: 28,045675595952 м/с^2
Ускорение свободного падения на поверхность Сатурна: 30,11504056344 м/с^2
Ускорение свободного падения на поверхность Урана: 50,03416556705146 м/с^2
Ускорение свободного падения на поверхность Нептуна: 53,13261420590458 м/с^2

G(м) = 3,815718177965394 * 10^-11 м^3/ с^2 кг
G(в) = 10,87632433043935 *10^-11 м^3/ с^2 кг
G(мар.) =1,316762660420172*10^-11 м^3/ с^2 кг
G(ю) = 88,8123291602068 *10^-11 м^3/ с^2 кг
G(с) = 20,28984933928397*10^-11 м^3/ с^2 кг
G(у) = 1,487933144290646 *10^-11 м^3/ с^2 кг
G(н) = 0,6034862626497043*10^-11 м^3/ с^2 кг

Заключение.
Массы планет приведены в соответствии с ускорениями согласно третьему закону И. Ньютона. Согласно массам планет, найдены ускорения свободного падения на них.
Найдены гравитационные постоянные для каждой планеты.
Выводы.
Ускорения свободного падения на планетах приведены в соответствие с их массами.
Доказано, что гравитационная постоянная G, таковой не является.
Все планеты на орбитах вокруг Солнца располагаются в полном соответствии с массой и ускорением в соответствии с третьим законом И. Ньютона. И этот факт свидетельствует о том, что лёгкие тела падают на центральное тело быстрее, чем тяжёлые. Поэтому планеты расположены от Солнца по мере удаления более тяжёлые. Все приведённые факты подтверждены расчётами. В связи с новыми данными, появятся новые закономерности космологических параметров.

Библиографический список:

1. Законы Кеплера /электронный ресурс/

https://questions-physics.ru/mehanika/z

… plera.html
Дата посещения: 28.07.2021г
2. Астронет > Массы небесных тел (методы определения) /электронный ресурс/

http://www.astronet.ru/db/msg/1188435

Дата посещения: 28.07.2021г
3. Как измеряют массу планет, звёзд и галактик: просто о сложном /электронный ресурс/

https://spacegid.com/kak-izmerjajut-massu-planet.html

Дата посещения: 28.07.2021г
4. Массы планет [1948 Уиппл Ф. — Земля, Луна и Планеты] /электронный ресурс/

http://www.adeva.ru/books/item/f00/s00/

… t011.shtml
Дата посещения: 28.07.2021г
5. § 31. Вычисление массы Солнца, Земли и планет
Дата посещения: 28.07.2021г

https://scask.ru/e_book_p_phis1.php?id=33

6. Г. И Ширмин. МАССЫ НЕБЕСНЫХ ТЕЛ • Большая российская энциклопедия — электронная версия /электронный ресурс/

https://bigenc.ru/physics/text/2191424

Дата посещения: 28.07.2021г
7. Дудин А.Т. Скрытые параметры константы G. — Астрономия — Новая Теория /электронный ресурс/

http://www.newtheory.ru/astronomy/skrit

… t6139.html Дата размещения: 15.02.2021 г.
8. Дудин А.Т. Тайна закона всемирного тяготения. — Астрономия — Новая Теория /электронный ресурс/

http://www.newtheory.ru/astronomy/tayna

… t6143.html Дата размещения: 19.04.2021 г.
9. Дудин А.Т. Расширение закономерностей и определение массы у планет. — Астрономия — Новая Теория /электронный ресурс/

http://www.newtheory.ru/astronomy/rassh

… t6190.html Дата размещения: 21.04.2021 г.
10. Дудин А.Т. Закономерности и скорости планет. — Астрономия — Новая Теория /электронный ресурс/

http://www.newtheory.ru/astronomy/zakon

… t6162.html Дата размещения: 28.03.2021 г.
11. Дудин А.Т. Закономерности и скорости спутников планет. — Астрономия — Новая Теория

http://www.newtheory.ru/astronomy/zakon

… t6168.html Дата размещения: 01.04.2021 г.
12. Дудин А.Т. Объединение космических параметров более двух тел. — Астрономия — Новая Теория /электронный ресурс/

http://www.newtheory.ru/astronomy/obedi

… t6137.html Дата размещения: 15.01.2921 г.
13. Дудин А.Т. Открытие закономерностей в космологических параметрах Солнеч — Астрономия — Новая Теория /электронный ресурс/

http://www.newtheory.ru/astronomy/otkri

… t6117.html Дата размещения: 27.01.2021 г.
14. Дудин А.Т. Выявлены закономерности в космологических параметрах. — Астрономия — Новая Теория /электронный ресурс/

http://www.newtheory.ru/astronomy/viyav

… t6127.html Дата размещения: 05.02.2021 г.
15. Дудин А.Т. Связь космических скоростей. — Астрономия — Новая Теория /электронный ресурс/

http://www.newtheory.ru/astronomy/svyaz

… t6136.html
Дата размещения: 15. 02.2021 г.

06.08. 2021 г. С уважением А.Т. Дудин.

Код ссылки на тему, для размещения на персональном сайте | Показать