ФЕДЕРАЛЬНОЕ
АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО
ОБРАЗОВАНИЯ
ДОНСКОЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра
физики
Определение ускорения свободного падения на машине Атвуда.
Методические
указания к лабораторной работе №20
(Раздел
«Механика»)
Ростов-на-Дону
2010
Составители:
В.С. Ковалёва, В.С. Кунаков, О.А. Лещёва,
О.М.
Холодова.
УДК
530.1
ОПРЕДЕЛЕНИЕ
УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ НА МАШИНЕ
АТВУДА: Метод. указания. -Ростов н/Д:
Издательский
центр ДГТУ, 2010. — 11 с.
Указания
содержат краткое описание рабочей
установки и методику определения
ускорения свободного падения с помощью
машины Атвуда.
Методические
указания предназначены для студентов
инженерных специальностей всех форм
обучения при выполнении лабораторных
работ по физике (раздел «Механика и
молекулярная физика»).
Печатается
по решению методической комиссии
факультета «Нанотехнологии и композиционные
материалы»
Научный
редактор канд. хим. наук, доц.
А.Я. Шполянский
©
Издательский центр ДГТУ, 2010
Лабораторная
работа №20
Определение ускорения свободного падения на машине Атвуда.
Цель
работы:
экспериментально определить ускорение
свободного падения.
Приборы
и принадлежности:
машина Атвуда ФПН02-ПС, набор основных
и дополнительных грузиков, электронный
секундомер.
Теоретическая часть.
Свободным
падением
называется движение, которое совершало
бы тело только под действием силы
тяжести. Такое движение может быть,
например, в трубке, из которой выкачали
воздух. При свободном падении тела с
небольшой высоты
от поверхности Земли (,
где
– радиус Земли) оно движется с постоянным
ускорением
,
направленным по вертикали вниз.
Ускорение
называется
ускорением
свободного падения.
Оно одинаково для всех тел и зависит
лишь от высоты над уровнем моря и от
географической широты на поверхности
Земли. Ускорение
максимально на полюсах и минимально
на экваторе Земли.
Впервые
ускорение свободного падения было
экспериментально определено итальянским
физиком Г.Галилеем.
Описание метода и экспериментальной установки для определения ускорения свободного падения.
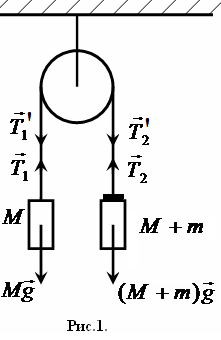
основан на исследовании движения двух
грузов, связанных нитью, перекинутой
через неподвижный блок (рис.1).
Грузы
имеют одинаковые массы
,
величина которых значительно превышает
массу нити. Если на один из грузов
положить дополнительный груз (перегрузок)
массы
,то
они начинают двигаться прямолинейно и
равно-ускоренно с некоторым ускорением
,
а блок начинает вращаться с угловым
ускорением.
Применяя
второй закон Ньютона, запишем уравнения
движения грузов в проекциях на оси:
а)
для груза без перегрузка:
,
(1)
б)
для груза с перегрузком:
, (2)
где
– ускорение движения грузов,
и
— силы натяжения нити (см. рис.1),
—
ускорение свободного падения.
Уравнение
вращения блока (т.к. по 3-му закону Ньютона
и
):
,
(3)
где
— момент инерции блока,
— угловое ускорение блока,
— радиус блока.
Решая
систему уравнений (1), (2) и (3), получим
формулу для определения ускорения
свободного падения в виде:
(4)
Из
выражения (4) следует, что для определения
ускорения свободного падения необходимо
знать массы грузов
и перегрузка
,
момент инерции блокаи
ускорение движения грузов.
Ускорение
движения грузов определяется из формулы
пути при равноускоренном движении:
,
откуда (5)
где
— время, в течение которого грузы
перемещаются на величину.
Подставив
в формулу (4) выражение ускорения (5),
получим:

(6).
Силы
натяжения нити
и
имеют различные значения и могут быть
определены из уравнений (1) и (2)
(7)
(8)
Если
момент инерции блока настолько мал, что
величиной
можно пренебречь по сравнению с массой
грузов,
то выражение (6) получает вид:
(9)
Силы
натяжения нити при условии
имеют одинаковые значения
.
Определить силу натяжения можно из
формул (7) либо (8).
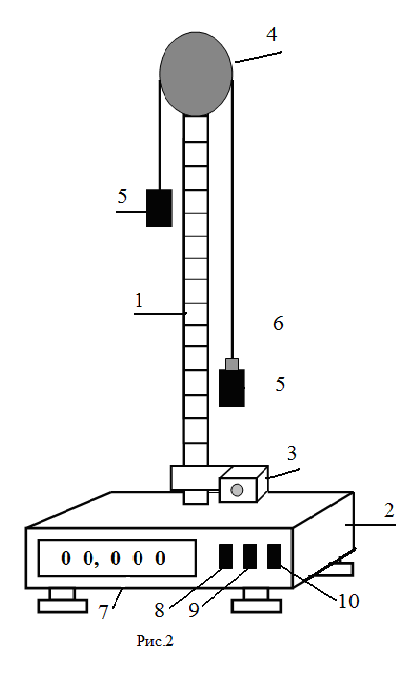
Общий
вид машины Атвуда приведен на рис.2.
Её
конструкция была предложена Д.Атвудом
и названа в его честь. Машина представляет
собой настольный прибор с вертикальной
стойкой 1, на которой крепятся все
основные элементы машины Атвуда, и
основание 2. На вертикальной стойке 1
расположены два кронштейна: нижний 3 и
верхний 4. На верхнем кронштейне 4 крепится
блок с узлом подшипников
качения,
через блок перекинута нить с грузами 5
одинаковой массы. Перегрузок 6 кладут
на правый груз 5. На верхнем кронштейне
находится электромагнит, который с
помощью фрикциона при подаче на него
напряжения, удерживает систему с грузами
в неподвижном состоянии. На нижнем
кронштейне 3 крепится фотодатчик,
который выдает электрический сигнал
окончания счета времени равноускоренного
движения грузов. Нижний кронштейн 3
представляет собой площадку с резиновым
амортизатором, о который ударяется груз
при его остановке. Нижний кронштейн
имеет возможность свободного перемещения
и фиксации на вертикальной стойке по
всей ее свободной длине. На вертикальной
стойке 1 укреплена миллиметровая линейка,
по которой определяют начальное и
конечное положения грузов, а следовательно,
и пройденный путь. Начальное положение
определяют визуально по нижнему срезу
грузов, конечное положение – по индексу
нижнего кронштейна. Секундомер 7 выполнен
самостоятельным прибором и соединен
кабелем с датчиком (фотоэлектрическим).
На установке кнопка 8 — «сброс времени»,
кнопка 9 – «пуск», кнопка 10 – «сеть»
Соседние файлы в папке Лаб.мех
- #
- #
- #
- #
- #
- #
- #
- Мой первый физический эксперимент.
- Определение ускорения свободного падения с помощью математического маятника.
- Надо делать все по-другому…
- Ускорение свободного падения и закон всемирного тяготения
- Ускорение свободного падения на различных широтах
- Как найти ускорение свободного падения на Марсе???
Мой первый физический эксперимент.
Свой самый первый физический эксперимент с гравитацией я поставил более 30 лет назад, когда мне было года 4 наверно.
Я скинул кота с балкона. К счастью, он остался жив, и даже позже сам повторил этот опыт, пытаясь поймать голубя. И опять же остался жив. Несмотря на то, что это был пятый этаж. Не даром говорят, что у кошек девять жизней.
Но так или иначе прошу вас не повторять мои ошибки, и не ставить опыты над животными. Или как Эрвин Шредингер делайте их мысленно.
Определение ускорения свободного падения с помощью математического маятника.
Здравствуйте дорогие друзья, меня зовут Валентин Анатольевич и сегодня я покажу вам как рассчитать ускорение свободного падения, не кидая котов с балкона.
Итак, нам понадобится яблоко и шнурок. Ну или толстая леска как в моем случае. Соединяем леску с яблоком. И получаем некое подобие математического маятника.
Я эту конструкцию называю яблотник. Моя последняя разработка.
Время, за которое маятник совершает полное колебание называется периодом. В нашем случае это время полета яблока туда и обратно. У меня оно составило 1,4 секунды.
Для математических маятников период определяется по следующему уравнению:
Где — это длинна маятника, а
— ускорение свободного падения. Его нам и необходимо найти. Вспоминаем зачем нам нужна алгебра и выражаем
.
Осталось только с помощью линейки найти длину нашего яблотника и произвести расчеты.
Обратите внимание, так как в нашем случае яблоко не является материальной точкой и его размерами пренебречь не получится, за длину маятника мы будем брать длину лески плюс половинку высоты яблока. Я намерил 49 сантиметров.
Подставляем значения и считаем.
Получается примерно 9.86 м/с 2
Надо делать все по-другому…
Да!!! По-хорошему стоило сделать по-другому. Позволить маятнику совершить несколько колебаний, потом общее время за которое эти колебания были совершены поделить на их количество, тем самым получить среднее значение периода колебаний, и только после этого производить расчеты.
Да и посчитать погрешность так же не помешало бы…
Ну, зато теперь вы знаете, как увлекательно провести выходные.
Ускорение свободного падения и закон всемирного тяготения
При желании ускорение свободного падения можно вычислить из закона всемирного тяготения. Сила, с которой тела притягиваются к Земле вычисляется по следующему уравнению:
Где F- сила тяжести, G — гравитационная постоянная, М — масса Земли, m — масса тела, а R — расстояние между их центрами масс. Если тело находится непосредственно на поверхности Земли, то за R можно принять её радиус.
Согласно второму закону Ньютона, сила тяжести, действующая на тело равна произведению массы тела на ускорение свободного падения.
Приравниваем правые части наших уравнений и сокращаем массу.
Осталось только подставить все необходимые значения переменных и произвести расчеты.
Получается 9.82 м/с 2. Все как в учебнике по Физике. И самое главное ни один котик не пострадал.
Ускорение свободного падения на различных широтах
Стоит отметить, что для расчетов я брал усреднённое значение радиуса Земли. В реальности ускорение свободного будет изменяться в зависимости от широты.
Так экваториальный радиус больше, чем полярный, соответственно на полюсах ускорение свободного падения будет чуть выше, чем на экваторе.
| Широта | g, м/с2 |
| 0° | 9.78030 |
| 10° | 9.78186 |
| 20° | 9.78634 |
| 30° | 9.79321 |
| 40° | 9.80166 |
| 50° | 9.81066 |
| 60° | 9.81914 |
| 70° | 9.82606 |
| 80° | 9.83058 |
| 90° | 9.83216 |
А если учесть еще и неровности рельефа, горы холмы…. В общем выходит довольно переменчивая константа.
Как найти ускорение свободного падения на Марсе???
А какое ускорение свободного падения на Марсе? И какой период колебаний будет там у нашего маятника? Пишите в комментариях. Ну а я с вами прощаюсь. Желаю счастья и до скорых встреч.
В статье обсуждается несколько подходов к нахождению ускорения свободного падения.
Ускорение свободного падения — это ускорение свободного падения объекта в вакууме с равномерной скоростью, несмотря на его массу, из-за силы тяжести. С помощью законов Ньютона, которые описывают силу тяжести, мы можем обнаружить ускорение силы тяжести или ускорение силы тяжести.
Ускорение свободного падения зависит от гравитирующего тела большой массы M, но не зависит от тела m малой массы. Вот почему тела небольшой массы падают вниз к гравитирующему телу, несмотря на его массу. Поэтому ускорение свободного падения называют ускорение свободного падения or ускорение силы тяжести, обозначается как ‘g’.
Поскольку сила вызывает такое ускорение, мы можем определить значение g с помощью нескольких подходов, использующих Законы движения Ньютона.
Прочтите, как рассчитать массу по гравитационной силе.
Как найти ускорение свободного падения с помощью законов Ньютона
Давайте рассчитаем значение g, используя второй закон движения Ньютона и закон всемирного тяготения.
Второй закон движения Ньютона дает силу тяжести между объектом и землей, тогда как закон всемирного тяготения дает силу гравитации между двумя объектами. Когда мы сравниваем обе силы гравитации, мы получаем значение ускорения свободного падения g.
Сила тяжести Fg определяется Второй закон Ньютона является,
Fg = мг …………………… .. (1)
Сила тяжести Fg определяется закон всемирного тяготения является,
Fg=GMм/об2
Где M — масса гравитирующего объекта, т. Е. Земли.
r — расстояние между центром масс объекта и земли.
А G — постоянная гравитационной пропорциональности.
Сравнивая обе силы тяжести Fg в уравнениях (1) и (2),
мг=ГМм/р2
г=ГМм/мр2
г=Гм/р2
Вышеупомянутая формула является стандартной формулой для расчета ускорения свободного падения g.
Как вы заметили, масса падающего тела m аннулируется при определении g, так как гравитационное ускорение зависит только от гравитации земной массы M.
Узнайте больше о законах Ньютона.
Рассчитайте ускорение свободного падения шара, падающего на земная поверхность. Масса земли 6 х 1024 кг, а расстояние между объектом и землей составляет 6.38 X 106 м. (G = 6.67 x 10-11 Нм2/ кг2)
Данный:
М = 6 х 1024 kg
г = 6.38 Х 106 m
G = 6.67 х 10-11 Nm2/ кг2
Найти: g =?
Формула:
Fg = мг
Решения:
Сила тяжести из-за Второй закон Ньютона находится в движении,
Fg = мг
г=Фg/m
Подставляя закон гравитации формулу (2) в приведенное выше уравнение,
г=ГМм/мр2
г=Гм/р2
Подставляя все значения,
г = 9.86
Ускорение свободного падения падающего у земной поверхности шара составляет 9.86 м / с.2.
Сила тяжести — это сила тяжести, которая различна для разных масс M. Следовательно, значение g также немного отличается для других планет из-за разной массы..
Прочтите, как рассчитать массу по силе и расстоянию.
Луна имеет массу 7.35 X 10.22 кг, а расстояние между центром масс 1.74 X 106м. Вычислите ускорение свободного падения космонавта, идущего по Луне.
Данный:
М = 7.35 х 1022 kg
г = 1.74 Х 106m
G = 6.67 х 10-11 Nm2/ кг2
Найти: г =?
Формула:
г=ГМ/р2
Решения:
Ускорение свободного падения космонавта рассчитывается с использованием Законы Ньютона,
г=ГМ/р2
Подставляя все значения,
г = 1.619
Ускорение свободного падения космонавта на Луне составляет 1.619 м / с.2.
Если объект движется на определенной высоте h от гравитирующей поверхности; подобно тому, как спутник вращается на высоте h от земли, радиус между ними становится R (r + h). Следовательно, величина ускорения свободного падения g также изменяется из-за изменения радиуса r.
Узнать больше о наклонной плоскости.
Если спутник движется по орбите на высоте около 280 км над земной поверхностью, какое гравитационное ускорение он испытывает?
Данный:
М = 6 х 1024 kg
G = 6.67 х 10-11 Nm2/ кг2
г = 6.38 Х 106 m
h = 280 км = 0.28 X 106 m
R = (r + h) = (6.38 Х 106 + 0.28 Х 106) = 6.66 х 106 m
Найти: g =?
Формула:
г=ГМ/р2
Решения:
Ускорение свободного падения рассчитывается с использованием Законы Ньютона,
г=ГМ/р2
Подставляя все значения,
г = 9.02
Ускорение свободного падения на спутнике, вращающемся над землей, составляет 9.02 м / с.2.
Как найти ускорение свободного падения с помощью третьего закона Кеплера
Рассчитаем значение g, используя Третий закон Кеплера следующим образом:
Третий закон Кеплера касается орбитального движения планет, согласно которому период обращения по орбите пропорционален ее большой полуоси. Период времени планеты получается путем сравнения центростремительной силы и силы тяжести, обусловленной законом всемирного тяготения.
(Кредит: Shutterstock)
Компания центростремительная сила на орбитальной планете
Fc=мв2/r
Сравнение центростремительная сила уравнение (4) с закон всемирного тяготения (2)
mv2/ г = Гм/р2
v2=ГМ/р
Скорость = Расстояние / Время
Расстояние до планеты, когда она движется по орбите = 2πr
v=2πr/T
v2=4π2r2
Подставляя указанное выше уравнение в уравнение (5),
4p2r2/T2=ГМ/р
T2=4π2r3/ГМ
Выше уравнение период времени на орбите планеты.
Давайте выведем гравитационное ускорение формула по времени.
Используя уравнение (3), M=gr2/G
Подставляя значение M в уравнение (6),
T2=4π2r3/гр2
г=4π2р/т2
Вот как мы можем вычислить значение g, используя период обращения объекта T.
Спутнику, движущемуся по орбите около 500 км, требуется 90 минут, чтобы совершить один оборот вокруг Земли. Какое будет гравитационное ускорение, которое он испытывает?
Данный:
г = 6.38 Х 106 m
h = 500 км
R = (R + h) = 6.88 Х 106 m
T = 90 мин. = 90 X 60 = 5.4 X 103 сек
Найти: g =?
Формула:
г=4π2р/т2
Решения:
Ускорение свободного падения на орбитальном спутнике рассчитывается по формуле
г=4π2р/т2
Подставляя все значения,
г = 9.28
Ускорение свободного падения на орбитальном спутнике Земли составляет 9.28 м / с.2
Узнать больше об угловом движении.
Как найти ускорение свободного падения, используя сферически-симметричные тела
Рассчитаем значение g для сферически симметричных тел следующим образом:
Гравитационно притягивающие тела обладают сферически-симметричным распределением массы, поскольку вся их масса сосредоточена в его центре. Следовательно, мы можем достичь ускорения свободного падения для симметричных тел, используя закон всемирного тяготения Ньютона.
(Кредит: физика)
Поскольку, масса = плотность / объем
Когда тела, имеющие симметричное распределение массы,
Где ρ0 плотность объекта
Подставляя приведенное выше уравнение в Закон тяготения Ньютона уравнение (2)
Подставляя Уравнение второго закона Ньютона (1) в приведенное выше уравнение,
Вот как мы можем вычислить значение g, используя плотность объекта ρ0.
Рассчитайте ускорение свободного падения шара, падающего на землю, который имеет плотность около 17 кг / см.3.
Данный:
G = 6.67 х 10-11 Nm2/ кг2
г = 6.38 Х 106 m
ρ0 = 17 кг / см3 = 17 х 103 г / см3
Найти: g =?
Формула:
Решения:
Ускорение свободного падения шара рассчитывается по формуле
Подставляя все значения,
г=(2893.71*10-2) / 3
г = 9.64
Ускорение свободного падения при падении мяча на землю составляет 9.64 м / с.2

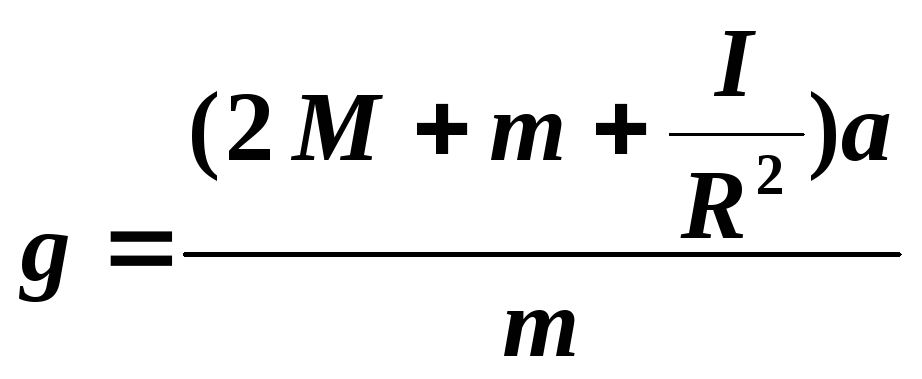

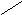

![Rendered by QuickLaTeX.com [T=2pi sqrt{frac{l}{g}}]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-29425af3eec4256686ccf44fde46b3ca_l3.png)




















