Векторные и кинематические уравнения в инерциальной системе отсчета. Для составления уравнений движения судна, необходимых для изучения маневренности судна, прежде всего нужно выбрать систему отсчета: инерциальную (неподвижную) или неинерциальную (подвижную).
Если рассматривать движение судна в инерциальной системе отсчета, то уравнение движения в общем случае определяется на основании второго закона динамики двумя векторными уравнениями:
m1dvdt=F; Форм. 1
J1=dωcdtMc Форм. 2
Первое уравнение (формула 1) представляет собой равенство главного вектора (результирующей силыОпределение результирующих сил инерции многоцилиндрового двигателя) внешних сил F произведению массы судна с учетом присоединенной массы воды m1 на линейное ускорение судна dvc/dt. Это уравнение характеризует поступательное движение центра инерции или центра тяжести судна.
Второе уравнение (формула 2) представляет собой равенство вектора главного момента внешних сил относительно вертикальной оси вращения судна Мс произведению момента инерции судна с учетом присоединенного момента инерции масс воды относительно той же оси J1 на угловое ускорение dω/dt. Это уравнение характеризует вращательное движение судна.
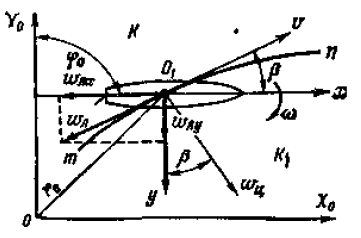
Положение судна на плоскости в инерциальной системе отсчета К с осями Х0 ОУ0 в любой момент времени можно определить, задав радиус-вектор r0 произвольной точки судна O1 и угол курса ф0 (рис. 1). Тогда кинематические уравнения движения в инерциальной системе отсчета в полярных координатах будут иметь вид:
ro=ro(t); Форм. 3
φ0=φ0(t); Форм. 4
В теории маневренности большое распространение получила неинерциальная система отсчета K1 с началом в центре тяжести судна и правой системой координат, при которой положительное направление оси O1x — это направление в сторону носа судна, оси O1y — в сторону правого борта, оси r — вниз. Ось O1x совпадает с диаметральной плоскостью судна.
Для того чтобы решить задачу о движении судна, необходимо знать законы действующих на судно сил и их моментов, которые можно подразделить на два вида: силы и моменты инерционной природы (внутренние силы), возникающие в результате действующих на судно ускорений, и силы и моменты гидроаэродинамической природы (внешние силы). При составлении уравнений будем считать, что движение судна происходит в горизонтальной плоскости с изменяющейся линейной скоростью v и угловой скоростью ω.
Силы и моменты инерционной природы. В неинерциальной, жестко связанной с судном, системе отсчета К1 при движении по криволинейной траектории m—n на судно будут действовать два ускорения: линейное ωл = dv/dt и центростремительное ωц = ωv. В общем случае при движении по криволинейной траектории скорость судна уменьшается, поэтому вектор ускорения ωл будет направлен в противоположную сторону вектору скорости v и отклонен от отрицательного направления оси O1x на величину угла дрейфа β. Вектор центростремительного ускорения ωц всегда направлен в сторону поворота и отклонен от оси О1γ на угол β.
Как видно из рис. 1, проекция векторов ωл и ωц на оси координат неинерциальной системы К1 соответственно равны:
ωлх=–ωлcosβ=–dvdt–cosβ=–dvxdt; Форм. 5
ωлу=ωл sinβ=ωusinβ=ωuy; Форм. 6
ωлх=ωцsinβ=ωusinβ=ωuу; Форм. 7
ωцу=ωцcosβ=ωucosβ=ωux. Форм. 8
Ускорения ωл и ωц вызовут появление сил инерции Fл и Fц, которые будут равны произведению соответствующих масс на величину ускорений и направлены в сторону, противоположную ускорениям (рис. 3). Обозначим коэффициенты присоединенных масс воды по оси О1х—λ11, по оси О1у—λ22, тогда масса судна с учетом присоединенной массы воды вдоль оси 01х будет равна m(1 + λ11), вдоль оси О1у — m(1+λ22). После суммирования проекций инерционных сил по оси 01x и О1у будем иметь следующие выражения для сил инерционной природы:
Fхл–Fцх=m(1+λ11)duxdt·m(1+λ22)ωuy, Форм. 9
Fул–Fцу=–m(1+λ22)duуdt–m(1+λ11)ωuх. Форм. 10
Если скорость судна при движении по кривой будет увеличиваться, то знаки сил Fxл и Fvл изменятся на обратные.
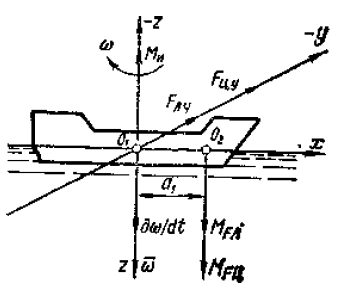
При неустановившемся движении по криволинейной траектории угловая скорость поворота ω является переменной величиной, поэтому на судно будет действовать угловое ускорение dω/dt = φ″. При увеличении угловой скорости судна вектор углового ускорения будет направлен вдоль вектора угловой скорости ω, т. е. вниз, в сторону положительного значения оси z (рис. 2).
Предлагается к прочтению: Основы маневренности крупнотоннажных судов
Угловое ускорение вызывает появление инерционного углового момента Мц, который препятствует повороту судна.
Угловой инерционный момент направлен в сторону, противоположную угловому ускорению, и численно равен произведению момента инерции судна (с учетом присоединенного момента инерции от масс воды) на угловое ускорение
Ми=–J(1+λ66)dωdt, Форм. 11
где:
- λ66 — коэффициент присоединенного момента инерции от масс воды.
Так как фактически ось вращения судна при движении по криволинейной траектории находится не в точке О1 а в точке О2, т. е. сдвинута к носу судна на величину а1, то в создании инерционных моментов будут участвовать проекции инерционных сил Fлу и Fцу. Проекции сил Fлx и Fцх пересекают ось вращения и моментов не создают.
Моменты от сил Fлv и Fцv способствуют повороту судна, поэтому их векторы MFл и MFu в рассматриваемом случае совпадают по направлению с вектором угловой скорости и и будут направлены вниз. Модули этих моментов будут равны MFл = Fлуa1; MFu=Fцуa1. Определим суммарный момент:
MFл+МFц=m(1–λ22)dvvdtα1+m(1+λ11)ωuxα1. Форм. 12
Учитывая, что ωа1 = vv, произведение (dvv-/dt) а1 = = ωvxa1 = vxvу, можем записать
MFл+МFц=m(2+λ22+λ11)uxuy . . . Форм. 13
Если движение судна по криволинейной траектории происходит с увеличением скорости поступательного движения, то момент изменит знак на обратный, в этом случае будем иметь:
MFл+МFц=m(1+λ22)duydtα1+m(1+λ11)ωuxα1, Форм. 14
- или в окончательном виде
MFл+МFц=m(λ11–λ22)uxuy. Форм. 15
Суммарный инерционный момент при увеличении скорости поворота судна и уменьшении линейной скорости движения будет иметь вид:
Mи+МFл+МFц=–J(1+λ66)dωdt+m(2+λ22+λ11)uxuy. Форм. 16
Этот момент при увеличении скорости поворота и линейной скорости судна будет равен:
Mи+МFл+МFц=J(1+λ66)dωdt+m(λ22–λ11)uxuy. Форм. 17
Значение именно этого момента приводится в большинстве работ по управляемости судов.
Силы и моменты аэрогидродинамической природы, силы тяжести и водоизмещения. Все внешние силы и моменты, действующие на судно, могут быть разбиты на пять категорий:
- аэродинамические силы и моменты, возникающие на надводной части корпуса судна;
- гидродинамические силы и моменты на корпусе судна;
- силы веса и водоизмещения;
- управляющие силы и моменты, создаваемые рулями, движителями и подруливающими устройствами;
- возмущающие силы и моменты, обусловленные воздействием течений, волнением, гидродинамическим воздействием корпуса судна с грунтом дна и берегов или корпусом другого судна.
Обычно при определении сил и моментов, действующих на судно, принято опираться на так называемую гипотезу стационарности, согласно которой величины аэро- и гидродинамических сил полностью определяются кинематическими параметрами движения судна в данный момент времени. Силы и моменты, действующие при прямолинейном движении с углами дрейфа, называют позиционными, а силы и моменты, обусловленные вращением судна,—демпфирующими.
Проекции главного вектора и главного момента гидродинамических сил на оси связанной системы координат определяются следующими формулами:
Fx1Fy1Fz1=12ρ1Su2Cx1Cy1Cz1; Форм. 18
Мx1Мy1Мz1=12ρ1Su2Lmx1my1mz1; Форм. 19
где:
- p1 — массовая плотность воды, кг/м2;
- S, L — площадь, м2, и длина, м, корпуса судна;
- v — скорость судна, м/с;
- Cу1, Cv1, Cz1 — характеристики (коэффициенты) продольной, нормальной и поперечной гидродинамических сил соответственно;
- mх1, mу1, mг1 —характеристики (коэффициенты) гидродинамических моментов крена, рыскания и дифферента соответственно.
Проекции главного вектора и главного момента аэродинамических сил на те же оси определяются аналогично.
На капитанском мостике должны находиться таблицы и графики, позволяющие вахтенному помощнику капитана достаточно быстро произвести приближенный расчет сил, воздействующих на судно от внешних факторов. В качестве примера (табл. 1) приведен расчет сил давления ветра на нефтерудовоз типа «Маршал Буденный», произведенный по формуле:
Fв=0,59Свu2в(Асcos2Θ+Bcsin2Θ), Форм. 20
где:
- FB — сила воздействия ветра, Н;
- CВ — коэффициент, учитывающий уменьшение скоростного напора ветра по высоте (по исследованиям автора CВ=0,7 — при стоянке судна у причалов;
- CВ — = 0,8 — на свободной поверхности воды);
- >vВ — скорость ветра, м/с;
- Ас — лобовая парусность судна, м2;
- ВC — боковая парусность судна, м2;
- 9 — курсовой угол ветра, °.
Ниже приведена зависимость от скорости сил течения на подводную часть корпуса того же судна при осадке 16,5 м на глубокой воде.
| Таблица 1. Воздействие ветра на нефтерудовоз типа “Маршал Буденный” | ||||
|---|---|---|---|---|
| Скорость ветра, м/с |
Воздействие ветра при Θ = 90°, Н |
Воздействие ветра при Θ = 45°, Н |
||
| Судно в балласте |
Судно в грузе | Судно в балласте (поперечная составляющая) |
Судно в балласте (продольная составляющая) |
|
| 10 | 1,96·105 | 1,47·105 | 9,81·104 | 3,92·104 |
| 20 | 7,65·105 | 6,78·105 | 3,43·105 | 1,18·105 |
| 30 | 1,67·106 | 1,42·106 | 7,85·105 | 1,96·105 |
| 40 | 2,94·106 | 2,35·106 | 1,37·106 | 3,92·105 |
Расчет произведен по формуле:
F1=Ku2ТSKsinΘ Форм. 21
где:
- FT — сила воздействия воды от течения, Н;
- К — коэффициент, равный 343,35;
- Sk2 — площадь боковой поверхности подводной части корпуса судна, м2;
- v — скорость течения, м/с;
- Θ — курсовой угол течения, °.
- Скорость течения, м/с (уз) 0,25 (0,5) 0,51 (1) 1,03 (2) 1,54 (3);
- Воздействие течения при Θ – 90°. 7,8· 104 3,14 ·105 1.29·106 2,88·106.
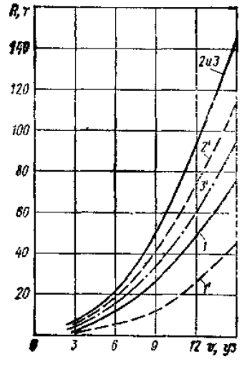
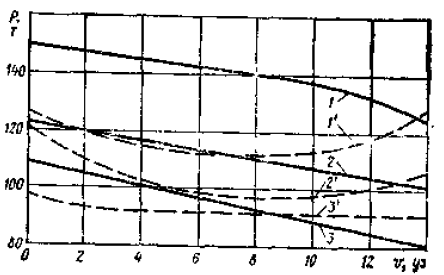
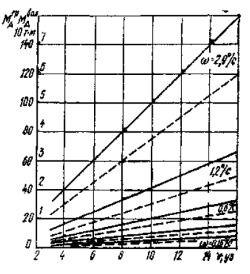
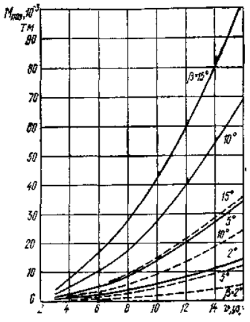
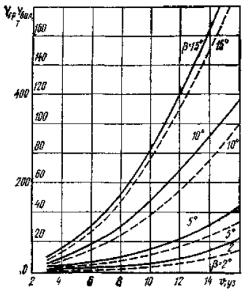
В качестве примера на рис. 4 приведены графики сил сопротивления воды корпусу судна на глубокой воде для крупнотоннажных танкеров при движении без учета угла дрейфа. На рис. 5 для этих же судов приведены силы упора винта при оборотах полного хода в зависимости от скорости движения на переднем и заднем ходу. На рис. 6 показаны графики поперечных сил на корпусе для нефтерудовоз а «Борис Бутома», а на рис. 7 и рис. 8 — значение позиционных и демпфирующих моментов, воздействующих на корпус того же теплохода в грузу (МДГР) и в балласте Мдбал в зависимости от скорости и угла дрейфа.
1 – танкер “Лисичанск” в грузу; 1″ – то же в балласте, 2 – нефтерудовоз “Борис Бутома” в грузу; 2″ – то же в балласте, 3 – нефтерудовоз “Маршал Жуков” в грузу; 3″ – то же в балласте
У крупнотоннажных судов при движении на участках пути (проливах, реках), где имеется течение и уклон поверхности воды, под действием веса возникают значительные силы соскальзывания. В практике управления судами типа «Крым» и крупнотоннажными одновинтовыми судами других типов Новороссийского морского пароходства имелись случаи, когда вследствие тех или иных технических причин главный двигатель мог работать только на малых оборотах, обеспечивая скорость движения в спокойной воде 6—8 уз. При движении в проливе Дарданеллы, а иногда в Эгейском море, где скорость встречного течения не превышает 3—5 уз, судно, имеющее ход относительно воды 6—8 уз, останавливалось. И после длительной многочасовой попытки преодолеть участок судно, заняв положение под углом к течению, начинало сноситься в сторону берега. Для предотвращения возникавшей аварийной ситуации машина останавливалась, и на заднем ходу судно выходило из пролива.
1- нефтерудовоз “Маршал Жуков” на переднем ходу; 1″ – то же при реверсировании; 2 – нефтерудовоз “Борис Бутома” на переднем ходу; 2″ – то же при реверсировании; 3 – танкер “Лисичанск” на переднем ходу; 3″ – то же при реверсировании
После одной-двух неудачных попыток капитаны обращались в пароходство с просьбой выслать для проводки буксировщик, в ожидании которого крупнотоннажное судно простаивало 2—3 сут.
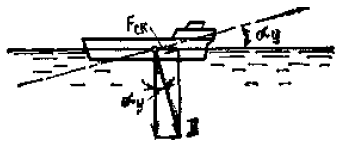
Причиной невозможности преодолеть участки пути со скоростями течения 5 уз, когда крупнотоннажное судно способно развивать скорость 6—8 уз, является действие силы соскальзывания FCK, которая, как видно из рис. 9, равна:
Fck=Dsinαy, Форм. 22
где:
- D — весовое водоизмещение судна, Н;
- αv — угол, характеризующий продольный уклон поверхности воды, °.
Продольный уклон i = sin αv поверхности воды можно определить, воспользовавшись широко известным в гидротехнике уравнением Шези, имеющим вид:
uT cp=CiH, Форм. 23
где:
- vт.ср — средняя скорость течения, м/с;
- C — коэффициент Шези, Н — глубина.
При ориентировочных расчетах можно принимать С≈22. На основании формулы 24 i = vт2/C2Н, тогда сила соскальзывания, действующая на судно, для практических расчетов может быть определена по формуле:
FCK=DH(uTC)2. Форм. 24
Если упор двигателя Fд ≤FCK + RT (RT — сопротивление сил трения на корпусе судна от течения), то проход данного участка пути невозможен. Как показывают расчеты, величина силы соскальзывания, действующей на судно водоизмещением 100 тыс. — 150 тыс. т, может достигать в проливах 15—25 т, что при скорости 7—8 уз приводит к потере скорости 2—3 уз.
Управляющими силами на крупнотоннажных судах являются силы давления на рули и силы упора подруливающих устройств. Рулевая сила Pv в случае расположения руля за гребным винтом может быть определена по формуле:
Py=52r1CpSpu3cp(xp+β), Форм. 25
где:
- r1 — поправочный коэффициент, учитывающий влияние сопротивления корпуса, r1≈1,2, Ср — коэффициент, зависящий от относительного удлинения руля λ = hp/lp (здесь hp — высота, lp — длина руля);
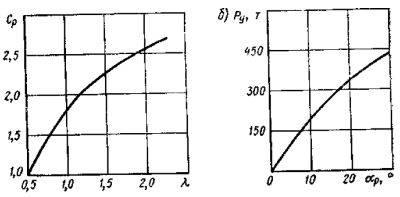
- Cp — определяется по графику, (рис. 12, а);
- SP — площадь руля, м2;
- vp — средняя скорость воды, набегающей на руль, м/с;
- αp — угол перекладки руля, °;
- β — угол дрейфа, °.
а – судно водоизмещением 180 тыс. т; б – рулевая сила танкера
На танкерах типа «Крым» и других крупнотоннажных судах устанавливаются водометные подруливающие устройства (ВПУ). Рабочим органом ВПУ является осевой насос, который всасывает воду, а затем выбрасывает ее через одно из двух сопел, расположенных перпендикулярно бортам. Сила упора ВПУ на танкере «Крым» составляет 57,8 кН. Величина упора изменяется перекрытием поперечных каналов с помощью затворов. Время изменения направления упора с одного борта на другой не более 30 с. В настоящее время разработан нормализованный ряд ВПУ, приведенный в табл. 2.
| Таблица 2. Нормализованный ряд ВПУ | |||||||
|---|---|---|---|---|---|---|---|
| Типоразмер (индекс) ВПУ |
Номинальная мощность привода, Вт |
Тяга, кН (не менее) |
Диаметр осевого насоса, м |
Типоразмер (индекс) ВПУ |
Номинальная мощность привода, Вт |
Тяга, кН (не менее) |
Диаметр осевого насоса, м |
| 1 | 22·103 | 2,94 | 0,42 | 5 | 315·103 | 41,7 | 1,43 |
| 2 | 45·103 | 6,87 | 0,7 | 500·103 | 57,8 | – | |
| 75·103 | 9,6 | – | 6 | 500·103 | 67,7 | – | |
| 3 | 110·103 | 1,4 | 0,87 | 800·103 | 92 | 1.85 | |
| 4 | 200·103 | 25,5 | 1,1 | 7 | 800·103 | 116 | – |
| 1250·103 | 158 | 2.60 |
На очень малых ходах обычные рули малоэффективны. Существующие носовые ВПУ эффективны в использовании, когда скорость судна равна нулю или не превышает 3 уз. ВПУ не только способствуют сокращению времени выполнения ряда маневров, но при плавании в узкостях, проливах, реках, каналах могут оказать судоводителю неоценимую помощь при расхождении с другими судами, когда требуется снизить до минимума скорость или остановиться, при постановке на якорь, особенно при ветре и в других случаях.
Из сравнения сил упора, создаваемых ВПУ, с силами воздействия ветра можно сделать вывод что для гарантированного управления крупнотоннажными судами при сильных ветрах существующие ВПУ обладают недостаточной силой упора. Возмущающие силы под действием волнения трудно поддаются расчету. Как показывают исследования Д. Н. Ньюмена, сила от воздействия волн может быть выражена следующим соотношением:
Fyα=KyDh2вλ2в, Форм. 26
где:
- KУ — коэффициент, равный 0,05 (зависит от глубины воды);
- D — водоизмещение судна;
- hB — высота волны, м;
- λВ — длина волны, м.
Короткие волны, которые почти полностью гасятся судном, передают ему почти всю свою кинетическую энергию, в результате чего возникает значительный напор в направлении распространения волн, в то же время длинные волны возбуждают только колебательные движения, не создавая горизонтального напора.
Вращающий момент, порождаемый волнением FМ.В, может быть выражен следующим образом:
Fм.а=КмDh2вλ2вsinψн, Форм. 27
где:
- Kм — коэффициент момента;
- ψВ — угол волновой атаки, °.
При волнении, направленном в корму FМ.В. достигает наибольшего значения и судно трудно удерживается на курсе. Крупные суда очень подвержены действию длинных волн в отношении влияния на стабилизацию курса.
Читайте также: Социально-психологические аспекты управления судовым экипажем
Уравнения движения судна в неинерциальной системе отсчета. Для рассматриваемого случая движения точки mi, расположенной на диаметральной плоскости судна, можно считать сложным движением: движением относительно неинерциальной системы и движением переносным в отношении инерциальной системы отсчета. Тогда в силу общих геометрических свойств сложного движения абсолютное ускорение точки mi будет равно:
ωiабс=ωiоτа+ωiпер. Форм. 28
На основании второго закона Ньютона можно записать miωiабс=Fi, или
mi(ωiоτ1+ωiпер)Fi. Форм. 29
Второе соотношение можно переписать так:
mi ωiоτ=Fi–miωiпер. Форм. 30
Формулу 30 можно трактовать как запись закона Ньютона применительно к неинерциальной системе отсчета. Второй член в правой части формулы 30 имеет размерность силы. На основании этой формулы, распространяя массу точки mi на всю массу судна, с учетом соответствующих присоединенных масс воды можем записать уравнения движения судна в неинерциальной системе отсчета:
m(1+λ11)duxdt–m(1+λ22)ωuy=ΣFx;m(1+λ22)duydt+m(1+λ11)ωux=ΣFy;J(1+λ66)dωdt+m(λ22–λ11)uxuy=ΣMz. Форм. 31
В левой части уравнений стоят инерционные члены, в правой — силы и моменты неинерционной природы. Интегрируя систему (формула 31), можно найти три функции v (t), β(t), ω (t). В свою очередь эти функции позволяют определить изменения угла курса φ(t) и угла скорости ψ(t). Далее по значениям v (t), ψ(t) и β(t) можно определить координаты центра тяжести судна x (t) и у (t) и на их основе построить траекторию движения судна в горизонтальной плоскости.
Сноски

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
что предупреждение всегда полезнее наказания, поэтому нельзя использовать власть до тех пор, пока другие средства не испробованы, например, выговоры в форме приказа дают меньше пользы, чем обсуждение провинившегося в коллективе. Не рекомендуется делать замечания в присутствии третьего лица, выговор следует делать наедине, так как «распекание» в присутствии других вызывает неприязнь к командиру. Но если никакие средства не помогают, командиру следует применять власть без колебаний.
ГЛАВА 2 ОСНОВЫМАНЕВРЕННОСТИ КРУПНОТОННАЖНЫХ СУДОВ
Движение судна, происходящее с изменением направления или скорости под действием рулевых средств или движителей, называют маневром1. Мореходное качество судна, характеризующее его способность выполнятьманевры, называютманевренностью.
Аналитическое изучение движения судов впервые было начато действительным членом Петербургской академии наук Леонардом Эйлером. В 1776 г. закончилось издание его книги «Полное умозрение строения и вождения кораблей», в которой были составлены уравнения для определений ветрового дрейфа и уравнения движения судна, описывающего циркуляцию. Согласно имевшейся уже в то время теории сопротивления движению тел Ньютона использовалась квадратичная зависимость сил от скорости движения. Поперечная сила при этом принималась пропорциональной второй степени угла дрейфа.
Начиная с 1870 г. начали выполнять модельные исследования для изучения свойств маневренности судов,
1Произошлоотлатинскихслов«manus» — рукаи«operar» — действую.
–32 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
целью которых было определение способности судна совершать повороты. В 1912 г. Ховгорд на основе эмпирических данных циркуляционных испытаний ряда кораблей американского и датского военно-морских флотов разработал формулы для оценки диаметра установившейся циркуляции судна в предположении, что результирующая гидродинамическая сила определяется суммой давлений на элементы диаметральной плоскости, пропорциональных квадрату скорости и синусу местного угла дрейфа.
На развитие учения о маневренности судов большое влияние оказывали работы Н. Е. Жуковского и его последователей в области теории крыла, а также работы Г. Кирхгофа и Ж- Л. Лагранжа.
В 1920—1930 гг. проводились исследования взаимного влияния руля и корпуса судна. Первой попыткой количественной оценки маневренности судна при маневре зигзаг явилась работа И. Ф. Кемпфа, который проанализировал результаты выполненных им натурных испытаний при движении по зигзагообразной траектории.
В 1932 г. была опубликована работа А. Кухарско-го, явившаяся первой попыткой применения результатов аэродинамической теории обтекания крыльев для определения гидродинамического воздействия жидкости на корпус и руль.
Существенный вклад в развитие теории маневренности сделал проф. И. Г. Ханович. В 1944 г. в СССР вышло его первое учебное пособие по управляемости «Поворотливость корабля», в предисловии к которому акад. А. Н. Крылов отметил: «Профессор И. Г. Ханович заполнил существовавшие до этого «чистые листы» обоснованной научно разработанной дисциплиной, вполне соответствующей практической важности предмета, сделав его доступным всякому морскому инженеру, а также штурману и плавающему составу в тех отделах, которые до этого состава непосредственно относятся».
Благодаря работам А. М. Басина, Г. А. Фирсова, К. К. Федявского, Р. Я. Першица в СССР к 1952 г. была создана первая практическая методика расчета радиуса установившейся циркуляции кораблей, и учение о поворотливости судов получило широкое распространение.
– 33 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
В настоящее время применяются два метода составления уравнений, характеризующих динамику движения судна.
Первый метод, получивший наибольшее применение в нашей стране в работах А. М. Басина, Я. И. Войткунского, В. Г. Павленко, Р. И. Першица, Г. В. Соболева, И. А. Титова и др., состоит в аналитическом и экспериментальном определении коэффициентов гидродинамических составляющих сил и моментов, действующих на корпуссудна.
Второй метод, нашедший отражение в работах Н. X. Норрбина, К. Номото, X. Эди, К. Л. Крэйн и других авторов, заключается в разложении составляющих сил и моментов в ряд Тейлора и определении его коэффициентовнаосновеиспытаниймоделисудна.
В существующей литературе по управляемости судов при выводе уравнений криволинейного движения авторами обычно не указывается, для какого вида криволинейного движения приняты силы и моменты инерции (ускоренного или замедленного), поэтому знаки у инерционных сил и моментов у ряда авторов не совпадают.
За последние годы как в нашей стране, так и за рубежом, значительно повысился интерес к маневренности крупнотоннажных судов. Из работ, посвященных этому вопросу, следует отметить работы М. М. Лескова, А. М. Оганова, С. И. Демина, А. И. Цурбана и др.; из зарубежных — работы Ж. П. Хофта, Г. Ф. Ремари, Я. Фудзи, Ё. Огава, К. Тадзима и др.
Знание динамики, особенно крупнотоннажных судов, позволяет на научной основе подходить к решению задач по управлению движением судов и конструированию автоматических систем удержания судна на заданной траектории, чтоспособствует:
повышению экономической эффективности морских судов путем реализации наилучшей траектории движения с учетом навигационных и гидрометеорологических условийплавания;
решению задачи реализации оптимальной траектории движения судна при расхождении с другими судами;
повышению безопасности мореплавания вблизи навигационных опасностей в результате более точного управлениядвижением судна.
– 34 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
§5 УРАВНЕНИЯ ДВИЖЕНИЯ СУДНА
Векторные и кинематические уравнения в инерциальной системе отсчета. Для составления уравнений движения судна, необходимых для изучения маневренности судна, прежде всего нужно выбрать систему отсчета: инерциальную (неподвижную) или неинерциальную (подвижную).
Если рассматривать движение судна в инерциальной системе отсчета, то уравнение движения в общем случае определяется на основаниивторогозакона динамикидвумя векторнымиуравнениями:
|
m |
dv |
= F; |
(8) |
|||
|
dt |
||||||
|
1 |
||||||
|
J |
1 |
dωc |
= M |
c |
(9) |
|
|
dt |
Первое уравнение (8) представляет собой равенство главного вектора (результирующей силы) внешних сил F произведению массы судна с учетом присоединенной массы воды т1 на линейное ускорение судна dvс/dt. Это уравнение характеризует поступательное движение центра инерции или центра тяжести судна.
Второе уравнение (9) представляет собой равенство вектора главного момента внешних сил относительно вертикальной оси вращения судна Мс произведению момента инерции судна с учетом присоединенного момента инерции масс воды относительно той же оси J1 на угловое ускорение dω/dt. Это уравнение характеризует вращательноедвижениесудна.
Положение судна на плоскости в инерциальной системе отсчета К с осями Х0 ОУ0 в любой момент времени можно определить, задав радиус-вектор r0 произвольной точки судна O1 и угол курса φ0 (рис. 3). Тогда кинематические уравнения движения в инерциальной системе отсчета в полярных координатах будут иметь вид:
|
ro = ro (t); |
(10) |
|
ϕ0 = ϕ0 (t); |
(11) |
|
В теорииманевренностибольшое |
распространение |
получила неинерциальная система отсчета K1 с началом
– 35 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
|
в центре тяжести судна и |
рис. 3 Инерциальная (К) и |
|||
|
правой |
при |
системой |
||
|
координат, |
которой |
неинерциальная(К1) системыот- |
||
|
положительное |
счета |
|||
|
направление оси O1х — |
||||
|
это |
направление |
в |
||
|
сторону носа судна, оси |
||||
|
O1y — в сторону правого |
||||
|
борта, оси г — вниз. Ось |
||||
|
O1х совпадает с диамет- |
||||
|
ральной |
плоскостью |
|||
|
судна. |
того |
чтобы |
||
|
Для |
||||
|
решить |
задачу |
о |
движении судна, необходимо знать законы действующих на судно сил и их моментов, которые можно подразделить на два вида: силы и моменты инерционной природы (внутренние силы), возникающие в результате действующих на судно ускорений, и силы и моменты гидроаэродинамической природы (внешние силы). При составлении уравнений будем считать, что движение судна происходит в горизонтальной плоскости с изменяющейся линейной скоростью v и угловой скоростьюω.
Силы и моменты инерционной природы. В неинерци-
альной, жестко связанной с судном, системе отсчета К1 при движении по криволинейной траектории т — п на судно будут действовать два ускорения: линейное ωл = = dv/dt и центростремительное ωц = ωv. В общем случае при движении по криволинейной траектории скорость судна уменьшается, поэтому вектор ускорения ωл будет направлен в противоположную сторону вектору скорости судна v и отклонен от отрицательного направления оси O1x на величину угла дрейфа β. Вектор центростремительного ускорения ωц всегда направлен в сторону поворота иотклоненотоси01у на уголβ.
Как видно из рис. 3, проекция векторов ωл и ωц на оси координат неинерциальной системы K1 соответственно равны:
(12)
(13)
(14)
(15)
– 36 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
Ускорения ωл и ωц вызовут появление сил инерции Fл и Fц, которые будут равны произведению соответствующих масс на величину ускорений и направлены в сторону, противоположную ускорениям (рис. 5). Обозначим коэффициенты присоединенных масс воды по оси 01х—λ11, по оси O1y—λ22, тогда масса судна с учетом присоединенной массы воды вдоль оси 01х будет равна m(1+λ11), вдоль оси O1y — m (1+λ22). После суммирования проекций инерционных сил по оси 01х и O1y будем иметь следующие выражения для сил инерционной природы:
(16)
( 17 )
Если скорость судна при движении по кривой будет увеличиваться, то знаки сил Fхл и Fул изменятся на обратные.
При неустановившемся движении по криволинейной траектории угловая скорость поворота ω является переменной величиной, поэтому на судно будет действовать угловое ускорение dω/dt = φ». При увеличении угловой скорости судна вектор углового ускорения будет направлен вдоль вектора угловой скорости ω, т. е. вниз, в сторону положительного значения оси z (рис. 4).
Угловое ускорение вызывает появление инерционного углового момента Ми, который препятствует повороту
|
рис. 4 Инерционныемоментыпри |
рис. 5 Инерционныесилы(FлиFц) |
|
увеличенииугловойскорости |
иихпроекциинаоси |
|
неинерциальнойсистемы |
– 37 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
судна. Угловой инерционный момент направлен в сторону, противоположную угловому ускорению, и численно равен произведению момента инерции судна (с учетом присоединенного момента инерции от масс воды) на угловоеускорение
(18)
где λ66 — коэффициент присоединенного момента инерции от масс воды.
Так как фактически ось вращения судна при движении по криволинейной траектории находится не в точке О1 а в точке Ο2, т. е. сдвинута к носу судна на величину а1, то в создании инерционных моментов будут участвовать проекции инерционных сил Fлу и Fцу. Проекции сил Fлx и Fцx пересекают ось вращения и моментов не создают.
Моменты от сил Fлу и Fцу способствуют повороту судна, поэтому их векторы МFл и МFц в рассматриваемом случае совпадают по направлению с вектором угловой скорости и и будут направлены вниз. Модули этих
моментов будут равны МFл = Fлуа1; МFц=Fцуа1. Определимсуммарныймомент
(19)
Учитывая, что ωа1 = vy, произведение (dvy/dt) а1 = = ωvxа1 = vxvy, можемзаписать
(20)
Если движение судна по криволинейной траектории происходит с увеличением скорости поступательного движения, то момент изменит знак на обратный, в этом случае будем иметь
иливокончательном виде
(21)
– 38 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
Суммарный инерционный момент при увеличении скорости поворота судна и уменьшении линейной скорости движениябудетиметьвид:
(22)
Этотмоментприувеличениискоростиповоротаилинейнойскорости суднабудетравен:
(23)
Значение именно этого момента приводится в большинствеработпоуправляемостисудов.
Силы и моменты аэрогидродинамической природы, силы тяжести и водоизмещения. Все внешние силы и моменты, действующие на судно, могут быть разбиты на пятькатегорий:
аэродинамические силы и моменты, возникающие на надводнойчастикорпуса судна;
гидродинамическиесилыимоментынакорпусесудна; силывесаиводоизмещения;
управляющие силы и моменты, создаваемые рулями, движителямииподруливающимиустройствами;
возмущающие силы и моменты, обусловленные воздействием течений, волнением, гидродинамическим воздействием корпуса судна с грунтом дна и берегов или корпусомдругогосудна.
Обычно при определении сил и моментов, действующих на судно, принято опираться на так называемую гипотезу стационарности, согласно которой величины аэро- и гидродинамических сил полностью определяются кинематическими параметрами движения судна в данный момент времени. Силы и моменты, действующие при прямолинейном движении с углами дрейфа, называют позиционными, а силы и моменты, обусловленные вращениемсудна, — демпфирующими.
– 39 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
Проекции главного вектора и главного момента гидродинамических сил на оси связанной системы координат определяютсяследующимиформулами:
(24)
(25)
где ρ1 — массовая плотность воды, кг/м3; S, L — площадь, м2, и длина, м, корпусасудна; v — скорость судна, м/с; Cχ1 , Cy1 ,
CZ1 —характеристики (коэффициенты) продольной, нормальной и поперечнойгидродинамическихсилсоответственно; тх1 , ту1 , тг1 —характеристики (коэффициенты) гидродинамических моментов
крена, рысканияидифферентасоответственно.
Проекции главного вектора и главного момента аэродинамических сил на те же оси определяются аналогично1.
На капитанском мостике должны находиться таблицы и графики, позволяющие вахтенному помощнику капитана достаточно быстро произвести приближенный расчет сил, воздействующих на судно от внешних факторов. В качестве примера (табл. 2) приведен расчет сил давления ветра на нефтерудовоз типа «Маршал Буденный», произведенный по формуле
(26)
где FВ — сила воздействия ветра, Н; СВ — коэффициент, учитывающий уменьшение скоростного напора ветра по высоте (по исследованиям автора, СВ=0,7 — при стоянке судна у причалов; СВ— = 0,8— на свободной поверхности воды); vВ — скорость ветра, м/с; АС—лобовая парусность судна, м2; ВС — боковая парусность судна, м2; 9 — курсовойуголветра, º.
Ниже приведена зависимость от скоростисилтечения на подводную часть корпуса того же судна при осадке 16,5 м на глубокойводе.
1 ‘Войткуиский Я. И., Першиц Р. Я., Титов И. А. Справочник потеориикорабля. М.: Судостроение, 1973. 511с.
– 40 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
Таблица 2 Воздействие ветра нанефтерудовозтипа«МаршалБуденный»
|
Воздействие |
ветра при |
Воздействие ветра при |
|||
|
Скорость |
Θ = 90°, Н |
Θ =45°, Н |
|||
|
ветра, |
м/с |
||||
|
Суднов |
Судно в грузу |
Судно в балласте |
Судно в балласте |
||
|
(поперечная со- |
(продольная |
||||
|
балласте |
|||||
|
ставляющая) |
составляющая) |
||||
|
10 |
1,96·105 |
1,47·105 |
9,81 ·104 |
3,92·104 |
|
|
20 |
7,65 ·105 |
6,87 ·105 |
3,43·105 |
1,18 · 105 |
|
|
30 |
1,67·106 |
1,42·106 |
7,85·105 |
1,96· 105 |
|
|
40 |
2,94 ·106 |
2,35·106 |
1,37·106 |
3,92· 105 |
|
Расчетпроизведенпоформуле
(27)
где FT—сила воздействия воды от течения, Н; К. — коэффициент, равный 343,35; SK — площадь боковой поверхности подводной части корпуса судна, м2; v — скорость течения, м/с; Θ — курсовой угол течения, °.
Скорость течения, м/с (уз)
Воздействие течения приΘ — 90°.
|
0,25 (0,5) |
0,51 (1) |
1,03 (2) |
1,54 (3) |
|
7,8· 104 |
3,14 ·105 |
1.29·106 |
2,88·106 |
В качестве примера на рис. 6 приведены графики сил сопротивления воды корпусу судна на глубокой воде для крупнотоннажных танкеров при движении без учета угла дрейфа. На рис. 7 для этих же судов приведены силы упора винта при оборотах полного хода в зависимости от ско-
рис. 6 Сила сопротивления корпуса крупнотоннажных танкеров:
|
1 —танкер «Лисичанск» |
в |
грузу; |
|
|
1 ‘-—то же в балласте, |
2 |
— |
|
|
нефтерудовоз «Борис Бутома» в грузу, |
|||
|
2′ — то же в балласте, 3 |
— нефте- |
||
|
рудовоз «Маршал Жуков» в грузу |
3′ — |
||
|
то же в балласте |
– 41 –

1 — нефтерудовоз «Маршал Жуков» на переднем ходу, 1′ — то же при реверсировании, 2 — нефтерудовоз «Борис Бутома» на переднем ходу, 2′ — то же при реверсировании,
3 — танкер «Лисичанск» на переднем ходу, 3′ — то же при реверсировании
УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
роста движения на рис. 7 Зависимость силы упора винта переднем и заднем крупнотоннажных танкеров от скорости
ходу. На рис. 8 по- напереднемходуиприреверсировании:
казаны графики поперечных сил на корпусе для нефтерудовоз а «Борис Бутома», а на рис. 9 и рис. 10— значение позиционных и демпфирующих моментов, воздействующих на корпус того же теплоходавгрузу(МДГР) ивбалласте Мдбал в зависимости
от скорости и угла дрейфа.
У крупнотоннажных судов при движении на участках пути (проливах,
реках), где имеется течение и уклон поверхности воды, под действием веса возникают значительные силы соскальзывания. В практике управления судами типа «Крым» и крупнотоннажными одновинтовыми судами других типов Новороссийского морского пароходства имелись случаи, когда вследствие тех или иных технических причин главный двигатель мог работать только на малых оборотах, обеспечивая скорость движения в спокойной воде 6—8 уз. При движении в проливе Дарданеллы, а иногда в Эгейском море, где скорость встречного течения не превышает 3—5 уз, судно, имеющее ход относительно воды 6—8 уз, останавливалось. И после длительной многочасовой попытки преодолеть участок судно, заняв положение под углом к течению, начинало сноситься в сторону берега. Для предотвращения возникавшей аварийной ситуации машина останавливалась, и на заднем ходу судно выходило из пролива.
После одной-двух неудачных попыток капитаны обращались в пароходство с просьбой выслать для проводки буксировщик, в ожидании которого крупнотоннажное суднопростаивало 2—3 сут.
Причиной невозможности преодолеть участкипути
– 42 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
|
рис. 9 Зависимость поперечной силы |
рис. 8 Зависимость позиционного мо- |
рис. 10 Зависимость демпфирующего |
|
от скорости для нефтерудовоза «Бо- |
мента от скорости нефтерудовоза |
момента от скорости нефтерудовоза |
|
рис Бутома» при различных значени- |
«Борис Бутома» при различных углах |
«Борис Бутома» при различных |
|
ях угла дрейфа β (сплошная линия— |
дрейфа β (сплошная линия — в грузу, |
значениях угловой скорости v (сплош- |
|
в грузу; штриховал — в балласте) |
штриховая — в балласте) |
ная линия — в грузу; штриховая — В |
|
балласте) |
– 43 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
|
со скоростями течения 5 уз, |
рис. 11 Силасоскальзывания |
|
когдакрупнотоннажноесудно |
|
|
способно развивать скорость |
|
|
6—8 уз, является действие |
|
|
силы соскальзывания FCK, |
|
|
которая, как видно из рис. 11, |
|
|
равна |
|
|
(28) |
где D — весовое водоизмещение судна, Н; αу — угол, характеризующийпродольныйуклонповерхностиводы, °.
Продольный уклон i=sin αy поверхности воды можно определить, воспользовавшись широко известным в гидротехникеуравнениемШези, имеющимвид
(29)
где vт.ср. — средняя скорость течения, м/с; С — коэффициент Шези, Н— глубина.
При ориентировочных расчетах можно принимать С≈22. На основании формулы (29) i = vт2/С2H, тогда сила соскальзывания, действующая на судно, для практических расчетов может быть определена по формуле
(30)
Если упор двигателя FД ≤FСК + RТ (RT— сопротивление сил трения на корпусе судна от течения), то проход данного участка пути невозможен. Как показывают расчеты, величина силы соскальзывания, действующей на судно водоизмещением 100 тыс. — 150 тыс. т, может достигать в проливах 15—25 т, что при скорости 7—8 уз приводиткпотерескорости2—3 уз.
Управляющими силами на крупнотоннажных судах являются силы давления на рули и силы упора подруливающих устройств. Рулевая сила Ру в случае расположения руля за гребным винтом может быть определена поформуле
(31)
где r1 — поправочный коэффициент, учитывающий влияние сопротивления корпуса, r1≈l,2, Ср— коэффициент, зависящий от относительного удлинения руля λ=hр/lр (здесь hр — высота, lР — длина руля; Ср — определяется по графику, рис. 12,а); SР — площадь руля, м2; vp — средняя скорость воды, набегающей на руль, м/с; αр — угол перекладкируля, °; β— уголдрейфа, °.
– 44 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
рис. 12 К определению силы давления на перо руля:
а — судно водоизмещением 180 тыс. т, б —рулевая сила танкера
На танкерах типа «Крым» и других крупнотоннажных судах устанавливаются водометные подруливающие устройства (ВПУ). Рабочим органом ВПУ является осевой насос, который всасывает воду, а затем выбрасывает ее через одно из двух сопел, расположенных перпендикулярно бортам. Сила упора ВПУ на танкере «Крым» составляет 57,8 кН. Величина упора изменяется перекрытием поперечных каналов с помощью затворов. Время изменения направления упора с одного борта на другой не более 30 с. В настоящее время разработан нормализованный ряд ВПУ, приведенныйвтабл. 3.
Таблица 3 Нормализованный ряд ВПУ
|
, |
, |
||||||||
|
)ВПУ |
Номинальная |
, Вт |
кН |
насоса |
)ВПУ |
Номинальная |
, Вт |
кН |
насоса |
|
индекс( |
привода |
Тяга |
осевого |
индекс( |
привода |
Тяга |
осевого |
||
|
Типоразмер |
мощность |
не ( |
Диаметр м |
Типоразмер |
мощность |
не ( |
Диаметр м |
||
|
менее |
менее |
||||||||
|
) |
) |
||||||||
|
, |
, |
|
1 |
22·103 |
2,94 |
0,42 |
5 |
315·103 |
41,7 |
1,43 |
|
2 |
45·103 |
6,87 |
0,7 |
6 |
500·103 |
57,8 |
— |
|
75·103 |
9,6 |
— |
500· 103 |
67,7 |
— |
||
|
3 |
110·103 |
1,4 |
0,87 |
800·103 |
92 |
1.85 |
|
|
4 |
200·103 |
25,5 |
1,1 |
7 |
800·103 |
116 |
— |
|
1250· 103 |
158 |
2.60 |
– 45 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
На очень малых ходах обычные рули малоэффективны. Существующие носовые ВПУ эффективны в использовании, когда скорость судна равна нулю или не превышает 3 уз. ВПУ не только способствуют сокращению времени выполнения ряда маневров, но при плавании в узкостях, проливах, реках, каналах могут оказать судоводителю неоценимую помощь при расхождении с другими судами, когда требуется снизить до минимума скорость или остановиться, при постановке на якорь, особенно при ветре и в других случаях.
Из сравнения сил упора, создаваемых ВПУ, с силами воздействия ветра (см. стр. 40) можно сделать вывод что для гарантированного управления крупнотоннажными судами при сильных ветрах существующие ВПУ обладают недостаточной силой упора. Возмущающие силы под действием волнения трудно поддаются расчету. Как показывают исследования Д. Н. Ньюмена, сила от воздействия волн может быть выражена следующим соотношением:
(32)
где КУ — коэффициент, равный 0,05 (зависит от глубины воды); D
— водоизмещениесудна; hВ — высотаволны, м; λВ — длинаволны, м.
Короткие волны, которые почти полностью гасятся судном, передают ему почти всю свою кинетическую энергию, в результате чего возникает значительный напор в направлении распространения волн, в то же время длинные волны возбуждают только колебательные движения, не создавая горизонтального напора.
Вращающиймомент, порождаемыйволнениемFм.в, может быть выражен следующим образом:
(33)
где Км— коэффициент момента; ψВ — угол волновой атаки, °.
При волнении, направленном в корму FM.B. достигает наибольшего значения и судно трудно удерживается на курсе. Крупные суда очень подвержены действию длинных волн в отношении влияния на стабилизацию курса.
– 46 –

УПРАВЛЕНИЕ КРУПНОТОННАЖНЫМИ СУДАМИ
Уравнения движения судна в неинерциальной системе отсчета. Для рассматриваемого случая движения точки mi, расположенной на диаметральной плоскости судна, можно считать сложным движением: движением относительно неинерциальной системы и движением переносным в отношении инерциальной системы отсчета. Тогда в силу общих геометрических свойств сложного движения абсолютное ускорение точки mi будет равно
(34)
На основании второго закона Ньютона можно записатьmiωia6c=Fi, или
(35)
Второесоотношениеможнопереписатьтак:
(36)
Формулу (36) можно трактовать как запись закона Ньютона применительно к неинерциальной системе отсчета. Второй член в правой части формулы (36) имеет размерность силы. На основании этой формулы, распространяя массу точки mi на всю массу судна, с учетом соответствующих присоединенных масс воды можем записать уравнения движения судна в неинерциальной системеотсчета:
(37)
В левой части уравнений стоят инерционные члены, в правой — силы и моменты неинерционной природы. Интегрируя систему(37), можно найти три функции v ( t ) , β(t), ω (t). В свою очередь эти функции позволяют определить изменения угла курса φ(t) и угла скорости ψ(t). Далее по значениям v ( t ) , ψ(t) и β(t) можно определить координаты центра тяжести судна x ( t ) и у (t) и на их основе построить траекторию движения судна в горизонтальнойплоскости.
– 47 –
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для решения задачи движения судна в горизонтальной плоскости необходимо знать силы и моменты, действующие на корпус судна и его средства управления. Они разделяются на три группы: движущие, внешние и реактивные.
Движущие силы: упор гребного винта, боковая сила руля, силы, создаваемые средствами активного управления и т. п.
Внешние силы: силы давления ветра, волнения моря, течения. Эти силы, как правило, создают помехи при маневрировании.
Реактивные силы: силы и моменты, возникающие в результате движения судна под действием движущих и внешних сил. Реактивные силы зависят от линейных и угловых скоростей и разделяются по своей природе на инерционные и неинерционные.
Инерционные силы и моменты, Rи, обусловлены инертностью судна и присоединенных масс жидкости. Они возникают только при наличии ускорений – линейного, углового, центростремительного. Инерционная сила всегда направлена в сторону, противоположную ускорению. При равномерном прямолинейном движении судна инерционные силы не возникают.
Неинерционные силы и моменты, Rв, обусловлены вязкостью забортной воды, т. е. являются гидродинамическими силами и моментами. Гидродинамические силы и моменты принято подразделять по характеру движения судна, при котором они возникают, на позиционные и демпфирующие.
Позиционные силы и моменты, Rn, действуют на судно при прямолинейном движении судна с углом дрейфа.
Демпфирующие силы и моменты, Rд, – добавочные силы и моменты, обусловленные вращением судна вокруг вертикальной оси.
Общие выражения для сил и моментов, действующих на корпус судна при его криволинейном движении записываются в виде:
При рассмотрении задач управляемости используется подвижная система координат, связанная с судном с началом в центре тяжести ЦТ. Положительные направления осей: X – в нос; Y – в правый борт; Z – вниз.
Положительный отсчет углов принимается по часовой стрелке, однако, за исключением в отношении угла перекладки руля δ, угла дрейфа β и курсового угла ветра (течения) КУ.
За положительное направление перекладки руля δ принимают перекладку, вызывающую циркуляцию по часовой стрелке, т. е. перекладку на правый борт (перо руля при этом перемещается против часовой стрелки).
За положительный угол дрейфа принимается угол β, при котором поток воды набегает со стороны левого борта и создает при этом положительную поперечную гидродинамическую силу на корпусе. Такой угол дрейфа возникает при правой циркуляции судна.
Общий случай движения судна описывается системой из трех дифференциальных уравнений: двух уравнений сил по продольной Х и поперечной Y осям и уравнения моментов вокруг вертикальной оси Z.
выражения в упрощенном виде и в параметрах скорости V, угла дрейфа β и угловой скорости ωz записываются в виде:
В этих системах:
m – масса судна;
Rx – продольная гидродинамическая сила на корпусе (сопротивление воды);
Ry – поперечная гидродинамическая сила на корпусе;
Mz – общий момент сил, приложенных к корпусу при криволинейном движении;
V – скорость судна;
β – угол дрейфа;
ωz – угловая скорость судна относительно оси Z;
Іz – момент инерции судна относительно оси Z;
Rp – продольная составляющая силы действия воды на руль;
P – упор гребного винта;
XA – продольная составляющая силы ветра;
YA – поперечная составляющая силы ветра;
MA – момент силы ветра YA относительно оси Z;
Fцв – центробежная сила инерции;
Yp – боковая сила руля, отклоненного от диаметральной плоскости ДП;
Mp – момент боковой силы руля относительно оси Z;
Ryв – поперечная гидродинамическая сила, приложенная к корпусу при его движении с углом дрейфа;
Mв – момент поперечной гидродинамической силы Ryв относительно оси Z;
λ11 – присоединенная масса воды при движении судна по оси X (λ11 = md/2L);
λ22 – присоединенная масса воды при движении судна по оси Y:;
λ26 – статический момент присоединенных масс воды;
λ66 – момент инерции присоединенных масс воды:;
L – длина судна;
B – ширина судна;
d – осадка судна.
Приведенные формулы для определения присоединенных масс по трем осям дают приближенные значения – более точно можно посчитать через коэффициенты присоединенных масс k11, k22, k66, которые можно выбрать из графиков, приведенных в справочниках по теории корабля.
Определение сил и моментов осуществляется тремя способами: теоретическим, экспериментальным и расчетно-экспериментальным. Для практических расчетов силы и моменты, действующие на корпус, винт и руль, определяют по отдельности, вводя в результаты коэффициенты взаимодействия.
Скачать материал

Скачать материал


- Сейчас обучается 620 человек из 78 регионов


- Сейчас обучается 98 человек из 37 регионов


- Сейчас обучается 81 человек из 38 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
«Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.»
Алексей Николаевич Крылов
(1863-1945)
Советский кораблестроитель, механик и математик, академик -
2 слайд
Цель урока: формирование умений применять полученные знания при решении профессиональных задач судовождения, решаемых с использованием производной.
Применение производной при решении задач судовождения. -
3 слайд
Производная.
Дайте определение производной.
В чем заключается физический смысл производной.
Каков геометрический смысл производной?
Какие задачи можно решить при помощи производной?
Что необходимо знать, чтобы решать задачи на нахождение производной элементарных функций? -
-
5 слайд
v(t)= x’(t)
Производная от координаты точки по времени есть скорость.
Производная от скорости по времени есть ускорениеКратко: производная функции – это скорость изменения этой функции
-
6 слайд
Нахождение производной функции
в точке– это вычисление углового
коэффициента касательной к данной
функции в этой точке.
f’(x0 ) = tqα -
7 слайд
1. Уравнение касательной к графику функции в заданной точке.
2. Задачи на нахождение скорости изменения функции.
3. Определение промежутков монотонности функции
4. Определение точек экстремума функции
5. Задачи на наибольшее и наименьшее значение (оптимизацию). -
8 слайд
1.Производная функции равна
0;
1;
с.
0 -
9 слайд
2.Производная функции равна
0;
1;
х.
1 -
10 слайд
3.Производная функции равна
х;
2х;
х2.
2х -
11 слайд
4.Производная функции равна
0;
1;
k.
k -
12 слайд
5.Производная функции равна
;;
.
-
13 слайд
6.Производная функции равна
;;
.
-
14 слайд
7.Производная функции равна
;;
.
-
15 слайд
8.Производная функции равна
10 ;0 ;
.
0 -
16 слайд
Составьте пары
«функция – производная функции»
0
1 -
17 слайд
Составьте пары
«функция – производная функции»
0
1 -
18 слайд
Проверка:
1 вариант: 1—7, 2—23, 3—10, 4—11, 5—19.
2 вариант: 6—15, 7—21, 8—24, 9—2, 10—13.
3 вариант: 11—22, 12—20, 13—18, 14—16, 15—5.
4 вариант: 16—23, 17—8, 18—3, 19—6, 20—23.перевод в оценку:
«5» – 5 правильных ответов
«4» – 3-4 правильных ответа
«3» – 2 правильных ответа -
19 слайд
Правила дифференцирования
1.2.
3.
4.
-
20 слайд
Найти производную функции
-
21 слайд
Найти производную функции
-
22 слайд
Для каких целей, по вашему мнению, может применятся производная в судовождении?
Основная задача судовождения – определение места судна в море.
Главные понятия:
Навигационный параметр(скорость, направление, углы, расстояния, разности расстояний и т.п.)
Навигационный ориентир(объекты с отличительными признаками и известным положением)
Навигационная функция – математическое выражение, устанавливающая связь между навигационным параметром и координатами места судна — U = f(x, y, t, φ, λ) -
23 слайд
Какие задачи из других изучаемых дисциплин решались на уроках математики с использованием производной?
В чем заключается физический смысл производной?
Как определить скорость тела, пользуясь понятием производной, если задано уравнение движения тела?
Производная – это скорость.
Скорость судна – это навигационный параметр?
Если известно уравнение движения судна, как найти его скорость? -
24 слайд
Задача
Судно движется прямолинейно по закону
x — в милях, t – часах.
а) Выведите формулу для вычисления скорости движения в любой момент времени t.
б) Найдите скорость судна в момент времени t = 2.1 часа.
в) Через сколько часов после начала движения теплоход остановится? -
-
26 слайд
Какие задачи с практическим содержанием вы решали на уроках математики?
Задачи на наибольшее и наименьшее значение функции на отрезке.
Задачи на наибольшее и наименьшее. значение функции на интервале.
Задачи на оптимизацию. -
27 слайд
наибольшее
значение
наименьшее
значение
a
b
a
b
Наибольшее , наименьшее значение функции на интервале.Если функция f имеет на интервале (области определения) одну точку экстремума.
Если это точка минимума, то в этой точке функция будет принимать наименьшее значение.
Если это точка максимума, то в этой точке функция будет принимать наибольшее значение.
-
28 слайд
Алгоритм нахождения наибольшего и наименьшего значения функции на интервале.
Найти производную функции.Найти критические точки функции
Найти область определения функции (интервал исследования)
Отметить интервал и критические точки на числовой прямой
Определить знаки производной на получившихся промежутках
Определить вид экстремума -
29 слайд
Основные этапы, при решении задач прикладного характера на оптимизацию:
Формализация (перевод задачи на математический язык – составление математической задачи);решение полученной математической задачи;
интерпретация найденного решения.
-
30 слайд
Экономический расчет рейса.
Стоимость топлива необходимого для движения т/х «Амур» пропорциональна кубу его скорости и составляет 68000 рублей при скорости 10 узлов. Все другие виды расходов составляют 408 000 рублей. Найдите наиболее экономическую скорость движения и вычислите дополнительную прибыль за экономию топлива на рейс Архангельск – Нарьян – Мар (расстояние 1250 км). -
31 слайд
1. Формализация (перевод задачи на математический язык – составление математической задачи);
Расходы на эксплуатацию судна на 1 милю пути определяются по формуле
S = k·v3 + b, где
K – коэффициент пропорциональности
V – скорость судна в узлах
b – прочие виды расходов в рублях.
На практике расходы рассчитывают не на 1 милю пути, а на 1 час, поэтому функция определяющая расходы будет иметь вид
f(v) = S/v = (k·v3 + b)/v = k·v2 + b/v -
32 слайд
f(v) = S/v = k·v2 + b/v
Наиболее экономичная скорость –это какая скорость?
При которой расходы будут минимальны.
Как сформулировать математическую задачу?
Исследовать функцию f(v) = S/v= k·v2 + b/v на минимум. -
33 слайд
f(v) = k·v2 + b/v
v – неизвестное.Стоимость топлива необходимого для движения т/х «Амур» пропорциональна кубу его скорости и составляет 68000 рублей при скорости 10 узлов. Все другие виды расходов составляют 408 000 рублей. Найдите наиболее экономическую скорость движения и вычислите дополнительную прибыль за экономию топлива на рейс Архангельск – Нарьян – Мар (расстояние 1250 км).
b = 408 000 руб.
Стоимость топлива
T = k·v3
68000 = k· 103
k = 68000/1000 =68
Получаем функцию
f(v) = 68·v2 + 408000/v
Исследовать данную функцию на минимум -
34 слайд
2. Решение математической задачи:
( алгоритм исследования функции на экстремум).
f(v) = 68·v2 + 408000/vНайти производную функции.
Найти критические точки функции
Найти область определения функции?
f'(v) =(68·v2 + 408000/v)’=
= 68·2·v – 408000/v2f'(v) = 68·2·v – 408000/v2 =0
(136·v3 – 408000)/v2 =0v≠0, 136·v3 – 408000 = 0
v 3 = 408000 /136 = 3000v ≈ 14.5
V > 0
-
35 слайд
f'(v) = 136·v – 408000/v2
Отметить критические точки на числовой прямойОпределить знаки производной на получившихся интервалах
Определить вид экстремума
3. Интерпретация найденного решения
Наиболее экономичная скорость 14,5 узлов
0
14,5
___
+
х
min -
36 слайд
Определим дополнительную прибыль за рейс
f(v) = k·v2 + b/vРейс: Архангельск – Нарьян – Мар ,
расстояние 1250 км.
Переведем 1250 км в мили:
1 миля = 1852 м,
1250 км = 1250000/1852 =
674,95 миль
При скорости 10 узлов время рейса —
t1 = 674.95/10 =67,95 час
При скорости 14,5 узлов время рейса –
t2 = 674.95/14,5 =46,55 час -
37 слайд
b = 408 000 руб. , k = 68
При скорости 10 узлов
f(10) = 68·102 + 408000/10 = 6800 +40800 =
47600 руб. в часСтоимость рейса
S1 = 47600·67.95 = 3 234 420 руб.При скорости 14,5 узлов
f(14,5) = 68·14,52 + 408000/14,5 = 14297 +28137,9 = 42434,9 руб. в часСтоимость рейса
S2 = 42434,9 ·46,55= 1 975 344,6 руб.
Определим дополнительную прибыль за рейс
f(v) = k·v2 + b/v -
38 слайд
Дополнительная прибыль
S1 — S2 = 3 234 420 — 1 975 344,6 =
= 1 259 075,4 руб.
Определим дополнительную прибыль за рейс
f(v) = k·v2 + b/v -
39 слайд
Домашнее задание
1.Теплоход движется по прямой согласно закону , где S(t) путь в милях и t – время в часах. В какой момент времени скорость теплохода будет наибольшей и какова величина этой скорости, если движение рассматривать за промежуток времени от
до ? -
40 слайд
Надо ли знать формулы для вычисления
производных функций?
В чем заключается механический смысл производной?
Как называется производная расстояния по времени?
Как найти ускорение, зная скорость?
Нужно ли, по Вашему мнению, изучать тему «Производная» с точки зрения подготовки к профессии?
Почему?
Довольны ли Вы своей оценкой успеваемости за урок?
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 264 852 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 27.04.2016
- 781
- 1
- 27.04.2016
- 1071
- 4
- 27.04.2016
- 1285
- 8
Рейтинг:
4 из 5
- 27.04.2016
- 5780
- 521
- 27.04.2016
- 502
- 0
- 27.04.2016
- 490
- 2
- 27.04.2016
- 920
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»