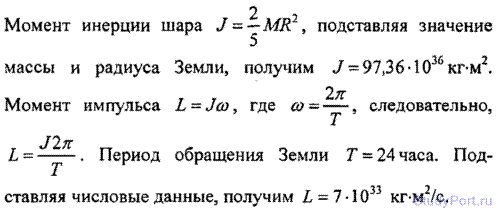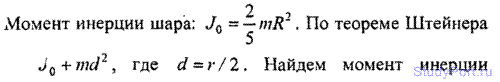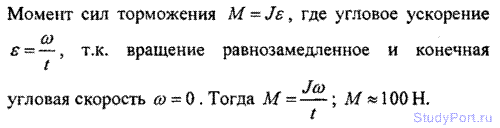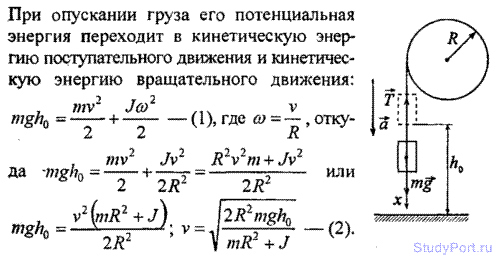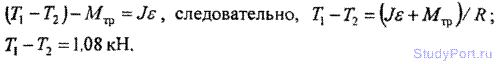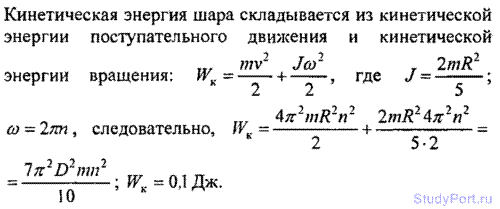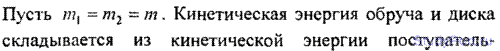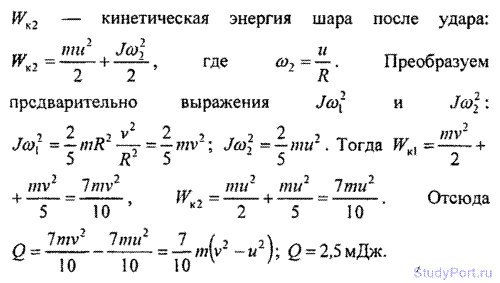2017-12-10
Две гири с массами $m_{1} = 2 кг$ и $m_{1} = 1 кг$ соединены нитью, перекинутой через блок массой $m = 1 кг$. Найти ускорение $a$, с которым движутся гири, и силы натяжения $T_{1}$ и $T_{2}$ нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
Решение:
Запишем в векторной форме уравнения поступательного движения первой и второй гири: $m_{1} vec{a} = m_{1} vec{g} + vec{T}_{1}; m_{2} vec{a} = vec{T}_{2} + m_{2} vec{g}$ и уравнение вращательного движения диска $J cdot vec{ epsilon} = vec{M}_{1} + vec{M}_{2}$, где $M_{1}$ — момент силы натяжения нити $T_{1}$, $M_{2}$ — момент силы натяжения нити $T_{2}$. Спроектируем первые два уравнения на ось х, а последнее на ось у и добавим уравнение кинематической связи. Получим систему 4 уравнений: $m_{1}a = m_{1}g — T_{1}$ — (1); $- m_{2}a = m_{2}g — T_{2}$ — (2); $J epsilon = RT_{1} — RT_{2}$ — (3); $a = epsilon R$. Подставим (4) в (3): $J frac{a}{R} = R(T_{1} — T_{2})$ — (5). Вычтем (2) из (1), подставим в полученное выражение (5) и найдем $a = frac{(m_{1} — m_{2})g}{m_{1} + m_{2} + m/2} = 2,8 м/с^{2}$ — (6) 2,8 м/с2 — (6). Подставляя (6) в (1) и (2), получим $T_{1} = m_{1} (g — a); T_{1} = 14 H. T_{2} = m_{2} (g + a); T_{2} = 12,6 H$.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

две гири массами 2 кг и 1 кг соединены нитью перекинутой через блок. найти ускорение, с которым движутся гири и силу натяжения нити. Трением в блоке и его массой пренебречь. чему равна сила давления на ось блока.
Светило науки — 16 ответов — 0 раз оказано помощи
на каждый из грузов действуют 2 силы:сила тяжести ,сила натяжения нити
сила натяжении нити действует на каждый из грузов с одной и той же силой ,модули перемещения,модули скорости и ускорения равны
модуль ускорения грузов
а1=а2=а
уравнение второго закона Ньютона для грузов запишем
в проекции на ось У получим
m1g-T=-m1a
m2g-T=m2a
вычтем из второго выражения первое
m2g-m1g=m2a+m1a
g(m2-m1)=a*(m2+m1)
a=g*(m2-m1)/(m2+m1)-ускорение грузов
сила натяжения -вес каждого груза
из уравнения 1 системы получим T=m1g+m1a
из уравнения 2 получим T=m2g+m2a
T=m1g+m1a-вместо а подставим формулу для ускорения грузов
T=m1g+m1g*(m2-m1)/(m2+m1)=m1g(1+(m2-m1)/(m2+m1))=m1g((m2+m1+m2-m1)/(m2+m1))=m1g((2m2)/(m2+m1))=2g*((m1*m2)/(m2+m1))
T=2g*((m1*m2)/m2+m1))- сила натяжения нити!
m2-2 кг
m1-1 кг
g=10 м /с
считайте!
776*. Две гири А и B массами по 1 кг соединены легкой нерастяжимой нитью, перекинутой через блок (рис. 229). Найдите ускорение, с которым движутся гири; силу натяжения нити. (Трением можно пренебречь.)
№776.
Дано:
Решение:
Повторяем рассуждения, приведенные в задаче № 774, касающиеся невесомости и нерастяжимости нити, невесомости блока и отсутствия силы трения в оси. Приходим к выводу, что тела будут двигаться с одинаковым по абсолютной величине ускорением а и величина силы натяжения нити Т постоянна вдоль всей ее длины. Нарисуем рисунок.
Изобразим на нем силы, действующие на грузы, их ускорения и координатные оси. На тело А действует сила тяжести m1g и сила натяжения нити Т1. На тело В действуют три силы: сила тяжести m1g, сила реакции
опоры N и сила натяжения нити T1. Запишем основной закон динамики (второй закон Ньютона) для каждого тела:
Мы поставили знак системы между уравнениями, так как они должны выполняться одновременно. Теперь запишем проекции векторных уравнений системы на оси координат:
Теперь легко находим натяжение нити:
Ответ из учебника(задачника): 776*. 4,9 м/с2; 4,9 Н.
Страница 1 из 3
3.1. Найти момент инерции J и момент импульса L земного шара относительно оси вращения.
Решение:
3.2. Два шара одинакового радиуса R = 5 см закреплены на концах невесомого стержня. Расстояние между шарами r = 0,5 м. Масса каждого шара m = 1 кг. Найти: а) момент инерции J1 системы относительно оси, проходящей через середину стержня перпендикулярно к нему; б) момент инерции J2 системы относительно той же оси, считая шары материальными точками, массы которых сосредоточены в их центрах; в) относительную ошибку б = (J1 — J2)/ J2, которую мы допускаем при вычислении момента инерции системы, заменяя величину J1 величиной J2.
Решение:
3.3. К ободу однородного диска радиусом R = 0,2 м прило касательная сила F = 98,1 Н. При вращении на диск действует момент сил трения Mтр=98,1 Н*м. Найти массу m дисков, если известно, что диск вращается с угловым ускоре е = 100 рад/с2.
Решение:
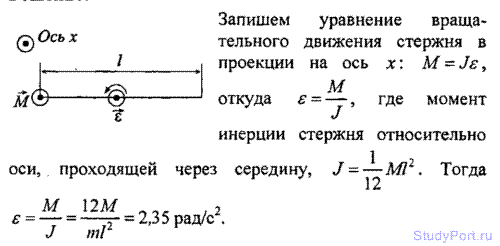
3.4. Однородный стержень длиной l = 1 м и массой m = 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением е вращается стержень, если на него действует момент сил М = 98,1 мН*м?
Решение:
3.5. Однородный диск радиусом R = 0,2 м и массой m = 0,5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости w вращения диска от времени t дается уравнением w = А + Bt, где В = 8 рад/с2. Найти касательную силу F, приложенную к ободу диска. Трением пренебречь.
Решение:
3.6. Маховик, момент инерции которого J = 63,6кгм2 враща с угловой скоростью w = 31,4 рад/с. Найти момент сил тор М, под действием которого маховик останавливается через время t = 20 с. Маховик считать однородным диском.
Решение:
3.7. К ободу колеса радиусом 0,5м и массой m = 50 кг при касательная сила F = 98,1 Н. Найти угловое ускорение s колеса. Через какое время t после начала действия силы колесо будет иметь частоту вращения n = 100 об/с? Колесо считать однородным диском. Трением пренебречь.
Решение:
3.8. Маховик радиусом R = 0,2 м и массой m = 10 кг соединен с мотором при помощи приводного ремня. Сила натяжения ремня, идущего без скольжения, T = 14,7Н. Какую частоту вра n будет иметь маховик через время t = 10 с после начала движения? Маховик считать однородным диском. Трением пренебречь.
Решение:
3.9. Маховое колесо, момент инерции которого J = 245 кг л, вращается с частотой n = 20 об/с. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения и число оборотов N, которое сделало колесо до полной остановки после прекра действия сил. Колесо считать однородным диском.
Решение:
З.10. Две гири с массами m1 =2 кг и m2 =1кг соединены нитью, перекинутой через блок массой m = 1 кг. Найти ускорение а, с которым движутся гири, и силы натяжения T1 и T2 нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
Решение:
3.11. На барабан массой m0=9кг намотан шнур, к концу которого привязан груз массой m = 2 кг. Найти ускорение а гру. Барабан считать однородным цилиндром. Трением прене.
Решение:
3.12. На барабан радиусом R = 0,5 м намотан шнур, к концу которого привязан груз массой m = 10 кг. Найти момент инерции J барабана, если известно, что груз опускается с ускорением а = 2,04 м/с2.
Решение:
3.13. На барабан радиусом R = 20 см, момент инерции кото J = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом hQ = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию WK груза в момент удара о пол и силу натяжения нити T. Трением пренебречь.
Решение:
3.14. Две гири с разными массами соединены нитью, переки через блок, момент инерции которого J = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока = 98,1 Нм. Найти разность сил натяжения нити T1 -T2 по обе стороны блока, если известно, что блок вращается с угловым ускорением e = 2,36 рад/с2. Блок считать однородным диском.
Решение:
3.15. Блок массой m = 1 кг укреплен на конце стола ( см. рис. и задачу 2.31). Гири 1 и 2 одинаковой массы m1=m2=1кг соединены нитью, перекинутой через блок. Коэффициент трения гири 2 о стол к = 0,1 . Найти ускорение а, с которым движутся гири, и силы натяжения T1 и T2 нитей. Блок считать однород диском. Трением в блоке пренебречь.
Решение:
3.16. Диск массой m = 2 кг катится без скольжения по гори плоскости со скоростью v = 4 м/с. Найти кинети энергию Wk диска.
Решение:
3.17. Шар диаметром D = 6 см и массой m = 0,25 кг катится без скольжения по горизонтальной плоскости с частотой враще n = 4 об/с. Найти кинетическую энергию WK шара.
Решение:
3.18. Обруч и диск одинаковой массы m1 = m2 катятся без скольжения с одной и той же скоростью v. Кинетическая энер обруча WKl =4кгсм. Найти кинетическую энергию Wk2 диска.
Решение:
3.19. Шар массой m = 1 кг катится без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку v = 10 см/с, после удара u = 8 см/с. Найти количество теплоты Q, выделившееся при ударе шара о стенку.
Решение:
3.20. Найти относительную ошибку б, которая получится при вычислении кинетической энергии WK катящегося шара, если не учитывать вращения шара.
Решение: