2020-02-12
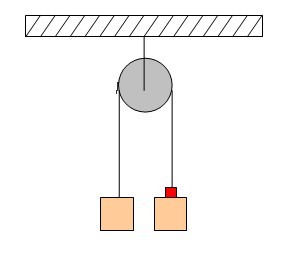
Найдите ускорение оси блока О в системе, состоящей из невесомых блоков, легких нерастяжимых нитей и грузов, массы которых указаны на рисунке. Трением пренебречь. Ускорение свободного падения равно $g$. Участки нитей, не лежащие на блоках, вертикальны.
Решение:
Поскольку нити и блоки невесомы и трения нет, сила натяжения нити $T$ должна быть одинакова вдоль всей длины нити (рис.). В проекции на вертикальную ось х уравнение движения невесомого блока О имеет вид
$2T — T = 0 cdot a_{O} = 0$,
где $a_{O}$ — искомое ускорение оси этого блока. Отсюда следует, что сила натяжения нити равна нулю и каждый из грузов падает под действием только силы тяжести с ускорением $g$:
$T = 0, a_{1} = a_{2} = a_{3} = g$.
Из условия нерастяжимости нитей можно получить уравнение кинематической связи ускорений грузов $a_{1}, a_{2}, a_{3}$ и ускорения оси интересующего нас блока $a_{O}$. Для этого выразим постоянную длину нити $l$ через координаты грузов и оси блока:
$l = x_{1} + x_{2} + (x_{2} — x_{O}) + (x_{3} — X_{O}) + x_{3} + X_{O} + const = x_{1} + 2x_{2} + 2x_{3} — x_{O} + const$
(здесь $const$ включает в себя длины участков нитей, лежащих на блоках и соединяющих блоки с грузами). Дифференцируя это соотношение два раза по времени, получаем связь ускорений:
$a_{1} + 2a_{2} + 2a_{3} — a_{O} = 0$,
откуда
$a_{O} = a_{1} + 2a_{2} + 2a_{3} = g + 2g + 2g = 5g$.
Итак, ось блока О движется вертикально вниз с ускорением $a_{O} = 5g$.
Общий случай решения
Рассмотрим общий случай. Имеется неподвижный блок, через который перекинута нить, к концам которой подвешены два грузика массой и
, где
.
Рис. 1. Схема блока
;
;
На первый грузик действует сила притяжения к земле и сила натяжения нити, которая направлена вверх. Соответственно, на второй грузик будут действовать те же силы. Величины сил натяжения их будут одинаковы по модулю при условии, что трение в оси блока отсутствует и сам блок невесом, то есть его не нужно раскручивать какой-то парой сил. Сила натяжения – это внутренняя сила, возникающая в системе связанных тел, друг на друга они действуют посредством нити. Ускорение у этих грузиков будет иметь разное направление, так как первый грузик тяжелее, то он будет двигаться вниз, а второй вверх, но величины ускорений будут одинаковы и равны а, при условии, что нить нерастяжима. К блоку приложены три силы – две силы натяжения, которые тянут блок вниз, и сила реакции крепления оси блока, направленная вверх и равная удвоенной силе натяжения, так как центр блока никуда не перемещается и сумма сил, приложенных к нему должна быть равна нулю. При разборе таких задач оси рисовать не обязательно, потому что подразумевается, что для каждого тела можно выбрать свое направление оси. Так как первое тело движется вниз, то ось необходимо направить вниз так, как направлено ускорение. Второе тело движется вверх и
направлено вверх согласно второму ускорению. Записываем второй закон Ньютона для этих тел, при сложении внутренние силы у нас сократятся, и мы получим общий вид для ускорения. Это отношение у нас будет всегда, то есть какое-то числовое значение, умноженное на
, которое заставляет систему всегда двигаться.
Задача 1
Одинаковые бруски, связанные нитью, движутся под действием внешней силы по гладкой горизонтальной поверхности (рис. 2). Как изменится сила натяжения нити
, если третий брусок переложить с первого на второй?
- Увеличится в 2 раза
- Увеличится в 3 раза
- Уменьшится в 1,5 раза
- Уменьшится в 2раза
Рис. 2. Иллюстрация к задаче 1 (Источник)
В этой задаче необходимо найти отношение силы натяжения к
;
;
Рис. 3. Решение задачи 1 (Источник)
Растянутая нить в этой системе действует на брусок 2, заставляя его двигаться вперед, но она также действует и на брусок 1, пытаясь препятствовать его движению. Эти две силы натяжения равны по величине, и нам как раз необходимо найти эту силу натяжения. В таких задачах необходимо упростить решение следующим образом: считаем, что сила является единственной внешней силой, которая заставляет двигаться систему трех одинаковых брусков, и ускорение остается неизменным, то есть сила заставляет двигаться все три бруска с одинаковым ускорением. Тогда натяжение
всегда двигает только один брусок и будет равно mа по второму закону Ньютона.
будет равно удвоенному произведению массы на ускорение, так как третий брусок находится на втором и нить натяжения должна уже двигать два бруска. В таком случае отношение
к
будет равно 2. Правильный ответ – первый.
Задача 2
Два тела массой и
, связанные невесомой нерастяжимой нитью, могут без трения скользить по гладкой горизонтальной поверхности под действием постоянной силы
(рис. 4). Чему равно отношение сил натяжения нити в случаях а и б?
Выбор ответа: 1. 2/3; 2. 1; 3. 3/2; 4. 9/4.
Рис. 4. Иллюстрация к задаче 2 (Источник)
Рис. 5. Решение задачи 2 (Источник)
На бруски действует одна и та же сила, только в разных направлениях, поэтому ускорение в случае «а» и случае «б» будет одним и тем же, так как одна и та же сила вызывает ускорение двух масс. Но в случае «а» эта сила натяжения заставляет двигаться еще и брусок 2, в случае «б» это брусок 1. Тогда отношение этих сил будет равно отношению их масс и мы получим ответ – 1,5. Это третий ответ.
Задача 3
На столе лежит брусок массой 1 кг, к которому привязана нить, перекинутая через неподвижный блок. Ко второму концу нити подвешен груз массой 0,5 кг (рис. 6). Определить ускорение, с которым движется брусок, если коэффициент трения бруска о стол составляет 0,35.
Рис. 6. Иллюстрация к задаче 3 (Источник)
Записываем краткое условие задачи:
Рис. 7. Решение задачи 3 (Источник)
Необходимо помнить, что силы натяжения и
как векторы разные, но величины этих сил одинаковы и равны
Точно также у нас будут одинаковы и ускорения этих тел, так как они связаны нерастяжимой нитью, хотя направлены они в разные стороны:
– горизонтально,
– вертикально. Соответственно, и оси для каждого из тел выбираем свои. Запишем уравнения второго закона Ньютона для каждого из этих тел, при сложении внутренние силы натяжения сократятся, и получим обычное уравнение, подставив в него данные, получим, что ускорение равно
.
Для решения таких задач можно пользоваться методом, который использовался в прошлом веке: движущей силой в данном случае является результирующая внешних сил, приложенных к телу. Заставляет двигаться эту систему сила тяжести второго тела, но мешает движению сила трения бруска о стол, в этом случае:
, так как движутся оба тела, то движущая масса будет равна сумме масс
, тогда ускорение будет равно отношению движущей силы на движущую массу
Так можно сразу прийти к ответу.
Задача 4
В вершине двух наклонных плоскостей, составляющих с горизонтом углы и
, закреплен блок. По поверхности плоскостей при коэффициенте трения 0,2 движутся бруски
кг и
, связанные нитью, перекинутой через блок (рис. 8). Найти силу давления на ось блока.
Рис. 8. Иллюстрация к задаче 4 (Источник)
Выполним краткую запись условия задачи и поясняющий чертеж (рис. 9):
Рис. 9. Решение задачи 4 (Источник)
Мы помним, что если одна плоскость составляет угол в 600 с горизонтом, а вторая плоскость – 300 с горизонтом, то угол при вершине будет 900, это обычный прямоугольный треугольник. Через блок перекинута нить, к которой подвешены бруски, они тянут вниз с одной и той же силой, и действие сил натяжения Fн1 и Fн2 приводит к тому, что на блок действует их результирующая сила. Но между собой эти силы натяжения будут равны, составляют они между собой прямой угол, поэтому при сложении этих сил получается квадрат вместо обычного параллелограмма. Искомая сила Fд является диагональю квадрата. Мы видим, что для результата нам необходимо найти силу натяжения нити. Проведем анализ: в какую сторону движется система из двух связанных брусков? Более массивный брусок, естественно, перетянет более легкий, брусок 1 будет соскальзывать вниз, а брусок 2 будет двигаться наверх по склону, тогда уравнение второго закона Ньютона для каждого из брусков будет выглядеть:
Решение системы уравнений для связанных тел выполняется методом сложения, далее преобразовываем и находим ускорение:
=
Это значение ускорения необходимо подставить в формулу для силы натяжения и найти силу давления на ось блока:
Мы выяснили, что сила давления на ось блока приблизительно равна 16 Н.
Заключение
Мы рассмотрели различные способы решения задач, которые многим из вас пригодятся в дальнейшем, чтобы понять принципы устройства и работы тех машин и механизмов, с которыми придется иметь дело на производстве, в армии, в быту.
Список литературы
- Тихомирова С. А., Яворский Б. М. Физика (базовый уровень) – М.: Мнемозина, 2012.
- Генденштейн Л. Э., Дик Ю. И. Физика 10 класс. – М.: Мнемозина, 2014.
- Кикоин И. К., Кикоин А. К. Физика-9. – М.: Просвещение, 1990.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «bambookes.ru» (Источник)
- Интернет-портал «10klass.ru» (Источник)
- Интернет-портал «festival.1september.ru» (Источник)
Домашнее задание
- Каким законом мы пользуемся при составлении уравнений?
- Какие величины одинаковы у тел, связанных нерастяжимой нитью?
Два тела
массами по 0,2 кг, на одном из которых лежит перегрузок массой 0,05 кг, связаны
невесомой нерастяжимой нитью, переброшенной через неподвижный блок. Определите
ускорения тел, силу давления перегрузка на тела и силу давления на ось блока.
Решение.
Систему
отсчета свяжем с лабораторией и будем считать ее инерциальной. Начало координат
выберем в точке, совпадающей с осью блока, ось OY направим вертикально вниз.
В качестве
физических систем будем поочерёдно рассматривать первое тело, второе тело,
перегрузок и блок. Причем, тела и перегрузок примем за материальные точки, а
блок будем считать абсолютно твердым телом.
Взаимодействием
с воздухом, массой
блока, массой нити и ее деформацией, а также трением в оси
блока пренебрегаем.
Для решения
задачи воспользуемся законами динамики (вторым законом Ньютона и законами для
частных сил). Движущиеся тела m1 , m2 и ∆m
взаимодействуют с
гравитационным полем Земли, т.е. на них действуют силы тяжести m1g , m2g и ∆m , направленные вертикально вниз;
взаимодействие тел m1 и m2 с нитью дает силы упругости T1 и T2 , направленные вертикально вверх;
кроме того, тело m2 взаимодействует с перегрузком ∆m , что дает силу давления перегрузка
на это тело F
и силу реакции N
, действующую со стороны этого тела на перегрузок.
Согласно
второму закону Ньютона, для каждого из движущихся тел получим систему
.
Если спроецировать
векторные величины на ось OY,
получим:
Поскольку нить
невесомая и нерастяжимая, то T1 = T2 = T
и a1 = a2 = a.
Согласно третьему закону
Ньютона F
= N. По условию задачи m1 = m2 = m. С учетом того динамические законы
движения тел можно записать следующим образом
Если решить эту систему
уравнений относительно неизвестных, получим:
Для нахождения силы
давления на ось блока рассмотрим силы, действующие на него. Взаимодействие блока
с нитью дает две силы упругости T’1
и T’2 направленные вертикально
вниз. С учетом того, что нить невесома и нерастяжима, имеем: T’1 = T’2 = T . Откуда найдем силу натяжения
Кроме того, на блок
действует сила реакции оси N’
, на которой этот блок закреплен. Таким образом, N’ + T’1 + T’2 = 0 , откуда N’ = T’1 + T’2 = 2T .
По третьему закону
Ньютона сила давления F’
на ось блока равно по модулю силе реакции оси N’ , т.е.
Численно: a = 1.1 м/с2; F = 0.44 H; F’ = 19 H.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
Условие задачи: Двухступенчатый блок (см. рис.) состоит из лёгких, жёстко соединённых дисков, которые могут вращаться без трения вокруг оси О пренебрежимо малой массы. Диаметры дисков отличаются в два раза. К концам лёгких нерастяжимых нитей, намотанных на диски блока, присоединены грузы массой: m1 = 0,5 кг и m2 = 0,4 кг. Система находится на гладком горизонтальном столе. К оси блока приложена сила, равная F = 1,8 Н. Найдите ускорение оси блока а0.
Рисунок здесь: https://mosphys.olimpiada.ru/upload/files/11_1_2021.pdf
Здравствуйте! Не удается разобраться с этой задачей. Записываю кинематическую связь — получаю выражение для ускорения а0 через ускорения грузов. Но сами ускорения найти не удается — не хватает уравнений.
В официальном очень кратком решении каким-то образом сразу из того, что блок невесомый, делается вывод, что силы натяжения нитей относятся как 1:2. Было бы здорово, если бы кто-нибудь объяснил, откуда это следует.
5.ДИНАМИКА МЕХАНИЧЕСКОЙ СИСТЕМЫ
5.1.Описание движений твёрдых тел на основе общих теорем динамики
системы Поступательное движение твердого тела описывается теоремой о дви-
жении центра масс механической системы. В проекциях на координатные оси дифференциальные уравнения поступательного движения твердого тела имеют
|
вид: m&x& |
= å F e |
, |
m&y& |
= å F e |
, |
m&z& = åF e |
, где m – масса тела; |
x |
C |
, y |
C |
,z |
C |
– |
|||
|
C |
kx |
C |
ky |
C |
kz |
||||||||||||
|
координаты центра масс тела; F e |
, F e |
, |
F e |
– проекции на оси координат внеш- |
|||||||||||||
|
kx |
ky |
kz |
них сил, действующих на твердое тело.
Вращательное движение твердого тела относительно неподвижной оси
z описывается теоремой об изменении кинетического момента.
Дифференциальное уравнения вращательного движения тела имеет вид:
|
dω |
e |
e |
||||
|
J z |
=åM z (Fk ) или |
J z ϕ = å M z (Fk ), |
||||
|
dt |
||||||
|
где ω – угловая скорость тела; |
& |
&& |
e |
) – |
||
|
ω = ϕ; ϕ |
– угол поворота тела; åM z (Fk |
|||||
|
моменты внешних сил относительно оси z; |
Jz – момент инерции тела относи- |
|||||
|
тельно оси z. |
||||||
|
Уравнение вращательного движения можно представить в алгебраической |
||||||
|
e |
& |
|||||
|
форме: J zε = åM z (Fk ), где ε – угловое ускорение тела; ε = ω. |
Плоскопараллельное движение твердого тела описывается на основа-
нии теорем о движении центра масс и изменении кинетического момента отно-
сительно оси, проходящей через центр масс перпендикулярно плоскости дви-
жения. В проекции на координатные оси уравнения плоскопараллельного дви-
жения тела имеют вид:
|
ma = åF e |
, ma |
Cy |
= åF e |
, |
J |
zC |
ε = å M |
zC |
(F e ), |
|
Cx |
kx |
ky |
k |
где aCx , aCy – проекции ускорения центра масс тела на координатные оси; Fkxe ,
103
Fkye – проекции на оси координат внешних сил, действующих на тело; J zC –
момент инерции тела относительно оси z, проходящей через центр масс, пер-
пендикулярно плоскости движения; ε – угловое ускорение тела; M zC (Fke ) –
моменты внешних сил относительно оси, проходящей через центр масс.
Проводя динамический расчет механической системы, следует рассмат-
ривать движение тел системы в отдельности, предварительно освободив их от связей и заменив действие связей реакциями. Далее на основании общих теорем динамики системы следует составить уравнения движения каждого тела.
5.2. Задание Д4. Динамический расчет механической системы
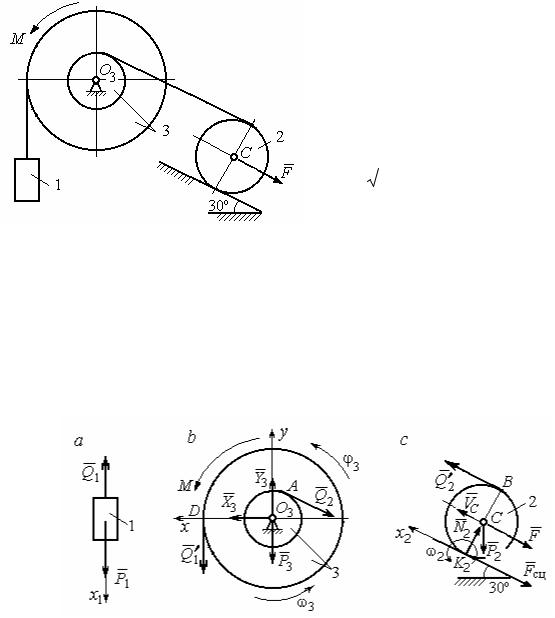
Механизм состоит из трёх тел – груза 1, катка 2 и блока 3, соединенных нерастяжимыми нитями или невесомыми стержнями.
Движение механизма происходит в вертикальной плоскости под действи-
ем сил тяжести P1 , P2 , P3 , силы F и пары сил с моментом М. Направление дей-
ствия силы F определяется углом α. Качение катка 2 происходит без скольже-
ния. Проскальзывание между дисками и соединяющими их невесомыми стерж-
нями или нитями отсутствует.
Сплошные диски считать однородными. Радиусы ступеней катка 2 и бло-
ка 3 на схемах обозначены R2 , r2 и R3 , r3.
Радиусы инерции неоднородных (ступенчатых) дисков относительно осей, проходящих через центры масс перпендикулярно плоскости движения равны iz2 , iz3 .
Найти ускорение груза 1 и динамические реакции, действующие на ось блока 3.
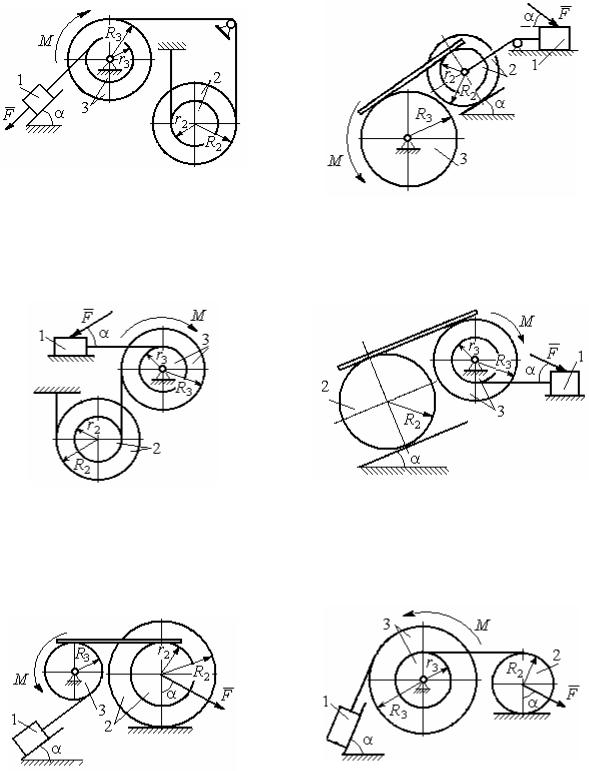
Варианты заданий представлены на рис. 5.1 – 5.2. Исходные данные при-
ведены в табл. 5.1.
104
|
Варианты № 1, 11, 21 |
Варианты № 2, 12, 22 |
|
Варианты № 3, 13, 23 |
Варианты № 4, 14, 24 |
|
Варианты № 5, 15, 25 |
Варианты № 6, 16, 26 |
Рис. 5.1. Задание Д4. Динамический расчёт механической системы. Номера вариантов задания 1 – 6, 11 – 16, 21 – 26
105
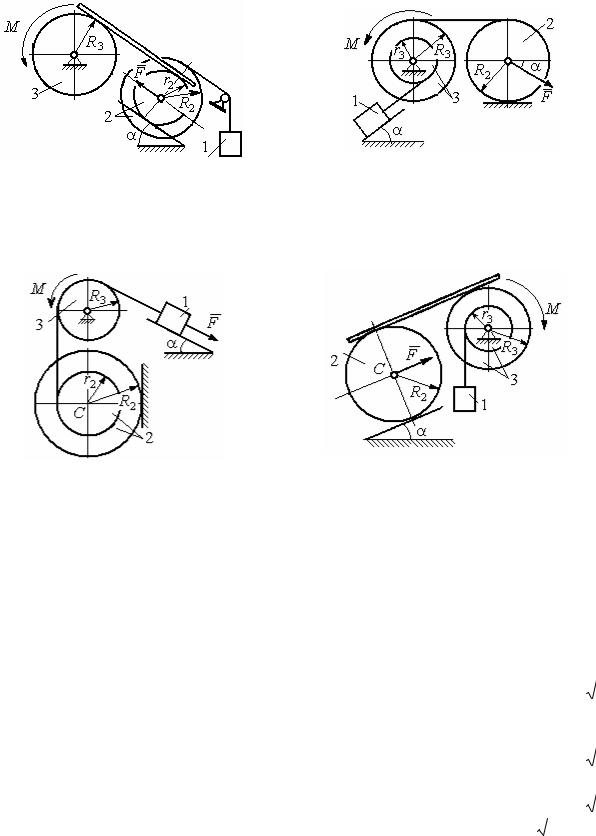
|
Окончание вариантов задания Д4 |
|
|
Варианты № 7, 17, 27 |
Варианты № 8, 18, 28 |
|
Варианты № 9, 19, 29 |
Варианты № 10, 20, 30 |
Рис. 5.2. Задание Д4. Динамический расчёт механической системы. Номера вариантов задания 7 – 10, 17 – 20, 27 – 30
Таблица 5.1
Исходные данные задания Д4. Динамический расчёт механической системы
|
Номер |
Р1, Н |
Р2, Н |
Р3, Н |
F, Н |
М, |
α , |
R2, м |
r2, м |
R3, м |
r3, м |
iz 2 , м |
iz3 , м |
|||
|
варианта |
Н·м |
град |
|||||||||||||
|
задания |
|||||||||||||||
|
1 |
Р |
Р |
2Р |
Р |
2Рr |
60 |
3r |
r |
2r |
r |
2r |
r |
|||
|
2 |
|||||||||||||||
|
2 |
3Р |
Р |
3Р |
3Р |
Рr |
30 |
2r |
r |
2r |
– |
2r |
– |
|||
|
3 |
4Р |
3Р |
4Р |
2Р |
2Рr |
60 |
2r |
r |
2r |
r |
2r |
2r |
|||
|
4 |
2Р |
2Р |
4Р |
Р |
4Рr |
45 |
3r |
– |
3r |
r |
– |
r |
|||
|
2 |
|||||||||||||||
|
5 |
Р |
3Р |
3Р |
2Р |
3Рr |
30 |
3r |
r |
r |
– |
2r |
– |
|||
|
6 |
Р |
2Р |
4Р |
4Р |
6Рr |
60 |
3r |
– |
3r |
r |
– |
r |
|||
|
2 |
|||||||||||||||
|
7 |
Р |
2Р |
3Р |
2Р |
3Рr |
45 |
3r |
r |
r |
— |
r |
– |
|||
|
3 |
106
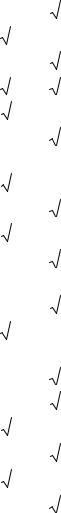
Окончание табл. 5.1
|
Номер |
Р1, Н |
Р2, Н |
Р3, Н |
F, Н |
М, |
α , |
R2, м |
r2, м |
R3, м |
r3, м |
iz 2 , м |
iz3 , м |
||||||||
|
варианта |
Н·м |
град |
||||||||||||||||||
|
задания |
||||||||||||||||||||
|
8 |
2Р |
3Р |
3Р |
Р |
3Рr |
30 |
2r |
– |
2r |
r |
– |
r |
||||||||
|
3 |
||||||||||||||||||||
|
9 |
3Р |
Р |
3Р |
Р |
2Рr |
30 |
2r |
r |
2r |
– |
r |
– |
||||||||
|
2 |
||||||||||||||||||||
|
10 |
Р |
Р |
3Р |
Р |
2Рr |
60 |
3r |
– |
3r |
r |
– |
r |
||||||||
|
3 |
||||||||||||||||||||
|
11 |
Р |
Р |
3Р |
2Р |
3Рr |
30 |
3r |
2r |
2r |
r |
r |
r |
||||||||
|
2 |
2 |
|||||||||||||||||||
|
12 |
2Р |
Р |
2Р |
4Р |
Рr |
60 |
3r |
r |
3r |
– |
r |
– |
||||||||
|
3 |
||||||||||||||||||||
|
13 |
3Р |
Р |
3Р |
3Р |
2Рr |
30 |
3r |
2r |
2r |
r |
2r |
r |
||||||||
|
2 |
||||||||||||||||||||
|
14 |
2Р |
Р |
3Р |
2Р |
4Рr |
60 |
2r |
– |
3r |
2r |
– |
2r |
||||||||
|
15 |
Р |
2Р |
4Р |
Р |
4Рr |
45 |
3r |
2r |
2r |
– |
r |
– |
||||||||
|
3 |
||||||||||||||||||||
|
16 |
Р |
3Р |
4Р |
2Р |
3Рr |
30 |
2r |
– |
2r |
r |
– |
r |
||||||||
|
2 |
||||||||||||||||||||
|
17 |
Р |
Р |
3Р |
2Р |
6Рr |
60 |
3r |
r |
3r |
— |
r |
|||||||||
|
3 |
||||||||||||||||||||
|
18 |
2Р |
2Р |
3Р |
Р |
3Рr |
60 |
2r |
– |
3r |
r |
– |
r |
||||||||
|
2 |
||||||||||||||||||||
|
19 |
2Р |
Р |
2Р |
3Р |
4Рr |
30 |
3r |
r |
3r |
– |
2r |
– |
||||||||
|
20 |
Р |
Р |
3Р |
Р |
2Рr |
45 |
2r |
– |
2r |
r |
– |
r |
||||||||
|
3 |
||||||||||||||||||||
|
21 |
2Р |
Р |
4Р |
2Р |
4Рr |
60 |
2r |
r |
3r |
r |
r |
2r |
||||||||
|
2 |
||||||||||||||||||||
|
22 |
Р |
Р |
2Р |
5Р |
2Рr |
45 |
3r |
2r |
2r |
– |
2r |
– |
||||||||
|
23 |
2Р |
2Р |
3Р |
3Р |
2Рr |
60 |
3r |
r |
2r |
r |
2r |
r |
||||||||
|
2 |
||||||||||||||||||||
|
24 |
4Р |
Р |
3Р |
Р |
3Рr |
30 |
2r |
– |
3r |
r |
– |
r |
||||||||
|
3 |
||||||||||||||||||||
|
25 |
Р |
3Р |
2Р |
Р |
2Рr |
60 |
3r |
r |
r |
– |
r |
– |
||||||||
|
3 |
||||||||||||||||||||
|
26 |
Р |
3Р |
4Р |
3Р |
3Рr |
45 |
2r |
– |
3r |
2r |
– |
r |
||||||||
|
3 |
||||||||||||||||||||
|
27 |
Р |
Р |
4Р |
2Р |
4Рr |
30 |
2r |
r |
2r |
— |
r |
|||||||||
|
3 |
||||||||||||||||||||
|
28 |
2Р |
3Р |
3Р |
Р |
6Рr |
30 |
2r |
– |
3r |
2r |
– |
r |
||||||||
|
2 |
||||||||||||||||||||
|
29 |
2Р |
Р |
2Р |
2Р |
2Рr |
45 |
2r |
r |
r |
– |
2r |
– |
||||||||
|
30 |
Р |
Р |
4Р |
Р |
4Рr |
60 |
3r |
– |
3r |
2r |
– |
2r |
Пример выполнения задания Д4. Динамический расчёт механической системы
Механизм (рис. 5.3) состоит из груза 1, однородного диска – катка 2 и не-
однородного диска – блока 3, соединённых друг с другом нерастяжимыми ни-
тями. Система движется в вертикальной плоскости из состояния покоя.
Движение происходит под действием сил тяжести P1, P2 , P3 , равных по
|
модулю: Р1 = 2Р, |
Р2 = 2Р, |
Р3 = 3Р, силы F , |
приложенной в центре масс |
|
катка 2, равной по |
величине: |
F = 3Р, и пары |
сил с моментом М = Рr, |
|
107 |
приложенных к блоку 3. Механизм является неизменяемой механической сис-
|
темой. Радиус катка 2 R2 = 2r . Каче- |
||
|
ние катка по наклонной плоскости |
||
|
происходит без проскальзывания. Ра- |
||
|
диусы ступенчатого блока 3: R3 = 3r , |
||
|
r3 = r . |
Радиус инерции блока 3 |
|
|
i3 = r |
. Найти ускорение груза 1 и |
|
|
3 |
||
|
динамические реакции, действующие |
|
Рис. 5.3. Схема механической системы |
на ось вращающегося блока 3, с по- |
|
мощью метода динамического расчета механической системы. |
Решение
Освобождаем систему от связей. На рис. 5.4 изображены внешние силы,
действующие на каждое тело, после освобождения его от связей.
Рис. 5.4. Расчетные схемы для описания движения тел, входящих в систему:
а– поступательное движение груза 1; b – вращательное движение блока 3;
с– плоское движение катка 2
Груз 1 совершает поступательное движение. К нему приложены сила тя-
жести P1 и реакция нити (натяжение) Q1 (рис. 5.4, а). Предположим, груз 1
движется вниз, и направим ось x1 в сторону движения груза.
Уравнение движения груза вдоль оси x1 в соответствии с теоремой о дви-
жении центра масс механической системы имеет вид:
108

m1a1 = å Fkx = P1 − Q1 = 2P − Q1 ,
где m1, a1 – соответственно, масса груза 1 и его ускорение, m1 = Pg1 = 2gP .
Блок 3 вращается вокруг неподвижной оси z , проходящей через его центр масс О3, перпендикулярно плоскости диска. Направление вращения блока, со-
ответствующее выбранному движению вниз груза 1, показано на рис. 5.4, b ду-
говой стрелкой ω3 .
На блок действуют сила тяжести P3 , силы реакции подшипника X 3 , Y3 ,
момент М и натяжения нитей Q1′ и Q2 (рис. 5.4, b). При составлении уравнения вращательного движения блока 3 моменты сил считаем положительными, если
они поворачивают блок в сторону его вращения.
Уравнение вращения блока 3 имеет вид:
J zO3 ε3 = åM zO3 (Fk )= Q1′R3 + M − Q2r3 = Q13r + Pr− Q2r ,
|
где J zO |
– момент инерции блока 3 относительно оси z; ε3 – угловое ускорение |
||||||||||||
|
3 |
|||||||||||||
|
P |
9Pr 2 |
||||||||||||
|
диска 3, |
J |
zO |
= m i2 |
= |
3 |
(r 3)2 = |
. |
||||||
|
3 |
3 3 |
g |
g |
||||||||||
|
Каток 2 совершает плоскопараллельное движение. К нему приложены си- |
|||||||||||||
|
ла тяжести P2 , сила F , |
′ |
||||||||||||
|
реакция нити Q2 и реакция наклонной плоскости, со- |
|||||||||||||
|
стоящая из нормальной реакции |
N2 и силы сцепления катка с поверхностью |
Fсц . Согласно принципу равенства действия и противодействия модули сил Q2
и Q2′ равны. На рис. 5.4, с показаны направления действия сил, приложенных к диску 2. В соответствии с выбранным направлением движения груза 1, центр масс катка 2 движется вверх параллельно наклонной плоскости. Направление движения центра масс катка 2 показано направлением оси х2, направление вра-
щения катка 2 – угловой скоростью ω2 (см. рис 5.4, с).
109
Плоскопараллельное движение катка 2 описывается уравнением движе-
ния его центра масс и уравнением вращения вокруг оси, проходящей через центр масс, перпендикулярно плоскости диска. Составляя уравнение движения
центра масс катка 2 в проекции на ось х2 и считая в уравнении вращательного движения диска момент силы положительным, если создаваемый им поворот направлен в сторону вращения диска, получим:
|
′ |
o |
||||||
|
m2aC = Q2 − F − Fсц − P2cos60 |
=Q2 − 3P − Fсц − P , |
||||||
|
′ |
+ Fсц R2 = Q2 2r + Fсц 2r , |
||||||
|
JC ε2 = Q2 R2 |
|||||||
|
где m2 |
– масса катка 2, m2 = |
P2 |
= |
2P |
; aC – ускорение центра масс катка 2; e2 – |
||
|
g |
g |
||||||
|
угловое ускорение катка 2; JC |
– момент инерции однородного катка 2 относи- |
тельно оси, проходящей через центр масс, перпендикулярно плоскости диска,
|
m |
R2 |
PR2 |
4Pr 2 |
||||
|
JC = |
2 2 |
= |
2 |
= |
. |
||
|
2 |
g |
g |
|||||
К системе четырех уравнений, описывающих движения тел в системе, не-
обходимо добавить уравнения связей. Если предположить, что скорость центра масс катка 2 равна VC , то угловая скорость катка определится по формуле:
|
ω2 = |
VC |
= |
VC |
, где CK2 – расстояние от центра масс катка 2 до его мгновен- |
|
CK2 |
||||
|
R2 |
ного центра скоростей (см. рис. 5.4, с). Продифференцировав по времени по-
следнее равенство, получим уравнение связи между ускорением центра масс
|
V& |
a |
C |
a |
C |
|||||||||||||||
|
катка 2 и его угловым ускорением ε2 = ω2 = |
C |
= |
= |
. |
|||||||||||||||
|
& |
R2 |
R2 |
2r |
||||||||||||||||
|
Скорость точки В катка 2 (см. рис. 5.4, с) можно выразить через скорость |
|||||||||||||||||||
|
его центра масс следующим образом: V |
B |
= w |
2 |
× BK |
2 |
= |
VC |
2R |
2 |
= |
2V . Точка В |
||||||||
|
R2 |
C |
||||||||||||||||||
катка 2 и точка А блока 3 соединены нитью (см. рис. 5.3), поэтому их скорости
110

равны. Приравняв скорость точки А к скорости точки В, получим равенство: 2VC = VB = VA = ω3r3 = ω3r , откуда ω3 = 2VrC .
После дифференцирования последнего выражения найдём соотношение между ускорениями: ε3 = 2arC .
Скорость груза 1 связана со скоростью центра масс диска 2 следующим образом: V1 = VD = ω3R3 = 2VrC 3r = 6VC . Тогда a1 = 6aC . В результате получены четыре уравнения, описывающие движение груза 1, блока 3 и катка 2:
|
2P |
a = 2P − Q , |
9Pr |
2 |
ε |
= Q 3r + Pr− Q r , |
||||||||||||||||
|
g |
g |
||||||||||||||||||||
|
1 |
1 |
3 |
1 |
2 |
|||||||||||||||||
|
2P |
a |
C |
= Q − 3P − F − P , |
4Pr 2 |
ε |
2 |
= Q 2r + F 2r |
||||||||||||||
|
g |
2 |
aC |
сц |
2aC |
g |
2 |
сц |
||||||||||||||
|
и три уравнения связей: ε |
2 |
= |
, ε |
3 |
= |
, a |
= 6a |
C |
. |
||||||||||||
|
2r |
r |
1 |
|||||||||||||||||||
После подстановки уравнений связи в уравнения движения тел, получим
систему четырёх уравнений с четырьмя неизвестными:
|
12P |
a |
C |
= 2P − Q , |
18P |
a |
C |
= 3Q + P − Q |
2 |
, |
||
|
g |
1 |
g |
1 |
||||||||
|
2P |
a |
C |
=Q − 4P − F , |
P |
a |
C |
= Q + F . |
||||
|
g |
2 |
сц |
g |
2 сц |
Исключим из первых двух уравнений неизвестную величину Q1 , а из третьего и четвёртого уравнений – величину Fсц . С этой целью умножим первое
уравнение на 3 и сложим со вторым. Третье уравнение сложим с четвертым.
|
Получим систему двух уравнений |
54P |
a |
C |
= 7P − Q |
, |
3P |
a |
C |
= 2Q − 4P , откуда: |
|
|
g |
2 |
g |
2 |
aC = 11110 g , Q2 = 3779 P . Величину натяжения нити Q1 находим из первого урав-
нения исходной системы: Q1 = 3734 P .
111

Динамические реакции X 3 , Y3 , действующие на ось вращающегося бло-
ка 3 (рис. 5.4, b), определяются из уравнений, которые можно получить, приме-
нив теорему о движении центра масс.
Так как центр масс блока 3 неподвижен, его ускорение равно нулю и уравнения движения центра масс блока 3 в проекциях на оси x, y имеют вид:
m3aO3x = X 3 − Q2cos 30o = 0 , m3aO3 y = Y3 − Q1 − P3 − Q2cos60o = 0 .
Отсюда, с учетом значений Q1 = 3437 P и Q2 = 3779 P , динамические реакции
оси блока 3 равны: X3 = Q2cos30o = 1,85Р, Y3 = Q1 + P3 + Q2cos60o = 4,98Р.
Полная величина динамической реакции оси блока 3
R3 = 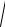
5.3. Теорема об изменении кинетической энергии системы.
|
Кинетическая энергия |
тела при |
поступательном |
движении: |
|||||
|
T = |
1 |
mV 2 |
, где m – масса тела; V |
– скорость центра масс тела. Кинетическая |
||||
|
2 |
C |
C |
||||||
|
энергия тела |
при вращательном движении |
вокруг неподвижной оси z: |
||||||
|
T = |
1 |
J zω2 |
, где |
J z – момент инерции тела относительно оси z; |
ω – угловая |
|||
|
2 |
||||||||
скорость тела. Для дисков с равномерно распределённой массой момент инер-
ции относительно оси z, проходящей через центр масс: J z = 12 mR2 , где R – ра-
диус диска. Для тел с неравномерно распределённой массой J z = miz2 , где iz –
радиус инерции. Кинетическая энергия тела при плоскопараллельном дви-
|
жении: T = |
1 |
mV 2 |
+ |
1 |
J |
ω2 |
, где m – масса тела; V , ω – скорость центра масс |
|
|
2 |
2 |
|||||||
|
C |
zС |
C |
||||||
|
и угловая скорость тела; J zС |
– момент инерции тела относительно оси z, прохо- |
дящей через центр масс перпендикулярно плоскости движения.
112
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #