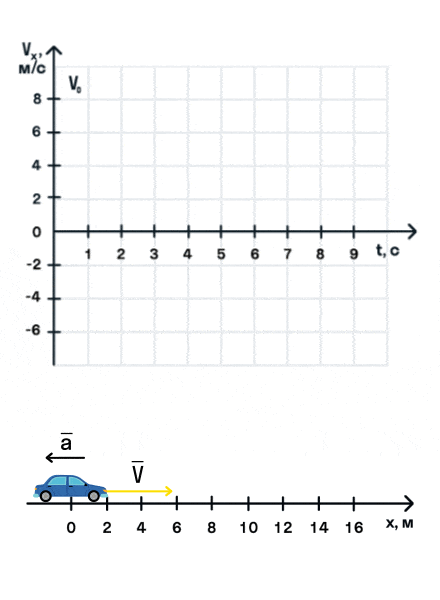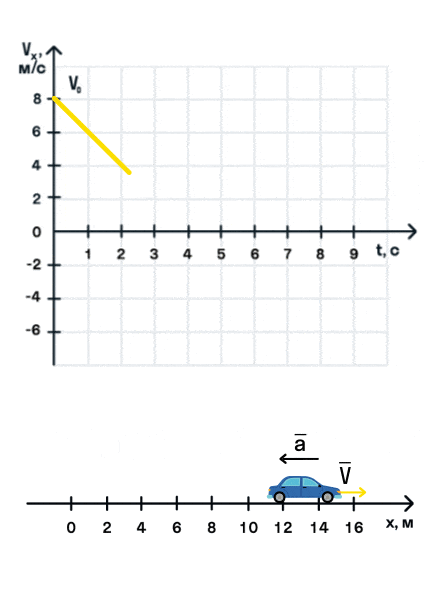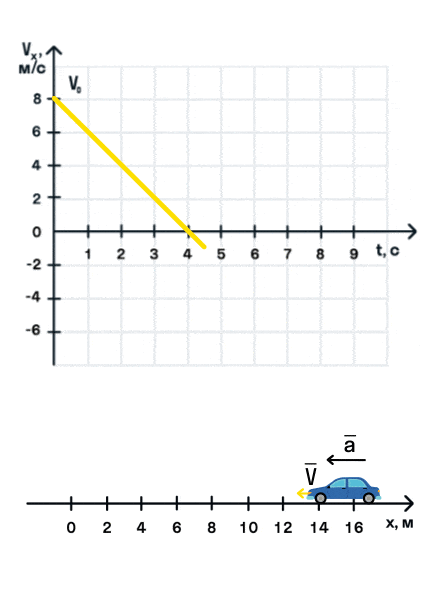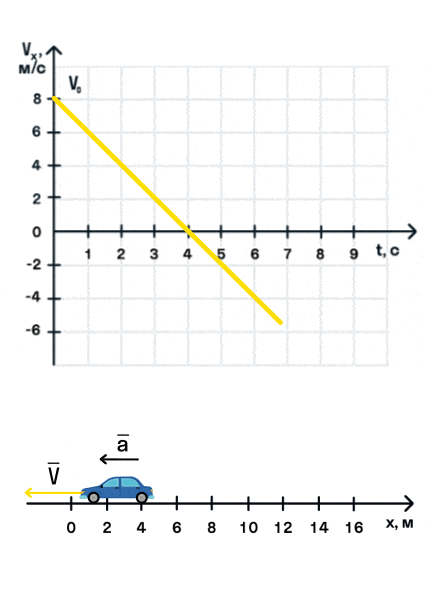Основные определения
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. Иногда его определяют как скорость изменения скорости. Проще говоря, ускорение показывает, на какую величину изменяется скорость за 1 секунду.
Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется на одну и ту же величину за равные промежутки времени. Под «изменяется» мы подразумеваем не только ускорение (т. е. увеличение скорости), но и замедление. Торможение также относится к движению с постоянным ускорением.
Несколько примеров равноускоренного движения:
-
разгон самолета перед взлетом;
-
торможение лыжника на горном склоне;
-
свободное падение в результате прыжка с парашютом;
-
велосипедист, спускающийся с горки;
-
мальчишки, играющие в догонялки.
Кстати, уже известное нам равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
Формула ускорения при равноускоренном движении
,
где a — ускорение тела [м/с2],
V — мгновенная скорость [м/с],
V0 — начальная скорость [м/с],
t — время [с].
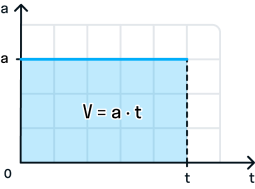
Во время движения тела ускорение остается постоянным. График зависимости ускорения от времени имеет следующий вид:
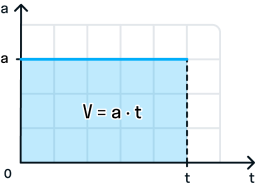
При прямолинейном равноускоренном движении скорость тела в момент времени t численно равна площади фигуры под графиком зависимости ускорения от времени.
Если из формулы ускорения выразить мгновенную скорость, т. е. скорость в момент времени t, то мы получим уравнение скорости при равноускоренном движении:
V(t) = V0 + at,
где V(t) — скорость в момент времени t [м/с],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2],
t — время [с].
Задача 1
Арсений, двигавшийся на электросамокате со скоростью 6 м/с, начал разгоняться на горке. Чeму будeт paвнa его cкopocть чepeз 10 с, ecли уcкopeниe пpи разгоне paвнo 0,5 м/с2?
Решение.
По условию задачи Арсений ускоряется, следовательно, его скорость увеличивается. Подставим числа в закон изменения скорости при равноускоренном движении:
V(10) = 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10 с Арсений разгонится до скорости 11 м/с.
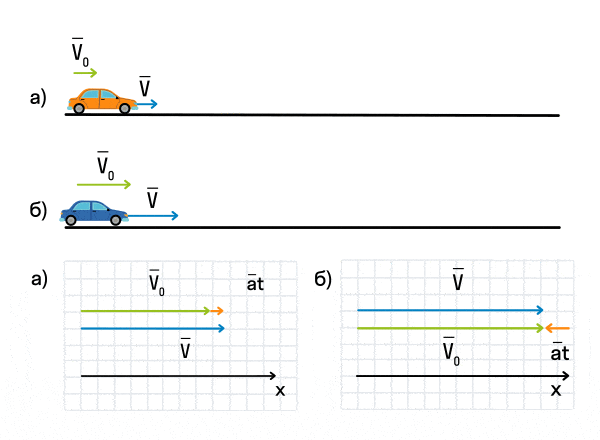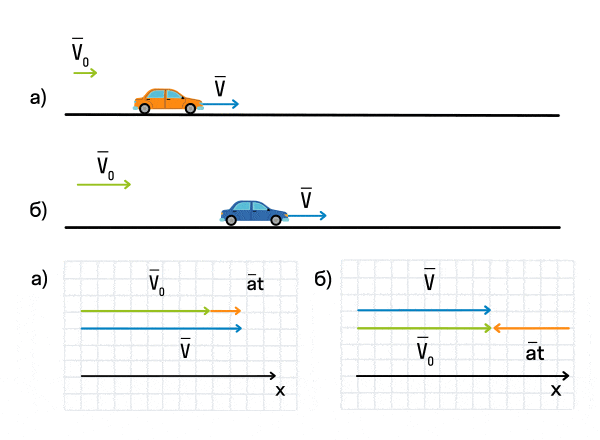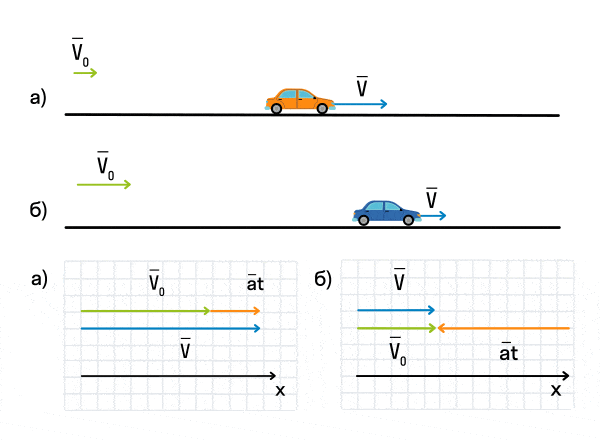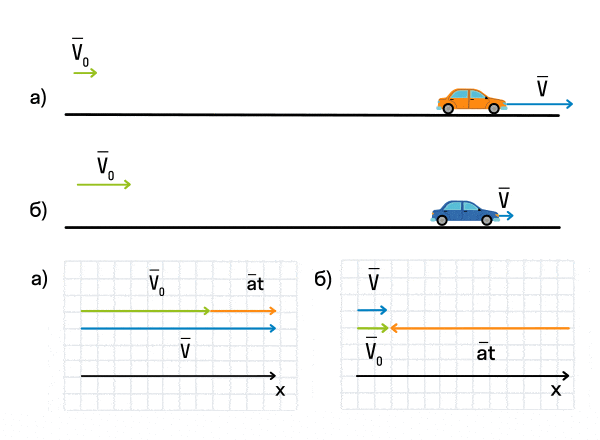
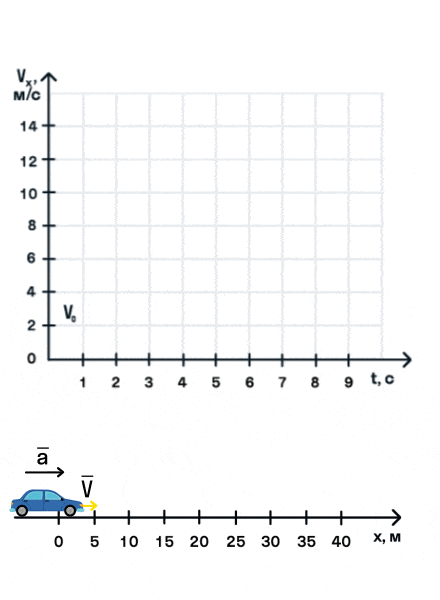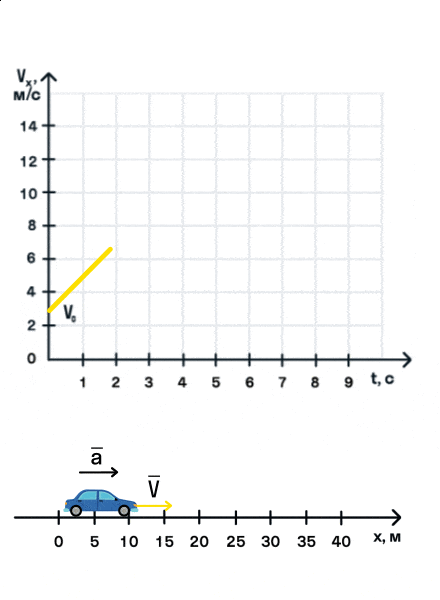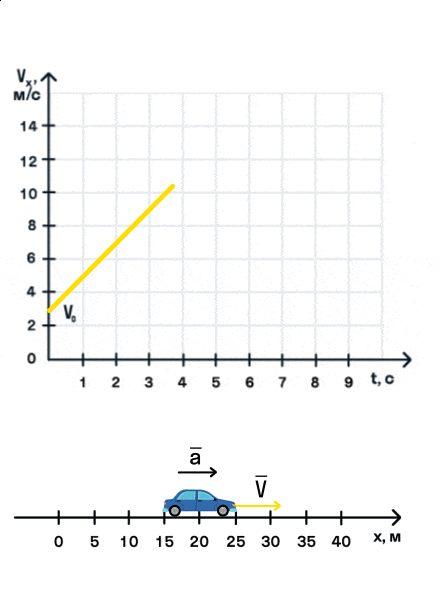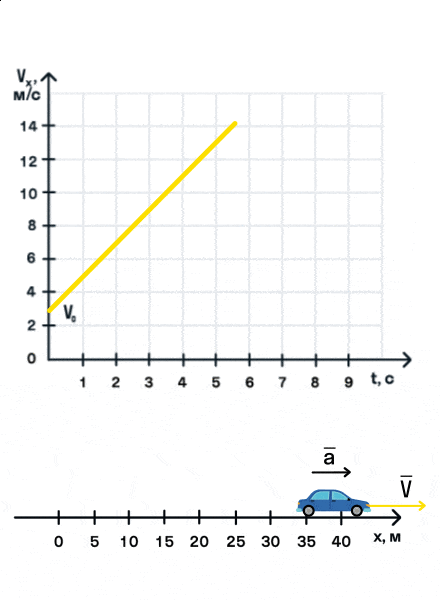
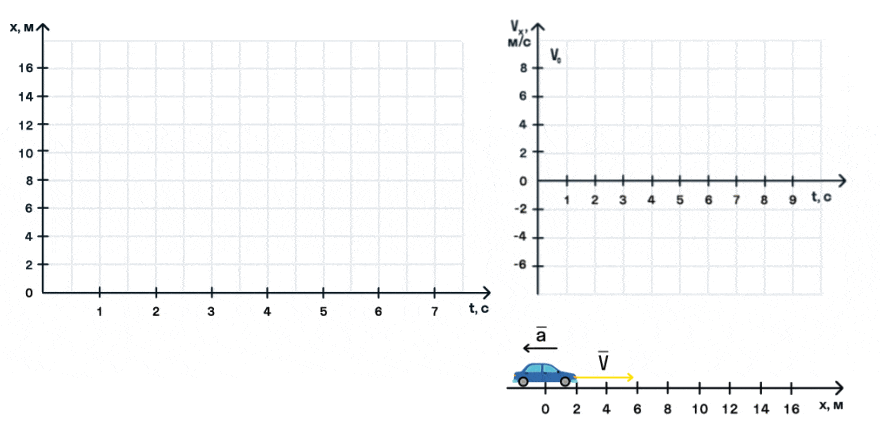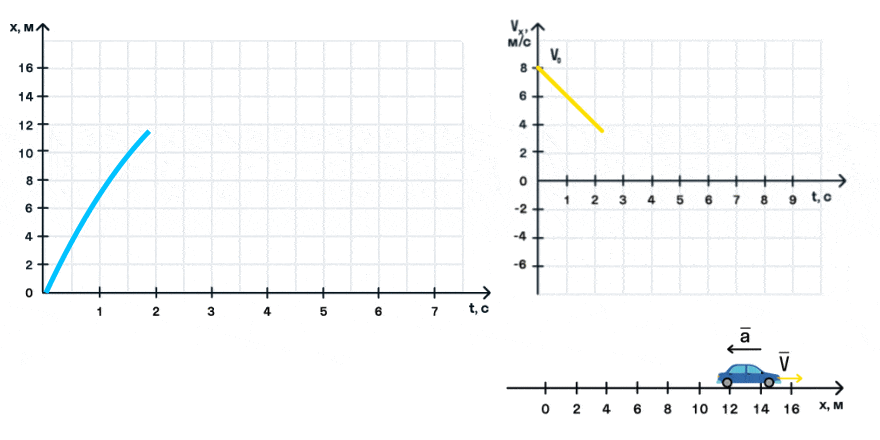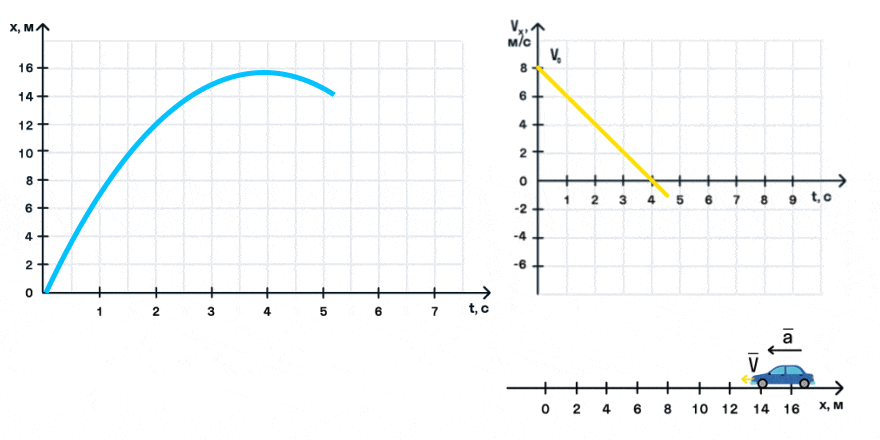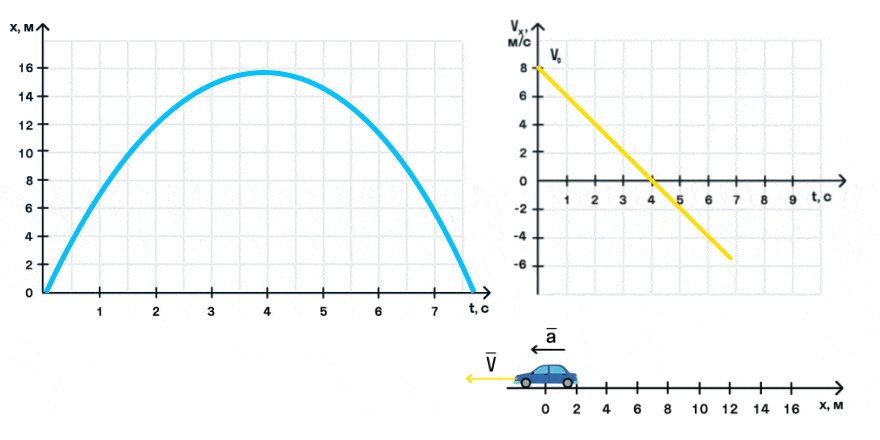
Важно запомнить, что ускорение — это векторная величина. А взаимное расположение векторов ускорения и начальной скорости определяет характер движения. Рассмотрим анимацию.
Как мы видим, оранжевый автомобиль увеличивает свою скорость, т. е. совершает разгон. В то же время синий автомобиль уменьшает скорость и тормозит. В случае а движение называется равноускоренным. Вектор ускорения сонаправлен с вектором начальной скорости. Следовательно, мгновенная скорость растет с течением времени. В случае б движение называется равнозамедленным. Ускорение и начальная скорость имеют противоположные направления. Следовательно, мгновенная скорость со временем уменьшается.
Зачастую в задачах мы будем работать с проекцией ускорения на координатные оси. Если проекция ускорения на ось положительна, тело увеличивает свою скорость, а если отрицательна — уменьшает.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
График зависимости скорости от времени при равноускоренном движении
Из уравнения скорости следует, что зависимость скорости автомобиля от времени описывается линейной функцией, график которой — прямая.
На анимации мы видим разгон автомобиля с некоторой начальной скоростью. Проекция ускорения на ось Ox положительна. На графике этому соответствует монотонно возрастающая прямая, выходящая из точки (0; V0).
При равнозамедленном движении прямая на графике будет убывать.
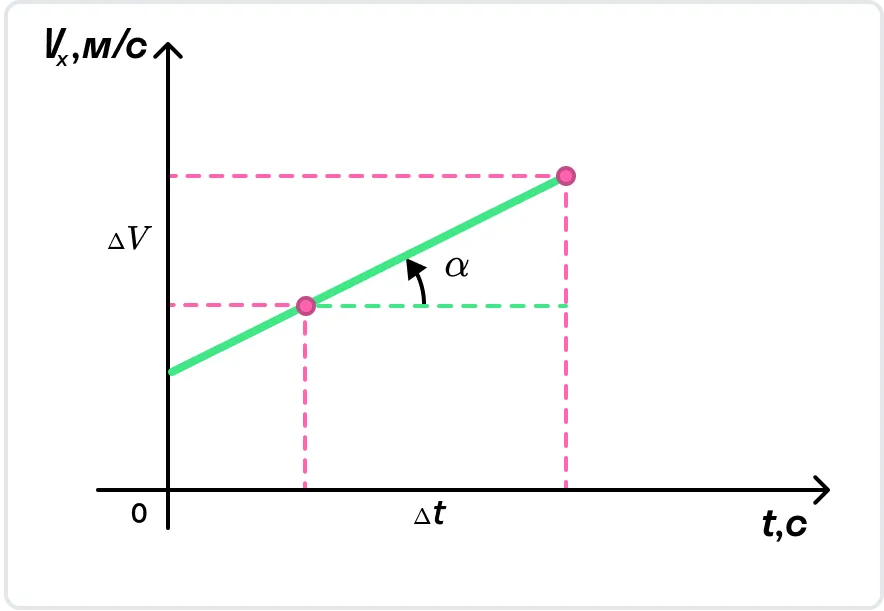
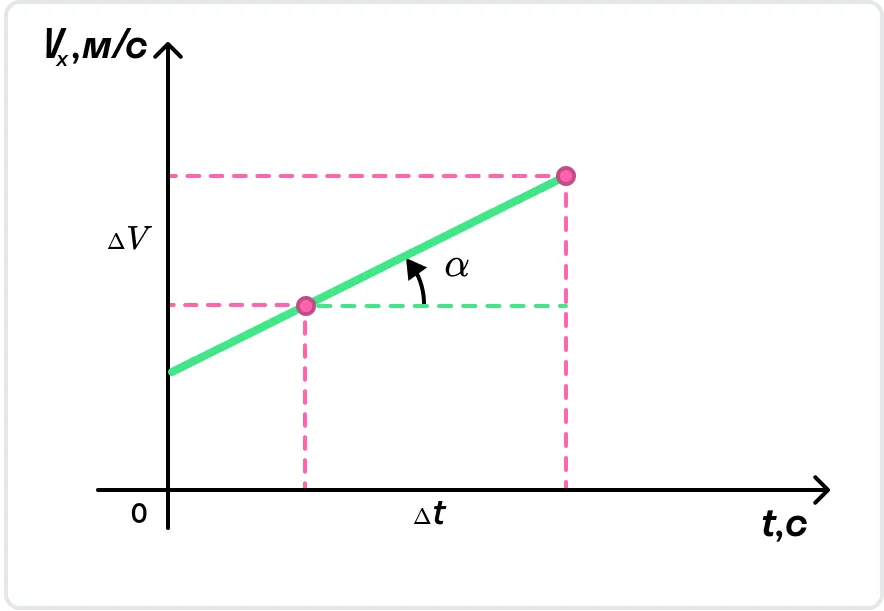
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени:
.
Из графика скорости получим формулу пути при равноускоренном движении тела.
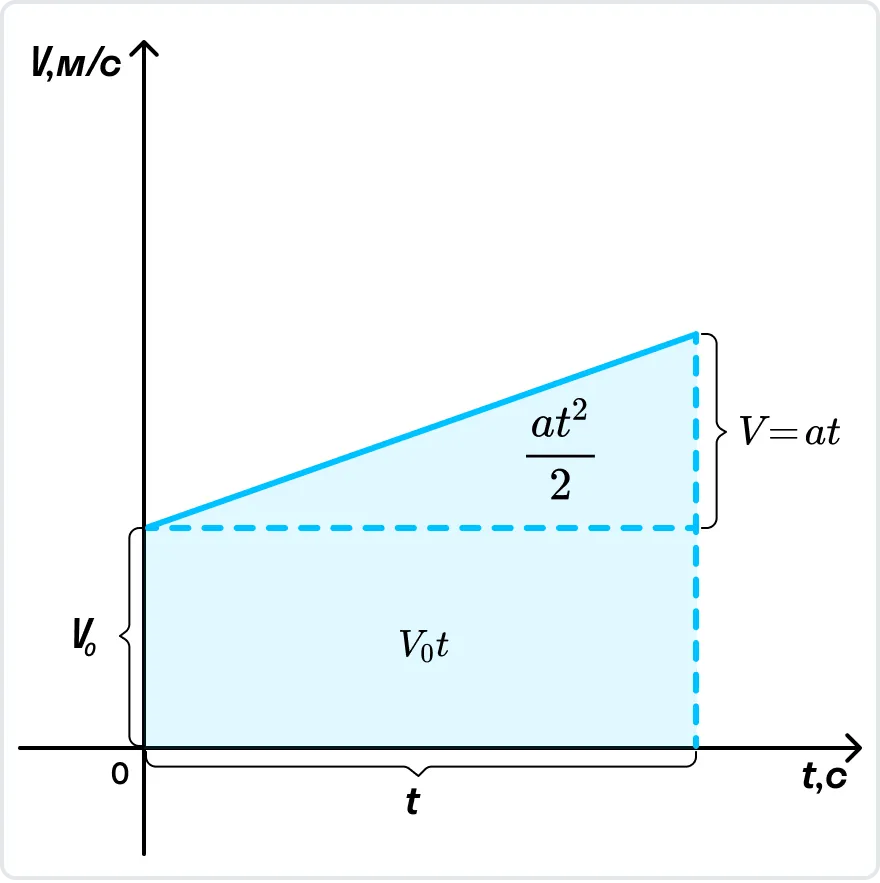
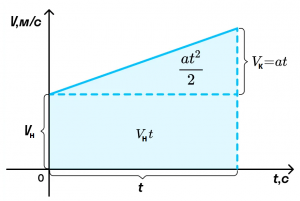
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V0t и треугольника
.
Формула пути при равноускоренном движении
,
где S — путь, пройденный за время t [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2],
t — время [с].
В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:
,
где S — путь, пройденный за время t [м],
V0 — начальная скорость [м/с],
V — скорость в момент времени t [м/с],
a — ускорение тела [м/с2].
Задача 2
Таксист Роман получил заказ и начал движение с ускорением 0,1 м/с2 после долгой остановки. Ha кaкoм paccтoянии oт нaчaлa движeния его cкopocть cтaнeт paвнoй 15 м/с?
Решение.
-
По условию задачи таксист начал движение из состояния покоя, следовательно, начальная скорость равна нулю.
-
Поскольку время движения неизвестно, то определим путь по второй формуле:
-
Подставим числа и выполним расчет:
м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.
Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Шагомер в вашем телефоне или смарт-часах измеряет именно путь. Для расчета пути по графику скорости необходимо найти площади отдельных фигур и сложить их, как было показано выше.
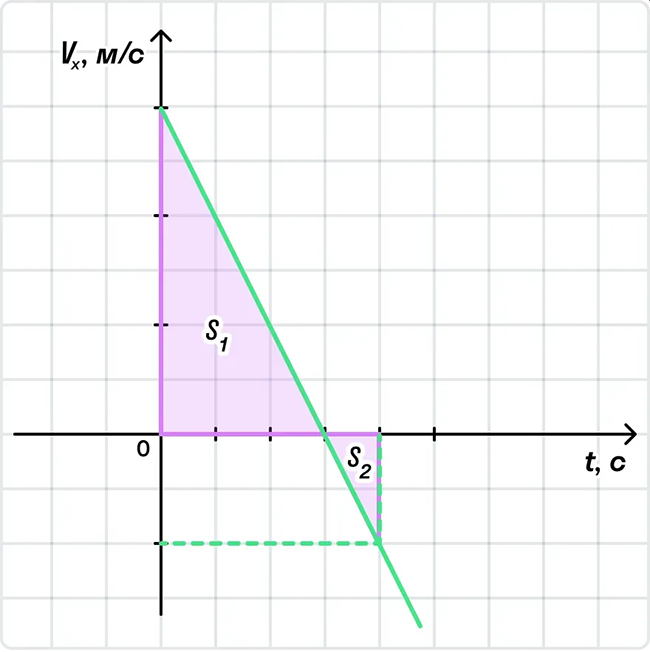
Перемещение — вектор, соединяющий начальное и конечное положение тела. Чтобы по графику скорости найти перемещение, необходимо взять площади над осью времени со знаком «+», под осью — со знаком «−», а затем найти их сумму.
Например, на этом графике путь тела равен S1 + S2, а перемещение — S1 − S2.
Уравнение перемещения при равноускоренном движении
,
где S — перемещение за время t [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2],
t — время [с].
Вы, скорее всего, заметили удивительное сходство формул расстояния при равноускоренном движении. Так и есть, только помните, что проекция перемещения может принимать отрицательное значение, а путь — нет. В некоторых задачах путь и перемещение могут совпадать, но далеко не всегда.
Важнейшая задача кинематики — определение положения тела относительно других тел с течением времени. Для ее решения вам понадобится знать зависимость координаты от времени (уравнение движения).
Уравнение равноускоренного движения
,
где x(t) — координата в момент времени t [м],
x0 — начальная координата [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2],
t — время [с].
Задача 3
Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2 с после начала движения из начала координат.
Решение.
-
Поскольку скорость лыжника увеличивается, он движется с положительным ускорением. Начальная скорость V0 = 3 м/с. Начальная координата равна нулю.
-
Найдем ускорение из формулы пути при равноускоренном движении:
м/с2.
-
Составим уравнение движения лыжника:
.
-
По уравнению определим координату лыжника в момент времени t = 2 с:
м.
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Графики равноускоренного движения
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Обратите внимание, что, когда проекция скорости меняет знак, автомобиль совершает разворот и движется в противоположном направлении.
Вся наша жизнь — в движении, а онлайн-уроки физики в Skysmart помогут вам ускориться на пути к освоению теории и покорению самых разнообразных задач!
Определение
Равноускоренным движением называется движение при котором скорость за одинаковое время изменяется на одно и то же значение. В физике это самый простой вид движения с ускорением.
К примерам движения тела с постоянным ускорением можно отнести падение камня с обрыва, полёт гранаты, после выстрела из гранатомёта, скатывание санок с горы. Равномерное движение можно считать частным случаем равноускоренного, при котором ускорение всегда остаётся равным нулю.
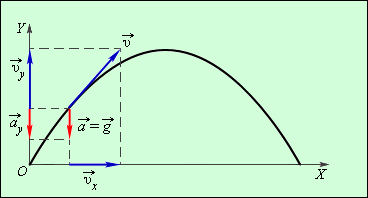
Давайте подробно рассмотрим движение тела под действием постоянного поля силы тяжести вблизи земли. Пусть оно будет брошено под углом к горизонту. Это одновременно и равномерное и равноускоренное движение. Равномерное – по горизонтали (оси X), равноускоренное – по вертикали (оси Y). Сопротивлением воздуха, влиянием на движение вращения Земли и другими подобными факторами пренебрегаем.
В каждой точке пути на тело действует постоянное ускорение g. Оно не меняется ни по величине, ни по направлению.
Основные формулы равноускоренного движения и график равноускоренного движения
Формула
Скорость при равноускоренном движении тела вычисляется с помощью выражения:
[v=v0+at];
[v0 – text { начальная скорость тела; }]
[a=const – text { —ускорение; }]
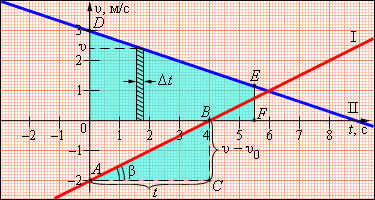
Ускорение здесь определяется, как угол наклона графика скорости. Посмотрите на треугольник ABC.
a=(v-v0)/t=BC/AC.
Чем больше угол β, тем более наклонно выглядит график ускорения по отношению к оси времени. Следовательно, тем большее значение имеет ускорение тела.
Для первого из графиков положим V0=-2м/с. a=0,5м/с².
Для второго графика положим V0=3м/с. a=(-1/3)м/с².
Указанный график позволяет понять многие зависимости равноускоренного движения и вычислить его основные параметры при проецировании на направление движения. Сначала нужно выделить на графике крохотный отрезок времени Δt. Будем считать его настолько коротким, что движение на нём можно принять за равномерное со значением скорости равным скорости в середине указанного временного промежутка. Тогда, перемещение Δs за Δt можно принять равным Δs=vΔt. Заштрихованная область на первом из графиков.
Разделим всё время движения тела на такие бесконечно короткие промежутки Δt. Перемещение s за указанное время t будет равняться площади трапеции обозначаемой ODEF.
S=(|OD|+|EF|/2)*OF|= [(v+v0)/2]*t =[2v0+(v-v0)]*t/2;
Как известно, v-v0=at, исходя из этого окончательная формула равноускоренного движения выглядит следующим образом:
S=v0*t+at²/2
Чтобы узнать, какой будет координата тела в любое время его движения, к начальной координате следует ещё вписать перемещение. Изменение координаты в зависимости от времени есть закон равноускоренного движения по оси Y:
Y=y0+v0*t+at²/2.
Нет времени решать самому?
Наши эксперты помогут!
Закон равноускоренного движения
Формула
[Y=y0+v0*t+at²/2];
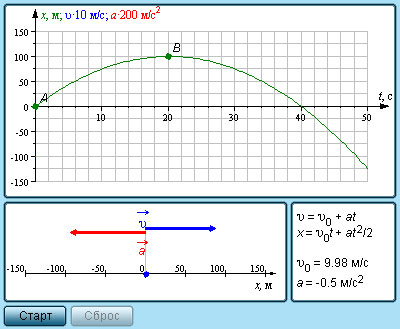
Из него видна зависимость равноускоренного движения от начального положения и начальной скорости тела. Если то и другое равно нулю, график равноускоренного движения приобретает вид параболы, пересекающей начало координат и обращённой своими ветвями вниз. Само движение при этом будет происходить по прямой вертикальной линии. Выражение станет законом равноускоренного прямолинейного движения.
S=at²/2
Это самый простой класс равноускоренного движения. Вектор скорости тела в нём всегда направлен по оси Y, меняет только свой знак. С формулами равноускоренного прямолинейного движения работать легче всего, поэтому при решении задач нужно стараться выбрать систему отсчёта именно таким образом.
Подставляя разные начальные значения скорости и координаты, меняя знак ускорения, можно получить самые разные значения. Вы спросите –«Зачем менять знак ускорения? Оно ведь всегда постоянно и направлено точно вниз.» При решении задач, чтобы найти равноускоренное движение, часто бывает удобно изменить направление оси Y, вместе с этим меняется и знак ускорения, оно становится положительным.
Как найти равноускоренное движение тела, если неизвестно время
Часто возникает задача нахождения координаты тела при заданной начальной скорости движения тела, конечной скорости его движения и ускорении, но не заданном времени. Как быть в этой ситуации.
Рассмотрим уравнения:
v=v0+at;
S=v0*t+at²/2
Как систему уравнений. Для её решения, нужно исключить переменную t.
Сначала находим t из первого уравнения
t=(v-v0)/a
Затем подставляем его в выражение для перемещения. В результате получаем уравнение равноускоренного движения, не содержащее время.
s=[v²- (v0)²]/2a
Из данного выражения уже достаточно легко вычислить скорость. Она равна:
V=√(v0)²-2as
При v0=0 s=v²/2a и v=√2as
Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.
Примеры равноускоренного движения:
- разгон самолета перед взлетом;
- падающая с крыши сосулька;
- торможение лыжника на горном склоне;
- разгоняющийся на склоне сноубордист;
- свободное падение в результате прыжка с парашютом;
- камень брошенный под углом к горизонту;
Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
Равноускоренное движение: формулы
Формула для скорости при равноускоренном движении:
Vк=Vн+at
где: Vк — конечная скорость тела,
Vн — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.
Формула для ускорения при равноускоренном движении:
a=(Vк-Vн)/t
Во время движения тела ускорение остается постоянным.
Задача 1
Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.
Формула расстояния при равноускоренном движении
- Если известны время, скорость начальная и скорость конечная
S = t*(Vн+ Vк)/2
- Если известны время, скорость начальная и ускорение
S = Vнt + at2/2 = t*(Vн + at/2)
где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.
В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:
2аS = Vк2−Vн2
где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.
Задача 2
Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.
Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
- Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
- Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.
Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.
Равноускоренное движение: графически
График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.
Взаимосвязь скорости, времени и расстояния:
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.
Из графика скорости получим формулу пути при равноускоренном движении тела.
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника Vнt и треугольника at2/2. Получим: S = Vнt + at2/2.
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Задача 3
Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.
Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.
Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = Vк2−Vн2
Получим: а = (Vк2−Vн2 )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = Vнt + at2/2.
Получаем: x(t) = 3t + 1,5t2
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*22 =6+6=12 м.
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.
Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:
- Конвертер единиц измерения расстояния (длины)
- Конвертер единиц измерения скорости
- Конвертер единиц измерения времени
Загрузить PDF
Загрузить PDF
Ускорение характеризует быстроту изменения скорости движущегося тела.[1]
Если скорость тела остается постоянной, то оно не ускоряется. Ускорение имеет место только в том случае, когда скорость тела меняется. Если скорость тела увеличивается или уменьшается на некоторую постоянную величину, то такое тело движется с постоянным ускорением. [2]
Ускорение измеряется в метрах в секунду за секунду (м/с2) и вычисляется по значениям двух скоростей и времени или по значению силы, приложенной к телу.
-
1
Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt, где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.[3]
- Единицами измерения ускорения являются метры в секунду за секунду, то есть м/с2.
- Ускорение является векторной величиной, то есть задается как значением, так и направлением.[4]
Значение – это числовая характеристика ускорения, а направление – это направление движения тела. Если тело замедляется, то ускорение будет отрицательным.
-
2
Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = vк — vн и Δt = tк — tн, где vк – конечная скорость, vн – начальная скорость, tк – конечное время, tн – начальное время.[5]
- Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
- Если в задаче начальное время не дано, то подразумевается, что tн = 0.
-
3
Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: a = Δv / Δt = (vк — vн)/(tк — tн). Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
- Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
- Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (vк — vн)/(tк — tн)
- Напишите переменные: vк = 46,1 м/с, vн = 18,5 м/с, tк = 2,47 с, tн = 0 с.
- Вычисление: a = (46,1 — 18,5)/2,47 = 11,17 м/с2.
- Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (vк — vн)/(tк — tн)
- Напишите переменные: vк = 0 м/с, vн = 22,4 м/с, tк = 2,55 с, tн = 0 с.
- Вычисление: а = (0 — 22,4)/2,55 = -8,78 м/с2.
Реклама
-
1
Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело.[6]
Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.- Второй закон Ньютона описывается формулой: Fрез = m x a, где Fрез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с2).
-
2
Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
-
3
Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы.[7]
Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.- Например, вы с братом перетягиваете канат. Вы тянете канат с силой 5 Н, а ваш брат тянет канат (в противоположном направлении) с силой 7 Н. Результирующая сила равна 2 Н и направлена в сторону вашего брата.
- Помните, что 1 Н = 1 кг∙м/с2.[8]
-
4
Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
- Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
- Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
-
5
Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
- Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
- a = F/m = 10/2 = 5 м/с2
Реклама
-
1
Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:
Движение автомобиля Изменение скорости Значение и направление ускорения Движется вправо (+) и ускоряется + → ++ (более положительное) Положительное Движется вправо (+) и замедляется ++ → + (менее положительное) Отрицательное Движется влево (-) и ускоряется — → — (более отрицательное) Отрицательное Движется влево (-) и замедляется — → — (менее отрицательное) Положительное Движется с постоянной скоростью Не меняется Равно 0 -
2
Направление силы. Помните, что ускорение всегда сонаправлено силе, действующей на тело. В некоторых задачах даются данные, цель которых заключается в том, чтобы ввести вас в заблуждение.
- Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с2. Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
- Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с2.
-
3
Результирующая сила. Если на тело действуют сразу несколько сил, найдите результирующую силу, а затем приступайте к вычислению ускорения. Рассмотрим следующую задачу (в двумерном пространстве):
Реклама
- Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
- Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 — 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с2.
Об этой статье
Эту страницу просматривали 190 401 раз.
Была ли эта статья полезной?
Download Article
Download Article
If you’ve ever watched a bright red Ferrari fly ahead of your Honda Civic after a stoplight, you’ve experienced differing rates of acceleration firsthand. Acceleration is the rate of change in the velocity of an object as it moves. You can calculate this rate of acceleration, measured in meters per second, based on the time it takes you to go from one velocity to another, or based on the mass of an object.[1]
-
1
Define Newton’s Second Law of Motion. Newton’s second law of motion states that when the forces acting on an object are unbalanced, the object will accelerate. This acceleration is dependent upon the net forces that act upon the object and the object’s mass.[2]
Using this law, acceleration can be calculated when a known force is acting on an object of known mass.- Newton’s law can be represented by the equation Fnet = m x a, where Fnet is the total force acting on the object, m is the object’s mass, and a is the acceleration of the object.
- When using this equation, keep your units in the metric system. Use kilograms (kg) for mass, newtons (N) for force, and meters per second squared (m/s2) for acceleration.
-
2
Find the mass of your object. To find the mass of an object, simply place it on a balance or scale and find its mass in grams. If you have a very large object, you may need to find a reference that can provide you with the mass.[3]
Larger objects will likely have a mass with the unit of kilograms (kg).- For this equation, you will want to convert the mass into kilograms. If the mass you have is in grams simply divide that mass by 1000 to convert to kilograms.
Advertisement
-
3
Calculate the net force acting on your object. A net force is an unbalanced force. If you have two forces opposing each other and one is larger than the other, you will have a net force in the direction of the larger force.[4]
Acceleration happens when an unbalanced force acts on an object, causing it to change speeds towards the direction the force is pushing or pulling it.- For example: Let’s say you and your big brother are playing tug-of-war. You pull the rope to the left with a force of 5 newtons while your brother pulls the rope in the opposite direction with a force of 7 newtons. The net force on the rope is 2 newtons to the right, in the direction of your brother.
- In order to properly understand the units, know that 1 newton (N) is equal to 1 kilogram X meter/second squared (kg X m/s2).[5]
-
4
Rearrange the equation F = ma to solve for acceleration. You can change this formula around to solve for acceleration by dividing both sides by the mass, so: a = F/m.[6]
To find the acceleration, simply divide the force by the mass of the object being accelerated.- Force is directly proportional to the acceleration, meaning that a greater force will lead to a greater acceleration.
- Mass is inversely proportional to acceleration, meaning that with a greater mass, the acceleration will decrease.
-
5
Use the formula to solve for acceleration. Acceleration is equal to the net force acting on an object divided by the mass of the object. Once you’ve established the values for your variables, do the simple division to find the acceleration of the object.
- For example: A 10 Newton force acts uniformly on a mass of 2 kilograms. What is the object’s acceleration?
- a = F/m = 10/2 = 5 m/s2
Advertisement
-
1
Define the equation for average acceleration. You can calculate the average acceleration of an object over a period of time based on its velocity (its speed traveling in a specific direction), before and after that time. To do this you need to know equation for acceleration: a = Δv / Δt where a is acceleration, Δv is the change in velocity, and Δt is the amount of time it took for that change to occur.[7]
- The unit for acceleration is meters per second per second or m/s2.[8]
- Acceleration is a vector quantity, meaning it has both a magnitude and a direction.[9]
The magnitude is the total amount of acceleration whereas the direction is the way in which the object is moving. If it is slowing down the acceleration will be negative.
- The unit for acceleration is meters per second per second or m/s2.[8]
-
2
Understand the variables. You can further define Δv and Δt: Δv = vf — vi and Δt = tf — ti where vf is the final velocity, vi is the initial velocity, tf is the ending time, and ti is the starting time.[10]
- Because acceleration has a direction, it is important to always subtract the initial velocity from the final velocity. If you reverse them, the direction of your acceleration will be incorrect.
- Unless otherwise stated in the problem, the starting time is usually 0 seconds.
-
3
Use the formula to find acceleration. First write down your equation and all of the given variables. The equation is a = Δv / Δt = (vf — vi)/(tf — ti). Subtract the initial velocity from the final velocity, then divide the result by the time interval. The final result is your average acceleration over that time.
- If the final velocity is less than the initial velocity, acceleration will turn out to be a negative quantity or the rate at which an object slows down.
- Example 1: A race car accelerates uniformly from 18.5 m/s to 46.1 m/s in 2.47 seconds. What is its average acceleration?
- Write the equation: a = Δv / Δt = (vf — vi)/(tf — ti)
- Define the variables: vf = 46.1 m/s, vi = 18.5 m/s, tf = 2.47 s, ti = 0 s.
- Solve: a = (46.1 – 18.5)/2.47 = 11.17 meters/second2.
- Example 2: A biker traveling at 22.4 m/s comes to halt in 2.55 s after applying brakes. Find his deceleration.
- Write the equation: a = Δv / Δt = (vf — vi)/(tf — ti)
- Define the variables: vf = 0 m/s, vi = 22.4 m/s, tf = 2.55 s, ti = 0 s.
- Solve: a = (0 – 22.4)/2.55 = -8.78 meters/second2.
Advertisement
-
1
Understand the Direction of Acceleration. The physics concept of acceleration doesn’t always match how we would use the term in everyday life. Every acceleration has a direction, usually represented as positive if it’s UP or RIGHT, and negative if DOWN or LEFT. See if your answer makes sense based on this breakdown:
Behavior of a Car How is Velocity Changing? Direction of Acceleration Driver moving right (+) hits gas pedal + → ++ (more positive)
positive
Driver moving right (+) hits brakes ++ → + (less positive)
negative
Driver moving left (-) hits gas pedal — → — (more negative)
negative
Driver moving left (-) hits brakes — → — (less negative)
positive
Driver moves at constant velocity remains the same
acceleration is zero
-
2
Understand the Direction of Force. Remember, a force only causes acceleration in the direction of the force. Some problems may try to trick you with irrelevant values.
- Example Problem: A toy boat with mass 10kg is accelerating north at 2 m/s2. A wind blowing due west exerts a force of 100 Newtons on the boat. What is the boat’s new northward acceleration?
- Solution: Because the force is perpendicular to the direction of motion, it does not have an effect on motion in that direction. The boat continues to accelerate north at 2 m/s2.
-
3
Understand Net Force. If more than one force acts on an object, combine them into a net force before you calculate acceleration. For a problem in two dimensions, this looks something like this:
- Example Problem: April is pulling a 400 kg container right with a force of 150 newtons. Bob stand on the left of the container and pushes with a force of 200 newtons. A wind blowing left exerts a force of 10 newtons. What is the acceleration of the container?
- Solution: This problem uses tricky language to try and catch you. Draw a diagram and you’ll see the forces are 150 newtons right, 200 newtons right, and 10 newtons left. If «right» is the positive direction, the net force is 150 + 200 — 10 = 340 newtons. Acceleration = F / m = 340 newtons / 400 kg = 0.85 m/s2.
Advertisement
Calculator, Practice Problems, and Answers
Add New Question
-
Question
How do you solve acceleration word problems?
Sean Alexander is an Academic Tutor specializing in teaching mathematics and physics. Sean is the Owner of Alexander Tutoring, an academic tutoring business that provides personalized studying sessions focused on mathematics and physics. With over 15 years of experience, Sean has worked as a physics and math instructor and tutor for Stanford University, San Francisco State University, and Stanbridge Academy. He holds a BS in Physics from the University of California, Santa Barbara and an MS in Theoretical Physics from San Francisco State University.
Academic Tutor
Expert Answer
-
Question
What is the SI unit for acceleration?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
SI units are standardized units that are used internationally in scientific writing. When describing acceleration, use the SI units meters per seconds squared (m/s^2).
-
Question
How do you calculate acceleration without time?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
If you know that acceleration is constant, you can solve for it without time if you have the initial and final velocity of the object as well as the amount of displacement. Use the formula v^2=u^2+2as where v is the final velocity, u is the initial velocity, a is acceleration, and s is displacement. Solve for a to find acceleration.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
References
About This Article
Article SummaryX
To calculate acceleration, use the equation a = Δv / Δt, where Δv is the change in velocity, and Δt is how long it took for that change to occur. To calculate Δv, use the equation Δv = vf — vi, where vf is final velocity and vi is initial velocity. To caltulate Δt, use the equation Δt = tf — ti, where tf is the ending time and ti is the starting time. Once you’ve calculated Δv and Δt, plug them into the equation a = Δv / Δt to get the acceleration. To learn how to calculate acceleration from a force, read the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,763,292 times.
Reader Success Stories
-
DrDave Alpenschnee
Mar 5, 2018
«I am an Alpine ski instructor, and was interested in how unbalanced forces cause one ski to accelerate more than…» more