Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:
Приняв вектор k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.
Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.
Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.
Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.
Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела
Способы определения
углового ускорения:
1. Если известен
угол поворота или угловая скорость в
зависимости от времени, то угловое
ускорение
определяем путем дифференцирования их
по времени, т.е.
2
.
Обычно требуется определить угловое
ускорение в какой-либо момент времени
по другим величинам, известным в этот
же момент времени. В этом случае угловое
ускорение тоже можно получить путем
дифференцирования угловой скорости по
времени. Угловую скорость можно найти:
,
где А
– точка плоской фигуры; Р
– мгновенный центр скоростей.
Дифференцируя
по времени, получаем
В тех случаях,
когда АР постоянно,
,
так как
Рис.
37
;
,
где
— касательное ускорение точки А.
Так, например, при
качении колеса без скольжения по
неподвижной прямой линии, если за точку
А
взять центр колеса О,
то, учитывая, что он движется прямолинейно,
получим
.
При качении без
скольжения одного колеса по неподвижному
другому колесу (рис. 37)
,
где R
– радиус неподвижного колеса; r
– радиус подвижного колеса.
Дифференцируя по
времени, имеем
,
так как
;
.
9. Теоерма о конечном перемещении плоской фигуры
Ф
игуру
в ее плоскости из заданного положения
I
в любое другое положение II
(рис.38) можно перевести одним поворотом
в этой плоскости вокруг точки P,
называемой центром конечного вращения.
Рис.
38
10. Мгновенный центр вращения. Центроиды
Для двух бесконечно
близких положений плоской фигуры вместо
центра конечного вращения получим так
называемый мгновенный центр вращения.
Любое плоское перемещение фигуры можно
приближенно заменить последовательностью
вращательных перемещений вокруг своих
центров конечного вращения. В пределе
плоское перемещение фигуры можно
заменить бесконечной последовательностью
элементарных мгновенных поворотов
вокруг мгновенных центров вращений,
расположенных в определенной
последовательности.
Отсюда следует,
что любое плоское движение фигуры можно
заменить последовательностью мгновенных
вращений, совершаемых за тот же промежуток
времени, что и рассматриваемое плоское
движение.
При плоском движении
фигуры мгновенный центр вращения
перемещается как в неподвижной, так и
в подвижной плоскости, скрепленной с
движущейся плоской фигурой. Геометрическое
место мгновенных центров вращения на
неподвижной плоскости называют
неподвижной центроидой, а геометрическое
место этих же мгновенных центров вращения
на подвижной плоскости, скрепленной с
движущейся фигурой, – подвижной
центроидой.
При плоском движении
фигуры подвижная центроида катится без
скольжения по неподвижной центроиде.
Эта теорема позволяет плоское движение
твердого тела рассматривать как качение
без скольжения одной плоской кривой по
другой.
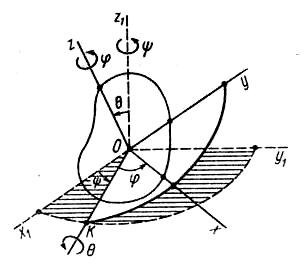
Вращение твердого тела вокруг неподвижной точки. Общий случай движения тела
Ч
ерез
неподвижную точку О
твердого тела проведем неподвижную
систему координат O1x1y1
относительно которой будем рассматривать
движение тела (рис. 39). Другую систему
координат Oxyz
скрепим с телом, вращающимся вокруг
неподвижной точки О.
Для определения положения движущегося
тела относительно системы координат
O1x1y1
следует
задать относительно этой системы
координат положение другой, подвижной,
системы координат Oxyz, скрепленной с
движущимся телом. Для этой цели Эйлер
предложил три независимых параметра –
углы Эйлера.
Первый из этих
углов – угол прецессии
– определяет положение линии узлов ОК,
которая является линией пересечения
координатных плоскостей O1x1y1
и Оху относительно неподвижной
координатной оси Ox1.
Для изменения этого угла тело должно
вращаться вокруг координатной оси Oz1
которую называют осью прецессии.
Вторым углом Эйлера
является угол между координатными
плоскостями Ox1y1
и Оху. Его измеряют углом
между перпендикулярами к этим координатным
плоскостям, которыми являются оси Oz1
и Oz.
У
Рис.
39
гол
называют углом нутации, а ось ОК, вокруг
которой вращается тело при изменении
угла
,
соответственно называют осью нутации
или линией узлов.
Для полного
определения положения рассматриваемого
тела относительно системы координат
O1x1y1z1
нужно задать угол между подвижной осью
координат Ох и положительным направлением
линии узлов ОК – угол собственного
вращения
.
Угол
от линии узлов ОК до оси Ох считается
положительным, если вокруг оси Oz поворот
оси Ох от линии ОК виден происходящим
против часовой стрелки.
При изменении угла
тело вращается вокруг так называемой
оси собственного вращения Oz, перпендикулярной
плоскости, в которой лежат прямые ОК и
Ох, образующие этот угол.
Углы Эйлера широко
применяются в теории гироскопов.
В технике особенно
важное значение имеет так называемая
регулярная прецессия, когда угловые
скорости вращения вокруг оси собственного
вращения и вокруг неподвижной оси
прецессии постоянны и угол между этими
осями (угол нутации) остается тоже
постоянным.
Итак, для определения
положения тела с одной неподвижной
точкой в любой момент времени надо
задать углы Эйлера как однозначные
функции времени, т. е.
;
;
.
Эти уравнения
являются уравнениями вращения твердого
тела вокруг неподвижной точки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Часто задаваемые вопросы как найти ускорение с учетом угла и коэффициента кинетического трения. В системе ускорения коэффициент трения является одним из основных факторов.
Ускорение в движущейся системе может быть разных форм. Например, в наклонной плоскости мы должны учитывать угол, под которым движется тело. Итак, учитывая все эти атрибуты, мы будем иметь дело с факторами, в основном ответственными за ускорение тела.
Когда наклон имеет тело или любой объект, который находится в постоянном движении, он будет рассчитываться в соответствии с поднятой проблемой. Здесь мы обсудим, как найти ускорение с углом и коэффициентом кинетического трения.
Мы должны знать, как нас ускоряют в движущейся машине. Когда машина движется с определенной скоростью, мы, как правило, возвращаемся на сиденье, когда скорость повышается. Когда в машине применяются тормоза, мы стремимся двигаться вперед, а на поворотах мы склонны двигаться боком. Это способы ускорения.
Ускорению способствуют несколько различных факторов. В одном из них нам нужно сосредоточиться на данных деталях. Здесь мы будем иметь дело с коэффициентом трения и углом, под которым он будет ускоряться.
Подробная информация о коэффициенте трения и его влиянии на ускорение
Коэффициент трения — это, по сути, наименьший фактор, влияющий на ускорение любого объекта, который уже находится в движении. Он основан на силах, действующих на тело, находящееся в постоянном движении.
Во-первых, это сила тяжести, одна из основных причин, по которой тело оказывается на земле без какой-либо левитации. Далее будет нормальная сила, действующая на тело. Эта нормальная сила — это сила, исходящая от окружающей среды. Далее идет сила трения, которая в основном отвечает за то, чтобы тело действительно могло совершать любые движения.
Нормальная сила и сила трения являются одними из основных факторов ускорения. Когда тело движется с определенной скоростью, внезапно набирает скорость и движется с другой скоростью, это называется ускорением.
На самом деле мы должны были знать, как это трение влияет на ускорение и как работает коэффициент трения при ускорении. Когда тело находится в процессе ускорения, в игру вступают несколько аспектов.
На тело в движении действует так много сил. В этой системе ускорения мы должны найти силы, присутствующие и действующие на это тело. Затем нам нужно соответственно рассчитать ускорение.
Сосредоточение внимания на силе трения является одним из факторов, влияющих на движение тела по земле. Например, автомобиль движется из-за трения между шиной автомобиля и дорогой, или в данном случае это может быть любая поверхность.
Как найти ускорение по углу и коэффициенту кинетического трения
Здесь нам нужно рассмотреть столько же примеров, как найти ускорение с учетом угла и коэффициента кинетического трения. Сначала идет угол, затем коэффициент трение. От угла болота зависит, как тело движется по наклонной плоскости.
Теперь рассмотрим случай, когда объект помещен на поверхность, ниже которой он фактически наклонен. Теперь по каким-то причинам объект теряет равновесие и скатывается по наклонной поверхности. Следовательно, необходимо оценить ускорение тела, движущегося в наклонной плоскости.
В этом сценарии сила трения кинетическая, она действует противоположно силе тяжести. Чистая сила также должна быть рассчитана. Нам нужно определить чистую силу, чтобы найти ускорение тела с учетом угла и коэффициента трения.
F = Fg + Fk; F = мг (синус θ) + мкг (cos θ)
Мы знаем, что ускорение — это [сила, деленная на массу, следовательно, a = F / m. Следовательно, из формулы чистой силы мы получаем ускорение как а = g (синус θ) + μ g (cos θ).
Используя эту формулу, мы можем найти ускорение с коэффициентом трения с углом, под которым он движется.
Задача о том, как найти ускорение с учетом угла и коэффициента кинетического трения
1 задачи:
Допустим, автомобиль весом 1200 кг движется по неровной дороге. Значение коэффициента трения равно 0.8. Fnet = 7000N будет расчетной чистой силой, действующей на это движущееся тело. Теперь первое, что нужно оценить, — это ускорение данной конкретной системы.
Решение 1:
Поскольку дана результирующая сила, мы можем найти нормальную силу, используя значение массы и силы тяжести, поскольку сила тяжести и нормальная сила равны друг другу, но действуют в разных направлениях. Сила трения находится с помощью коэффициент величины трения и значения нормальной силы.
м = 1200; Fnet = 7000N; μ = 0.8
Нормальная сила = сила тяжести x масса тела
Fn = 9.8 х 1200; Fn = 11270
Сила трения = μ x нормальная сила; Ff = 0.8x 11270 = 9016 Н
а = ф / м
а = 9016 / 1200
a = 7.51 мс-2
2 задачи:
Как найти ускорение, если задан коэффициент трения и угол наклона.
Итак, в задаче указаны коэффициент трения и угол, под которым он движется. Масса 100 кг движется вниз в наклонной плоскости под углом θ = 45⁰. Коэффициент трения μ = 0.9.
С каким ускорением тело движется вниз?
Решение 2:
Коэффициент силы, действующей на плоскости, равен mgSinθ, а коэффициент, перпендикулярный плоскости, равен mgCosθ. И мы знаем, что f = ma, поэтому a = f / m. исходя из этого, мы можем использовать значение коэффициента трения или нет.
Таким образом, мы получаем формулу как a = μgCosθ
а = 0.9 × 9.8 × 0.52
a = 4.58 мс-2.
Часто задаваемые вопросы
Как найти ускорение с трением и под углом?
Трение — единственная причина, по которой тело перемещается в любом направлении, и когда движение происходит под наклоном, угол будет учитываться.
Формула для определения ускорения с трением, а также угла: a = μgCosθ. Нам нужно знать, что действующие силы будут двух типов: одна будет соответствовать уклону, а другая сила будет перпендикулярна наклону.
Как найти ускорение по чистой силе и массе?
Масса и сила имеют прямое воздействие на тело, независимо от того, находится оно в движении или нет. Таким образом, масса и сила будут основными причинами движения конкретного тела.
Когда тело находится в движении, частью движения будет несколько различных факторов. В одном из таких случаев сила будет иметь большое влияние. Основная сила, действующая на движущееся тело, будет силой тяжести и нормальной силой, которая будет действовать перпендикулярно направлению движения. числовые силы, действующие на эту конкретную систему, должны быть найдены и затем оценены.
Масса имеет прямое воздействие на тело, поскольку это основная причина, по которой тело движется; когда масса тела увеличивается, ускорение уменьшается. Когда масса тела уменьшается, ускорение увеличивается, поэтому действующая сила больше, и телу будет легче двигаться, если только масса будет больше. Таким образом, формула ускорения с чистой силой и массой дается как a = f / m.
Download Article
Different ways to calculate rotation speed
Download Article
Most people have a general understanding of the idea of velocity and acceleration. Velocity is the measure of how fast an object is moving, and acceleration is the measure of how quickly the object’s velocity is changing (i.e., speeding up or slowing down). When the object is moving in a circle, such as a spinning tire or a rotating CD, velocity and acceleration are generally measured by the angle of rotation. They are then called angular velocity and angular acceleration. If you know the object’s velocity over some period of time, you can calculate its average angular acceleration. Alternatively, you may have a function to calculate the object’s position. With this information, you can calculate its angular acceleration at any chosen instant.
-
1
Determine the function for angular position. In some cases, you may be provided with a function or formula that predicts or assigns the position of an object with respect to time. In other cases, you may derive the function from repeated experiments or observations. For this article, we assume that the function has been provided or previously calculated.[1]
-
2
Find the function for angular velocity. Velocity is the measure of how fast an object changes its position. In layman’s terms, we think of this as its speed. In mathematical terms, the change of position over time can be found by finding the derivative of the position function. The symbol for angular velocity is
. Angular velocity is generally measured in units of radians divided by time (radians per minute, radians per second, etc.).[2]
Advertisement
-
3
Find the function for angular acceleration. Acceleration is the measure of how fast an object’s velocity is changing over time. You can mathematically calculate the angular acceleration by finding the derivative of the function for angular velocity. Angular acceleration is generally symbolized with
, the Greek letter alpha. Angular acceleration is reported in units of velocity per time, or generally radians divided by time squared (radians per second squared, radians per minute squared, etc.).[3]
-
4
Apply the data to find instantaneous acceleration. Once you have derived the function for instantaneous acceleration as the derivative of velocity, which in turn is the derivative of position, you are ready to calculate the instantaneous angular acceleration of the object at any chosen time.[4]
Advertisement
-
1
-
2
Measure final angular velocity. The second piece of information that you need is the angular velocity of the spinning or rotating object at the end of the time period that you want to measure. This is to be called the “final” velocity.[6]
- A compact disc plays in the machine by rotating at an angular velocity of 160 radians per second.
- The roller coaster, after applying its brakes to the spinning wheels, ultimately reaches an angular velocity of zero when it stops. This will be its final angular velocity.
-
3
Measure the elapsed time. To calculate the average angular velocity of the spinning or rotating object, you need to know the amount of time that passes during your observation. This can be found by direct observation and measurement, or the information can be provided for a given problem.[7]
- The owner’s manual for the CD player provides the information that the CD reaches its playing speed in 4.0 seconds.
- From observations of roller coasters being tested, it has been found that they can come to a complete stop within 2.2 seconds from when the brakes are initially applied.
-
4
Calculate the average angular acceleration. If you know the initial angular velocity, the final angular velocity, and the elapsed time, fill that data into the equation and find the average angular acceleration.[8]
- For the example of the CD player, the calculation is as follows:
- For the roller coaster example, the calculation looks like this:
- Note that acceleration is always going to be in units of some distance measurement “per” time squared. With angular acceleration, the distance is generally measured in radians, although you could convert that to number of rotations if you wish.
Advertisement
-
1
Understand the concept of angular motion. When people think of the speed of an object, they often consider linear motion — that is, objects traveling mostly in a straight line. This would include a car, a plane, a ball that is thrown or any number of other objects. However, angular motion describes objects that spin or rotate. Think of the earth spinning on its axis. The position or speed of the earth can be measured with angular quantities. A spinning compact disc (or record player, if you’re old enough), electrons on their axes, or the wheels of a car on the axle are other examples of rotating objects that can be measured through angular motion.[9]
-
2
Visualize angular position. When you measure the position of a moving vehicle, for example, you can measure the distance traveled in a straight line from the starting point. With a rotating object, the measurement is generally done in terms of the angle around a circle. By convention, the starting or “zero” point is generally a horizontal radius from the center to the right side of the circle. The distance traveled is measured by the size of the angle
, measured from that horizontal radius.[10]
- The angle that is being measured is commonly represented by
, the Greek letter theta.
- Positive motion is measured in a counterclockwise direction. Negative motion is measured in a clockwise direction.
- The angle that is being measured is commonly represented by
-
3
Measure angular motion in radians. Linear travel is generally measured in some unit of distance, such as miles, meters, inches or some other unit of length. Rotational or angular motion is generally measured in units called radian. A radian is a fraction of the circle. For standard reference, mathematicians use the “unit circle,” which has a standard radius of 1 unit.[11]
- One full rotation around the unit circle is said to measure 2π radians. Therefore, a half circle is π radians, and a quarter circle is π/2 radians.
- Sometimes it is useful to convert from radians to degrees. If you recall that a full circle is 360 degrees, you can find the conversion as follows:
- Thus, one radian is about equal to 57.3 degrees.
-
4
Understand the concept of angular acceleration. Angular acceleration is the measurement of how fast or slow a rotating object is changing its velocity. In other words, is the spinning speeding up or slowing down? If you know the angular velocity at a starting time and then at a later ending time, you can calculate the average angular acceleration over that time interval. If you know the function for the object’s position, you can use calculus to derive the instantaneous angular acceleration at any chosen time.[12]
- People often use the word “acceleration” to mean speeding up, and “deceleration” to mean slowing down. In mathematical and physical terms, however, only the word “acceleration” is used. If the object is speeding up, the acceleration is positive. If it is slowing down, the acceleration is negative.
Advertisement
Add New Question
-
Question
What are the formulas to find the initial acceleration of an object?
Initial acceleration generally has to be given as a condition of the problem or the experiment.
-
Question
What is the direction of radial and tangential acceleration and how do they affect each other?
Angular (or radial) measurements are generally counterclockwise. Tangential acceleration means the straight line direction of the tangent at some measured point along the circle. The tangent is a line that is perpendicular to the radius at that point.
-
Question
How can you find angular acceleration in revolutions per second squared?
This article shows how to find acceleration in radians per second squared. To convert the number of radians to the number of revolutions, recall that 1 full circle (or 1 revolution) is equal to 2pi radians. This is roughly equivalent to 6.28 radians per revolution. If you know the acceleration in radians per second squared, divide that answer by 6.28 to get revolutions per second squared.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Remember to express final results with the proper units. Angular position is usually expressed in radians. Angular velocity is expressed in radians per time. Angular acceleration is expressed in units of radians per time squared.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To calculate instantaneous angular acceleration, start by determining the function for angular position, or the position of the object with respect to time. Next, find the angular velocity, which is the measure of how fast the object changes its position. Then, find the derivative of the function for angular velocity in order to determine the function for angular acceleration. Finally, plug in the data to find the instantaneous acceleration of the object at any chosen time. To learn more, including how to calculate average angular acceleration, read on.
Did this summary help you?
Thanks to all authors for creating a page that has been read 91,103 times.
Did this article help you?
Угловое ускорение – что это?
Угловое ускорение (varepsilon) – физическая величина, характеризующая изменение угловой скорости при движении тела.
Единица измерения: (lbrackvarepsilonrbrack=frac1{с^2}) или (с^{-2})
Угловая скорость
Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Угловая скорость (omega) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.
При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).
Вектор угловой скорости направлен вдоль оси вращения.
Основные формулы для вычисления угловой скорости
Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):
- (omega=frac nt), где (n) – количество оборотов за единицу времени (t).
- (omega=fracvarphi t), где (varphi) – угол поворота, (t) – время, за которое он совершен.
- (omega=frac{2pi}T), где (Т) – период обращения (время, за которое тело/точка совершает один оборот).
- (omega=2pinu), где (nu) – числом оборотов в единицу времени.
Единица измерения угловой скорости в СИ: (lbrackomegarbrack=frac{рад}с)
Связь между угловой скоростью и нормальным (центростремительным) ускорением
Центростремительное (нормальное) ускорение (a_n) – это составляющая полного ускорения, которая характеризует изменение направления вектора скорости при криволинейном движении. Другим компонентом полного ускорения является тангенциальное ускорение, оно характеризует изменение величины скорости.
Центростремительное ускорение определяется по формуле:
(a_n=frac{V^2}R),
где (V) – скорость движения, (R) – радиус окружности.
Единица измерения в СИ: (lbrack a_nrbrack=frac м{с^2})
Итак, формула связывающая эти две величины:
(a_n=omega^2R)
Основные формулы для расчета углового ускорения
Значение углового ускорения в определенный момент времени вычисляется как первая производная от угловой скорости или вторая производная от угла поворота по времени.
(varepsilon=lim_{triangle trightarrow0}frac{triangleomega}{triangle t}=frac{domega}{dt}=frac{d^2varphi}{dt}=overset.omega=overset{..}varphi)
Угловое ускорение маховика
(varepsilon=fracomega t=frac{2pi n}t), где (n) – количество оборотов за единицу времени (t).
Среднее угловое ускорение
Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.
(leftlanglevarepsilonrightrangle=frac{triangleomega}{triangle t})
Тангенциальное ускорение
Тангенциальным (касательным) ускорением (a_tau) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.
(a_tau=varepsilon r), где (varepsilon) – угловое ускорение, (r) – радиус кривизны траектории в заданной точке.
Мгновенное угловое ускорение
Мгновенное угловое ускорение (alpha) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.
(alpha=tg(varepsilon)=frac{;domega}{dt}=frac{d^2phi}{dt^2})