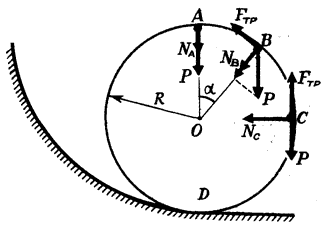
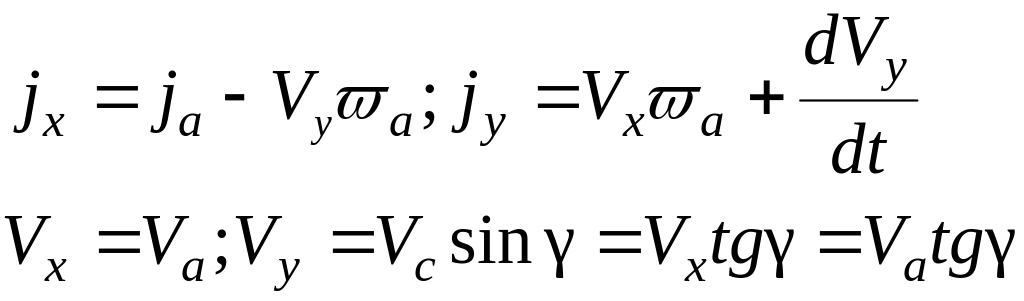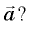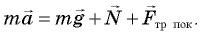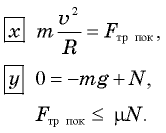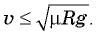Для
определения сил, действующих на автомобиль
при его повороте, когда угол поворота
управляемых колес и скорость движения
автомобиля переменны, найдем вначале
силы инерции. Для этого воспользуемся
следующим приемом. Найдем абсолютные
ускорения центра тяжести автомобиля,
рассматривая автомобиль как твердое
тело. Умножив затем полученные ускорения
на массу автомобиля, найдем силы инерции,
а затем, считая другие силы, действующие
на автомобиль, заданными, определим
реакции дороги.
Пусть
автомобиль движется относительно
неподвижной системы координат ζ0η
, причем
в рассматриваемый момент времени его
продольная ось расположена под углом
β
к
оси 0η этой системы, а колеса повернуты,
как показано на рис. 44а, на угол θ. Зная
средний угол поворота управляемых
колес, можно способом, показанным ранее,
найти положение центра поворота Оп.
Скорость Vc
центра тяжести С автомобиля направлена
перпендикулярно радиусу и равна Vс
=
ωaОпС.
Обозначим y
угол
между продольной осью автомобиля и
вектором скорости Vс.Проекции
скорости Vc
на неподвижные оси координат равны
;(143)
;
(144)
где
VX
= VC
Cos
γ
– проекция
скорости Vc
на
продольную ось x
автомобиля
(продольная составляющая скорости
движения автомобиля);
Vx
= VC
Cos
γ
– проекция
скорости Vc
на
поперечную ось автомобиля (скорость
бокового смещения автомобиля).
а) б)
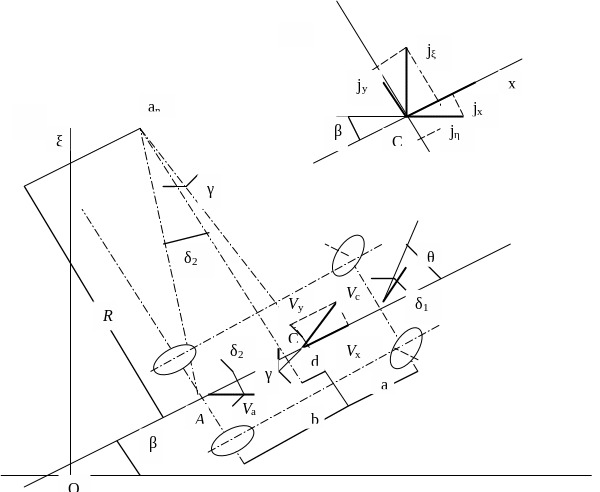
Рис.
44. Схема для определения сил, действующих
на автомобиль при повороте
Продифференцировав
равенства (143), (144) по времени, получим
проекции на оси неподвижной системы
ускорения центра тяжести автомобиля:
;
(145)
;
(146)
Поскольку
положение автомобиля относительно
неподвижной системы координат непрерывно
меняется, то положение ускорений Jη
и Jζ
относительно продольной и поперечной
осей также изменяется. Удобнее иметь
дело с ускорениями, а, следовательно, и
силами, не изменяющими свое направление
относительно автомобиля. Поэтому
спроектируем полученные в неподвижной
системе ускорения на продольную и
поперечную оси автомобиля.
Согласно
рис. 44б, сумма jx
проекций
ускорений Jη
и Jζ
на продольную ось автомобиля равна:
;
(147)
Сумма
jy
проекций ускорений jη
и Jζ
на поперечную ось автомобиля равна:
;
(148)
Подставляя
в равенства (147), (148) значения Jη
и Jζ
из равенств (145), (146) после соответствующих
преобразований, получим:
;
(149)
Пользуясь
рис.44а, найдем:
,
,
откуда
,
где
точками обозначено дифференцирование
по времени.
Подставляя
полученные значения Vy
и
в
равенства (149), найдем:
;
(150)
;
(151)
Продольная
и поперечная составляющие сил инерции,
действующих на автомобиль при повороте,
равны произведению массы автомобиля
на продольную и поперечную составляющие
ускорения центра тяжести автомобиля и
направлены в сторону, противоположную
направлению соответствующих ускорений.
Продольная
составляющая силы инерции:
;
(152)
направлена
в сторону, противоположную движению
автомобиля.
Поперечная
составляющая силы инерции:
;
(153)
направлена
от центра поворота автомобиля.
Пользуясь
формулами (151), (152), можно, как частный
случай, получить формулы для определения
продольной и поперечной составляющих
сил инерции без учета увода (у автомобиля
с жесткими колесами).
Принимая
,
получим:
;
(154)
;
(155)
Из
формул (154), (155) видно, что как с учетом
увода, так и без учета увода поперечная
составляющая Py
силы
инерции может быть представлена в виде
трех составляющих:
Ру=Рy‘+Рy»+Ру‘
(156)
Первая
из этих составляющих является центробежной
силой:
;
(157)
Как
видно из равенства (157), если заданы R
и Va,
то выражения для центробежной силы
одинаковы как с учетом, так и без учета
увода.
В
формулах (152)-(157) скорость Va
выражена в м/с. Если задана скорость в
км/ч, то в этих формулах вместо Va
нужно
поставить Va/3,6.
Вторая
составляющая Ру
поперечной
силы инерции возникает в результате
изменения угла поворота управляемых
колес и изменения углов увода. Для
автомобиля с жесткими колесами эта
составляющая всегда положительна при
входе автомобиля в поворот и отрицательна
при выходе из поворота. С учетом увода
в случае, когда скорости изменения углов
увода велики, эта составляющая может
быть отрицательной при входе в поворот
и положительной при выходе.
Третья,
составляющая Py‘«поперечной
силы инерции возникает в результате
изменения скорости движения автомобиля.
Для автомобиля с жесткими колесами эта
составляющая положительна при ускоренном
движении и отрицательная при замедлении.
При небольших углах θ и больших углах
увода положительное значение третьей
составляющей поперечной силы может
иметь место и в процессе торможения.
В
большинстве случаев движения автомобиля
центробежная сила значительно больше
остальных составляющих. Поэтому в
качестве основных критериев устойчивости
автомобиля обычно принимаются предельная
по устойчивости скорость или предельный
радиус поворота при круговом движении,
когда две последние составляющие
поперечной силы инерции равны нулю. В
некоторых случаях при больших радиусах
поворота, больших скоростях движения,
а также резком изменении углов поворота
управляемых колес и кривизны траектории
движения автомобиля существенную роль
может играть составляющая Py».
Составляющая
Ру‘«в
большинстве случаев мала. Только при
резком торможении влияние этой
составляющей на устойчивость автомобиля
может быть заметным.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Если автомобиль на повороте движется по дуге окружности, значит, ускорение автомобиля 
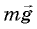
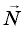
Этой силой является сила трения, действующая на колеса со стороны дороги, и направленная по горизонтали перпендикулярно скорости.
Какая это сила трения — покоя или скольжения? Мы уже знаем, что при качении без проскальзывания нижняя точка колеса покоится относительно дороги (см. § 5. Примеры решения задач). Значит, возникающая на повороте сила трения — это сила трения покоя — именно она вызывает центростремительное ускорение автомобиля при повороте. А для силы трения покоя, как мы уже знаем, должно выполняться неравенство 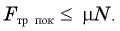
Изобразим все силы, действующие на автомобиль при повороте (рис. 15.3).
Согласно второму закону Ньютона,
Центростремительное ускорение связано со скоростью соотношением 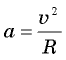
Запишем уравнение второго закона Ньютона в проекциях на оси координат. Совместим начало координат с положением автомобиля в данный момент, ось 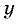
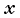
Из второго уравнения следует, что 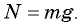
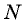
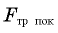
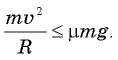
В нашем случае, подставляя численные данные из условия, получаем, что скорость автомобиля на повороте не может превышать 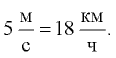
Как мы видим, скорость на повороте должна быть значительно меньше обычной скорости при движении по городу (около 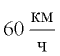
При гололеде коэффициент трения между шинами и дорогой значительно уменьшается: он становится равным 0,2 вместо 0,5 на сухой дороге. Поэтому ограничение на скорость становится более строгим: подставляя 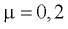
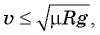
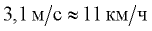
Для описания движения по окружности наряду с линейной скоростью вводят понятие угловой скорости. Если точка при движении по окружности за время (Delta t) описывает дугу, угловая мера которой (Delta varphi), то угловая скорость (omega = frac{{Delta varphi }}{{Delta t}}).
Угловая скорость (omega) связана с линейной скоростью (upsilon) соотношением (upsilon = omega r), где (r) — радиус окружности, по которой движется точка (рис. 1). Понятие угловой скорости особенно удобно для описания вращения твердого тела вокруг оси. Хотя линейные скорости у точек, находящихся на разном расстоянии от оси, будут неодинаковыми, их угловые скорости будут равны, и можно говорить об угловой скорости вращения тела в целом.
Задача
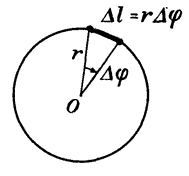
Диск, радиуса (r) катится без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянная и равна (upsilon_п). С какой угловой скоростью при этом вращается диск?
Каждая точка диска участвует в двух движениях — в поступательном движении со скоростью (upsilon_п) вместе с центром диска и во вращательном движении вокруг центра с некоторой угловой скоростью (omega).
Для нахождения (omega) воспользуемся отсутствием проскальзывания, то есть тем, что в каждый момент времени скорость точки диска, соприкасающейся с плоскостью, равна нулю. Это означает, что для точки А (рис. 2) скорость поступательного движения (upsilon_п) равна по величине и противоположна по направлению линейной скорости вращательного движения ({upsilon _{вр}} = omega r). Отсюда сразу получаем (omega = frac{{{upsilon _п}}}{r}).
Задача
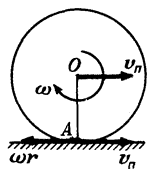
Найти скорости точек В, С и D того же диска (рис. 3).
Рассмотрим вначале точку В. Линейная скорость ее вращательного движения направлена вертикально вверх и равна ({upsilon _{вр}} = omega r = frac{{{upsilon _п}}}{R}r = {upsilon _п}), то есть по величине равна скорости поступательного движения, которая, однако, направлена горизонтально. Складывая векторно эти две скорости, находим, что результирующая скорость (upsilon_B) по величине равна ({upsilon _п}sqrt 2 ) и образует угол 45° с горизонтом. У точки С скорости вращательного и поступательного движения направлены в одну сторону. Результирующая скорость (upsilon_C) равна (2upsilon_п), и направлена горизонтально. Аналогично находится и скорость точки D (см. рис. 3).
Даже в том случае, когда скорость точки, движущейся по окружности, не меняется по величине, точка имеет некоторое ускорение, так как меняется направление вектора скорости. Это ускорение называется центростремительным. Оно направлено к центру окружности и равно
[{a_ц} = {omega ^2}r = frac{{{upsilon ^2}}}{R}]
((R) — радиус окружности, (omega) и (upsilon) — угловая и линейная скорости точки).
Если же скорость точки, движущейся по окружности, меняется не только по направлению, но и по величине, то наряду с центростремительным ускорением существует и так называемое тангенциальное ускорение. Оно направлено по касательной к окружности и равно отношению (frac{{Delta upsilon }}{{Delta t}}) (({Delta upsilon }) — изменение величины скорости за время (Delta t)).
Задача
Найти ускорения точек А, В, С и D диска радиуса (r), катящегося без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянна и равна (upsilon_п) (рис. 3).
В системе координат, связанной с центром диска, диск вращается с угловой скоростью (omega), а плоскость движется поступательно со скоростью (upsilon_п). Проскальзывание между диском и плоскостью отсутствует, следовательно, (omega = frac{{{upsilon _п}}}{r}). Скорость поступательного движения (upsilon_п) не меняется, поэтому угловая скорость вращения диска постоянная и точки диска имеют только центростремительное ускорение ({a_ц} = {omega ^2}r = frac{{{upsilon_п^2}}}{R}), направленное к центру диска. Так как система координат движется без ускорения (с постоянной скоростью (upsilon_п)), то в неподвижной системе координат ускорения точек диска будут теми же.
Перейдем теперь к задачам на динамику вращательного движения. Вначале рассмотрим простейший случай, когда движение по окружности происходит с постоянной скоростью. Так как ускорение тела при этом направлено к центру, то и векторная сумма всех сил, приложенных к телу, должна быть тоже направлена к центру, и по II закону Ньютона (m{a_ц} = sum F).
Следует помнить, что в правую часть этого уравнения входят только реальные силы, действующие на данное тело со стороны других тел. Никакой центростремительной силы при движении по окружности не возникает. Этим термином пользуются просто для обозначения равнодействующей сил, приложенных к телу, движущемуся по окружности. Что касается центробежной силы, то она возникает только при описании движения по окружности в неинерциальной (вращающейся) системе координат. Мы пользоваться здесь понятием центростремительной и центробежной силы вообще не будем.
Задача
Определить наименьший радиус закругления дороги, которое автомобиль может пройти при скорости (upsilon=70) км/ч и коэффициенте трения шин о дорогу (k=0,3).
На автомобиль действуют сила тяжести (P=mg), сила реакции дороги (N) и сила трения (F_{тр}) между шинами автомобиля и дорогой. Силы (P) и (N) направлены вертикально и равны по величине: (P=N). Сила трения, препятствующая проскальзыванию («заносу») автомобиля, направлена к центру поворота и сообщает центростремительное ускорение: ({F_{тр}} = frac{{m{upsilon ^2}}}{R}). Максимальное значение силы трения ({F_{трmax}} = kN = kmg), поэтому минимальное значение радиуса окружности, по которой еще возможно движение со скоростью (upsilon), определяется из уравнения (frac{{m{upsilon ^2}}}{R} = kmg). Отсюда (R = frac{{{upsilon ^2}}}{{kg}} approx 130;м).
Сила реакции дороги (N) при движении автомобиля по окружности не проходит через центр тяжести автомобиля. Это связано с тем, что ее момент относительно центра тяжести должен компенсировать момент силы трения, стремящийся опрокинуть автомобиль. Величина силы трения тем больше, чем больше скорость автомобиля (left( {{F_{тр}} = frac{{m{upsilon ^2}}}{R}} right)). При некотором значении скорости момент силы трения превысит момент силы реакции и автомобиль опрокинется.
Задача
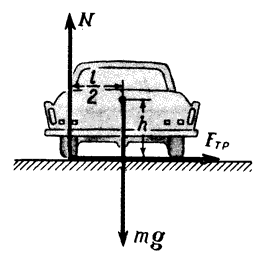
При какой скорости автомобиль, движущийся по дуге окружности радиуса (R=130) м, может опрокинуться? Центр тяжести автомобиля находится на высоте (h=1) м над дорогой, ширина следа автомобиля (l=1,5) м (рис. 4).
В момент опрокидывания автомобиля как сила реакции дороги (N), так и сила трения (F_{тр}) приложены к «внешнему» колесу. При движении автомобиля по окружности со скоростью (upsilon) на него действует сила трения (left( {{F_{тр}} = frac{{m{upsilon ^2}}}{R}} right)). Эта сила создает момент относительно центра тяжести автомобиля ({M_{тр}} = frac{{m{upsilon ^2}}}{R}h). Максимальный момент силы реакции дороги (N=mg) относительно центра тяжести равен (mgfrac{l}{2}) (в момент опрокидывания сила реакции проходит через внешнее колесо). Приравнивая эти моменты, найдем уравнение для максимальной скорости, при которой автомобиль еще не опрокинется:
[frac{{m{upsilon ^2}}}{R}h = frac{{mgl}}{2},]
откуда
[upsilon = sqrt {frac{{glR}}{{2h}}} approx 30;м/с approx 110;км/ч.]
Чтобы автомобиль мог двигаться с такой скоростью, необходим коэффициент трения (k geq frac{{{upsilon ^2}}}{{gR}}) (см. предыдущую задачу).
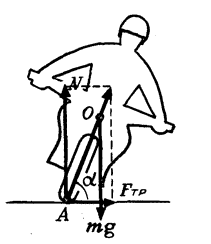
Аналогичная ситуация возникает при повороте мотоцикла или велосипеда. Сила трения, создающая центростремительное ускорение, имеет момент относительно центра тяжести, стремящийся опрокинуть мотоцикл. Поэтому для компенсации этого момента моментом силы реакции дороги мотоциклист наклоняется в сторону поворота (рис. 5).
Задача
Мотоциклист едет по горизонтальной дороге со скоростью (upsilon=70) км/ч, делая поворот радиусом (R=100) м. На какой угол (alpha) к горизонту он должен при этом наклониться, чтобы не упасть?
Сила трения между мотоциклом и дорогой ({{F_{тр}} = frac{{m{upsilon ^2}}}{R}}), так как она сообщает мотоциклисту центростремительное ускорение. Сила реакции дороги (N=mg). Условие равенства моментов силы трения и силы реакции относительно центра тяжести дает уравнение: ({F_{тр}} cdot lsin alpha = Nlcos alpha), где (l) — расстояние OA от центра тяжести до следа мотоцикла (см. рис. 5).
Подставляя сюда значения (F_{тр}) и (N), находим что ({text{tg}}alpha = frac{{gR}}{{{upsilon ^2}}}) или (alpha = {text{arctg}}frac{{gR}}{{{upsilon ^2}}} approx 70^circ). Отметим, что равнодействующая сил (N) и (F_{тр}) при этом угле наклона мотоцикла проходит через центр тяжести, что и обеспечивает равенство нулю суммарного момента сил (N) и (F_{тр}).
Для того, чтобы увеличить скорость движения по закруглению дороги, участок дороги на повороте делают наклонным. При этом в создании центростремительного ускорения, кроме силы трения, участвует и сила реакции дороги.
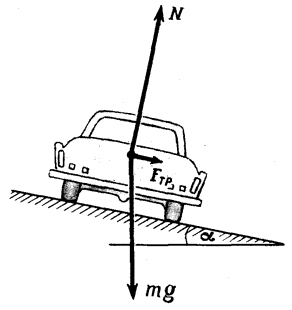
Задача
С какой максимальной скоростью (upsilon) может двигаться автомобиль по наклонному треку с углом наклона (alpha) при радиусе закругления (R) и коэффициенте трения шин о дорогу (k)?
На автомобиль действуют сила тяжести (mg), сила реакции (N), направленная перпендикулярно плоскости трека, и сила трения (F_{тр}), направленная вдоль трека (рис. 6). Так как нас не интересуют в данном случае моменты сил, действующих на автомобиль, мы нарисовали все силы приложенными к центру тяжести автомобиля. Векторная сумма всех сил должна быть направлена к центру окружности, по которой движется автомобиль, и сообщать ему центростремительное ускорение. Поэтому сумма проекций сил на направление к центру (горизонтальное направление) равна (frac{{m{upsilon ^2}}}{R}), то есть (frac{{m{upsilon ^2}}}{R} = Nsin alpha + {F_{тр}}cos alpha).
Сумма проекций всех сил на вертикальное направление равна нулю:
[Ncos alpha – mg – {F_{тр}}sin alpha = 0.]
Подставляя в эти уравнения максимальное возможное значение силы трения (F_{тр}=kN) и исключая силу (N), находим максимальную скорость (upsilon = sqrt {gRfrac{{k + {text{tg}}alpha }}{{1 – k{text{tg}}alpha }}}), с которой еще возможно движение по такому треку. Это выражение всегда больше значения (sqrt {kgR}), соответствующего горизонтальной дороге.
Разобравшись с динамикой поворота, перейдем к задачам на вращательное движение в вертикальной плоскости.
Задача
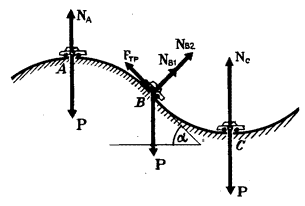
Автомобиль массы (m=1,5) т движется со скоростью (upsilon=70) км/ч по дороге, показанной на рисунке 7. Участки дороги АВ и ВС можно считать дугами окружностей радиуса (R=200) м, касающимися друг друга в точке В. Определить силу давления автомобиля на дорогу в точках А и С. Как меняется сила давления при прохождении автомобилем точки В?
В точке A на автомобиль действуют сила тяжести (P=mg) и сила реакции дороги (N_A). Векторная сумма этих сил должна быть направлена к центру окружности, то есть вертикально вниз, и создавать центростремительное ускорение: (frac{{m{upsilon ^2}}}{R} = P – {N_A}), откуда ({N_A} = mg – frac{{m{upsilon ^2}}}{R} approx 12 cdot {10^3};Н). Сила давления автомобиля на дорогу равна по величине и противоположна по направлению силе реакции. В точке С векторная сумма сил направлена вертикально вверх: (frac{{m{upsilon ^2}}}{R} = {N_C} – P) и ({N_C} = mg + frac{{m{upsilon ^2}}}{R} = 18 cdot {10^3};Н).
Таким образом, в точке А сила давления меньше силы тяжести, а в точке С — больше.
В точке В автомобиль переходит с выпуклого участка дороги на вогнутый (или наоборот). При движении по выпуклому участку проекция силы тяжести на направление к центру должна превышать силу реакции дороги (N_{B1}), причем (Pcos alpha – {N_{B1}} = frac{{m{upsilon ^2}}}{R}). При движении по вогнутому участку дороги, наоборот, сила реакции дороги (N_{B2}) превосходит проекцию силы тяжести:
[{N_{B2}} – Pcos alpha = frac{{m{upsilon ^2}}}{R}.]
Из этих уравнений получаем, что при прохождении точки В сила давления автомобиля на дорогу меняется скачком на величину (frac{{2m{upsilon ^2}}}{R} approx 6 cdot {10^3}) Н. Разумеется, такие ударные нагрузки действуют разрушающе как на автомобиль, так и на дорогу. Поэтому дороги и мосты всегда стараются делать так, чтобы их кривизна менялась плавно.
При движении автомобиля по окружности с постоянной скоростью сумма проекций всех сил на направление, касательное к окружности, должна быть равна нулю. В нашем случае касательная составляющая силы тяжести уравновешивается силой трения между колесами автомобиля и дорогой.
Величина силы трения регулируется вращательным моментом, прикладываемым к колесам со стороны мотора. Этот момент стремится вызвать проскальзывание колес относительно дороги. Поэтому возникает сила трения, препятствующая проскальзыванию и пропорциональная приложенному моменту. Максимальное значение силы трения равно (kN), где (k) — коэффициент трения между шинами автомобиля и дорогой, (N) — сила давления на дорогу. При движении автомобиля вниз сила трения играет роль тормозящей силы, а при движении вверх, наоборот, роль силы тяги.
Задача
Автомобиль массой (m=0,5) т, движущийся со скоростью (upsilon=200) км/ч, совершает «мертвую петлю» радиуса (R=100) м (рис. 8). Определить силу давления автомобиля на дорогу в верхней точке петли A; в точке B, радиус-вектор которой составляет угол (alpha=30^circ) с вертикалью; в точке С, в которой скорость автомобиля направлена вертикально. Возможно ли движение автомобиля по петле с такой постоянной скоростью при коэффициенте трения тин о дорогу (k=0,5)?
В верхней точке петли сила тяжести и сила реакции дороги (N_A) направлены вертикально вниз. Сумма этих сил создает центростремительное ускорение: (frac{{m{upsilon ^2}}}{R} = {N_A} + mg).
Поэтому ({N_A} = frac{{m{upsilon ^2}}}{R} – mg approx {10^4};Н).
Сила давления автомобиля на дорогу равна по величине и противоположна по направлению силе (N_A).
В точке В центростремительное ускорение создается суммой силы реакции и проекции силы тяжести на направление к центру: (frac{{m{upsilon ^2}}}{R} = {N_B} + mgcos alpha). Отсюда
[{N_B} = frac{{m{upsilon ^2}}}{R} – mgcos alpha approx 11 cdot {10^3};Н]
Легко видеть, что ({N_B} > {N_A}); с увеличением угла (alpha) сила реакции дороги увеличивается.
В точке С сила реакции ({N_C} = frac{{m{upsilon ^2}}}{R} approx 15 cdot {10^3}) Н; центростремительное ускорение в этой точке создается только силой реакции, а сила тяжести направлена по касательной. При движении по нижней части петли сила реакции будет превышать (frac{{m{upsilon ^2}}}{R}) и максимальное значение (frac{{m{upsilon ^2}}}{R} – mg approx 20 cdot {10^3}) Н сила реакции имеет в точке D. Значение ({N_A} = frac{{m{upsilon ^2}}}{R} – mg), таким образом, является минимальным значением силы реакции.
Скорость автомобиля будет постоянной, если касательная составляющая силы тяжести не превышает максимальной силы трения (kN) во всех точках петли. Это условие заведомо выполняется, если минимальное значение (kN = k{N_A} = kmleft( {frac{{{upsilon ^2}}}{R} – g} right)) превосходит максимальное значение касательной составляющей силы веса. В нашем случае это максимальное значение равно (mg) (оно достигается в точке С), и условие (kmleft( {frac{{{upsilon ^2}}}{R} – g} right) > mg) выполняется при (k=0,5), (upsilon=200) км/ч, (R=100) м.
Таким образом, в нашем случае движение автомобиля по «мертвой петле» с постоянной скоростью возможно.
Рассмотрим теперь движение автомобиля по «мертвой петле» с выключенным мотором. Как уже отмечалось, обычно момент силы трения противодействует моменту, приложенному к колесам со стороны мотора. При движении автомобиля с выключенным мотором этого момента нет, и силой трения между колесами автомобиля и дорогой можно пренебречь.
Скорость автомобиля уже не будет постоянной — касательная составляющая силы тяжести замедляет или ускоряет движение автомобиля по «мертвой петле». Центростремительное ускорение тоже будет меняться. Создается оно, как обычно, равнодействующей силы реакции дороги и проекции силы тяжести на направление к центру петли.
Задача
Какую наименьшую скорость должен иметь автомобиль в нижней точке петли D (см. рис. 8 ) для того, чтобы совершить ее с выключенным мотором? Чему будет равна при этом сила давления автомобиля на дорогу в точке В? Радиус петли (R=100) м, масса автомобиля (m=0,5) т.
Посмотрим, какую минимальную скорость может иметь автомобиль в верхней точке петли А, чтобы продолжать двигаться по окружности?
Центростремительное ускорение в этой точке дороги создается суммой силы тяжести и силы реакции дороги (frac{{mupsilon _A^2}}{R} = mg + {N_A}). Чем меньшую скорость имеет автомобиль, тем меньшая возникает сила реакции (N_A). При значении ({upsilon _A} = sqrt {gR}) эта сила обращается в нуль. При меньшей скорости сила тяжести превысит значение, необходимое для создания центростремительного ускорения, и автомобиль оторвется от дороги. При скорости ({upsilon _A} = sqrt {gR}) сила реакции дороги обращается в нуль только в верхней точке петли. В самом деле, скорость автомобиля на других участках петли будет большей, и как легко видеть из решения предыдущей задачи, сила реакции дороги тоже будет большей, чем в точке А. Поэтому, если автомобиль в верхней точке петли имеет скорость ({upsilon _A} = sqrt {gR}), то он нигде не оторвется от петли.
Теперь определим, какую скорость должен иметь автомобиль в нижней точке петли D, чтобы в верхней точке петли А его скорость ({upsilon _A} = sqrt {gR}). Для нахождения скорости (upsilon_D) можно воспользоваться законом сохранения энергии, как если бы автомобиль двигался только под действием силы тяжести. Дело в том, что сила реакции дороги в каждый момент направлена перпендикулярно перемещению автомобиля, а следовательно, ее работа равна нулю (напомним, что работа (Delta A = FDelta Scos alpha), где (alpha) — угол между силой (F) и направлением перемещения (Delta S)). Силой трения между колесами автомобиля и дорогой при движении с выключенным мотором можно пренебречь. Поэтому сумма потенциальной и кинетической энергии автомобиля при движении с выключенным мотором не меняется.
Приравняем значения энергии автомобиля в точках А и D. При этом будем отсчитывать высоту от уровня точки D, то есть потенциальную энергию автомобиля в этой точке будем считать равной нулю. Тогда получаем
[frac{{mupsilon _D^2}}{2} = frac{{mupsilon _A^2}}{2} + 2mgR.]
Подставляя сюда значение ({upsilon _A} = sqrt {gR}) для искомой скорости (upsilon _D), находим:
[{upsilon _D} = sqrt {5gR} approx 70;м/с approx 260;км/ч.]
Если автомобиль въедет в петлю с такой скоростью, то он сможет совершить ее с выключенным мотором.
Определим теперь, с какой силой при этом автомобиль будет давить на дорогу в точке В. Скорость автомобиля в точке В опять легко находится из закона сохранения энергии:
[frac{{mupsilon _D^2}}{2} = frac{{mupsilon _B^2}}{2} + mgRleft( {1 + cos alpha } right).]
Подставляя сюда значение ({upsilon_D} = sqrt {5gR}), находим, что скорость ({upsilon _B} = sqrt {gRleft( {3 – 2cos alpha } right)}).
Воспользовавшись решением предыдущей задачи, по заданной скорости находим силу давления в точке В:
[{N_B} = frac{{mupsilon _B^2}}{R} – mgcos alpha = 3mgleft( {1 – cos alpha } right) approx 2 cdot {10^3};Н]
Аналогично можно найти силу давления в любой другой точке «мертвой петли».
Упражнения
- Найти угловую скорость искусственного спутника Земли, вращающегося по круговой орбите с периодом обращения (T=88) мин. Найти линейную скорость движения этого спутника, если известно, что его орбита расположена на расстоянии (R=200) км от поверхности Земли.
- Диск радиуса (R) помещен между двумя параллельными рейками. Рейки движутся со скоростями (upsilon_1) и (upsilon_2). Определить угловую скорость вращения диска и скорость его центра. Проскальзывание отсутствует.
- Диск катится по горизонтальной поверхности без проскальзывания. Показать, что концы векторов скоростей точек вертикального диаметра находятся на одной прямой.
- Самолет движется по окружности с постоянной горизонтальной скоростью (upsilon=700) км/ч. Определить радиус (R) этой окружности, если корпус самолета наклонен на угол (alpha=5^circ).
- Груз массы (m=100) г, подвешенный на нити длины (l=1) м, равномерно вращается по кругу в горизонтальной плоскости. Найти период обращения груза, если при его вращении нить отклонена по вертикали на угол (alpha=30^circ). Определить также натяжение нити.
- Автомобиль движется со скоростью (upsilon=80) км/ч по внутренней поверхности вертикального цилиндра радиуса (R=10) м по горизонтальному кругу. При каком минимальном коэффициенте трения между шинами автомобиля и поверхностью цилиндра это возможно?
- Груз массой (m) подвешен на нерастяжимой нити, максимально возможное натяжение которой равно (1,5mg). На какой максимальный угол (alpha) можно отклонить нить от вертикали, чтобы при дальнейшем движении груза нить не оборвалась? Чему будет равно при этом натяжение нити в тот момент, когда нить составит угол (frac{alpha}{2}) с вертикалью?
Источник: Журнал “Квант”, №5 1972 г. Автор: Л. Асламазов.
Софья Макарова
19 ноября, 20:05
0
Для определения значения ускорения указанного автомобиля на повороте необходимо использовать формулу (учитываем, что при постоянной скорости аτ (касательное ускорение) = 0 м/с²) : а = ац = V² / R.
Переменные: V — постоянная скорость указанного автомобиля (V = 36 км/ч = 10 м/с); R — радиус круговой траектории (R = 50 м).
Произведем расчет: а = V² / R = 10² / 50 = 2 м/с².
Ответ: Ускорение указанного автомобиля на повороте составляло 2 м/с².
- Комментировать
- Жалоба
- Ссылка