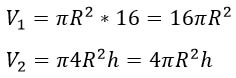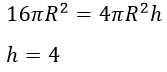Как найти уровень жидкости в цилиндре

07
Янв 2012

05 Задание (2022)

Задание 8: находим уровень жидкости в сосуде

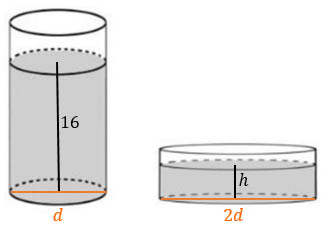
Задание B12 (№ 27046) В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.

Решение.

Вспомним формулу для вычисления объема цилиндра:

V=∏R²H, где R- радиус цилиндра, H — его высота.

По условию задачи уровень жидкости равен 16, следовательно, высота равна 16:

V=∏R²16

После того, как жидкость перелили в другой цилиндрический сосуд, ее объем не изменился. Диаметр второго сосуда в два раза больше диаметра первого. Т.к. D=2R, следовательно радиус второго сосуда также в два раза больше радиуса первого, и равен 2R.

Запишем, чему равен объем жидкости во втором сосуде:

V=∏(2R)²h= ∏4R²h, где h — высота жидкости во втором сосуде.

Приравняем объемы жидкости в первом и втором сосудах:

∏R²16= ∏4R²h

Сократим одинаковые величины в левой и правой частях равенства. Получим:

16=4h.

Отсюда: h=4

Ответ: 4 см.

То есть при одинаковом объеме высота обратно пропорциональна квадрату радиуса, и, следовательно, диаметра. Если мы диаметр увеличили в 2 раза, то высота уменьшится в 4 раза.

Вероятно, Ваш браузер не поддерживается. Попробуйте скачать

Firefox

|
Отзывов (24)
| Метки: решение задния В11

Источник

Partially filled cylinder

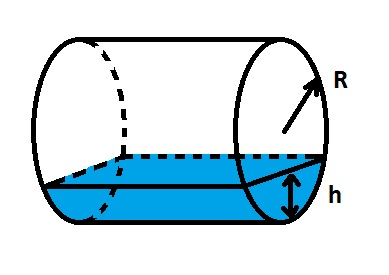
Задачу можно сформулировать следующим образом: Найти уровень жидкости в цилиндрическом баке, лежащем на боку, до которого нужно заполнить бак, чтобы получить требуемый объем.

Эта задача прямо противоположна задаче, описанной в калькуляторе Объем жидкости в цилиндрической таре.

Вот уравнение, которая описывает связь уровня жидкости и объема жидкости в цилиндре:

$pi R^2 p = R^2 acos((R - h) / R) - (R - h)sqrt{(2Rh - h^2)}$

где p — требуемый объем заполнения, в долях единицы (например, 0.25 соответствует четверти бака), R — радиус цилиндра, h — уровень жидкости.

Это уравнение нельзя решить аналитически относительно h, но можно найти ответ используя численные методы, например, Метод секущих, который, собственно, и используется в этом калькуляторе.

Также стоит заметить, что здесь уже есть решения для более сложного случая цилиндра, лежащего под наклоном — Уровень жидкости в наклоненном цилиндрическом баке и Объем жидкости в наклоненном цилиндрическом баке.

Уровень жидкости в цилиндрическом баке

Требуемый процент наполнения

Точность вычисления

Знаков после запятой: 4

Источник

Задание

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.

Решение

Для решения данной задачи необходимо знать формулу для нахождения объема цилиндра:

Объем цилиндра равен произведению его высоты на площадь основания (основание цилиндра – это круг, поэтому площадь основания равна площади круга): V = h * S_осн = h * πr² = h * π * D²/ 4

Найдем объем жидкости для первого сосуда:
V₁ = 16 * π * D²/ 4

Найдем объем жидкости для второго сосуда:
V₂ = h * π * (2D)²/ 4

Объем переливаемой жидкости одинаков, следовательно, V₁ = V₂:
16 * π * D²/ 4 = h * π * (2D)²/ 4

Осталось найти высоту уровня воды во втором цилиндре:
h = (16 * π * D²/ 4) / (π * (2D)²/ 4)
h = 16 / 4 = 4
4 см – высота уровня воды во втором цилиндре.

Ответ: 4

Источник