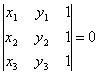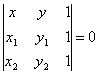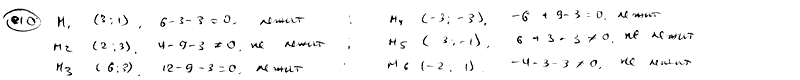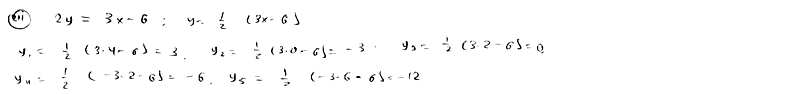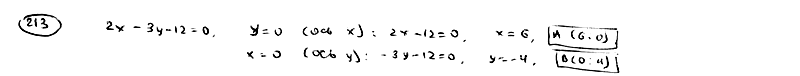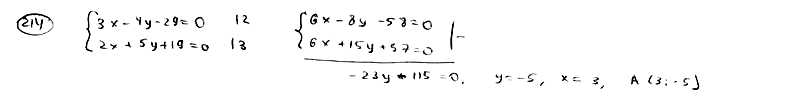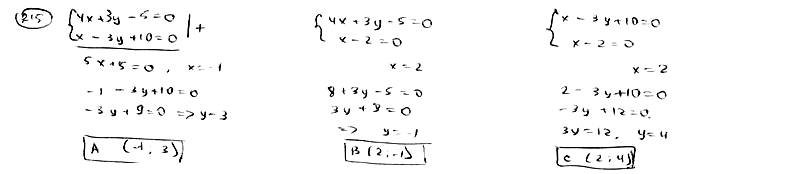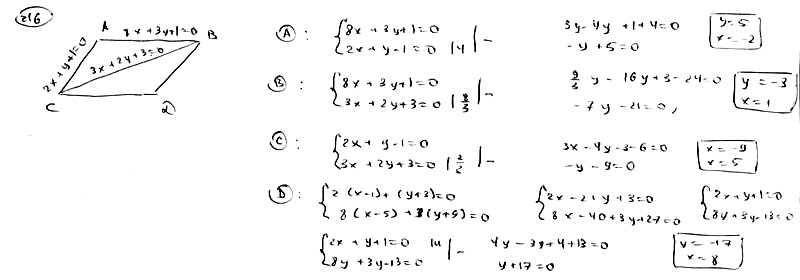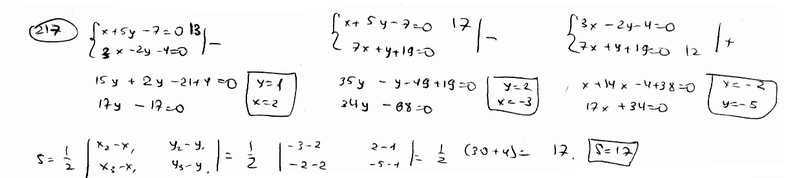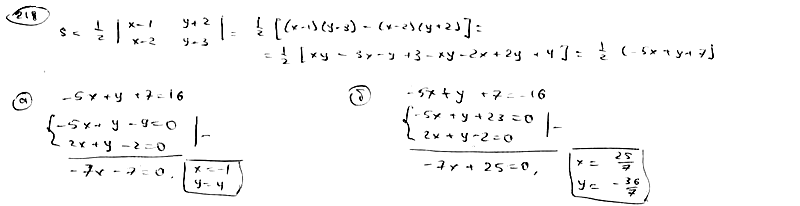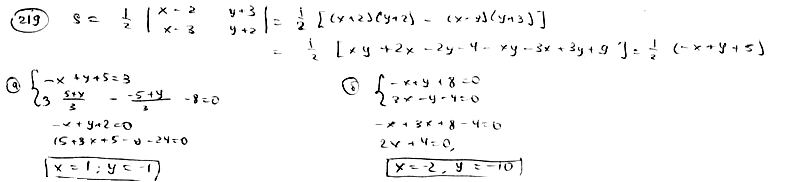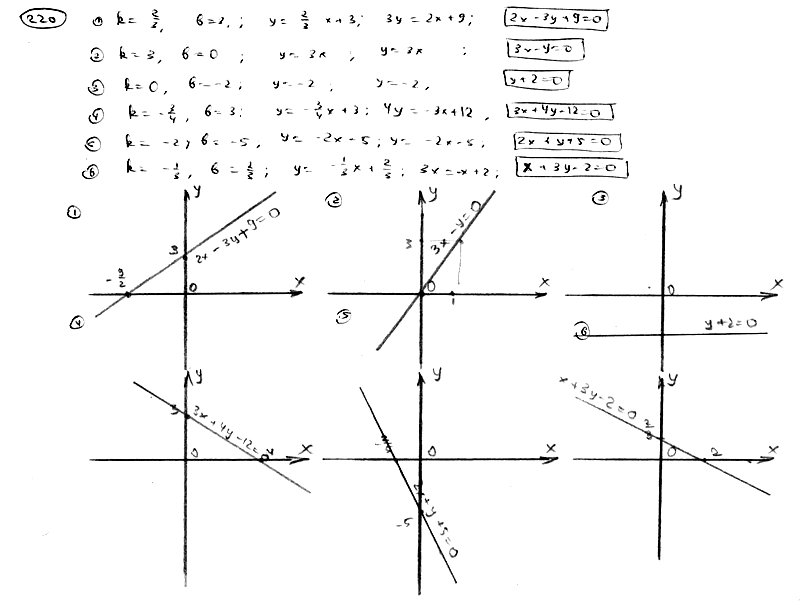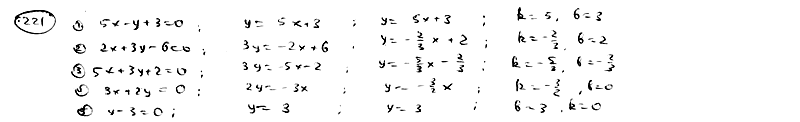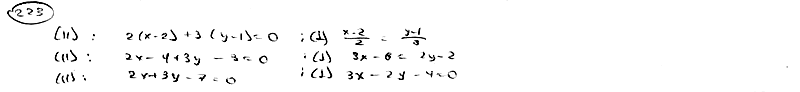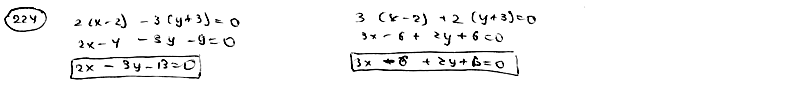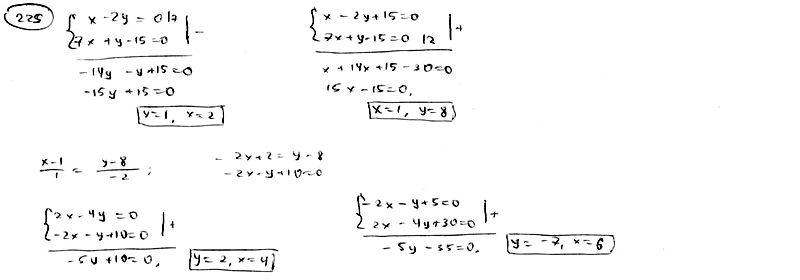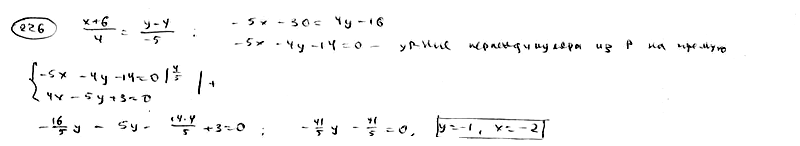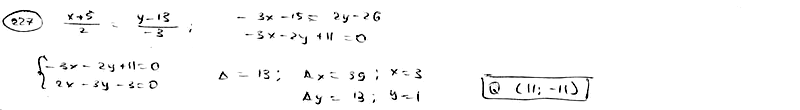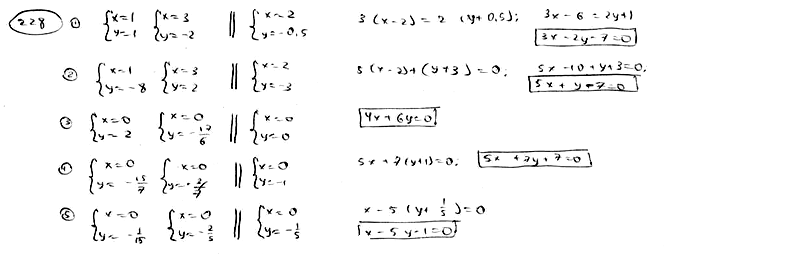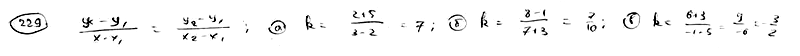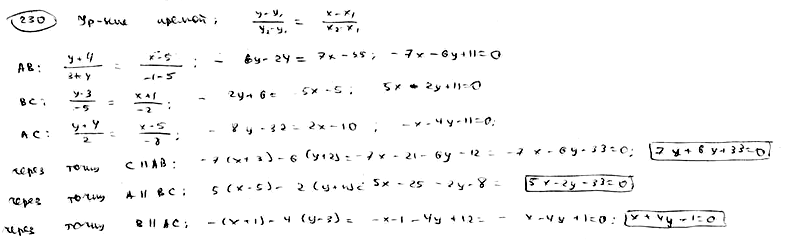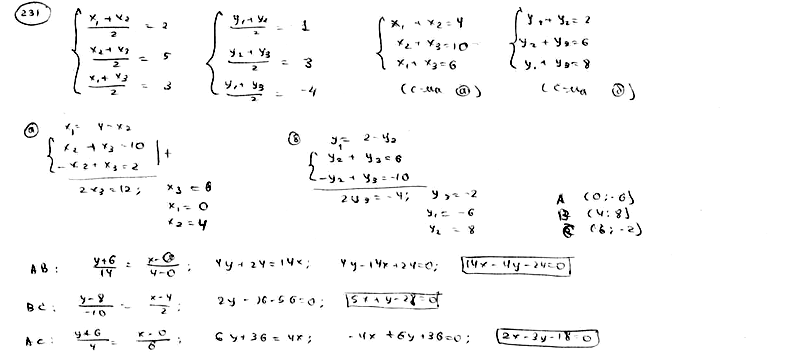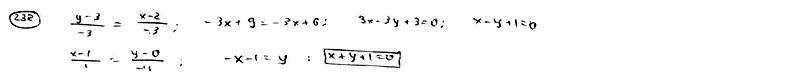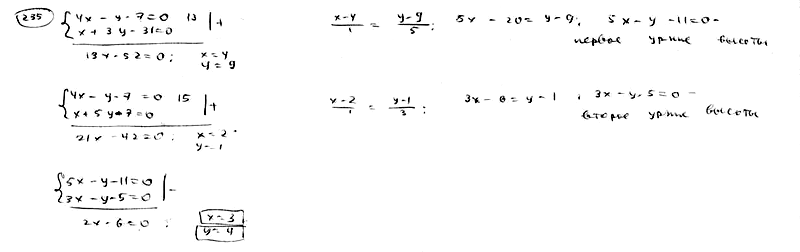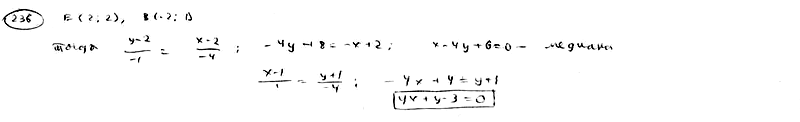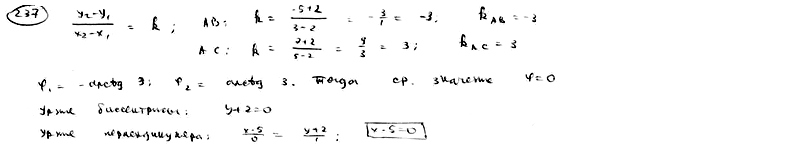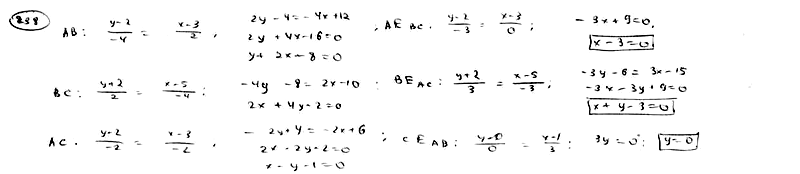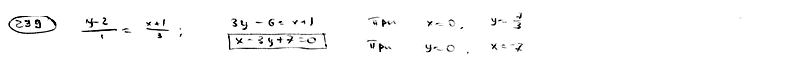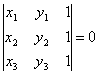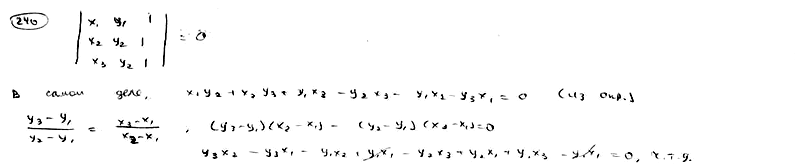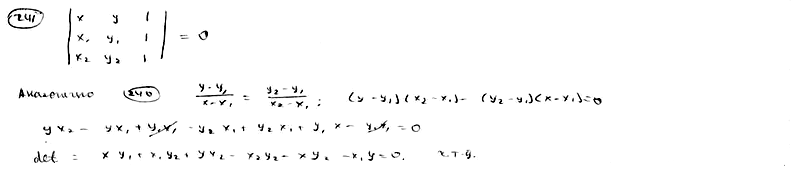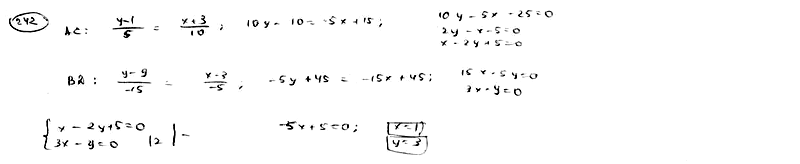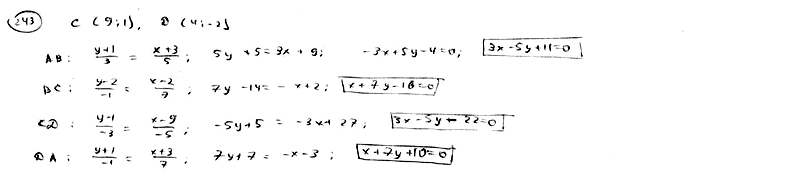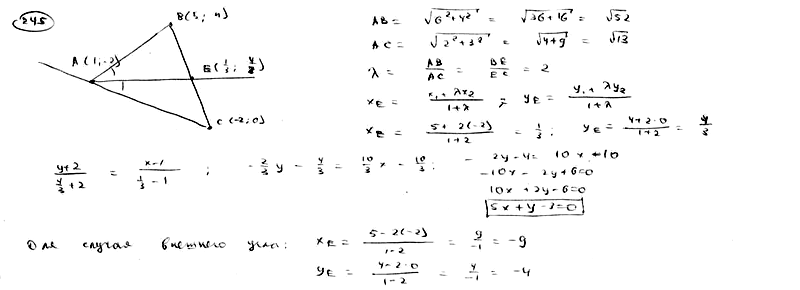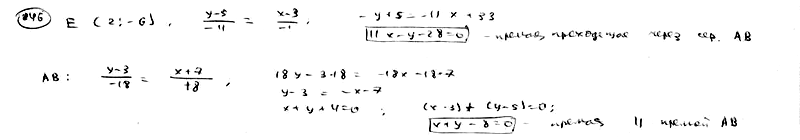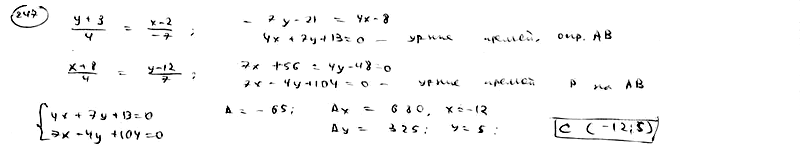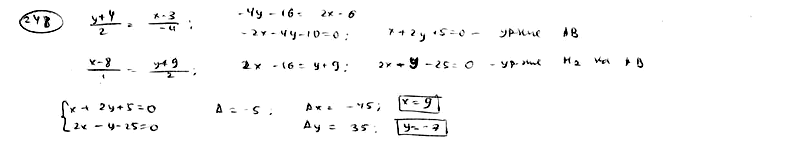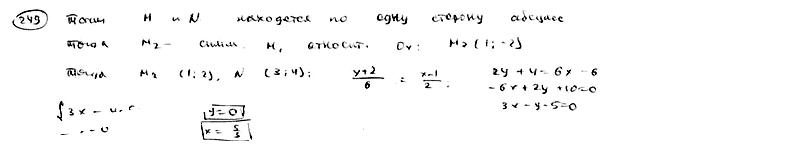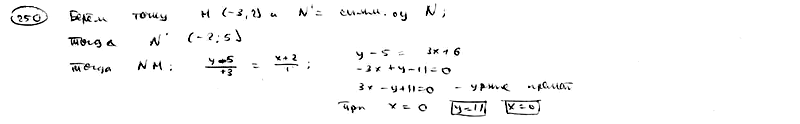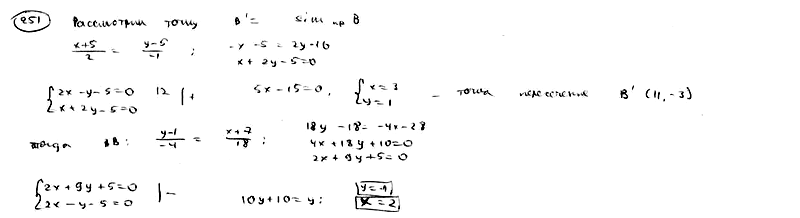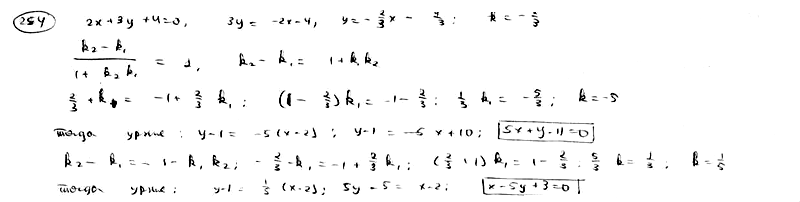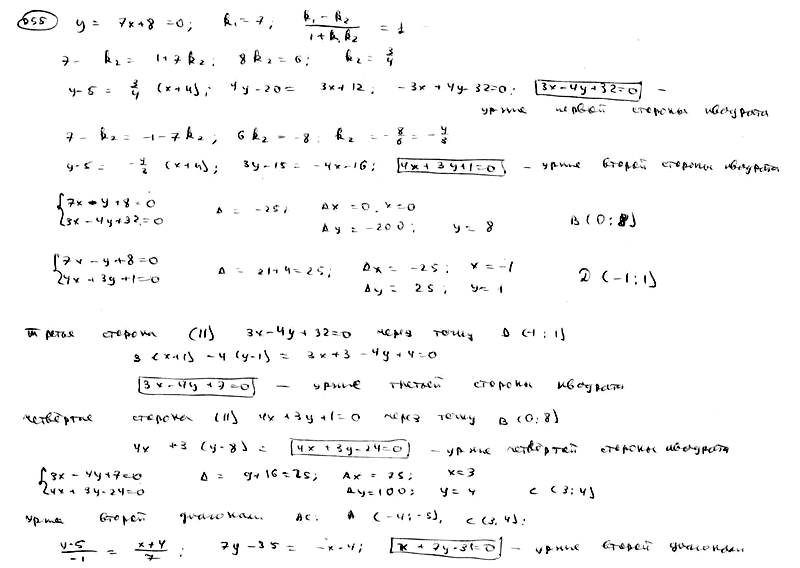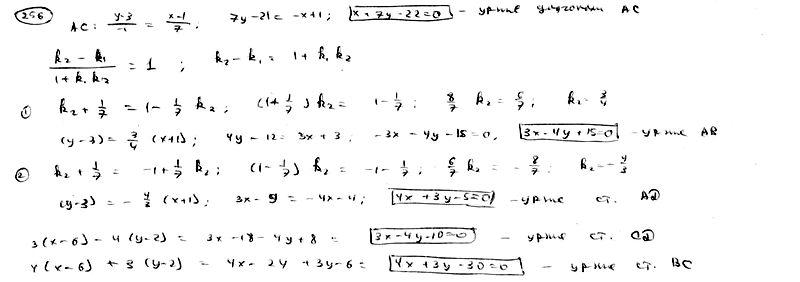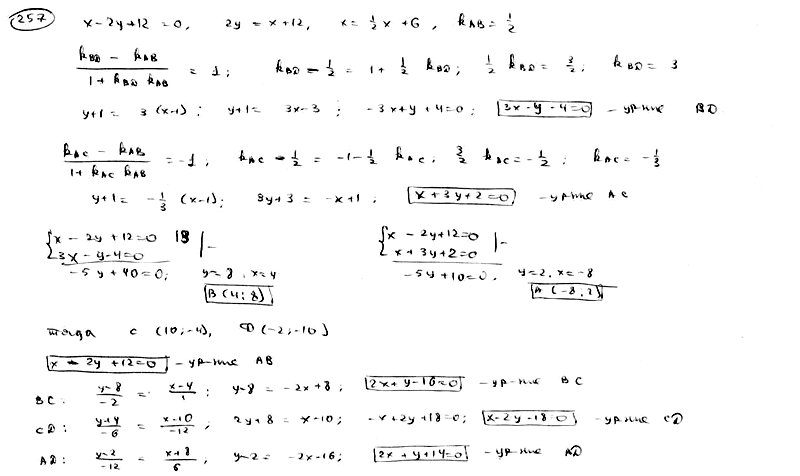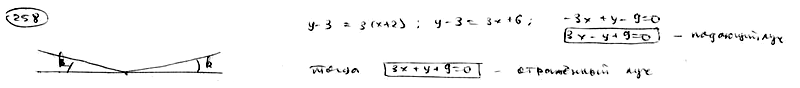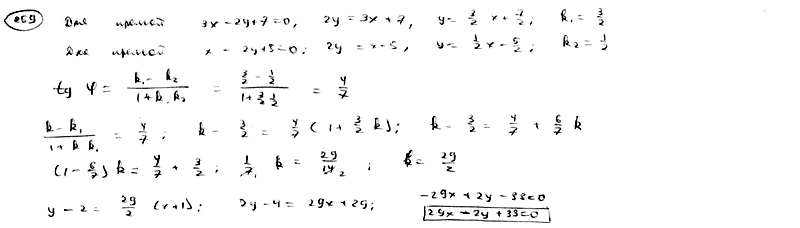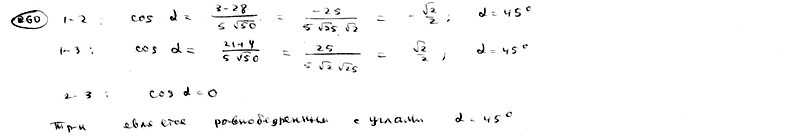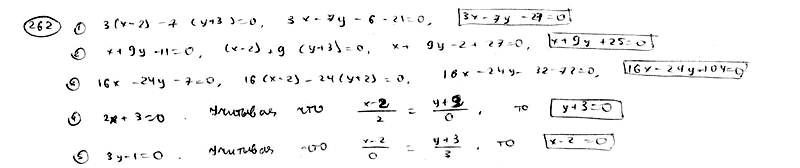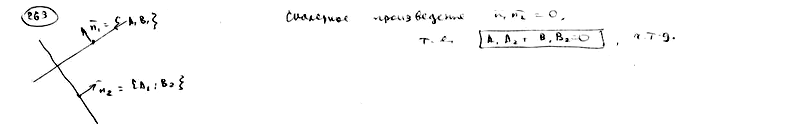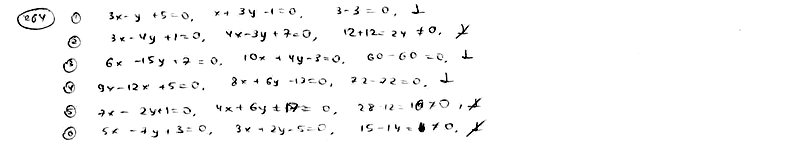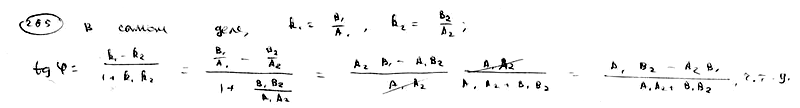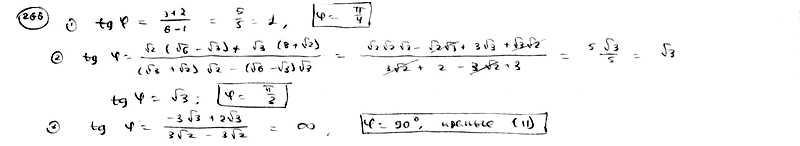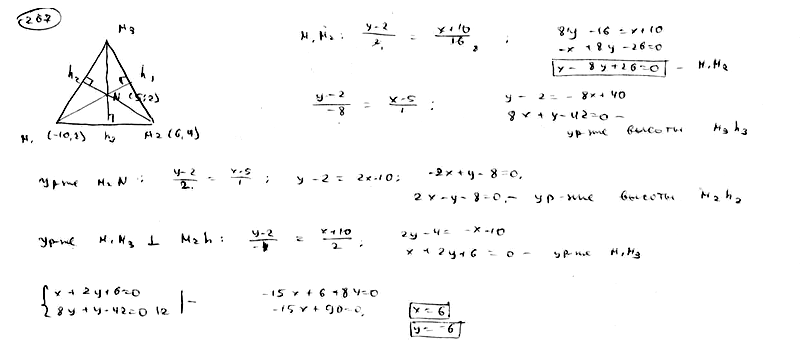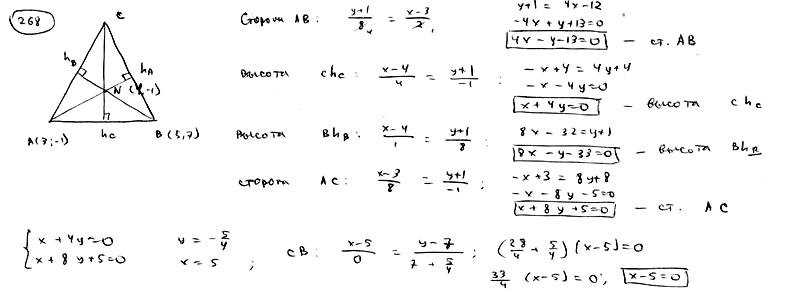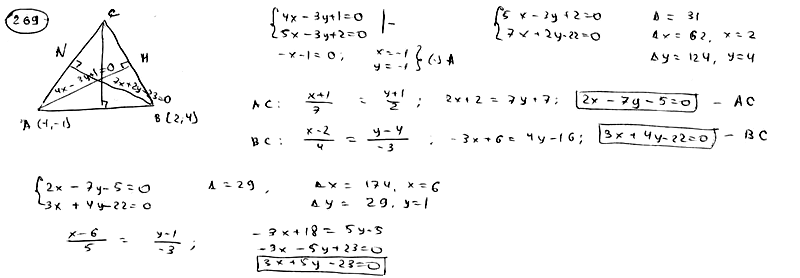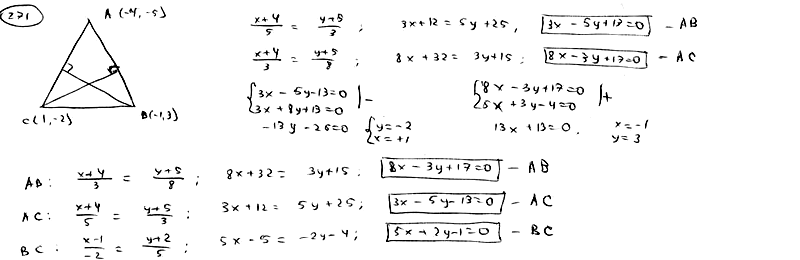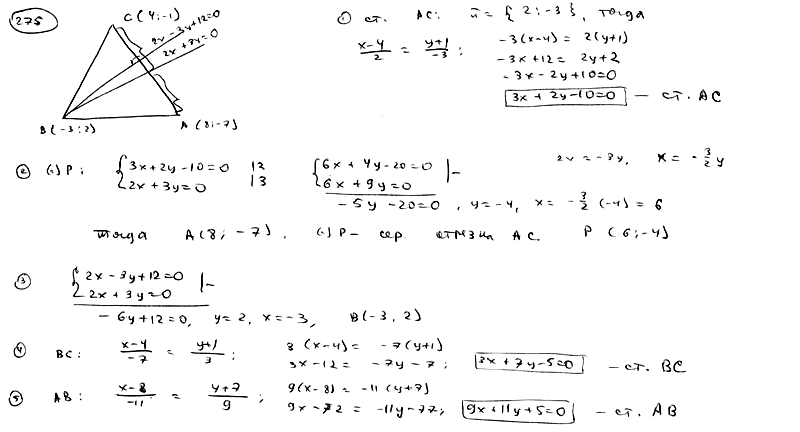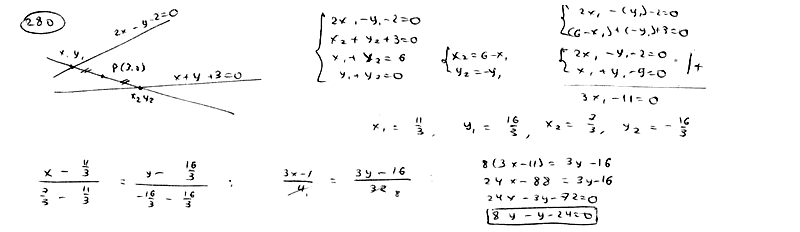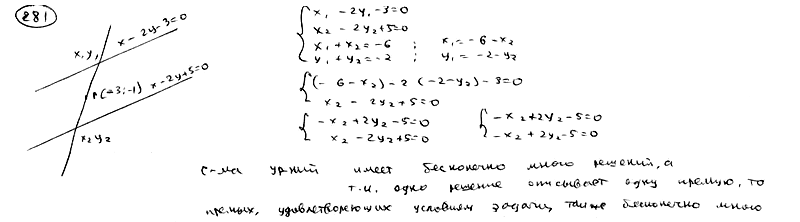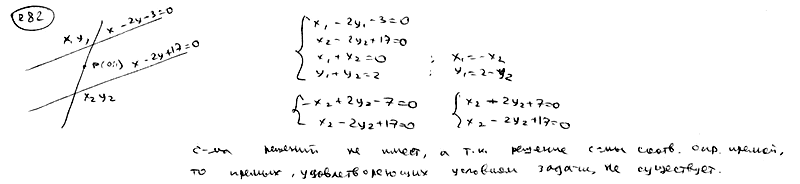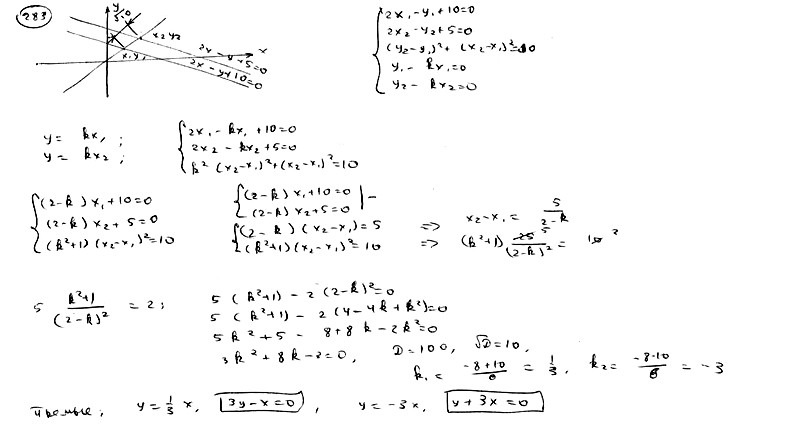Как найти уравнение стороны прямоугольника по координатам

Воспользуемся тем что прямая, которая проходит через точку $%(x_0;y_0)$% и параллельно прямой $%ax+by+c=0,$% имеет фурмулу $%a(x-x_0)+b(y-y_0)=0,$% а прямая, которая проходит через точку $%(x_0;y_0)$% и пепендикулярно прямой $%ax+by+c=0,$% имеет формулу $%b(x-x_0)-a(y-y_0)=0.$%

Точки $%(-2;1)$% и $%(5;7)$% находятся на разные стороны прямой $%2x+3y-6=0,$% значит точка$%(-2;1)$% принадлежит прямой, которая перпендикулярна $%2x+3y-6=0.$% уравнение этой стороны будет $%3(x+2)-2(y-1)=0 Leftrightarrow 3x-2y=-8.$%
А уравнение прямой которое проходит через точку $%(5;7)$% и перпендикулярно $%2x+3y-6=0,$% будет $% 3(x-5)-2(y-7)=0Leftrightarrow 3x-2y=1.$%

Параллельные прямие $%3x-2y=-8$% и $% 3x-2y=1$% пересекают ос $%Oy$% в точках $%(0;4)$% и $%(0;-0,5)$% расстояние которых $%4,5$%.По теореме Фалеса продолжение второй стороны которая параллельна $%3x-2y=-8,$% пересекает $%Oy$% в точке $%(0;-5)$%, следовательно её уравнение будет $%3x-2(y+5)=0Leftrightarrow 3x-2y=10.$%

Через точку $%(5;7)$% проведем еще одну вспомогательную прямую параллельно $%2x+3y-6=0,$%её уравнение $% 2(x-5)+3(y-7)=0Leftrightarrow 2x+3y=31.$%

Параллельные прямые $%2x+3y=6$% и $% 2x+3y=31$% пересекают ос $%Oy$% в точках $%(0;2)$% и $%(0;31/3)$% расстояние которых $%25/3$%.По теореме Фалеса продолжение второй стороны, которая параллельна $%2x+3y=6,$% пересекает $%Oy$% в точке $%(0;56/3)$%, следовательно её уравнение будет $%2x+3(y-56/3)=0Leftrightarrow 2x+3y=56.$%

Ответ. $% 3x-2y=-8,3x-2y=10,2x+3y=6,2x+3y=56$%

Задача 36077 Помогите, пожалуйста, с задачей. Даны.

Условие

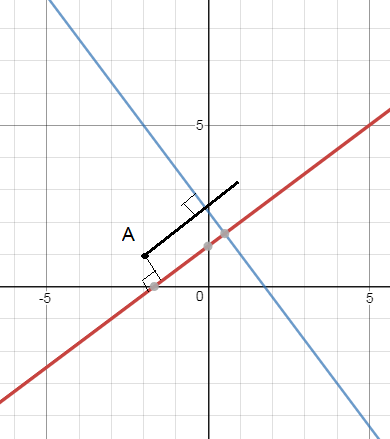
Помогите, пожалуйста, с задачей. Даны уравнения сторон прямоугольника 3х-4у+5=0, 4х+3у-7=0 и одна из его вершин А(-2;1). Составить уравнения двух других сторон прямоугольника.

Решение

Очевидно, что точка А не принадлежит ни одной из данных сторон, подставляем ее координаты в уравнение и убеждаемся, что координаты не удовлетворяют ни первому , ни второму уравнению
3*(-2)-4*1+5=0- неверно
4*(-2)+3*1-7=0 -неверно

Так как прямые
3х–4у+5=0 и 4х+3у–7=0
пересекаются под прямым углом, то дальнейшее решение видно из рисунка.
На рисунке проводим через точку А две прямые, перпендикулярные данным ( или параллельные данным как хотите)
Можно и так и так.

Находим уравнение прямой перпендикулярной
3х–4у+5=0
y=(3/4)x+(5/4)
k=3/4

Значит k=-4/3 — угловой коэффициент перпендикулярной прямой

y=(-4/3)x+b
Чтобы найти b подставляем координаты точки А
1=(-4/3)*2+b
b=11/3
y=(-4/3)x+(11/3)
[b]4x+3y-11=0[/b]

Находим уравнение прямой перпендикулярной
4х+3у–7=0
y=(-4/3)x+(7/3)
k=-4/3

Значит k=3/4 — угловой коэффициент перпендикулярной прямой

y=(3/4)x+b
Чтобы найти b подставляем координаты точки А
1=(3/4)*2+b
b=-1/2
y=(3/4)x+(-1/2)
[b]3x-4y-1=0[/b]

Уравнения сторон треугольника

Как составить уравнение сторон треугольника по координатам его вершин?

Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.

Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)

Составить уравнения сторон треугольника.

1) Составим уравнение прямой AB, проходящей через 2 точки A и B.

Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:

Таким образом, уравнение стороны AB

2) Прямая BC проходит через точки B(7;-4) и C(3;7):

Отсюда уравнение стороны BC —

3) Прямая AC проходит через точки A(-5;1) и C(3;7):

Прямоугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.

Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

• 1. Стороны прямоугольника являются его высотами.
• 2. Все углы прямоугольника прямые.
• 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
• 4. Диагонали прямоугольника равны.
• 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Диагональ прямоугольника

Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

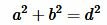(1)

Из равенства (1) найдем d:

.

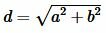(2)

Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:

Ответ:

Окружность, описанная около прямоугольника

Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника

Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.

Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть

( small R=frac<large d> <large 2>)

(3)

Подставляя (3) в (2), получим:

( small R=frac<large sqrt> <large 2>)

(4)

Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:

Ответ:

Периметр прямоугольника

Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Периметр прямоугольника вычисляется формулой:

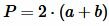(5)

где ( small a ) и ( small b ) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:

Ответ:

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

(6)

(7)

Из формулы (7) найдем ( small b ) и подставим в (6):

(8)

(9)

Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):

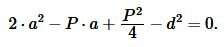(10)

Вычислим дискриминант квадратного уравнения (10):

Сторона прямоугольника вычисляется из следующих формул:

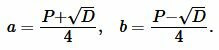(12)

После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

( frac< P><2>>d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*).

Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим , в (11):

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения и в формулу, получим:

Ответ: ,

Признаки прямоугольника

Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.

Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.

В общем виде прямоугольник , действительно задаётся (описывается системой четырёх уравнений , два из которых представляет собой прямые линии , параллельные оси ОХ , но с разными значениями ординат : у1 = a ,y2 = b , , а два уравнения параллельны оси ОУ . И также два эти уравнения отличаются только значениями абцисс : х1 = с , х2 = d .При таком задании стороны прямоугольника равны соответственно a-b ).(a>b) , и ( c-d ),(c>d). Отсюда зная параметры обоих сторон прямоугольника , найдём и периметр , и площадь прямоугольника.

Конечно , есть другие возможности описать уравнением прямоугольник.При этом описываются уравнения диагоналей , допустим.

210

Определить, какие из точек M₁(3; 1), M₂(2; 3), M₃(6; 3), M₄(-3;
-3), M₅(3; -1), M₆(-2; 1) лежат
на прямой и какие на ней не лежат. 211 Точки P₁,
P₂, P₃, P₄, P₅ расположены
на прямой ; их абсциссы соответственно равны
числам 4; 0; 2; -2; -6. Определить ординаты этих точек. 212 Точки Q₁,
Q₂, Q₃, Q₄, Q₅ расположены
на прямой ; их ординаты соответственно равны
числам 1; 0; 2; -1, 3. Определить абсциссы этих точек. 213 Определить точки
пересечения прямой с координатными
осями и построить эту прямую на чертеже. 214 Найти точку
пересечения двух прямых , . 215 Стороны АВ, ВС и АС
треугольника АВС даны соответственно
уравнениями , , . Определить
координаты его вершин. 216 Даны уравнения двух
сторон параллелограмма , и уравнение одной из
его диагоналей .
Определить координаты вершин
этого параллелограмма. 217 Стороны
треугольника лежат на прямых , , . Вычислить его площадь S. 218 Площадь
треугольника S=8, две его вершины суть точки А(1; -2),
В(2; 3), а третья вершина С лежит на прямой . Определить координаты вершины С. 219 Площадь
треугольника S=1,5, две его вершины суть точки А(2;
-3), В(3; -2), центр масс этого треугольника лежит на
прямой .
Определить координаты третьей
вершины С. 220 Составить
уравнение прямой и построить прямую на чертеже,
зная ее угловой коэффициент k и отрезок b,
отсекаемый ею на оси Oy: 220.1 k=2/3, b=3; 220.2 k=3, b=0; 220.3 k=0, b=-2; 220.4 k=-3/4, b=3; 220.5 k=-2, b=-5; 220.6 k=-1/3, b=2/3. 221 Определить угловой
коэффициент k и отрезок b, отсекаемый на оси Oy, для
каждой из прямых: 221.1 ; 221.2 ; 221.3 ; 221.4 ; 221.5 . 222 Дана прямая . Определить угловой коэффициент k
прямой: 222.1 Параллельной
данной прямой; 222.2 Перпендикулярно к
данной прямой. 223 Дана прямая . Составить уравнение прямой,
проходящей через точку М₀(2; 1): 223.1 Параллельно данной
прямой; 223.2 Перпендикулярно
данной прямой. 224 Даны уравнения двух
сторон прямоугольника , и одна из его вершин
А(2; -3). Составить уравнения двух других сторон
этого прямоугольника. 225 Даны уравнения двух
сторон прямоугольника , и уравнение одной из
его диагоналей .
Найти вершины прямоугольника. 226 Найти проекцию
точке Р(-5; 13) относительно прямой . 227 Найти точку Q,
симметричную точке Р(-5; 13) относительно прямой . 228 В каждом из
следующих случаев составить уравнение прямой,
параллельной двум данным прямым и проходящей
посередине между ними: 228.1 , ; 228.2 , ; 228.3 , ; 228.4 , ; 228.5 , . 229 Вычислить угловой
коэффициент k прямой, проходящей через две данные
точки: 229.1 M₁(2;
-5), M₂(3; 2); 229.2 P(-3, 1), Q(7; 8); 229.3 A(5; -3), B(-1; 6). 230 Составить
уравнения прямых, проходящих через вершины
треугольника A(5; -4), B(-1; 3), C(-3; -2) параллельно
противоположным сторонам. 231 Даны середины
сторон треугольника M₁(2; 1), M₂(5;
3), M₃(3; -4). Составить
уравнение его сторон. 232 Даны две точки P(2; 3),
Q(-1; 0). Составить уравнение прямой, проходящей
через точку Q перпендикулярно к отрезку . 233 Составить
уравнение прямой, если точка P(2; 3) служит
основанием перпендикуляра, опущенного из начала
координат на эту прямую. 234 Даны вершины
треугольника M₁(2; 1), M₂(-1; -1),
M₃(3; 2). Составить уравнения
его высот. 235 Стороны
треугольника даны уравнениями , , . Определить точку пересечения его
высот. 236 Даны вершины
треугольника A(1; -1), B(-2; 1), C(3; 5). Составить
уравнение перпендикуляра, опущенного из вершины
А на медиану, проведенную из вершины В. 237 Даны вершины
треугольника A(2; -2), B(3; -5), C(5; 7). Составить
уравнение перпендикуляра, опущенного из вершины
С на биссектрису внутреннего угла при вершине А. 238 Составить
уравнения сторон и медиан треугольника с
вершинами A(3; 2), B(5; -2), C(1; 0). 239 Через точки M₁(-1; 2), M₂(2; 3) проведена
прямая. Определить точки пересечения этой прямой
с осями координат. 240

Доказать,
что условие, при котором три точки M₁(x₁,
y₁), M₂(x₂, y₂), M₃(x₃,
y₃) лежат на одной прямой,
может быть записано в следующем виде:

241

Доказать,
что уравнение прямой, проходящей через две
данные точки M₁(x₁, y₁),
M₂(x₂, y₂), может
быть записано в следующем виде:

242 Даны
последовательные вершины выпуклого
четырехугольника A(-3; 1), B(3; 9), C(7; 6), D(-2; -6).
Определить точку пересечения его диагоналей. 243 Даны две смежные
вершины A(-3; -1), B(2; 2) параллелограмма ABCD и точка Q(3;
0) пересечения его диагоналей. Составить
уравнения сторон этого параллелограмма. 244 Даны уравнения двух
сторон прямоугольника , и уравнение его
диагонали . Составить уравнения остальных
сторон и второй диагонали этого прямоугольника. 245 Даны вершины
треугольника A(1; -2), B(5; 4), C(-2; 0). Составить
уравнения биссектрис его внутреннего и внешнего
углов при вершине А. 246 Составить
уравнение прямой, проходящей через точку P(3; 5) на
одинаковых расстояниях от точек A(-7; 3) и B(11; -15). 247 Найти проекцию
точки P(-8; 12) на прямую, проходящую через точки A(2;
-3), B(-5; 1). 248 Найти точку M₁, симметричную точке М₂(8;
-9) относительно прямой,
проходящей через точки А(3; -4), B(-1; -2). 249 На оси абсцисс
найти такую точку P, чтобы сумма ее расстояний до
точек M(1; 2), N(3; 4) была наименьшей. 250 На оси ординат
найти такую точку P, чтобы сумма ее расстояний до
точек M(-3; 2), N(2; 5) была наибольшей. 251 На прямой найти такую точку Р, сумма
расстояний которой до точек A(-7; 1), B(-5; 5) была бы
наименьшей. 252 На прямой найти такую точку Р, разность
расстояний которой до точек A(4; 1), B(0; 4) была бы
наибольшей. 253 Определить угол между двумя прямыми: 253.1 , ; 253.2 , ; 253.3 , ; 253.4 , . 254 Дана прямая . Составить уравнение прямой,
проходящей через точку M₀(2; 1) под углом 45⁰ к данной прямой. 255 Точка А(-4; 5)
является вершиной квадрата, диагональ которого
лежит на прямой . Составить
уравнения сторон и второй диагонали этого
квадрата. 256 Даны две
противоположные вершины квадрата A(-1; 3), C(6; 2).
Составить уравнения его сторон. 257 Точка E(1; -1) является
центром квадрата, одна из сторон которого лежит
на прямой . Составить уравнения
прямых, на которых лежат остальные стороны этого
квадрата. 258 Из точки M₀(-2; 3) под углом к оси
Ox направлен луч света. Известно, что . Дойдя
до оси Ox, луч от нее отразился. Составить
уравнения прямых, на которых лежат падающий и
отраженный лучи. 259 Луч света направлен
по прямой , луч от нее отразился.
Составить уравнение прямой, на которой лежит
отраженный луч. 260 Даны уравнения
сторон треугольника , , . Доказать, что этот треугольник
равнобедренный. Решить задачу при помощи
сравнения углов треугольника. 261 Доказатть, что
уравнение прямой, проходящей через точку M₁(x₁; y₁) параллельно
прямой , может быть записано в виде . 262 Составить
уравнение прямой, проходящей через точку М₁(2: -3) параллельно
прямой: 262.1 ; 262.2 ; 262.3 ; 262.4 ; 262.5 . 263 Доказать, что
условие перпендикулярности прямых ; может быть записано
в следующем виде: . 264 Установить, какие
из следующих пар прямых перпендикулярны. Решить
задачу, не вычисляя угловых коэффициентов данных
прямых. 264.1  , ; 264.2 , ; 264.3 , ; 264.4 , ; 264.5 , ; 264.6 , . 265

Доказать,
что формула для определения угла между
прямыми , может
быть записана в следующей форме:

266 Определить угол , образованный двумя прямыми. Решить
задачу, не вычисляя угловых коэффициентов данных
прямых. 266.1 , ; 266.2  , ; 266.3  , . 267 Даны две вершины
треугольника M₁(-10; 2), M₂(6; 4);
его высоты пересекаются в точке
N(5; 2). Определить координаты третьей вершины M₃. 268 Даны две вершины A(3;
-1), B(5; 7) треугольника ABC и точка N(4; -1) пересечения
его высот. Составить уравнения сторон этого
треугольника. 269 В треугольнике АВС
даны: уравнение стороны АВ: , уравнения
высот АМ: и BN: . Составить уравнения двух
других сторон и третьей высоты этого
треугольника. 270 Составить
уравнения сторон треугольника АВС, если даны
одна из его вершина А(1; 3) и уравнения двух медиан , . 271 Составить
уравнения сторон треугольника, сли даны одна из
его вершин B(-4; -5) и уравнения двух высот , . 272 Составить
уравнения сторон треугольника, зная одну из его
вершин A(4; -1) и уравнения двух биссектрис , . 273 Составить
уравнения сторон треугольника, зная одну из его
вершин B(2; 6), а также уравнения высоты и
биссектрисы , проведенных из одной вершины. 274 Составить
уравнения сторон треугольника, зная одну его
вершину B(2; -1), а также уравнения высоты и биссектрисы , проведенных из
различных вершин. 275 Составить
уравнения сторон треугольника, зная одну его
вершину C(4; -1), а также уравнения высоты и медианы , проведенной из
одной вершины. 276 Составить
уравнения сторон треугольника, зная одну его
вершину B(2; -7), а также уравнения высоты и медианы , проведенных из
различных вершин. 277 Составить
уравнения сторон треугольника, зная одну его
вершину C(4; 3), а также уравнения биссектрисы и медианы , проведенных из
одной вершины. 278 Составить
уравнения сторон треугольника, зная одну его
вершину A(3; -1), а также уравнения биссектрисы и медианы , проведенных из
различных вершин. 279 Составить
уравнение прямой, которая проходит черезначало
координат и вместе с прямыми , образует
треугольник с площадью, равной 1,5. 280 Среди прямых,
проходящих через точку P(3; 0), найти такую, отрезок
которой, заключенный между прямыми , , делится в точке Р
пополам. 281 Через точку Р(-3; -1)
проведены всевозможные прямые. Доказать, что
отрезок каждой из них, заключенный между прямыми , , делится
в точке Р пополам. 282 Через точку Р(0; 1)
проведены всевозможные прямые. Доказать, что
среди них нет прямой, отрезок которой,
заключенный между прямыми , , делился бы в точке Р
пополам. 283 Составить
уравнение прямой, проходящей через начало
координат, зная, что длина ее отрезка,
заключенного между прямыми , , равна . 284 Составить
уравнение прямой, проходящей через точку С(-5; 4),
зная, что длина ее отрезка, заключенного между
прямыми , , равна 5.

210

Определить,
какие из точек M₁(3;
1), M₂(2;
3), M₃(6;
3), M₄(-3;
-3), M₅(3;
-1), M₆(-2;
1) лежат на прямой
и
какие на ней не лежат.

211

Точки
P₁,
P₂,
P₃,
P₄,
P₅
расположены на прямой
;
их абсциссы соответственно равны
числам 4; 0; 2; -2; -6. Определить ординаты
этих точек.

212

Точки
Q₁,
Q₂,
Q₃,
Q₄,
Q₅
расположены на прямой
;
их ординаты соответственно равны
числам 1; 0; 2; -1, 3. Определить абсциссы
этих точек.

213

Определить
точки пересечения прямой
с
координатными осями и построить эту
прямую на чертеже.

214

Найти
точку пересечения двух прямых
,.

215

Стороны
АВ, ВС и АС треугольника АВС даны
соответственно уравнениями
,,.
Определить координаты его вершин.

216

Даны
уравнения двух сторон параллелограмма
,и
уравнение одной из его диагоналей.
Определить координаты вершин этого
параллелограмма.

217

Стороны
треугольника лежат на прямых
,,.
Вычислить его площадь S.

218

Площадь
треугольника S=8, две его вершины суть
точки А(1; -2), В(2; 3), а третья вершина С
лежит на прямой
.
Определить координаты вершины С.

219

Площадь
треугольника S=1,5, две его вершины суть
точки А(2; -3), В(3; -2), центр масс этого
треугольника лежит на прямой
.
Определить координаты третьей вершины
С.

220

Составить
уравнение прямой и построить прямую
на чертеже, зная ее угловой коэффициент
k и отрезок b, отсекаемый ею на оси Oy:

220.1

k=2/3,
b=3;

220.2

k=3,
b=0;

220.3

k=0,
b=-2;

220.4

k=-3/4,
b=3;

220.5

k=-2,
b=-5;

220.6

k=-1/3,
b=2/3.

221

Определить
угловой коэффициент k и отрезок b,
отсекаемый на оси Oy, для каждой из
прямых:

221.1

;

221.2

;

221.3

;

221.4

;

221.5

.

222

Дана
прямая
.
Определить угловой коэффициент k
прямой:

222.1

Параллельной
данной прямой;

222.2

Перпендикулярно
к данной прямой.

223

Дана
прямая
.
Составить уравнение прямой, проходящей
через точку М₀(2;
1):

223.1

Параллельно
данной прямой;

223.2

Перпендикулярно
данной прямой.

224

Даны
уравнения двух сторон прямоугольника
,и
одна из его вершин А(2; -3). Составить
уравнения двух других сторон этого
прямоугольника.

225

Даны
уравнения двух сторон прямоугольника
,и
уравнение одной из его диагоналей.
Найти вершины прямоугольника.

226

Найти
проекцию точке Р(-5; 13) относительно
прямой
.

227

Найти
точку Q, симметричную точке Р(-5; 13)
относительно прямой
.

228

В
каждом из следующих случаев составить
уравнение прямой, параллельной двум
данным прямым и проходящей посередине
между ними:

228.1

,
;

228.2

,
;

228.3

,
;

228.4

,
;

228.5

,
.

229

Вычислить
угловой коэффициент k прямой, проходящей
через две данные точки:

229.1

M₁(2;
-5), M₂(3;
2);

229.2

P(-3,
1), Q(7; 8);

229.3

A(5;
-3), B(-1; 6).

230

Составить
уравнения прямых, проходящих через
вершины треугольника A(5; -4), B(-1; 3), C(-3;
-2) параллельно противоположным
сторонам.

231

Даны
середины сторон треугольника M₁(2;
1), M₂(5;
3), M₃(3;
-4). Составить уравнение его сторон.

232

Даны
две точки P(2; 3), Q(-1; 0). Составить уравнение
прямой, проходящей через точку Q
перпендикулярно к отрезку
.

233

Составить
уравнение прямой, если точка P(2; 3)
служит основанием перпендикуляра,
опущенного из начала координат на эту
прямую.

234

Даны
вершины треугольника M₁(2;
1), M₂(-1;
-1), M₃(3;
2). Составить уравнения его высот.

235

Стороны
треугольника даны уравнениями
,,.
Определить точку пересечения его
высот.

236

Даны
вершины треугольника A(1; -1), B(-2; 1), C(3;
5). Составить уравнение перпендикуляра,
опущенного из вершины А на медиану,
проведенную из вершины В.

237

Даны
вершины треугольника A(2; -2), B(3; -5), C(5;
7). Составить уравнение перпендикуляра,
опущенного из вершины С на биссектрису
внутреннего угла при вершине А.

238

Составить
уравнения сторон и медиан треугольника
с вершинами A(3; 2), B(5; -2), C(1; 0).

239

Через
точки M₁(-1;
2), M₂(2;
3) проведена прямая. Определить точки
пересечения этой прямой с осями
координат.

240

Доказать,
что условие, при котором три точки
M₁(x₁,
y₁),
M₂(x₂,
y₂),
M₃(x₃,
y₃)
лежат на одной прямой, может быть
записано в следующем виде:

241

Доказать,
что уравнение прямой, проходящей через
две данные точки M₁(x₁,
y₁),
M₂(x₂,
y₂),
может быть записано в следующем виде:

242

Даны
последовательные вершины выпуклого
четырехугольника A(-3; 1), B(3; 9), C(7; 6), D(-2;
-6). Определить точку пересечения его
диагоналей.

243

Даны
две смежные вершины A(-3; -1), B(2; 2)
параллелограмма ABCD и точка Q(3; 0)
пересечения его диагоналей. Составить
уравнения сторон этого параллелограмма.

244

Даны
уравнения двух сторон прямоугольника
,и
уравнение его диагонали.
Составить уравнения остальных сторон
и второй диагонали этого прямоугольника.

245

Даны
вершины треугольника A(1; -2), B(5; 4), C(-2;
0). Составить уравнения биссектрис его
внутреннего и внешнего углов при
вершине А.

246

Составить
уравнение прямой, проходящей через
точку P(3; 5) на одинаковых расстояниях
от точек A(-7; 3) и B(11; -15).

247

Найти
проекцию точки P(-8; 12) на прямую,
проходящую через точки A(2; -3), B(-5; 1).

248

Найти
точку M₁,
симметричную точке М₂(8;
-9) относительно прямой, проходящей
через точки А(3; -4), B(-1; -2).

249

На
оси абсцисс найти такую точку P, чтобы
сумма ее расстояний до точек M(1; 2), N(3;
4) была наименьшей.

250

На
оси ординат найти такую точку P, чтобы
сумма ее расстояний до точек M(-3; 2),
N(2; 5) была наибольшей.

251

На
прямой
найти
такую точку Р, сумма расстояний которой
до точек A(-7; 1), B(-5; 5) была бы наименьшей.

252

На
прямой
найти
такую точку Р, разность расстояний
которой до точек A(4; 1), B(0; 4) была бы
наибольшей.

253

Определить
угол
между
двумя прямыми:

253.1

,
;

253.2

,
;

253.3

,
;

253.4

,
.

254

Дана
прямая
.
Составить уравнение прямой, проходящей
через точку M₀(2;
1) под углом 45⁰
к данной прямой.

255

Точка
А(-4; 5) является вершиной квадрата,
диагональ которого лежит на прямой
.
Составить уравнения сторон и второй
диагонали этого квадрата.

256

Даны
две противоположные вершины квадрата
A(-1; 3), C(6; 2). Составить уравнения его
сторон.

257

Точка
E(1; -1) является центром квадрата, одна
из сторон которого лежит на прямой
.
Составить уравнения прямых, на которых
лежат остальные стороны этого квадрата.

258

Из
точки M₀(-2;
3) под углом
к
оси Ox направлен луч света. Известно,
что.
Дойдя до оси Ox, луч от нее отразился.
Составить уравнения прямых, на которых
лежат падающий и отраженный лучи.

259

Луч
света направлен по прямой
,
луч от нее отразился. Составить
уравнение прямой, на которой лежит
отраженный луч.

260

Даны
уравнения сторон треугольника
,,.
Доказать, что этот треугольник
равнобедренный. Решить задачу при
помощи сравнения углов треугольника.

261

Доказатть,
что уравнение прямой, проходящей через
точку M₁(x₁;
y₁)
параллельно прямой
,
может быть записано в виде.

262

Составить
уравнение прямой, проходящей через
точку М₁(2:
-3) параллельно прямой:

262.1

;

262.2

;

262.3

;

262.4

;

262.5

.

263

Доказать,
что условие перпендикулярности прямых
;может
быть записано в следующем виде:.

264

Установить,
какие из следующих пар прямых
перпендикулярны. Решить задачу, не
вычисляя угловых коэффициентов данных
прямых.

264.1

 ,
;

264.2

,
;

264.3

,
;

264.4

,
;

264.5

,
;

264.6

,
.

265

Доказать,
что формула для определения угла
между
прямыми,может
быть записана в следующей форме:

266

Определить
угол
,
образованный двумя прямыми. Решить
задачу, не вычисляя угловых коэффициентов
данных прямых.

266.1

,
;

266.2

 ,
;

266.3

 ,
.

267

Даны
две вершины треугольника M₁(-10;
2), M₂(6;
4); его высоты пересекаются в точке
N(5; 2). Определить координаты третьей
вершины M₃.

268

Даны
две вершины A(3; -1), B(5; 7) треугольника
ABC и точка N(4; -1) пересечения его высот.
Составить уравнения сторон этого
треугольника.

269

В
треугольнике АВС даны: уравнение
стороны АВ:
,
уравнения высот АМ:и
BN:.
Составить уравнения двух других сторон
и третьей высоты этого треугольника.

270

Составить
уравнения сторон треугольника АВС,
если даны одна из его вершина А(1; 3) и
уравнения двух медиан
,.

271

Составить
уравнения сторон треугольника, сли
даны одна из его вершин B(-4; -5) и уравнения
двух высот
,.

272

Составить
уравнения сторон треугольника, зная
одну из его вершин A(4; -1) и уравнения
двух биссектрис
,.

273

Составить
уравнения сторон треугольника, зная
одну из его вершин B(2; 6), а также уравнения
высоты
и
биссектрисы,
проведенных из одной вершины.

274

Составить
уравнения сторон треугольника, зная
одну его вершину B(2; -1), а также уравнения
высоты
и
биссектрисы,
проведенных из различных вершин.

275

Составить
уравнения сторон треугольника, зная
одну его вершину C(4; -1), а также уравнения
высоты
и
медианы,
проведенной из одной вершины.

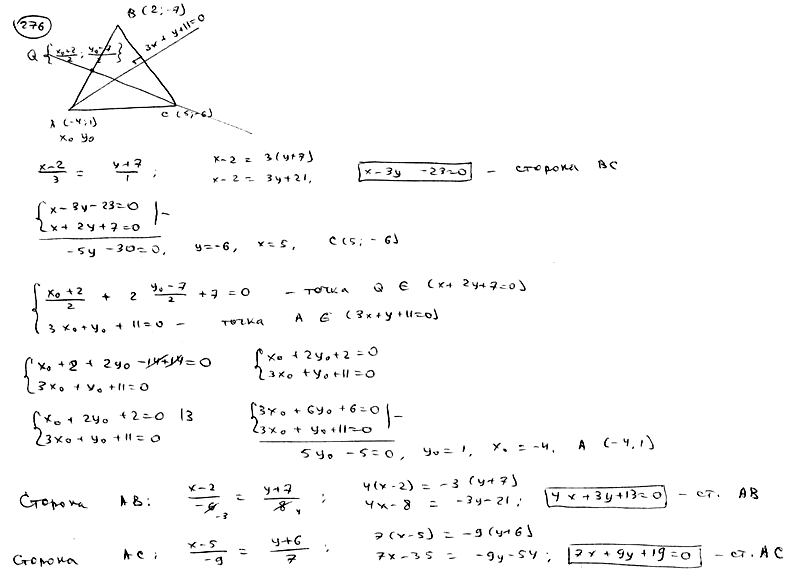
276

Составить
уравнения сторон треугольника, зная
одну его вершину B(2; -7), а также уравнения
высоты
и
медианы,
проведенных из различных вершин.

277

Составить
уравнения сторон треугольника, зная
одну его вершину C(4; 3), а также уравнения
биссектрисы
и
медианы,
проведенных из одной вершины.

278

Составить
уравнения сторон треугольника, зная
одну его вершину A(3; -1), а также уравнения
биссектрисы
и
медианы,
проведенных из различных вершин.

279

Составить
уравнение прямой, которая проходит
черезначало координат и вместе с
прямыми
,образует
треугольник с площадью, равной 1,5.

280

Среди
прямых, проходящих через точку P(3; 0),
найти такую, отрезок которой, заключенный
между прямыми
,,
делится в точке Р пополам.

281

Через
точку Р(-3; -1) проведены всевозможные
прямые. Доказать, что отрезок каждой
из них, заключенный между прямыми
,,
делится в точке Р пополам.

282

Через
точку Р(0; 1) проведены всевозможные
прямые. Доказать, что среди них нет
прямой, отрезок которой, заключенный
между прямыми
,,
делился бы в точке Р пополам.

283

Составить
уравнение прямой, проходящей через
начало координат, зная, что длина ее
отрезка, заключенного между прямыми
,,
равна.

284

Составить
уравнение прямой, проходящей через
точку С(-5; 4), зная, что длина ее отрезка,
заключенного между прямыми
,,
равна 5.