Сторона ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти длину стороны ромба по известным элементам. Для нахождения стороны ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Открыть онлайн калькулятор
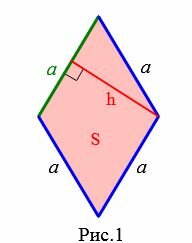
1. Сторона ромба через высоту и площадь
Пусть известны площадь и высота ромба (Рис.1).
Покажем, что сторона ромба через высоту и площадь вычисляется формулой
| (small a=frac<large S><large h>.) | (1) |
Формула площади ромба через сторону и высоту имеет следующий вид:
Откуда легко вывести формулу (1).
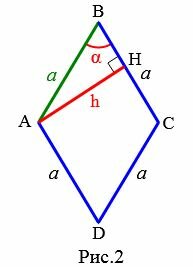
2. Сторона ромба через высоту и угол
Рассмотрим ромб с высотой h и углом α между сторонами (Рис.2). Выведем формулу вычисления стороны ромба через высоту и угол.
Для прямоугольного треугольника AHB применим теорему синусов:
(small frac<large a><large sin 90°>=frac<large h><large sin alpha>.)
Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:
| (small a=frac<large h><large sin alpha>.) | (2) |
Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: (small angle C=180°-alpha.) Следовательно (small sin angle C=sin(180°-alpha)=sin alpha.) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.
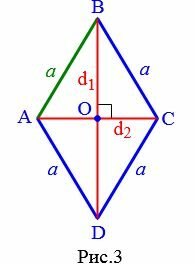
3. Сторона ромба через диагонали
Выведем формулу вычисления сторон ромба через диагонали.
Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).
Применим к прямоугольному треугольнику AOB теорему Пифагора:
(small a^2= left( frac<large d_1> <large 2>right)^2+left( frac<large d_2> <large 2>right)^2.)
| (small a= frac<sqrt<large d_1^2+d_2^2>> <large 2>) | (3) |
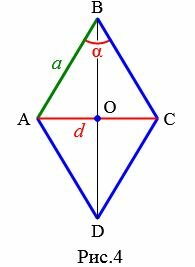
4. Сторона ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления сторон ромба.
Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Кроме этого, диагонали ромба делят углы ромба пополам. Применим теорему синусов для прямоугольного треугольника AOB:
Откуда получим формулу стороны ромба через угол и противолежащую диагональ:
| (small a=frac<large d><large 2 cdot sin frac< alpha>< 2>>.) | (4) |
Формулу (4) можно записать и в другом виде, применяя формулу синуса половинного угла:
| (small sin frac< alpha>< 2>=sqrt<frac<large 1-cos alpha><large 2 >>.) | (5) |
Подставляя (5) в (4), получим:
(small a=frac<large d><large 2 cdot sqrt<frac<large 1-cos alpha><large 2 >>>.)
| (small a=large frac< d>< sqrt< 2-2 cdot cos alpha>>.) | (6) |
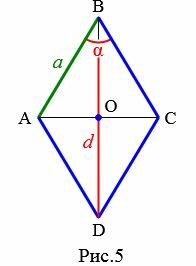
5. Сторона ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.
Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Для прямоугольного треугольника AOB, имеем:
| (small frac<large OB > <large a>=cos angle ABO.) | (7) |
Учитывая, что ( small BO=frac<large d><large 2>) и ( small angle ABO=frac<large alpha><large 2>), формулу (13) можно записать так:
(small frac< large frac<large d > <large 2>><large a>= cos frac<large alpha> <large 2>.)
| (small a=frac<large d><large 2 cdot cos large frac< alpha>< 2>>.) | (8) |
Формулу (8) можно записать и в другом виде, применяя формулу косинуса половинного угла:
| (small cos frac< alpha>< 2>=sqrt<frac<large 1+cos alpha><large 2 >>.) | (9) |
Подставляя (9) в (8), получим:
(small a=frac<large d><large 2 cdot sqrt<frac<large 1+cos alpha><large 2 >>>.)
| (small a=large frac< d>< sqrt< 2+2 cdot cos alpha>>.) | (10) |
6. Сторона ромба через площадь и радиус вписанной в ромб окружности
В статье Площадь ромба показали, что площадь ромба через сторону и радиус вписанной в ромб окружности вычисляется формулой
| (small S= 2 cdot a cdot r.) | (11) |
Из формулы (11) получим:
| ( small a=frac<large S> <large 2 cdot r>) | (12) |
7. Сторона ромба через площадь и угол
В статье Площадь ромба показали, что площадь ромба через сторону и угол вычисляется формулой
| (small S= a^2 cdot sin alpha.) | (13) |
Из формулы (13) найдем a:
| ( small a=frac<large S> <large sin alpha>) | (14) |
Получили формулу сторон ромба через площадь и угол.
Электронная библиотека
Пример 1. Вычислить координаты вершин ромба, если известны уравнения двух его сторон: и и уравнение одной из его диагоналей: . Решение. Выясним взаимное расположение известных сторон ромба. Угловой коэффициент k прямой определяется по формуле:
Стороны параллельны, так как имеют одинаковый угловой коэффициент:
Для построения рисунка (рис. 4.1) запишем уравнения в отрезках для данных прямых:
Наметим план решения: 1) находим вершины ромба P и Q ; 2) находим точку пересечения диагоналей ромба N ; 3) через точку N проводим диагональ D 2 ; 4) находим оставшиеся вершины ромба R и S .1) Так как точка P является точкой пересечения прямых L 2 и D 1 , то ее координаты находим из системы уравнений:
Из рис. 4.1 сразу находим координаты точки Q (- 2, 0) . 2) Так как диагонали ромба в точке пересечения делятся пополам, то точка является серединой отрезка PQ , поэтому ее координаты — полусумма соответствующих координат точек P и Q :
3) Так как диагонали ромба взаимно перпендикулярны, то прямая D 2 перпендикулярна вектору . Найдем его координаты:
По формуле (3.1) находим уравнение диагонали D 2 как уравнение прямой, проходящей через точку N (- 3, 1) перпендикулярно вектору = <2; — 2>:
2( x — (- 3)) + (- 2)( y — 1) = 0, x — y + 4 = 0.
4) Вершины ромба R и S — точки пересечения прямых L 2 и D 2 , L 1 и D 2 , соответственно, находим из уравнений:
Ответ: P (- 4, 2) R (- 6, — 2), Q (- 2, 0), S (0, 4).
Пример 2. Составить уравнения сторон треугольника, зная одну его вершину P (2, — 7), уравнения высоты 3 x + y + 11 = 0 и медианы x + 2 y + 7 = 0, проведенных из разных вершин. Решение. Для построения рисунка (рис. 4.2) приведем уравнения данных прямых к уравнениям в отрезках:
h : 3 x + y + 11 = 0, m : x + 2 y + 7 = 0 ,
План решения:1) находим уравнение прямой PQ ;2) находим координаты точки R ;3) находим уравнения прямых RP и RQ .1) Находим нормальный вектор прямой h : . Уравнение стороны PQ , проходящей через точку P (2, — 7) параллельно вектору , запишем в виде:
Находим координаты точки Q — точки пересечения прямых PQ и m :
2) По свойству медианы треугольника PQR точка S ( x S , y S ) является серединой отрезка RP . Следовательно:
Точка S лежит на медиане m , значит,
Точка R лежит на высоте h , значит,
Из последних двух уравнений определяем координаты точки R , решая систему: 3) Используя формулу (3.4), составим уравнение прямой RP , проходящей через две заданные точки R и P : Аналогично, составим уравнение прямой RQ : Ответ: x — 3 y — 23 = 0, ,
как составить уравнения сторон ромба.
как составить уравнения сторон ромба ABCD и найти его площадь, если известны уравнения сторон AB u BC и координаты вершины Д.
АВ: 2x+y-2=0
BC: 2x-y-2=0
D(4,2)
составить уравнение прямой проходящей через точку А, перпендикулярно к плоскости, которая проходит через точки А, В и С.
А (0,-1,0) В (2,1,-2) С (1,4,1)
Найти точку пересечения плоскости ХОУ и прямой проходящей через точки А и В.
А (-9,7,-2) В (-11,2,3)
найти проекцию точки А на прямую, заданную как пересечение двух плоскостей.
А (-2,1,-1)
1: x+4y+2z-3=0
2: 2x+5y+z=0
найти радиус и координаты центра окружности, заданной уравнением:
x^2+y^2+6x-8y=0
4. приведи к виду (x-a)^2 + (y-b)^2 = r^2, тогда А и В — координаты центра,
http://libraryno.ru/4-3-pryamaya-na-ploskosti-algandgeom/
http://sprashivalka.com/tqa/q/7177995
We can use parallel vector properties and similitude shrink ratio $sigma$ for entire figure of rhombus of 4 lines built around the origin $O$. Let vertices of rhombus be
$$O(9,0),quad A(3,4),quad B(5,12),quad D(3+5=8, 4+12=16);$$
Diagonal length is $sqrt{8^2+16^2}={8sqrt5} $ and scale-down ratio $sigma= dfrac{12}{8sqrt5} =dfrac{3}{2sqrt 5} $
Equations of lines $ (OA,OB)$
$$ dfrac{y-16}{x-8}=dfrac{12}{5},quaddfrac{y-16}{x-8}=dfrac{4}{3}, $$
and corresponding outer parallel scaled lines $ (DB,DA)$ become
$$ dfrac{y-16sigma}{x-8sigma}=dfrac{12}{5},quaddfrac{y-16sigma}{x-8sigma}=dfrac{4}{3}. $$
which can be further simplified.
Next we find perpendicular bisector of new shortened $OD$ to find points of intersection with old/given line equations of $(OA,OB);$ the slopes do not change but the constant term $y-$ intercept changes.
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Найти уравнения сторон ромба по двум вершинам и прямой
|
|||
|
Точки А(4;5) и С(2;-1) являются двумя противоположными вершинами ромба, а прямая x-y+1=0 одной из его сторон. Найти уравнения остальных сторон ромба.
|
||
| Вернуться к началу |
|
||
|
olya-kolbasova |
Заголовок сообщения: Re: Найти уравнения сторон
|
|
Как определить то, если ничего не сказано!
|
|
| Вернуться к началу |
|
|
olya-kolbasova |
Заголовок сообщения: Re: Найти уравнения сторон
|
|
Так получается точка А принадлежит прямой! А дальше что?
|
|
| Вернуться к началу |
|
|
Alexdemath |
Заголовок сообщения: Re: Найти уравнения сторон
|
|
olya-kolbasova Так так точки [math]A,B[/math] — противоположные вершины ромба, то, следовательно, они лежат на одной диагонали. Для отыскания уравнение второй диагонали воспользуйтесь тем, что диагонали ромба пересекаются под прямым углом. А ещё можно вспомнить, что диагонали ромба являются его биссектрисами.
|
|
| Вернуться к началу |
|
| За это сообщение пользователю Alexdemath «Спасибо» сказали: mad_math |
|
|
olya-kolbasova |
Заголовок сообщения: Re: Найти уравнения сторон ромба по двум вершинам и прямой
|
|
как я могу найти уравнение диагонали по двум точкам, если я знаю только 1 это точка А, а точка В не известна! И для чего нужны вообще диагонали, если мне нужны уравнения сторон ромба!
|
|
| Вернуться к началу |
|
|
olya-kolbasova |
Заголовок сообщения: Re: Найти уравнения сторон ромба по двум вершинам и прямой
|
|
Всё понятно, ну найду я две диагонали, а дальше что?
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти уравнении остальных сторон ромба
в форуме Аналитическая геометрия и Векторная алгебра |
focus |
1 |
274 |
24 мар 2017, 15:35 |
|
Найти уравнение второй диагонали ромба и сторон
в форуме Аналитическая геометрия и Векторная алгебра |
butoxors |
4 |
920 |
01 янв 2015, 19:31 |
|
Составить уравнение прямой по вершинам
в форуме Аналитическая геометрия и Векторная алгебра |
hahaha1 |
1 |
151 |
03 дек 2018, 22:13 |
|
Уравнение прямой, перпендикулярной двум заданным
в форуме Аналитическая геометрия и Векторная алгебра |
Tsvirotka |
4 |
817 |
12 окт 2018, 19:50 |
|
Найти уравнения сторон параллелограмма
в форуме Аналитическая геометрия и Векторная алгебра |
lanvandance |
3 |
495 |
05 ноя 2018, 18:17 |
|
Найти уравнения сторон треугольника
в форуме Аналитическая геометрия и Векторная алгебра |
yol145 |
19 |
1273 |
10 ноя 2015, 16:34 |
|
Найти уравнения сторон треугольника
в форуме Аналитическая геометрия и Векторная алгебра |
andreta |
16 |
2101 |
22 дек 2013, 22:41 |
|
Даны уравнения сторон, найти точку пересечения медиан
в форуме Линейная и Абстрактная алгебра |
dora77 |
7 |
210 |
26 фев 2021, 20:44 |
|
По вершинам пирамиды найти всё
в форуме Аналитическая геометрия и Векторная алгебра |
Ksusha++ |
1 |
294 |
18 ноя 2014, 14:26 |
|
Найти корд-ы вершины треугольника по другим вершинам
в форуме Геометрия |
vlad_miloslavskij |
1 |
115 |
06 фев 2020, 21:01 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 3 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Основные
методы составления уравнений прямых
наглядно можно продемонстрировать на
примере построения уравнений линейных
элементов треугольника .
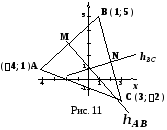
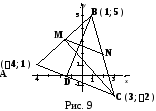
Пример15.
Треугольник
задан координатами своих вершин:
,
и
(Рис. 9)
Найти:
-
м
едиану
;
-
среднюю
линию
;
-
высоту
;
-
биссектрису
;
-
центр
описанной окружности.
Решение.
-
Найдем
медиану
.
Вычислим координаты точки
середины отрезка
.
.
Уравнениенайдем
по двум точкам:
.
-
Найдем
среднюю линию
.
Способ
1. Вычислим
координаты середины стороны
точки
.
.
Уравнениенайдем по двум точкам:
.
Способ
2. Найдем
по
точкеи направляющему вектору, в качестве
которого можно взять вектор.
Вычислим:
.
Тогда:
Очевидно,
что для
получилось то же уравнение, что и при
первом способе.
-
Уравнение
высоты
найдем по точке и перпендикулярному
вектору, в качестве которого можно
взять вектор.
.
-
Биссектрису
можно найти разными способами (Рис.
10). Но, если числовые данные в задаче
специально не подобраны, то все эти
способы приводят к громоздким
вычислениям. Наиболее легким для
запоминания является способ, основанный
на следующем факте:
в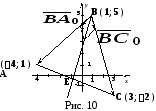
суммы векторов одинаковой длины идет
в точности по биссектрисе угла,
образованного этими векторами (свойство
ромба).
Поскольку
требуется найти биссектрису угла
,
то возьмем два вектора, исходящих именно
из этой вершины:и
.
Вычислим их длины:
;
.
Очевидно,
что их длины не равны. А теперь от
векторов
и
перейдем к их ортам
и
,
векторам с тем же направлением, но
одинаковой единичной длины.
;
.
Построим
новый вектор
.
Этот
вектор уже можно использовать в качестве
направляющего для биссектрисы, но
работать с ним нелегко. Вместо него
можно взять другой вектор, попроще.
Корни,
конечно, никуда не исчезли, но, по крайней
мере, не стало дробей.
По
формуле (9) имеем:
Если
Вам не нравится отрицательный коэффициент
при
,
умножьте все уравнение на (1
):
-
Найдем
центр окружности, описанной вокруг
треугольника
.
Он,
как известно, находится в точке
пересечения любых двух серединных
перпендикуляров треугольника
(Рис.11)..
Поскольку ранее
были найдены координаты середин сторон
и
,
найдем уравнения серединных перпендикуляров
именно к этим сторонам:и
.
Для
имеем:
|
точка
|
|
Для
имеем:
|
точка
|
|
Найдем
точку пересечения полученных серединных
перпендикуляров:
и
Воспользуемся
формулами Крамера:
;
;
.
;
Задачи
для самостоятельного решения
-
Известны уравнения двух сторон ромба ,и уравнение одной из его диагоналей. Составить уравнение второй диагонали.Ответ: .
-
Известны
уравнения двух сторон ромба
,
и уравнение одной из его диагоналей
.
Составить уравнение второй
диагонали.Ответ:.
-
Даны
уравнения двух сторон параллелограмма
,
и точка пересечения его диагоналей
.
Найти уравнения двух других сторон.
Ответ:,
.
-
Даны
вершины треугольника
,
и
.
Составить уравнение перпендикуляра,
опущенного из вершинына
биссектрису внутреннего угла при
вершине.Ответ:
.
-
Найти
точку
,
симметричную точкеотносительно прямой, проходящей
через точкии
.
Ответ:.
-
Точки
и
являются
противоположными вершинами квадрата.
Определить координаты двух других
вершин квадрата.
Ответ:и
-
Найти прямые,
принадлежащие пучку
и
перпендикулярные основным прямым
пучка.
Ответ: ,
.
-
Даны стороны
треугольника:
;
и
.
Составить уравнения медианы ,
проходящей через вершину,
и высоты, проходящей через вершину.Ответ:
,
.
-
Составить
уравнения трех сторон квадрата, если
известно, что четвертой стороной
являются отрезок прямой
,
концы которого лежат на осях координат.
Ответ: ,
,
или
.
-
Доказать,
что четырехугольник с вершинами
,
,
и
–
трапеция. Найти точку пересечения
средней линии трапеции и высоты,
опущенной из вершины С на сторону
.
Ответ:
-
Вершины
четырехугольника:
,
,
,
.
Доказать, что этот четырехугольник
ромб. Найти точку пересечения
перпендикуляра из вершины
на
сторонус прямой, проходящей через вершину
и середину.
Ответ:
-
Даны
три из четырёх вершин трапеции
:
.
Известно, что диагонали трапеции
взаимно перпендикулярны. Найти
координаты вершиныэтой трапеции.
Ответ:
ГЛАВА
2. Плоскость
§
1 Вступление
В
аналитической геометрии плоскость
это геометрическое множество точек в
пространстве, координаты которых
удовлетворяют уравнению
.
общее уравнение
плоскости;
уравнение
плоскости в отрезках,
где
абсцисса точки пересечения плоскости
с
осью;
ордината точки пересечения
с
осью,
ааппликата точки
пересеченияс
осью.
§
2 Вывод уравнения плоскости при разных
способах
ее задания.
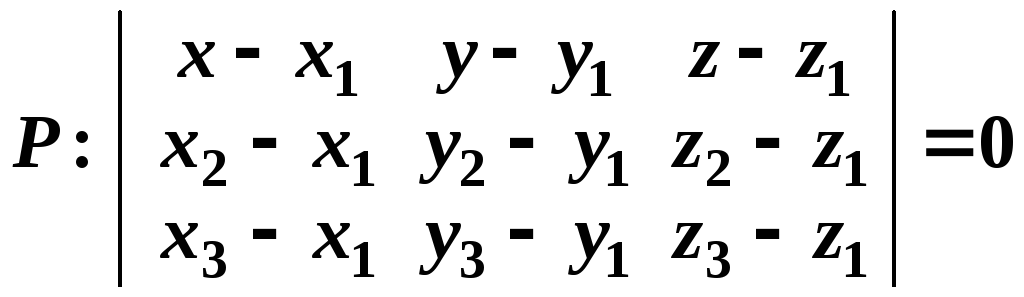
Чтобы
получить общее уравнение плоскости
,
нужно символьно вычислить этот
определитель, например, разложив его
по первой строке.
Пример16.
Даны вершины тетраэдра:
,
,
и
.
Найти уравнение грани.
Р
D(-1;0;5)
С(2;2;0)
А(3;-1;1)
В(-4;1;0)

«вслепую», без чертежа. Но для лучшего
понимания методов решения, чертеж (хотя
бы схематический) лучше все-таки
нарисовать.
Обозначимпроизвольная точка
плоскости, в которой лежит основание.
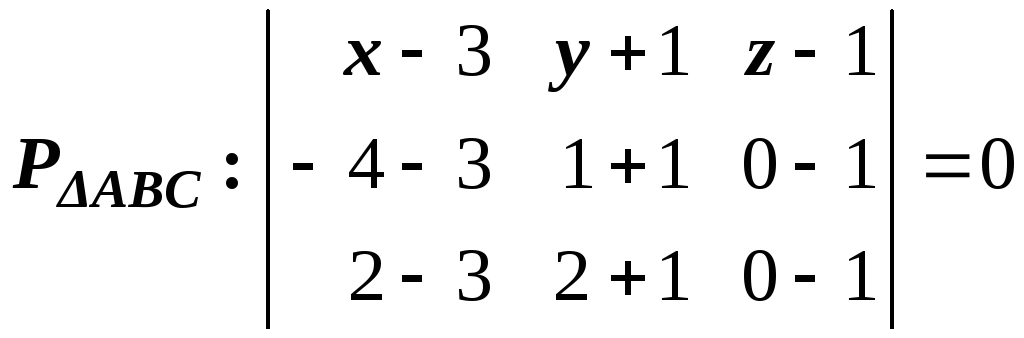
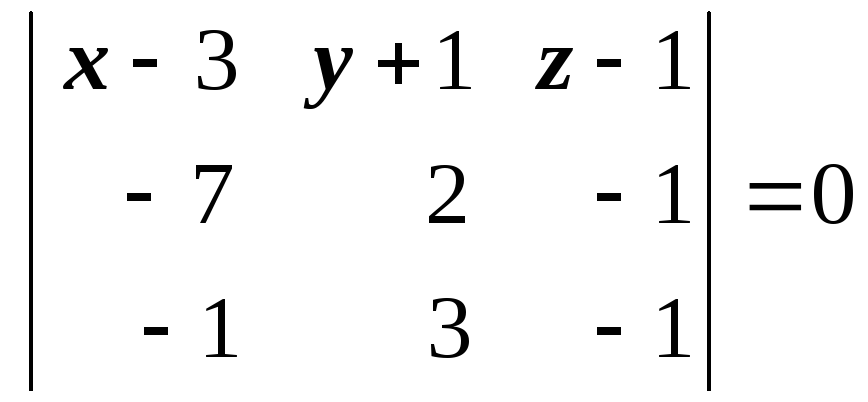
-
.
Окончательно
.
-
Уравнение
плоскости, проходящей через данную
точку
перпендикулярно данному вектору
(16)
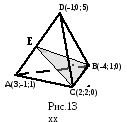
Пример17.Даны вершины тетраэдра:,
,
и
.
Найти уравнение плоскости, проходящей
через вершинуперпендикулярно ребру
.
Решение.Искомая плоскостьизображена на Рис 13. Так как по условию
плоскостьперпендикулярна боковому ребру
,
то векторперпендикулярен плоскости треугольника
.
Точка.
Тогда
.
Пример
18.
Известно, что точки:
и
симметричны относительно некоторой
плоскости.
Найти уравнение этой плоскости.
Р
B
Искомая плоскость изображена на Рис.14.
Поскольку по условию точки
и
симметричны
относительно плоскости,
то они лежат на перпендикуляре к этой
плоскости, проходящем черези
.
Так каки
равноудалены
от плоскости,
то эта плоскость проходит через середину
отрезка
точку
.
Нарисуем вектори введем его аналитически
.
Вычислим координаты точки:
. По формуле (16 ) построим
уравнение искомой плоскости
/
поделим на (
4) /
.
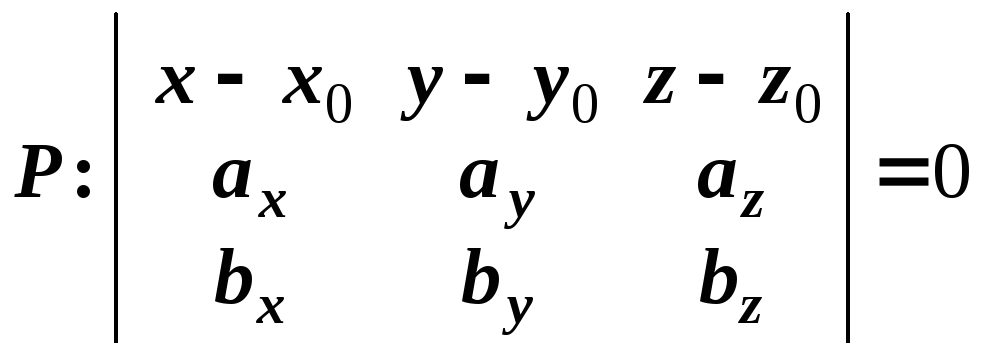
Замечание.
Решение многих задач на составление
уравнения плоскости на практике сводится
к поиску трех компланарных векторов.
Их смешанное произведение, как известно,
равно нулю. В координатах смешанное
произведение вычисляется с помощью
определителя 3-го порядка, строки
которого и есть координаты этих трех
векторов. Именно в этом и заключается
смысл формул (15) и (17 ).
П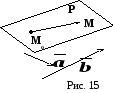
19.
Составить уравнение плоскости, проходящей
через точку
параллельно двум векторам
и
.
Решение.
Прежде всего заметим, что векторы
и
не параллельны, так как их координаты
не пропорциональны(Рис.15). Далее, обозначим
произвольная точка искомой плоскости.
Нарисуем вектор
и введем его аналитически
.
По условию искомая плоскость параллельна
векторами
или, что то же самое, векторы
и
параллельны искомой плоскости . Это в
свою очередь означает, что параллельным
переносом векторыи
можно переместить в плоскость вектора
.
Следовательно все три вектора,
и
компланарны и их смешанное произведение
,
что в координатах дает уравнение
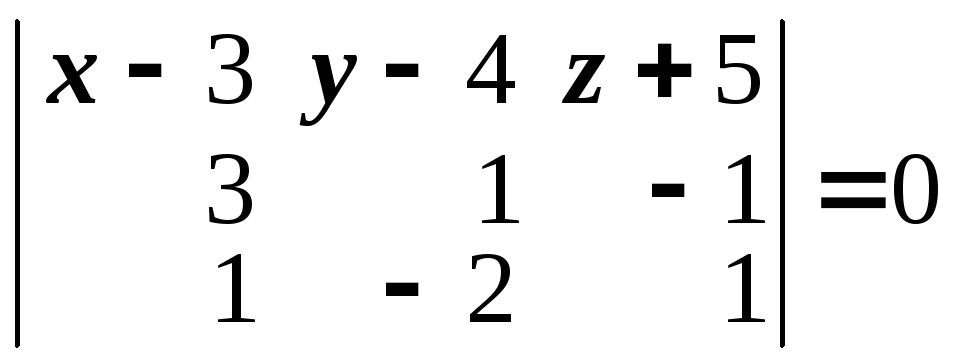
или
.
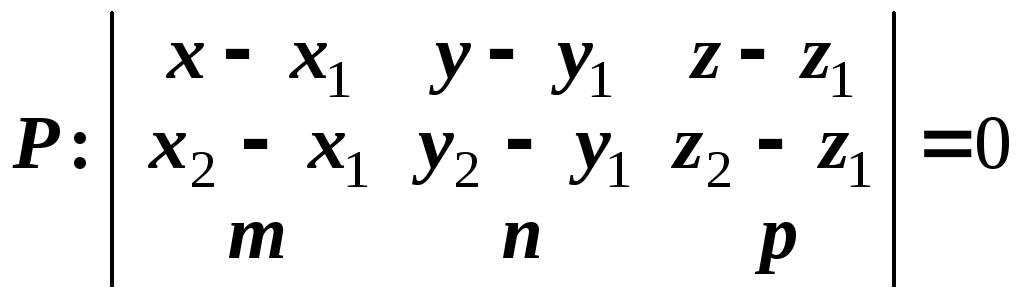
Пример
20.
Известно, что пространственная прямая
,
проходящая через точку,
пересекает плоскостьв точке
.
Найти уравнение плоскости,
проектирующей прямуюна
данную плоскость(Рис. 16).
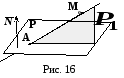
Две точки, через которые проходит
искомая плоскость
,
уже имеются
это точки
и
.
По этим точкам можно ввести вектор,
заведомо лежащий в искомой плоскости.
Далее, как всегда, введем точку
произвольную точку искомой плоскости.
По ней и по точке, например,
введем
еще один вектор, также лежащий в искомой
плоскости, а именно.
Осталось найти вектор, которому плоскостьпараллельна
или, что то же самое, который параллелен
этой плоскости. Таковым является вектор
нормальный вектор данной плоскости
.
Введенные три вектора компланарны, а
значит их смешанное произведение,
что в координатах дает уравнение:

.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Даны уравнения сторон ромба x+3y-8=0, 3x-y+16=0 и его диагонали 2x+y+4=0. Найти уравнения остальных сторон ромба.
Я выяснил, что стороны и диагонали выходят из одной точки (-4;4). Также легко понять, что каждая сторона будет параллельна одной из данных, т.е. уравнения будут отличать свободным членом. А что дальше то? Нам неизвестны ни центр диагонали, никакие другие точки.
Это задача по теме «Пучок прямых». Т.е. прямую можно задать как прямую пучка: α(A1x + B1y + C1) +β(A2y + B2y + C2) = 0. Дальше мои мысли кончились и я прошу помощи. Задачу сдавать уже завтра, а я даже не знаю с чего начать.






 едиану
едиану