Содержание
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Краткие теоретические сведения
Кривая в пространстве
Рассмотрим в пространстве гладкую кривую $gamma$.
-
Векторное уравнение $gamma:, vec{r}=vec{r}(t)$.
-
Параметрическое уравнение $gamma:,, x=x(t),, y=y(t),, z=z(t)$.
Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:
begin{equation*}
vec{r_0}=vec{r}(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0).
end{equation*}
Пусть в точке $M$ $ vec{r’}(t_0)neqvec{0}$, то есть $M$ не является особой точкой.
Касательная к кривой
Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec{r’}(t_0)$.
Пусть $vec{R}$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид
begin{equation*}
vec{R}=vec{r}(t_0)+lambdavec{r’}(t_0).
end{equation*}
Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec{R}$).
Если $vec{R}={X,Y,Z}$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:
begin{equation*}
frac{X-x(t_0)}{x'(t_0)}=frac{Y-y(t_0)}{y'(t_0)}=frac{Z-z(t_0)}{z'(t_0)}.
end{equation*}
Нормальная плоскость
Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.
Пусть $vec{R}$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec{R}-vec{r}(t_0)$ и $vec{r’}(t_0)$:
begin{equation*}
(vec{R}-vec{r}(t_0))cdotvec{r’}(t_0)=0.
end{equation*}
Если расписать покоординатно, то получим следующее уравнение:
begin{equation*}
x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0.
end{equation*}
Соприкасающаяся плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec{r’}(t_0)$, $vec{r»}(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.
Если $vec{R}$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec{R}-vec{r}(t_0)$, $vec{r’}(t_0)$, $vec{r»}(t_0)$:
begin{equation*}
(vec{R}-vec{r}(t_0), vec{r’}(t_0), vec{r»}(t_0))=0.
end{equation*}
Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:
begin{equation*}
left|
begin{array}{ccc}
X-x(t_0) & Y-y(t_0) & Z-z(t_0) \
x'(t_0) & y'(t_0) & z'(t_0)\
x»(t_0) & y»(t_0) & z»(t_0) \
end{array}
right|=0
end{equation*}
Плоская кривая лежит в своей соприкасающейся плоскости.
Бинормаль и главная нормаль
Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.
Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.
Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.
Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec{r’}(t_0)timesvec{r»}(t_0)$, тогда ее уравнение можно записать в виде:
begin{equation*}
vec{R}=vec{r}(t_0)+lambda,vec{r’}(t_0)timesvec{r»}(t_0).
end{equation*}
Как и раньше, $vec{R}$ — радиус-вектор произвольной точки бинормали.
Каноническое уравнение прямой:
begin{equation*}
frac{X-x(t_0)}{left|
begin{array}{cc}
y'(t_0) & z'(t_0) \
y»(t_0) & z»(t_0) \
end{array}
right|
}=frac{Y-y(t_0)}{left|
begin{array}{cc}
z'(t_0) & x'(t_0) \
z»(t_0) & x»(t_0) \
end{array}
right|
}=frac{Z-z(t_0)}{left|
begin{array}{cc}
x'(t_0) & y'(t_0) \
x»(t_0) & y»(t_0) \
end{array}
right|
}.
end{equation*}
Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec{r’}(t_0) timesleft[vec{r’}(t_0),vec{r»}(t_0)right]$:
begin{equation*}
vec{R}=vec{r}(t_0)+lambda,vec{r’}(t_0) timesleft[vec{r’}(t_0),vec{r»}(t_0)right].
end{equation*}
Уравнение в каноническом виде распишите самостоятельно.
Спрямляющая плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.
Другое определение:
Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.
Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec{R}-vec{r}(t_0)$, $vec{r’}(t_0)$, $vec{r’}(t_0)timesvec{r»}(t_0)$:
begin{equation*}
left(vec{R}-vec{r}(t_0),, vec{r’}(t_0),, vec{r’}(t_0)timesvec{r»}(t_0)right)=0.
end{equation*}
Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.
Репер Френе
Орт (то есть единичный вектор) касательной обозначим:
$$ vec{tau}=frac{vec{r’}(t_0)}{|vec{r’}(t_0)|}. $$
Орт бинормали:
$$ vec{beta}=frac{vec{r’}(t_0)timesvec{r»}(t_0)}{|vec{r’}(t_0)timesvec{r»}(t_0)|}. $$
Орт главной нормали:
$$ vec{nu}=frac{vec{r’}(t_0) times[vec{r’}(t_0),,vec{r»}(t_0)]}{|vec{r’}(t_0) times [vec{r’}(t_0),,vec{r»}(t_0)]|}. $$
Правая тройка векторов $vec{tau}$, $vec{nu}$, $vec{beta}$ называется репером Френе.

Решение задач
Задача 1
Кривая $gamma$ задана параметрически:
$$
x=t,,, y=t^2,,, z=e^t.
$$
Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$.
Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.
Решение задачи 1
Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.
Начнем с производных.
begin{gather*}
gamma: vec{r}(t)=left{ t,, t^2,, e^tright} ,, Rightarrow \
vec{r’}(t)=left{ 1,, 2t,, e^tright},\
vec{r»}(t)=left{ 0,, 2,, e^tright}.
end{gather*}
В точке $M(t_0=0)$:
begin{gather*}
vec{r}(t_0)={ 0,, 0,, 1},\
vec{r’}(t_0)={ 1,, 0,, 1},\
vec{r»}(t_0)={ 0,, 2,, 1}.
end{gather*}
-
Зная координаты точки $M(0,0,1)$ и направляющего вектора $ vec{r’}(t_0)={ 1,0,1 }$, можем записать уравнение касательной:
begin{equation*}
frac{X}{1}=frac{Y}{0}=frac{Z-1}{1}.
end{equation*}
-
Нормальная плоскость проходит через точку $M(0,0,1)$ перпендикулярно вектору $vec{r’}(t_0)={ 1,0,1 }$, поэтому ее общее уравнение имеет вид:
begin{equation*}
1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1.
end{equation*}
-
Запишем теперь уравнение соприкасающейся плоскости, определяемой точкой $M(0,0,1)$ и векторами: $vec{r’}(t_0)={ 1,, 0,, 1}$, $vec{r»}(t_0)={ 0,, 2,, 1}$:
begin{equation*}
left|
begin{array}{ccc}
X-0 & Y-0 & Z-1 \
1 & 0 & 1\
0 & 2 & 1 \
end{array}
right|=0
end{equation*}
Раскрываем определитель, получаем уравнение:
begin{equation*}
-2X-Y+2Z-2=0
end{equation*}
-
Направление бинормали задается вектором $vec{r’}(t_0) times vec{r»}(t_0)$. Координаты этого вектора мы уже нашли, когда вычисляли миноры в определителе, задающем уравнение соприкасающейся плоскости.
$$
{ 1,, 0,, 1} times { 0,, 2,, 1}= left|
begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
1 & 0 & 1\
0 & 2 & 1 \
end{array}
right|= {-2,, -1,, 2}.
$$
Уравнение бинормали:
begin{equation*}
frac{X}{-2}=frac{Y}{-1}=frac{Z-1}{2}.
end{equation*}
-
Направление главной нормали задается вектором $vec{r’}(t_0) times (vec{r’}(t_0)timesvec{r»}(t_0))$.
$$
{ 1,, 0,, 1} times {-2,, -1,, 2}= left|
begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
1 & 0 & 1\
-2 & -1 & 2 \
end{array}
right|= {1,, -4,, -1} ,, Rightarrow ,,
frac{X}{1}=frac{Y}{-4}=frac{Z-1}{-1}.
$$
-
Спрямляющая плоскость перпендикулярна главной нормали, а значит, вектору ${1,, -4,, -1}$, поэтому можем сразу записать ее общее уравнение:
begin{equation*}
1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0.
end{equation*}
Орт касательной: $vec{tau} =frac{1}{sqrt{2}}{1,,0,,1}$,
Орт главной нормали: $vec{nu} =frac{1}{sqrt{18}}{1,,-4,,-1}$,
Орт бинормали: $vec{beta }=frac{1}{3}{-2,,-1,,2}$.
Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec{tau}$, $vec{nu}$, $vec{beta}$ не будет правой (по определению векторного произведения вектор $vec{tau}timesvec{beta}$ направлен так, что тройка векторов $vec{tau}$, $vec{beta}$, $vec{nu}=vec{tau}timesvec{beta}$ — правая). Изменим направление одного из векторов. Например, пусть
$$ vec{nu} =frac{1}{sqrt{18}}{-1,,4,,1}.$$
Теперь тройка $vec{tau}$, $vec{nu}$, $vec{beta}$ образует репер Френе для кривой $gamma$ в точке $M$.
Задача 2
Написать уравнение соприкасающейся плоскости к кривой
$$
x=t,,, y=frac{t^2}{2},,, z=frac{t^3}{3},
$$
проходящей через точку $N(0,0,9)$.
Решение задачи 2
Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.
Найдем значение параметра $t_0$.
Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.
begin{align*}
gamma: vec{r}(t)&=left{ t,, frac{t^2}{2},, frac{t^3}{3}right} ,, Rightarrow \
vec{r’}(t)&=left{ 1,, t,, 3t^2right},\
vec{r»}(t)&=left{ 0,, 1,, 6tright}.
end{align*}
В точке $M(t=t_0)$:
begin{align*}
vec{r}(t_0)&=left{t_0,, frac{t_0^2}{2},, frac{t_0^3}{3}right} \
vec{r’}(t_0)&=left{1,, t_0,, 3t_0^2right},\
vec{r»}(t_0)&=left{0,, 1,, 6t_0right}.
end{align*}
Соприкасающаяся плоскость определяется векторами $vec{r’}(t_0)$, $vec{r»}(t_0)$, поэтому записываем определитель
begin{equation*}
left|
begin{array}{ccc}
X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \
&&\
1 & t_0 & t^2_0 \
&&\
0 & 1 & 2t_0
end{array}
right|=0 quad Rightarrow
end{equation*}
begin{equation*}
(X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0.
end{equation*}
Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$:
begin{equation*}
9-t_0^3/3=0 quad Rightarrow quad t_0=3.
end{equation*}
Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости:
$$ 9X-6Y+Z-9=0. $$
Задача 3
Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой:
$$
x=t^2,,, y=1+t,,, z=2t.
$$
Решение задачи 3
Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.
Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec{r’}(t_0)$ и $vec{r’}(t_0)timesvec{r»}(t_0)$.
В произвольной точке $M(t=t_0)$:
begin{align*}
vec{r}(t_0)&=left{t^2_0,, 1+t_0,, 2t_0right} \
vec{r’}(t_0)&=left{2t_0,, 1,, 2right},\
vec{r»}(t_0)&=left{2,, 0,, 0right}.
end{align*}
begin{equation*}
vec{r’}(t_0)timesvec{r»}(t_0)= left|
begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
2t_0 & 1 & 2\
2 & 0 & 0
end{array}
right|= {0,, 4,, -2}
end{equation*}
Записываем уравнение спрямляющей плоскости:
begin{equation*}
left|
begin{array}{ccc}
X-t_0^2 & Y-1-t_0 & Z-2t_0 \
2t_0 & 1 & 2\
0 & 4 & -2
end{array}
right|= 0
end{equation*}
Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$:
begin{equation*}
5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_{01}=2,, t_{02}=-frac25.
end{equation*}
Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид:
begin{align*}
& 5X-4Y-8Z+24=0,\
& 25X+4Y+8Z=0.
end{align*}
Рассмотрим
плоскости, проходящие через касательную
кривой

в точке Р=Р (t0)
кривой. При изменении параметра t
получаем вектор

Для вектора
имеет
место формула Тейлора:


+
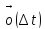

Точка
М(t0+∆t)
кривой и касательная






ꞌ(t0+∆t)
Нормальный
вектор плоскости есть


Плоскость

,


плоскостью
кривой в точке t0
.
Уравнение
соприкасающейся плоскости:
Практическая
часть нахождения соприкасающейся
плоскости в произвольной и в выбранной
точке
Найдем
формулу соприкасающейся плоскости в
произвольной и выбранной точке:


Мы
нашли формулу соприкасающейся плоскости
в произвольной точке. Теперь найдем в
произвольной точке, которую мы ранее
приняли равной



Соприкасающаяся
плоскость в выбранной точке найдена.
1.3 Кривизна и кручение кривой. Вычислительные формулы для кривизны и кручения.
Величина
k1
называется кривизной
или первой
кривизной
кривой r(s)
в точке Р; функция k1
= k1(s)
называется функцией
кривизны кривой
r(s),
k1
≥
0,

–вектор кривизны кривой
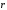
Величина
k2
называется кручением
кривой

или второй
кривизной кривой

в точке Р. При движении точки Р по кривой

т.е. с изменением параметра s,
имеем функцию k2=
k2(s)
–
функцию кручения.
Знак величины k2
может
быть и положительным, и отрицательным
k1=
k2
=

Практическая
часть вычисления кривизны и кручения
в произвольной и выбранной точке
Вычислим,
имея компоненты нашей кривой: кривизну
и кручение в произвольной и выбранной
точке.
Кривизна
кривой (
в произвольной точке вычисляется
согласно формуле (1).Подставляем наши
координаты в эту формулу, получаем:
Мы
нашли кривизну кривой в произвольной
точке. Найдем кривизну выбранной точке,
подставив вместо

ранее.
Кривизна
кривой в выбранной точке найдена.
Кручение
кривой (
в произвольной точке вычисляется
согласно формуле (2).Подставляем наши
координаты в эту формулу, получаем:
Мы
нашли кручение кривой в произвольной
точке. Найдем кручение выбранной точке,
подставив вместо

ранее.
Кручение
кривой в выбранной точке найдена.
1.4 Построение кривой
Изобразим
нашу кривую; она будет иметь следующий
вид:
-
2.Поверхности евклидова пространства.
Нам
даны компоненты поверхности: x=

плоскости и нормали, первую и вторую
квадратичные формы в произвольной и
выбранной точке. Вычислим полную и
среднюю кривизны поверхности. Изобразим
поверхность.
2.1 Касательная плоскость и нормаль поверхности.
Пусть
P
– точка регулярной поверхности

В этой точке имеем неколлинеарные
векторы
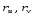
Для любой линии
=

выполняется

Касательная
прямая

,



=

поверхности

лежит в плоскости

Касательные всех линий поверхности
,проходящих через точку Р, образуют
плоскость.
Пусть
Р=(x0,y0,z0)
и производные

в точке Р.
Тогда
уравнение касательной плоскости таково

Прямая


в точке Р. Ее уравнение
Нахождение
касательной плоскости и нормали в
произвольной и выбранной точке.
Вычислим
производные по u
и v.
Получим следующее:
Возьмем
точки




Найдем
касательную плоскость в произвольной
точке:
Уравнение
касательной плоскости в произвольной
точке найдено.
Найдем
в выбранной точке, подставив значения

и ch
Мы
нашли уравнение касательной плоскости
в выбранной точке.
Теперь
найдем уравнение нормали в произвольной
и выбранной точке, используя теоретическую
часть нашего вопроса, получим:
Получено
уравнение нормали в произвольной точке.
Найдем в выбранной:
Уравнение
нормали в выбранной точке найдено.
Соседние файлы в папке курсач docx180
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение.
Плоскость, проходящую через касательную и главную нормаль в данной точке кривой, называют соприкасающейся плоскостью.
Отсюда и из определения главной нормали следует, что соприкасающаяся плоскость определена для точек кривой, в которых кривизна (kneq 0).
Утверждение 1.
Если гладкая кривая (Gamma={textbf{r}=textbf{r}(t),;alphaleq tleqbeta}) дважды дифференцируема и ее кривизна в точке (M_{0}=M(t_{0})) не равна нулю, то уравнение соприкасающейся плоскости (Q) в точке (M_{0}) имеет вид
$$
(r-r(t_0),r'(t_0),r″(t_0))=0.label{ref41}
$$
Доказательство.
(circ) Если (s=s(t)) — переменная длина дуги кривой (Gamma), то дифференцируя (r(t)) как сложную функцию и используя эту и эту формулы, получаем
$$
textbf{r}_{t}’=textbf{r}_{s}’s_{t}’=s_{t}’tau,quad textbf{r}_{tt}″=frac{d}{dt}(s_{t}’tau)=s_{tt}″tau+s_{t}’tau_{s}’s_{t}’=s_{tt}″tau+(s_{t}’)^{2}knu,nonumber
$$
где индексы указывают, по каким переменным производится дифференцирование. Отсюда следует, что векторы (textbf{r}_{t}’) и (textbf{r}_{tt}″) параллельны плоскости (Q). По условию (kneq 0), и поэтому ([textbf{r}_{t}’,textbf{r}_{tt}″]neq 0). Следовательно, векторы (textbf{r}_{t}’) и (textbf{r}_{tt}″) не коллинеарны.
Так как векторы (textbf{r}-textbf{r}(t_{0}), textbf{r}'(t_{0})=textbf{r}_{t}'(t_{0}), textbf{r}″(t_0)=textbf{r}_{tt}″(t_{0})) параллельны плоскости (Q) (рис. 22.8), то их смешанное произведение равно нулю, то есть во всех точках плоскости (Q) (и только в этих точках) должно выполняться условие eqref{ref41}. (bullet)
Запишем уравнение eqref{ref41} в координатной форме:
$$
begin{vmatrix}x-x(t_0)&y-y(t_0)&z-z(t_0)\x'(t_0)&y'(t_0)&z'(t_0)\x″(t_0)&y″(t_0)&z″(t_0)end{vmatrix}=0nonumber
$$
Во-первых, уравнение соприкасающейся плоскости имеет вид:
[math]left|{begin{array}{*{20}{c}}{X — x}&{Y — y}&{Z — z}\{x’}&{y’}&{z’}\{x»}&{y»}&{z»}end{array}}right|=0[/math],
а то, что вы написали просто какой-то определитель.
Во-вторых, вы забыли дописать фразу:
Цитата:
где X, Y, Z — текущие координаты, а х, у, z, х’, у’, z’, х», у», z» вычисляются в точке соприкосновения
из которой, по-моему, всё предельно ясно относительно параметров уравнения плоскости.
Marusya писал(а):
По логике вещей, нужно подобрать такое t ,при котором выполнялось бы следующее:
В вашей задаче не написано, что точка М принадлежит кривой. Написано только, что через неё проходит соприкасающаяся плоскость. Найдите сначала производные и составьте уравнение плоскости с параметром t.
Соприкасающиеся плоскости и окружности
Говорят, что кривые (y = fleft( x right)) и (y = gleft( x right)) имеют в точке (left( <,> right)) касание (n)-го порядка , если выполняются следующие условия: [ > right) = gleft( <> right),>;; > right) = g’left( <> right),>;; > right) = g»left( <> right),;ldots,;> <>left( <> right) = >left( <> right),>;; <right)>>left( <> right) ne right)>>left( <> right).> ] В частности, если (n = 1,) то кривые (y = fleft( x right)) и (y = gleft( x right)) имеют общую касательную .
Случай (n = 0) означает, что кривые имеют общую точку (left( <,> right):) (fleft( <> right) = gleft( <> right),) но их первые производные при этом не совпадают: (f’left( <> right) ne g’left( <> right).) В этом случае кривые просто пересекаются в точке (.)
Можно рассмотреть разность функций (varphi left( x right) = gleft( x right) — fleft( x right)) в окрестности точки () и разложить ее в ряд Тейлора с остаточным членом в форме Пеано. Если кривые (gleft( x right)) и (fleft( x right)) имеют порядок касания (n,) то первые (n) членов ряда равны нулю и разность (varphi left( x right)) представляется в виде [ <varphi left( x right) = frac<<<varphi ^<left( right)>>left( <> right) + alpha >> <<left( right)!>><left( > right)^> > = <frac<<right)>>left( <> right) — right)>>left( <> right) + alpha >> <<left( right)!>><left( > right)^>,> ] т.е. пропорциональна (<left( > right)^>.) Следовательно, при четном значении (n) разность (varphi left( x right)) имеет разные знаки слева и справа от точки касания (,) т.е. в этом случае кривые пересекаются в точке (.) Частный случай (n = 0) рассмотрен выше.
При нечетном (n) кривые (y = fleft( x right)) и (y = gleft( x right)) касаются друг друга в точке () без взаимного пересечения.
Рассмотрим следующую задачу. Дано уравнение кривой (y = fleft( x right)) и семейство кривых [Gleft( right) = 0] с (n + 1) параметрами (.) Требуется, изменяя значения параметров, выбрать из данного семейства такую кривую, которая с кривой (y = fleft( x right)) в точке (left( <,> right)) имела бы наивысший возможный порядок касания. Такая кривая будет называться соприкасающейся кривой .
Введем обозначение [Phi left( right) = Gleft( right).] Условия касания записываются в виде: [left< begin Phi left( <,a,b, ldots ,ell> right) = 0\ <Phi’_x>left( <,a,b, ldots ,ell> right) = 0\ <Phi»_>left( <,a,b, ldots ,ell> right) = 0\ cdots cdots cdots cdots cdots cdots cdots \ Phi _<>^<left( n right)>left( <,a,b, ldots ,ell> right) = 0 end right..] В результате мы получаем систему из (n + 1) уравнений с (n + 1) неизвестными значениями параметров. Решая эту систему, находим параметры () и уравнение соприкасающейся кривой. Обычно ее порядок касания будет не ниже, чем (n) (в случае (n + 1) параметров). Таким образом, порядок касания соприкасающейся кривой, как правило, на единицу меньше числа параметров.
Выведем уравнение соприкасающейся окружности. Пусть задана функция (y = fleft( x right),) которая является по меньшей мере дважды дифференцируемой. Семейство окружностей описывается уравнением [ <left( right)^2> + <left( right)^2> = .] Как видно, здесь мы имеем дело с тремя параметрами − координатами центра окружности (a, b) и ее радиусом (R.) Ясно, что в данном случае максимально возможный порядок касания равен (2.)
Будем считать, что парабола задана уравнением (y = gleft( x right) = a + bx + c.) Данная функция содержит (3) параметра. Поэтому можно предположить, что порядок касания кривых равен (2.) Тогда коэффициенты (a, b, c) находятся из следующих условий: [left< begin fleft( <> right) = gleft( <> right)\ f’left( <> right) = g’left( <> right)\ f»left( <> right) = g»left( <> right) end right..] Производные функций (fleft( x right) = ) и (gleft( x right) = a + bx + c) выражаются формулами [ > right)^prime > = ,>;;; > right)^prime > = ;> ] [ + bx + c> right)^prime > = 2ax + b,>;;; right)^prime > = 2a.> ] Тогда система уравнений принимает такой вид: [left< begin >> = ax_0^2 + b + c\ >> = 2a + b\ >> = 2a end right..] Подставляя ( = 0,) получаем: [ left< begin c = 1\ b = 1\ 2a = 1 end right. ;;text<или>;; left< begin a = frac<1><2>\ b = 1\ c = 1 end right.. ] Итак, парабола, соприкасающаяся с экспоненциальной функцией в точке ( = 0,) имеет второй порядок касания и определяется формулой [y = frac<<>> <2>+ x + 1.] Если записать ее уравнение в виде [ >> <2>+ x + 1 > = <frac<1><2>left( <+ 2x> right) + 1 > = <frac<1><2>left( <+ 2x + 1 — 1> right) + 1 > = <frac<1><2> <left( right)^2> + frac<1><2>,> ] то видно, что вершина параболы находится в точке (left( < — 1,largefrac<1><2>normalsize> right).) Схематически обе соприкасающиеся кривые показаны на рисунке (2.)
Полагая, что семейство парабол является трехпараметрическим, т.е. описывается уравнением [y = a + bx + c] с тремя параметрами (a, b) и (c,) введем функцию [Phi left( right) = a + bx + c — fleft( x right)] и запишем условие касания в точке () в виде [left< begin Phi left( <,a,b,c> right) = 0\ <Phi ‘_x>left( <,a,b,c> right) = 0\ <Phi »_>left( <,a,b,c> right) = 0 end right..] В нашем случае (fleft( x right) = cos x.) Следовательно, [ right)^prime > = — sin x,>;;; right)^prime > = — cos x.> ] В результате имеем следующую систему для определения коэффициентов (a, b, c:) [left< begin ax_0^2 + b + c — cos = 0\ 2a + b + sin = 0\ 2a + cos = 0 end right..] Подставляя ( = 0,) получаем: [left< begin c — 1 = 0\ b = 0\ 2a + 1 = 0 end right.,;; Rightarrow left< begin a = — frac<1><2>\ b = 0\ c = 1 end right..] Таким образом, парабола, соприкасающаяся с функцией косинус в точке ( = 0,) описывается уравнением [y = — frac<<>> <2>+ 1.] Как видно, это уравнение соответствует первым двум членам разложения косинуса в ряд Маклорена .
Здесь мы имеем дело с семейством функций, содержащих (4) параметра. Следовательно, наивысший возможный порядок касания кривых равен (3.) Для определения коэфициентов (a, b, c) и (d) запишем следующие условия касания: [left< begin fleft( <> right) = gleft( <> right)\ f’left( <> right) = g’left( <> right)\ f»left( <> right) = g»left( <> right)\ f»’left( <> right) = g»’left( <> right) end right..] Производные кубической функции имеют такой вид: [g’left( x right) = <left( + b + cx + d> right)^prime > = 3a + 2bx + c,] [g»left( x right) = <left( <3a+ 2bx + c> right)^prime > = 6ax + 2b,] [g»’left( x right) = <left( <6ax + 2b>right)^prime > = 6a.] Вычислим производные тангенса: [f’left( x right) = <left( <tan x>right)^prime > = frac<1><<<<cos >^2>x>>,] [ <<<<cos >^2>x>>> right)^prime > > = <<left[ <<<left( <cos x>right)>^< — 2>>> right]^prime > > = < — 2<left( <cos x>right)^< — 3>> cdot left( < — sin x>right) > = <frac<<2sin x>><<<<cos >^3>x>>,> ] [ ><<<<cos >^3>x>>> right)^prime > > = <frac<<<<left( <2sin x>right)>^prime ><<cos >^3>x — 2sin x<<left( <<<cos >^3>x> right)>^prime >>><<<<cos >^6>x>> > = <frac<<2,cos x,<<cos >^3>x — 2sin x cdot 3,<<cos >^2>x cdot left( < — sin x>right)>><<<<cos >^6>x>> > = <frac<<2,<<cos >^3>x + 6,<<sin >^2>x,<<cos >^2>x>><<<<cos >^6>x>> > = <frac<<<<cos >^2>xleft( <2,<<cos >^2>x + 2,<<sin >^2>x + 4,<<sin >^2>x> right)>><<<<cos >^6>x>> > = <frac<<2 + 4,<<sin >^2>x>><<<<cos >^4>x>>.> ] Тогда система уравнений принимает вид: [left< begin tan = ax_0^3 + bx_0^2 + c + d\ frac<1><<<<cos >^2>>> = 3ax_0^2 + 2b + c\ frac<<2sin >><<<<cos >^3>>> = 6a + 2b\ frac<<2 + 4<<sin >^2>>><<<<cos >^4>>> = 6a end right..] Подставляя значение ( = 0,) получаем: [left< begin d = 0\ c = 1\ 2b = 0\ 6a = 2 end right.,;; Rightarrow left< begin a = frac<1><3>\ b = 0\ c = 1\ d = 0 end right..] Таким образом, соприкасающаяся кубическая функция записывается как [y = frac<<>> <3>+ x.] Данная кривая имеет третий порядок касания с кривой тангенса в начале координат.
Заметим, что найденная кубическая функция представляет собой разложение тангенса в ряд Маклорена до третьего порядка.
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Краткие теоретические сведения
Кривая в пространстве
Рассмотрим в пространстве гладкую кривую $gamma$.
Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:
begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end
Пусть в точке $M$ $ vec(t_0)neqvec<0>$, то есть $M$ не является особой точкой.
Касательная к кривой
Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.
Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид
Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).
Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:
Нормальная плоскость
Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.
Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:
Если расписать покоординатно, то получим следующее уравнение:
begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end
Соприкасающаяся плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.
Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:
Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:
begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end
Бинормаль и главная нормаль
Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.
Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.
Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.
Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:
Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:
Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:
Уравнение в каноническом виде распишите самостоятельно.
Спрямляющая плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.
Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.
Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.
Репер Френе
Орт (то есть единичный вектор) касательной обозначим: $$ vec<tau>=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec<beta>=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec<nu>=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$
Правая тройка векторов $vec<tau>$, $vec<nu>$, $vec<beta>$ называется репером Френе.
Решение задач
Задача 1
Кривая $gamma$ задана параметрически:
Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.
Решение задачи 1
Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.
Начнем с производных.
begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end
begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end
begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end
Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec<tau>$, $vec<nu>$, $vec<beta>$ не будет правой (по определению векторного произведения вектор $vec<tau>timesvec<beta>$ направлен так, что тройка векторов $vec<tau>$, $vec<beta>$, $vec<nu>=vec<tau>timesvec<beta>$
— правая). Изменим направление одного из векторов. Например, пусть
Теперь тройка $vec<tau>$, $vec<nu>$, $vec<tilde<beta>>$ образует репер Френе для кривой $gamma$ в точке $M$.
Задача 2
Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac<2>,,, z=frac<3>, $$ проходящей через точку $N(0,0,9)$.
Решение задачи 2
Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.
Найдем значение параметра $t_0$.
Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.
Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end
begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$
Задача 3
Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$
Решение задачи 3
Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.
Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.
Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end
Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_<01>=2,, t_<02>=-frac25. end
Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end
Соприкасающаяся плоскость
Плоскость, проходящую через касательную и главную нормаль в данной точке кривой, называют соприкасающейся плоскостью.
Отсюда и из определения главной нормали следует, что соприкасающаяся плоскость определена для точек кривой, в которых кривизна (kneq 0).
Если гладкая кривая (Gamma=<textbf=textbf(t),;alphaleq tleqbeta>) дважды дифференцируема и ее кривизна в точке (M_<0>=M(t_<0>)) не равна нулю, то уравнение соприкасающейся плоскости (Q) в точке (M_<0>) имеет вид
$$
(r-r(t_0),r'(t_0),r″(t_0))=0.label
$$
(circ) Если (s=s(t)) — переменная длина дуги кривой (Gamma), то дифференцируя (r(t)) как сложную функцию и используя эту и эту формулы, получаем
$$
textbf_’=textbf_’s_’=s_’tau,quad textbf_″=frac
$$
где индексы указывают, по каким переменным производится дифференцирование. Отсюда следует, что векторы (textbf_’) и (textbf_″) параллельны плоскости (Q). По условию (kneq 0), и поэтому ([textbf_’,textbf_″]neq 0). Следовательно, векторы (textbf_’) и (textbf_″) не коллинеарны.
Рис. 22.8
Так как векторы (textbf-textbf(t_<0>), textbf'(t_<0>)=textbf_'(t_<0>), textbf″(t_0)=textbf_″(t_<0>)) параллельны плоскости (Q) (рис. 22.8), то их смешанное произведение равно нулю, то есть во всех точках плоскости (Q) (и только в этих точках) должно выполняться условие eqref. (bullet)
Запишем уравнение eqref в координатной форме:
$$
beginx-x(t_0)&y-y(t_0)&z-z(t_0)\x'(t_0)&y'(t_0)&z'(t_0)\x″(t_0)&y″(t_0)&z″(t_0)end=0nonumber
$$
http://vmath.ru/vf5/diffgeom/seminar1
http://univerlib.com/mathematical_analysis/derivative/osculating_plane/






























