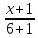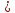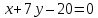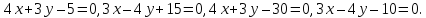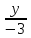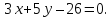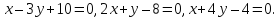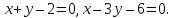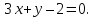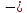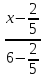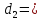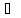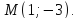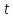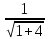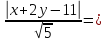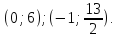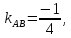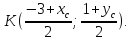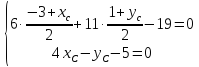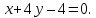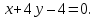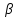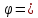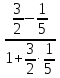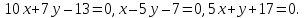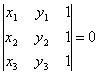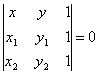Уравнение квадрата в декартовой системе координат.
Проанализируем расположение квадрата на координатной плоскости.
В общем случае уравнение квадрата в декартовой (прямоугольной) системе координат принимает вид:
где точка О`(a;b) – точка пересечения диагоналей квадрата;
d – длина диагонали квадрата.
В частном случае, когда точка О(0;0) — начала координат, является одновременно и точкой пересечения диагоналей квадрата, уравнение квадрата принимает вид:
где d– длина диагонали квадрата.
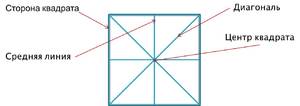
Задача 34286 Пусть прямая l1(4x–y+1=0) одна из.
Условие
Пусть прямая l1(4x–y+1=0) одна из сторон квадрата, а точка M(1;2) его вершина. Составить уравнение остальных сторон квадрата
Решение
Расстояние d от точки M(1;2) до прямой 4х-у+1=0
это длина стороны квадрата
Уравнение прямой 4x-y+1=0 можно записать
y=4x+1
k=4
k=tg α ;
Значит прямая c угловым коэффициентом 4 — это диагональ прямоугольника, размеры 1 × 4 ( длина 1, высота 4: tgα=4/1)
Параллельная ей прямая проходит через точку М
k=4
y=4x+m
Чтобы найти m подставляем координаты точки M
2=4*1+m
m=-2
Перпендикулярная ей прямая имеет угловой k=-1/4
(потому что произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1))
Чтобы найти b подставляем координаты точки M
2=(-1/4)*1+b
b=2 целых 1/4
[b]y=(-1/4)x + 2 целых 1/4⇒ 4y+x-9=0[/b]
Третья сторона имеет угловой коэффициент k=(-1/4) и находится на расстоянии 3/sqrt(17) от точки M (1;2)
9-4n=-3 или 9-4n=3
n=3 или n=3/2
[b]4y+x-12 =0[/b] или [b]4y+x-6=0[/b]
О т в е т. [b]y=4x-2[/b]; [b]4y+x-9=0[/b]; [b]4y+x-12 =0[/b] (или [b] 4y+x-6=0[/b])
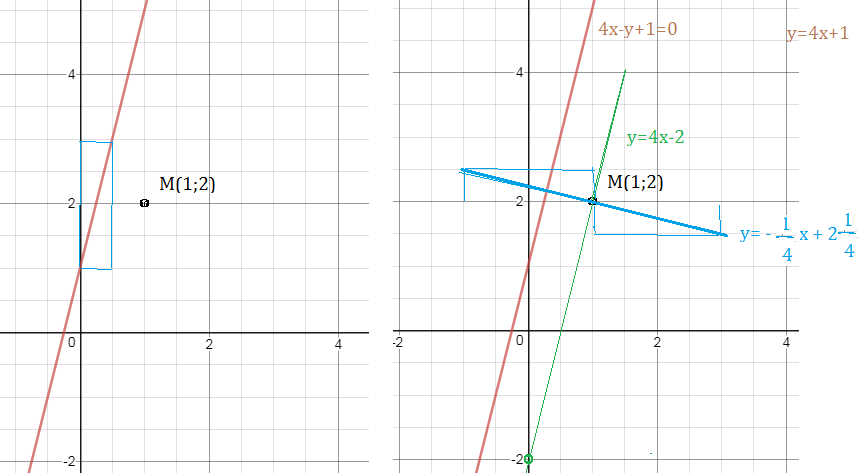
Формулы и способы как находить диагональ квадрата
При решении задач по школьной математике часто требуется определить, чему равняется диагональ заданного квадрата. При кажущейся некоторой сложности, эта задача является весьма простой и имеет несколько несложных способов решения. Рассмотрим их, для начала введём некоторые понятия и определения.
Определения и соглашения
- Квадрат — это четырёхугольник с равными сторонами, все углы которого являются прямыми, то есть равны 90 градусов. Данная фигура одновременно и ромб, и прямоугольник, поэтому сохраняет все их свойства.
- Диагональ многоугольника — это отрезок, соединяющий две его противоположные вершины. В статье её будем обозначать буквой d.
- Противоположными называются вершины, не лежащие на одной стороне.
- Корень квадратный из числа, это такое число, которое при умножении само на себя даст исходное. В геометрии используются только положительные значения квадратного корня. В статье его будем обозначать сокращением rad (от латинского radical — корень).
- Сторону квадрата будем обозначать буквой a.
Как понятно из вышеизложенного, у квадрата только две диагонали. Поскольку квадрат является прямоугольником и сохраняет его свойства, то они равны между собой. Рассмотрим различные методы нахождения её длины.
Вычисление диагонали квадрата по известной стороне
Самым простым способом является вычисление диагонали, если известна сторона квадрата. Здесь действует широко известная теорема Пифагора для прямоугольных треугольников. Запишем эту формулу: c^2 = a^2+b^2.
Отметим, что в нашем случае диагональ квадрата есть гипотенуза треугольника с равными катетами. Перепишем формулу исходя из наших условий: d^2 = a^2+a^2. Преобразуем, получим: d^2 = 2*a^2. Следующим шагом извлечём квадратный корень, получится: d = rad2*a. Это и есть наша конечная формула.
Рассмотрим вычисление на примере. Пусть a = 64. Подставим наше значение в формулу. Получим d = 64*rad2. Это и есть ответ.
Вычисление диагонали квадрата по известной площади
Пусть нам дана площадь квадрата, её обозначают латинской буквой S, найдём его диагональ.
Используем свойства прямоугольника и запишем формулу его площади.
S = a*b. Перепишем для b = a. Получим: s = a^2. Отсюда найдём сторону: a = radS. Итак, нам удалось выразить сторону через площадь. Подставим полученное выражение в конечную формулу из предыдущей части. Формула примет вид: d = rad2*a = rad2*radS.
Пример: допустим, площадь равна 32 квадратных метра. Подставим это число. Получим rad2*rad32 = rad2*4*rad2 = 4*2 = 8 метров.
Вычисление диагонали по известному периметру
Пусть нам известен периметр. В дальнейшем его будем записывать латинской буквой P, найдём его d. Воспользуемся свойствами прямоугольника и запишем формулу его периметра.
P = два*(a + b). Перепишем для b = a. У нас получится: P = два*(a + a) = 2*2a = 4*a. Выразим из последней формулы сторону. Имеем: a = P/4. Воспользуемся тем, что: d = rad2*a. Выразим сторону через периметр. Наша формула примет видd = rad2*P/4.
Примере: пусть периметр равен 128 метров. Проведём несложный расчёт. Имеем, rad =d2*128/4 = 32*rad2 метров.
Вычисление по радиусу описанной и вписанной окружности
Ещё один способ, который на само деле очень простой. Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.
Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R. Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.
И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r.
Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.
Заключение
Таким образом, мы рассмотрели в статье пять принципиально различных методов вычисления диагонали квадрата. Если, на первый взгляд, задача казалась сложной, то после проведённых нами рассуждений стало очевидно, что особых проблем здесь нет. Сведём все полученные нами формулы в одну таблицу.
Хочется ещё отметить, что с помощью первой из наших формул очень легко построить отрезок, равный корню квадратному из двух. Для этого строим квадрат со стороной единица, его диагональ и будет равняться искомому отрезку.
Если на полученной диагонали мы построим прямоугольник, используя её как длину, а ширину возьмём равной единице, то получим отрезок равный ещё одному иррациональному числу корень квадратный из трёх.
Продолжая нашу цепочку и далее, мы научимся строить отрезки равные любому иррациональному числу.
Видео
Из видео вы узнаете, как найти диагональ квадрата, если известна его площадь.
http://reshimvse.com/zadacha.php?id=34286
http://liveposts.ru/articles/education-articles/matematika/formuly-i-sposoby-kak-nahodit-diagonal-kvadrata
Определение.
Любой ненулевой вектор, перпендикулярный
прямой называется её нормальным
вектором,
и обозначается
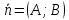
Теорема.
Алгебраическое уравнение 1-й степени
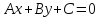
где
коэффициенты
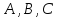
одновременно не равные нулю, являетсяуравнением
прямой на плоскости
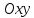
а вектор
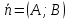
Верно
обратное:
на координатной плоскости
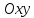
любой прямой с нормальным вектором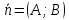
может быть записано в виде алгебраического
уравнения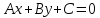
Определение.
Уравнение прямой вида
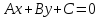
где
коэффициенты
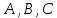
одновременно не равные нулю, называетсяобщим
уравнением прямой.
Известно,
что прямая определяется двумя точками.
Пусть
и
–
точки, лежащие на прямой
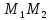
–
произвольная точка этой прямой. Тогда
векторы
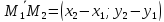
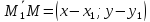
пропорциональны. Получаемуравнение
прямой, проходящей через две точки:
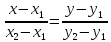
Определение.
Вектор,
параллельный прямой, называется
направляющим
вектором прямой.
Определение.
Пусть
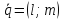
предыдущего уравнения получаемканоническое
уравнение прямой:
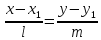
Определение.
В
тех же обозначениях, параметрическое
уравнение прямой
имеет вид:
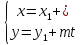
Определение.
Уравнение прямой вида
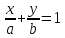
где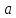
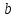
действительные числа, называетсяуравнением
прямой в отрезках.
Теорема.
Пусть
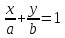
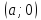
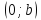
прямой с осями координат.
Определение.
Уравнение прямой вида

где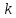
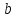
называетсяуравнением
прямой с угловым коэффициентом,
коэффициент
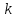
коэффициентом данной
прямой.
Теорема.
Пусть
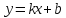
Тогда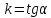
где угол
α
равен углу наклона данной прямой к оси
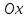
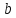
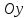
Если
известны угловые коэффициенты
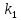
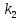
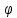
формуле:
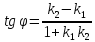
Признаком
параллельности двух прямых является
равенство их угловых коэффициентов:
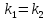
Признаком
перпендикулярности двух прямых является
соотношение:
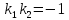
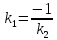
Теорема.
(Связь нормального вектора прямой с её
направляющим вектором и её угловым
коэффициентом.)
1)
Если
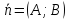
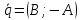
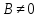
то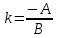
2)
Если
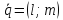
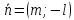
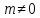
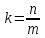
3)
Если
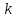
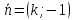
–
направляющий вектор.
Взаимное
расположение двух прямых на плоскости.
Две
прямые на плоскости могут пересекаться,
совпадать или быть параллельными.
Теорема.
Пусть прямые заданы общими уравнениями:
L1: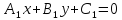
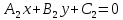
Тогда:
1)
если
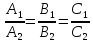
то прямые совпадают, и система уравнений
имеет
бесконечное множество решений;
2)
если
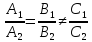
уравнений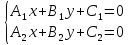
3)
если
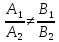
точки их пересечения являются единственным
решением системы уравнений
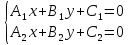
Определение.
Уравнение вида
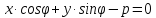
где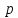
координат, называетсянормальным
уравнением прямой,
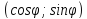
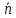
Чтобы
привести прямую к указанному виду,
разделим общее уравнение прямой на
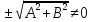
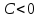
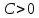
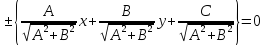
Теорема.
Орт нормального вектора
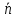
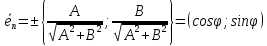
где
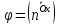
Теорема.
Расстояние от прямой до произвольной
точки
находится
по формуле:
Чтобы
найти расстояние
между двумя параллельными прямыми,
нужно взять произвольную точку на одной
из прямых и найти расстояние от нее до
другой прямой.
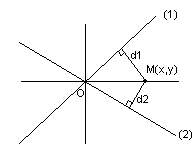
Чтобы
найти множество
точек, равноудаленных от двух прямых
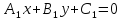
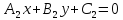
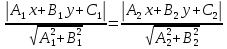
Раскрывая
модули в случае параллельных прямых,
получаем параллельную им прямую, лежащую
между данными прямыми, а в случае
пересекающихся прямых – биссектрисы
углов,
образованных пересечением прямых.
Определение.
Совокупность прямых, проходящих через
некоторую точку S,
называется пучком
прямых с центром S.
Теорема.
Если
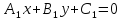
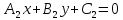
в точкеS,
то уравнение:
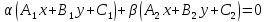
где
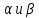
одновременно нулю, определяют прямую,
также проходящую через точкуS.
Более
того, в указанном уравнении числа всегда
возможно подобрать так, чтобы оно
определяло любую (заранее назначенную)
прямую, проходящую через точку S,
иначе говоря, любую прямую пучка с
центром S.
Поэтому уравнение вида называется
уравнением пучка с центром S.
Решение
типовых задач
Задача
№1:
Даны
уравнения двух сторон параллелограмма
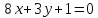
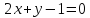
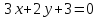
Определить координаты вершин этого
параллелограмма.
Решение:
Найдём
координаты т.
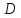
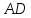
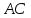
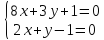
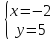
т.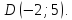
Подставим
координаты т.
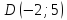
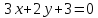
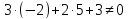
т.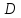
следовательно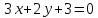
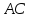
Найдём
координаты т.
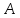
как точки пересечения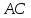
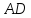
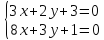
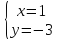
т.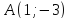
Найдём
координаты т.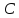
как точки пересечения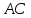
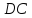
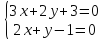

т.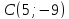
Найдём
координаты т.B:
в параллелограмме диагонали делят друг
друга пополам:
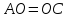
Найдём координаты т.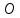
т.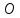
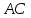
следовательно, т.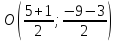
т.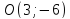
но т.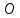
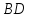
следовательно,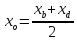
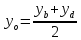
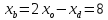
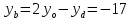
т.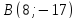
Ответ:
Задача
№2:
Дана
прямая
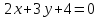
Составить уравнение прямой, проходящей
через точку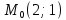
-
параллельно
данной прямой. -
перпендикулярно
к данной прямой.
Решение:
-
Искомая
прямая параллельна прямой
,
поэтому её уравнение имеет вид:.
Найдём
т.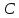
точка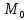
координаты удовлетворяют записанному
уравнению: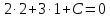
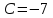
Итак, прямая принимает вид: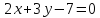
-
Т.к.
заданная и искомые прямые перпендикулярны,
то их угловые коэффициенты удовлетворяют
условию:
.
Найдём
угловой коэффициент прямой
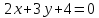
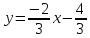
итак,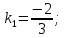
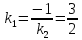
Запишем уравнение искомой прямой: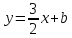
Точка
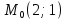
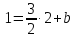
Уравнение
прямой принимает вид:
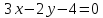
Ответ:
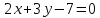
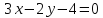
Задача
№3:
Определить,
при каких значениях a
и b
две прямые
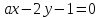
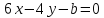
-
имеют
одну общую точку; -
параллельны;
-
совпадают.
Решение:
-
Прямые
имеют одну общую точку, когда они не
параллельны (их коэффициенты при x
и y
не пропорциональны):
;
-
Прямые
параллельны, когда коэффициенты при x
и y
пропорциональны:
;
.
-
Прямые
совпадают, когда все их коэффициенты
пропорциональны:
;
.
Задача
№4:
Найти
проекцию точки
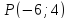
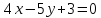
Решение:
Проведём
через т.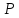
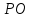
перпендикулярную прямой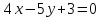
Точка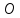
проекцией.
Прямая
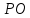
её направляющим вектором служит
нормальный вектор прямой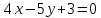
т.е.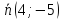
Запишем
уравнение прямой
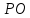
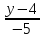
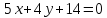
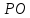
Найдём
координаты т.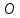
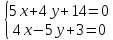
т.
Ответ:
Задача
№5:
Найти
точку
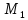
симметричную точке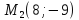
точки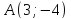
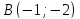
Решение:
Составим
уравнение
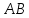
как прямой проходящей через 2 точки:
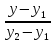
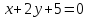
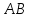
Найдём
уравнение прямой
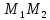
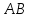
Нормальный
вектор
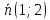
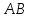
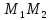
поэтому используем каноническое
уравнение прямой: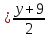
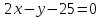
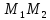
Найдём
координат т.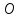
как точки пересечения прямых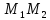
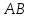
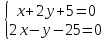
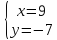
т.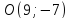
Так
как точка

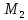
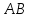
следовательно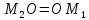
то есть т.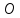
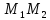
Найдём координаты точки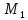
зная начало и середину отрезка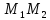
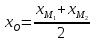
, тогда
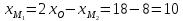
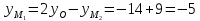
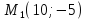
Ответ:
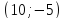
Задача
№6:
Даны
вершины треугольника
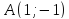
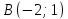
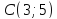
Составить уравнение перпендикуляра,
опущенного из вершины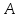
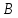
Решение:
Найдём
координаты т.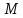
как середины отрезка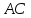
т.
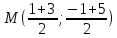
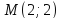
Запишем
уравнение медианы
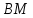
как прямой, проходящей через две известные
точки:
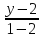
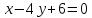
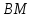
Нормальный
вектор для
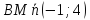
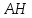
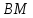
тогда уравнение примет вид:
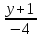
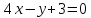
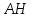
Ответ:
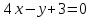
Задача
№7:
Даны
вершины треугольника

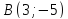
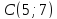
Составить уравнение перпендикуляра,
опущенного из вершины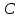
вершине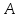
Решение:
Пусть
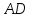
Найдём
координаты т.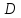
Тогда:
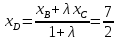
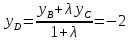
т.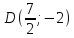
Уравнение
биссектрисы
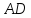
=
⇒
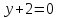
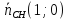
Точка
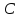
поэтому уравнение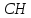
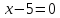
Ответ:
Задача
№8:
Две
стороны квадрата лежат на прямых
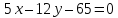
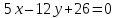
Вычислить его площадь.
Решение:
-
Выберем
на прямой
некоторую точку
:
пусть
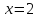
тогда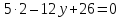
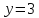
т.е.
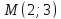
-
Найдём
расстояние от точки
до прямой
:
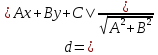
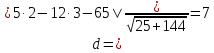
где
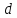
-
т.е.
.
Ответ:
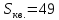
Задача
№9:
Даны
две противоположные вершины квадрата
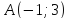
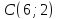
Составить уравнения его сторон.
Решение:
Зная
вершины
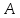

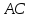
как прямой проходящей через две точки: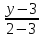
– уравнение прямой
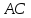
Т.к.
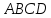
биссектрисами, поэтому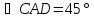
найдём угловой коэффициент
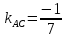
Зная
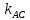

найдём угловой коэффициент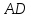
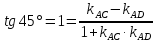
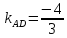
Уравнение
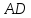
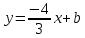
Найдём
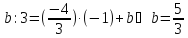
Тогда уравнение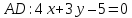
Т.к.
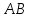
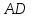
угловой коэффициент
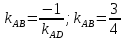
Уравнение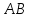
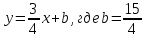
тогда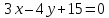
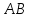
Т.к.
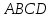
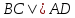
то уравнение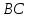
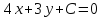
Зная,
что точка
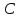
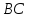
найдём свободный член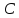
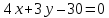
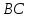
Аналогично
найдём уравнение стороны
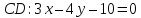
Ответ:
Задача
№10:
Вычислить
площадь треугольника, отсекаемого
прямой
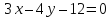
Решение:
Запишем
уравнение прямой
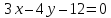
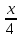
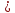
Из
этого уравнения следует, что длины
отрезков
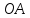
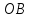
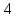
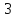
поэтому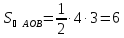
Ответ:
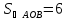
Задача
№11:
Составить
уравнения сторон треугольника, зная
одну из его вершин

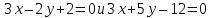
Решение:
Выясним,
что точка
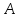
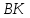
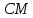
Найдём
координаты точки
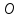
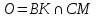
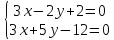
т.
Продолжим
медиану
и на её продолжении отложим отрезок
Соединим точку
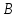
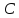
Полученный четырёхугольник
пересекаясь в точке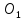
делятся пополам).
Найдём
координаты точки
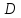
как конца отрезка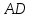

Найдём
уравнение прямой
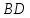
зная, что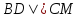

Найдём
координаты вершины
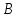
как точки пересечения прямых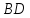
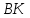
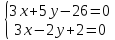
т.
Точка
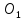
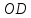
поэтому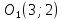
Найдём
координаты точки
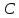
как конца отрезка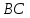
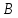
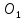
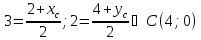
Зная
координаты всех вершин треугольника
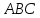
найдём уравнения его сторон, как прямых
проходящих через две точки.
Ответ:
Задача
№12:
Составить
уравнения сторон треугольника, зная
одну из его вершин
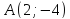
Решение:
Очевидно,
что точка

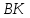
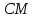
Найдём точку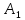
симметричную точке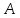
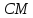
Можно доказать, что точка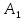
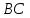
Опустим из т.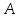
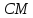
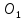
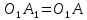
Т.к.
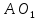
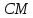
то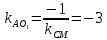
точка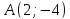
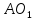
поэтому её уравнение примет вид:
Координаты
точки
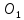
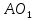
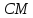
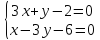
т.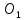
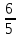
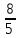
Найдём
координаты точки
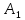
как конца отрезка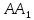
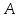
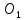
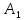
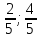
Аналогично
найдём точку
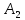
симметричную т.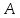
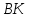
Точка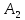
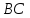
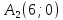
Тогда
уравнение стороны
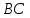
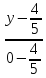
Найдём
координаты точек
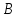
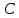
как точек пересечения прямой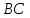
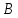
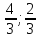
Зная
координаты вершин треугольника
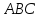
найдём уравнения его сторон.
Ответ:
Задача
№13:
Составить
уравнения биссектрис углов, образованных
двумя пересекающимися прямыми:
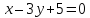
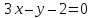
Решение:
Известно
свойство: биссектриса есть геометрическое
место точек, равноудалённых от сторон
угла.
Пусть
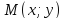
тогда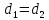
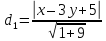
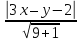
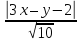
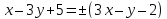
Тогда
уравнения биссектрис примут вид:
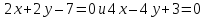
Ответ:
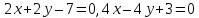
Задача
№14:
Составить
уравнение биссектрисы угла между прямыми
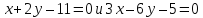
в котором лежит точка
Решение:
Найдём
отклонение точки
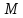
прямых, для этого приведём их уравнения
к нормальному виду: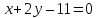
нормирующий множитель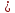
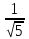
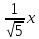
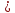
Найдём
отклонение
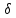
т.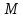
нормального уравнения подставим
координаты т.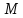
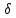
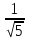
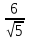
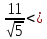
Аналогично
найдём отклонение
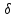
т.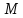
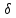
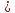
Отклонения имеют разные знаки, поэтому
при раскрытии модулей (см. решение
предыдущей задачи) справа ставим знак
«минус».
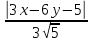
Уравнение
биссектрисы принимает вид:
Ответ:
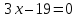
Задача
№15:
На
прямой
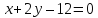
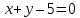
Решение:
Точки
равноудалённые от прямых
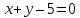
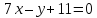
лежат на биссектрисах углов, образованных
этими прямыми. Аналогично решению
предыдущих задач найдём их:
Тогда
искомые точки являются точками пересечения
этих биссектрис и прямой
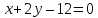
поэтому найдём их, решая системы: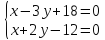
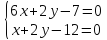
Ответ:
Задача
№16:
Составить
уравнения сторон треугольника, зная
одну из его вершин
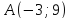
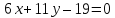
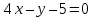
проведённых из различных вершин.
Решение:
Убедимся,
что точка
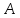
высоте.
Найдём
уравнение стороны
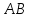
зная, что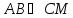
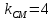
тогда уравнение примет вид:
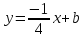
зная координаты т.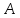
принадлежащей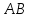
найдём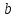
тогда уравнение примет вид: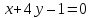
Найдём
координаты т.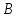
как точки пересечения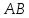
медианы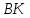
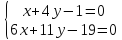
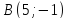
Пусть
точка
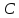
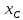
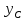
найдём их. Точка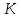
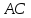
поэтому
Точка
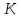
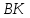
точка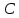
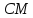
поэтому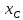
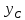
Откуда
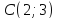
найдём уравнения всех его сторон.
Ответ:
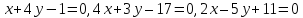
Задача
№17:
Через
точку
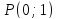
заключённый между прямыми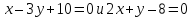
делился бы в точке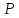
Решение:
Обозначим
через
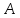
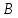
искомой прямой и пусть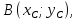
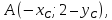
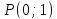
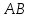
Координаты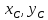
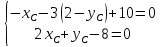
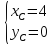
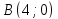
Составим
уравнение искомой прямой, которая
проходит через две точки, например,
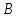
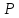
Ответ:
Задача
№18:
Составить
уравнения сторон треугольника
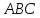
зная одну из его вершин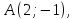
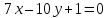
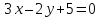
проведённых из одной вершины. Решить
задачу, не вычисляя координат вершин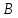
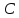
Решение:
Можно
проверить, что т.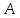
ни биссектрисе.
Найдём уравнение стороны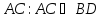
поэтому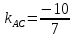
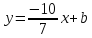
зная координаты т.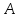
найдём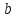
Итак,
уравнение
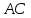
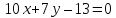
Рассмотрим
пучок с центром в т.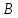
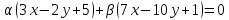
Пусть
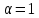
тогда уравнение пучка примет вид:
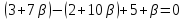
(1)
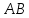
пучка, причём координаты т.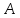
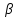
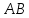
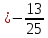
поэтому уравнение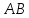
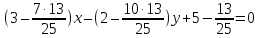
т.е.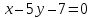
Найдём
угол между прямыми
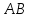
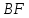
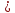
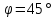
Тогда
угол
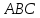
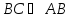
—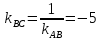
С другой стороны найдём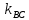
Итак,
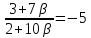
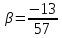
Найдём
уравнение стороны
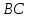
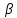
стороны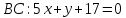
Ответ:
Образовательным
результатом после изучения данной темы
является сформированность компонент,
заявленных во введении, совокупности
компетенций (знать, уметь, владеть) на
двух уровнях: пороговый и продвинутый.
Пороговый уровень соответствует оценке
«удовлетворительно», продвинутый
уровень соответствует оценкам «хорошо»
или «отлично» в зависимости от результатов
защиты кейс-заданий.
Для
самостоятельной диагностики данных
компонент вам предлагаются следующие
задания.
Решение: согласно условия задачи нужно найти уравнение прямых, на которых лежат диагонали параллелограмма. Уравнения прямых будем искать по формуле уравнения прямой, проходящей через две заданные точки, т.е. нужно найти все четыре вершины параллелограмма.
1. Известна одна вершина с координатами A(3,-1), проверим принадлежит ли она данным прямым:
A(3,-1) ( l_1: quad 2x-y+3 = 0 => 2*3 — (-1)+3 ne 0 )
A(3,-1) ( l_2: quad x+3y-2 = 0 => 3 + 3(-1)-2 ne 0 )
Получили, что точка не принадлежит прямым.
Согласно условия задачи, две стороны параллелограмма лежат на двух прямых ( l_1: quad 2x-y+3=0 ) и ( l_2: quad x+3y-2=0), определим взаимное расположение этих прямых.
Прямые могут быть коллинеарными или пересекающимися
Проверяем прямые на коллинеарность
Две прямые называются коллинеарными, если они параллельны или совпадают
Прямые (l_1: quad A_1x+B_1y+C_1=0 ) и (l_2: quad A_2x+B_2y+C_2=0) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число ( lambda ne 0) , что (A_1 = lambda A_2), (B_1 = lambda B_2) , но ( C_1 ne lambda C_2).
По другому это условие можно записать $$l_1||l_2: quad frac{A_1}{A_2} =frac{B_1}{B_2} ne frac{C_1}{C_2} $$
Прямые (l_1, l_2) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны: (A_1 = lambda A_2), (B_1 = lambda B_2) , ( C_1 = lambda C_2).
По другому это условие можно записать $$ l_1≡ l_2: quad frac{A_1}{A_2} =frac{B_1}{B_2} = frac{C_1}{C_2} $$
Проверяем на коллинеарность прямые ( l_1: quad quad 2x-y+3=0) и ( l_2: quad x+3y-2=0). $$ frac{2}{1} ne frac{-1}{3} ne frac{3}{-2} $$
Вывод: прямые не являются коллинеарными.
2. Найдем вторую вершину — точку пересечения прямых ( l_1: quad 2x-y+3=0 ) и ( l_2: quad x+3y-2=0)
Составим систему уравнений $$ begin{cases}2x-y+3=0 \ x+3y-2=0end{cases} => begin{cases} 2x-y+3=0 \ 2x+6y-4=0 end{cases} => begin{cases}x=-1\ y=1end{cases}$$
Получили точку пересечения С(-1;1)
Вывод: точка пересечения двух сторон — вершина параллелограмма С(-1;1).
Получили две вершины, которые лежат на одной диагонали A(3;-1) и C(-1;1).
Найдем уравнение первой диагонали, проходящей через две заданные точки по формуле ( frac{x-x_1}{x_2-x_1} = frac{y-y_1}{y_2-y_1}).
Подставляем координаты вершин A(3;-1) и C(-1;1) в уравнение и получим искомое уравнение диагонали $$ frac{x-3}{-1-3} = frac{y+1}{1+1} => y = frac{1}{2} — frac{1}{2}x$$
Ответ: получили первое уравнение прямой, на которой лежит диагональ ( y = frac{1}{2} — frac{1}{2}x )
3. Найдем третью вершину.
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Получаем, что через вершину C проходит две прямые, параллельные известным, найдем их, для этого применим формулу уравнения прямой, проходящей через заданную точку в заданном направлении. Направление — угловой коэффициент прямой (y — y_0 = k(x-x_0)). Для параллельных прямых известно свойство — угловые коэффициенты параллельных прямых равны (k_1=k_2).
Рассмотрим прямую ( l_1: quad quad 2x-y+3=0 ) преобразуем канонической уравнение прямой в уравнение прямой с угловым коэффициентом ( y = kx+b)
( l_1: quad quad 2x-y+3=0 => y = 2x+3 => k=2)
Найдем искомое уравнение прямой, для точки A(3;-1) с угловым коэффициентом ( k =2), получаем (y+1 = 2(x-3) => y = 2x-7)
найдем точку пересечения полученной прямой ( y = 2x-7 ) и ( l_2: quad x+3y-2 = 0 ). Составим и решим систему уравнений $$ begin{cases}y = 2x-7 \ x+3y-2 = 0end{cases} => begin{cases}y = 2x-7 \ 2x+6y-4 = 0end{cases} => begin{cases}y = — frac{3}{7} \ x = frac{23}{7} end{cases}$$
Получили координаты искомой вершины (B( frac{23}{7}; — frac{3}{7} ))
Рассмотрим прямую ( l_2: quad x+3y-2 = 0 ) преобразуем канонической уравнение прямой в уравнение прямой с угловым коэффициентом ( y = kx+b)
( l_2: quad quad x+3y-2 = 0 => y = frac{2}{3} — frac{1}{3}x => k = — frac{1}{3})
Найдем искомое уравнение прямой, для точки A(3;-1) с угловым коэффициентом ( k = — frac{1}{3}), получаем (y+1 = — frac{1}{3}(x-3) => y = — frac{1}{3}x )
4. Найдем четвертую вершину.
Найдем точку пересечения полученной прямой ( y = — frac{1}{3}x ) и ( l_1: quad 2x-y+3 = 0 ). Составим и решим систему уравнений $$ begin{cases} y = — frac{1}{3}x \ 2x-y+3 = 0 end{cases} => begin{cases} y = frac{3}{7} \ x = -frac{9}{7} end{cases} $$
Получили координаты искомой вершины (D( -frac{9}{7}; frac{3}{7} ))
Найдем уравнение второй диагонали, проходящей через две заданные точки по формуле ( frac{x-x_1}{x_2-x_1} = frac{y-y_1}{y_2-y_1}).
Подставляем координаты вершин (B( frac{23}{7}; — frac{3}{7} )) и (D( -frac{9}{7}; frac{3}{7} )) в уравнение и получим искомое уравнение диагонали $$ frac{x-frac{23}{7}}{- frac{9}{7}-frac{23}{7}} = frac{y+ frac{3}{7}}{frac{3}{7}+ frac{3}{7}} => y = -frac{3}{16}x + frac{3}{16}$$
Ответ: получили второе уравнение прямой, на которой лежит диагональ ( y = -frac{3}{16}x + frac{3}{16} )
Ответ: уравнения диагоналей параллелограмма ( y = frac{1}{2} — frac{1}{2}x ) и ( y = -frac{3}{16}x + frac{3}{16} )
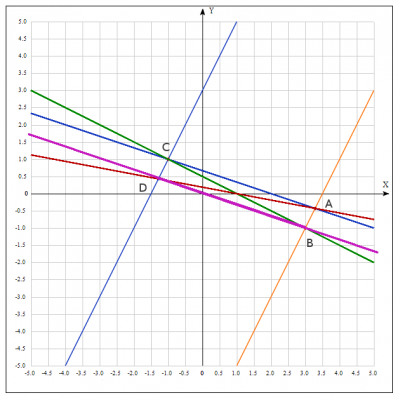
Строим рисунок:
210
-3), M5(3; -1), M6(-2; 1) лежат
на прямой
P2, P3, P4, P5 расположены
на прямой
числам 4; 0; 2; -2; -6. Определить ординаты этих точек.
Q2, Q3, Q4, Q5 расположены
на прямой
числам 1; 0; 2; -1, 3. Определить абсциссы этих точек.
пересечения прямой
осями и построить эту прямую на чертеже.
пересечения двух прямых
треугольника АВС даны соответственно
уравнениями
координаты его вершин.
сторон параллелограмма
его диагоналей
Определить координаты вершин
этого параллелограмма.
треугольника лежат на прямых
треугольника S=8, две его вершины суть точки А(1; -2),
В(2; 3), а третья вершина С лежит на прямой
треугольника S=1,5, две его вершины суть точки А(2;
-3), В(3; -2), центр масс этого треугольника лежит на
прямой
Определить координаты третьей
вершины С.
уравнение прямой и построить прямую на чертеже,
зная ее угловой коэффициент k и отрезок b,
отсекаемый ею на оси Oy:
коэффициент k и отрезок b, отсекаемый на оси Oy, для
каждой из прямых:
прямой:
данной прямой;
данной прямой.
проходящей через точку М0(2; 1):
прямой;
данной прямой.
сторон прямоугольника
А(2; -3). Составить уравнения двух других сторон
этого прямоугольника.
сторон прямоугольника
его диагоналей
Найти вершины прямоугольника.
точке Р(-5; 13) относительно прямой
симметричную точке Р(-5; 13) относительно прямой
следующих случаев составить уравнение прямой,
параллельной двум данным прямым и проходящей
посередине между ними:
коэффициент k прямой, проходящей через две данные
точки:
-5), M2(3; 2);
уравнения прямых, проходящих через вершины
треугольника A(5; -4), B(-1; 3), C(-3; -2) параллельно
противоположным сторонам.
сторон треугольника M1(2; 1), M2(5;
3), M3(3; -4). Составить
уравнение его сторон.
Q(-1; 0). Составить уравнение прямой, проходящей
через точку Q перпендикулярно к отрезку
уравнение прямой, если точка P(2; 3) служит
основанием перпендикуляра, опущенного из начала
координат на эту прямую.
треугольника M1(2; 1), M2(-1; -1),
M3(3; 2). Составить уравнения
его высот.
треугольника даны уравнениями
высот.
треугольника A(1; -1), B(-2; 1), C(3; 5). Составить
уравнение перпендикуляра, опущенного из вершины
А на медиану, проведенную из вершины В.
треугольника A(2; -2), B(3; -5), C(5; 7). Составить
уравнение перпендикуляра, опущенного из вершины
С на биссектрису внутреннего угла при вершине А.
уравнения сторон и медиан треугольника с
вершинами A(3; 2), B(5; -2), C(1; 0).
прямая. Определить точки пересечения этой прямой
с осями координат.
Доказать,
что условие, при котором три точки M1(x1,
y1), M2(x2, y2), M3(x3,
y3) лежат на одной прямой,
может быть записано в следующем виде:
Доказать,
что уравнение прямой, проходящей через две
данные точки M1(x1, y1),
M2(x2, y2), может
быть записано в следующем виде:
последовательные вершины выпуклого
четырехугольника A(-3; 1), B(3; 9), C(7; 6), D(-2; -6).
Определить точку пересечения его диагоналей.
вершины A(-3; -1), B(2; 2) параллелограмма ABCD и точка Q(3;
0) пересечения его диагоналей. Составить
уравнения сторон этого параллелограмма.
сторон прямоугольника
диагонали
сторон и второй диагонали этого прямоугольника.
треугольника A(1; -2), B(5; 4), C(-2; 0). Составить
уравнения биссектрис его внутреннего и внешнего
углов при вершине А.
уравнение прямой, проходящей через точку P(3; 5) на
одинаковых расстояниях от точек A(-7; 3) и B(11; -15).
точки P(-8; 12) на прямую, проходящую через точки A(2;
-3), B(-5; 1).
-9) относительно прямой,
проходящей через точки А(3; -4), B(-1; -2).
найти такую точку P, чтобы сумма ее расстояний до
точек M(1; 2), N(3; 4) была наименьшей.
найти такую точку P, чтобы сумма ее расстояний до
точек M(-3; 2), N(2; 5) была наибольшей.
расстояний которой до точек A(-7; 1), B(-5; 5) была бы
наименьшей.
расстояний которой до точек A(4; 1), B(0; 4) была бы
наибольшей.
проходящей через точку M0(2; 1) под углом 450 к данной прямой.
является вершиной квадрата, диагональ которого
лежит на прямой
уравнения сторон и второй диагонали этого
квадрата.
противоположные вершины квадрата A(-1; 3), C(6; 2).
Составить уравнения его сторон.
центром квадрата, одна из сторон которого лежит
на прямой
прямых, на которых лежат остальные стороны этого
квадрата.
Ox направлен луч света. Известно, что
до оси Ox, луч от нее отразился. Составить
уравнения прямых, на которых лежат падающий и
отраженный лучи.
по прямой
Составить уравнение прямой, на которой лежит
отраженный луч.
сторон треугольника
равнобедренный. Решить задачу при помощи
сравнения углов треугольника.
уравнение прямой, проходящей через точку M1(x1; y1) параллельно
прямой
уравнение прямой, проходящей через точку М1(2: -3) параллельно
прямой:
условие перпендикулярности прямых
в следующем виде:
из следующих пар прямых перпендикулярны. Решить
задачу, не вычисляя угловых коэффициентов данных
прямых.
Доказать,
что формула для определения угла между
прямыми ,
может
быть записана в следующей форме:
задачу, не вычисляя угловых коэффициентов данных
прямых.
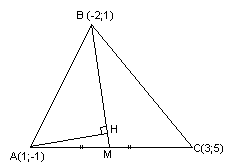
треугольника M1(-10; 2), M2(6; 4);
его высоты пересекаются в точке
N(5; 2). Определить координаты третьей вершины M3.
-1), B(5; 7) треугольника ABC и точка N(4; -1) пересечения
его высот. Составить уравнения сторон этого
треугольника.
даны: уравнение стороны АВ:
высот АМ:
других сторон и третьей высоты этого
треугольника.
уравнения сторон треугольника АВС, если даны
одна из его вершина А(1; 3) и уравнения двух медиан
уравнения сторон треугольника, сли даны одна из
его вершин B(-4; -5) и уравнения двух высот
уравнения сторон треугольника, зная одну из его
вершин A(4; -1) и уравнения двух биссектрис
уравнения сторон треугольника, зная одну из его
вершин B(2; 6), а также уравнения высоты
биссектрисы
уравнения сторон треугольника, зная одну его
вершину B(2; -1), а также уравнения высоты
различных вершин.
уравнения сторон треугольника, зная одну его
вершину C(4; -1), а также уравнения высоты
одной вершины.
уравнения сторон треугольника, зная одну его
вершину B(2; -7), а также уравнения высоты
различных вершин.
уравнения сторон треугольника, зная одну его
вершину C(4; 3), а также уравнения биссектрисы
одной вершины.
уравнения сторон треугольника, зная одну его
вершину A(3; -1), а также уравнения биссектрисы
различных вершин.
уравнение прямой, которая проходит черезначало
координат и вместе с прямыми
треугольник с площадью, равной 1,5.
проходящих через точку P(3; 0), найти такую, отрезок
которой, заключенный между прямыми
пополам.
проведены всевозможные прямые. Доказать, что
отрезок каждой из них, заключенный между прямыми
в точке Р пополам.
проведены всевозможные прямые. Доказать, что
среди них нет прямой, отрезок которой,
заключенный между прямыми
пополам.
уравнение прямой, проходящей через начало
координат, зная, что длина ее отрезка,
заключенного между прямыми
уравнение прямой, проходящей через точку С(-5; 4),
зная, что длина ее отрезка, заключенного между
прямыми
Решение типового варианта контрольной работы. Аналитическая геометрия.
Задача №1.
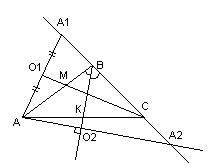
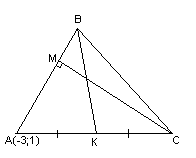
Даны три последовательные вершины параллелограмма А(2;-3), В(5;1),С(3;-4). Не находя координаты вершины D, найти:
1) уравнение стороны AD;
2) уравнение высоты BK, опущенной из вершины В на сторону AD;
3) длину высоты BK;
4) уравнение диагонали BD;
5) тангенс угла между диагоналями параллелограмма.
Записать общие уравнения найденных прямых. Построить чертеж.
Решение.
Сначала построим чертеж. Построим в прямоугольной декартовой системе координат точки ,
,
. Построим отрезки
и
.
Рис. 1
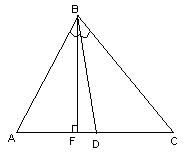
Достроим полученный рисунок до параллелограмма и нанесем на чертеж высоту BK.
Рис. 2
1) Составим уравнение прямой AD.
А) Предварительно найдем уравнение прямой BС. Уравнение прямой, проходящей через точки и
, имеет вид
(3.1)
По условию ,
. Подставим координаты точек
и
в уравнение (3.1):
, т. е.
.
Запишем полученное уравнение в общем виде, то есть в виде . Для этого в последнем уравнении избавимся от знаменателей
и проведем преобразования, перенося все слагаемые в левую часть равенства:
или
.
Из этого уравнения выразим :
;
. Получили уравнение вида
— уравнение с угловым коэффициентом.
Б) Воспользуемся тем фактом, что противоположные стороны параллелограмма параллельны. Составим искомое уравнение прямой AD как уравнение прямой, проходящей через точку параллельно прямой
.
Уравнение прямой, проходящей через данную точку в данном направлении, имеет вид
(3.2)
Где направление определяется угловым коэффициентом .
Условие параллельности двух прямых и
имеет вид
(3.3)
По условию задачи , прямая
. Подставим координаты точки
в уравнение (3.2):
. Так как прямая
параллельна прямой
, то в силу формулы (3.3) их угловые коэффициенты совпадают. Угловой коэффициент прямой
равен
, следовательно, уравнение прямой
имеет вид
.
Запишем уравнение прямой в общем виде. Для этого раскроем скобки и все слагаемые перенесем в левую часть равенства:
. Умножим обе часть равенства на (-2) и получим общее уравнение прямой
:
.
Запишем уравнение прямой в виде с угловым коэффициентом. Для этого выразим
из общего уравнения:
.
2) Составим уравнение высоты , проведенной из вершины
на сторону
как уравнение прямой, проходящей через точку
перпендикулярно прямой
.
Условие перпендикулярности двух прямых и
имеет вид
(3.4)
Подставим координаты точки в уравнение (3.2):
. Так как высота
перпендикулярна прямой
, то их угловые коэффициенты связаны соотношением (3.4). Угловой коэффициент прямой
равен
, следовательно, угловой коэффициент высоты
равен
и уравнение прямой
имеет вид
. Запишем уравнение высоты
в общем виде:
. Запишем это же уравнение в виде с угловым коэффициентом:
.
3) Найдем длину высоты как расстояние от точки
до прямой
.
Расстояние от точки
до прямой
представляет собой длину перпендикуляра, опущенного из точки на прямую и определяется формулой
(3.5)
Так как перпендикулярна
, то длина
может быть найдена с помощью формулы (3.5). По условию
, прямая
определяется уравнением
. В силу формулы (3.5) длина высоты
равна

.
4) Найдем уравнение диагонали как уравнение прямой, проходящей через точки
И
, где
— середина отрезка
.
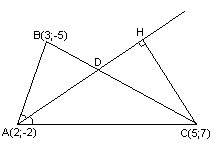
А) Если и
, то координаты точки
— середины отрезка
, определяются формулами
(3.6)
По условию ,
. В силу формул (3.6) имеем:
,
. Следовательно
.
Б) Так как точка пересечения диагоналей является их серединой, то точка (середина отрезка
) является точкой пересечения диагоналей и диагональ
проходит через точку
.
Воспользуемся уравнением (3.1). По условию ,
. В силу формулы (3.1) уравнение прямой
(диагонали
) имеет вид:


. Запишем это же уравнение в виде с угловым коэффициентом:
.
5) Найдем тангенс угла между диагоналями и
.
А) Найдем уравнение диагонали как уравнение прямой, проходящей через две данные точки.
Воспользуемся уравнением (3.1). По условию ,
. Следовательно,
. Общее уравнение диагонали
имеет вид
, уравнение с угловым коэффициентом – вид
, угловой коэффициент
прямой
равен
.
Б) Уравнение диагонали имеет вид
, ее угловой коэффициент
.
В) Тангенс угла между прямыми
и
определяется формулой
Следовательно, 
.
Задача №2.
Условие задачи №2 несколько различается в зависимости от номера варианта контрольной работы. Приведем решения простейших задач, входящих в это задание.
1) Составить уравнение плоскости, проходящей через точки ,
,
.
Решение.
Уравнение плоскости, проходящей через точки ,
,
имеет вид:

Тогда уравнение плоскости в силу уравнения (3.7) имеет вид


Запишем полученное уравнение в общем виде, т. е. в виде . Для этого раскроем определитель по первой строке
. После преобразований получим:
.
2) Найти нормальный вектор плоскости .
Решение.
Нормальный вектор — это вектор, перпендикулярный плоскости. Если плоскость задана общим уравнением
, то нормальный вектор имеет координаты
.
Рис. 3
Для плоскости нормальным является вектор
=
.
Отметим, что любой вектор, коллинеарный вектору =
так же является нормальным вектором плоскости
. Таким образом, при каждом ненулевом
вектор с координатами
будет являться нормальным вектором рассматриваемой плоскости.
3) Найти косинус угла между плоскостями и
.
Решение.
Угол между двумя плоскостями
и
представляет собой угол между их нормальными векторами и определяется равенством
Для плоскости координаты нормального вектора
определяются равенствами
,
,
. Для плоскости
— равенствами
,
,
. Следовательно,
=
.
4) Составить уравнение плоскости , проходящей через точку
параллельно плоскости
:
.
Решение.
Уравнение плоскости, проходящей через точку , имеет вид
(3.8)
Подставим в уравнение (3.8) координаты точки :
.
Условие параллельности плоскостей и
имеет вид
(3.9)
Так как плоскости и
параллельны, то в качестве нормального вектора
Плоскости
можно взять нормальный вектор
плоскости
, т. е. в формуле (3.9) отношение
можно принять равным единице. Следовательно, уравнение плоскости
примет вид
. Запишем это уравнение в общем виде:
.
5) Найти расстояние от точки до плоскости
:
.
Решение.
Расстояние от точки
до плоскости
представляет собой длину перпендикуляра, опущенного из точки на плоскость, и определяется формулой
(3.10)
Для плоскости координаты нормального вектора
определяются равенствами
,
,
. Следовательно,

6) Составить канонические уравнения прямой, проходящей через точки и
.
Решение.
Уравнения прямой, проходящей через точки и
имеют вид
(3.11)
Так как ,
, то в силу (3.11) получим уравнения
или
.
7) Найти направляющий вектор прямой .
Решение.
Направляющий вектор — это вектор, параллельный прямой.
Если прямая задана каноническими уравнениями , то направляющий вектор
имеет координаты
.
Рис. 4
Для рассматриваемой прямой направляющим вектором является вектор
.
Отметим, что любой вектор, коллинеарный вектору так же является направляющим вектором прямой
. Таким образом, при каждом ненулевом
вектор с координатами
будет являться направляющим вектором рассматриваемой прямой.

и
.
Решение.
Угол между двумя прямыми
и
представляет собой угол между их направляющими векторами и определяется равенством
Для прямой координаты направляющего вектора
определяются равенствами
,
,
. Для прямой
— равенствами
,
,
. Значит,
.
9) Составить канонические уравнения прямой , проходящей через точку
параллельно прямой
:
.
Решение.
Канонические уравнения прямой имеют вид . Здесь
— координаты точки, через которую проходит прямая.
В канонические уравнения прямой подставим координаты точки
. Получим:
.
Условие параллельности прямых и
имеет вид
(3.12)
Так как прямые и
параллельны, то в качестве направляющего вектора
прямой
можно взять направляющий вектор
прямой
, т. е. в формуле (3.12) отношение
можно принять равным единице. Следовательно, уравнение прямой
примет вид
.
10) Найти угол между прямой :
и плоскостью
:
.
Решение.
Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость. Угол между прямой и плоскостью равен
, где
— угол между направляющим вектором
прямой и нормальным вектором
плоскости.
Рис. 5
Угол между прямой
и плоскостью
определяется формулой
Для плоскости :
координаты нормального вектора
определяются равенствами
,
,
. Для прямой
:
координаты направляющего вектора
— равенствами
,
,
. Синус угла между прямой и плоскостью равен
=
. Следовательно,
.
11) Составить уравнение плоскости , проходящей через точку
перпендикулярно прямой
:
.
Решение.
Уравнение плоскости, проходящей через данную точку, имеет вид .
Подставим в указанное уравнение координаты точки . Получим:
.
Условие перпендикулярности плоскости и прямой
имеет вид
(3.13)
Так как искомая плоскость перпендикулярна прямой
, то в качестве нормального вектора
плоскости можно взять направляющий вектор
прямой
, т. е. в формуле (3.13) отношение
можно принять равным единице. Следовательно, уравнение плоскости
примет вид
. Запишем это уравнение в общем виде:
.
12) Составить канонические уравнения прямой , проходящей через точку
перпендикулярно плоскости
:
.
Решение.
Канонические уравнения прямой, проходящей через данную точку, имеют вид .
Подставим в эти уравнения координаты точки . Получим:
Условие перпендикулярности прямой и плоскости
имеет вид
.
Так как прямая перпендикулярна плоскости
, то в качестве направляющего вектора
прямой
можно взять нормальный вектор
плоскости
, т. е. в формуле (3.13) отношение
можно принять равным единице. Следовательно, уравнение прямой
примет вид:
.
13) Найти координаты точки пересечения прямой :
и плоскости
:
.
Решение.
Координаты точки пересечения прямой

представляют собой решение системы

Запишем параметрические уравнения прямой :

в уравнение плоскости
:
. Отсюда
;
. Подставим найденное значение
в параметрические уравнения прямой
:

.
Задача №3.
К кривым второго порядка относятся эллипс (рис.6), гипербола (рис. 7 и 8), парабола (рис. 9-12). Приведем рисунки и канонические уравнения этих кривых.
Эллипс
Рис. 6
Гипербола Гипербола
.
Рис. 7 Рис. 8
Парабола Парабола
Рис. 9
Рис. 10
Парабола Парабола
Рис. 11
Рис. 12
Приведем примеры решения задачи №3.
Пример 1. Привести уравнение кривой второго порядка к каноническому виду и построить кривую.
Решение.
Для приведения уравнения кривой второго порядка к каноническому виду применяют метод выделения полного квадрата.
Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при и
вынесем за скобки:
.
Выделим полный квадрат: . Отсюда
. Разделим обе части равенства на 25:
. Запишем полученное уравнение в каноническом виде:

Выполним параллельный перенос осей координат по формулам 
, уравнение эллипса принимает канонический вид
.
В нашем примере ,
,
,
.
Итак, рассматриваемое уравнение определяет эллипс с центром в точке и полуосями
и
.
Рис. 13
Пример 2. Привести уравнение кривой второго порядка к каноническому виду и построить кривую.
Решение.
Как и в предыдущем примере, сгруппируем слагаемые, содержащие текущие координаты: .
В скобках выделим полный квадрат: ;
. Отсюда
.
Выполним замену переменных 
, вершина параболы в системе координат
расположена в точке
.
Рис. 14
Задача №4.
Кривая задана в полярной системе координат уравнением .
Требуется:
1) найти точки, лежащие на кривой, давая значения через промежуток, равный
, начиная от
до
;
2) построить полученные точки;
3) построить кривую, соединив построенные точки (от руки или с помощью лекала);
4) составить уравнение этой кривой в прямоугольной декартовой системе координат.
Решение.
Сначала построим таблицу значений и
:
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,00 |
1,92 |
1,71 |
1,38 |
1,00 |
0,62 |
0,29 |
0,08 |
0,00 |
0,08 |
0,29 |
0,62 |
1,00 |
1,38 |
1,71 |
1,92 |
Построим эти точки в полярной системе координат. Полярная система координат состоит из начала координат (полюса) и полярной оси
. Координаты точки
в полярной системе координат определяются расстоянием
от полюса (полярным радиусом) и углом
между направлением полярной оси и полярным радиусом (полярным углом). Для того, чтобы построить точку
, необходимо построить луч, выходящий из точки
под углом
к полярной оси; отложить на этом луче отрезок длиной
.
Рис. 15
Построим все точки, определенные в таблице и соединим их плавной линией
Рис. 16
Запишем уравнение рассматриваемой кривой в прямоугольной декартовой системе координат. Для этого воспользуемся формулами перехода от декартовой к полярной системе координат.
Если полюс совпадает с началом координат прямоугольной декартовой системы координат, полярная ось – с осью абсцисс, то между прямоугольными декартовыми координатами и полярными координатами
существует следующая связь:
,
Откуда
Рис. 17
Итак, в уравнении исходной кривой ,
. Поэтому уравнение
принимает вид
. После преобразований получим уравнение
.
Задача №5.
Построить на плоскости геометрическое место точек, определяемое неравенствами
1)
2)
Решение.
Для того, чтобы решить неравенство на плоскости, надо построить график линии
. Кривая
разбивает плоскость на части, в каждой из которых выражение
сохраняет свой знак. Выбирая пробную точку в каждой из этих частей, найдем часть плоскости, являющуюся искомым решением неравенства.
1) Построим прямые и
, заштрихуем область, в которой
. Затем построим параболу
и заштрихуем область, содержащую ось симметрии параболы (расположенную внутри параболы); построим прямую
и заштрихуем область, лежащую выше прямой. Пересечение всех заштрихованных областей и определит множество точек, представляющих решение рассматриваемой системы.
Рис. 18
2) Построим линию, определяемую уравнением . Эта линия представляет собой ту часть окружности
или
, на которой
. Далее построим прямую
(
). Решением рассматриваемого двойного неравенства является часть плоскости, расположенная между нижней половиной окружности
с центром в точке
радиуса
прямой
.
Рис. 19
| < Предыдущая | Следующая > |
|---|

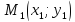
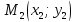
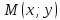


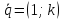
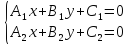
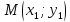
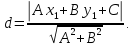

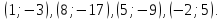
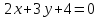 ,
,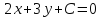 .
.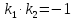 .
.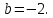
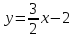
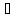
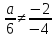 ;
;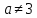
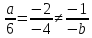 ;
;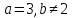 .
.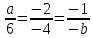 ;
;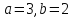 .
.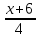
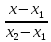
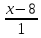
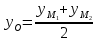
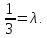
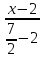
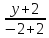
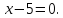
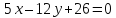 некоторую точку
некоторую точку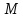 :
: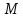 до прямой
до прямой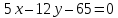 :
: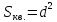 т.е.
т.е.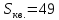 .
.