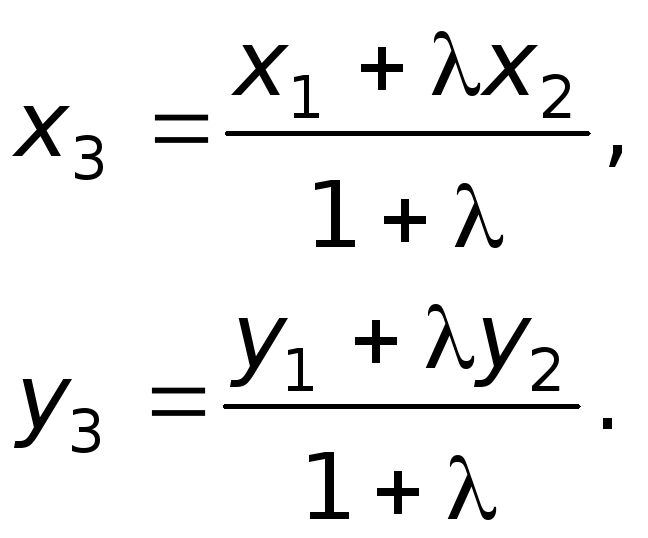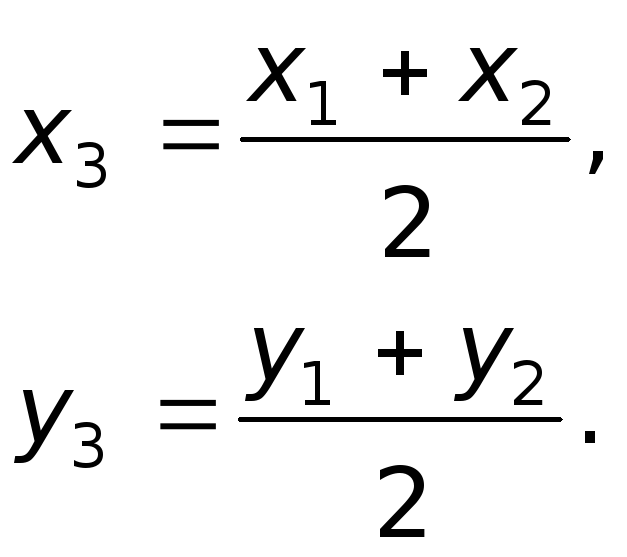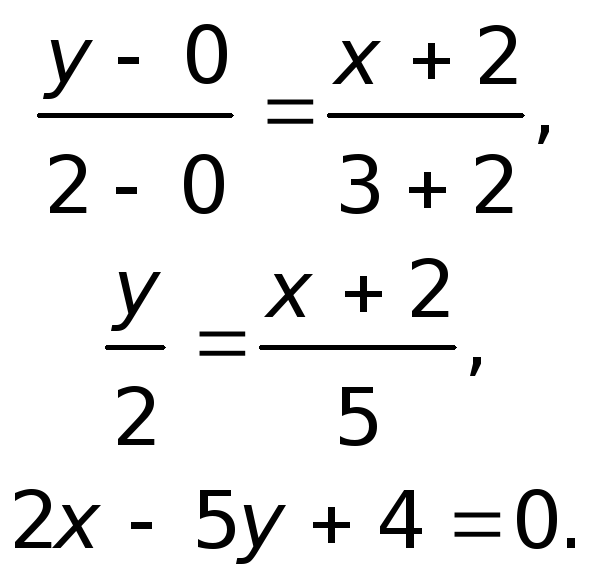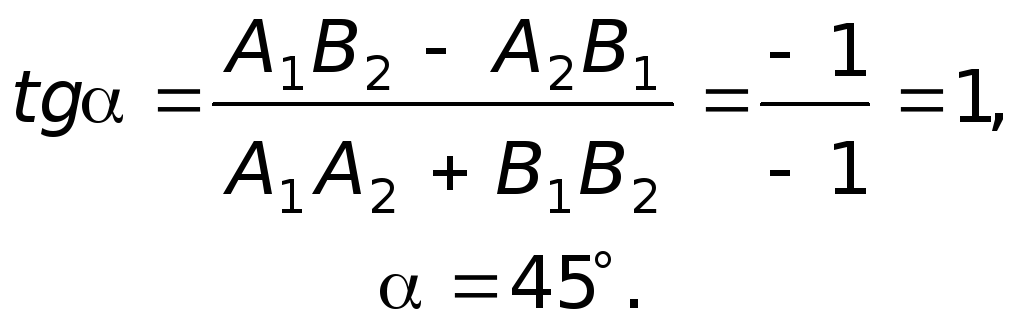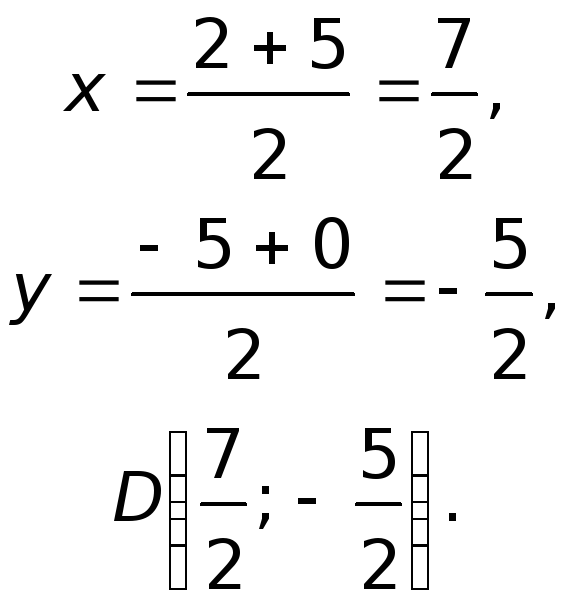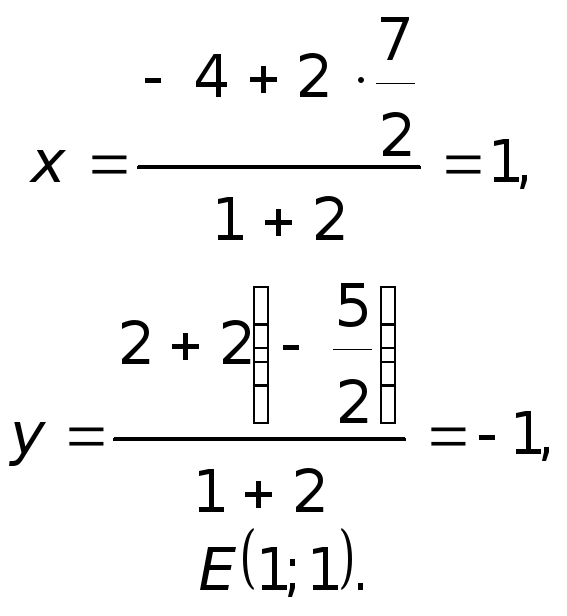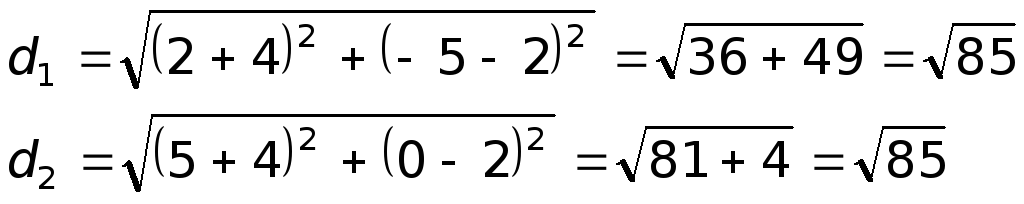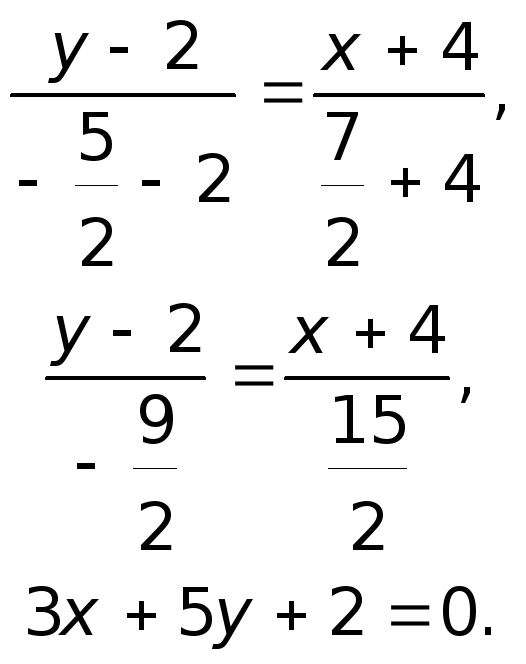Как найти уравнение прямой через высоту - AvtoShod.ru

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

Найти уравнение стороны треугольника.
Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

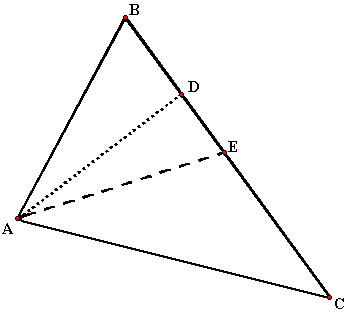
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Общее уравнение прямой: описание, примеры, решение задач

Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.

Общее уравнение прямой: основные сведения

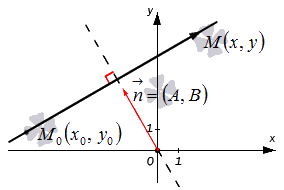
Пусть на плоскости задана прямоугольная система координат O x y .

Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .

указанная теорема состоит из двух пунктов, докажем каждый из них.

Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.

Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .

Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.

Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.

Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .

Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .

Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0

Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .

Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.

Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .

Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.

Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .

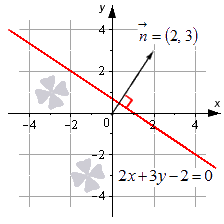
Рассмотрим конкретный пример общего уравнения прямой.

Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.

Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.

Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.

Неполное уравнение общей прямой

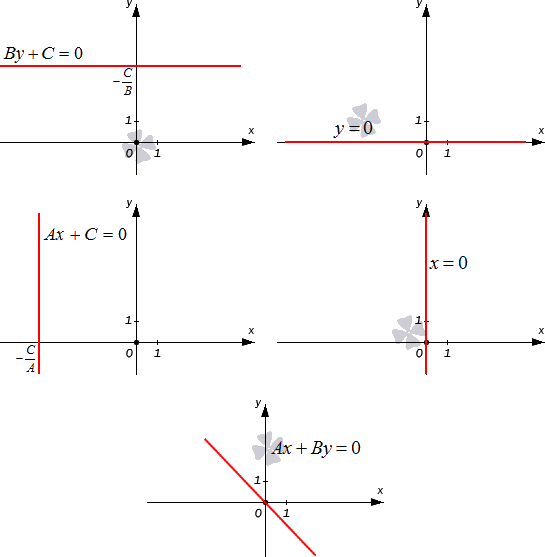
Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.

Разберем все вариации неполного общего уравнения прямой.

Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .

Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.

Решение

Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:

Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0

Ответ: 7 x — 2 = 0

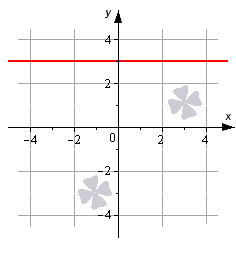
На чертеже изображена прямая, необходимо записать ее уравнение.

Решение

Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .

Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .

Ответ: y — 3 = 0 .

Общее уравнение прямой, проходящей через заданную точку плоскости

Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .

Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.

Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.

Решение

Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:

A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0

Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:

A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0

Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .

Ответ: x — 2 · y + 11 = 0 .

Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.

Решение

Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:

2 3 x 0 — y 0 — 1 2 = 0

Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2

Ответ: — 5 2

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно

Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.

Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .

Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .

Это равенство возможно записать как пропорцию: x + C A — B = y A .

В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .

Перепишем равенство в виде пропорции: x — B = y + C B A .

Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.

Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.

Решение

Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .

Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.

Ответ: x — 3 = y — 4 3 0 .

Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.

Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.

Решение

Осуществим переход от общего уравнения к каноническому:

2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2

Теперь примем обе части полученного канонического уравнения равными λ , тогда:

x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R

Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R

Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .

Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.

Решение

Произведем нужные действия по алгоритму:

2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x

Ответ: y = — 2 7 x .

Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :

A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1

Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.

Решение

Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .

Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .

Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .

Ответ: x — 1 2 + y 1 14 = 1 .

В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.

Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:

x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0

Каноническое уравнение преобразуется к общему по следующей схеме:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0

Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0

Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.

Решение

Осуществим переход от параметрических уравнений к каноническому:

x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0

Перейдем от канонического к общему:

x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0

Ответ: y — 4 = 0

Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.

Решение:

Просто перепишем уравнение в необходимом виде:

x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0

Ответ: 1 3 x + 2 y — 1 = 0 .

Составление общего уравнения прямой

Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.

Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.

Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.

Решение

Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:

A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0

Ответ: 2 x — 3 y — 5 = 0 .

Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.

Решение

Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .

Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:

A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0

Прямая на плоскости. Примеры решений

Решение проводим с помощью калькулятора.
Даны координаты треугольника: A(2,1), B(1,-2), C(-1,0).
1) Координаты векторов
Координаты векторов находим по формуле:
X = x_j — x_i; Y = y_j — y_i
здесь X,Y координаты вектора; x_i, y_i — координаты точки А_i; x_j, y_j — координаты точки А_j
Например, для вектора AB
X = x₂ — x₁; Y = y₂ — y₁
X = 1-2 = -1; Y = -2-1 = -3
AB(-1;-3)
AC(-3;-1)
BC(-2;2)
2) Модули векторов
Длина вектора a(X;Y) выражается через его координаты формулой:

3) Угол между прямыми
Угол между векторами a₁(X₁;Y₁), a₂(X₂;Y₂) можно найти по формуле:

где a₁a₂ = X₁X₂ + Y₁Y₂
Найдем угол между сторонами AB и AC

γ = arccos(0.6) = 53.13 0
4) Проекция вектора
Проекцию вектора b на вектор a можно найти по формуле:

Найдем проекцию вектора AB на вектор AC

5) Площадь треугольника
Пусть точки A₁(x₁; y₁), A₂(x₂; y₂), A₃(x₃; y₃) — вершины треугольника, тогда его площадь выражается формулой:

В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Решение. Принимая A за первую вершину, находим:

Пример. Даны координаты вершин треугольника АВС: А(–3; –1), В(4; 6), С(8; –2).
Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

Задание. Даны координаты вершин треугольника ABC: A(7;4), B(-9;-8), C(-2;16). Требуется:

составить уравнение медианы, проведенной из вершины B, и вычислить ее длину.
составить уравнение высоты, проведенной из вершины A, и вычислить ее длину.
найти косинус внутреннего угла B треугольника ABC.

Сделать чертеж.

Пример №3. Даны вершины A(1;1), B(7;4), C(4;5) треугольника. Найти: 1) длину стороны AB ; 2) внутренний угол A в радианах с точностью до 0,001. Сделать чертеж.
Скачать

Пример №4. Даны вершины A(1;1), B(7;4), C(4;5) треугольника. Найти: 1) уравнение высоты, проведенной через вершину C ; 2) уравнение медианы, проведенной через вершину C ; 3) точку пересечения высот треугольника; 4) длину высоты, опущенной из вершины C. Сделать чертеж.
Скачать

Пример №5. Даны вершины треугольника ABC: A(-5;0), B(7;-9), C(11;13). Определите: 1) длину стороны AB ; 2) уравнение сторон AB и AC и их угловые коэффициенты; 3) площадь треугольника.

Решение
Видео решение

Задание. Найти острый угол между прямыми x + y -5 = 0 и x + 4y — 8 = 0 .
Рекомендации к решению. Задача решается посредством сервиса Угол между двумя прямыми.
Ответ: 30.96 o

Пример №1. Даны координаты точек А1(1;0;2), A2(2;1;1), А3(-1;2;0), A4(-2;-1;-1). Найти длину ребра А1А2. Составить уравнение ребра А1А4 и грани А1А2А3. Составить уравнение высоты опущенной из точки А4 на плоскость А1А2А3. Найти площадь треугольника А1A2A3. Найти объем треугольной пирамиды А1A2А3A4.

Решение
Видео решение

Задание. По координатам вершин пирамиды А1,А2,А3,А4 найти: 1) длины ребер А1А2 и А1А3; 2) угол между ребрами А1А2 и А1А3; 3) площадь грани А1А2А3;4) объем пирамиды А1А2А3А4
A₁(3;5;4,0,0), A₂(8;7;4,0,0), A₃(5;10;4,0,0), A₄(4;7;9,0,0):Пример №10

Пример. В декартовой прямоугольной системе координат даны вершины пирамиды A, B, C, D. Найдите длину ребра AB, косинус угла между векторами, уравнение ребра, уравнение грани, уравнение высоты.
Решение

Пример. Даны вершины треугольника А(1, –1, -3), В(2, 0, -10), С(3, 0, -2).
а) Найти уравнение биссектрисы и высоты данного треугольника, проведенных из вершины A .
б) Найти уравнения всех его медиан и координаты точки их пересечения.
см. также Как найти периметр треугольника

источники:

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-prjamoj/

http://math.semestr.ru/line/example-analytic-geometry.php

Источник

Тема
2.2. Прямая на плоскости

Д
ве
взаимно перпендикулярные прямые, на
каждой из которых указано
положительное направление и масштаб,
образуют прямоугольную декартову
систему координат (рис: 2.6). :

Рис. 2.6

Точка

называется началом координат, ось

—
осью абсцисс, ось

-осью ординат. Положение на плоскости
любой точки

определяется двумя числами (координатами):

(рис.2.6).

Теорема 2.9 Расстояние

между точками

и

(рис.2.7) измеряется по
формуле

Рис. 2.7

Теорема 2.10 Если
точка

делит отрезок

в отношении

(
называется коэффициентом
пропорциональности), то ее координаты
находят так;

Следствие В частном случае, когда
отрезок делится пополам,
,
получим так называемые формулы половинного
деления;

Теорема 2.11 Площадь
треугольника

с известными вершинами

равна;

В декартовом базисе прямая изображается
уравнением первой степени с двумя
неизвестными

и

Рассмотрим различные формы задания
уравнения прямой на плоскости.

Теорема 2.12 В прямоугольной системе
координат

любая прямая задается уравнением первой
степени, называемым общим уравнением
прямой

где

— постоянные коэффициенты, причем
.

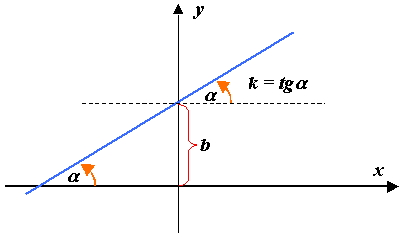
Уравнение прямой с угловым коэффициентом:

З
десь
параметры

и

имеют определенный геометрический
смысл (рис2.8).

Рис. 2.8

и называется угловым коэффициентом.

— угол, образованный прямой
с положительным направлением
.
В качестве положительного направления
измерения угла а принято направление
против хода часовой стрелки (рис.
2.8).

– отрезок, отсекаемый прямой на оси
ординат.

Выполнив несложные алгебраические
преобразования, можно от общего уравнения
прямой перейти к уравнению прямой с
угловым коэффициентом. При этом

Уравнение прямой в отрезках
выглядит так:

Здесь

и
—
отрезки, отсекаемые прямой на осях
абсцисс и ординат соответственно. Их
связь с коэффициентами общего уравнения

В этой форме можно представить уравнение
прямой, не проходящей через начало
координат, т.е. если
.

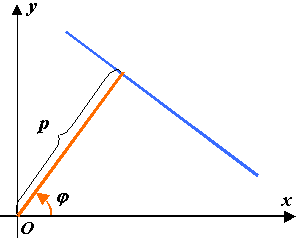
Нормальное уравнение прямой:

Геометрический смысл коэффициентов
этого уравнения:

— длина перпендикуляра,
опущенного из начала координат на
прямую;

— угол, образованный этим перпендикуляром,
с положительным направлением оси
(рис.2.9).

Рис. 2.9

Чтобы перейти к этому виду уравнения
прямой, надо умножить все члены общего
уравнения на нормирующий множитель

Знак

выбирается таким образом, чтобы

Уравнение пучка прямых описывает
множество прямых, проходящих через
точку

с известными координатами:

Уравнение прямой, проходящей через
две точки

и
:

Угол между прямыми

в зависимости от формы задания уравнений
прямых может быть найден по формуле:

или

З
десь
угол

измеряется от прямой с угловым
коэффициентом

или

до прямой с параметрами

или

(рис.2.10):

Рис. 2.10

Из этих формул легко выводятся условия
параллельности:

или

и перпендикулярности прямых:

или
.

Координаты точки пересечения
двух прямых определяются как
решение системы, составленной из
уравнений прямых.

Теорема 2.13
Расстояние

от точки

до прямой

(или
)
определяется по формулам:

или

Задача 2.5 Дано общее уравнение прямой
.

Написать: а) уравнение с угловым
коэффициентом; б) уравнение в отрезках;
в) нормальное уравнение. Построить
прямую.

Решение

а) Оставим член с

слева, а остальные перенесем в правую
часть уравнения. Затем разделим обе
части на коэффициент при
,
т.е. на -3. В результате
получим уравнение с угловым коэффициентом

Задача 2.6 Написать
уравнение прямой, проходящей через
точку

и отсекающей от координатного угла
треугольник, площадью равной
3.

Решение

О
чевидно,
что таких прямых будет 2,
а треугольники образованы во
втором и четвертом квадрантах (рис.2.11):

Рис. 2.11

Запишем уравнение пучка прямых, проходящих
через точку
:

Преобразуем его к уравнению в отрезках:

Таким образом,

Так как

и

имеют разные знаки, то площадь указанных
в условии задачи треугольников может
быть найдена по формуле

Отсюда

или

Решив квадратное уравнение, найдем

Тогда уравнения прямых будут иметь вид:

Задача 2.7 Дан
треугольник с вершинами

и
.
Написать уравнения сторон треугольника,
медианы
,
высоты
,
найти длины медианы

и высоты
,
угол при вершине
,
площадь треугольника
.

Решение

П
остроим
треугольник с указанными вершинами и
отметим все перечисленные элементы
(рис. 2.12).

Рис. 2.12

Уравнения, сторон треугольника получим,
используя уравнения прямой, проходящей
через две точки.

Уравнение

можно было записать и без таких выкладок,
учитывая, что обе точки лежат на оси
.

Для нахождения уравнения медианы

предварительно определим координаты
точки

как середины отрезка
:

Тогда уравнение медианы

будет иметь вид

Длину

определим как расстояние между точками

и
:

Запишем уравнение пучка прямых, проходящих
через вершину
:

Так как высота

перпендикулярна стороне треугольника
,
то их угловые коэффициенты связаны так:

Из уравнения

легко найти

Тогда
,
и уравнение высоты

будет

или

Длину высоты

определим как расстояние от точки

до прямой
:

Так как мы установили общие уравнения
прямых

и
,
то воспользуемся соответствующей
формулой для определения угла при
вершине

треугольника
.

Площадь треугольника

равна

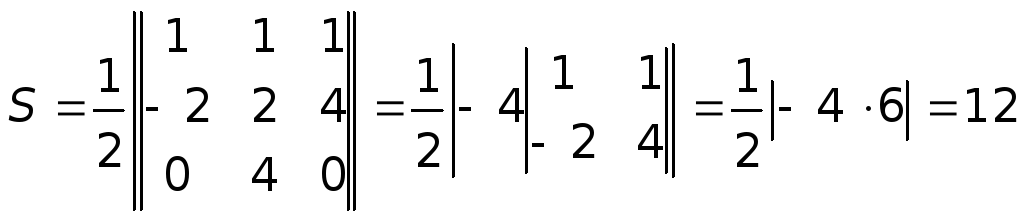
Задача 2.8 Найти
точку пересечения медиан и точку
пересечения высот треугольника, вершины
которого

и
.

Решение

С
троим
треугольник, показываем точки пересечения
его медиан и высот (рис.2.13).

Рис.2.13

Определим координаты точки

как середины отрезка
,
воспользовавшись формулами половинного
деления

Для определения координат точки
пересечения медиан

воспользуемся свойством этой точки,
согласно которому она делит медиану

в отношении
,
считая от вершины, т.е.
.
Тогда для точки

Треугольник

является равнобедренным, так как длины
сторон

и

равны:

Следовательно, медиана

будет и высотой. Отсюда уравнение высоты

определим как уравнение прямой, проходящей
через точки
:

Уравнение пучка прямых, проходящих
через точку

может быть записано как

Уравнение

находим через известные координаты
концов отрезка:

Так как высота

перпендикулярна
,
то ее угловой коэффициент

и уравнение

будет

или

Координаты точки

пересечения высот

и

определим из решения системы, составленной
из уравнений высот:

Соседние файлы в папке высшая математика

Источник

Уравнения прямых в пространстве

Уравнение прямой как линии пересечения двух плоскостей

Пусть в координатном пространстве Oxyz (в прямоугольной системе координат) две плоскости заданы общими уравнениями

$begin{aligned}rho_{1}colon & ,A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1}=0;\[2pt] rho_{2}colon & ,A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2}=0,end{aligned}$

в которых коэффициенты при неизвестных непропорциональны, т.е. $operatorname{rang}!begin{pmatrix}A_{1}&B_{1}&C_{1}\A_{2}&B_{2}&C_{2}end{pmatrix}=2$ . Это условие означает, что плоскости $rho_{1}$ и $rho_{2}$ пересекаются (см. условие (4.25)), поскольку их нормали $vec{n}_{1}=A_{1}vec{i}+B_{1}vec{j}+C_{1}vec{k}$ и $vec{n}_{2}=A_{2}vec{i}+B_{2}vec{j}+C_{2}vec{k}$ неколлинеарны (рис.4.25). Тогда линия пересечения плоскостей описывается системой уравнений

$begin{cases} A_{1}cdot x+D_{1}cdot y+C_{1}cdot z+D_{1}=0,\ A_{2}cdot x+D_{2}cdot y+C_{2}cdot z+D_{2}=0. end{cases}$

(4.31)

Система (4.31) называется общим уравнением прямой в пространстве.

Общее уравнение прямой в пространстве как пересечение двух плоскостей

Пример 4.13. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы вершины A(1;2;3), B(3;0;2), C(7;4;6) треугольника (рис.4.26). Требуется составить уравнение прямой, содержащей высоту треугольника.

Решение. Прямая является линией пересечения двух плоскостей: плоскости $rho_{1}$ , треугольника ABC и плоскости $rho_{2}$ , проходящей через точку перпендикулярно вектору overrightarrow{BC} (рис.4.26). По формуле (4.21) составим уравнение плоскости $rho_{1},$ проходящей через три точки A,,B,,C:

$begin{vmatrix}x-1&y-2&z-3\3-1&0-2&2-3\7-1&4-2&6-3end{vmatrix}= begin{vmatrix} x-1&y-2&z-3\ 2&-2&-1\ 6&2&3 end{vmatrix}=0 quad Leftrightarrow quad x+3y-4z+5=0.$

По формуле (4.14) составим уравнение плоскости $rho_{2}$ , проходящей через точку перпендикулярно вектору overrightarrow{BC}=(7-3)vec{i}+(4-0)vec{j}+(6-2)vec{k}=4vec{i}+4vec{j}+4vec{k}:

4cdot(x-1)+4cdot(y-2)+4cdot(z-3)=0 quad Leftrightarrow quad x+y+z-6=0.

Следовательно, общее уравнение (4.31) прямой имеет вид $begin{cases}x+3y-4z+5=0,\x+y+z-6=0.end{cases}$

Параметрическое уравнение прямой в пространстве

Напомним, что направляющий вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.

Пусть в координатном пространстве Oxyz заданы точка $M_{0}(x_{0}, y_{0}, z_{0})$ и ненулевой вектор vec{p}= avec{i}+ bvec{j}+ cvec{k} (рис.4.27). Требуется составить уравнение прямой, коллинеарной вектору vec{p} и проходящей через точку $M_{0}(x_{0},y_{0},z_{0})$ .

Выберем на прямой произвольную точку $M_{0}(x,y,z)$ . Обозначим vec{r}=overrightarrow{OM}, $vec{r}_{0}=overrightarrow{OM_{0}}$ — радиус-векторы точек M(x,y,z) и $M_{0}(x_{0},y_{0},z_{0})$ (рис.4.28).

Параметрическое уравнение прямой в пространстве и направляющий вектор прямой

Точка принадлежит заданной прямой тогда и только тогда, когда векторы $overrightarrow{M_{0}M}$ и vec{p} коллинеарны. Запишем условие коллинеарности: $overrightarrow{M_{0}M}=tvec{p}$ , где — некоторое действительное число (параметр). Учитывая, что $overrightarrow{M_{0}M}=vec{r}-vec{r}_{0}$ , получим векторное параметрическое уравнение прямой в пространстве:

$vec{r}=vec{r}_{0}+tcdotvec{p}, quad tinmathbb{R},,$

(4.32)

где vec{p} — направляющий вектор прямой, а $vec{r}_{0}$ — радиус-вектор заданной точки $M_{0}(x_{0},y_{0},z_{0})$ принадлежащей прямой.

Координатная форма записи уравнения (4.32) называется параметрическим уравнением прямой в пространстве

$begin{cases}x=x_{0}+acdot t,\y=y_{0}+bcdot t,\z=z_{0}+ccdot t,end{cases}tinmathbb{R},,$

(4.33)

где a,b,c — координаты направляющего вектора vec{p} прямой. Параметр в уравнениях (4.32),(4.33) имеет следующий геометрический смысл: величина пропорциональна расстоянию от заданной точки $M_{0}(x_{0}, y_{0}, z_{0})$ до точки $M(x,y,z)equiv M(x_{0}+at,y_{0}+bt,z_{0}+ct)$ . Физический смысл параметра в параметрических уравнениях (4.32),(4.33) — это время при равномерном и Прямолинейном движении точки по прямой. При t=0 точка M(x,y,z) совпадает с заданной точкой $M_{0}$ . При возрастании параметра движение происходит в направлении направляющего вектора.

Каноническое уравнение прямой в пространстве

Выразим параметр из каждого уравнения системы (4.33): $t=frac{x-x_{0}}{a},, t=frac{y-y_{0}}{b},, t=frac{z-z_{0}}{c}$ , а затем исключим этот параметр:

$frac{x-x_{0}}{a}=frac{y-y_{0}}{b}=frac{z-z_{0}}{c}, quad a^2+b^2+c^2ne0.$

(4.34)

Уравнение (4.34) называется каноническим уравнением прямой в пространстве. В этом уравнении коэффициенты a,b,c не равны нулю одновременно, так как это координаты направляющего вектора прямой.

Замечания 4.6.

1. Если один или два из трех знаменателей дробей в (4.34) равны нулю, то считается, что соответствующий числитель дроби равен нулю. Например:

а) каноническое уравнение $frac{x-x_{0}}{0}=frac{y-y_{0}}{0}=frac{z-z_{0}}{c}$ — это уравнение $begin{cases}x=x_{0},\y=y_{0}end{cases}$ прямой, параллельной оси аппликат (рис.4.29,а);

б) каноническое уравнение $frac{x-x_{0}}{a}=frac{y-y_{0}}{b}=frac{z-z_{0}}{0}$ — это уравнение $begin{cases}z=z_{0},\dfrac{x-x_{0}}{a}=dfrac{y-y_{0}}{b}end{cases}$ прямой, параллельной координатной плоскости Oxy (рис.4.29,б).

Прямые в пространстве, параллельные координатным плоскостям

2. Направляющий вектор vec{p} прямой определяется неоднозначно. Например, любой ненулевой вектор lambdacdotvec{p} , где lambdainmathbb{R} , также является направляющим вектором для той же прямой.

Переход от общего уравнение к каноническому

3. Для перехода от общего уравнения прямой (4.31) к каноническому (4.34) нужно выполнить следующие действия:

1) найти любое решение $(x_{0},y_{0},z_{0})$ системы $begin{cases} A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1}=0,\ A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2}=0, end{cases}$ определяя тем самым координаты точки $M_{0}(x_{0},y_{0},z_{0})$ , принадлежащей прямой;

2) найти направляющий вектор vec{p} прямой как векторное произведение нормалей $vec{n}_{1}=A_{1}vec{i}+B_{1}vec{j}+C_{1}vec{k},$ $vec{n}_{2}= A_{2}vec{i}+ B_{2}vec{j}+ C_{2}vec{k},$ заданных плоскостей:

$vec{p}= begin{bmatrix}vec{n}_{1},vec{n}_{2}end{bmatrix}= acdotvec{i}+ bcdotvec{j}+ ccdotvec{k}= begin{vmatrix} vec{i}&vec{j}&vec{k}\ A_{1}&B_{1}&C_{1}\ A_{2}&B_{2}&C_{2} end{vmatrix}.$

3) записать каноническое уравнение (4.34) с учетом пунктов 1 и 2.

4. Чтобы перейти от канонического уравнения к общему, достаточно двойное равенство (4.34) записать в виде системы

$left{!begin{aligned}frac{x-x_{0}}{a}&=frac{y-y_{0}}{b},,\frac{y-y_{0}}{b}&=frac{z-z_{0}}{c},,end{aligned}right.$ и привести подобные члены.

5. Чтобы перейти от канонического уравнения к параметрическому, следует приравнять каждую дробь в уравнении (4.34) параметру t и записать полученные равенства в виде системы (4.33):

$frac{x-x_{0}}{a}=frac{y-y_{0}}{b}=frac{z-z_{0}}{c}=t quad Leftrightarrow quad begin{cases}x=x_{0}+acdot t,\y=y_{0}+bcdot t,\z=z_{0}+ccdot t,end{cases} tinmathbb{R},.$

6. Если в каноническом уравнении (4.34) прямой фиксировать координаты $x_{0},y_{0},z_{0}$ точки $M_{0}$ , а коэффициентам a,b,c придавать произвольные значения (не равные нулю одновременно), то получим уравнение связки прямых с центром в точке $M_{0}(x_{0},y_{0},z_{0})$ , т.е. совокупность всех прямых, проходящих через точку $M_{0}$ .

7. Параметрическое (4.33) и каноническое (4.34) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.

Пример 4.14. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы вершины A(1;2;3), B(3;0;2), C(7;4;6) треугольника (рис. 4.30). Требуется:

В координатном пространстве Oxyz (в прямоугольной системе координат) заданы вершины A(1,2,3), B(3,0,2), C(7,4,6) треугольника

а) составить каноническое уравнение прямой, содержащей высоту треугольника;

б) составить общее уравнение прямой, содержащей биссектрису треугольника.

Решение. а) Общее уравнение прямой получено в примере 4.13: $begin{cases}x+3cdot y-4cdot z+5=0,\x+y+z-6=0.end{cases}$ Перейдем от общего уравнения к каноническому.

1) Найдем любое решение $(x_{0},y_{0},z_{0})$ системы, например, $x_{0}=1,$ $y_{0}=2,$ $z_{0}=3$ (это координаты точки A(1;2;3) ).

2) Найдем направляющий вектор vec{p} прямой как векторное произведение нормалей $vec{n}_{1}=vec{i}+3vec{j}-4vec{k},$ $vec{n}_{2}=vec{i}+vec{j}+vec{k}$ заданных плоскостей

$vec{p}= begin{bmatrix}vec{n}_{1},vec{n}_{2}end{bmatrix}= begin{vmatrix} vec{i}&vec{j}&vec{k}\ 1&3&-4\ 1&1&1 end{vmatrix}= 7cdotvec{i}-5cdotvec{j}-2cdotvec{k},.$

3) Запишем каноническое уравнение (4.34): $frac{x-1}{7}=frac{y-2}{-5}=frac{z-3}{-2}$ .

б) Сначала составим каноническое уравнение прямой . Для этого нужно найти направляющий вектор vec{l} этой прямой. Учитывая, что диагональ ромба является биссектрисой, vec{l}=vec{b}+vec{c} , где vec{b} и vec{c} — единичные векторы, одинаково направленные с векторами overrightarrow{AB} и overrightarrow{AC} соответственно. Находим

$begin{gathered}overrightarrow{AB}= 2cdotvec{i}-2cdotvec{j}-1cdotvec{k}, quad begin{vmatrix}overrightarrow{AB}end{vmatrix}=3, quad vec{b}= frac{overrightarrow{AB}}{begin{vmatrix} overrightarrow{AB}end{vmatrix}}= frac{2}{3}cdot vec{i}-frac{2}{3} cdotvec{j}-frac{1}{3}cdot vec{k},;\[3pt] overrightarrow{AC}= 6cdot vec{i}+ 2cdotvec{j}+3cdotvec{k}, quad begin{vmatrix} overrightarrow{AC} end{vmatrix}=7, quad vec{c}= frac{overrightarrow{AC}}{begin{vmatrix} overrightarrow{AC}end{vmatrix}}= frac{6}{7}cdotvec{i}+ frac{2}{7}cdotvec{j}+ frac{3}{7}cdotvec{k},;\[3pt] vec{l}=vec{a}+vec{c}= left(frac{2}{3}cdotvec{i}-frac{2}{3}cdotvec{j}-frac{1}{3}cdotvec{k}right)+ left(frac{6}{7}cdotvec{i}+frac{2}{7}cdotvec{j}+frac{3}{7}cdotvec{k}right)= frac{32}{21}cdotvec{i}-frac{8}{21}cdotvec{j}+frac{2}{21}cdotvec{k},. end{gathered}$

Составляем каноническое уравнение прямой $ALcolon,frac{x-1}{32/21}=frac{y-2}{-8/21}=frac{z-3}{2/21}$ .

Записывая двойное равенство в виде системы, получаем общее уравнение прямой AL:

$left{!begin{aligned}frac{x-1}{32/21}&=frac{y-2}{-8/21},\ frac{y-2}{-8/21}&=frac{z-3}{2/21},end{aligned}right. quad Leftrightarrow quad begin{cases}x+4cdot y-9=0,\ y+4cdot z-14=0.end{cases}$

Расстояние от точки до прямой, заданной каноническим уравнением

Расстояние от точки до прямой в пространстве

Найдем расстояние от точки $M_{1}(x_{1},y_{1},z_{1})$ до прямой , заданной каноническим уравнением (рис.4.31)):

$lcolon, frac{x-x_{0}}{a}= frac{y-y_{0}}{b}= frac{z-z_{0}}{c},.$

Искомое расстояние равно высоте параллелограмма, построенного на векторах

vec{p}=avec{i}+bvec{j}+cvec{k} и $vec{m}=overrightarrow{M_{0}M_{1}}=(x_{1}-x_{0})vec{i}+(y_{1}-y_{0})vec{j}+(z_{1}-z_{0})vec{k}$ , то есть.

$d=frac{begin{vmatrix}begin{bmatrix}vec{m},vec{p}end{bmatrix}end{vmatrix}}{begin{vmatrix}vec{p}end{vmatrix}}= frac{sqrt{begin{vmatrix}x_{1}-x_{0}&y_{1}-y_{0}\a&bend{vmatrix}^2+ begin{vmatrix}y_{1}-y_{0}&z_{1}-z_{0}\b&cend{vmatrix}^2+ begin{vmatrix}x_{1}-x_{0}&z_{1}-z_{0}\a&cend{vmatrix}^2}}{sqrt{a^2+b^2+c^2}},.$

(4.35)

Уравнение прямой, проходящей через две заданные точки

Уравнение прямой в пространстве, проходящей через две заданные точки

Пусть в координатном пространстве Oxyz заданы две точки $M_{0}(x_{0},y_{0},z_{0})$ и $M_{1}(x_{1},y_{1},z_{1})$ . Требуется составить уравнение прямой, проходящей через заданные точки.

Как показано в разд., точка M(x,y,z) принадлежит прямой $M_{0}M_{1}$ тогда и только тогда, когда ее радиус-вектор overrightarrow{OM} удовлетворяет условию (рис.4.32): $overrightarrow{OM}= (1-t)cdot overrightarrow{OM_{0}}+ tcdotoverrightarrow{OM_{1}}$ , где — некоторое действительное число (параметр). Это уравнение, а также его координатную форму

$begin{pmatrix}x\y\zend{pmatrix}= (1-t)cdot!begin{pmatrix}x_{0}\y_{0}\z_{0}end{pmatrix}+tcdot!begin{pmatrix}x_{1}\y_{1}\z_{1}end{pmatrix}! quad Leftrightarrow quad !begin{cases} x=(1-t)cdot x_{0}+tcdot x_{1},\ y=(1-t)cdot y_{0}+tcdot y_{1},\ z=(1-t)cdot z_{0}+tcdot z_{1}.end{cases} tinmathbb{R}$

(4.36)

будем называть аффинным уравнением прямой, проходящей через две точки $M_{0}(x_{0},y_{0},z_{0})$ и $M_{1}(x_{1},y_{1},z_{1})$ .

Выражая параметр из каждого уравнения системы (4.36), получаем: $frac{x-x_{0}}{x_{1}-x_{0}}=frac{y-y_{0}}{y_{1}-y_{0}}=frac{z-z_{0}}{z_{1}-z_{0}}=t$ . Исключая параметр , приходим к уравнению прямой, проходящей через две точки $M_{0}(x_{0},y_{0},z_{0})$ и $M_{1}(x_{1},y_{1},z_{1})$ :

$frac{x-x_{0}}{x_{1}-x_{0}}=frac{y-y_{0}}{y_{1}-y_{0}}=frac{z-z_{0}}{z_{1}-z_{0}},.$

(4.37)

Уравнение (4.37) можно получить из канонического уравнения (4.34), выбирая в качестве направляющего вектора vec{p}=avec{i}+bvec{j}+cvec{k} вектор $overrightarrow{M_{0}M_{1}}=(x_{1}-x_{0})vec{i}+(y_{1}-y_{0})vec{j}+(z_{1}-z_{0})vec{k},$ т.е. подставляя $a=x_{1}-x_{0},$ $b=y_{1}-y_{0},$ $c=z_{1}-z_{0}.$

Треугольник в пространстве по координатам вершин, его высота и медиана

Пример 4.15. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы вершины A(1;2;3), B(3;0;2), C(7;4;6) треугольника (рис.4.33). Требуется:

а) составить уравнение прямой ;

б) составить уравнение прямой, содержащей медиану треугольника;

в) найти высоту h=|AH| треугольника, опущенную на сторону .

Решение. а) Записываем уравнение (4.37) прямой, проходящей через точки B(3;0;2), C(7;4;6):

$frac{x-3}{7-3}=frac{y-0}{4-0}=frac{z-2}{6-2}~ Leftrightarrow~ frac{x-3}{1}=frac{y}{1}=frac{z-2}{1},.$

б) Находим координаты середины стороны BCcolon M(5;2;4) . Составляем уравнение (4.37) прямой AM:

$frac{x-1}{5-1}=frac{y-2}{2-2}=frac{z-3}{4-3}~ Leftrightarrow~ frac{x-1}{4}=frac{y-2}{0}=frac{z-3}{1},.$

в) Искомую высоту находим по формуле (4.35), полагая vec{m}=overrightarrow{BA}=-2vec{i}+2vec{j}+vec{k} и vec{p}=vec{i}+vec{j}+vec{k}:

$h=|AH|=frac{begin{vmatrix}begin{bmatrix}vec{m},vec{p}end{bmatrix}end{vmatrix}}{begin{vmatrix}vec{p}end{vmatrix}}= frac{sqrt{begin{vmatrix}-2&2\1&1end{vmatrix}^2+begin{vmatrix}2&1\1&1end{vmatrix}^2+begin{vmatrix}-2&1\1&1end{vmatrix}^2}}{sqrt{1^2+1^2+1^2}}=frac{sqrt{16+1+9}}{sqrt{3}}= sqrt{frac{26}{3}},.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Содержание:

Прямые на плоскости
Уравнения прямых
Уравнение прямой, которая проходит через две точки
Уравнения прямой, которая проходит через заданную точку с известным направляющим вектором
Уравнение прямой, которая проходит через данную точку перпендикулярно к данному вектору (нормальное уравнение прямой)
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой
Угол между прямыми
Пересечение прямых
Расстояние от точки до прямой
Прямая линия на плоскости и её определение
Уравнение прямой с угловым коэффициентом
Уравнение прямой, проходящей через заданную точку в данном направлении
Уравнение прямой в отрезках
Угол между двумя прямыми
Общее уравнение прямой и его исследование
Нормальное уравнение прямой
Расстояние от точки до прямой
Плоскость и ее уравнение
Исследование общего уравнения плоскости
Уравнение плоскости в отрезках
Угол между двумя плоскостями. условия параллельности и перпендикулярности плоскостей
Нормальное уравнение плоскости
Расстояние от точки до плоскости
Прямая линия на плоскости
Уравнения прямой
Угол между прямыми, условия параллельности и перпендикулярности
Основные формулы, связанные с прямой на плоскости
Неравенства, задающие полуплоскости
Экономические задачи, использующие уравнение прямой
Прямая линия на плоскости с примерами
Прямая на плоскости
Понятие об уравнении линии на плоскости. Основные задачи аналитической геометрии
Разновидности уравнений прямой на плоскости
Уравнение прямой с заданным нормальным вектором
Общее уравнение прямой и его исследование
Каноническое и параметрическое уравнение прямой
Уравнение прямой, проходящей через две заданные точки
Уравнение прямой, проходящей через заданную точку в заданном направлении
Уравнения прямой с угловым коэффициентом
Уравнение прямой в отрезках на осях
Нормальное уравнение прямой
Свойства нормального уравнения прямой
Основные задачи о прямой линии на плоскости
Взаимное расположение двух прямых
Угол между двумя прямыми, которые заданные общими уравнениями
Возведение общего уравнения прямой к нормальному виду
Расстояние от точки до прямой
Уравнение биссектрис углов, образованных двумя прямыми
Разновидности уравнений прямой

Прямые на плоскости

Понятие «прямая» тесно связано с понятием «линия». Любая линия может рассматриваться как траектория движения точки, а «прямая линия» – как кратчайшее расстояние между двумя точками. Плоскость, в свою очередь, может быть задана тремя точками, прямой и точкой, двумя пересекающимися прямыми, двумя параллельными прямыми, любой плоской фигурой.

Уравнения прямых

Известно, что прямую линию на плоскости можно провести, если:

1) заданы две точки;

2) задана точка и параллельный ей вектор (такой вектор называем направляющим для данной прямой);

3) задана точка и перпендикулярный ей вектор (такой вектор называем нормальным для данной прямой);

4) задана точка и угол, который данная прямая образует с положительным направлением оси Ох.

Составим уравнения таких прямых.

Уравнение прямой, которая проходит через две точки

Пусть на прямой I заданы точки А(х_I, у_I),

Если точка М(х, у) принадлежит прямой I, то вектор коллинеарный вектору

Запишем условие коллинеарных векторов

Данное уравнение вычисляет уравнение прямой, которая проходит через две точки. Следовательно, уравнение составлено.

Если заданные точки лежат на осях координат, то есть то уравнение прямой, которая проходит через две точки записано так:

Последнее уравнение ещё называют уравнением прямых в отрезках.

Уравнения прямой, которая проходит через заданную точку с известным направляющим вектором

Пусть точка принадлежит прямой I, которая параллельна вектору . Если точка принадлежит прямой I, то вектор коллинеарный вектору . Согласно условию коллинеарных векторов получаем:

Данное уравнение определяет уравнение прямой, которая проходит через заданную точку с заданным направляющим вектором.

Уравнение прямой, которая проходит через данную точку перпендикулярно к данному вектору (нормальное уравнение прямой)

Пусть точка принадлежит прямой I, а вектор перпендикулярный этой прямой (рис. 4). Если точка принадлежит прямой I, то вектор перпендикулярный вектору .

Согласно условию перпендикулярности векторов , следовательно

Данное уравнение и является уравнением прямой, которая проходит через заданную точку перпендикулярно заданному вектору (нормальное уравнение прямой).

Уравнение прямой с угловым коэффициентом

Пусть прямая I наклонена к положительному направлению оси Ох под углом и проходит через заданную точку (рис. 5). Построим треугольник АМК, в котором

Если точка принадлежит I, то

Следовательно,

Если обозначить , то получим уравнение прямой с угловым коэффициентом k

Если , то и k=0, а это значит, что прямая I параллельна оси Ох.

Если не имеет содержания, а это значит, что прямая I параллельна оси Оу (перпендикулярна оси Ох).

Если прямая пересекает ось Оу в заданной точке А(0, b), то уравнение прямой приобретает вид

Рассмотрим ряд примеров.

Пример 1. Дано треугольник АВС, с заданными координатами вершин А(-3; 2), В(1; 5) и С(5; -7). Записать уравнение медианы, которая выходит из вершины А.

Решение:

Если точка М — середина стороны ВС, то легко вычислить координаты точки:

Подставив координаты точек А и М в уравнение прямой, которая проходит через две точки, получим:

или

Ответ: — уравнение медианы проведённой из вершины А.

Пример 2. Записать уравнение прямой, которая проходит через точку А(4; -3) и отсекает на осях треугольник площадью три квадратные единицы (рис. 6).

Решение:

Для решения задачи воспользуемся уравнением прямой на отрезках

По условию задачи кв. ед. Площадь прямоугольных треугольников можно представить через длину отрезков, которые отсекает прямая на осях координат, . Поэтому, (два знака, поскольку могут иметь и разные знаки).

Искомая прямая проходит через данную точку А(4; -3), поэтому её координаты удовлетворяют уравнения прямой в отрезках и мы можем записать , то есть получили ещё одну зависимость между .

Для вычисления имеет две системы:

Из первой системы находим а решив вторую систему получим .

Запишем уравнения искомых прямых:

Ответ:

Пример 3. Записать уравнение прямой, которая проходит через точку и образует с положительным направлением оси Ох угол 30°.

Решение: Поскольку Подставив значения в уравнение прямой с угловым коэффициентом, получим

Ответ:

Общее уравнение прямой

Если в полученных выше уравнениях прямой выполнить определённые алгебраические преобразования, то все они будут сведены до уравнения:

которое называется общим уравнением прямой.

Например, рассмотрим уравнение прямой, которая проходит через данные две точки:

Как видим, коэффициенты в общем уравнении прямой это координаты нормального вектора этой прямой.

Отметим, что зная общее уравнение прямой, можно всегда получить хотя бы одно из вышеуказанных уравнений прямой.

Рассмотрим размещение прямой относительно системы координат в зависимости от значений коэффициентов общего уравнения прямой.

1. Если , то уравнение будет иметь вид , или , то есть все точки прямой будут иметь туже самую ординату ; это означает, что прямая параллельна оси Ох.

2. Если , с=0, то уравнение будет иметь вид у=0, то есть получим уравнение оси Ох.

3. Если b=0, то уравнение будет иметь вид , или , то есть все точки прямой будут иметь туже самую абсциссу , это означает, что прямая параллельна оси Оу.

4. Если b=0, с=0, то уравнение приобретает вид х=0, то есть получим уравнение оси Оу.

5. Если с=0, то уравнение будет иметь вид . Это уравнение удовлетворяют координаты точки О(0;0) и, следовательно, прямая будет проходить через начало координат.

Зная общее уравнение прямой можно вычислить угол между прямыми, как угол между их нормальными векторами.

Угол между прямыми

Пример 4. Вычислить угол между прямыми

Решение: Запишем нормальные векторы заданных прямых

Согласно выше приведённой формуле получим

воспользовавшись калькулятором получим

Ответ:

Если уравнение прямых записаны, как уравнения прямых с угловыми коэффициентами , то записав их в виде

получим координаты нормальных векторов и формула для вычисления косинуса угла между прямыми приобретёт вид

Если знаменатель в последней формуле преобразуется в ноль, то есть , то прямые перпендикулярны, а угол

Пример 5. Найти угол между прямыми

Решение:

Уравнение прямых записано, как уравнение прямых с угловыми коэффициентами

следовательно

Угол между прямыми равен 45º.

Ответ:

Пример 6. Доказать, что прямые перпендикулярны.

Решение:

Проверим, выполняются ли условия перпендикулярности прямых с угловыми коэффициентами

Следовательно, прямые перпендикулярны.

Пересечение прямых

Если прямые не параллельны, то нахождение точки их пересечения сводится к решению системы двух уравнений с двумя неизвестными:

Пример 7. Найти координаты точки пересечения прямых

Решение:

Ответ: (-1; 2).

Совокупность прямых, которые проходят через данную точку называют пучком прямых на плоскости с центром в этой точке.

является уравнением пучка прямых с центром в заданной точке М₀ (рис. 9).

Пример 8. Записать уравнение пучка прямых с центром в точке М(2; -3).

Решение: Запишем уравнение пучка прямых в общем виде:

Подставим координаты точки М, получим: уравнение пучка прямых с центром в точке М.

Ответ:

Расстояние от точки до прямой

Под расстоянием от точки до прямой которое задано уравнением

понимают длину перпендикуляра где

Известно, что это нормальный вектор данной прямой, а вектор нормальный единичный вектор этой же прямой.

Векторы перпендикулярны к прямой поэтому они коллинеарные.

Следовательно,

Запишем последнее равенство в координатах:

Поскольку точка Подставим, получим уравнение расстояния от точки до прямой:

Пример 8. Вычислить расстояние от точки М(3;2) до прямой .

Решение: Подставим данные условия в уравнение расстояния от точки до прямой:

Ответ: d=4.

Пример 9. Даны вершины треугольника А(-2; 7), В(2; -1), С(8;3). Записать уравнения:

1) высоты опущенной с вершины А на сторону ВС;

2) медианы проведённой с вершины В.

Решение:

1) Запишем уравнение высоты АК, выполнив предварительно следующие действия:

а) Выберем произвольно точку М(х, у), которая принадлежит прямой АК.

б) Найдём координаты вектора :

в) Используя условие перпендикулярности векторов и запишем уравнение высоты АК:

Следовательно, уравнение высоты АК.

2) Для того, чтобы записать уравнение медианы BD, необходимо найти координаты точки D, которая делит отрезок АС напополам. Поэтому:

Запишем уравнение медианы BD медианы, как уравнение прямой, которая проходит через две точки В и D:

Следовательно, уравнение медианы BD.

Ответ: уравнение высоты АК; уравнение медианы BD.

Прямая линия на плоскости и её определение

Уравнение линии является важным понятием аналитической геометрии. Пусть на плоскости мы имеем некоторую линию (кривую) (рис. 22).

Рис. 22.

Определение. Уравнением линии (кривой) на плоскости Oxy называется уравнение, которому удовлетворяют координаты x и y каждой точки, находящейся на этой линии, и не удовлетворяют координаты другой точки, не находящейся на этой линии.

В общем случае уравнение линии будем записывать в виде F (x, y) = 0 или y = f (x). Если точка M (x, y) движется по линии, то ее координаты меняются, и поэтому эти координаты называются бегущими.

Уравнение прямой с угловым коэффициентом

Пусть прямая l (рис.23) пересекает ось ординат в точке A (0, b) и образует с положительным направлением оси Ox угол φ .

Рис. 23.

Возьмем на прямой l произвольную точку M (x, y). Из точки A проведем прямую, параллельную Ox до пересечения с отрезком MN. Обозначим через k = tg φ — угловой коэффициент. Таким образом, величины k и b полностью определяют положение прямой на плоскости. Найдем уравнение прямой l по заданными параметрами k и b. Другими
словами, покажем, каким уравнением связаны координаты произвольной точки M (x, y) прямой. Из прямоугольного треугольника АМN находим
(2.50)

Из равенства (2.50), считая tg φ = k, получим
y = kx + b. (2.51)

Уравнение (2.51) называется уравнением прямой с угловым коэффициентом.

Можно легко доказать, что формула (2.51) также справедлива для случая, когда
Значит, координаты произвольной точки прямой удовлетворяют уравнению (2.51).
Рассмотрим частные случаи уравнения.

Рис. 24.

а) Если b = 0, то получим y = kx — уравнение прямой, проходящей через начало координат (рис. 24). Когда k = tg φ > 0, то угол φ — острый, а когда k = tg φ < 0, то угол φ тупой.

б) Если φ = 0, k = tg φ = 0 , и уравнение прямой, параллельной оси Ox, имеет вид y = b, а уравнение оси Ox будет y = 0 (рис.25).

Рис. 25. Рис. 26.

в) Если, , то не существует, и прямая перпендикулярна оси Ox, то есть вертикальная прямая не имеет углового коэффициента. Пусть эта прямая отсекает на оси Ox отрезок, равный a (рис.26). Тогда ее уравнение будет x = a, а уравнение оси Oy будет x = 0.

Уравнение прямой, проходящей через заданную точку в данном направлении

Пусть задана точка M₁ (x₁, y₁) , и нужно написать уравнение прямой линии, проходящей через эту точку.
Пусть прямая l, проходящая через точку M₁ (x₁, y₁), образует с осью Ox угол (рис.27).

Рис. 27.

Поскольку точка M₁ (x₁, y₁) находится на прямой, то ее координаты удовлетворяют уравнению (2.51), то есть
y₁ = kx₁ b (2.52)

Вычитая уравнение (2.52) из (2.51), получим уравнение искомой прямой
y – y₁ = k (x – x₁). (2.53)

Уравнение (2.53) называют формулой «пучка» прямых, где k — произвольное число. Через точку M₁ (x₁, y₁) проходит множество прямых, кроме прямой, параллельной оси Oy.

16.3. Уравнение прямой, проходящей через две заданные точки

Пусть заданы две точки M₁ (x₁, y₁) и M₂ (x₂, y₂).
Для получения уравнения прямой M₁M₂ (рис. 28) запишем уравнение прямой, проходящей через точку M₁ (x₁, y₁), а именно y – y₁ = k (x – x₁).

Рис. 28.

Поскольку точка M₂ (x₂, y₂) находится на прямой l, то подставив координаты этой точки в равнение пучка прямых (2.53), получим y₂ – y₁ = k (x₂ – x₁). Из этого равенства найдем угловой коэффициент прямой
(2.54)
Теперь, подставив выражение для k, то есть (2.54) в уравнение (2.53), получим искомое уравнение прямой
(2.55)

Примечание. Если точки M₁иM₂ лежат на прямой, параллельной оси Oy, то есть x₁ = x₂, то уравнение прямой будет x₁ = x. Когда упомянутые точки лежат на прямой, параллельной оси Ox, y₁ = y₂, и уравнение прямой будет y₁ = y.

Пример 1. Составить уравнение прямой, проходящей через точки A (–3; 4) и B (5; –1).

Решение. Используя формулу (2.55), запишем
или
Раскрыв пропорцию, имеем 8 (y – 4) = –5 (х + 3). Упростив, получим .

Уравнение прямой в отрезках

Пусть прямая отсекает от начала координат на оси Ox отрезок a ≠ 0, а на оси Oy — отрезок b ≠ 0, тогда прямая проходит через две точки A (a; 0) и B (0; b).

Рис. 39.

Использовав формулу (2.55) для точек A (a; 0) и B (0; b), получим ,
и после упрощения имеем
. (2.56)
Уравнение (2.56) называется уравнением прямой в отрезках.

Пример 2. Составить уравнения прямой, проходящей через точку A (1; 2), которая отсекает на положительный оси Oy отрезок в два раза больший, чем на положительный оси Ox.

Решение. У равенства (2.56) по условию b = 2a (a > 0). Подставляя координаты точки A (1; 2) и b = 2a в уравнение (2.56), получим
или и a = 2.
Тогда уравнение искомой прямой будет .

Угол между двумя прямыми

Пусть заданы две прямые l₁ и l₂:
y₁ = k₁ x + b₁, l₁
y₂ = k₂ x + b₂, l₂
и нужно найти угол φ между ними (рис.40).

Рис. 40.

Из рис. 40 видно, что φ = φ₂ – φ₁, причем k₁ = tg φ₁, k₂ = tg φ_{2 ,}.
Тогда
или , (2.57)

где стрелка на рис. 40 означает, что угол φ берется против часовой стрелки от l₁ к l₂.

Формула (2.57) является формулой для нахождения угла между двумя прямыми.

Если , то φ = 0 и tg φ = 0. Тогда из формулы (2.57) имеем, что
k₁ = k₂ (2.58)

Условие (2.58) является необходимым и достаточным условием параллельности двух прямых.
Если , то тогда и tg φ не существует. Перейдем к
Теперь формула (2.57) запишется так
, и когда , то .
Получим условие перпендикулярности двух прямых:
k₁ k₂ = –1 (2.59)

Вывод. Прямые l₁ к l₂параллельны тогда и только тогда, когда их угловые коэффициенты равны, и эти прямые перпендикулярны, когда произведение их угловых коэффициентов равно «–1».

Пример 3. Найти угол между прямыми и .
Решение. Находим и . Подставив значения этих угловых коэффициентов в формулу (2.57), получим

Отсюда находим φ = 45^о.

Пример 4. Затраты перевозок двумя средствами транспорта выражаются функциями y = 75 + 25 x и y = 125 + 15 x, где x — расстояние перевозок в сотнях километров, а y — транспортные расходы. Начиная с какого расстояния, наиболее экономичным является второе средство транспорта?

Решение. Нарисуем графики заданных функций и увидим, что они пересекаются в
точке (5; 200). Чтобы проверить данный результат, решим систему уравнений

75 + 25 x = 125 + 15 x или 10 x = 50, x = 5, y = 200.

Из данного рисунка видно, что при расстоянии, превышающем 500 км, наиболее экономичным является второе транспортное средство.

Общее уравнение прямой и его исследование

Пусть задана точка М₀ (x₀; y₀), через которую проходит прямая l и вектор перпендикулярный к прямой l (рис. 41).

Рис. 41.

На прямой l берем произвольную точку M (x; y). Поскольку вектор перпендикулярен вектору то скалярное произведение этих векторов равно нулю, то есть
. (2.60)
Уравнение (2.60) является векторным уравнением прямой l. Распишем это уравнение в координатной форме. Поскольку = (x – x₀; y – y₀), то уравнение (2.60) перепишется в виде A (x – x₀) + B (y – y₀) = 0.
Раскрыв скобки, получим
Ax + By + C = 0, (2.61)
где С = –Ax₀ – By₀.

Уравнение (2.61) называется общим уравнением прямой. Исследуем, как размещена прямая, заданная уравнением (2.61), если некоторые коэффициенты A, B и С будут равны нулю.
1) Если С = 0, A ≠ 0, B ≠ 0, то уравнение (2.61) имеет вид
Ax + By = 0 или , где .
Значит, если свободный член, а именно С = 0, то прямая проходит через начало координат.

2) Если A = 0, B ≠ 0, С ≠ 0, то уравнение примет вид
By + С = 0 или , то есть прямая параллельна оси Ox.

3) Если B = 0, A ≠ 0, C ≠ 0, то уравнение (2.61) имеет вид
Ax + C = 0 или является уравнением прямой, параллельной оси ординат.

4) Если A = 0, B ≠ 0, С = 0, то уравнение примет вид By = 0, отсюда y = 0. Это и есть уравнение оси Ox.

5) Если A ≠ 0, B = 0, С = 0, то уравнение (2.61) будет иметь вид Ax = 0 или x = 0. Это уравнение оси Oy.

Если заданы две прямые l₁ и l₂ общими уравнениями

то чтобы найти координаты точки пересечения этих прямых, которые должны
удовлетворять уравнение каждой прямой, то нужно решить систему уравнений

Если прямые l₁ и l₂ параллельны, то их угловые коэффициенты
и равны. Итак, k₁ = k₂ или .

Значит, условием параллельности прямых, заданных общими уравнениями, является пропорциональность коэффициентов при неизвестных.
Условие перпендикулярности прямых k₁k₂ = –1 в этом случае имеет вид или .

Итак, для прямых , заданных общими уравнениями, условием перпендикулярности является равенство нулю суммы произведений коэффициентов при переменных x и y.

Нормальное уравнение прямой

Пусть положение прямой на плоскости определяется двумя величинами (параметрами прямой): длиной и направлением перпендикуляра ОР, опущенного из начала координат на прямую, и величиной угла , который образует данный перпендикуляр с осью Ox (рис. 42).

Рис. 42.

На прямой l возьмем произвольную точку M (x, y). Обозначим длину перпендикуляра через p, а орт нормали через . Проекция радиус-вектора на нормаль будет
всегда равной p.

Таким образом, прямая l определяется как геометрическое место точек плоскости, проекции радиус-векторов которых на нормаль равны постоянной величине p.

На основании скалярного произведения имеем
(2.62)
Уравнение (2.62) является нормальным уравнением прямой в векторной форме.

Поскольку , координаты , вектор то в координатной форме уравнение (2.62) будет иметь вид:
(2.63)

Если прямая линия задана общим уравнением Ax + By + C = 0, то это уравнение можно свести к нормальному уравнению прямой (2.63). Умножим общее уравнение прямой на некоторое множитель μ :
(2.64)

Полученное уравнение и общее уравнение прямой равносильны. Чтобы уравнение (2.64) было нормальным, то есть имело вид (2.63) необходимо, чтобы выполнялись равенства:
(2.65)

Первые два равенства в (2.65) возведем в квадрат и сложим. Тогда получим, что
, (2.66)

μ называется нормировочным множителем.

Третье равенство (2.65) устанавливает знак множителя μ, а именно знак μ противоположный знаку свободного члена C.

Пример 4. Привести к нормальному виду уравнение 4x – 3y – 7 = 0.

Решение. Находим нормировочный множитель

(выбираем знак плюс, поскольку C = –7 < 0).
Умножив на данное уравнение, получим:

Полученное уравнение и является нормальным уравнением прямой. В этом уравнении

Расстояние от точки до прямой

Пусть имеем прямую l, заданную уравнением x cos α + y sin α – p = 0 и точку М₀ (х₀; у₀) . Нужно найти расстояние от этой точки до прямой l.

Через точку М₀ (х₀; у₀) проведем прямую l₁ , параллельную прямой l. Искомое расстояние от точки М до прямой l обозначим через d = М₀D. Поскольку OP = p, а OP₁ = p₁, то d = p₁–p.

Если бы точка М₀ находилась на том же расстоянии от прямой l, но с другой стороны, то тогда d = –(p₁ – p).

Таким образом, искомое расстояние определяется равенством

Нормальное уравнение прямой l₁ , параллельной l имеет вид
. (2.67)

Поскольку точка М₀ (х₀; у₀) находится на прямой l₁, то ее координаты удовлетворяют уравнению (2.67), т.е.
и отсюда .

Рис. 43.

Подставляя значение p₁ в равенство получим
(2.68)

Формула (2.68) является формулой расстояния от точки М₀ (х₀; у₀) до прямой, заданной нормальным уравнением.
Если же прямая задана общим уравнением, то расстояние от точки М₀ (х₀; у₀) находится по формуле:
(2.69)

Пример. Найти расстояние от точки М₀ (3; 4) до прямой 4 x – 3 y + 10 = 0.

Решение. Теперь подставляем вместо х₀ и у₀ координаты точки М₀, то есть х₀ = 3, у₀ = 4 в формулу (2.69) и находим искомое расстояние:

Плоскость и ее уравнение

Пусть в системе координат Оxyz задана произвольная плоскость . Возьмем на этой плоскости какую-нибудь точку М₀ (х₀; у₀;z₀).
Выберем вектор , перпендикулярный плоскости , и назовем его нормальным вектором, или просто нормалью. Этими двумя величинами (точкой, через которую проходит плоскость, и вектором, перпендикулярным к плоскости) плоскость определяется однозначно. На плоскости возьмем произвольную точку M (x, y, z) (рис. 44).

Рис. 44.

Поскольку точка М (x, y, z) находится на плоскости, то вектор  перпендикулярен к
вектору , а это значит, что их скалярное произведение равно нулю, то есть    (2.70).
Уравнение (2.70) является векторным уравнением плоскости. Распишем
уравнения (2.70) в координатной форме, зная, что
. Получим
A (x – х₀) + B (y – у₀) + C (z –z₀) = 0 (2.71).

Уравнение (2.71) является уравнением плоскости, проходящей через заданную точку М₀ (х₀; у₀;z₀) и перпендикулярную к заданному вектору
Уравнение (2.71) удовлетворяют координаты произвольной точки, которая находится на этой плоскости , и не удовлетворяют координат произвольной точки, не находящейся на этой плоскости.
Раскрыв скобки в уравнении (2.71), получим
Ax + By + Сz + D = 0, (2.72)
где D = –Aх₀ – Bу₀ – Cz₀. Уравнение (2.72) называется общим уравнением плоскости.

Каждая плоскость в декартовых прямоугольных координатах определяется уравнением первой степени относительно бегущих координат x, y, z. Верно и обратное утверждение: каждое уравнение первой степени относительно бегущих координат x, y, z определяет плоскость.

Действительно, пусть х₀, у₀,z₀ – какое-нибудь решение уравнения (2.72), т.е.
Aх₀ + Bу₀ + Сz₀ + D = 0 (2.73).

Вычитая почленно из уравнения (2.72) равенство (2.73), получим уравнение A (x – х₀) + B (y – у₀) + C (z –z₀) = 0 , которое и является уравнением плоскости, проходящей через точку М₀ (х₀; у₀;z₀) и перпендикулярно вектору) .
.

Исследование общего уравнения плоскости

Под исследованием общего уравнения плоскости понимается то, какое положение занимает плоскость, когда некоторые из коэффициентов A, B, C и D превращаются в ноль.

1) D = 0, A ≠ 0, B ≠ 0, C ≠ 0, то уравнение плоскости имеет вид Ax + By + Cz = 0, то есть плоскость проходит через начало координат;

2) C = 0, A ≠ 0, B ≠ 0, D ≠ 0, то уравнение (2.72) будет иметь вид Ax + By + D = 0. В плоскости Оxy это уравнение определяет прямую линию, а в пространстве это будет уравнение плоскости, параллельной оси Оz.

3) B = 0, A ≠ 0, C ≠ 0, D ≠ 0, то уравнение (2.72) будет иметь вид Ax + Cz + D = 0 и является уравнением плоскости, параллельной оси Оy.

4) A = 0, B ≠ 0, C ≠ 0, D ≠ 0, то уравнение (2.72) имеет вид By + Cz + D = 0 и является уравнением плоскости, параллельной оси Оx. Итак, если в уравнении плоскости (2.72) отсутствует одна из координат x, y или z , то плоскость параллельна оси Оx, Оy или Оz.

5) Если D = C = 0, A ≠ 0, B ≠ 0, то уравнению Ax + By = 0 соответствует плоскость, проходящая через начало координат и параллельно оси Оz, то есть эта плоскость проходит через ось Оz;

6) Аналогично, когда D = B = 0, A ≠ 0, C ≠ 0, то уравнению Ax + Cz = 0 соответствует плоскость, проходящая через ось Оy.

7) Когда D = A = 0, C ≠ 0, B ≠ 0, то уравнению By + Cz = 0 соответствует плоскость, проходящая через ось Оx.

Если A = B = 0, C ≠ 0, D ≠ 0, то уравнение Сz + D = 0 определяет плоскость, параллельную оси Оx и оси Оy, то есть плоскость параллельна координатной плоскости Оxy. Эта плоскость отсекает на оси Оz отрезок .
9) Аналогично, когда A = C = 0, B ≠ 0, D ≠ 0, то уравнение By + D = 0 определяет плоскость, параллельная координатной плоскости Оxz и отсекает на оси Оy отрезок .
10) Когда B = C = 0, A ≠ 0, D ≠ 0, то уравнение Ax + D = 0 определяет плоскость, параллельная координатной плоскости Оyz и отсекает на оси Оx отрезок .
11) Если B = C = D = 0, A ≠ 0, то уравнение Ax = 0 равносильное x = 0, а это и есть уравнение координатной плоскости Оyz.

12) Аналогично, когда A = 0, C = 0, D = 0, B ≠ 0, то уравнение By = 0, (y = 0) представляет соответственно координатную плоскость Оzx.

13) Если A = B = D = 0, C ≠ 0, то уравнение C = 0 (или z = 0) являются соответственно уравнением координатной плоскости Oxy.

Уравнение плоскости в отрезках

Пусть в уравнении (2.72) каждый из коэффициентов A, B, C, D не равен нулю, то есть плоскость пересекает все оси координат и не проходит через начало координат. Преобразуем уравнение (2.72) таким образом: Aх + Bу + Сz = –D,

Для сокращения записи обозначим

тогда уравнение плоскости будет иметь вид

(2.73)

Уравнение (2.73) называют уравнением плоскости в отрезках, где числа a, b, c являются величины отрезков, которые отсекает плоскость на осях координат.

Угол между двумя плоскостями. условия параллельности и перпендикулярности плоскостей

Пусть заданы две плоскости
A₁х + B₁у + С₁z + D₁ = 0 (2.74)
A₂х + B₂у + С₂z + D₂ = 0 (2.75)

Если эти плоскости пересекаются, то углом между ними назовем любой смежный двугранный угол. Один из них равен углу φ между векторами и , а второй — .
Значит, искомый угол φ можно найти по формуле (2.21) §11
(2.76)
Если то из формулы (2.76) получаем, что

A₁A₂ + B₁B₂ + С₁С₂ = 0. (2.77)

Условие (2.77) получается из условия перпендикулярности векторов и . Равенство (2.77) называется условием перпендикулярности двух плоскостей.

Если плоскости (2.74) и (2.75) параллельны, то нормали этих плоскостей
и будут коллинеарны, и тогда по формуле (2.23) получим

. (2.78)

Условие (2.78) выражает условие параллельности двух плоскостей.

Пример 1. Записать уравнение плоскости, проходящей через точки M₁(8; –3; 1) и M₂(4; 7; 2) и перпендикулярной к плоскости 3x + 5y – 72 + 21 = 0.

Решение. Поскольку плоскость проходит через точку M₁(8; –3; 1), то ее координаты удовлетворяют уравнению (2.71), то есть
A (x – + B (y + 3) + C (z – 1) = 0. (2.79)

Аналогично, плоскость проходит и через точку M₂(4; 7; 2), то ее координаты удовлетворяют уравнению (2.79), то есть
A (4 – + B (7 + 3) + C (2 – 1) = 0. (2.80)

Используем условие перпендикулярности (2.77) для плоскости (2.79) и заданной плоскости 3x + 5y – 7z + 21 = 0, то есть 3A + 5B – 7C = 0. Для нахождения А, В, С имеем систему двух уравнений с тремя неизвестными, а именно

Из данной системы находим A и B через C, то есть , и подставляем полученные значения в уравнение (2.79):

Сделав упрощение в последнем уравнении, получаем искомое уравнение плоскости 3x + y + 2z – 23 = 0.

Нормальное уравнение плоскости

Положение плоскости в пространстве можно определить через нормальный вектор
, начало которого совпадает с началом координат, а конец находится на плоскости . Пусть длина этого вектора равна p, то есть , а углы наклона этого вектора к осям координат являются α, β, γ (рис. 45). Значит p является расстоянием от плоскости к началу координат.

Рис. 45.

Если через обозначим единичный вектор нормали , то координаты будут (сos α, cos β, cos γ). На основании §8 их называют направляющими косинусами нормального вектора. Возьмем произвольную точку M (x, y, z) на плоскости и обозначим радиус-вектор через . Тогда . Теперь на основе формулы (2.15) имеем

потому что .
Значит, мы получим, что или . (2.81)
Уравнение (2.81) называется нормальным уравнением плоскости в векторной форме. Распишем уравнения (2.81) в координатной форме, получим

x cos α + y cos β + z cos γ – p = 0. (2.82).

В этом уравнении p расстояние от плоскости до начала координат и
сos²α + cos²β + cos² γ = 1. (2.83)

Чтобы общее уравнение плоскости привести к нормальному виду, нужно общее уравнение плоскости умножить на постоянный множитель μ. Получим

μAx + μBy + μCz + μD = 0, где μA = cos α, μB = cos β, μC = cos γ, μD = –p.

Возведя первые три равенства в квадрат и сложив их,учитывая (2.83), получим
μ² (A² + B² + C²) = 1, или (2.84)

В формуле (2.84) необходимо брать знак, противоположный знаку свободного члена в общем уравнении плоскости, так как μD = –p, где p — всегда положительное, как расстояние.

Итак, чтобы уравнение (2.72) привести к нормальному виду, надо умножить его на нормировочный множитель (2.84).

Расстояние от точки до плоскости

Пусть задано нормальное уравнения плоскости : х cosα + y cosβ + z cos γ — p = 0 и точка М₀ (х₀; у₀;z₀) вне плоскости. Нужно вычислить расстояние от точки М₀ к плоскости (рис. 46).

Рис. 46.

Решение. Проведем через точку М₀ плоскость , параллельную плоскости (рис. 46). Нормальное уравнение плоскости запишем так
x cos α + y cos β + z cos γ – p₁ = 0 , где p₁ — расстояние плоскости от начала координат.

Искомое расстояние равно AB = p₁ – p . Поскольку точка М₀ (х₀; у₀;z₀) находится на плоскости , то
х₀ cos α + у₀ cos β + z₀ cos γ – p₁ = 0 и значит
d = p₁ – p = х₀ cos α + у₀ cos β + z₀ cos γ – p. Вообще
(2.85)
или
(2.86)

Прямая линия на плоскости

Рассмотрим равенство, связывающее переменные. и :

. (1)

Равенство (1) называют уравнением с двумя переменными и , если это равенство выполняется не для всех пар чисел , , и тождеством, если оно справедливо для всех значений и . Например, равенства и являются уравнениями, а равенства и — тождествами.

Равенство (1) называют уравнением линии, заданной на плоскости относительно определенной системы координат, если этому уравнению удовлетворяют координаты и каждой точки линии , и не удовлетворяют координаты и ни одной точки, которая не лежит на этой линии.

Пусть линия относительно системы координат определяется уравнением (1). В аналитической геометрии линии классифицируют в зависимости от свойств уравнения. Если выражение в уравнении (1) является многочленом от переменных и (то есть суммой конечного числа одночленов , где а — постоянный коэффициент, а показатели и — целые положительные числа или нули), то линия, которая задается этим уравнением, называется алгебраической.

Алгебраические линии различают в зависимости от их порядка. Степенью одночлена называется сумма + показателей при переменных. Степенью уравнения (1) называется наивысшая степень одночлена, входящего в его состав. Алгебраической линией -го порядка называется линия, которая выражается уравнением -й степени. Порядок алгебраической линии не изменяется при замене одной декартовой системы на другую.

Линия, не являющаяся алгебраической, называется трансцендентной. Мы изучаем линии первого и второго порядков, то есть линии, задаваемые уравнениями

Таким образом, линию на плоскости можно задать геометрически как совокупность точек с определенными геометрическими свойствами и аналитически — с помощью уравнения. В связи с этим возникают две типичные для аналитической геометрии задачи: составить уравнение линии, которая задана геометрически, и наоборот, установить геометрический образ линии, заданной аналитически. Отметим, что в аналитической геометрии вторая задача решается лишь для алгебраических линий первого и второго порядков. Общий метод исследования линий, заданных уравнениями, дается в курсе математического анализа.

Пример №1

а) Уравнение определяет на плоскости прямую линию.

б) Уравнения или определяют две прямые — биссектрисы координатных углов.

в) Уравнению удовлетворяет только одна точка (0:0) — вырожденная линия.

г) Уравнение не определяет ни какого геометрического места точек, поскольку для любых действительных значении и имеем .

Уравнения прямой

Рассмотрим уравнение

. (2)

Ее графиком является прямая в координатной плоскости. Уравнение (2) в аналитической геометрии называется уравнением прямой с угловым коэффициентом. Параметр равен тангенсу угла , образованного прямой и положительным направлением оси . Этот параметр называется угловым коэффициентом или коэффициентом наклона прямой. Параметр b — ордината точки пересечения прямой и оси .

Вторым распространенным типом уравнения прямой является общее уравнение прямой.

. (3)

Рассмотрим особые случаи:

а) при С = 0 — прямая проходит через начало координат;

б) при В = 0 — прямая параллельна оси ;

в) при А = 0 — прямая параллельна оси ;

г) при В = С = 0 = 0, = 0 — ось ;

д) при А = С = 0 = 0, = 0 — ось .

Уравнение прямой в отрезках на осях

, (4)

где а и b — величины отрезков, отсекаемых прямой на осях координат.

Угол между прямыми, условия параллельности и перпендикулярности

Угол отсчитанный против часовой стрелки от прямой до прямой , определяется формулой

. (5)

Для прямых, заданных общими уравнениями , формула (5) примет вид

(6)

Пример №2

Определить угол между прямыми: а) и ; б) и .

Решение:

а) , , поэтому .

б) , , поэтому .

Условие параллельности:

(7)

Условие перпендикулярности:

. (8)

Основные формулы, связанные с прямой на плоскости

Уравнение пучка прямых, проходящих через данную точку :

. (9)

Уравнение прямой, проходящей через две данные точки и :

. (10)

Чтобы найти точку пересечения непараллельных прямых, нужно составить из них систему уравнений и решить ее относительно неизвестных и . Например, даны прямые и . Составив из них систему

(11)

и решив ее, рассчитаем координаты точки пересечения прямых.

Расстояние от точки () до прямой находят по формуле

(12)

Пример №3

Найти уравнение прямой, проходящей через точки А(1; 4) и В(-2; 3). Определить уравнение высоты , опущенной на прямую АВ из точки С(0; -5),и вычислить ее длину. Найти координаты точки пересечения прямой АВ и высоты .

Решение:

Уравнение прямой АВ найдем по формуле (10):

Угловой коэффициент высоты найдем из условия перпендикулярности (8):

Подставив координаты точки С(0:-5) и = -3 в уравнение пучка прямых (9), найдем уравнение высоты :

Длину высоты найдем, как расстояние от точки С (0; -5) до прямой АВ. Запишем уравнение прямой АВ в общем виде

Воспользовавшись (12), получим

Обозначим точку пересечения прямой АВ и высоты через . Для нахождения ее координат составим систему уравнений:

Итак,

Заметим, что ,

поэтому

Таким образом, результаты расчетов совпали.

Неравенства, задающие полуплоскости

Множество точек, лежащих на некоторой прямой и по одну сторону от нее, называется полуплоскостью. Очевидно, что любая прямая делит плоскость на две полуплоскости, для которых она является общей границей. Эти полуплоскости определяются неравенствами

Выбрав произвольную точку , не принадлежащую границе, подставим ее координаты в выражение . Если окажется, что

то неравенство

определяет полуплоскость, содержащую точку . Если же

то полуплоскость задается неравенством

Пример №4

По данным примера 2.3 найти неравенство, которое определяет полуплоскость, содержащую прямую АВ и точку С(0; -5).

Решение:

Общее уравнение прямой АВ: .

Подставляя координаты точки С(0; -5) в выражение , получим 0-3 • (-5) + 11 0.

Поэтому искомым неравенством будет

Экономические задачи, использующие уравнение прямой

Приведем примеры использования уравнения прямой в экономике.

1) Если через обозначить тариф перевозки груза за единицу расстояния; b — издержки при перевозке груза, не зависящие от расстояния , то общую стоимость перевозки груза на расстояние можно вычислить по формуле

2) Если обозначить через издержки предприятия в течение месяца при выпуске единиц однородной продукции, то они могут быть определены по формуле

где — издержки предприятия в течение месяца на выпуск единицы продукции, b -постоянные издержки, не зависящие от объема выпуска продукции (амортизация здания, заработная плата, охраны, коммунальные услуги и т.д.).

Пример №5

Издержки производства =10 единиц продукции составляют =1000 ден.ед., =50 единиц — =2000 ден.ед. Пусть функция издержек производства от объема продукции является функцией линейного типа.

Требуется определить: 1) издержки производства на выпуск единицы продукции; 2) постоянные издержки b, не зависящие от объема выпуска продукции; 3) издержки производства =30 единиц продукции.

Решение:

Пусть — объем продукции, — издержки производства. Тогда данные задачи будут определять две точки на плоскости с координатами: А(10; 1000), В(50; 2000). Определим согласно (10) уравнение прямой (т.е. линейной зависимости) по этим двум точкам:

1) Издержки производства на выпуск единицы продукции: = 25. 2) Постоянные издержки, не зависящие от объема выпуска продукции: b = 750. 3) Издержки производства = 30 единиц продукции: (30) = 1500.

Пример №6

Стоимость перевозки груза железнодорожным и автомобильным транспортом линейно зависит от расстояния . Автотранспортный тариф перевозки составляет =50 ден.ед. за единицу расстояния и за перевозку на =2 ед. расстояния было уплачено = 250 ден.ед. Услуги железнодорожного транспорта за перевозку на = 2 ед. расстояния стоят = 300 ден.ед., на = 6 ед. расстояния — = 400 ден.ед.

Требуется определить: 1) постоянные издержки , автотранспортных перевозок, не зависящие от расстояния; 2) железнодорожный тариф за единицу расстояния и постоянные издержки железнодорожных перевозок, не зависящие от расстояния; 3) при каких расстояниях более выгоден тот или иной вид транспортировки. Проиллюстрировать эти выводы графически.

Решение:

Данные задачи имеют вид:

1) Общий вид линейной зависимости ,

поэтому постоянные издержки автотранспортных перевозок, не зависящие от расстояния, равны:

(ден.ед.).

2) Числовые данные задачи определяют две точки на плоскости: А(2; 300), В(6; 400). Определим уравнение прямой (т.е. линейной зависимости) по этим двум точкам:

Т.о., железнодорожный тариф за единицу расстояния и постоянные издержки железнодорожных перевозок, не зависящие от расстояния, равны: .

3) Для того, чтобы определить при каких расстояниях выгоден тот или иной вид транспортировки, надо решить систему уравнений:

Корни системы: =4, = 350. Следовательно, при расстоянии =4 стоимость перевозки одинакова для автомобильного и железнодорожного транспорта, и равна: = 350 (ден.ед.). Построим обе прямые в координатной плоскости (рис. 1).

Судя по графику, при >4 прямая = 50 + 150 расположена выше прямой = 25+ 250, т.е. более дорогой вид транспорта — автомобильный. Поэтому при расстоянии > 4 более выгоден железнодорожный вид транспортировки, а при расстоянии < 4 более выгоден автомобильный вид транспортировки.

Рис. 1. Иллюстрация к примеру 6

Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:

Другие темы которые вам помогут понять высшую математику:

Прямая линия на плоскости с примерами

В прямоугольной системе координат уравнения прямой на плоскости задается одним из следующих видов.

1. Уравнение прямой с угловым коэффициентом:

где — угловой коэффициент прямой, то есть тангенс этого угла, который прямая образует с положительным направлением оси причем, этот угол отсчитывается от оси к прямой против часовой стрелки; — величина отрезка, что отсекает прямая на оси ординат. При уравнения (2.6) имеет вид и соответственная ему прямая проходит через начало координат.

Уравнение прямой с угловым коэффициентом решенное относительно текущей координаты

2. Общее уравнение прямой

Если то и прямая, что обозначается этим уравнением, проходит через начало координат, так как координаты начала координат удовлетворяют этому уравнению.

б) если в общем уравнении (2.7) то уравнение получит вид:

или

Уравнение не содержит переменной и этим уравнением обозначается прямая, которая параллельна оси

в) если в общем уравнении (2.7) то уравнение получит вид:

или

Уравнение не содержит переменной и этим уравнением обозначается прямая, которая параллельна оси

Необходимо запомнить, если прямая параллельна какой — нибудь координатной оси, то в ее уравнении отодвинутый член, который содержит координату, одноименную с этой осью.

г) При и — уравнение (2.7) имеет вид или Эти уравнения оси

д) При и уравнение (2.7) запишется в виде или Эти уравнения оси

3. Уравнение прямой в отрезках на осях:

где — величина отрезка, который отделяет прямая на оси — величина отрезка, который отделяет прямая на оси Каждый из этих отрезков выкладывается от начала координат.

4. Если прямая имеет угловой коэффициент и проходит через заданную точку то ее уравнение имеет вид:

Если в этом уравнении параметра придавать разные значения, то получим разные прямые, которые проходят через заданную точку Тогда уравнение (2.9) дает связку прямых с центром в точке

5. Если прямая проходит через две заданные точки и то уравнения:

называется уравнением прямой, что проходит через две заданные точки и

6. Если задан вектор параллельный прямой и точку на этой прямой, то уравнение прямой можно записать в виде:

Вектор называется направляющим вектором прямой.

7. Углом между прямыми и называется угол, на которой необходимо повернуть прямую, к соприкасанию ее с второй прямой, против часовой стрелки.

и этот угол вычисляется по формуле:

Необходимо обратить внимание на то, что в числителе дроби от углового коэффициента второй прямой отнимается угловой коэффициент первой прямой.

Условие параллельности двух прямых:

Условие перпендикулярности двух прямых:

или

Если прямые заданы уравнениями в общем виде:

то условием параллельности будет равенство а перпендикулярности будет

Координаты точек пересечения двух прямых обозначаются путем решения системы уравнений этих прямых:

где

Отклонения вычисляются по формуле:

Расстояние от точки к прямой является абсолютная величина отклонения точки от прямой

Примеры решения задач:

Задача 2.21.

Построить прямую

Общий метод построения прямой: Положение прямой на плоскости обозначается двумя точками, которые принадлежат этот прямой. Для построения прямой достаточно знать координаты двух произвольных точек этой прямой. Для этого вычисляется значение из данного равенства: при произвольных значениях

при значении

Складывается следующая таблица:

Таким образом, через полученные две точки, координаты которых и строим прямую (рис. 2.6).

Задача 2.22.

Построить прямую

Решение. Так как произвольный член уравнения равен нулю, то прямая проходит через начало координат. Если мы зададим произвольное значение найдем соответственное значение из заданного уравнения, то получим еще одну точку, которая лежит на прямой. Если то Через точки и проводим прямую, уравнение которой (рис. 2.7).

Задача 2.23.

Построим прямые и

Решение. 1) Рассмотрим уравнение Запишем его в виде Это говорит, что каждая точка прямой имеет постоянную абсциссу, то есть прямая проходит слева от оси на расстоянии 4 единицы масштаба от нее. Следует, прямая параллельна оси и отделяет на оси отрезок, равный -4,

2) Аналогично уравнение показывает, что все точки этой прямой имеют одну и ту же ординату, то есть прямая параллельна оси и отделяет на оси отрезок, равный 3 (единицы масштаба) (рис. 2.8),

Задача 2.24

Сложить уравнение прямой, что отделяет на оси отрезок. равный 4 и образует с осью угол

Решение. Воспользуемся уравнениями прямой с заданным угловым коэффициентом Согласно условию

Искомое уравнение прямой будет:

или

Задача 2.25

Найти уравнение сторон треугольника, вершины которого

Решение. Воспользуемся формулой (2.10):

Для нахождения уравнения стороны берем и

Пусть

Подставим в уравнение (2.10):

или

Для нахождения уравнения стороны берем и

Пусть

Подставим в уравнения (2.10):

или

Для нахождение уравнения стороны берем и

Пусть

Подставим в уравнение (2.10):

или

Задача 2.26

Найти углы и площадь треугольника, стороны которого заданы уравнениями:

Решение. Построим заданный треугольник.

Обозначим его вершины буквами Уравнения первой стороны является Угловой коэффициент прямой

Уравнение прямой является Угловой коэффициент прямой

Углы треугольника будем искать по формуле (2.11)

Для того, чтобы найти площадь треугольника, необходимо обозначить координаты его вершин. Точки и мы найдем, решив систему уравнений прямых, что дают эти прямые в пересечении.

Решим систему:

Сложим к первому уравнению второе:

Подставим полученное значение переменной в любое уравнение системы, например во второе:

Получили точку

Отнимем от первого уравнения второе:

Подставим полученное значение переменной в любое уравнение системы, например во второе:

Получили точку

Прибавим к первому уравнению второе:

Подставим полученное значение переменной в любое уравнение системы, например во второе:

Получили точку

Найдем плоскость треугольника по формуле:

Площадь треугольника кв.

Задача 2.28

Найти уравнение прямой, что проходит через точку параллельно прямой

Решение. Исходя из того, что искомая прямая параллельна заданной, ее угловой коэффициент равен угловому коэффициенту заданной прямой, то есть

Сложим уравнение искомой прямой по формуле:

Искомое уравнение прямой

Задача 2.29

Найти уравнение прямой, что проходит через точку и перпендикулярна к прямой

Решение. Так как искомая прямая перпендикулярна заданной, то произведение угловых коэффициентов обоих прямых может быть равен -1, то есть Таким образом, угловой коэффициент искомой прямой может быть обратной абсолютной величиной и противоположной к знаку углового коэффициента заданной прямой:

Найдем угловой коэффициент заданной прямой:

По условию перпендикулярности:

Находим уравнение искомой прямой по формуле:

Искомое уравнение прямой:

Задача 2.30

Найти проекцию точки на прямую, что проходит через точки и

Решение. Уравнение прямой найдем по формуле (2.10):

Проекцию точки на прямую будет основа перпендикуляра, который опущен из точки на прямую . Уравнение перпендикуляра можно найти по формуле так как координаты точки заданы, а угловой коэффициент, согласно условию перпендикулярности равен:

Получили уравнение перпендикуляра

Решили систему уравнений и найдем проекцию точки на прямую .

Используя формулы (2.14) находим и

Искомая точка

Задача 2.31.

Найти расстояние между двумя параллельными прямыми:

Решение. Искомое расстояние мы найдем как расстояние от произвольной точки одной прямой к второй прямой. Возьмем на первой прямой произвольную точку, например точку с абсцисой в ее ордината будет:

Следует, на первой прямой выбрана точка Найдем расстояние от точки к заданной второй прямой по формуле (2.15):

Задача 2.32.

Заданы вершины треугольника Найти:

1) длины сторон;

2) уравнение сторон;

3) уравнение высоты, что проведена из вершины

4) длина этой высоты;

5) уравнение медианы, что проведена из вершины

6) точку пересечения высоты, что проведена из вершины и медианы, что проведена из точки

7) уравнение биссектрисы угла

центр тяжести треугольника;

9) угол

10) площадь треугольника.

Решение.

1) Длина сторон обозначим с помощью формулы расстояния между двумя точками:

2) каждая сторона треугольника проходит через две точки, для нахождения уравнения сторон используем формулу (2.10):

Найдем уравнение сторон:

2) Чтобы сложить уравнение высоты, которая проведена из точки на сторону необходимо найти угловой коэффициент высоты.

Сначала найдем угловой коэффициент стороны

Из условия перпендикулярности двух прямых найдем угловой коэффициент высоты

Сложим уравнение высоты, воспользуемся формулой:

4) Для нахождения длины используем формулу (2.15):

с помощью которой найдем расстояние от точки к прямой

5) Для нахождения уравнения медианы нужно найти координаты точки

координаты точек

Уравнение медианы находится как уравнение прямой, что проходит через две точки и

6) Чтобы найти координаты точки пересечения высоты и медианы , необходимо решить систему уравнений этих прямых:

Искомая точка пересечения

7) Для нахождения уравнения биссектрисы внутреннего угла необходимо найти координаты точки Согласно свойствам биссектрисы внутреннего угла треугольника, которая делит сторону в соотношении находим Находим координаты точки по формуле:

Искомая точка

Находим уравнение биссектрисы внутреннего угла

Центр тяжести треугольника обозначается по формулам:

Искомая точка центра треугольника

9) Величину угла находим по формуле:

Из решения получим: тогда,

Величина угла

10) Найдем площадь треугольника по формуле:

Искомая площадь (кв. ед.).

Прямая на плоскости

Понятие об уравнении линии на плоскости. Основные задачи аналитической геометрии

Любую линию на плоскости в аналитической геометрии рассматривают как совокупность точек, обладающих некоторой общей свойством. На основании этого свойства между координатами , точек линии устанавливают соотношение, содержащее две переменные величины и, возможно, некоторые числовые параметры и константы.

Уравнения называется уравнением линии , если координаты любой точки, принадлежащей данной линии, удовлетворяют это уравнение и наоборот, если пара чисел удовлетворяет уравнение, то и являются координатами точки, принадлежащей линии:

уравнение

где закон, отражающий свойство точек линии.

Переменные и , входящих в уравнение линии, называются текущими координатами ее точек, то есть , — это координаты любой точки линии.

Составим уравнение окружности радиуса с центром в точке (рис. 7.1)

Рис. 7.1

Кругом называется линия, все точки которой находятся на одинаковом расстоянии , которую называют радиусом круга, от заданной точки плоскости — центру круга.

Из определения следует геометрическое свойство точек, принадлежащих данной линии.

Применим стандартную схему решения следующих задач:
1) выбираем на координатной плоскости произвольную точку , которая принадлежит линии ;
2) записываем средствами алгебры в аналитическом виде условие, которое удовлетворяет любая точка линии.

Пусть — произвольная точка окружности с текущими координатами, тогда согласно свойством точек окружности и формуле расстояния между двумя точками имеем:

откуда

Уравнение (7.2) называют каноническим уравнением окружности.
Если центр окружности лежит в начале координат, то его каноническое уравнение имеет вид:

Найдем уравнение линии, все точки которой равноудалены от двух точек и

Выбираем точку , которая принадлежит линии (рис. 7.2).

Рис. 7.2

По свойству точек линии: и формулой расстояния между двумя точками имеем:

Упростим полученное уравнение, для чего поднимем к квадрату обе части:

раскроем скобки и сведем подобные члены:

Получили уравнение прямой линии, перпендикулярной отрезку , разделяет его пополам и является биссектрисой первого и третьего координатных углов.

К основным задачам аналитической геометрии на плоскости относят следующие задачи:
1. Составить уравнение кривой по заданной геометрической свойством ее точек. Примером такой задачи является задача на составление канонического уравнения круга. Аналогичным образом находят уравнение других известных линий: прямой, гиперболы, параболы, эллипса. Изучение таких линий является одной из задач данного раздела.
2. Построить линию по заданным ее уравнением. Эта задача в общем случае не дает ответа на вопрос о геометрических свойств точек линии и является задачей математического анализа.

Разновидности уравнений прямой на плоскости

Понятие «прямая линия», или просто «прямая», является первичным в геометрии, то есть неопределенным через другие математические понятия. С аксиом элементарной геометрии известно через две точки можно провести прямую и притом только одну; через точку, которая не принадлежит заданной прямой, можно провести параллельную (перпендикулярную) ей прямую и притом только одну, и др.

В зависимости от того, какие исходные данные, определяющие единую прямую, положено в основу построения ее аналитического образа — уравнение — одна и та же прямая может описываться уравнениями различного вида. Рассмотрим основные их разновидности.

Зададим на плоскости систему координат и некоторую прямую.

Уравнение прямой с заданным нормальным вектором

Любой ненулевой вектор , перпендикулярный к прямой, называется нормальным вектором прямой (рис. 7.3).

Рис. 7.3

Найдем уравнение прямой, проходящей через точку и имеет нормальный вектор . Для этого возьмем на прямой произвольную точку , которая отличается от и введем в рассмотрение вектор

С условия ортогональности векторов и имеем:

Уравнение (7.4) называется уравнением прямой с заданным нормальным вектором. Если в нем раскрыть скобки, то получим стандартную запись линейного уравнения с двумя переменными:

где свободный член уравнения (некоторое число).

Общее уравнение прямой и его исследование

Уравнения вида

где . линейное относительно переменных и , называется общим
уравнением прямой на плоскости, или уравнением прямой в общем виде.

Теорема 7.1 (о общее уравнение прямой). Любая прямая описывается уравнением и каждое уравнение вида определяет прямую линию.

Доказательство базируется на уравнении (7.4):

Отсюда имеем (7.5):

общее уравнение прямой.

Пусть задано уравнение (7.5), где — ненулевой вектор, то есть , в котором . Тогда,

Уравнение (7.6) определяет прямую, проходящую через точку и имеет нормальный вектор .

Исследование общего уравнения прямой предполагает выяснение особенностей расположения прямой относительно координатных осей в зависимости от значения тех или иных из чисел — параметров уравнения:

уравнение прямой общего расположения;

уравнение прямой, параллельной оси ;

уравнение прямой, параллельной оси

уравнение прямой, проходящей через начало координат;

уравнение оси ;

уравнение оси .

Каноническое и параметрическое уравнение прямой

Любой ненулевой вектор , что параллельный прямой или лежит на ней, называется направляющим вектором прямой. Координаты направляющего вектора согласно определению подаются так:

где направляющие косинусы вектора

Составим уравнение прямой, проходящей через точку и имеет направляющий вектор . Для этого выберем на прямой (рис. 7.4) произвольную точку , которая не совпадает с точкой , и введем в рассмотрение вектор

Рис. 7.4

Вектор и направляющий вектор прямой коллинеарны, поэтому их координаты пропорциональны:

Уравнение (7.9) называют каноническим уравнением прямой.

Если за направляющий вектор взять единичный вектор , то , , а уравнение (7.9) принимает вид:

это каноническое уравнение прямой с единичным направляющим вектором.
Если в (7.9) положить каждое отношение равным , то получим:

Уравнение (7.11) называют параметрическим уравнением прямой.
В случаях, когда одна из координат, или , равна нулю, получаем параметрические уравнения прямых, параллельных соответственно оси или оси .

Уравнение прямой, проходящей через две заданные точки

Составим уравнение прямой, проходящей через заданные точки и . Для этого выберем на прямой (рис. 7.5) произвольным образом точку , которая отличается от точек и , и введем в рассмотрение векторы и

Рис. 7.5

По условию коллинеарности этих векторов получим искомое уравнение прямой:

Уравнение (7.12) называют уравнением прямой, проходящей через две заданные точки.

Заметим, что вектор является направляющим вектором прямой, как и противоположный ему вектор .

Уравнение прямой, проходящей через заданную точку в заданном направлении

Найдем уравнение прямой, проходящей через точку и наклонена к оси под углом (рис. 7.6).

Рис. 7.6

С канонического уравнения прямой (7.9) и соотношения (7.8) получаем:

Окончательно имеем:

где называют угловым коэффициентом прямой.

Уравнение (7.13) называется уравнением прямой, проходящей через заданную точку в заданном направлении.

Изменяя в уравнении (7.13) произвольным образом значение параметра , мы сможем получить любое число прямых (даже бесконечно много!), Поэтому его называют также уравнением семьи прямых с центром в точке

Уравнения прямой с угловым коэффициентом

Составим уравнение прямой, которая наклонена к оси под углом и отсекает на оси отрезок величины (рис. 7.7).

Рис. 7.7

Уравнение получаем как следствие из (7.13), если по взять координаты точки

Уравнение

называют уравнением прямой с угловым коэффициентом.

Уравнение прямой в отрезках на осях

Построим уравнение прямой, которая пересекает оси координат и соответственно в точках и (рис. 7.8).

Рис. 7.8

Уравнение

называется уравнением прямой в отрезках на осях.

Нормальное уравнение прямой

Построим уравнение прямой в условиях: расстояние от начала координат до прямой равно , нормальный вектор прямой образует с осью угол (рис. 7.9).

Рис. 7.9

Для этого выберем на прямой произвольную точку и введем в рассмотрение вектор . Пусть — прямая, имеет единичный направляющий вектор . На этой прямой отложим отрезок длины .

Используя скалярное произведение двух векторов, получаем: с одной стороны

а с другой —

Таким образом, искомое уравнение имеет вид:

или

Уравнение (7.16) называется нормальным уравнением прямой.

Свойства нормального уравнения прямой

1. Сумма квадратов коэффициентов при текущих координатах , равна единице
2. Свободный член уравнения всегда отрицательный .

Эти свойства используются при возведении общего уравнения прямой к нормальному виду.

Основные задачи о прямой линии на плоскости

Взаимное расположение двух прямых

Пусть прямые и заданные общими уравнениями:

Установим условия: 1) сечения; 2) параллельности; 3) совпадения двух прямых.
Задача сводится к исследованию системы двух линейных уравнений

каждое из которых является уравнением соответствующей прямой.

1. Если прямые пересекаются, то они имеют общую точку и к тому же только одну. Это значит, что координаты этой точки удовлетворяют оба уравнения, следовательно, система совместима и имеет единственное решение.

По правилу Крамера определитель этой системы должен быть отличаться от нуля. Это обстоятельство определяет условие пересечения двух прямых, заданных общими уравнениями:

Отсюда

2. Если прямые параллельны, то они не имеют общих точек. это значит, что система несовместима, то есть:

или

Значит, надо проверить выполнение условия:

которая и является условием параллельности двух прямых.

3. Если прямые совпадают, то они имеют множество общих точек. Это значит, что система совместима и неопределенная, то есть: . Тогда имеем условие совпадения двух прямых:

Угол между двумя прямыми, которые заданные общими уравнениями

Пусть прямые и заданные общими уравнениями

Углом между двумя прямыми, которые описываются общими уравнениями, называют один из смежных углов между их нормальными векторами , и , (рис. 7.10).

По формуле угла между векторами и имеем:

Отсюда

Рис. 7.10

Если нормальные векторы и образуют тупой угол (рис. 7.10), то и угол между прямыми тоже тупой; если в качестве нормального вектора прямой выбрать вектор , то угол между прямыми будет острый.

С (7.20) получаем условие ортогональности прямых:

Поскольку каждое из уравнений, приведенных в предыдущем параграфе 7.2 (пункты 1-6), допускает запись в общем виде, то формулы (7.17) — (7.21) можно записать через параметры
соответствующего вида уравнения прямой.

Пусть прямые заданные уравнениями с угловыми коэффициентами (рис. 7.11):

По свойству внешнего угла треугольника и формуле тангенса разности двух углов получим:

Отсюда для двух прямых устанавливаем:
1) условие параллельности:
2) условие перпендикулярности:

Возведение общего уравнения прямой к нормальному виду

Выше выведено девять разновидностей уравнений прямых, которые отличаются по форме символического представления, но все они являются линейными уравнениями относительно переменных , — текущих координат точек прямой. Каждое из них можно свести к другому с помощью тождественных преобразований.

Покажем, как осуществляется переход от уравнения (7.5): , к нормальному уравнению (7.16): .

В нормальном уравнении коэффициенты при переменных и являются координатами единичного нормального вектора прямой , а в общем уравнении — это параметры , которые являются координатами нормального вектора .

По определению направляющих косинусов вектора (6.5) относительно вектора имеем:

где

Это значит: чтобы перейти от произвольного вектора к единичному , надо умножить вектор на скаляр . Отсюда следует, что для перехода к нормальному уравнению прямой надо левую и правую части ее общего уравнения (7.5) умножить на число , знак которого выбирается противоположным знаку свободного члена (по второму свойству нормального уравнения должно выполняться условие: ):

Число , взятое с определенным знаком, называется нормируемых множителем общего уравнения прямой.

Пусть прямая задана общим уравнением:

Определим расстояние от прямой до начала координат.

Перейдем от общего уравнения прямой (7.5) к нормальному (7.16). По заданным уравнениям прямой определяем ее нормальный вектор: , находим его модуль и вычисляем нормировочный множитель. Поскольку свободный член общего уравнения прямой , то имеем:

Осуществляем нормирования общего уравнения, умножая его левую и правую части на :

За нормальным уравнением устанавливаем, что расстояние от начала координат до прямой равно .

Расстояние от точки до прямой

Пусть прямая задана нормальным уравнением: .
Найдем расстояние от точки к этой прямой.

Для этого на прямой (рис. 7.12) выбираем произвольную точку и вводим в рассмотрение вектор

Рис. 7.12

Запишем скалярное произведение векторов и

поскольку

Поскольку то расстояние равно модулю скалярного произведения векторов и :

Для любой точки прямой выполняется равенство: , следовательно, окончательно получаем:

Если прямая описывается общим уравнением , то имеем:

Уравнение биссектрис углов, образованных двумя прямыми

Пусть прямые и заданные общими уравнениями:

Найдем уравнения биссектрис углов, образованных этими прямыми. Напомним, что точки биссектрисы равноудалены от сторон угла (рис. 7.13). Именно на этом свойстве с привлечением формулы (7.26) основывается построение их уравнений.

Рис. 7.13

Обозначим текущие координаты точек биссектрисы через ; выберем на ней точку найдем расстоянии и приравняем их:

где модули нормальных векторов.

Снимаем символы модулей и, возвращаясь к обозначению текущих координат точек биссектрис строчными буквами, получим два уравнения биссектрис:

Запишем уравнения биссектрис углов между двумя прямыми, которые заданные уравнениями:

Согласно (7.27) находим модули нормальных векторов , и записываем уравнения биссектрис:

Итог рассматриваемого представим в виде таблицы.

Разновидности уравнений прямой

Разновидности уравнений прямой в Таблица 7.1

Лекции:

Выпуклость и вогнутость графика функции
Матанализ для чайников
Производные некоторых элементарных функций
Векторы
Объем конуса
Уравнения с одной переменной
Найдите координаты точки пересечения графиков
Геометрический смысл производной в точке
Двойной интеграл: примеры решения
Асимптотическое поведение функций. Сравнение бесконечно малых функций

Источник

Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.

Здесь будет калькулятор

Уравнение прямой с угловым коэффициентом

y=kx+by=kx+b,

где kk — угловой коэффициент, а bb — свободный коэффициент.

Уравнения данного вида составляются следующим образом по формуле:

y−y0=k(x−x0)y-y_0=k(x-x_0),

где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.

Задача 1

Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.

Решение

Подставляем значения в формулу:

y−y0=k(x−x0)y-y_0=k(x-x_0)

y−2=1⋅(x−1)y-2=1cdot(x-1)

Приводим подобные слагаемые:

y=x+1y=x+1

Ответ

y=x+1y=x+1

Общее уравнение прямой

Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:

y−x−1=0y-x-1=0

Уравнение прямой по двум точкам

Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:

Уравнение прямой по двум точкам

x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},

где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.

Задача 2

Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).

Решение

x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1

x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}

x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}

x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}

x−4=−y−12x-4=frac{-y-1}{2}

y+1=2⋅(4−x)y+1=2cdot(4-x)

y=8−2x−1y=8-2x-1

y=−2x+7y=-2x+7

Ответ

y=−2x+7y=-2x+7

Уравнение прямой при помощи точки и вектора нормали

Уравнение прямой по точке и нормали

(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,

где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.

Задача 3

Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).

Решение

x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5

(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,

(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,

x−7+40−5y=0x-7+40-5y=0

x−5y=−40+7x-5y=-40+7

x−5y=−33x-5y=-33

5y=x+335y=x+33

y=x5+335y=frac{x}{5}+frac{33}{5}

Проверка

Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.

8=75+3358=frac{7}{5}+frac{33}{5}

8=88=8 — верно, ответ правильный.

Ответ

y=x5+335y=frac{x}{5}+frac{33}{5}

Прямая в пространстве

Уравнение прямой, заданной в пространстве имеет такой вид:

Уравнение прямой в пространстве

x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},

где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.

Задача 4

Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).

Решение

x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7

x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}

x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}

Проверка

Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:

1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.

Такой вид уравнения прямой называется каноническим.

Ответ

x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}

Тест по теме “Составление уравнения прямой”

Источник

Уравнение высоты треугольника

Общее уравнение прямой: описание, примеры, решение задач

Общее уравнение прямой: основные сведения

Неполное уравнение общей прямой

Общее уравнение прямой, проходящей через заданную точку плоскости

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно

Составление общего уравнения прямой

Прямая на плоскости. Примеры решений

Тема 2.2. Прямая на плоскости

Уравнение прямой с угловым коэффициентом:

Уравнения прямых в пространстве

Уравнение прямой как линии пересечения двух плоскостей

Параметрическое уравнение прямой в пространстве

Каноническое уравнение прямой в пространстве

Переход от общего уравнение к каноническому

Расстояние от точки до прямой в пространстве

Уравнение прямой, проходящей через две заданные точки

Прямые на плоскости

Уравнения прямых

Уравнение прямой, которая проходит через две точки

Уравнения прямой, которая проходит через заданную точку с известным направляющим вектором

Уравнение прямой, которая проходит через данную точку перпендикулярно к данному вектору (нормальное уравнение прямой)

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой

Угол между прямыми

Пересечение прямых

Расстояние от точки до прямой

Прямая линия на плоскости и её определение

Уравнение прямой с угловым коэффициентом

Уравнение прямой, проходящей через заданную точку в данном направлении

Уравнение прямой в отрезках

Угол между двумя прямыми

Общее уравнение прямой и его исследование

Нормальное уравнение прямой

Расстояние от точки до прямой

Плоскость и ее уравнение

Исследование общего уравнения плоскости

Уравнение плоскости в отрезках

Угол между двумя плоскостями. условия параллельности и перпендикулярности плоскостей

Нормальное уравнение плоскости

Расстояние от точки до плоскости

Прямая линия на плоскости

Пример №1

Уравнения прямой

Угол между прямыми, условия параллельности и перпендикулярности

Пример №2

Основные формулы, связанные с прямой на плоскости

Пример №3

Неравенства, задающие полуплоскости

Пример №4

Экономические задачи, использующие уравнение прямой

Пример №5

Пример №6

Прямая линия на плоскости с примерами

Прямая на плоскости

Понятие об уравнении линии на плоскости. Основные задачи аналитической геометрии

Разновидности уравнений прямой на плоскости

Уравнение прямой с заданным нормальным вектором

Общее уравнение прямой и его исследование

Каноническое и параметрическое уравнение прямой

Уравнение прямой, проходящей через две заданные точки

Уравнение прямой, проходящей через заданную точку в заданном направлении

Уравнения прямой с угловым коэффициентом

Уравнение прямой в отрезках на осях

Нормальное уравнение прямой

Свойства нормального уравнения прямой

Основные задачи о прямой линии на плоскости

Взаимное расположение двух прямых

Угол между двумя прямыми, которые заданные общими уравнениями

Возведение общего уравнения прямой к нормальному виду

Расстояние от точки до прямой

Уравнение биссектрис углов, образованных двумя прямыми

Разновидности уравнений прямой

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой

Уравнение прямой по двум точкам

Уравнение прямой при помощи точки и вектора нормали

Прямая в пространстве

Тест по теме “Составление уравнения прямой”

Не пропустите также:

Тема
2.2. Прямая на плоскости