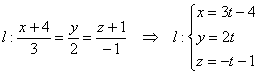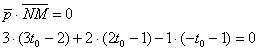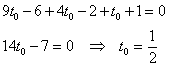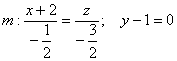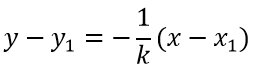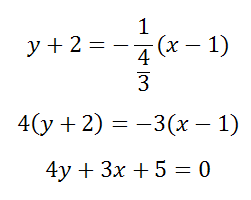Как найти уравнение перпендикулярной прямой через точку - AvtoShod.ru

Как составить уравнение прямой перпендикулярной данной прямой и проходящей через данную точку?

Пусть y=k₁x+b₁ — данная прямая. С учётом условия перпендикулярности прямых уравнение прямой, перпендикулярной данной, имеет вид

$[y = - frac{1}{{k_1 }}x + b_2 .]$

Если эта прямая проходит через точку M(x_o; y_o), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение x_o и y_o, мы найдем b.

Примеры.

1) Написать уравнение прямой, проходящей через точку A(-10;3), перпендикулярной прямой y=5x-11.

Решение:

Так как прямые перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, то

$[k_2 = - frac{1}{{k_1 }} = - frac{1}{5} = - 0,2.]$

Значит уравнение прямой, перпендикулярной прямой y=5x-11, имеет вид

Так как прямая проходит через точку A(-10;3), то координаты A удовлетворяют уравнению прямой:

откуда b=1.

Итак, уравнение прямой, перпендикулярной прямой y=5x-11 и проходящей через точку A(-10;3)

Ответ: y= -0,2x+1.

2) Написать уравнение прямой, перпендикулярной прямой x= -2, проходящей через точку M(-5;9).

Решение:

Прямая x= -2 перпендикулярна оси абсцисс. Значит, прямая, уравнение которой мы ищем, параллельна оси абсцисс, то есть ищем уравнение прямой в виде y=b.

Так как искомая прямая проходит через точку M(-5;9), то координаты M удовлетворяют уравнению прямой: y=9.

Ответ: y=9.

3) Написать уравнение прямой, перпендикулярной прямой y=4, проходящей через точку F(7;-5).

Решение:

Прямая y=4 перпендикулярна оси ординат. Следовательно, прямая, уравнение которой мы ищем, параллельна оси ординат, а значит, её уравнение имеет вид x=a.

Так как эта прямая проходит через точку F(7;-5), то координаты F удовлетворяют уравнению прямой: x=7.

Ответ: x=7.

Источник

1

Simplify the equation of the line. If you are given the equation of a line and one common point and asked to find a line that runs perpendicular to it, it is important that you first convert the equation into the format. To do this, you want to get the by itself.^[3]
2

Calculate the opposite reciprocal of the slope. When a line is perpendicular to another line, the slope will be the negative opposite of the original line. This is called the opposite reciprocal. The lines cross each other at a right angle, so the slopes must be opposite. Two perpendicular slopes multiplied together will always equal .^[4]

Advertisement
3

Plug the point into the slope equation to find the y-intercept. Now that you have the slope of the perpendicular line, you can plug the value of the slope and the point you were given into a slope equation. This will give you the value of the y-intercept. Using the y-intercept, you can move on to complete the slope equation.^[5]
4

Solve the equation for the y-intercept. Once you have your values entered into the slope equation, it is time to isolate , or the y-intercept. To isolate , you must move all other numbers from one side of the equation. After you solve for the y-intercept, you will know all of the numbers needed to write the equation of the perpendicular line.^[6]
5

1

Understand the coordinates you were given. If you are given three coordinates from two perpendicular lines, they cannot all be used for the same equations. The first two coordinates will be used for one line, and the third will be used once you begin calculating the equation of the perpendicular line. The goal is finding two perpendicular equations.^[8]
2
3
4

Simplify the equation to solve for . Once you have your chosen point and slope plugged into the equation, it is time to simplify. This will give you the equation of one line. After you know the equation of this line, you will be able to figure out the equation of the line that runs perpendicular to it.^[11]
5

Find the slope of the perpendicular line using the opposite reciprocal. A line perpendicular to another line will always have an opposite slope. If the slope of the original line is a positive whole number, then the slope of the perpendicular line will be a negative fraction. Two perpendicular slopes multiplied together will always equal .^[12]
6

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

References

About This Article

Thanks to all authors for creating a page that has been read 70,530 times.

Did this article help you?

Get all the best how-tos!

You’re all set!

Источник

5.5.6. Как найти прямую, перпендикулярную данной?

Обращаю внимание, что для скрещивающихся прямых таких прямых можно провести бесконечно много, а вот для

пересекающихся – задача имеет единственное решение:

Задача 157

а) Составить уравнения прямой, проходящей через точку перпендикулярно

прямой (прямые пересекаются).

б) Найти расстояние от точки до прямой , в) симметричную точку .

а) Решение: обозначим неизвестную прямую через :

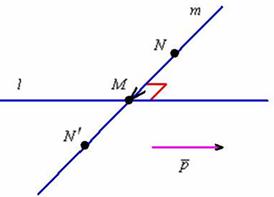
И начинаем

раскручивать задачу: что нам известно об этой прямой?

Известна её точка . Неплохо бы найти направляющий вектор. В качестве

такого вектора вполне подойдёт вектор . Но мы не знаем точку . Вот ей-то и займёмся

План есть, и мы счастливы:

1) Вытащим из уравнений прямой «эль» её направляющий вектор , а сами

уравнения перепишем в параметрической форме:

И вот уже в третий раз используем тот же самый фокус. Рассмотрим точку с пока ещё неизвестными координатами. Поскольку точка , то её

координаты удовлетворяют параметрическим уравнениям прямой «эль» и им

соответствует конкретное значение параметра :
, или в строчку:

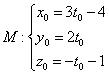
Тогда:

2) По условию прямые должны быть перпендикулярны, следовательно, их направляющие векторы – ортогональны. А если векторы ортогональны, то их скалярное

произведение равно нулю:

Что получилось? Простейшее линейное уравнение с одной неизвестной:

3) Значение параметра известно, находим точку:

И направляющий вектор: .

4) Уравнения прямой составим по точке и вектору… избавимся-ка мы от дробей и возьмём направляющий вектор :

Ответ:

Но, разумеется, тут можно было взять и вектор :

Проверка состоит из двух этапов:

1) проверяем направляющие векторы прямых на ортогональность;

2) подставляем координаты точки в уравнения каждой прямой, они должны «подойти» и там и там.

Об этих действиях говорилось много, поэтому я выполнил проверку на черновике.

5.5.7. Как найти расстояние от точки до прямой?

5.5.5. Пересекающиеся прямые в пространстве

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

1.Пусть прямая, проходит через точку T₁(x₁;y₁) и перпендикулярно прямой y=kx+b, тогда её можно представить уравнением (уравнение прямой перпендикулярной данной прямой):

Это и есть уравнение прямой, проходящей через точку перпендикулярно к прямой.
2. Если прямая проходит через ту же точку T₁(x₁;y₁) и перпендикулярно прямой, но только записанной в виде Ax+By+C = 0, то уравнение можно представить как:

A (y − y₁) − B (x − x₁ ) = 0

Пример 1
Составить уравнение прямой, проходящей через точку L(1;-2) и перпендикулярно прямой

4x-3y-1 = 0 (на рисунке прямая, обозначенная красным цветом)

Решение
Данную прямую можно представить уравнением y = 4/3x-1/3 (здесь a = 4/3). Уравнение искомой прямой есть

Пример 2
Составить уравнение прямой, проходящей через точку M(-1;-2) и перпендикулярной к прямой 3y+2=0

Решение
Здесь A=0, B=3, получаем 3(x+1)=0, т.е. x+1=0. В этом случае формула неприменима.

23272

Источник

Пусть дана прямая y=kx+b. И пусть дана точка M(x,y). Необходимо написать уравнение пямой, перпендикулярной данной прямой. Коэффициент k1 искомой прямой равен k1=-1/k. Далее в искомое уравнение прямой подставим координаты точки M. И найдем значение b .

Например пусть дана прямая y=2x+6. M(5,3). Запишем уравнение прямой, перпендикулярной данной. K1=-1/2. Подставляем координаты точки M, получим

3=-1/2×5+b.

3=-2,5+b

b=3+2,5

b=5,5.

Тогда искомое уравнение прямой имеет вид y=-1/2x+5,5.

Источник

References

About This Article

Did this article help you?

5.5.6. Как найти прямую, перпендикулярную данной?

Не пропустите также: