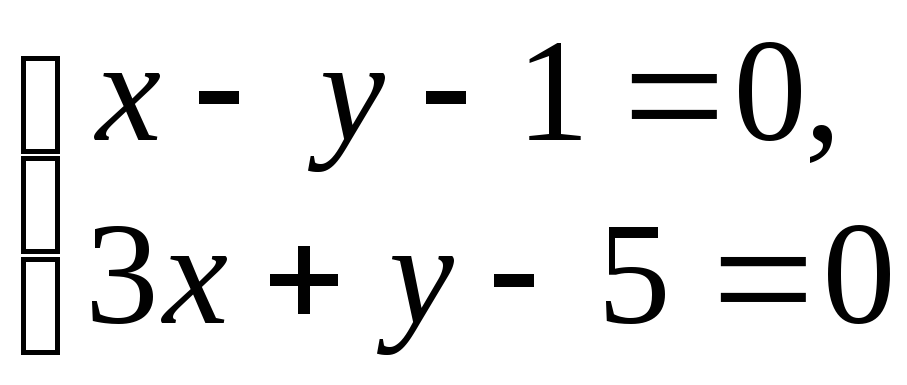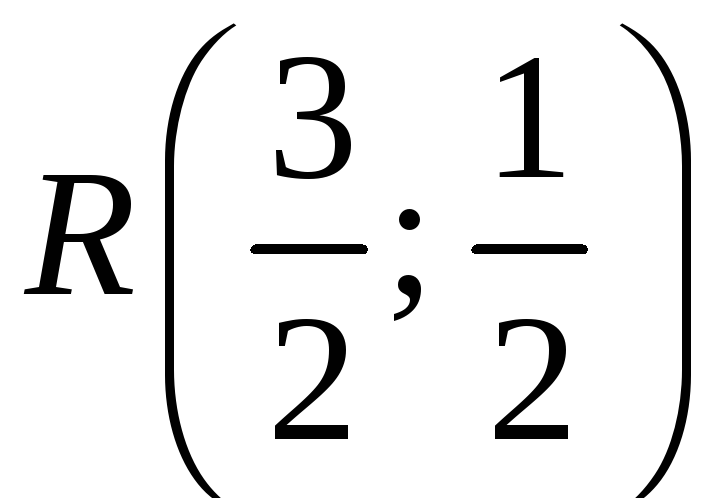Найти уравнение высоты и медианы треугольника
Уравнение медианы треугольника
Как составить уравнение медианы треугольника по координатам его вершин?
Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:
- Найти координаты середины отрезка по координатам его концов.
- Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).
Найти уравнения медиан треугольника.
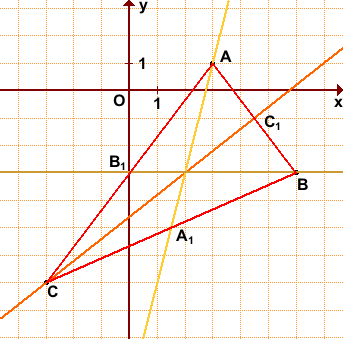
Обозначим середины сторон BC, AC, AB через A1, B1, C1.
Уравнение медианы AA1 будем искать в виде y=kx+b.
Найдём уравнение прямой, проходящей через точки A(3;1) и A1(1,5;-5). Составляем и решаем систему уравнений:
Отсюда k= 4; b= -11.
Уравнение медианы AA1: y=4x-11.
2) Аналогично, координаты точки B1 — середины отрезка AC
Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B1(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB1 можно найти ещё быстрее: y= -3.
3) Координаты точки C1 — середины отрезка BC:
Отсюда уравнение медианы CC1 : y=0,8x-4,6.
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) |
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Примеры решений по аналитической геометрии на плоскостиВ этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п. Решения задач о треугольнике онлайнЗадача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти: Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$. Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти: Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$. Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон. Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$. Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$. Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$. источники: http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik http://www.matburo.ru/ex_ag.php?p1=agtr |
Как составить уравнение медианы треугольника по координатам его вершин?
Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:
- Найти координаты середины отрезка по координатам его концов.
- Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.
Пример.
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).
Найти уравнения медиан треугольника.
Решение:
Обозначим середины сторон BC, AC, AB через A1, B1, C1.
1) По формулам координат середины отрезка
Уравнение медианы AA1 будем искать в виде y=kx+b.
Найдём уравнение прямой, проходящей через точки A(3;1) и A1(1,5;-5). Составляем и решаем систему уравнений:
Отсюда k= 4; b= -11.
Уравнение медианы AA1: y=4x-11.
2) Аналогично, координаты точки B1 — середины отрезка AC
Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B1(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB1 можно найти ещё быстрее: y= -3.
3) Координаты точки C1 — середины отрезка BC:
C(-3;-7), C(4,5;-1), y=kx+b:
Отсюда уравнение медианы CC1 : y=0,8x-4,6.
Решить треугольник Онлайн по координатам
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
1) Зная координаты вершин Можем узнать координаты вектора BC (2-3; -3-1) = BC(-1; -4)
Прямая проходящая через точку A должна идти коллинеарно вектору BC, то есть
(х-0) = k•(-1)
(y-4) = k•(-4)
откуда получаем -х=k и -y/4 +1 = k, приравниваем k
-x = -y/4 + 1 или
4x — y = -4
2) Медиана треугольника приходит в середину противоположной стороны. То есть в точку М — середина AС. Её координаты х = (0+2)/2 = 1; y = (4+(-3))/2 = 0,5; M(1; 0,5)
Получаем медиана идет из точки B в направлении вектора MB (3-1; 1-0,5) = MB (2; 0,5)
Получаем (x-3)/2 = (y-1)/0,5
0,5х — 1,5 = 2y — 2
x — 4y = -1
3) Высота из вершины С перпендикулярна стороне AB. То есть Вектора AB и CH ортогональны и их скалярное произведение = 0
AB (3-0; 1-4) = AB(3; -3)
CH (x-2; y-(-3))
<AB•СH> = 3•(х-2) + (-3)•(y+3) = 0
3x-6 — 3y — 9 = 0
x-y = 5 — получили уравнение прямой высоты CH
Уравнение прямой AB: (х-0)/3 = (y-4)/(-3)
x+y = 4
Точка Н — пересечение этих двух прямых:
Решая систему уравнений подстановкой, находим х=4,5; y=-0,5
CH (4,5-2; -0,5+3) = CH(2,5; 2,5)
|CH| = √(2,5² + 2,5²) = 2,5•√2
Ответ:
1) 4x — y = -4;
2) x — 4y = -1;
3) 2,5•√2
Раздел V.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
И В ПРОСТРАНСТВЕ
В раздел включены
задачи, которые рассматриваются в теме
«Аналитическая геометрия на плоскости
и в пространстве»: составление различных
уравнений прямых на плоскости и в
пространстве; определение взаимного
расположения прямых на плоскости,
прямых, прямой и плоскости, плоскостей
в пространстве; изображение кривых
второго порядка. Необходимо отметить,
что в данном разделе представлены задачи
экономического содержания, при решении
которых применяются сведения из
аналитической геометрии на плоскости.
При решении задач
аналитической геометрии целесообразно
воспользоваться учебными пособиями
следующих авторов: Д.В. Клетеника, Н. Ш.
Кремера, Д.Т. Письменного В.И. Малыхина,
т.к. в данной литературе рассматривается
более широкий круг задач, которые можно
использовать для самостоятельной
подготовки по данной теме. Применение
аналитической геометрии к решению
экономических задач изложено в учебных
изданиях М.С. Красса и В.И. Ермакова.
Задача 5.1. Даны
координаты вершин треугольника АВС.
Необходимо
а) написать
уравнения сторон треугольника;
б) написать
уравнение высоты треугольника проведенной
из вершины С
к стороне АВ
и найти ее длину;
в) написать
уравнение медианы треугольника,
проведенной из вершины В
к стороне АС;
г) найти углы
треугольника и установить его вид
(прямоугольный, остроугольный,
тупоугольный);
д) найти длины
сторон треугольника и определить его
тип (разносторонний, равнобедренный,
равносторонний);
е) найти координаты
центра тяжести (точка пересечения
медиан) треугольника АВС;
ж) найти координаты
ортоцентра (точка пересечения высот)
треугольника АВС.
К каждому из
пунктов а) – в) решения сделать рисунки
в системе координат. На рисунках
обозначить соответствующие пунктам
задачи линии и точки.
Данные к условию
задачи, соответствующие вариантам:
|
1)
2)
3)
7)
9)
10)
11)
12)
13)
14)
15)
16)
17) 18) |
4)
5)
6)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
29) 30) |
Пример 5.1
Даны координаты
вершин треугольника АВС:
.
Необходимо а) написать уравнения сторон
треугольника; б) написать уравнение
высоты треугольника проведенной из
вершины С
к стороне АВ
и найти ее длину; в) написать уравнение
медианы треугольника, проведенной из
вершины В
к стороне АС;
г) найти длины сторон треугольника и
определить его тип (разносторонний,
равнобедренный, равносторонний); д)
найти углы треугольника и установить
его вид (прямоугольный, остроугольный,
тупоугольный); е) найти координаты центра
тяжести (точка пересечения медиан)
треугольника АВС;
ж) найти координаты ортоцентра (точка
пересечения высот) треугольника АВС.
Решение
а)
Для каждой стороны треугольника известны
координаты двух точек, которые лежат
на искомых линиях, значит уравнения
сторон треугольника – уравнения прямых,
проходящих через две заданные точки
|
|
(5.1) |
где
и
соответствующие координаты точек.
Таким образом,
подставляя в формулу (5.1) координаты
соответствующих прямым точек получаем
,
,
,
откуда после
преобразований записываем уравнения
сторон
,
,
.
На рис. 7 изобразим
соответствующие сторонам треугольника
прямые.
Ответ:
,
,
.
|
Рис. 7 |
б)
Пусть
– высота, проведенная из вершины
к стороне
.
Поскольку
проходит через точку
перпендикулярно вектору
,
то составим уравнение прямой по следующей
формуле
|
|
(5.2) |
где
– координаты вектора перпендикулярного
искомой прямой,
– координаты точки, принадлежащей этой
прямой. Найдем координаты вектора,
перпендикулярного прямой
,
и подставим в формулу (5.2)
,
,
,
,
.
Найдем длину высоты
CH
как расстояние от точки
до прямой
|
|
(5.3) |
где
– уравнение прямой
,
– координаты точки
.
В предыдущем пункте
было найдено
.
Подставив данные
в формулу (5.3), получим
,
На рис. 8 изобразим
треугольник и найденную высоту СН.
Ответ:
.
|
Р |
в)
медиана
треугольника
делит сторону
на две равные части, т.е. точка
является серединой отрезка
.
Исходя из этого, можно найти координаты
точки
|
|
(5.4) |
где
и
– координаты соответственно точек
и
,
подставив которые в формулы (5.4), получим
;
.
Уравнение медианы
треугольника
составим как уравнение прямой, проходящей
через точки
и
по формуле (5.1)
,
.
Ответ:
(рис. 9).
|
Р |
г)
Длины сторон треугольника найдем как
длины соответствующих векторов, т.е.
,
,
.
Стороны
и
треугольника
равны, значит, треугольник является
равнобедренным с основанием
.
Ответ:
треугольник
равнобедренный с основанием
;
,
.
д)
Углы треугольника
найдем как углы между векторами,
исходящими из соответствующих вершин
данного треугольника, т.е.
,
,
.
Поскольку треугольник
равнобедренный с основанием
,
то
,
Углы между векторами
вычислим по формуле (4.4), для которой
потребуются скалярные произведения
векторов
,
.
Найдем координаты
и модули векторов, необходимых для
вычисления углов
,
;
,
,
.
Подставляя
найденные данные в формулу (4.4), получим
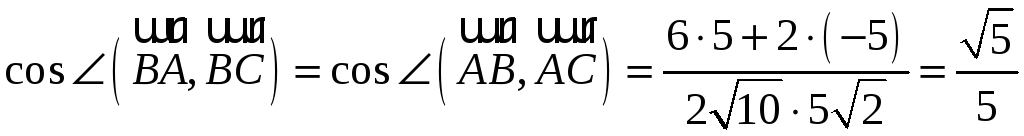
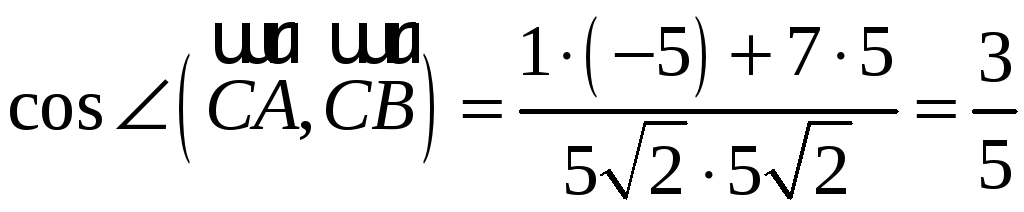
Поскольку значения
косинусов всех найденных углов
положительны, то треугольник
является остроугольным.
Ответ:
треугольник
остроугольный;
,
,
.
е)
Пусть
– центр тяжести треугольника
,
тогда координаты
точки
можно найти, по формулам (5.5)
|
|
(5.5) |
где
,
и
– координаты соответственно точек
,
и
,
следовательно,
,
.
Ответ:
– центр тяжести треугольника
.
ж) Пусть
– ортоцентр треугольника
.
Найдем координаты точки
как координаты точки пересечения высот
треугольника. Уравнение высоты
было найдено в пункте б).
Найдем уравнение высоты
:
,
,
,
.
Поскольку
,
то решение системы
является координатами
точки
,
откуда находим

Ответ:
– ортоцентр треугольника
.
Задача 5.2.
Фиксированные издержки на предприятии
при выпуске некоторой продукции
составляют F
руб. в месяц, переменные издержки – V0
руб. за
единицу продукции, при этом выручка
составляет R0
руб. за единицу изготовленной продукции.
Составить функцию прибыли P(q)
(q
– количество произведенной продукции);
построить ее график и определить точку
безубыточности.
Данные к условию
задачи, соответствующие вариантам:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;

;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
17)
;
18)
;
19)
;
20)
;
21)
;
22)
;
23)
;
24)
;
25)
;
26)
;
27)
;
28)
;
29)
;
30)
.
Пример 5.2
Фиксированные
издержки на предприятии при выпуске
некоторой продукции составляют
руб. в месяц, переменные издержки –
руб. за единицу
продукции, при этом выручка составляет
руб. за единицу
изготовленной продукции. Составить
функцию прибыли P(q)
(q
– количество произведенной продукции);
построить ее график и определить точку
безубыточности.
Решение
Вычислим совокупные
издержки на производстве при выпуске
q
единиц некоторой продукции
.
Если будет продано
q
единиц продукции, то совокупный доход
составит
.
Исходя из полученных
функций совокупного дохода и совокупных
издержек, найдем функцию прибыли
,
,
.
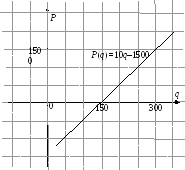
безубыточности – точка, в которой
прибыль равна нулю, или точка, в которой
совокупные издержки равны совокупному
доходу
,
,
откуда находим
– точка безубыточности.
Для построения
графика (рис. 10) функции прибыли найдем
еще одну точку
.
Рис. 10
Ответ:
функция прибыли
,
точка безубыточности
.
Задача 5.3. Законы
спроса и предложения на некоторый товар
соответственно определяются уравнениями
p=pD(q),
p=pS(q),
где p
– цена на товар, q
– количество товара. Предполагается,
что спрос определяется только ценой
товара на рынке pС,
а предложение – только ценой pS,
получаемой поставщиками. Необходимо
а) определить
точку рыночного равновесия;
б) точку равновесия
после введения налога, равного t.
Определить увеличение цены и уменьшение
равновесного объема продаж;
в) найти субсидию
s,
которая приведет к увеличению объема
продаж на q0
ед. относительно изначального
(определенного в пункте а));
г) найти новую
точку равновесия и доход правительства
при введении налога, пропорционального
цене и равного N%;
д) определить,
сколько денег будет израсходовано
правительством на скупку излишка при
установлении минимальной цены, равной
p0.
К каждому пункту
решения сделать рисунок в системе
координат. На рисунке обозначить
соответствующие пункту задачи линии и
точки.
Данные к условию
задачи, соответствующие вариантам:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;

;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
17)
;
18)
;
19)
;
20)
;
21)
;
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


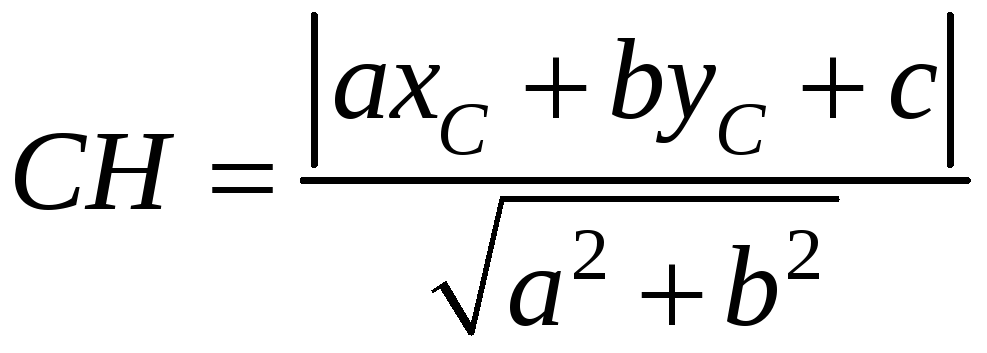 ,
, ис.
ис.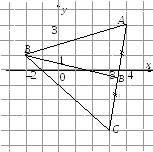 ис.
ис.