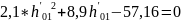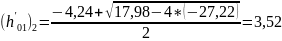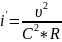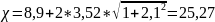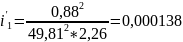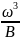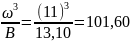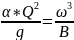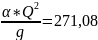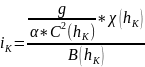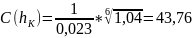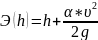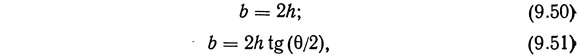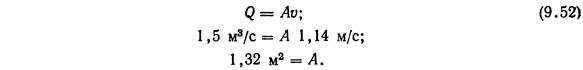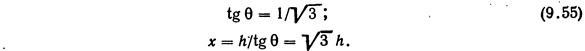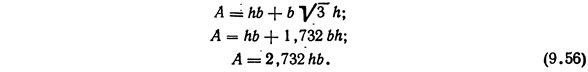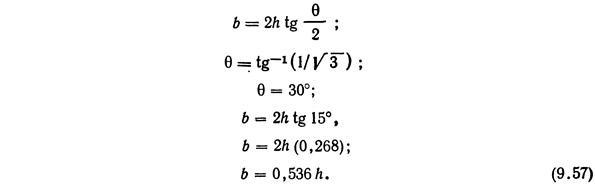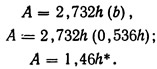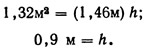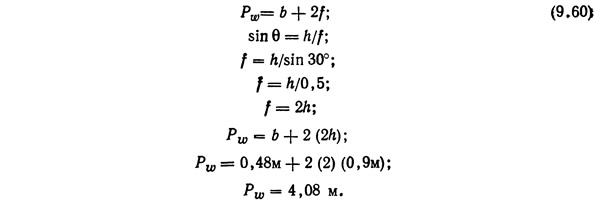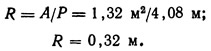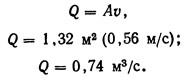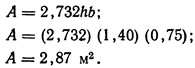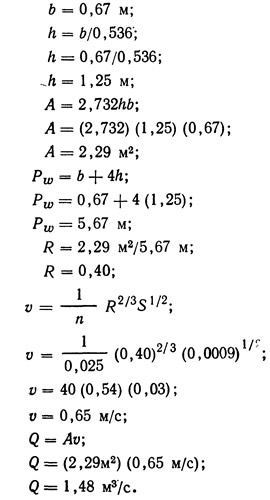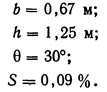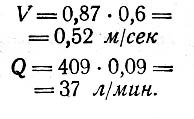-
Определение глубины наполнения и уклона дна канала на подводящем участке
Полагаем,
что υ = (υmax)неразм1
= 0,88 м/с.
Используя
формулы (1.4) и (3.1) найдём глубину наполнения
канала, решив квадратное уравнение:
;
;
;
;
м;
м.
Проверка
решения квадратного уравнения:
57,16 ≈ (8,9 + 2,1
* 3,52) * 3,52 = 57,12
В результате
получаем:
Новый уклон
канала можно определить по формуле:
, (4.1)
где
С = C(h’01)
и R = (h’01).
Найдём
новые коэффициент Шези (С) и гидравлический
радиус (R).
— по
формуле (1.4):
ω
= (8,9+ 2,1 * 3,52) * 3,52 = 57,12 м2;
— по формуле
(1.5):
м;
-по формуле
(1.6):
м;
— по формуле
(1.7):
м1/2/с.
Подставляем
найденные значения в формулу (4.1):
.
-
Определение критической глубины hK и критического уклона iK канала
Воспользуемся
уравнением для нахождения критической
глубины:
, (5.1)
где α –
корректив кинетической энергии ( пусть
α = 1,05).
Найдём
значение, соответствующее заданному
расходу в канале:
м2.
Составим
таблицу, отражающую зависимость значения
от
глубины канала (табл. 5.1).
Таблица
5.1
|
h |
B |
ω |
ω3/B |
|
м |
м |
м2 |
м5 |
|
1,00 |
13,10 |
11,00 |
101,60 |
|
1,20 |
13,94 |
13,70 |
184,62 |
|
1,40 |
14,78 |
16,58 |
308,15 |
|
1,60 |
15,62 |
19,62 |
483,23 |
|
1,80 |
16,46 |
22,82 |
722,35 |
Пример
расчёта таблицы (для h
= 1,00 м):
-
Ширина канала по
верху определяется по формуле (2.1):
B
= 8,9 + 2 * 2,1 * 1 = 13,10м.
-
Площадь живого
сечения определяется по формуле (1.4):
ω = (8,9 +
2,1 * 1) * 1 = 11,00 м2.
-
м5.
По данным
таблицы 5.1 строим график зависимости
значения
от глубины канала h (рис.
5.1).
Рис. 5.1
По построенному графику определяем
критическую глубину канала:
м2
=> hK
= 1,34 м.
Далее необходимо найти критический
уклон, который определяется по формуле:
, (5.2)
где g
– ускорение свободного падения (g
= 9,8 м2/с).
Величины С,
В, χ зависят от критической глубины hK.
Найдём их значения:
— по формуле
(1.4):
ω(hK)
= (8,9 + 2,1 * 1,34) * 1,34 = 15,70м2;
— по формуле
(2.1):
В(hK)
= 8,9 + 2 * 2,1 * 1,34 = 14,53 м;
— по формуле
(1.5):
м;
— по формуле
(1.6):
м;
— по формуле
(1.7):
м1/2/с.
Подставляем
найденные значения в формулу (5.2):
.
-
Построение графика удельной энергии сечения э(h)
Удельная
энергия сечения определяется по формуле:
. (6.1)
Составим
таблицу, отражающую зависимость удельной
энергии сечения от глубины (табл. 6.1).
Таблица
6.1
|
h |
ω |
υ |
αυ2/2g |
Э(h) |
|
м |
м2 |
м/с |
м |
м |
|
0,60 |
6,10 |
8,25 |
3,65 |
4,25 |
|
0,70 |
7,26 |
6,93 |
2,57 |
3,27 |
|
0,80 |
8,46 |
5,94 |
1,89 |
2,69 |
|
0,90 |
9,71 |
5,18 |
1,44 |
2,34 |
|
1,00 |
11,00 |
4,57 |
1,12 |
2,12 |
|
1,10 |
12,33 |
4,08 |
0,89 |
1,99 |
|
1,20 |
13,70 |
3,67 |
0,72 |
1,92 |
|
1,34 |
15,70 |
3,20 |
0,55 |
1,89 |
|
1,50 |
18,08 |
2,78 |
0,41 |
1,91 |
|
2,00 |
26,20 |
1,92 |
0,20 |
2,20 |
|
2,20 |
29,74 |
1,69 |
0,15 |
2,35 |
|
2,50 |
35,38 |
1,49 |
0,11 |
2,61 |
|
3,00 |
45,60 |
1,10 |
0,07 |
3,07 |
Пример
расчёта таблицы (для h
= 0,60 м):
-
Площадь живого
сечения определяется по формуле (1.4):
ω = (8,9 +
2,1 * 0,6) * 0,6 = 6,10 м2.
-
Скорость
определяется по формуле (3.1):
.
-
Скоростной напор:
м.
-
Удельная энергия
сечения определяется по формуле (6.1):
Э = 0,6 + 3,65
= 4,25 м.
По данным
табл. 6.1 строим график удельной энергии
сечения канала (рис. 6.1).
Рис. 6.1
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Topographic maps reveal the Earth’s contour. Contour lines on a map are those lines that reflect a consistent or constant elevation. Slope or gradient is the vertical distance divided by horizontal distance, and channel slope is how far a channel drops over a horizontal distance, according to the Austin Creek Watershed Department. Essentially, a channel slope is the valley between the peaks of elevation created by a stream. Channel patterns are influenced by the flow of streams and the accumulation of sediment. Channel slopes are generally measured as percentages based upon the area between a pair of adjacent contour lines where they cross the creek.
Things You’ll Need
- Topographic map
- Map wheel
Find the creek for the channel. Find the source and mouth of the creek. Begin tracing the blue line on the map denoting the creek. Document the elevation line starting at the source and following the creek upstream to each cross of the contour line.
Use a rule or map wheel to measure the distance along the blue line of the creek from contour line 1 to contour line 2. Convert the distance from a fraction to a decimal format. Repeat this for all adjacent contour lines to the source of the creek.
Calculate the change in elevation. Subtract the elevation for contour 1 from contour 2. For example, if contour 1 is 80 and contour 2 is 90, then the change in elevation equals 90 minus 80, or 10.
Calculate the channel slope. Using the formula, slope equals change in elevation divided by ground distance. For example, if the ground distance is 11/16 or 0.69 inches and the scale factor is 1 inch equals 2,000 feet per inch, this equals 1,380 feet. The channel slope is 10 divided by 1,380, which equals 0.0072. Multiply by 100 to get a percentage of 0.72 percent.
Движение жидкости в открытых каналах является результатом действия только гравитационных сил и характеризуется тем, что на свободной поверхности жидкости давление равно атмосферному.
Теоретическое решение задачи о такого рода режиме движения до некоторой степени ограниченно. Математически можно показать, что формула (9.44) справедлива для случая движения жидкости в открытых каналах:
где v — скорость потока; С — константа (опытная); R — гидравлический радиус (определение дано ниже); S — уклон канала; х и у — показатели степени (константы) .
Поперечное сечение открытого канала, показанного на рис. 9.12, имеет прямоугольную форму. Глубина канала h, ширина Ь. Таким образом, площадь живого сечения потока
Часть периметра сечения канала, которая соприкасается с водой, называется смоченным периметром
Гидравлическим радиусом называют отношение площади живого сечения к смоченному периметру:
Так, для прямоугольного сечения, показанного на рис. 9.12,
Уклон S в уравнении (9.44) — это уклон дна канала в сторону движения потока, определяемый как перепад высот канала, отнесенный к единице его длины.
Хотя уравнение (9.44) опирается на солидную теоретическую базу, его практическое применение без знания коэффициента С и констант х и у затруднительно. Различные исследователи определяли эти величины эмпирически. Наибольшее распространение получила формула Маннинга, на основе которой построено дальнейшее изложение. Эта формула, называемая формулой Маннинга, была впервые выведена в 1890 г. и записывается в единицах системы СИ в следующем виде:
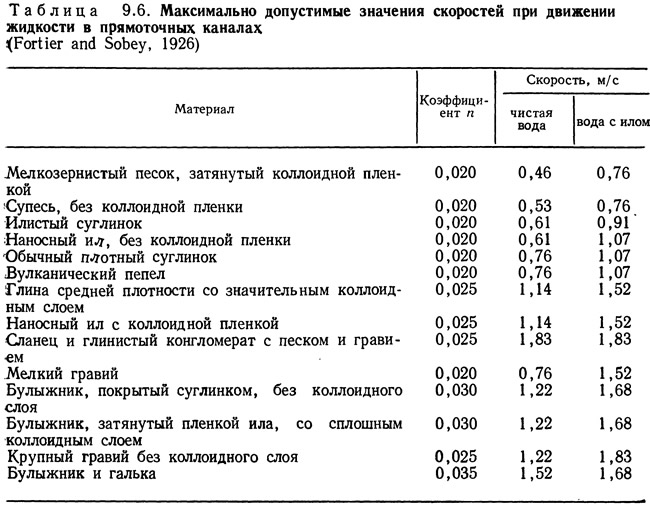
Полученные экспериментально значения коэффициента n для наиболее распространенных материалов и видов труб приведены в табл. 9.5. Минимальное значение n соответствует условиям движения жидкости в совершенно новых и чистых трубах или каналах; для труб, бывших в употреблении или открытых каналов, забитых растительностью и другими загрязнениями, значения n будут максимальными. При расчете труб и каналов обычно берут средние значения из соответствующего диапазона.
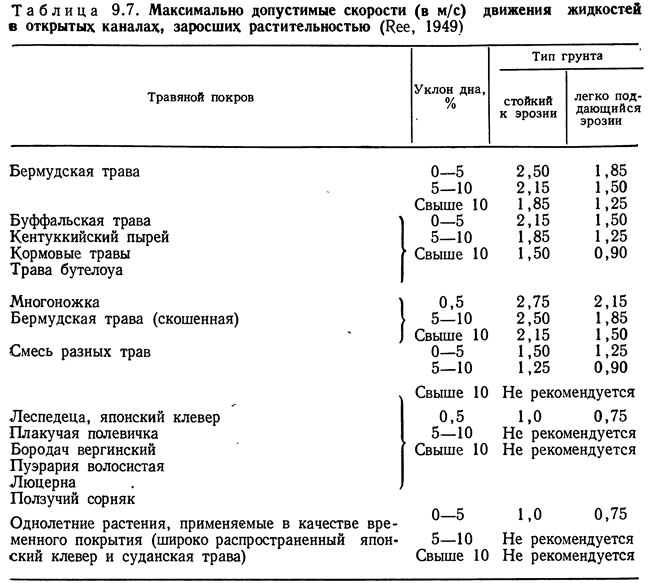
Большинство открытых каналов рассчитывается по формуле Маннинга и уравнению неразрывности. Среди них—открытые каналы, реки, ручьи, дренажные канавы, лотки и сточные желоба. При расчете земляных каналов или каналов, покрытых растительностью, необходимо учитывать ограничения влияния эрозии и толщины осадков (дополнительно к ограничениям, накладываемым формулой Маннинга и местным рельефом). Скорости, превышающие допустимые значения, вызывают эрозию стен каналов, а низкие скорости ускоряют рост отложений; последнее может вызвать необходимость увеличения поперечного сечения канала, что приводит к значительному возрастанию капитальных затрат. В табл. 9.6 и 9.7 приведены максимально допустимые значения скоростей для различных грунтов и отложений. Минимально допустимая скорость движения жидкости в канале определяется условием возможного образования отложений из материалов взвешенных в жидкости. Желательно, чтобы скорости превышали минимально допустимые значения, так как сооружение каналов с низкой скоростью движения воды обходится очень дорого.
Форма поперечного сечения канала определяется его назначением, видом материала, из которого выполнены дно и стенки, экономическими соображениями, а также из условия минимальных потерь жидкости на испарение. Каналы с бетонированными стенками или подобные им обычно имеют прямоугольную и трапецеидальную формы поперечного сечения. Каналы, прокладываемые в грунте, обычно делают трапецеидальной формы, так как при прямоугольной форме сечения боковые стенки таких каналов неустойчивы. Боковые стенки каналов с трапецеидальной формой сечения могут иметь различный уклон — от 3:1 (отношение горизонтального катета к вертикальному) до 1:1; последняя величина встречается лишь в условиях исключительно плотного грунта. Желоба для транспортировки рыбы или овощей часто имеют сечение прямоугольной формы, что объясняется конструктивными и экономическими соображениями. Глубокие узкие каналы позволяют значительно уменьшить площадь зеркала воды и сократить таким образом потери на испарение.
С точки зрения гидравлики форму поперечного сечения канала следует выбирать с таким расчетом, чтобы при минимальном смоченном периметре площадь живого сечения потока была максимальной, т. е. гидравлический радиус должен быть максимальным. Чем больше гидравлический радиус, тем меньше сопротивление преодолеваемое потоком, и тем больше расход воды при одинаковом поперечном сечении. В этом смысле наиболее совершенной является форма круга, так как у него максимальный радиус R. Однако для каналов больших размеров круглое сечение не применяется, так как это слишком сложно и дорого.
Уравнение (9.50) характеризует зависимость между шириной канала по дну и и глубиной h для наиболее выгодного с точки зрения гидравлики сечения при прямоугольной форме канала:
где θ — угол между боковой стенкой канала и горизонтальной плоскостью.
Облицовка внутренней поверхности открытых каналов имеет несколько преимуществ. Бетонирование, например, значительно сокращает утечки воды, максимально допустимые скорости, могут быть увеличены. За счет увеличения скоростей появляется возможность пропустить требуемый расход через меньшее поперечное сечение. При сооружении каналов малого сечения уменьшается стоимость постройки. Если экономия за счет уменьшения поперечного сечения канала с избытком компенсирует затраты на его облицовку, то облицовка становится экономически выгодной. Однако увеличение скоростей не всегда возможно, для этого необходим соответствующий уклон дна. Обслуживание облицованных каналов обходится дешевле, так как на внутренних стенках таких каналов не развивается растительность.
Пример 9.8. Определить размеры открытого канала трапециевидного сечения (рис. 9.13), по которому должна подводиться вода (1,5 м3/с) из реки к форелевому хозяйству. Канал прокладывается в плотном глинистом грунте, без облицовки. Уклон боковых стенок принять равным √
3:1
, т. е. максимальный для данного грунта. Топография местности ограничивает уклон дна 0,09%.
По табл. 9.6 максимально допустимая скорость равна 1,14 м/с, коэффициент шероховатости n=0,025. Если предположить, что скорость в канале равна максимально допустимой, то
Таким образом, площадь поперечного сечения канала при скорости движения в нем 1,14 м/с и расходе 1,5 м3/с должна составлять 1,32 м2.
Площадь поперечного сечения канала рассчитывается по формуле
Из уравнения (9.13) и определения тангенса
Из подобия треугольников
Подставив выражение (9.55) в формулу (9.53), получаем
Поперечное сечение канала должно быть максимально выгодным с точки зрения гидравлики. Для трапециевидной формы, сечения зависимость ширины канала по дну b от глубины канала h и угла наклона боковых стенок к горизонтальной плоскости θ имеет следующий вид:
Последнее выражение позволяет исключить одну из неизвестных величин в формуле (9.56):
Выше [уравнение (9.52)] площадь поперечного сечения была определена в 1,32 м2. Таким образом,
Ширину канала по дну можно подсчитать, воспользовавшись выражением (9.57):
Величины h, b и θ определяют поперечное сечение канала. Однако до сих пор не учитывался уклон дна канала и его влияние на скорость. Это ограничение учитывается расчетными величинами b и h и формулой Маннинга
Если значения n и S известны из условия задачи, то значение R следует определить
Площадь поперечного сечения была ранее определена в 1,32 м2. Длину смоченного периметра pw можно подсчитать из рис. 9.13, для b и h берутся полученные выше значения.
Отсюда
Подставляя в формулу (9.58), получим
(Уклон дна канала, заданный в процентах, переведен в десятичную величину).
Следовательно, скорость в канале равна 0,56 м/с, а не 1,14 м/с, как было принято. Действительный расход воды в канале составит
Однако в соответствии с проектным заданием расход должен равняться 1,5 м3/с. Поскольку уклон дна канала ограничен топографией местности, остается увеличивать поперечное сечение. Это можно выполнить различными способами, в нашем случае попробуем увеличить ширину канала по дну до 0,75 м.
Во всех случаях смоченный периметр должен быть минимальным, тогда условия, выраженные формулой (9.51), остаются в силе.
Поскольку уклон дна канала не изменился, выражение (9.56) может быть использовано для дальнейшего расчета.
Смоченный периметр можно определить по формуле (9.61).
Отсюда
Теперь, сделав соответствующие подстановки, можно выполнить расчет по формуле Маннинга
Полученное значение расхода превышает заданное, равное 1,5 м3/с; следовательно, наиболее подходящая ширина канала должна находиться где-то между значениями 0,75 и 0,48, фигурировавшими в расчете в качестве предположительных. Следуя той же методике подбора,
Поскольку значение 1,48 м3/с весьма близко к заданному 1,5 м3/с, на этом расчет можно прекратить и принять за окончательные следующие размеры поперечного сечения трапецеидального канала:
При расчете открытых каналов многие задачи решаются таким же, как в примере (9.8), методом последовательных приближений. Некоторые задачи можно решать непосредственно. Метод последовательных приближений отнимает много времени. Практический опыт работы помогает сократить количество промежуточных этапов решения такого рода задач. Кроме того, существует много справочников, в которых приводятся значения b, h и S. Такие справочники позволяют существенно сократить время, затрачиваемое на подсчеты.
Чтобы канализация не засорялась, сточная жидкость должна двигаться со скоростью, при которой не только не происходило бы выпадение осадков, но даже смывались бы осадки, случайно образовавшиеся. Такая самоочищающая скорость различна для разных диаметров труб и для небольших труб достаточна велика.
Точных опытных данных о ней не имеется. По английским данным она для домовой канализации некогда требовалась около 1,4 м/сек; однако это делалось для половинного наполнения сечения трубы, исходя из условий колебания расхода (с учетом, что наполнение бывает меньше и фактическая скорость понижается).
По G. Thomson минимум скорости для небольших диаметров считается 0,9 м/сек. Рекомендуемые в Англии уклоны (стр. 53) дают следующие скорости: для трубы 100 мм — 0,97 м/сек; для 125 мм-1,02, для 150 мм — 1,01 м/сек, т. е. скорость в среднем около 1 м/сек. Однако эти скорости действительны при расходе воды на человека около 160 л и более. При меньших расходах воды эта скорость считается: для 100 мм-1,12 м/сек; 125 мм — 1,13 м/сек; 150 мм — 1,09 м или в среднем около 1,1 м/сек.
При наших небольших расходах воды самоочищающую скорость для труб 100-150 мм следует принимать выше, и ориентировочно можно считать ее примерно в следующих пределах (табл. 2):
Таблица 2
|
Для расхода в сутки в л/чел |
20 40 60 |
80 100 |
120 |
150 и более |
|
Скорость в м/сек |
1,4 1,2 1,1 |
1,0 0,9 |
0,8 |
0,7 |
Для труб более 200-250 мм самоочищающую скорость безотносительно нормы воды на человека ввиду более равномерного расхода можно принимать около 0,8 м/сек; для 300-450 мм — 0,7 м/сек и для 500 мм и более — 0,6 м/сек. В последнее время некоторые организации в качестве наименьшей расчетной скорости для наружной канализационной сети вообще допускают 0,6 м/сек, тем самым последняя считается ими достаточной для самоочищения. .
При скорости, большей скорости самоочищения, движение сточных вод может рассматриваться как подчиняющееся законам гидравлики В частности скорость V движения жидкости в каналах по формуле Шези выражается в м/сек следующим образом
V = c √ R * i
где R — есть гидравлический радиус, представляющий отношение площади поперечного сечения канала, занятой водой, к смоченному периметру сечения,
i — гидравлический уклон поверхности жидкости в канале, который при небольших диаметрах может считаться равным уклону канала;
с — коэффициент сопротивления, зависящий от трения жидкости о стенки, выражаемый различно разными экспериментаторами.
Таким образом достигнуть требуемой скорости можно увеличением гидравлического радиуса и уклона канала.
Гидравлический радиус при круглой трубе и полном ее наполнении будет равен четверти диаметра трубы, а именно:
R = F/p = πd2 / 4 : πd = d / 4
Ту же величину он имеет и при половинном наполнении трубы, а именно:
R = F/p = πd2 / 4 * 2 : πd / 2 = d / 4
Но между половинным и полным наполнением круглого сечения гидравлический радиус больше, так как площадь сечения здесь возрастает больше, чем смачиваемый периметр. Максимум гидравлического радиуса имеет место при степени наполнения около 0,81 диаметра, т. е. это соответствует и наибольшей скорости движения жидкости. При наполнении меньше половины гидравлический радиус уменьшается, а значит уменьшается и скорость движения жидкости.
Из указанного видно, что увеличение гидравлического радиуса возможно в весьма ограниченных пределах. Значит достижение необходимой скорости движения жидкости приходится преимущественно основывать на увеличении уклона канала, тем более что благодаря колебанию рас-
хода в некоторые моменты при незначительном расходе гидравлический радиус бывает очень невелик.
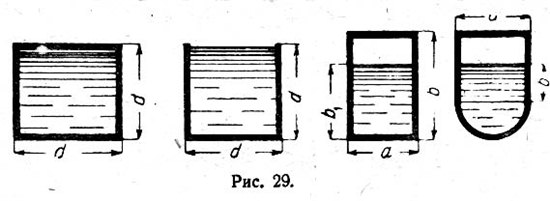
При некруглом сечении канала подсчет величины гидравлического радиуса также не представляет сложности. Рассмотрим этот вопрос для обычных в условиях промышленных зданий сечений (рис. 29).
При квадратном сечении со стороной d и полном наполнении:
F = d2, p = 4d, R = F / p = d / 4
Если жидкость заполняет квадратное, открытое сверху сечение, то:
F = d2, p = 3d, R = d / 3
Возьмем любое прямоугольное сечение шириной а, высотой b;
При полном заполнение
R = a * b / 2 (a + b)
Если сечение заполнено только на высоту b, то:
R = a * b / a + 2b
Подобным же образом можно подсчитать гидравлический радиус и для более сложных сечений: овоидального, лоткового и др.
По заданной скорости и выбранному наполнению каждый раз возможно подсчитать требуемый уклон, если знать коэффициент С. Он по так называемый старой формуле Куттера выражается следующим образом:
C = 100 √R / m + √R
Величина т называется коэффициентом сопротивления или шероховатости и потому же Куттеру равна: 0,25 для керамических и бетонных труб, бывших в употребления водопроводных труб, дощатых каналов; 0,30 — 0,35 — для гладких кирпичных каналов.
При т — 0,25 и для половинного (или полного) наполнения старая формула Куттера имеет вид
V = (0,5 √d / 0,5 + √d) * √d * i
где d — диаметр трубы.
Расход жидкости и скорость течения ее при различных уклонах и разных диаметрах круглых труб и при полном их наполнении, подсчитанные по указанной формуле, приведены в табл. 3 на стр. 51. В ней скорость дана в м/сек, а расход в л/мин.
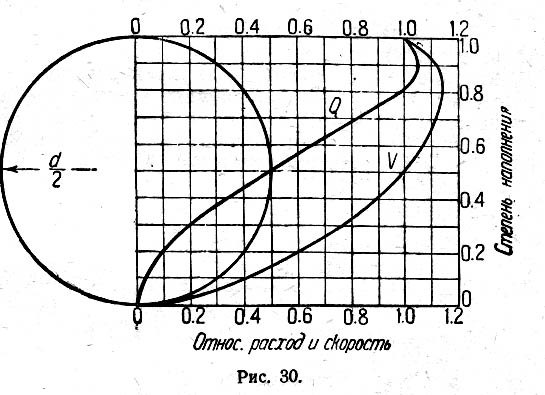
Нередко нужно бывает знать расход жидкости Q и скорость V ее движения при любой степени наполнения трубы. Для этой цели можно использовать график, представленный на рис. 30.
| Диаметр в мм | м/сек | 25 | 30 | 35 | 40 | 50 | 60 | 70 | 80 | 100 | 125 | 150 |
| Уклон | л/мин | |||||||||||
| 0.01 | V | 0.19 | 0.22 | 0.25 | 0.29 | 0.35 | 0.40 | 0.46 | 0.51 | 0.61 | 0.73 | 0.85 |
| Q | 5.6 | 9.3 | 14.4 | 21.7 | 41.3 | 61.6 | 106 | 154 | 286 | 540 | 900 | |
| 0.02 | V | 0.27 | 0.32 | 0.36 | 0.40 | 0.49 | 0.57 | 0.65 | 0.72 | 0.87 | 1.04 | 1.21 |
| Q | 7.9 | 13.6 | 20.7 | 30.0 | 57.9 | 93.4 | 150 | 217 | 409 | 770 | 1280 | |
| 0.03 | V | 0.33 | 0.39 | 0.44 | 0.49 | 0.60 | 0.70 | 0.80 | 0.89 | 1.06 | 1.27 | 1.47 |
| Q | 9.7 | 16.5 | 25.4 | 36.7 | 70.8 | 114.6 | 185 | 269 | 498 | 940 | 1560 | |
| 0.04 | V | 0.38 | 0.45 | 0.51 | 0.57 | 0.69 | 0.81 | 0.92 | 1.02 | 1.22 | 1.46 | 1.69 |
| Q | 11.2 | 19.4 | 29.5 | 42.8 | 81.2 | 132.3 | 212 | 307 | 573 | 1080 | 1790 | |
| 0.05 | V | 0.42 | 0.50 | 0.57 | 0.64 | 0.77 | 0.90 | 1.03 | 1.15 | 1.37 | 1.64 | 1.90 |
| Q | 12.4 | 21.2 | 32.9 | 48.0 | 90.9 | 147.5 | 238 | 346 | 644 | 1215 | 2015 | |
| 0.06 | V | 0.47 | 0.55 | 0.62 | 0.70 | 0.85 | 0.99 | 1.13 | 1.25 | 1.50 | 1.79 | 2.08 |
| Q | 13.8 | 23.3 | 35.7 | 52.50 | 100.1 | 162.5 | 260 | 376 | 705 | 1325 | 2205 | |
| 0.07 | V | 0.50 | 0.59 | 0.67 | 0.76 | 0.92 | 1.07 | 1.22 | 1.35 | 1.62 | 1.94 | 2.24 |
| Q | 14.7 | 25.0 | 38.6 | 56.2 | 108.5 | 175 | 281 | 408 | 761 | 1435 | 2386 | |
| 0.08 | V | 0.54 | 0.63 | 0.72 | 0.81 | 0.98 | 1.15 | 1.30 | 1.45 | 1.73 | 2.07 | 2.40 |
| Q | 15.9 | 26.7 | 41.5 | 60.9 | 115.6 | 188 | 300 | 437 | 812 | 1530 | 2540 | |
| 0.09 | V | 0.57 | 0.67 | 0.76 | 0.86 | 1.04 | 1.21 | 1.38 | 1.53 | 1.83 | 2.19 | 2.54 |
| Q | 16.8 | 28.4 | 43.8 | 64.5 | 122.4 | 198 | 318 | 461 | 860 | 1620 | 2690 | |
| 0.10 | V | 0.60 | 0.71 | 0.81 | 0.90 | 1.09 | 1.28 | 1.45 | 1.62 | 1.94 | 2.32 | 2.68 |
| Q | 17.6 | 30.0 | 46.6 | 67.5 | 128.3 | 210 | 335 | 489 | 911 | 1720 | 2840 | |
| 0.15 | V | 0.74 | 0.86 | 0.99 | 1.11 | 1.34 | 1.57 | 1.78 | 1.98 | 2.37 | 2.84 | 3.28 |
| Q | 21.8 | 36.4 | 57.0 | 83.2 | 158 | 258 | 411 | 598 | 1160 | 2100 | 3480 | |
| 0.20 | V | 0.85 | 1.00 | 1.14 | 1.28 | 1.55 | 1.81 | 2.06 | 2.29 | 2.74 | 3.28 | 3.79 |
| Q | 25.0 | 42.4 | 65.9 | 96.1 | 183 | 297 | 476 | 691 | 1285 | 2430 | 4020 | |
| 0.25 | V | 0.95 | 1.12 | 1.28 | 1.43 | 1.73 | 2.02 | 2.30 | 2.57 | 3.07 | 3.66 | 4.24 |
| Q | 28.0 | 47.5 | 73.9 | 107.5 | 204 | 331 | 532 | 776 | 1440 | 2710 | 4490 |
На нем изображены средние кривые, характеризующие изменения расхода и скорости жидкости в зависимости от изменения степени наполнения. Изменяясь от 0 до 1,0, последняя соответствует полному заполнению (равна диаметру). Расход и скорость при этом приняты также за 1 (относительная величина их откладывается по оси абсцисс). Как видно из графика, скорость движения жидкости имеет максимум при степени наполнения около 0,8 диаметра, что соответствует указанному выше. Наибольший расход жидкости может протечь по трубе при степени заполнения около 0,9 диаметра. Максимум скорости в 1,13 раза больше, чем скорость при полном заполнении; а максимум расхода больше, чем такой же при заполненной трубе, в 1,07 раза. Значит каждая труба в действительности при данном уклоне может пропустить больше жидкости, чем это дают таблицы для заполненного сечения.
Как видно из графика, при наполнении 0,5 относительная скорость V- 1, т. е. одинакова с такой же при полном наполнении; а относительный расход равен соответственно Q = 0,5 расхода при заполненной трубе. Таким образом можно определить их для любого заполнения.
Пример 1. Круглая труба диаметром 100 мм при уклоне 0,02 и полном наполнении пропускает расход 409 л/мин со скоростью 0,87 м/сек. Определить скорость и расход жидкости при наполнении 0,2. По графику
видно, что относи- ‘ тельная скорость равна 0,6, а относительный расход — 0,09. Отсюда:
Пример 2. Круглая труба диаметром 125 мм при уклоне 0,03 пропускает 940 л/мин со скоростью жидкости 1,27 м/сек. При какой степени наполнения и скорости имеет место в ней расход 658 л/мин?
Отношение обоих расходов равно 658:940 = 0,7. Этот относительный расход, как следует из графика, соответствует степени наполнения 0,62 при последней относительная скорость, как видно оттуда же, равна 1,08. Т. е. абсолютная скорость будет 1,27 * 1,08=1,37 м /сек..
Из указанного ранее ясно, что гидравлический уклон имеет первостепенное значение в канализации. С точки зрения более удобной прокладки отводных линий в межэтажных перекрытиях, а также во избежание излишнего заглубления в землю наружной канализационной сети нежелательно уклон делать большим. С другой стороны, слишком малый уклон вызовет возрастание засорения трубопроводов.
У нас II Всесоюзным (XIV) водопроводным и санитарно-техническим съездом в 1927 г. в г. Харькове были приняты в качестве минимальных допустимых уклонов следующие (табл. 4):
|
диаметр в мм уклон |
50 0,025 |
75 0,015 |
100 0,012 |
125 0,010 |
150 0,008 |
200 0,006 |
250 0,005 |
300 0,004 |
|
скорость в м/сек |
0,55 |
0,58 |
0,66 |
0,73 |
0,76 |
0,82 |
0,88 |
0,91 |
Приведенные в нижней строке скорости при полном наполнений показывают, что для мелких диаметров получающаяся скорость не велика. Поэтому не следует идти на уменьшение требуемых у нас во внутренней и дворовой сети (разделы 6 и 9) уклонов. Следует помнить, что они являются минимальными. Не нужно забывать, что степень разжижения сточной жидкости и условия эксплуатации устройств имеют огромное значение. Отметим, что за границей, например в Англии, США, даже при большом расходе воды на жителя, уклоны принимаются не меньше наших.
Для крупных диаметров скорость при вышеуказанных уклонах значительна. Поэтому некоторые проектные организации в последнее время допускают меньшие уклоны (для 200 мм — 0,005, для 250 мм — 0,004 и т. д.).
В Англии употребляют простое правило для определения допустимых минимальных уклонов канализационных труб:
Уклон для каждого диаметра равен единице, деленной на 10 диаметров трубы в дюймах, т. е. (табл. 5):
Таблица 5
| Для 100-мм трубы | 1:4*10 | 1:40 или 0.025 | |
| 125 | 1:5*10 | 1:50 | 0.02 |
| 150 | 1:6*10 | 1:60 | 0.016 |
Но при расходе воды на человека в 160 л/сутки считают вполне допустимыми уклоны (табл. 6):
Таблица 6
|
100-мм |
1 :40 или |
0,025 |
|
125″ |
1:52 |
0,019 |
|
150″ |
1:70 |
0,014 |
При расходе меньше чем 160 л/су тки на человека в Англии рекомендуется уже уклоны (табл. 7):
Таблица 7
|
100-мм |
1:30 |
0,033 |
|
125 |
1:42 |
0,024 |
|
150 |
1:60 |
0,016 |
Вообще ни одно общее указание о допустимых уклонах не должно механически распространяться на все случаи. В особенности нужно быть осторожным там, где водопотребление ничтожно, в домах и городах, где население не привыкло к пользованию канализацией, где не имеется ванн или душей, вода которых способствует самопромыванию.
Там, где это представляется возможным, лучше идти на увеличение уклона, чем диаметра трубы. Опыты, произведенные в США, показали, что твердые вещества проходят вдоль 100-мм трубы при уклоне 0,025 лучше, чем по трубе 150 мм при уклоне 0,016. В этих опытах спускались стоки от 2 клозетов и одной ванны, и естественно, что при таком небольшом расходе труба в 150 мм работала небольшой частью своего сечения, и твердые вещества оседали на дне.
Вообще трубы большого диаметра допустимы только тогда, когда имеется расход воды, обеспечивающий достаточное ее наполнение и промывание.
Погоня за малым уклоном за счет увеличения диаметра трубы не только ведет к удорожанию трубопроводов, но нередко и к ухудшению работы канализации. Наоборот, увеличение уклона в допустимых пределах всегда желательно. В равной мере уменьшение диаметра ниже известных пределов ведет к увеличению числа засорений сети.
Допустимым уклоном следует считать такой, при котором максимальная скорость движения жидкости не превышает 3-3,5 м/сек. Это дает для наружной сети и вообще крупных диаметров (от 125 мм) уклон не более 0,15, а лучше — 0,10, и для внутренней сети (50-100 мм) не более 0,25.
« Предыдущая | Оглавление | Следующая »
Топографические карты показывают контур Земли. Контурные линии на карте — это те линии, которые отражают постоянную или постоянную высоту. По данным Департамента водоразделов в Остине-Крик, наклон или уклон — это вертикальное расстояние, деленное на горизонтальное расстояние, а наклон канала — это расстояние, на которое канал падает на горизонтальное расстояние. По существу, уклон канала — это долина между пиками возвышения, созданными потоком. На характер каналов влияют потоки и накопление отложений. Наклоны канала обычно измеряются в процентах на основе площади между парой соседних контурных линий, где они пересекают ручей.
Найдите ручей для канала. Найдите источник и устье ручья. Начните отслеживать синюю линию на карте, обозначающую ручей. Документируйте линию возвышения, начиная с источника и следуя ручью вверх по течению до каждого пересечения линии контура.
Используйте правило или колесо карты, чтобы измерить расстояние вдоль синей линии ручья от контурной линии 1 до контурной линии 2. Преобразуйте расстояние от дроби до десятичного формата. Повторите это для всех смежных контурных линий к источнику ручья.
Рассчитайте изменение высоты. Вычтите отметку для контура 1 из контура 2. Например, если контур 1 равен 80, а контур 2 равен 90, то изменение отметки равняется 90 минус 80 или 10.
Рассчитайте наклон канала. Используя формулу, уклон равен изменению высоты, деленному на расстояние от земли. Например, если расстояние от земли составляет 11/16 или 0, 69 дюйма, а коэффициент масштабирования 1 дюйм равен 2000 футов на дюйм, это равно 1380 футам. Наклон канала равен 10, деленному на 1380, что равно 0, 0072. Умножьте на 100, чтобы получить процент 0, 72 процента.